Деление и умножение отрицательных и положительных дробей: Умножение и деление положительных и отрицательных чисел

Содержание

§ Деление отрицательных чисел. Деление рациональных чисел

Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел

Как выполнять деление отрицательных чисел легко понять, вспомнив, что деление — это действие, обратное умножению.

Если «a» и «b» положительные числа, то разделить число «a» на число «b», значит найти такое число «с», которое при умножении на «b» даёт число «a».

Данное определение деления действует для любых рациональных чисел, если делители отличны от нуля.

Поэтому, например, разделить число «−15» на число 5 — значит, найти такое число, которое при умножении на число 5 даёт число «−15». Таким числом будет «−3», так как

(−3) · 5 = −15

значит

(−15) : 5 = −3

Примеры деления рациональных чисел.

10 : 5 = 2, так как 12 · 5 = 10
(−4) : (−2) = 2, так как 2 · (−2) = −4

(−18) : 3 = −6, так как (−6) · 3 = −18
12 : (−4) = −3, так как (−3) · (−4) = 12

Из примеров видно, что частное двух чисел с одинаковыми знаками — число положительное (примеры 1, 2), а частное двух чисел с разными знаками— число отрицательное (примеры 3, 4).

Правила деления отрицательных чисел

Чтобы найти модуль частного, нужно разделить модуль делимого на модуль делителя.

Итак, чтобы разделить два числа с одинаковыми знаками, надо:

модуль делимого разделить на модуль делителя;
перед результатом поставить знак «+».

Примеры деления чисел с одинаковыми знаками:

(−9) : (−3) = +3
6 : 3 = 2

Чтобы разделить два числа с разными знаками, надо:

модуль делимого разделить на модуль делителя;
перед результатом поставить знак «−».

Примеры деления чисел с разными знаками:

(−5) : 2 = −2,5

28 : (−2) = −14

Для определения знака частного можно также пользоваться следующей таблицей.

Правило знаков при делении

+ : (+) = +	+ : (−) = −
− : (−) = +	− : (+) = −

При вычислении «длинных» выражений, в которых фигурируют только умножение и деление, пользоваться правилом знаков очень удобно. Например, для вычисления дроби

Можно обратить внимание, что в числителе два знака «минус», которые при умножении дадут «плюс». Также в знаменателе три знака «минус», которые при умножении дадут «минус». Поэтому в конце результат получится со знаком «минус».

Сокращение дроби (дальнейшие действия с модулями чисел) выполняется также, как и раньше:

Запомните!

Частное от деления нуля на число, отличное от нуля, равно нулю.

0 : a = 0, a ≠ 0

Делить на ноль НЕЛЬЗЯ!

Все известные ранее правила деления на единицу действуют и на множество рациональных чисел.

а : 1 = a
а : (−1) = −a
а : a = 1

, где «а» — любое рациональное число.

Зависимости между результатами умножения и деления, известные для положительных чисел, сохраняются и для всех рациональных чисел (кроме числа нуль):

если a · b = с; a = с : b; b = с : a;
если a : b = с; a = с · b; b = a : c

Данные зависимости используются для нахождения неизвестного множителя, делимого и делителя (при решении уравнений), а также для проверки результатов умножения и деления.

Пример нахождения неизвестного.

x · (−5) = 10

x = 10 : (−5)

x = −2

Знак «минус» в дробях

Разделим число «−5» на «6» и число «5» на «−6».

Напоминаем, что черта в записи обыкновенной дроби — это тот же знак деления, поэтому можно записать частное каждого из этих действий в виде отрицательной дроби.

Таким образом знак «минус» в дроби может находиться:

перед дробью;
в числителе;
в знаменателе.

Запомните!

При записи отрицательных дробей знак «минус» можно ставить перед дробью, переносить его из числителя в знаменатель или из знаменателя в числитель.

Это часто используется при выполнении действий с дробями, облегчая вычисления.

Пример. Обратите внимание, что после вынесения знака «минуса» перед скобкой мы из большего модуля вычитаем меньший по правилам сложения чисел с разными знаками.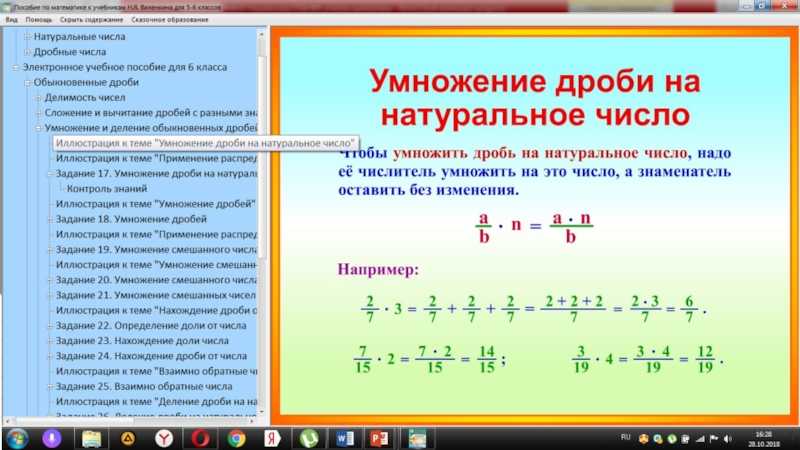

Пример.

Используя описанное свойство переноса знака в дроби, можно действовать, не выясняя, модуль какого из данных дробных чисел больше.

Умножения и деление отрицательных чисел. Решение примеров.

Альфашкола
Статьи
Умножения и деление отрицательных чисел

В этой статье мы будем изучать умножение и деление отрицательных чисел. Существуют определенные правила умножения отрицательных чисел.

$«—«-$ при умножении минус на минус результат становится положительным;

$«-+»-$ при умножении минуса на плюс результат становится отрицательным;
$«+-«-$ при умножении плюса на минус результат становится отрицательным;
$«++»-$ при умножении плюса на плюс результат становится положительным.

Примеры умножения отрицательных чисел.

Задача 1. Вычислить: $(-4)*(-4)$ и $(-6)*(-5).$

Решение.

Отрицательное число при умножении на отрицательное станет положительным согласно правилу.

$(-4)*(-4)=16$
$(-6)*(-5)=30$

Ответ: $16;30.$

Задача 2. Вычислить: $(-10)*12$ и $(-7)*4.$

Решение.

Отрицательное при умножении на положительное число станет отрицательным согласно правилу.

-10 * 12= -120

(-7)*4=-28

Ответ: $-120; -28$

Задача 3. Вычислить: $11*(-11)$ и $13*(-6).$

Решение.

Положительное при умножении на отрицательное число станет отрицательным согласно правилу.

$11*(-11)=-121$
$13*(-6)=-78$

Ответ: $-121;-78.$

Деление отрицательных чисел

При делении действуют те же правила знаков, что и при умножении. Делить на ноль нельзя.

$«—«-$ при делении минус на минус результат становится положительным;
$«-+»-$при делении минуса на плюс результат становится отрицательным;
$«+-«-$при делении плюса на минус результат становится отрицательным;
$«++»-$ при делении плюса на плюс результат становится положительным.

Задача 4. Вычислить: $(-16)*(-4)$ и $(-6)*(-2)$.

Решение.

$-16:(-4)=4$
$(-6):-2=3$

Ответ: $4;3.$

Задача 5. Вычислить: $(-10):5$ и $(-12):6$.

Решение.

$(-10):5=-2$
$(-12):6=-2$

Ответ: $-2;-2.$

Задача 3. Вычислить: $121:(-11)$ и $169:(-13)$.

Решение.

$121:(-11)=-11$
$169:(-13)=-13$

Ответ: $-11;-13.$

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Виолетта Грантовна Саркисян

Репетитор по математике

Стаж (лет)

Образование:

Тбилисский Государственный Педагогический Университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Адель Василевич Халиков

Репетитор по математике

Стаж (лет)

Образование:

Казанский федеральный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Надежда Геннадьевна Зубкова

Репетитор по математике

Стаж (лет)

Образование:

Астраханский педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

Математика
Репетитор по физике
Репетитор по химии
Репетитор по русскому языку
Репетитор по английскому языку
Репетитор по обществознанию
Репетитор по истории России
Репетитор по биологии
Репетитор по географии
Репетитор по информатике

Специализации

Репетитор по олимпиадной математике
Подготовка к ЕГЭ по математике (профильный уровень)
Репетитор по химии для подготовки к ОГЭ
Подготовка к олимпиадам по химии
Репетитор по русскому языку для подготовки к ОГЭ
Подготовка к олимпиадам по английскому языку
Английский язык для начинающих
Репетитор по разговорному английскому
Репетитор для подготовки к ВПР по обществознанию
Репетитор по географии для подготовки к ОГЭ

Как правильно умножать отрицательные числа?

Поможем понять и полюбить математику

Начать учиться

В 6 классе каждый школьник знает отличие между положительным и отрицательным числом и правила умножения. В этой статье объединим эти две темы и попрактикуемся в умножении отрицательных чисел.

Основные определения

Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.

Начнем с того, что проведем прямую и отметим на ней начало отсчета — точку нуль (0). А теперь укажем направление движения по прямой вправо от начала координат. В этом нам поможет красивая стрелка:

Два главных определения:

Положительные числа — это точки координатной прямой, которые лежат правее начала отсчета (нуля). Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают. То есть «+1» и «1» — это одно и тоже число.

Запоминаем!

Положительные числа — это те, что больше нуля, а отрицательные — меньшие.

Отрицательные числа — это точки координатной прямой, которые лежат левее начала отсчета (нуля). Их всегда обозначают знаком минус — «-».

Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!

Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).

Если стрелка направлена вверх, то в верхней части от начала отсчета всегда расположены положительные числа, а в нижней — отрицательные. Смотрите:

Прямая, на которой отмечена начальная точка, положительное направление и единичный отрезок, называется координатной или числовой осью.

Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.

Свойства умножения

От перестановки множителей местами произведение не меняется.
a * b = b * a
Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.
a * b * c = (a * b) * c = a * (b * c)

Вычислять можно в уме, при помощи таблицы умножения или в столбик. Продвинутые школьники могут использовать онлайн-калькулятор.

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Умножение отрицательных чисел

Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство:

(-а) * (-b) = a * b

А вот как умножить два числа с разными знаками:

перемножить модули этих чисел
перед полученным числом поставить знак минус

А теперь упростим правила. Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:

«—» — при умножении минус на минус ответ будет положительным
или минус на минус дает плюс
«-+» — при умножении минуса на плюс ответ будет отрицательным
или минус на плюс дает минус
«+-» — при умножении плюса на минус ответ будет отрицательным
или плюс на минус дает минус
«++» — при умножении плюса на плюс ответ будет положительным
или плюс на плюс дает плюс.

Примеры умножения отрицательных чисел

Пример 1. Вычислить: (-2)∗(-2) и (-3)∗(-7)

Как решаем:

Вспомним правило: отрицательное число умножить на отрицательное — получается ответ со знаком плюс. Считаем:

(-2)∗(-2) = 4

(-3)∗(-7) = 21

Ответ: 4; 21.

Пример 2. Вычислить: (-11)∗11 и (-20)∗2

Как решаем:

Вспомним правило: отрицательное число умножить на положительное — получается ответ со знаком минус. Считаем:

-11 * 11 = -121

(-20) * 2 = -40

Ответ: -121; -40.

Пример 3. Вычислить произведение: 5∗(-5) и 12∗(-8)

Как решаем:

Вспомним правило: умножение положительного на отрицательное число дает отрицательный результат. Считаем:

5 ∗ (-5)= -25

12 ∗ (-8)= -96

Ответ: -25; -96.

Пример 4. Вычислить произведение: (-0,125 ) * (-6)

Как решаем:

Используем правило умножения отрицательных чисел:
(-0,125 ) * (-6) = 0,125 * 6.

Выполним умножение десятичной дроби на натуральное число столбиком:

Ответ: 0,75.

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

Как найти координаты точки?

К следующей статье

503.5K

Признаки равенства треугольников

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс

Умножение положительных и отрицательных чисел

Задача 1. Точка движется по прямой слева направо со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка по прошествии 5 секунд?

Нетрудно сообразить, что точка будет находиться на 20 дм. вправо от A. Запишем решение этой задачи относительными числами. Для этого условимся в следующих знакоположениях:

1) скорость вправо будем обозначать знаком +, а влево знаком –, 2) расстояние движущейся точки от A вправо будем обозначать знаком + и влево знаком –, 3) промежуток времени после настоящего момента знаком + и до настоящего момента знаком –. В нашей задаче даны, след., такие числа: скорость = + 4 дм. в секунду, время = + 5 секунд и получилось, как сообразили арифметически, число + 20 дм., выражающее расстояние движущейся точки от A через 5 секунд. По смыслу задачи мы видим, что она относится к умножению. Поэтому решение задачи удобно записать:

(+ 4) ∙ (+ 5) = + 20.

Задача 2. Точка движется по прямой слева направо со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A. Где находилась эта точка 5 секунд назад?

Ответ ясен: точка находилась влево от A на расстоянии 20 дм.

Решение удобно, согласно условиям относительно знаков, и, имея в виду, что смысл задачи не изменился, записать так:

(+ 4) ∙ (– 5) = – 20.

Задача 3. Точка движется по прямой справа налево со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка спустя 5 секунд?

Ответ ясен: на 20 дм. слева от A. Поэтому, согласно тем же условиям относительно знаков, мы можем записать решение этой задачи так:

(– 4) ∙ (+ 5) = – 20.

Задача 4. Точка движется по прямой справа налево со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A. Где находилась движущаяся точка 5 секунд тому назад?

Ответ ясен: на расстоянии 20 дм. справа от A. Поэтому решение этой задачи следует записать так:

(– 4) ∙ (– 5) = + 20.

Рассмотренные задачи указывают, как следует распространить действие умножения на относительные числа. Мы имеем в задачах 4 случая умножения чисел со всевозможными комбинациями знаков:

1) (+ 4) ∙ (+ 5) = + 20;
2) (+ 4) ∙ (– 5) = – 20;
3) (– 4) ∙ (+ 5) = – 20;
4) (– 4) ∙ (– 5) = + 20.

Во всех четырех случаях абсолютные величины данных чисел следует перемножить, у произведения приходится ставить знак + тогда, когда у множителей одинаковые знаки (1-й и 4-й случаи) и знак –, когда у множителей разные знаки (случаи 2-й и 3-й).

Отсюда же видим, что от перестановки множимого и множителя произведение не изменяется.

Упражнения.

Выполним один пример на вычисление, где входят и сложение и вычитание и умножение.

Чтобы не спутать порядка действий, обратим внимание на формулу

ab + cd.

Здесь написана сумма произведений двух пар чисел: надо, следовательно, сперва число a умножить на число b, потом число c умножить на число d и затем полученные произведения сложить. Также в формуле

a – bc

надо сперва число b умножить на c и затем полученное произведение вычесть из a.

Если бы требовалось произведение чисел a и b сложить с c и полученную сумму умножить на d, то следовало бы написать: (ab + c)d (сравнить с формулой ab + cd).

Если бы надо было разность чисел a и b умножить на c, то написали бы (a – b)c (сравнить с формулой a – bc).

Поэтому установим вообще, что если порядок действий не обозначен скобками, то надо сначала выполнить умножение, а потом уже сложение или вычитание.

Приступаем к вычислению нашего выражения: выполним сначала сложения, написанные внутри всех маленьких скобок, получим:

Теперь надо выполнить умножение внутри квадратных скобок и затем из вычтем полученное произведение:

Теперь выполним действия внутри витых скобок: сначала умножение и потом вычитание:

Теперь останется выполнить умножение и вычитание:

16. Произведение нескольких множителей. Пусть требуется найти

(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5).

Здесь надо первое число умножить на второе, полученное произведение на 3-е и т. д. Не трудно на основании предыдущего установить, что абсолютные величины всех чисел надо между собою перемножить.

Если бы все множители были положительны, то на основании предыдущего найдем, что и у произведения надо написать знак +. Если бы какой-либо один множитель был отрицателен

напр., (+2) ∙ (+3) ∙ (+4) ∙ (–1) ∙ (+5) ∙ (+6),

то произведение всех предшествующих ему множителей дало бы знак + (в нашем примере (+2) ∙ (+3) ∙ (+4) = +24, от умножения полученного произведения на отрицательное число (в нашем примере +24 умножить на –1) получили бы у нового произведения знак –; умножив его на следующий положительный множитель (в нашем примере –24 на +5), получим опять отрицательное число; так как все остальные множители предполагаются положительными, то знак у произведения более изменяться не может.

Если бы было два отрицательных множителя, то, рассуждая, как выше, нашли бы, что сначала, пока не дошил до первого отрицательного множителя, произведение было бы положительно, от умножения его на первый отрицательный множитель новое произведение получилось бы отрицательным и таковы бы оно и оставалось до тех пор, пока не дойдем до второго отрицательного множителя; тогда от умножения отрицательного числа на отрицательно новое произведение получилось бы положительным, которое таким останется и в дальнейшем, если остальные множители положительны.

Если бы был еще третий отрицательный множитель, то полученное положительно произведение от умножения его на этот третий отрицательный множитель сделалось бы отрицательным; оно таковым бы и осталось, если остальные множители были все положительны. Но если есть еще четвертый отрицательный множитель, то от умножения на него произведение сделается положительным. Рассуждая так же, найдем, что вообще:

Чтобы узнать знак произведения нескольких множителей, надо посмотреть, сколько среди этих множителей отрицательных: если их вовсе нет, или если их четное число, то произведение положительно: если же отрицательных множителей нечетное число, то произведение отрицательно.

Итак, теперь мы легко узнаем, что

(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5) = +4200.

Также

(+3) ∙ (–2) ∙ (+7) ∙ (+3) ∙ (–5) ∙ (–1) = –630.

Теперь нетрудно видеть, что знак произведения, а также и его абсолютная величина, не зависят от порядка множителей.

Удобно, когда имеем дело с дробными числами, находить произведение сразу:

Удобно это потому, то не приходится делать бесполезных умножений, так как предварительно полученное дробное выражение сокращается, сколько возможно.

Пример на вычисление:

Умножение положительных и отрицательных чисел — «Семья и Школа»

Содержание

Умножение и деление положительных и отрицательных чисел

Умножение отрицательных чисел

Правило умножения отрицательных чисел:

Замечание 1

Для умножения двух отрицательных чисел нужно выполнить умножение их модулей.

Согласно правилу можно записать:

$(−a) \cdot (−b)=a \cdot b$,

где $a$ и $b$ – положительные действительные числа.

Из правила умножения следует, что результатом произведения двух отрицательных чисел является положительное число.

Правило умножения справедливо для целых, рациональных и действительных чисел.

Пример 1

Выполнить умножение двух отрицательных чисел $−8$ и $−11$.

Решение.

Найдем модули данных чисел:

$|-8|=8$;

$|-11|=11$.

Произведение модулей равно $8 \cdot 11=88$.

Краткая запись решения:

$(−8) \cdot (−11)= 8 \cdot 11=88$.

Ответ: $(−8) \cdot (−11)=88$.

Помощь со студенческой работой на тему

Умножение и деление положительных и отрицательных чисел

Замечание 2

Для умножения отрицательных рациональных чисел необходимо числа преобразовать к виду смешанных чисел, обыкновенных или десятичных дробей.

Умножение чисел с противоположными знаками

Правило умножения чисел с разными знаками:

Замечание 3

Для умножения чисел с противоположными знаками необходимо выполнить умножение чисел и перед полученным значением поставить знак $«–»$.

Согласно данному правилу можно записать:

$a \cdot (−b)=−(|a| \cdot |b|)$,

$(−a) \cdot b=−(|a| \cdot |b|)$,

где $a$ и $b$ – положительные действительные числа.

Данное правило умножения чисел с противоположными знаками применяется для целых, рациональных и действительных чисел.

Согласно рассмотренному правилу умножение чисел с противоположными знаками сводится к выполнению умножения положительных чисел.

Пример 2

Выполнить умножение положительного числа $7$ и отрицательного числа $–12$.

Решение.

Согласно правилу умножения чисел с противоположными знаками сначала выполним умножение модулей данных чисел:

$|7|=7$;

$|-12|=12$;

$7 \cdot 12=84$.

Поставим знак $«–»$ перед полученным значением и получим $−84$.

Краткая запись решения:

$7 \cdot (–12)=−(7 \cdot 12)=−84$.

Ответ: $7 \cdot (–12)=−84$.

Замечание 4

Для умножения дробных чисел с противоположными знаками необходимо преобразовать данные числа к удобному виду: обыкновенных или десятичных дробей.

Деление отрицательных чисел

Правило деления отрицательных чисел:

Замечание 5

Для деления одного отрицательного числа на другое необходимо выполнить деление модулей данных чисел.

Согласно данному правилу можно записать:

$a:b=|a|:|b|$,

где $a$ и $b$ – отрицательные числа.

Правило выполняется для целых, рациональных и действительных чисел. {−1}$.

Данное правило применимо для выполнения деления чисел с противоположными знаками.

Пример 3

Разделить отрицательные числа $−24$ и $−6$.

Решение.

Согласно правилу деления отрицательных чисел найдем модули данных чисел и выполним их деление. Получим:

$|-24|=24$;

$|-6|=6$;

$24:6=4$.

Краткая запись решения:

$(–24):(–6)=|–24|:|–6|=24:6=4$.

Ответ: $(–24):(–6)=4$.

Замечание 7

Для выполнения деления дробных рациональных чисел для удобства нужно преобразовать их к виду обыкновенных дробей, но можно делить и десятичные дроби.

Деление чисел с противоположными знаками

Правило деления чисел с противоположными знаками:

Замечание 8

Для деления положительного числа на отрицательное или отрицательного числа на положительное необходимо выполнить деление модулей данных чисел и перед полученным значением поставить знак $«–»$.

Согласно данному правилу можно записать:

$a:(–b)=−|a|:|–b|$,

$(–a):b=−|–a|:|b|$. {−1}$.

Данное правило применимо для деления отрицательных чисел.

Пример 4

Разделить положительное число $28$ на отрицательное число $–7$.

Решение.

Согласно правилу деления чисел с противоположными знаками найдем модули данных чисел и выполним их деление:

$|28|=28$;

$|-7|=7$;

$28:7=4$.

Поставим знак $«–»$ перед полученным значением и получим $–4$.

Краткая запись решения:

$28:(–7)=-|28|:|-7|=-(28:7)=-4$.

Ответ: $28:(–7) = –4$.

Замечание 10

Для деления дробных рациональных чисел с противоположными знаками числа удобнее представлять в виде обыкновенных дробей.

Умножение и деление отрицательных чисел

Мы уже умеем складывать и вычитать отрицательные числа.

Теперь давайте разберемся с умножением и делением.

Предположим, нам нужно умножить +3 на -4. Как это сделать?

Давайте рассмотрим такой случай. Три человека залезли в долги, и у каждого по 4 доллара долга. Чему равен общий долг? Для того чтобы его найти, надо сложить все три долга: 4 доллара + 4 доллара + 4 доллара = 12 долларов. Мы с вами решили, что сложение трех чисел 4 обозначается как 3×4. Поскольку в данном случае мы говорим о долге, перед 4 стоит знак «-». Мы знаем, что общий долг равен 12 долларам, так что теперь наша задача имеет вид 3х(-4)=-12.

Мы получим тот же результат, если по условию задачи каждый из четырех человек имеет долг по 3 доллара. Другими словами, (+4)х(-3)=-12. А поскольку порядок сомножителей значения не имеет, получаем (-4)х(+3)=-12 и (+4)х(-3)=-12.

Давайте обобщим результаты. При перемножении одного положительного и одного отрицательного числа результат всегда будет отрицательным числом. Численная величина ответа будет той же самой, как и в случае положительных чисел. Произведение (+4)х(+3)=+12. Присутствие знака «-» влияет только на знак, но не влияет на численную величину.

А как перемножить два отрицательных числа?

К сожалению, на эту тему очень трудно придумать подходящий пример из жизни. Легко себе представить долг в сумме 3 или 4 доллара, но совершенно невозможно вообразить -4 или -3 человека, которые залезли в долги.

Пожалуй, мы пойдем другим путем. В умножении при изменении знака одного из множителей меняется знак произведения. Если мы меняем знаки у обоих множителей, мы должны дважды сменить знак произведения, сначала с положительного на отрицательный, а затем наоборот, с отрицательного на положительный, то есть у произведения будет первоначальный знак.

Следовательно, вполне логично, хотя немного странно, что (-3)х(-4)=+12.

Положение знака при умножении изменяется таким образом:

положительное число х положительное число = положительное число;
отрицательное число х положительное число = отрицательное число;
положительное число х отрицательное число = отрицательное число;
отрицательное число х отрицательное число = положительное число.

Иначе говоря, перемножая два числа с одинаковыми знаками, мы получаем положительное число. Перемножая два числа с разными знаками, мы получаем отрицательное число.

Такое же правило справедливо и для действия противоположного умножению – для деления.

(+12):(+3)=+4;

(+12):(-3)=-4;

(-12):(+3)=-4;

(-12):(-3)=+4.

Вы легко можете в этом убедиться, проведя обратные операции умножения. Если в каждом из примеров, приведенных выше, вы умножите частное на делитель, то получите делимое, и убедитесь, что оно имеет тот же самый знак, например (-3)х(-4)=(+12).

Поскольку скоро зима, то пора уже подумать о том, в что переобуть своего железного коня, что бы не скользить по льду и чувствовать себя уверено на зимних дорогах. Можно, например, взять шины йокогама на сайте: mvo.ru или какие-то другие, главное, что бы качественный, больше информации и цены вы можете узнать на сайте Mvo.ru.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

Отрицательные дроби.

Действия с отрицательными дробями

Отрицательные дроби — это дроби, числитель или знаменатель которых является отрицательным числом.

Отрицательные дроби могут быть записаны по-разному. Например, рассмотрим два частных:

-2 : 7 и 2 : (-7),

каждое из них равно отрицательному числу

Каждое из данных частных можно записать в виде дроби, в которой дробная черта заменит знак деления:

-2 : 7	=	-2	и	2 : (-7)	=	2	.
		7				-7

Следовательно, при записи отрицательных дробей знак минус можно ставить перед дробью, перед числителем или перед знаменателем:

Сложение и вычитание

Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел.

Пример.

Приведём дроби к общему знаменателю:

—	2	+ (-	1	) =	-8	+	-5	.
	5		4		20		20

Теперь сложим числители дробей по правилам сложения рациональных чисел:

-8	+	-5	=	-8 + (-5)	=	-13	=	—	13	.
20		20		20		20			20

Таким образом:

—	2	+ (-	1	) =	-8	+	-5	=
	5		4		20		20

=	-8 + (-5)	=	-13	=	—	13	.
	20		20			20

Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.

Пример.

—	5	— (-	11	) =	—	5	+ (+	11	) =
	12		12			12		12

=	—	5	+	11	=	-5 + 11	=	6	.
		12		12		12		12

Сложение и вычитание отрицательных дробей производится по правилам сложения обыкновенных дробей, то есть сначала идёт приведение к общему знаменателю, если это нужно, а затем производятся вычисления.

Умножение и деление

Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей.

Пример.

—	2	· (-	4	) =	-2	·	-4	=	-2 · (-4)	=	8	.
	3		5		3		5		3 · 5		15

Так как при умножении двух отрицательных чисел результат будет положительным, то данный пример можно решить сразу, отбросив оба минуса:

—	2	· (-	4	) =	2	·	4	=	2 · 4	=	8	.
	3		5		3		5		3 · 5		15

При умножении отрицательной дроби на положительную результат будет отрицательным.

Пример.

—	2	·	4	=	—	2 · 4	=	—	8	.
	3		5			3 · 5			15

К отрицательным дробям можно применять любые законы умножения. Поэтому предыдущий пример можно переписать так:

4	· (-	2	) =	—	4 · 2	=	—	8	.
5		3			5 · 3			15

То есть при умножении положительной дроби на отрицательную результат будет отрицательным.

Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.

Пример.

—	2	: (-	4	) =	-2	:	-4	=
	3		5		3		5

=	-2 · 5	=	-10	=	10	.
	3 · (-4)		-12		12

Знак результата умножения или деления отрицательных дробей можно узнать по правилам знаков целых чисел.

Умножение положительных и отрицательных чисел

(+ 4) ∙ (+ 5) = + 20.

Ответ ясен: точка находилась влево от A на расстоянии 20 дм.

(+ 4) ∙ (– 5) = – 20.

(– 4) ∙ (+ 5) = – 20.

Ответ ясен: на расстоянии 20 дм. справа от A. Поэтому решение этой задачи следует записать так:

(– 4) ∙ (– 5) = + 20.

1) (+ 4) ∙ (+ 5) = + 20;
2) (+ 4) ∙ (– 5) = – 20;
3) (– 4) ∙ (+ 5) = – 20;
4) (– 4) ∙ (– 5) = + 20.

Отсюда же видим, что от перестановки множимого и множителя произведение не изменяется.

Упражнения.

Выполним один пример на вычисление, где входят и сложение и вычитание и умножение.

Чтобы не спутать порядка действий, обратим внимание на формулу

ab + cd.

a – bc

надо сперва число b умножить на c и затем полученное произведение вычесть из a.

Если бы надо было разность чисел a и b умножить на c, то написали бы (a – b)c (сравнить с формулой a – bc).

Теперь надо выполнить умножение внутри квадратных скобок и затем из вычтем полученное произведение:

Теперь выполним действия внутри витых скобок: сначала умножение и потом вычитание:

Теперь останется выполнить умножение и вычитание:

16. Произведение нескольких множителей. Пусть требуется найти

(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5).

напр., (+2) ∙ (+3) ∙ (+4) ∙ (–1) ∙ (+5) ∙ (+6),

Итак, теперь мы легко узнаем, что

(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5) = +4200.

Также

(+3) ∙ (–2) ∙ (+7) ∙ (+3) ∙ (–5) ∙ (–1) = –630.

Удобно, когда имеем дело с дробными числами, находить произведение сразу:

Пример на вычисление:

правило, примеры, умножение отрицательных чисел на положительные

В данной статье сформулируем правило умножения отрицательных чисел и дадим ему объяснение. Будет подробно рассмотрен процесс умножения отрицательных чисел. На примерах показаны все возможные случаи.

Умножение отрицательных чисел

Определение 1

Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел –a, -b данное равенство считается верным.

(-а)·(-b)=a·b.

Выше приведено правило умножения двух отрицательных чисел. Исходя из него, докажем выражение: (-а)·(-b)=a·b. Статья умножение чисел с разными знаками рассказывает о том, что равенств а·(-b)=-a·b справедливое, как и (-а)·b=-a·b. Это следует из свойства противоположных чисел, благодаря которому равенства запишутся следующим образом:

(-a)·(-b)=(-a·(-b))=-(-(a·b))= a·b.

Тут явно видно доказательство правила умножения отрицательных чисел. Исходя из примеров явно, что произведение двух отрицательных чисел – положительное число. При перемножении модулей чисел результат всегда положительное число.

Данное правило применимо для умножения действительных чисел, рациональных чисел, целых чисел.

Примеры умножения отрицательных чисел

Теперь рассмотрим подробно примеры умножения двух отрицательных чисел. При вычислении необходимо пользоваться правилом, написанным выше.

Пример 1

Произвести умножение чисел -3 и -5.

Решение.

По модулю умножаемые данные два числа равны положительным числам 3 и 5. Их произведение дает в результате 15. Отсюда следует, что произведение заданных чисел равно 15

Запишем кратко само умножение отрицательных чисел:

(-3)·(-5)=3·5=15

Ответ: (-3)·(-5)=15.

При умножении отрицательных рациональных чисел, применив разобранное правило, можно мобилизоваться к умножению дробей, умножению смешанных чисел, умножению десятичных дробей.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Пример 2

Вычислить произведение (-0,125)·(-6).

Решение.

Используя правило умножения отрицательных чисел, получим, что (−0,125)·(−6)=0,125·6. Для получения результата необходимо выполнить умножение десятичной дроби на натуральное число столбиков. Это выглядит так:

Получили, что выражение примет вид (−0,125)·(−6)=0,125·6=0,75.

Ответ: (−0,125)·(−6)=0,75.

В случае, когда множители – иррациональные числа, тогда их произведение может быть записано в виде числового выражения. Значение вычисляется только по необходимости.

Пример 3

Необходимо произвести умножение отрицательного -2 на неотрицательное log5 13.

Решение

Находим модули заданных чисел:

-2=2 и log513=-log5 3=log5 3.

Следуя из правил умножения отрицательных чисел, получим результат -2·log5 13=-2·log5 3=2·log5 3. Это выражение и является ответом.

Ответ: -2·log5 13=-2·log5 3=2·log5 3.

Для продолжения изучения темы необходимо повторить раздел умножение действительных чисел.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Сложение и вычитание отрицательных и положительных чисел.

Решение примеров.

Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.

Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:

Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.

$(-2)+(-3)=-5$

Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:

$(-8)+4=4-8=-4$

$9+(-4)=9-4=5$

Для каждого числа кроме $0$ существует противоположный элемент, при сумме с ним образуется ноль:

$-9+9=0$ $7,1+(-7,1)=0$

При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.

$(-7)-(-6)=(-7)+6=(-1)$

Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.

$7-9=-2$ так как $9>7$

Также не стоит забывать минус на минус дает плюс:

$7-(-9)=7+9=16$

Задача 1. Вычислите:

$4+(-5)$
$-36+15$
$(-17)+(-45)$
$-9+(-1)$

Решение:

$4+(-5)=4-5=-1$
$-36+15=-21$
$(-17)+(-45)$ $=-17-45=-62$
$-9+(-1)=-9-1=-10$

Задача 2. Вычислите:

$3-(-6)$
$-16-35$
$-27-(-5)$
$-94-(-61)$

Решение:

$3-(-6)=3+6=9$
$-16-35=-51$
$-27-(-5)=-27+5=-22$
$-94-(-61)=-94+61=-33$

Запишитесь на бесплатное тестирование знаний!

Наши преподаватели

Оставить заявку

Репетитор по математике

Омский государственный педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 7-11 классов. Реализую дифференцированный подход к обучению, осуществляю подготовку учеников к ОГЭ и ЕГЭ. Почему я люблю математику? Меня завораживают строки формул и выражений, кажется, что это шифр, к которому нужно подобрать ключ. Поэтому математика — это ключ к тайнам Вселенной.

Оставить заявку

Репетитор по математике

Гомельский государственный университет им. Ф. Скорины

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-9 классов. Математикой я был увлечен со школы, часто участвовал в олимпиадах. За время своей работы понял, что в изучении предмета большую роль играет эмоциональное отношение ученика к предмету. В школе часто создается впечатление, что математика — это сложно. На занятиях я стараюсь помочь ученикам преодолеть этот психологический барьер (если он есть) и начать решать легко и весело. При обучении использую примеры не только из книг, но и из жизни, помогая формировать образное мышление, которое позволяет просто запоминать формулы и табличные данные.

Оставить заявку

Репетитор по математике

БГПУ им.М.Танка

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-6 классов. Люблю математику за её красоту и элегантность. «Математика — это музыка в цифрах.» При обучении всегда провожу параллели с примерами из жизни.

Математика 10 класс

— Индивидуальные занятия
— В любое удобное для вас время
— Бесплатное вводное занятие

Курсы ОГЭ

— Индивидуальные занятия
— В любое удобное для вас время
— Бесплатное вводное занятие

Математика по Skype

— Индивидуальные занятия
— В любое удобное для вас время
— Бесплатное вводное занятие

Как правильно умножать отрицательные числа?

Основные определения

Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.

Два главных определения:

Запоминаем!

Положительные числа — это те, что больше нуля, а отрицательные — меньшие.

Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!

Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).

Свойства умножения

От перестановки множителей местами произведение не меняется.
a * b = b * a
Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.
a * b * c = (a * b) * c = a * (b * c)

А вот как умножить два числа с разными знаками:

перемножить модули этих чисел
перед полученным числом поставить знак минус

А теперь упростим правила. Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:

«—» — при умножении минус на минус ответ будет положительным
или минус на минус дает плюс
«-+» — при умножении минуса на плюс ответ будет отрицательным
или минус на плюс дает минус
«+-» — при умножении плюса на минус ответ будет отрицательным
или плюс на минус дает минус
«++» — при умножении плюса на плюс ответ будет положительным
или плюс на плюс дает плюс.

Примеры умножения отрицательных чисел

Пример 1. Вычислить: (-2)∗(-2) и (-3)∗(-7)

Как решаем:

Вспомним правило: отрицательное число умножить на отрицательное — получается ответ со знаком плюс. Считаем:

(-2)∗(-2) = 4

(-3)∗(-7) = 21

Ответ: 4; 21.

Пример 2. Вычислить: (-11)∗11 и (-20)∗2

Как решаем:

-11 * 11 = -121

(-20) * 2 = -40

Ответ: -121; -40.

Пример 3. Вычислить произведение: 5∗(-5) и 12∗(-8)

Как решаем:

Вспомним правило: умножение положительного на отрицательное число дает отрицательный результат. Считаем:

5 ∗ (-5)= -25

12 ∗ (-8)= -96

Ответ: -25; -96.

Пример 4. Вычислить произведение: (-0,125 ) * (-6)

Как решаем:

Используем правило умножения отрицательных чисел:
(-0,125 ) * (-6) = 0,125 * 6.

Выполним умножение десятичной дроби на натуральное число столбиком:

Ответ: 0,75.

Умножение отрицательных дробей — Видео и стенограмма урока

Умножение отрицательных дробей

Вот четыре шага для умножения отрицательных дробей. Давайте воспользуемся следующей задачей, чтобы проиллюстрировать шаги.

Помните, что числители — это числа над чертой в дробной части, а знаменатели — это числа под чертой в долях.

Помните, что целое число можно превратить в дробь, просто поместив целое число над 1.Например, целое число 7 становится 7/1.

Попрактикуемся

Давайте вместе попробуем. Давайте найдем произведение -2/7 * 3/4

Шаг 1) Когда мы умножим числители (2 * 3), ответ будет 6.

Шаг 2) Когда мы умножим знаменатели (7 * 4), ответ равно 28.

Шаг 3) Новая дробь — 6/28. Оба числа делятся на 2 и могут быть упрощены до 3/14.

Шаг 4) У дробей разные знаки, так как одна положительная, а другая отрицательная, поэтому ответ отрицательный.

Произведение -2/7 * 3/4 = -3/14.

Попробуем еще парочку. Не стесняйтесь брать лист бумаги и карандаш и самостоятельно решать следующие задачи, прежде чем искать решение.

Решить: -3/4 * 2/3

Шаг 1) Умножить числители: 3 * 2 = 6

Шаг 2) Умножить знаменатели: 4 * 3 = 12

Шаг 3) Упростить 6/12 ( оба делятся на 6) до 1/2

Шаг 4) Знаки разные, поэтому ответ отрицательный.

Ответ -1/2.

Решить: -1/2 * 3/4

Шаг 1) Умножить числители: 1 * 3 = 3

Шаг 2) Умножить знаменатели: 2 * 4 = 8

Шаг 3) 3/8 уже в простейшей форме

Шаг 4) Знаки разные, поэтому ответ отрицательный.

Итак, -1/2 * 3/4 = -3/8.

Краткое содержание урока

При умножении дробей помните, что если дроби имеют одинаковый знак, ответ будет положительным, а если дроби имеют разные знаки, ответ будет отрицательным.Также помните, что умножение отрицательных дробей состоит из четырех простых шагов, и это, безусловно, положительный момент!

Умножение и деление на целые числа (предалгебра, изучение и понимание целых чисел) — Mathplanet

Вы также должны обращать внимание на знаки при умножении и делении. Следует помнить два простых правила:

Когда вы умножаете отрицательное число на положительное, произведение всегда отрицательное.

Когда вы умножаете два отрицательных числа или два положительных числа, произведение всегда будет положительным.

Это похоже на правило сложения и вычитания: два знака минус становятся плюсом, а плюс и минус становятся минусом. Однако при умножении и делении вы вычисляете результат, как если бы не было знаков минус, а затем смотрите на знаки, чтобы определить, положительный или отрицательный результат. Два примера быстрого умножения:

$$ 3 \ cdot (-4) = — 12 $$

3 умножить на 4 равно 12. Поскольку существует одно положительное и одно отрицательное число, произведение равно отрицательному 12.

$$ (- 3) \ cdot (-4) = 12 $$

Теперь у нас есть два отрицательных числа, поэтому результат положительный.

Переходя к делению, вы можете вспомнить, что вы можете подтвердить полученный ответ, умножив частное на знаменатель. Если вы ответили правильно, то произведение этих двух чисел должно совпадать с числителем. Например,

$$ \ frac {12} {3} = 4 $$

Чтобы проверить, является ли 4 правильным ответом, мы умножаем 3 (знаменатель) на 4 (частное):

$$ 3 \ cdot 4 = 12 $$

Что произойдет, если разделить два отрицательных числа? Например,

$$ \ frac {(- 12)} {(- 3)} = \:? $$

Чтобы знаменатель (-3) стал числителем (-12), вам нужно умножить его на 4, поэтому частное равно 4.

Итак, частное отрицательного и положительного чисел отрицательно, и, соответственно, частное положительного и отрицательного чисел также отрицательно. Можно сделать вывод, что:

Если вы разделите отрицательное число на положительное, то частное будет отрицательным.

Когда вы делите положительное число на отрицательное, частное также становится отрицательным.

Когда вы делите два отрицательных числа, получается положительное частное.

Те же правила верны и для умножения.

Видеоурок

Вычислить следующие выражения

$$ (- 4) \ cdot (-12), \: \: \: \: \ frac {-12} {3} $$

Умножение и деление отрицательных чисел

Purplemath

Если перейти от сложения и вычитания, как вы производите умножение и деление с отрицательными числами? Собственно, сложную часть мы уже рассмотрели: вы уже знаете правила «знака»:

плюс раз плюс плюс
(добавление большого количества горячих кубиков повышает температуру)

минус раз плюс минус
(удаление большого количества горячих кубиков снижает температуру)

плюс умножить на минус — это минус
(добавление большого количества холодных кубиков снижает температуру)

минус умножить на минус равно плюс
(удаление большого количества холодных кубиков повышает температуру)

MathHelp.

com

Правила знаков действуют одинаково для деления; просто замените «раз» на «деленное на». Вот пример правил в разделе:

(Помните, что дроби — это просто еще одна форма деления! «Дроби — это деление»!)

Некоторым людям нравится думать об отрицательных числах в терминах долгов.Так, например, если вы должны 10 долларов шести людям, ваш общий долг составит 6 × 10 долларов = 60 долларов. В этом контексте имеет смысл получить отрицательный ответ. Но в каком контексте может иметь смысл деление отрицательного на отрицательное (и получение положительного)?

Подумайте о том, чтобы перекусить в кафе. Когда вы идете платить, у ребенка возникают проблемы с использованием вашей дебетовой карты. Он проводит по ней шесть раз, прежде чем, наконец, вернуть карту вам. Вернувшись домой, вы проверяете свой банковский счет в Интернете. По сумме можно сказать, что да, он действительно взимал с вас или более одного раза.Некоторая часть этого общего дебета (отрицательная на вашем счете) неверна.

Прежде чем звонить в банк для исправления ситуации, вы хотите подтвердить количество превышенных комиссий. Как в этом разобраться? Вы можете разделить всю сумму (скажем, 76,02 доллара США) на сумму, указанную в квитанции (скажем, 12,67 доллара США), которая является суммой одного платежа. Каждое списание является минусом на вашем счету, поэтому математика составляет:

(- 76,02 доллара) ÷ (- 12 долларов.67) = 6

Итак, всего действительно было шесть зарядов. Количество зарядов, 6, при подсчете количества событий, должно быть положительным. В этом реальном контексте деление минуса на минус и получение плюса имеет смысл. И теперь вы знаете, что нужно указать службе поддержки клиентов отменить ровно пять начислений.

Вы можете заметить, что люди отменяют знак минус.Они пользуются тем, что «минус, умноженный на минус, есть плюс». Например, предположим, что у вас есть (–2) (- 3) (- 4). Любые два отрицательных результата при умножении становятся одним положительным. Так что выберите любые два из перемноженных (или разделенных) отрицаний и «отмените» их знаки:

Начну с того, что уберу одну пару знаков «минус».Потом размножу как обычно.

(–2) (- 3) (- 4)

= (–2) (- 3) (–4)

= (+6) (–4)

= –24

Если вам дано длинное умножение с отрицательными числами, просто уберите знаки «минус» в парах:

Первое, что я сделаю, это подсчитаю знаки «минус». Один два три четыре пять шесть семь. Итак, есть три пары, которые я могу отменить, оставив одну. В результате мой окончательный ответ должен быть отрицательным. Если я получу положительный результат, я буду знать, что сделал что-то не так.

(–1) (- 2) (- 1) (- 3) (- 4) (- 2) (- 1)

= (–1) (- 2) (–1) (- 3) (- 4) (- 2) (- 1)

= (+1) (+ 2) (–1) (- 3) (- 4) (- 2) (- 1)

= (1) (2) (–1) (- 3) (–4) (- 2) (- 1)

= (1) (2) (+1) (+ 3) (–4) (- 2) (- 1)

= (1) (2) (1) (3) (–4) (- 2) (–1)

= (1) (2) (1) (3) (+4) (+ 2) (–1)

= (1) (2) (1) (3) (4) (2) (- 1)

= (2) (3) (4) (2) (- 1)

= 48 (–1)

= –48

Я получил отрицательный ответ, поэтому знаю, что мой знак правильный.

Вот еще один пример, показывающий тот же процесс отмены в контексте разделения:

Отрицательные скобки

Основная трудность, с которой люди сталкиваются с негативом, заключается в том, чтобы иметь дело со скобками; в частности, в переносе отрицания через круглые скобки. Обычная ситуация примерно такая:

Если бы у вас было «3 ( x + 4)», вы бы знали, что нужно «распределить» 3 «над» круглыми скобками:

3 ( x + 4) = 3 ( x ) + 3 (4) = 3 x + 12

Те же правила применяются, когда вы имеете дело с негативом.Если у вас проблемы с отслеживанием, используйте маленькие стрелки:

← проведите по экрану , чтобы просмотреть изображение полностью →

Мне нужно взять 3 в скобки:

3 ( x — 5) = 3 ( x ) + 3 (–5) = 3 x — 15

Здесь я возьму «минус» в скобках; Я буду распределять –2 на x и минус 3.

–2 ( x — 3) = –2 ( x ) — 2 (–3) = –2 x + 2 (+3) = –2 x + 6

Обратите внимание, как я внимательно следил за знаками в круглых скобках. «Минус» был сохранен рядом с цифрой 3 за счет использования еще одного набора круглых скобок. Не стесняйтесь использовать символы группировки, чтобы обозначить предполагаемый смысл как для оценщика, так и для вас самих.

Другая проблема, связанная с предыдущей, связана с вычитанием скобок. Вы можете отслеживать знак вычитания, преобразовав вычитание в умножение на минус:

Я начну с написания маленькой цифры «1» перед круглыми скобками. Затем я нарисую стрелки от этой единицы к терминам в круглых скобках, чтобы напомнить себе о том, что мне нужно сделать.

← проведите по экрану , чтобы просмотреть изображение полностью →

Не бойтесь написать эту маленькую цифру «1» и нарисовать эти маленькие стрелки.Вы должны делать все, что вам нужно, чтобы ваша работа была прямой и постоянно получала правильный ответ.

Упростить 6 — (3
x — 4 [1 — x ]).

Я буду работать изнутри, упрощая сначала символы внутренней группировки в соответствии с Порядком операций. Итак, первое, что я сделаю, это возьму –4 через скобки.Тогда я упрощу; Я продолжу, поставив 1 перед круглыми скобками и, чтобы помочь мне отслеживать тот -1, который я буду распространять, я нарисую маленькие стрелки.

← проведите по экрану , чтобы просмотреть изображение полностью →

Филиал

Упростить
¹/₃—^{( x -2)}/₃.

Это хитрый. Они заставляют меня вычесть дробь. Мне нужно объединить дроби, что означает объединение числителей. Чтобы не упустить из виду, что именно означает этот «минус» (а именно, что я вычитаю весь числитель второй дроби, а не только x ), я конвертирую минус с плюсом –1:

← проведите по экрану , чтобы просмотреть изображение полностью →

Обратите внимание, что я преобразовал вычитание дроби в добавление отрицательного числа, умноженного на единицу дроби.Очень легко «потерять» минус, когда вы добавляете такие беспорядочные полиномиальные дроби. Самая распространенная ошибка — ставить минус на x и забывать отнести его к –2. Будьте особенно осторожны с дробями!

Для дополнительной практики со скобками попробуйте здесь.

URL: https://www.purplemath.com/modules/negative3.htm

Рационалов (числа со знаком, включая дроби)

Рационалы (числа со знаком, включая дроби)

Напомним, что целые числа — это положительные и отрицательные целые числа и ноль.Когда дроби и завершающие или повторяющиеся десятичные дроби между целыми числами включены, полная группа чисел упоминается как рациональное число. Это числа со знаком, включая дроби. Более техническое определение рационального числа — это любое число, которое может быть записано в виде дроби, где числитель является целым числом или целым числом, а знаменатель — натуральным числом. Обратите внимание, что дроби могут быть помещены в числовую линию, как показано на рисунке 1

. Числовая строка, показывающая целые числа и дроби.

Дроби могут быть как отрицательными, так и положительными. Отрицательные дроби обычно записываются следующим образом:

Хотя все они равны.

Правила для знаков при сложении целых чисел применимы и к дробям. Помните: Чтобы сложить дроби, вы должны сначала получить общий знаменатель.

Добавьте следующее.

Правила для знаков при сложении целых чисел также применимы к смешанным числам.

Добавьте следующее.

Правила для знаков при вычитании целых чисел применимы и к дробям. Запомните: Чтобы вычесть дроби, вы должны сначала получить общий знаменатель.

Вычтите следующее.

Правила для знаков при вычитании целых чисел также применимы к смешанным числам. Помните: Чтобы вычесть смешанные числа, вы должны сначала получить общий знаменатель. Если заимствование из столбца необходимо, остерегайтесь простых ошибок.

Вычтите следующее.

Проблемы, подобные предыдущим, обычно легче всего решить, сложив число с большим абсолютным значением наверху, вычтя и сохранив знак числа с большим абсолютным значением.

Правила для знаков при умножении целых чисел применимы и к дробям. Помните: Чтобы умножить дроби, умножьте числители, а затем знаменатели. По возможности всегда упрощайте до минимальных условий.

Умножьте следующее.

Можно отменить при умножении положительной и отрицательной дробей. Просто отмените, как вы это делаете при умножении положительных дробей, но обратите особое внимание на соответствующие знаки.Следуйте правилам знаков при умножении целых чисел, чтобы получить правильный знак. Помните: Отсутствие знака означает, что понимается положительный знак.

Умножьте следующее.

Следуйте правилам знаков при умножении целых чисел, чтобы получить правильный знак. Запомните: Перед умножением смешанных чисел вы должны сначала преобразовать их в неправильные дроби.

Умножьте следующее.

Следуйте правилам знаков при делении целых чисел, чтобы получить правильный знак. Помните: При делении дробей сначала инвертируйте делитель, а затем умножайте.

Разделите следующее.

Следуйте правилам знаков при делении целых чисел, чтобы получить правильный знак. Запомните: Перед тем, как делить смешанные числа, вы должны сначала изменить их на неправильные дроби. Затем вы должны инвертировать делитель и умножить.

Разделите следующее.

Упрощение выражения с помощью дроби

Результаты обучения

Определите отрицательные дроби, которые эквивалентны, учитывая, что их отрицательный знак находится в другом месте
Упростите выражения, содержащие дробные черты, используя порядок операций

Где идет знак минус в дроби? Обычно перед дробью ставится знак минус, но иногда можно увидеть дробь с отрицательным числителем или знаменателем.Помните, что дроби представляют собой деление. Дробь [латекс] — \ frac {1} {3} [/ latex] может быть результатом деления [latex] \ frac {-1} {3} [/ latex], отрицательного на положительный или деления [latex] \ frac {1} {- 3} [/ latex], положительное за отрицательным. Когда числитель и знаменатель имеют разные знаки, частное отрицательное.

Если и числитель, и знаменатель отрицательны, тогда сама дробь положительна, потому что мы делим отрицательное значение на отрицательное.

[латекс] \ frac {-1} {- 3} = \ frac {1} {3} \ frac {\ text {negative}} {\ text {negative}} = \ text {positive} [/ latex]

Знак минус в дробной части

Для любых положительных чисел [латекс] a \ text {и} b [/ latex],

[латекс] \ frac {-a} {b} = \ frac {a} {- b} = — \ frac {a} {b} [/ latex]

Пример

Какая из следующих фракций эквивалентна [latex] \ frac {7} {- 8}? [/ Latex]

[латекс] \ frac {-7} {- 8}, \ frac {-7} {8}, \ frac {7} {8}, — \ frac {7} {8} [/ latex]

Решение:
Частное положительного и отрицательного отрицательно, поэтому [latex] \ frac {7} {- 8} [/ latex] отрицательно.Из перечисленных фракций [latex] \ frac {-7} {8} \ text {и} — \ frac {7} {8} [/ latex] также отрицательны.

Упрощение выражения с помощью дроби

Полоски дроби действуют как символы группировки. Выражения над и под дробной чертой следует рассматривать так, как если бы они были заключены в круглые скобки. Например, [латекс] \ frac {4 + 8} {5 — 3} [/ latex] означает [латекс] \ left (4 + 8 \ right) \ div \ left (5 — 3 \ right) [/ latex] . Порядок операций говорит нам сначала упростить числитель и знаменатель — как если бы были круглые скобки — перед тем, как делить.
Мы добавим дробные черты к нашему набору символов группировки из раздела «Использование языка алгебры», чтобы получить здесь более полный набор.

Группировка символов

Упростите выражение с помощью дробной линейки

Упростим числитель.
Упростим знаменатель.
Упростите дробь.

Пример

Упростить: [латекс] \ frac {4 + 8} {5 — 3} [/ латекс]

Показать решение

Решение:

» data-label=»»>

	[латекс] \ frac {4 + 8} {5 — 3} [/ латекс]
Упростите выражение в числителе.	[латекс] \ frac {12} {5 — 3} [/ латекс]
Упростим выражение в знаменателе. {2} +2} [/ latex]
Используйте порядок операций.{2}} {64 — 16} [/ латекс]
Упростим числитель и знаменатель.	[латекс] \ frac {16} {48} [/ латекс]
Упростим дробь.	[латекс] \ frac {1} {3} [/ латекс]

Пример

Упростить: [латекс] \ frac {4 \ left (-3 \ right) +6 \ left (-2 \ right)} {- 3 \ left (2 \ right) -2} [/ latex]

Показать решение

Решение:

[латекс] \ frac {4 \ left (-3 \ right) +6 \ left (-2 \ right)} {- 3 \ left (2 \ right) -2} [/ латекс]
Умножить.	[латекс] \ frac {-12+ \ left (-12 \ right)} {- 6 — 2} [/ латекс]
Упростить.	[латекс] \ frac {-24} {- 8} [/ латекс]
Разделить.	[латекс] 3 [/ латекс]

Посмотрите это видео, чтобы увидеть еще один пример того, как упростить выражение с помощью дробной линейки, содержащей несколько различных операций.

Умножение положительных и отрицательных чисел: 3 простых правила

При умножении положительных и отрицательных чисел существует меньше правил, чем при сложении и вычитании положительных и отрицательных чисел.Следует запомнить всего три правила:

Правило 1. Положительное число, умноженное на положительное, равно положительному числу.

Это умножение, которое вы делали все время: положительные числа, умноженные на положительные числа, равны положительным числам.

Например, 5 x 3 = 15. 5 — положительное число, 3 — положительное число, а умножение дает положительное число: 15.

Ответ: 5 x 3 = 15.

Правило 2: Отрицательное число, умноженное на положительное, равняется отрицательному числу.

Когда вы умножаете отрицательное число на положительное, ваш ответ — отрицательное число. Не имеет значения, в каком порядке вы умножаете положительные и отрицательные числа, ответ всегда будет отрицательным.

Например: -2 x 4, что по сути то же самое, что -2 + (-2) + (-2) + (-2)

Ответ: -2 х 4 = -8.

И, как мы уже сказали, если около 4 x -2 наоборот, ответ все тот же: -8.

Ответ: 4 х -2 = -8.

Правило 3. Отрицательное число, умноженное на отрицательное число, равняется положительному числу.

Два отрицательных числа дают положительное число, поэтому отрицательное число, умноженное на отрицательное число, дает положительное число. Если вы посмотрите на него на числовой прямой, идя назад и повернувшись лицом в отрицательном направлении, вы двинетесь в положительном направлении.

Например. -2 x -4 отрицательны, поэтому мы знаем, что ответ будет положительным.

Ответ: -2 x -4 = 8.

Вот общее правило, которое следует помнить при умножении положительных и отрицательных чисел:

Два одинаковых знака дают положительный знак:

Два непохожих знака образуют знак минус:

Если вы все еще не понимаете, почему отрицательное число, умноженное на отрицательное, дает положительное число, Диана Браун с факультета математики Университета Джорджии объясняет это разными способами в этой статье.

Скотт из About.com также собрал удобное видео о том, как создать шпаргалку для умножения отрицательных и положительных чисел (прокрутите страницу вниз, и вы найдете видео).

Как складывать, вычитать, умножать и делить положительные и отрицательные числа

Давайте посмотрим на следующую числовую строку и заметим, что каждая точка (точка) на числовой прямой соответствует одному числу:

В числовой строке выше мы видим три типа чисел или целых чисел: отрицательные числа, ноль и положительные числа. Отрицательные числа находятся слева от нуля, поэтому они меньше нуля. Положительные числа справа от нуля, поэтому они больше нуля. Ноль, разделительная точка, не является ни положительным, ни отрицательным.

Для числовой строки выше «1» соответствует или относится к красной точке, «2» относится к зеленой точке, «3» относится к синей точке и так далее. Когда мы перемещаемся вправо по числовой строке, мы увеличиваем числа. Мы определили это как дополнение. Когда мы движемся влево, мы уменьшаемся.И мы определили это как вычитание. Обычно так работает числовая линия.

Когда мы складываем два положительных числа или умножаем два положительных числа, мы получаем положительное число. Однако мы можем вычесть положительное число из положительного, и внезапно мы не получим положительное число!

Например, если мы вычтем 7 из 4, мы начнем с 4 в числовой строке и переместимся влево на 7 позиций. Это подводит нас к -3. Поскольку -3 находится слева от 0, оно меньше нуля.

Глядя на обратную операцию, мы можем сказать, что если 4-7 = -3, то -3 + 7 = 4. И это правильно. Если мы начнем с -3 и переместим на 7 делений вправо, мы получим 4.

Положительные числа — это не только целые числа справа от нуля, но и все типы чисел, такие как дроби, десятичные дроби и радикалы. Отрицательные числа также включают различные формы и различные типы чисел, которые появляются слева от нуля.

У нас не всегда есть числовая линия, с которой можно работать, поэтому нам нужно выучить несколько правил работы с отрицательными числами.Во-первых, нам нужно определить абсолютное значение. Абсолютное значение числа — это количество единиц, отсчитываемых от нуля. Он всегда выражается положительно, но без знака «плюс».

Абсолютное значение 3 равно 3. Абсолютное значение -3 также равно 3. И 3, и -3 — три единицы от нуля. Абсолютное значение обозначается путем написания числа между двумя вертикальными полосами.

| 3 | = 3 и | -3 | = 3

Добавление отрицательных чисел

Если перед числом вы не видите отрицательный или положительный знак, это положительный знак.

При сложении чисел одного знака (положительного или отрицательного) сложите их абсолютные значения и дайте результату тот же знак.

6 + 5 = 11 (6 и 5 положительны; 6 + 5 равно 11, что положительно)

-7 + -8 = -15

(-7 и -8 оба отрицательны; сложите | 7 | + | 8 |, что равно 7 + 8, чтобы получить 15; ответ -15)

Если все числа в добавляемой группе отрицательные: -2 + -3 + -4 = -9, снова сложите абсолютные значения 2 + 3 + 4, чтобы получить 9 и поставить отрицательный знак.

Сложение положительных и отрицательных чисел

При сложении чисел с противоположным знаком возьмите их абсолютные значения, вычтите меньшее из большего и присвойте результату знак числа с большим абсолютным значением.

7 + -3 = | 7 | — | 3 | = 4

-8 + 6 = | 8 | что равно 8 и | 6 | что составляет 6. Вычтите меньшее из большего:

8-6, что дает результат 2 и дает ему знак большего числа, равного 8.

Ответ — -2.

Вычитание положительных и отрицательных чисел

При вычитании положительного числа из отрицательного используйте то же правило, что и для сложения двух отрицательных чисел: сложите абсолютные значения и присвойте разнице отрицательный знак.

-5 — 4 = | 5 | + | 4 | = | 9 | = -9 (это как -5 + -4 = -9)

-2 — 12 = | 2 | + | 12 | = | 14 | = -14

При вычитании отрицательного числа из положительного, двойной отрицательный результат вычитания отрицательного становится положительным, поэтому используйте то же правило, что и для сложения двух положительных чисел: сложите абсолютные значения и присвойте разнице положительный знак.

5 — -4 = | 5 | + | 4 | = 5 + 4 = 9

Если бы вы использовали числовую строку, вы бы пошли влево для вычитания, а затем перевернули (вправо) для отрицательного числа, так что окончательный ответ будет справа от исходного числа.

16 — -10 = | 16 | + | 10 | = 16 + 10 = 26

Аддитивное обратное число — это число с противоположным знаком, так что при сложении двух результат равен нулю.

а + (-а) = 0

Как видите, это положительные и отрицательные числа одного и того же абсолютного значения.

10 + -10 = 0

-24 + 24 = 0

Умножение положительных и отрицательных чисел

При умножении положительного числа и отрицательного числа (или отрицательного числа на положительное число) умножьте абсолютные значения и дайте ответ отрицательный знак.

8 х -5 = | 8 | х | 5 | = 8 x 5 = 40, но дайте ему отрицательный знак, сделав -40

-13 x 3 = -39

9 х -3 = -27

Чтобы умножить несколько чисел, посчитайте количество отрицательных знаков в числах, которые нужно умножить.Если это четное число, произведение будет положительным, а если нечетное, произведение будет отрицательным.

6 х -2 х -3 х 5 = | 6 | х | 2 | х | 3 | х | 5 |

6 x 2 = 12, 12 x 3 = 36 и 36 x 5 = 180

Имеется два отрицательных знака (четное число), поэтому ответ положительный.

Если бы было -6 x -2 x -3 x 5, ответ был бы -180

Умножение двух отрицательных чисел

При умножении двух отрицательных чисел два отрицательных числа компенсируют друг друга, поэтому умножьте абсолютные значения и дайте ответ положительный знак.

-21 х -3 = | 21 | х | 3 | = 63 (остается положительным)

-7 x -8 = | 7 | х | 8 | = 56

Деление отрицательного числа на отрицательное

Чтобы разделить два числа с одинаковым знаком (два положительных или два отрицательных), используйте абсолютные значения, и результат будет положительным.

16 ¸ 4 = | 16 | ¸ | 4 | = 4

-20 ¸ -10 = | 20 | ¸ | 10 | = 2

Деление положительного числа на отрицательное или отрицательного числа на положительное

Чтобы разделить пару чисел с разными знаками (отрицательное на положительное или положительное на отрицательное), используйте абсолютные значения двух чисел и присвойте результату отрицательный знак.

-12 ¸ 3 = | 12 | ¸ | 3 | = 4, но это -4

18 ¸ -3 = | 18 | ¸ | 3 | = 6, но это -6

Использование отрицательных чисел

Отрицательные числа используются для обозначения низких температур. Цифры ниже 0 ° C отрицательны и ниже точки замерзания. (Помните, что значения ниже 32 ° F ниже точки замерзания, но температура часто опускается ниже 0 ° F.)

Отрицательные числа используются для отображения измерений ниже уровня моря.Уровень моря равен 0.

Отрицательные числа используются с деньгами, чтобы показать задолженность или денежную задолженность. Если человек или домохозяйство тратят больше денег, чем зарабатывают, мы говорим, что они «отрицательные на определенную сумму», или называем это «красным», потому что бухгалтеры используют красные чернила для отображения отрицательных чисел.

Больше и меньше и наборы чисел

Набор чисел — это группа чисел, которая соответствует заданному описанию.Например, набор целых чисел меньше 0 будет выражен как n Все целые числа больше 0 будут выражены как n> 0. Набор чисел, удовлетворяющий этим условиям, будет набором всех положительных целых чисел. Каждое из этих целых чисел будет называться членом или элементом этого набора.

Какие целые числа от 3 до 8? Это будет 4, 5, 6 и 7.Другой способ выразить это — набор чисел больше 3, но меньше 8, которые можно представить в виде математического предложения, которое выглядит так:

Прочтите это: n такое, что n больше 3 и меньше 8

Поскольку 3

И n

п = 4, 5, 6, 7

Мы могли бы сказать 3 n Часто эти ответы «больше» и «меньше» необходимо выражать с помощью числовой строки, потому что было бы невозможно перечислить все числа для ответа.

Умножение и деление чисел с разными знаками, отрицательных и положительных чисел в 2023 году

Умножение целых чисел

Правило умножения целых чисел звучит так:

Чтобы умножить целые числа, нужно перемножить их абсолютные величины и перед результатом поставить знак плюс, если оба сомножителя имеют одинаковые знаки или минус, если сомножители имеют разные знаки.

Например,

-4 ⋅ 5 = — (|-4|⋅|5|) = — (4 ⋅ 5) = -20

-4 ⋅ (-5) = |-4|⋅|-5|= 4 ⋅ 5 = 20

4 ⋅ 5 = |4|⋅|5|= 4 ⋅ 5 = 20

4 ⋅ (-5) = — (|4|⋅|-5|) = — (4 ⋅ 5) = -20

Умножение чисел с разными знаками

Чтобы умножить числа с разными знаками, нужно перемножить модули множителей и перед произведением поставить знак минус.

Например, 8 ⋅ (-7) = — (|8|⋅|-7|) = — (8 ⋅ 7) = -56

Как умножать отрицательные числа?

Чтобы умножить отрицательные числа, нужно перемножить их модули и перед произведением поставить знак плюс.

Например, -9 ⋅ (-10) = |-9|⋅|-10|= 9 ⋅ 10 = 90

Как умножать положительные числа?

О разных методах и правилах умножения натуральных чисел читайте в нашем уроке: Умножение натуральных чисел. Умножение в столбик. Законы, правила и примеры

Умножение нескольких целых чисел

Как определить знак произведения, если множителей больше двух и они имеют разные знаки? Для нахождения произведения нескольких множителей целых чисел нужно перемножить модули множителей и перед результатом поставить знак:

– если количество отрицательных сомножителей четное число, то произведение будет положительным, перед результатом ставим знак «+»;

– если количество отрицательных сомножителей нечетное число, то произведение будет отрицательным, перед результатом ставим знак «-»;

Пример. Найти произведение: -5 ⋅ 2 ⋅3 ⋅ (-4) ⋅ (-10)

-5 ⋅ 2 ⋅3 ⋅ (-4) ⋅ (-20) = — 2400

Объяснение: вычислили произведение абсолютных величин множителей, перед произведением ставим знак минус, ведь количество отрицательных сомножителей составляет 3, нечетное число

Пример. Найти произведение: 8 ⋅ 4 ⋅ (-2) ⋅ (-10) ⋅ 6

8 ⋅ 4 ⋅ (-2) ⋅ (-10) ⋅ 6 = 3840

Объяснение: выполнили умножение абсолютных величин множителей, перед произведением ставим плюс или ничего не ставим, поскольку количество отрицательных сомножителей равно 2 — четное число

Свойства умножения целых чисел: переместительный, сочетательный, распределительный законы

Для умножения целых чисел характерными являются переместительный, сочетательный, распределительный законы:

Переставное свойство: от перестановки множителей местами произведение не изменится. Для любых целых чисел выполняется равенство:

Проверим на примере:

-3 ⋅ (-9) = (-9) ⋅ (-3)

Ведь -3 ⋅ (-9) = 27 і (-9) ⋅ (-3) = 27

Сочетательное свойство:

Где a, b, c – любые целые числа

[–8 ⋅ (–3)] ⋅ 2 = 24 ⋅ 2 = 48

–8 × (–3 × 2) = -8 ⋅ (-6) = 48

Поэтому [–8 ⋅ (–3)] ⋅ 2 = –8 × (–3 × 2)

Распределительное свойство:

Для любых целых чисел a, b, c выполняется равенство:

Проверим распределительное свойство умножения целых чисел на примере:

(–5 + 9) ⋅ (–7) = 4 ⋅ (-7) = -28

(–5 + 9) ⋅ (–7) =- 5 ⋅ (-7) + 9 ⋅ (-7) = 35 – 63 = -28

Итак, (–5 + 9) ⋅ (–7) =- 5 ⋅ (-7) + 9 ⋅ (-7)

Умножение целых чисел на 0, 1 и -1

а ⋅ 0 = 0 , где а – любое целое число

Произведение целых чисел, хотя бы один множитель которых равен 0, равно нулю.

Для любых целых чисел выполняются следующие равенства:

Деление целых чисел

Деление двух отрицательных целых чисел и двух чисел с разными знаками имеет то же содержание, что и деление положительных чисел: по данному произведению и одному из множителей посредством деления определяют второй множитель.

Если (-4) ⋅ 6 = -24, то (-24) : (-4) = 6 и (-24) : 6 = -4

Рассмотрим подробнее равенство (-24) : (-4) = 6 – в ней делимое равно -24, делитель равен -4 и частное от деления равно 6

Найдем абсолютные величины каждого компонента:

|-24| = |24|, |-4| = |4|, |6|= |6|

Можно сделать вывод, что для нахождения модуля частного нужно поделить модуль делимого на модуль делителя. Если делимое и делитель являются отрицательными числами, то частное будет положительным числом.

Как правильно делить отрицательные числа?

Чтобы найти частное двух отрицательных целых чисел, нужно поделить модули этих чисел. Частное будет положительным числом.

Как правильно делить числа с разными знаками?

Чтобы разделить числа с разными знаками, нужно модуль делимого разделить на модуль делителя и перед результатом поставить знак минус.

–18 : 6 = –(|–18| : |6|) = – (18 : 6) = -3

Деление целых чисел, если делимое или делитель равно 0 или 1

а – любое целое число, но в первом и третьем равенствах а≠ 0.

Ведь целые числа на 0 делить нельзя.

Умножение отрицательных дробей — видео и расшифровка урока

Математические курсы / Алгебра для детей Курс / Работа с дробями для начальной школы Глава

Инструктор: Нола Бридженс Показать биографию

Нола преподавала в начальной школе и занималась репетиторством в течение четырех лет. Она имеет степень бакалавра в области начального образования, степень магистра в области маркетинга и является сертифицированным учителем.

Процесс умножения дробей можно разбить на четыре простых шага. Узнайте, как реализовать эти шаги и важные вещи, которые следует помнить при умножении отрицательных дробей. Обновлено: 22.12.2021

Хотя умножение отрицательных дробей может дать отрицательный оттенок, на самом деле это довольно просто и может часто пригодиться. Давайте научимся умножать отрицательные дроби. Я уверен, что нам будет весело.

Если вы будете обращать внимание на знаки перемножаемых дробей и следовать этим правилам, то сможете быстро умножать отрицательные дроби, как профессионал!

Если обе дроби имеют одинаковых знаков , либо обе положительные, либо обе отрицательные, ответ будет положительным.

Если обе дроби имеют различных знаков , один положительный и один отрицательный, то ответ будет отрицательным.

Мы рассмотрим примеры этих правил в следующих разделах.

Произошла ошибка при загрузке этого видео.

Попробуйте обновить страницу или обратитесь в службу поддержки.

Вы должны cСоздать учетную запись, чтобы продолжить просмотр

Зарегистрируйтесь, чтобы просмотреть этот урок

Вы студент или преподаватель?

Создайте свою учетную запись, чтобы продолжить просмотр

Как участник вы также получите неограниченный доступ к уроки математики, английского языка, науки, истории и многое другое. Кроме того, получите практические тесты, викторины и индивидуальное обучение, которые помогут вам преуспевать.

Получите неограниченный доступ к более чем 88 000 уроков.

Попробуй это сейчас

Настройка занимает всего несколько минут, и вы можете отменить ее в любое время.

Уже зарегистрированы? Войдите здесь для доступ

Ресурсы, созданные учителями для учителей

Более 30 000 видеоуроков и учебные ресурсы‐все в одном месте.

Видеоуроки

Тесты и рабочие листы

Интеграция в классе

Планы уроков

Я определенно рекомендую Study.com своим коллегам. Это как учитель взмахнул волшебной палочкой и сделал работу за меня. Я чувствую, что это спасательный круг.

Дженнифер Б.

Учитель

Попробуй это сейчас

Далее: Проценты: урок для детей

пройти викторину Смотреть Следующий урок

Повтор

Просто отмечаюсь. Вы все еще смотрите?

Да! Продолжай играть.

Ваш следующий урок будет играть в 10 секунд

0:00 Все дело в знаке
0:46 Умножение отрицательных дробей
1:30 Давайте потренируемся
3:11 Итоги урока

Сохранить
Хронология
Автовоспроизведение
Автовоспроизведение
Скорость
Скорость
Умножение отрицательных дробей
Вот четыре шага для умножения отрицательных дробей. Давайте используем следующую задачу, чтобы проиллюстрировать шаги.
Помните, что числителей — это числа над чертой в дроби, а знаменателя — это числа под чертой в дробях.
Помните, целое число можно превратить в дробь, просто поместив целое число над 1. Например, целое число 7 становится 7/1.
Давайте попрактикуемся
Давайте попробуем вместе. Найдем произведение -2/7 * 3/4
Шаг 1) При умножении числителей (2 * 3) ответ равен 6.
Шаг 2) При умножении знаменателей (7 * 4) ответ 28.
Шаг 3) Новая дробь 6/28. Оба числа делятся на 2 и могут быть упрощены до 3/14.
Шаг 4) Дроби имеют разные знаки, так как одна положительная, а другая отрицательная, поэтому ответ отрицательный.
Произведение -2/7 * 3/4 = -3/14.
Попробуем еще парочку. Не стесняйтесь взять лист бумаги и карандаш и решить следующие задачи самостоятельно, прежде чем искать решение.
Решите: -3/4 * 2/3
Шаг 1) Умножьте числители: 3 * 2 = 6
Шаг 2) Умножьте знаменатели: 4 * 3 = 12
Шаг 3) Упростите 6/12 ( оба делятся на 6) до 1/2
Шаг 4) Знаки разные, поэтому ответ отрицательный.
Ответ: -1/2.
Решите: -1/2 * 3/4
Шаг 1) Умножьте числители: 1 * 3 = 3
Шаг 2) Умножьте знаменатели: 2 * 4 = 8
Шаг 3) 3/8 уже в простейшей форме
Шаг 4) Знаки разные, поэтому ответ отрицательный.
Значит -1/2 * 3/4 = -3/8.
Краткое содержание урока
При умножении дробей помните, что если дроби имеют одинаковые знаки, ответ положительный, а если дроби имеют разные знаки, ответ отрицательный. Также помните, что умножение отрицательных дробей состоит из четырех простых шагов, и в этом, безусловно, есть что-то положительное!
Чтобы разблокировать этот урок, вы должны быть участником Study. com.
Создайте свою учетную запись
Зарегистрируйтесь для просмотра этого урока
Вы студент или преподаватель?
Разблокируйте свое образование
Убедитесь сами, почему 30 миллионов человек используют Study.com
Станьте участником Study.com и начните учиться прямо сейчас.
Стать участником
Уже зарегистрированы? Войти
Назад
Ресурсы, созданные учителями для учителей
Более 30 000 видеоуроков и учебные ресурсы‐все в одном месте.
Видеоуроки
Тесты и рабочие листы
Интеграция в классе
Планы уроков
Я определенно рекомендую Study.com своим коллегам. Это как учитель взмахнул волшебной палочкой и сделал работу за меня. Я чувствую, что это спасательный круг.
Дженнифер Б.
Учитель
Попробуй это сейчас
Спинка
Я настоятельно рекомендую вам использовать этот сайт! Это помогло мне сдать экзамен, а вопросы теста очень похожи на практические тесты на Study. com. Этот сайт помог мне пройти!
рабочих листов | TPT
by
My Teaching Pal
22,00 $
15,00 $
Bundle
Этот комплект содержит 263 ОГРОМНЫХ математических листа для первого класса! Рабочие листы охватывают сложение и вычитание, числа и разрядность, 2D и 3D фигуры, данные и графики, дроби и разбиение на части и время. Эти веселые рабочие листы отлично подходят для использования в течение всего года, они идеально подходят для занятий в классе, математических станций, быстрых финишеров, домашних заданий и повторения. Этот комплект состоит из следующих пакетов: Рабочие листы для сложения и вычитания для первого классаРабочие листы для первого класса 2D и 3D
Предметы:
Базовые операции, математика, числа
Классы:
Типы:
Печатные формы, рабочие тетради, рабочие листы ваши ученики тренируются в чтении коротких гласных слов CVC! Эти отрывки для чтения в детском саду помогают вашим ученикам развить уверенность в чтении, помогая им развить прочные базовые навыки. Идеальные отрывки для чтения, чтобы дополнить любую программу чтения. ♥ СОБЕРИТЕ И СОХРАНИТЕ ♥Возьмите комплект для беглости чтения, чтобы попрактиковаться в чтении коротких гласных слов, сочетаний и диграфов, а также длинных гласных слов. Это NO PREP, PRINT & GO readi
субъекты:
Английский языковой искусство, стратегии чтения
Оценки:
K — 1 -е
Типы:
Центры
Также включены в: вмешательство в небольшую группу Mega Bundle
. $14.00
Используйте эти уроки, чтобы развить навыки самоконтроля у детей! Действия сосредоточены на понимании самоконтроля, импульсивного контроля, остановке и обдумывании, чтобы принять решение, ожидании своей очереди, соблюдении правил и указаний, сохранении мотивации, выполнении нашей работы наилучшим образом, управлении эмоциями, использовании стратегий преодоления и практике самоконтроля для укрепления. навыки со временем. Также рассматриваются другие навыки, влияющие на самоконтроль, включая планирование, управление временем и настойчивость. Цифровая версия обновлена до 9.0003
Тема:
Школьное консультирование, социальное эмоциональное обучение, специальное образование
Оценки:
4 -й — 8 -е
Типы:
Урок, печатные изготовления
на
Lucky Littge.
Отрывки для чтения фонетики, или Phonics Mats, являются идеальным ресурсом без подготовки, распечатайте и идите, чтобы помочь учащимся превратить отдельные фонетические навыки в чтение текста! Учащиеся практикуют изолированные фонетические навыки, декодирование, беглость речи и понимание в одном ресурсе. *** НОВОЕ ОБНОВЛЕНИЕ *** Этот ресурс обновлен новой версией 2022 года! В новых ковриках для фонетики есть декодируемые отрывки, вопросы на понимание, практика написания слов и страница для разминки для каждого навыка. Обязательно загрузите превью
Предметы:
Акустика, чтение, письмо
Классы:
Типы:
Печатные формы, рабочие листы
CCSS:
RF. 2.3, RF.2.3c, RF.2.2.2.2 .2.3d…
by
Kaitlynn Albani
Внутри вы найдете 6 забавных и уникальных шрифтов в ZIP-файле! Большинство акцентных символов включены во все шрифты. Пожалуйста, проверьте предварительный просмотр, чтобы увидеть все шрифты, включенные в этот набор! Примечания. Включено 5 шрифтов + 1 шрифт для каракулей. Все шрифты с заглавными буквами Elementary. Проверьте предварительный просмотр, чтобы увидеть все шрифты в действии! $ СЭКОНОМЬТЕ ДЕНЬГИ $ БОЛЕЕ 400 ШРИФТОВ + КАЖДЫЙ НОВЫЙ ШРИФТ БЕСПЛАТНО! ПРОВЕРЬТЕ РАСШИРЯЮЩИЙСЯ НАБОР ШРИФТОВ ЗДЕСЬУсловия использования * Шрифты
Предметы:
Для всех предметов, Товары для продавцов ТРТ, Специальность
Классы:
PreK — 12th, Высшее образование, Обучение взрослых, Персонал by
Pocket of Preschool
Журналы мелкой моторики — это увлекательный способ обучения навыкам письма, основам письма и укреплению мелкой моторики. В дневнике так много упражнений на мелкую моторику! Это похоже на мини-портфолио всех их мелкой моторики, все организовано и собрано в одном месте, что позволяет легко визуально увидеть рост ученика. Вот некоторые действия, которые можно выполнять в дневниках мелкой моторики: написание типов строк/букв (также известный как забавный почерк), действия с именами, действия с буквами, действия с числами, печать ac
субъекты:
Английский язык искусства
Оценки:
Prek — K
Типы:
Действия
также включены в: Preschool, Pre -K и Cindergarten Complet Коннор
Есть ли в вашем классе учащиеся, нуждающиеся в дополнительной поддержке поведения? Вы тратите драгоценное учебное время, постоянно перенаправляя нескольких трудных учеников, и не знаете, что делать, чтобы поддержать их? Этот пакет ПОЛЕН ресурсов, идей и инструментов, которые помогут каждому учащемуся в вашем классе добиться успеха. Этот ресурс идеально подходит для любого учителя начальных классов, которому нужны дополнительные ресурсы по поведению для поддержки учеников в своем классе! Работая ВМЕСТЕ со студентом, вы сможете создать сильные
Предметы:
Classroom Community, Управление в классе, школьное консультирование
Оценки:
K — 2 -й
Типы:
Формы классной комнаты, печатные изделия
. пакет из 123 центров обучения грамоте первого и второго класса обеспечивает идеальный способ обеспечить увлекательную, дифференцированную практику ELA в течение всего года. Каждый центр имеет аналогичный формат, что делает его идеальным для самостоятельной практики, оставляя вам больше времени для обучения с меньшим количеством перерывов!Отлично для центровых или быстрых финишеров, с этим пакетом вы сможете легко дифференцировать потребности всех ваших учеников с огромным выбором игр на выбор.Каждое общее ядро соответствует
Предметы:
Английский язык, акустика, правописание
Классы:
1-2
CCSS:
RF.1.1a, RF.1.2, RF.1.2a, RF.1.2b, RF.1.2b, RF.1.2b, RF.1.2b, RF.1.2b c…
by
Кейтлин Олбани
Внутри вы найдете 60 отрывков для понимания детского сада! Эти отрывки отлично подходят для детей младшего возраста, а также подойдут для первоклассников или первоклассников, в зависимости от того, как вы их используете. В комплекте много разнообразия. Пожалуйста, проверьте изображения и просмотрите, чтобы увидеть, подойдут ли эти отрывки для ваших учеников. Отрывки разбиты на три категории… Первые 20 отрывков: Основная история с 3 вопросами. Студентам дается два ответа на выбор на каждый вопрос. Вторые 20 отрывков: Базовый
субъекты:
Английский язык искусства, чтение, стратегии чтения
Оценки:
K — 1st
Типы:
Центры, печатные изготовления, рабочие листы
на
Особенно образование
Если вы ищете индивидуальное. книга расписаний, наглядные расписания или сначала доска, в этом ресурсе поддержки позитивного поведения есть все! Обратите внимание: все редактируемые файлы совместимы с Microsoft PowerPoint. Некоторые страницы теперь можно редактировать с помощью Google Slides. В эту загрузку включены: — Варианты флипбука с 6 и 2 вкладками — Более 200 визуальных значков расписания (они не редактируются) — Сначала доска (отдельно от флипбука) — Сначала затем доска (отдельно от флипбука) — доски жетонов (wi
Предметы:
Снова в школу, Специальное образование, Логопедия
Классы:
PreK — 2-й
Типы:
Расписание занятий
Также включено в: НАБОР: First Book Then Boards & Visual реальные фотографии)
на
Ничего, кроме класса
15,75 $
Это новое исследование Луи Сашара «Дыры» содержит 124 страницы ресурсов, включая понимание и словарный запас по главам, задания по чтению ответов, оценки и многое другое. Стандарты фокусировки включают образный язык, тему, анализ персонажей, сюжет и написание мнений. Не требующее подготовки, предсказуемое и чрезвычайно удобное для пользователя, это руководство по литературе идеально подходит для всего класса, небольшой группы или самостоятельного изучения. ♥Вы можете использовать печатную или цифровую версию; ОБА входят в комплект поставки Pur 9.0003
субъекты:
Английский язык искусства, литература, чтение
Оценки:
3 -й — 6th
Типы:
Литературные круги, печатные изготовления
CCS:
RL.3.2, RL.3.3, RL. RL.3.6, RL.3.7…
Также включено в: Holes and The Lion, the Witch, and the Платяной шкаф | Novel Study Bundle
by
Ashleigh
Эти брошюры с фактами об умножении можно использовать, чтобы помочь учащимся понять концепцию умножения, а также запомнить факты умножения. Кроме того, их можно использовать при дистанционном обучении, так как в дополнение к версии в формате PDF есть цифровая версия! Всего имеется одиннадцать буклетов (2 факта — 12 фактов), каждый из которых состоит из восьми страниц. В конце каждого буклета есть две страницы, которые можно вырезать и использовать в качестве карточек. На каждой странице учащиеся будут: представлять выражение умножения
Субъекты:
Алгебра, базовые операции
Оценки:
2 -е — 4 -е
Типы:
Действия, печатные изготовления
CCSS:
3.OA.A.1, 3.OA.C.7
Также включено в: Набор фактов умножения
by
Deedee Wills
10,00 $
Практика рукописного ввода и инструкции здесь! Умение свободно писать буквы приводит к большим успехам в чтении. Исследования мозга подтверждают необходимость четкого почерка и инструкций по движению и связывают правильный почерк с лучшими письменными результатами учащихся! Быстро, лаконично, легко реализовать! Моя своеобразная инструкция по письму. УРОКИ ПОЧЕРКОПИСАНИЯ — ЭТО НЕ ТОЛЬКО ЕЩЕ ОДНА ВЕЩЬ! Когда вы обучаете учащихся письму во время обучения фонетике, у учащихся развивается кинестетическая мышечная память на все
Subjects:
Balanced Literacy, English Language Arts, Handwriting
Grades:
PreK — 1st
Types:
Activities, Printables
CCSS:
L. K.1a
by
Simply Kinder
$42.00
16,00 $
Редактируемая практика по отслеживанию имен❤️ Помогите своим ученикам выучить свои имена с помощью этого забавного редактируемого комплекта печатных форм. Легко запрограммируйте весь класс на создание пользовательских страниц для каждого из ваших учеников. ОБНОВЛЕНИЕ. Этот пакет был обновлен и теперь включает диаграмму классов для каждого набора редактируемых именных ресурсов, чтобы упростить вставку имен и их заполнение! Назовите свои классы на первой странице каждого набора a
Предметы:
Снова в школу, Английский язык, Письмо
Классы:
PreK — 1st
Типы:
Занятия, распечатки, рабочие листы
CCSS, RFKb, RFKb, RFKb, RFKb, 9.0029.00023 .3, RF.K.3c
на
Lucky Little Learners
Этот набор страниц для рукописного ввода дает вашим учащимся навыки письма в увлекательной форме. Они будут развивать выносливость при письме, повторять построение букв и цифр и практиковаться в словах, изучая новые шутки и забавные факты! и почерк, который не является «детским»? Глупые шутки и забавные факты привлекут ваших учеников, пока они
субъекты:
Сбалансированная грамотность, почерк, написание
. идеально подходит для того, чтобы помочь учащимся детского сада и первоклассникам осознать числа от 0 до 20. Учащиеся практикуются в упорядочивании чисел, сравнении чисел, построении чисел и выявлении различных способов составления чисел от 0 до 20. Что такое чувство числа? Чувство числа — это способность идентифицировать числа и осмысливать их. Мы хотим, чтобы наши ученики с раннего возраста могли определять различные величины и понимать, что означают эти цифры. В этом блоке студенты f
Предметы:
Математика, Цифры
Классы:
PreK — 1st
Типы:
Занятия, игры, распечатки
CCSS:
, KCCB.5.A.5.A.3 K. , K. NBT.A.1, 1.NBT.A.1
by
Games 4 Learning
Эта коллекция игр для печати содержит 35 игр, которые рассматривают умножение до 12 x 12. Это интересный способ помочь учащиеся развивают беглость фактов. Это игры PRINT and PLAY. Они НЕ требуют ПОДГОТОВКИ. Просто распечатайте и раздайте. Каждая игра требует определенного навыка умножения. Они разработаны, чтобы заставить студентов применять свои факты, а также заставить их думать. ПРАКТИКУЙТЕСЬ, А ТОГДА ИГРАЙТЕ: Каждая игра в этом наборе теперь имеет соответствующее задание в БЕЗ ПОДГОТОВКИ Упражнения на умножение.0003
Субъекты:
Основные операции, математика, ментальная математика
Оценки:
2 -е — 4 -е
Типы:
Центры, игры
CCS:
3.OA.C.7
Также включены в::
3.OA.C. Умножение с заданиями, играми и занятиями Умножение Факт Беглость
на
Peachie Speechie
39,00 $
Этот систематический, пошаговый подход к R-терапии — все, что вам нужно для обучения самым угрожающим звукам! Узнайте, почему он получил более 1300 5-звездочных отзывов! Эта тетрадь MUST HAVE у каждого логопеда! Профессиональные иллюстрации учат студентов анатомии рта, а подробные пошаговые изображения помогают врачу и студенту использовать различные методы для получения точных результатов. Вовлекающие действия включены для практики в изоляции, слоги, слова,
Предметы:
Специальное образование, логопедия
Классы:
1–6
Типы:
Занятия, рабочие тетради, рабочие листы
by
Games 4 Gains
30,10 $
25,95 $
Bundle
Мотивируйте своих учеников с помощью этих математических игр NO-PREP для 3-го класса! Этот огромный набор включает 77 увлекательных игр, которые идеально подходят для повторения математики в 3-м классе в течение всего учебного года. Ваши ученики ПОЛЮБЯТ уроки математики, когда вы достанете эти математические игры для практики! Эти математические центры содержат не требующие подготовки игры, которые можно распечатать и играть, чтобы поддерживать стандарты Common Core 3-го класса в следующих ключевых областях: операции, разрядное значение, дроби, измерения и геометрия. Наблюдайте, как ваши ученики погружаются в себя
Subjects:
Fractions, Math Test Prep, Place Value
Grades:
Types:
Centers, Games
by
Sight Word Activities
$22. 00
$12.50
Bundle
All the sight word рабочие листы, которые вам когда-либо понадобятся! Этот продукт представляет собой набор из 4 моих самых продаваемых рабочих листов, включая 3 редактируемых набора рабочих листов. Каждый из этих 4 продуктов содержит 220 готовых рабочих листов со словами. Это означает, что вы получаете 880 рабочих листов в этой загрузке! Три из этих рабочих листов доступны для редактирования, так что вы можете создавать рабочие листы для любого слова! Нажмите на кнопку предварительного просмотра, чтобы увидеть каждый из 4 рабочих листов крупным планом. Используйте эти страницы в качестве утренней работы, ежедневной практики в вашем центре грамотности
Субъекты:
Английский язык искусства, орфография
Оценки:
K — 3 -й
Типы:
Центры, рабочие листы
на
Симпа учебники для словесной практики, игры, раскраска по коду и многое другое для более чем 200 высокочастотных слов! ЛУЧШИЙ ПРОДАВЕЦ на TpT с более чем 7000 отзывов учителей! Оцените эту невероятную ценность всего, что вам нужно для практики словесного зрения! Ваша практика словесного зрения стала намного лучше благодаря этому огромному файлу печатных форм, занятий, центров и многого другого. Каждое включенное прицельное слово имеет отдельный файл с 67 страницами действий! Идеально подходит для детского сада, первого класса
Предметы:
Английский язык, чтение
Классы:
PreK — 1st
Типы:
Занятия, распечатки, рабочие листы
CCSS, RF.3.9002. .K.3c
by
Учитель по соседству
18,00 $
14,25 $
Bundle
Ищете способ сделать обучение написанию абзацев намного проще? Хотите помочь своим ученикам писать хорошо продуманные абзацы? Этот полный набор для написания абзацев как в печатном, так и в цифровом виде поможет вам научить каждую часть абзаца напрямую! Он сочетает в себе четыре из моих очень популярных наборов стратегий письма: цветовое кодирование и выделение абзацев, тематические предложения, переходы в письме и заключительные предложения. Здесь есть все, что вам нужно, чтобы помочь вашим ученикам по-настоящему понять, как создавать
Предметы:
Английская словесность, информационный текст, письменное объяснение
Классы:
3-8
Типы:
Графические органайзеры, плакаты
CCSS:
2, W.
3.3003, W.30003 .5.2, W.5.2a, W.5.2b…
by
Речевые размышления
$15.00
Целевая перспектива, делающая выводы и прогнозы с использованием реальных изображений с помощью этого ресурса! Этот ресурс включает 100 карточек с реальными изображениями, которые позволяют вам обеспечить эффективное, прямое обучение тому, как делать выводы из сцен с картинками. Каждая карточка включает в себя визуальный элемент в верхней части, на котором показаны «Посмотрите», «Думайте», «Вывод», «Предскажите». Стратегия (вместе с начальными предложениями для студентов, чтобы обеспечить дополнительную поддержку). Рядом с фотографией есть четыре вопроса, которые требуют от ваших учеников
субъекты:
Школьное консультирование, специальное образование, речевая терапия
Оценки:
K — 6th
Типы:
Действия, печатные изготовления
также включены в: Real Pictures Resource Bundle для речевой терапии
Patricia Pat Resources
Трудно ли вашим ученикам писать полные предложения или структуру предложений? Если это так, вам понравится, как эти рабочие листы для построения предложений помогут вам научить писать полные предложения. ✏️ Многочисленные изображения в рабочем листе помогут вашим ученикам ПОНЯТЬ и ЗАПОМНИТЬ правильную структуру предложения. ✏️ Это ресурс без подготовки, который понравится даже неохотным писателям, плюс вы сэкономите много времени с помощью ТРЕХ дифференциаций и строительных лесов, сделанных за вас. ✏️ Эти практические рабочие листы будут
Предметы:
EFL — ESL — ELD, английский язык, специальное образование
Классы:
K — 2nd
Типы:
Центры, Домашнее обучение, Домашнее задание
9.1002 CCSS3: SL.1.6, L.K.1f, L.1.1c, L.1.2b
Также включено в: Центр написания предложений | Полные предложения | Структура предложения | Небольшие группы
Умножение и деление действительных чисел
Результаты обучения
Умножение и деление действительных чисел
Умножение двух или более действительных чисел.
Разделить действительные числа
Упростите выражения с помощью умножения и деления
Умножение и деление являются обратными операциями , так же как сложение и вычитание. Вы, наверное, помните, что при делении дроби вы умножаете на обратную. Обратные операции «отменяют» друг друга.
Умножение действительных чисел
Умножение действительных чисел ничем не отличается от умножения целых чисел и положительных дробей. Однако вы не узнали, какое влияние оказывает отрицательный знак на продукт.
Умножение целых чисел можно представить как многократное сложение. Используя числовую линию, вы можете сделать несколько прыжков заданного размера. Например, на следующем рисунке показан продукт [latex]3\cdot4[/latex] в виде скачков [latex]3[/latex] по [latex]4[/latex] единиц каждый.
Итак, чтобы умножить [латекс]3(−4)[/латекс], вы можете повернуться налево (в отрицательную сторону) и сделать три «прыжка» вперед (в отрицательном направлении).
Произведение положительного числа и отрицательного числа (или отрицательного и положительного) отрицательно.
Произведение положительного числа на отрицательное число
Чтобы умножить положительное число на отрицательное число , умножьте их абсолютные значения. Продукт отрицательный .
Попробуйте
Следующее видео содержит примеры умножения десятичных чисел с разными знаками.

Произведение двух чисел с одинаковым знаком (как положительных, так и отрицательных)
Чтобы умножить два положительных числа , умножьте их абсолютные значения. Продукт положительный .
Чтобы умножить два отрицательных числа , умножьте их абсолютные значения. Продукт положительный .
В следующем видео показаны примеры умножения двух дробей со знаком, включая упрощение ответа.

Подведем итоги:
положительный [латекс]\cdot[/латекс] положительный : Продукт положительный .
отрицательный [латекс]\cdot[/латекс] отрицательный : Продукт положительный .
отрицательный [латекс]\cdot[/латекс] положительный : Произведение отрицательный .
положительный [латекс]\cdot[/латекс] отрицательный : Продукт отрицательный .
Вы можете видеть, что произведение двух отрицательных чисел является положительным числом. Итак, если вы умножаете более двух чисел, вы можете подсчитать количество отрицательных множителей.
Умножение более двух отрицательных чисел
Если есть четное число ([latex]0, 2, 4[/latex], …) отрицательных множителей, которые нужно умножить, произведение положительное .
Если имеется нечетное число ([латекс]1, 3, 5[/латекс], …) отрицательных множителей, произведение равно отрицательному .
Следующее видео содержит примеры умножения более чем двух целых чисел со знаком.

Деление действительных чисел
Возможно, вы помните, что при делении дробей вы умножали на взаимное . Обратное — это другое название мультипликативной инверсии (так же, как напротив — это другое название аддитивной инверсии).
Самый простой способ найти обратное мультипликативное число — просто «перевернуть» числитель и знаменатель, как вы это сделали, чтобы найти обратное. Вот несколько примеров:
Обратная величина [латекс]\frac{4}{9}[/latex] равна [латекс] \frac{9}{4}[/latex], потому что [латекс]\frac{4 {9}\left(\frac{9}{4}\right)=\frac{36}{36}=1[/latex].
Обратная величина [латекс]3[/латекс] равна [латекс]\фракция{1}{3}[/латекс], потому что [латекс]\фракция{3}{1}\левый(\фракция{1}{3 }\right)=\frac{3}{3}=1[/latex].
Обратная величина [латекс]-\frac{5}{6}[/latex] равна [латекс]\frac{-6}{5}[/latex], потому что [латекс]-\frac{5}{6} \left( -\frac{6}{5} \right)=\frac{30}{30}=1[/latex].
Обратная величина [латекс]1[/латекс] равна [латекс]1[/латекс], поскольку [латекс]1(1)=1[/латекс].
Когда вы делили на положительные дроби, вы научились умножать на обратную. Вы также делаете это, чтобы разделить действительные числа .
Подумайте о том, чтобы разделить мешок с [латексом]26[/латексом] шариков на два меньших мешка с одинаковым количеством шариков в каждом. Вы также можете сказать, что в каждом меньшем мешочке и половина шариков.
[латекс] 26\div 2=26\left( \frac{1}{2} \right)=13[/latex]
Обратите внимание, что [latex]2[/latex] и [latex] \frac{ 1}{2}[/latex] являются обратными.
Попробуйте еще раз, разделив мешок с [латексом]36[/латекс] шариков на мешочки поменьше.
Количество пакетов Деление на количество мешков Умножение на обратное
[латекс]3[/латекс] [латекс]\фракция{36}{3}=12[/латекс] [латекс] 36\влево( \frac{1}{3} \right)=\frac{36}{3}=\frac{12(3)}{3}=12[/latex]
[латекс]4[/латекс] [латекс]\фракция{36}{4}=9[/латекс] [латекс] 36 \ влево (\ гидроразрыва {1} {4} \ вправо) = \ гидроразрыва {36} {4} = \ гидроразрыва {9 \ влево (4 \ вправо)} {4} = 9 [/ латекс]
[латекс]6[/латекс] [латекс]\фракция{36}{6}=6[/латекс] [латекс] 36 \ влево (\ гидроразрыва {1} {6} \ вправо) = \ гидроразрыва {36} {6} = \ гидроразрыва {6 \ влево (6 \ вправо)} {6} = 6 [/ латекс]
Деление на число равносильно умножению на его обратную величину. (То есть вы используете обратную величину делителя , второго числа в задаче на деление.)
Теперь давайте посмотрим, что это означает, когда одно или несколько чисел отрицательные. Число и его обратное имеют один и тот же знак. Поскольку деление переписывается как умножение с использованием обратной величины делителя, а взятие обратной величины не меняет никаких знаков, деление подчиняется тем же правилам, что и умножение.
Правила деления
При делении перепишите задачу как умножение, используя в качестве второго множителя обратную величину делителя.
Когда одно число положительное , а другое отрицательное , частное равно отрицательному .
Когда оба числа отрицательные , частное положительное .
Когда оба числа положительны , частное равно положительный .
Попробуйте
В следующем видео показано, как разделить дроби со знаком.

Помните, что черта дроби также указывает на деление, поэтому знак минус перед дробью соответствует числителю, знаменателю или всей дроби: [латекс]-\frac{3}{4}=\frac {-3}{4}=\frac{3}{-4}[/latex].
В каждом случае общая дробь отрицательна, потому что в делении есть только одно отрицательное число.
В следующем видео показано, как разделить дроби со знаком.

Поддержите!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Отрицательные степени — правила, дроби, решения, вычисления
Отрицательная степень определяется как мультипликативная инверсия основания, возведенная в степень, противоположную знаку данной степени. Проще говоря, мы пишем обратное число, а затем решаем его как положительные показатели степени. Например, (2/3) ^-2 можно записать как (3/2) ² . Мы знаем, что показатель степени относится к тому, сколько раз число умножается само на себя. Например, 3 ² = 3 × 3. В случае положительных степеней мы легко умножаем число (основание) само на себя, но в случае отрицательных степеней мы умножаем обратное число само на себя. Например, 3 ^-2 = 1/3 × 1/3.
Давайте узнаем больше об отрицательных показателях вместе с соответствующими правилами и решим больше примеров.
1. Что такое отрицательные показатели?
2. Числа и выражения с отрицательными показателями
3. Правила отрицательного экспонента
4. Почему дроби с отрицательными показателями степени?
5. Показатели степени отрицательной дроби
6. Умножение отрицательных показателей
7. Как решать отрицательные показатели?
8. Часто задаваемые вопросы об отрицательных показателях
Что такое отрицательные показатели?
Мы знаем, что показатель степени числа говорит нам, во сколько раз мы должны умножить основание. Например, в 8 ² 8 — основание, а 2 — показатель степени. Мы знаем, что 8 ² = 8 × 8. Отрицательная экспонента говорит нам, сколько раз мы должны умножить обратную величину основания. Рассмотрим 8 ^-2 , здесь основание равно 8, и у нас отрицательный показатель степени (-2). 8 ^-2 выражается как 1/8 × 1/8 = 1/8 ² .
Числа и выражения с отрицательными показателями
Вот несколько примеров, которые выражают отрицательные показатели с помощью переменных и чисел. Обратите внимание на приведенную ниже таблицу, чтобы увидеть, как число/выражение с отрицательным показателем степени записывается в его обратной форме и как изменяется знак степени.
Отрицательная экспонента Результат
2 ^-1 1/2
3 ^-2 1/3 ² = 1/9
х ^-3 1/х ³
(2 + 4x) ^-2 1/(2 + 4x) ²
(х ² + у ² ) ^-3 1/(х ² + у ² ) ³
Правила отрицательного экспонента
У нас есть набор правил или законов для отрицательных показателей, которые облегчают процесс упрощения. Ниже приведены основные правила решения отрицательных показателей.
Правило 1: Правило отрицательного показателя степени гласит, что для основания ‘a’ с отрицательным показателем степени -n возьмите обратное основание (которое равно 1/a) и умножьте его само на себя n раз.
т. е. a ^(-n) = 1/a × 1/a × … n раз = 1/a ⁿ
Правило 2: Правило остается тем же, даже если в знаменателе есть отрицательный показатель степени.
т. е. 1/a ^(-n) = a × a × … .n раз = a ⁿ
Давайте применим эти правила и посмотрим, как они работают с числами.
Пример 1: Решить: 2 ^-2 + 3 ^-2
Решение:
Используйте правило отрицательного порядка a ^-n = 1/a ⁿ
2 ^-2 + 3 ^-2 = 1/2 ² + 1/3 ² = 1/4 + 1/9
Возьмите наименьшее общее кратное (НОК): (9 + 4)/36 = 13/36
Следовательно, 2 ^-2 + 3 ^-2 = 13/36
0069
Используйте второе правило с отрицательным показателем в знаменателе: 1/a ^-n =a ⁿ
1/4 ^-2 + 1/2 ^-3 = 4 ² + 2 ³ =16 + 8 = 24
Следовательно, 1/4 ^-2 + 1/2 ^-3 = 24.
Отрицательные показатели являются дробями
Отрицательная экспонента приводит нас к обратному числу. Другими словами, a ^-n = 1/a ⁿ и 5 ^-3 становятся 1/5 ³ = 1/125. Вот как отрицательные показатели превращают числа в дроби. Давайте возьмем другой пример, чтобы увидеть, как отрицательные показатели превращаются в дроби.
Пример: Выразите 2 ^-1 и 4 ^-2 в виде дробей.
Решение:
2 ^-1 можно записать как 1/2, а 4 ^-2 можно записать как 1/4 ² . Следовательно, отрицательные показатели превращаются в дроби при изменении знака их показателя.
Отрицательные степени дроби
Иногда у нас может быть отрицательная дробная экспонента, например 4 ^-3/2 . Мы можем применить то же правило a ^-n = 1/a ⁿ, чтобы выразить это через положительный показатель степени. т. е. 4 ^-3/2 = 1/4 ^3/2 . Кроме того, мы можем упростить это, используя правила экспоненты.
4 ^-3/2 = 1/4 ^3/2
= 1 / (2 ² ) ^3/2
= 1 / 2 ³
= 1/8
Умножение отрицательных показателей
Умножение отрицательных показателей такое же, как умножение любого другого числа. Как мы уже обсуждали, отрицательные показатели степени могут быть выражены в виде дробей, поэтому их можно легко решить после преобразования в дроби. После этого преобразования мы умножаем отрицательные показатели, используя то же правило умножения, которое мы применяем для умножения положительных показателей. Давайте разберемся с умножением отрицательных показателей на следующем примере. 9{3} \раз 4}\)
45/4 ⁴ = 45/256
Как решать отрицательные показатели?
Чтобы решить выражения с отрицательными показателями, сначала преобразуйте их в положительные показатели, используя одно из следующих правил, и упростите:
a ^-n = 1/a ⁿ
1/a ^-n = a ⁿ
Пример : Решите: (7 ³ ) × (3 9{4}}\)
Используйте правило: a ^m × a ⁿ = a ^(m+n), чтобы объединить общее основание (7).
7 ⁵/3 ² =16807/9
Важные примечания относительно отрицательных показателей:
Показатель степени или степень означает, сколько раз нужно умножить основание само на себя.
a ^м = a × a × a ….. m раз
a ^-m = 1/a × 1/a × 1/a ….. m раз
a ^-n также известен как мультипликативная инверсия ⁿ .
Если a ^-m = a ^-n, то m = n.
Отношение между показателем степени (положительные степени) и отрицательным показателем (отрицательная степень) выражается как ^x = 1/a ^-x
☛ Похожие темы:
Калькулятор отрицательных показателей
Калькулятор правил экспоненты
Калькулятор экспоненты

Примеры отрицательных показателей
Пример 1: Найдите решение данного выражения (3 ² + 4 ² ) ^-2 .
Решение:
Данное выражение:
(3 ² + 4 ² ) ^-2 = (9 + 16) ^-2
6 = (25) ^-2
= 1/25 ² (по правилу отрицательной степени)
= 1/625.
Следовательно, (3 ² + 4 ²) ^-2 = 1/625
Ответ: 1/625
Пример 2: Найдите значение x в 27/3 ^-x = 3 ⁶
Решение:
Здесь у нас есть отрицательные показатели степени с переменными.
27/3 ^-x = 3 ⁶
3 ³ /3 ^-x = 3 ⁶
3 ³ × 3 ^х = 3 ⁶
3 ^{(3 + x)} = 3 ⁶
Если основания одинаковые, то степени должны быть равны, поэтому 3 + x = 6. Решая это, x = 3.
Ответ: x = 3
Пример 3: Упростите следующее, используя правила отрицательной степени: (2/3) ^-2 + (5) ^-1
Решение:
Используя правила отрицательной степени, мы можем написать (2 /3) ^-2 как (3/2) ² и (5) ^-1 как 1/5. Таким образом, мы можем упростить данное выражение как,
= (3/2) ² + 1/5
= 9/4 + 1/5
После взятия LCM получаем, (45 + 4)/20
49/20
Следовательно, (2/3) ^-2 + (5) ^-1 упрощается до 49/20.
Ответ: 49/20.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.
Часто задаваемые вопросы об отрицательных показателях
Что означают отрицательные показатели?
Отрицательные показатели степени означают отрицательные числа, которые присутствуют вместо показателей степени. Например, в числе 2 ^-8 , -8 — отрицательная степень основания 2.
Приводят ли отрицательные степени к отрицательным числам?
Нет, отрицательные показатели степени не обязательно должны давать отрицательные числа. Например, 2 ^-3 = 1/8, что является положительным числом.
Как рассчитать отрицательные показатели?
Отрицательные показатели вычисляются с использованием тех же законов показателей, которые используются для вычисления положительных показателей. Например, чтобы решить: 3 ^-3 + 1/2 ^-4, сначала мы преобразуем их в обратную форму: 1/3 ³ + 2 ⁴ , затем упростите 1/27 + 16. Взяв НОК, [1+ (16 × 27)]/27 = 433/27.
Каково правило для отрицательных показателей?
Есть два основных правила, которые полезны при работе с отрицательными показателями:
a ^-n = 1/a ⁿ
1/a ^-n = a ⁿ
Как решать дроби с отрицательными показателями?
Дроби с отрицательными показателями можно решить, взяв обратную дробь. Затем найдите значение числа, взяв положительное значение данного отрицательного показателя степени. Например, (3/4) ^-2 = (4/3) ² = 4 ² /3 ² . Это приводит к 16/9, что является окончательным ответом.
Как разделить отрицательные степени?
Деление степеней с одинаковым основанием приводит к вычитанию степеней. Например, чтобы решить y ⁵ ÷ y ^-3 = y ^5-(-3) = y ⁸ . Это также можно упростить альтернативным способом. т. е. y ⁵ ÷ y ^-3 = y ⁵ /y ^-3 , сначала мы меняем отрицательный показатель степени (y ^-3 ) на положительный, написав его обратный. Получается: у ⁵ × у ³ = у ⁽⁵⁺³⁾ = у ⁸ .
Как умножать отрицательные степени?
При умножении отрицательных степеней сначала нам нужно преобразовать их в положительные степени, записав соответствующие числа в обратной форме. Как только они преобразуются в положительные, мы умножаем их, используя те же правила, что и для умножения положительных показателей. Например, у ^-5 × y ^-2 = 1/год ⁵ × 1/год ² = 1/год ⁽⁵⁺²⁾ = 1/год ⁷
Почему отрицательные экспоненты?
Когда нам нужно изменить отрицательную степень на положительную, мы должны написать обратную величину данного числа. Итак, отрицательный знак степени косвенно означает обратную величину данного числа, точно так же, как положительный показатель степени означает многократное умножение основания.
Сколько будет 10 в отрицательной степени числа 2?
10 в отрицательной степени 2 представляется как 10 ^-2 , что равно (1/10 ² ) = 1/100.
Умножение
Умножение — это математическая операция, которая масштабирует одно число на другое ( умножение — знак: x). Заменяет сложение большого количества чисел подряд. Умножение — математическая операция, обратная делению. Например: вы можете заменить математическое выражение 5+5+5+5 на 5×4 (число 5, умноженное на количество раз, которое оно появилось в строке).
Умножение имеет несколько свойств. Когда число умножается на число 1, произведение (результат умножения) совпадает с этим числом. Когда число умножается на ноль, произведение всегда равно нулю. Когда число умножается на отрицательное, результатом является отрицательная версия этого числа. Он также обладает свойствами коммутативности, ассоциативности и дистрибутивности.
Коммутативные и ассоциативные свойства подобны этим свойствам дополнительно. Распределение применяется, когда сложение и умножение комбинируются, как в этом примере:
a * (b + c) = a * b + a * c
Очень важно помнить, что порядок важности умножения всегда выше, чем порядок важности сложения или вычитания. Вы сначала умножаете числа (там, где это необходимо), а затем добавляете или вычитаете их. Вот пример:
5 * 4 + 3 = 20 + 3 = 23
Единственным исключением из правила является то, что сложение или вычитание имеют приоритет над умножением, когда числа, которые необходимо сложить, и оператор указаны в скобках, а оператора умножения нет.
Умножение экзаменов для учителей
Название экзамена Размер файла загрузок Дата загрузки
Положительные целые числа
Умножение целых положительных чисел — очень просто 78 КБ 3577 3 сентября 2019 г.
Умножение целых положительных чисел — просто 143 КБ 3562 3 сентября 2019 г.
Умножение положительных целых чисел – средний 166,3 КБ 3984 3 сентября 2019 г.
Умножение положительных целых чисел – средней сложности 173,1 КБ 3242 3 сентября 2019 г.
Умножение положительных целых чисел — жесткое 561,5 КБ 2597 3 сентября 2019 г.
Умножение целых положительных чисел — очень сложно 571,8 КБ 2868 3 сентября 2019 г.
Положительные десятичные дроби
Умножение положительных десятичных дробей – очень просто 554,5 КБ 2475 3 сентября 2019 г.
Умножение положительных десятичных дробей – легко 555,5 КБ 2428 3 сентября 2019 г.
Умножение положительных десятичных дробей – средний 579.2 КБ 2282 3 сентября 2019 г.
Умножение положительных десятичных дробей – средней сложности 580,2 КБ 2066 3 сентября 2019 г.
Умножение положительных десятичных дробей – жесткое 569,5 КБ 2241 3 сентября 2019 г.
Умножение положительных десятичных дробей – очень сложно 567,2 КБ 2035 3 сентября 2019 г.
Положительные дроби
Умножение положительных дробей – очень сложно 567,2 КБ 2035 3 сентября 2019 г.
Умножение положительных дробей – очень просто 172,7 КБ 3107 3 сентября 2019 г.
Умножение положительных дробей – легко 188,9 КБ 2889 3 сентября 2019 г.
Умножение положительных дробей – среднее 577,2 КБ 2314 3 сентября 2019 г.
Умножение положительных дробей – средней жесткости 591,9 КБ 2068 3 сентября 2019 г.
Умножение положительных дробей – трудно 575,7 КБ 2080 3 сентября 2019 г.
Умножение положительных дробей – очень сложно 581 КБ 2032 3 сентября 2019 г.
Положительные смешанные числа
Умножение положительных смешанных чисел — очень просто 176,8 КБ 2281 3 сентября 2019 г.
Умножение положительных смешанных чисел – просто 209,8 КБ 2251 3 сентября 2019 г.
Умножение положительных смешанных чисел – средний 585,6 КБ 2109 3 сентября 2019 г.
Умножение положительных смешанных чисел – средний уровень сложности 592,9 КБ 1986 3 сентября 2019 г.
Умножение положительных смешанных чисел — сложно 589,3 КБ 2026 3 сентября 2019 г.
Умножение положительных смешанных чисел – очень сложно 596,6 КБ 1942 3 сентября 2019 г.
Положительные неправильные дроби
Умножение положительных неправильных дробей – очень просто 166 КБ 2015 3 сентября 2019 г.
Умножение положительных неправильных дробей – легко 169,9 КБ 2130 3 сентября 2019 г.
Умножение положительных неправильных дробей – средний 571,6 КБ 2030 3 сентября 2019 г.
Умножение положительных неправильных дробей – средней сложности 569,5 КБ 1887 3 сентября 2019 г.
Умножение положительных неправильных дробей — трудно 560,5 КБ 1865 3 сентября 2019 г.
Умножение положительных неправильных дробей – очень сложно 571,8 КБ 1921 3 сентября 2019 г.
Не положительные целые числа
Умножение целых чисел – очень просто 137,9 КБ 2656 3 сентября 2019 г.
Умножение целых чисел – легко 143,6 КБ 2772 3 сентября 2019 г.
Умножение целых чисел – средний 173,3 КБ 2727 3 сентября 2019 г.
Умножение целых чисел – средней сложности 173,5 КБ 2504 3 сентября 2019 г.
Умножение целых чисел – жесткий 565,9 КБ 2252 3 сентября 2019 г.
Умножение целых чисел — очень сложно 568 КБ 2157 3 сентября 2019 г.
Неположительные десятичные дроби
Умножение десятичных дробей – очень просто 186,6 КБ 2496 3 сентября 2019 г.
Умножение десятичных дробей – легко 187 КБ 2664 3 сентября 2019 г.
Умножение десятичных дробей – средний 578,8 КБ 2170 3 сентября 2019 г.
Умножение десятичных дробей – средней сложности 577 КБ 1949 3 сентября 2019 г.
Умножение десятичных дробей – жесткое 564,9 КБ 2088 3 сентября 2019 г.
Умножение десятичных дробей – очень сложно 567,9КБ 1960 3 сентября 2019 г.
Неположительные дроби
Умножение дробей – очень просто 179,6 КБ 2266 3 сентября 2019 г.
Умножение дробей – легко 186,7 КБ 2538 3 сентября 2019 г.
Умножение дробей – среднее 583,8 КБ 2167 3 сентября 2019 г.
Размножающие дроби – средней твердости 589 КБ 1928 3 сентября 2019 г.
Умножение дробей – жесткое 588 КБ 1829 3 сентября 2019 г.
Умножение дробей – очень сложно 594,9 КБ 1912 3 сентября 2019 г.
Неположительные смешанные числа
Умножение смешанных чисел – очень просто 192,9 КБ 1959 3 сентября 2019 г.
Умножение смешанных чисел – легко 209 КБ 2094 3 сентября 2019 г.
Умножение смешанных чисел – средний 594,7 КБ 1945 3 сентября 2019 г.
Умножение смешанных чисел – средний уровень сложности 602,2 КБ 1769 3 сентября 2019 г.
Умножение смешанных чисел – трудно 586,3 КБ 1764 3 сентября 2019 г.
Умножение смешанных чисел – очень сложно 591,3 КБ 1755 3 сентября 2019 г.
Не положительные неправильные дроби
Умножение неправильных дробей – очень просто 171,2 КБ 1824 3 сентября 2019 г.
Умножение неправильных дробей – легко 174 КБ 1865 3 сентября 2019 г.
Умножение неправильных дробей – средний 574,7 КБ 1823 3 сентября 2019 г.
Умножение неправильных дробей – средней сложности 573,9 КБ 1765 3 сентября 2019 г.
Умножение неправильных дробей – трудно 570,7 КБ 1730 3 сентября 2019 г.
Умножение неправильных дробей – очень сложно 577,4 КБ 1768 3 сентября 2019 г.

Умножение рабочих листов для учащихся
Название рабочего листа Размер файла загрузок Дата загрузки
Положительный
Умножение положительных целых чисел 496,1 КБ 2972 3 сентября 2019 г.
Умножение положительных десятичных дробей 51,8 КБ 2243 3 сентября 2019 г.
Умножение положительных дробей 632,1 КБ 2043 3 сентября 2019 г.
Умножение положительных смешанных чисел 637,8 КБ 2218 3 сентября 2019 г.
Умножение положительных неправильных дробей 594,6 КБ 1790 3 сентября 2019 г.
Не положительный
Умножение целых чисел 166,8 КБ 2338 3 сентября 2019 г.
Умножение десятичных дробей 246,3 КБ 2093 3 сентября 2019 г.
Умножение дробей 393,1 КБ 2152 3 сентября 2019 г.
Умножение смешанных чисел 412,4 КБ 1940 3 сентября 2019 г.
Умножение неправильных дробей 334,1 КБ 1796 3 сентября 2019 г.
1.2: Математические операции — Workforce LibreTexts
Последнее обновление
Сохранить как PDF
Идентификатор страницы
20031
Келли Брукс
Общественный колледж Восточных ворот
Сложение целых и десятичных дробей
Сложение чисел с одинаковыми знаками
Сложение абсолютных значений чисел и присвоение результата общему знаку
ПРИМЕЧАНИЕ. Если оба знака положительные, добавьте значения
.
Пример: $23+18$
Общий знак +, поэтому ответ будет положительным, теперь мы складываем числа, чтобы получить
\[23+18=41\]
Пример: $ -17+(-31)$
Общий знак — -, поэтому ответ будет отрицательным, теперь складываем абсолютные значения чисел, чтобы получить:
\[-17+\left( -31\right ) =\]
Сначала вычислите сумму абсолютных значений :
\[\влево|-17\вправо|+\влево|-31\вправо|=\ 17+31=48\]
Затем присвойте результату общий знак, чтобы окончательный ответ был : -48.
\[-17+\left(-31\right)=-48\]
Сложение чисел с противоположными знаками
Взять абсолютное значение каждого числа
Вычесть меньшее из большего числа
Назначение знака результата на основе знака числа с большим абсолютным значением
ПРИМЕЧАНИЕ: Преобладает знак большего абсолютного значения. С практикой эти шаги начнут казаться плавными.
Пример: $21+(-13)$
Сначала вычислите абсолютное значение каждого числа :
\[\left|21\right|=21 \text{ и } \left|- 13\right|=13\]
Затем из большего числа вычтите меньшее :
\[21-13=8\]
Затем присвойте знак числу, абсолютное значение которого было больше , в данном случае знак 21 — это знак окончательного ответа (положительного), следовательно,
\[21+\left(-13\right)=8\]
Нажатие клавиш научного калькулятора:
Пример: $28+(-54)$
Сначала вычислите абсолютное значение каждого число :
$\влево|28\вправо|=28$ и $\влево|-54\вправо|=54$
Затем вычтите меньшее число из большего числа :
\[54-28=26\]
Затем присвойте знак числа, абсолютное значение которого было больше, в данном случае знак -54 — это знак окончательного ответа (отрицательного), следовательно,
\[28+\left(-54\right)=-26\]
Сокращение: теперь, когда мы прошли формальный процесс добавления целые числа, давайте получим общее представление о процессе:
Если знаки одинаковые, объедините числа и сохраните знак
Если знаки разные, то без учета знаков вычесть меньшее число из большего числа, затем сохранить знак большего числа
Пример: $13+(-29)$
Поскольку 29 больше 13, мы вычитаем 13 из 29, чтобы получить 16, и используем отрицательный знак 29: -16
Пример: $- 28+(-54)$
Поскольку знаки одинаковые, ответ будет иметь тот же знак (отрицательный), теперь объедините числа 28 + 54 = 82, так что окончательный ответ будет -82
Аналогично с десятичные числа :
Пример: $-2,34+\влево(-5,4\вправо)=$
Так как знаки одинаковые, складываем числа: 2,34 + 5,4 = 7,74 и сохраняем общий знак (минус ) получить – 7,74
Вычитание целых и десятичных дробей
При вычитании целого или десятичного числа мы прибавляем противоположное число после вычитания.
Пример: $15-7=$
В этом случае мы можем выполнить обычное вычитание, однако мы также можем применить правило вычитания, сложив противоположное, чтобы получить:
\[15+\left(- 7\right)=8\]
, так как 15 больше 7, мы вычитаем и сохраняем знак большего положительного числа
Пример: $3-12=$
Не забывая складывать противоположное 12, получаем
\[3+\left(-12\right)=-9\]
Поскольку знаки разные и 12 больше 3, вычитаем $12 -3$, чтобы получить 9, но используйте отрицательный знак 12, чтобы получить -9
Аналогично с десятичными значениями:
Пример: $8.23-(-1.2)=$
Сначала складываем противоположное из -1.2: $8.23+1.2=$
Затем мы объединяем числа, поскольку они имеют одинаковые знаки, чтобы получить:
\[8.23-\left(-1.2\right)=8.23+1.2=9.43\]
Умножение и деление целых и десятичных чисел
Чтобы умножить или разделить целые и десятичные числа, мы используем умножение чисел и применяем следующие правила для знака:
Если два числа имеют одинаковые знаки, результат положительный
Если два числа имеют разные (противоположные) знаки, результат будет отрицательным
Примеры:
$\влево(3\вправо)\влево(-7\вправо)=\ -21$
$\влево(-15\вправо)\влево(-10\вправо)=150$
$\влево(-5,2\вправо)\влево(2\вправо)=-10,4$
$\влево(2\вправо)\влево(7\вправо)=14$
$\влево(-25\вправо)\дел \влево(-5\вправо)=5$
$\влево(-12,8\вправо)\дел \влево(4\вправо)=-3,2$
$\влево(250\вправо)\дел \влево(-10\вправо)=-25$
$\влево(48\вправо)\дел \влево(6\вправо)=8$
Сложение, вычитание, умножение и деление целых и десятичных чисел с помощью научного калькулятора
Существует множество типов научных калькуляторов, доступных на розничном рынке, на наших персональных компьютерах и даже на наших персональных устройствах, таких как мобильные телефоны и планшеты. . В результате давайте сначала разберем два типа научных калькуляторов: калькулятор с дисплеем и калькулятор без дисплея. Некоторые примеры дисплейных калькуляторов: TI30XIIS, TI-36X Pro, TI-30XS Multiview и Casio fx-350ES PLUS. Некоторыми примерами калькуляторов без дисплея являются TI-30Xa, большинство калькуляторов для мобильных телефонов и большинство калькуляторов на персональных компьютерах.
Для наших целей мы определим, является ли калькулятор «дисплеем» или «без дисплея», выполнив следующие действия:
Введите 2 + 3 на своем калькуляторе.
Если на вашем экране отображается выражение 2 + 3 целиком, значит, у вас есть «Отображение» калькулятора.
Если ваш экран отображает только 3 после ввода 2 + 3, то у вас есть «неотображаемый» калькулятор.
На дисплее калькуляторов мы обычно можем ввести задачу так, как она написана. На калькуляторе без дисплея мы обычно должны вводить задачу в обратном порядке операций (дополнительную информацию см. в Модуле 2).
Давайте вернемся к некоторым из наших предыдущих примеров и рассчитаем их на научном калькуляторе. Для отрицательных чисел обязательно используйте отрицательный символ (-), который обычно находится внизу клавиатуры калькулятора TI, а не символ вычитания -, который обычно находится с правой стороны клавиатуры. Каждый калькулятор уникален, поэтому вам, возможно, придется поэкспериментировать со своим калькулятором, чтобы определить процесс.
Чтобы вычислить -17+(-31), используйте следующую последовательность нажатий клавиш, чтобы получить -48:
Дисплей Калькулятор: Калькулятор без дисплея:
(-) 17 + (-) 31 ВВОД 17 (-) + 31 (-)=
Введите знак минус перед числом Введите отрицательное число после знака
Для вычисления 8.23-(-1.2)= используйте следующую последовательность нажатий клавиш для получения 9. 43:
.
Показать калькулятор Калькулятор без дисплея:
8.23 - (-) 1.2 ВВОД 8,23 — 1,2 (-) =
Используйте клавишу вычитания, затем введите знак минус перед числом Используйте клавишу вычитания, затем введите знак минус после числа
Чтобы вычислить (-15)(-10) = используйте следующую последовательность нажатий клавиш для получения 150:
Дисплей калькулятора Калькулятор без дисплея:
(-)15 X (-)10 ВВОД 15 (-) Х 10 (-) =
Введите знак минус перед числом Введите знак минус после числа
Чтобы вычислить (250)$\div$(-10) = используйте следующую последовательность нажатий клавиш для получения -25:
Показать калькулятор Калькулятор без дисплея:
250$\дел$(-)10 ВВОД 250$\дел$10(-) =
Введите знак минус перед числом Введите знак минус после числа
Дроби
Дроби — это действительные числа, обозначающие часть целого. Дробь состоит из числителя и знаменателя. Знаменатель представляет количество равных частей объекта, а числитель представляет часть этих равных частей. Например, если труба разделена на 4 равные части, ¼ будет представлять 1 из 4 частей, 2/4 будет представлять 2 из 4 частей, ¾ будет представлять 3 из 4 частей, а 4/4 = 1 будет представлять все 4 части или всю трубу. Точно так же 0/4 будет представлять 0 из 4 частей или ничего, следовательно, 0/4 = 0,9.0003
Прямоугольник внизу разделен на две равные части. Следовательно, 1 из 2 частей будет представлять 1/2.
Показанный ниже круг разделен на 8 равных частей. 1 часть будет представлять 1/8. 2 части будут представлять 2/8, что уменьшится до 1/4 по нескольким причинам:
если бы мы заштриховали 2 из 8 частей, это также представляло бы 1 из 4 равных частей и
2/8 можно уменьшить, разделив числитель (2) и знаменатель (8) на одно и то же число, которое в данном случае будет равно 2, следовательно: $\frac{2}{8}=\frac{ 2\дел 2}{8\дел 2}=\разрыв{1}{4}$
«Черта» в дроби также обозначает деление, поэтому ¼ также означает $1\дел 4$. Это можно интерпретировать как целое, разделенное на 4 равные части или 1 из 4 равных частей.
Дроби имеют множество применений. Дроби также можно использовать для представления таких единиц измерения, как мили в час или $\frac{miles}{hour}$. Дроби также могут использоваться для обозначения соотношений и пропорций; мы увидим использование дробей в этих приложениях в более позднем разделе.
Умножение и деление дробей
Чтобы умножить дроби:
Умножьте числители и умножьте знаменатели.
Для упрощения уменьшите путем деления на одинаковые множители (числа, которые делятся на другие числа).
Примеры:
1. $\frac{2}{3}\cdot \frac{5}{7}$
a. Умножьте числители и умножьте знаменатели.
\[\frac{2}{3}\cdot \frac{5}{7}=\frac{10}{21}\nonumber \]
Поскольку числа 10 и 21 не имеют общих делителей, это упрощенный или сокращенный ответ.
2. $\frac{22}{63}\cdot \frac{9}{24}$
а. Умножьте числители и умножьте знаменатели.
\[\frac{22}{63}\cdot \frac{9}{24}=\frac{108}{1512}\nonumber \]
b. Упростите, уменьшив дробь (разделите числитель и знаменатель на одно и то же число(а))
\[\frac{108}{1512}=\frac{108\div 12}{1512\div 12}=\frac{ 9}{126}=\frac{9\div 9}{126\div 9}=\frac{1}{14}\nonumber \]
Другим вариантом решения этой задачи является сокращение перед умножением:
\[\frac{12}{63}\cdot \frac{9}{24}\nonumber \]
а. Сократите числители и знаменатели, разделив их на одно и то же число
\[\frac{12\div 12}{63\div 9}\cdot \frac{9\div 9}{24\div 12}=\frac{ 1}{7}\cdot \frac{1}{2}\nonumber \]
б. Умножить числители и знаменатели (умножить прямо)
\[\frac{1}{7}\cdot \frac{1}{2}=\frac{1}{14}\nonumber \]
3. \ (\frac{24}{72}\cdot \frac{18}{30}\)
Поскольку числа в дробях большие, давайте сначала уменьшим, а затем умножим.
Определить числа, которые делятся как на числитель, так и на знаменатель:
9 делится на 18 и 72; 6 делится на 24 и 30 ИЛИ 6 делится на 18 и 30; 24 делится на 24 и 72
\[\frac{24}{72}\cdot \frac{18}{31}=\frac{24\div 6}{72\div 9}\cdot \frac{18\ div 9}{30\div 6}=\frac{4}{8}\cdot \frac{2}{5}=\frac{4\div 4}{8\div 4}\cdot \frac{2} {5}=\frac{1}{2}\cdot \frac{2}{5}=\frac{1}{2\div 2}\cdot \frac{2\div 2}{5}=\frac {1}{5} \nonumber \]
ИЛИ
\[\frac{24}{72}\cdot \frac{18}{31}=\frac{24\div 24}{72\div 24} \cdot \frac{18\div 6}{30\div 6}=\frac{1}{3}\cdot \frac{3}{5}=\frac{1}{3\div 3}\cdot \ frac{3\div 3}{5}=\frac{1}{5} \nonumber \]
Чтобы разделить дроби: инвертируйте вторую дробь и измените операцию на умножение и продолжайте, как описано выше.
Пример: $\frac{3}{5}\div \frac{9}{10}$
\[\frac{3}{5}\div \frac{9}{10}= \ frac{3}{5}\cdot \frac{10}{9}=\frac{30}{45}=\frac{2}{3}\nonumber \]
Пример: $\frac{15} {7}\div \frac{25}{21}$
\[\frac{15}{7}\div \frac{25}{21}=\frac{15}{7}\cdot \frac {21}{25}=\frac{3}{1}\cdot \frac{3}{5}=\frac{9}{5}\nonumber \]
Сложение и вычитание дробей
С одинаковыми знаменателями
Чтобы складывать или вычитать дроби, дроби должны иметь одинаковый знаменатель:
Шаг 1: Убедитесь, что дроби подобны дробям (дроби с одинаковым знаменателем).
Шаг 2: Сложите или вычтите числители, сохранив знаменатель.
Примеры:
$\frac{2}{7}+\frac{3}{7}=\frac{2+3}{7}=\frac{5}{7}$
$\frac{14}{17}-\frac{5}{17}=\frac{14-5}{17}=\frac{9{17}$
С разными знаменателями
Шаг 1: Перепишите разные дроби (дроби с разными знаменателями) как одинаковые дроби (дроби с одинаковым знаменателем) с наименьшим общим кратным в качестве их нового знаменателя. Этот новый знаменатель называется наименьшим общим знаменателем (LCD).
Чтобы определить наименьший общий знаменатель (НОД), найдите наименьшее общее кратное знаменателей, другими словами, найдите наименьшее число, на которое оба знаменателя делятся на
Преобразуйте разные дроби в одинаковые, умножив числитель и знаменатель каждой дроби на число, при котором знаменатель каждого из них является наименьшим общим знаменателем.
Шаг 2: Сложите или вычтите числители и сохраните общий знаменатель.
Примеры:
$\frac{2}{3}+\frac{1}{9}=$
Сначала найдите наименьшее число, на которое делятся и 3, и 9, в данном случае это будет 9, поэтому 9 — это ЖК-дисплей.
Итак, нам нужно умножить первую дробь на 3/3, чтобы получить 9 в знаменателе:
\[\frac{3}{3}\cdot \frac{2}{3}+\frac{1 }{9}=\frac{6}{9}+\frac{1}{9}=\frac{7}{9}\nonumber \]
2. $\frac{3}{7}+ \frac{1}{4}=$
Наименьший общий знаменатель = 28 (поскольку 28 — наименьшее число, которое можно разделить и на 7, и на 4)
Затем умножьте числитель и знаменатель 3/7 на 4/4, чтобы получить знаменатель 28, и умножить числитель и знаменатель ¼ на 7/7, чтобы получить знаменатель 28, наконец, сложить числители и сохранить общий знаменатель.
\[\frac{4}{4}\cdot \frac{3}{7}+\frac{1}{4}\cdot \frac{7}{7}=\frac{12}{28} +\frac{7}{28}=\frac{19}{28}\nonumber \]
ПРИМЕЧАНИЕ. Мы складываем, вычитаем, умножаем и делим отрицательные дроби так же, как складываем, вычитаем, умножаем и делим отрицательные числа. в разделе ___.
Проценты
Процент определяется как сумма, основанная на 100. Если мы разделим слово на два слова, мы получим «процент» и «процент». Per означает деление на и цент означает 100, следовательно, деление на 100 или из 100.
Пример: 54% означает 54 из 100
Мы будем использовать проценты для расчета значений в Единице ____.
Преобразование между различными типами чисел (дробями, десятичными и процентами)
Чтобы преобразовать дробь в десятичную, разделите числитель на знаменатель.
Для преобразования десятичной дроби в дробь определите место последней цифры после запятой, запишите дробь как все цифры после запятой над последним знаком запятой.
Пример: 0,547 представляет 547 тысячных, так как последняя цифра после запятой стоит в тысячном разряде, мы имеем 547/1000.

Количество пакетов	Деление на количество мешков	Умножение на обратное
[латекс]3[/латекс]	[латекс]\фракция{36}{3}=12[/латекс]	[латекс] 36\влево( \frac{1}{3} \right)=\frac{36}{3}=\frac{12(3)}{3}=12[/latex]
[латекс]4[/латекс]	[латекс]\фракция{36}{4}=9[/латекс]	[латекс] 36 \ влево (\ гидроразрыва {1} {4} \ вправо) = \ гидроразрыва {36} {4} = \ гидроразрыва {9 \ влево (4 \ вправо)} {4} = 9 [/ латекс]
[латекс]6[/латекс]	[латекс]\фракция{36}{6}=6[/латекс]	[латекс] 36 \ влево (\ гидроразрыва {1} {6} \ вправо) = \ гидроразрыва {36} {6} = \ гидроразрыва {6 \ влево (6 \ вправо)} {6} = 6 [/ латекс]

1.	Что такое отрицательные показатели?
2.	Числа и выражения с отрицательными показателями
3.	Правила отрицательного экспонента
4.	Почему дроби с отрицательными показателями степени?
5.	Показатели степени отрицательной дроби
6.	Умножение отрицательных показателей
7.	Как решать отрицательные показатели?
8.	Часто задаваемые вопросы об отрицательных показателях

Отрицательная экспонента	Результат
2 ^-1	1/2
3 ^-2	1/3 ² = 1/9
х ^-3	1/х ³
(2 + 4x) ^-2	1/(2 + 4x) ²
(х ² + у ² ) ^-3	1/(х ² + у ² ) ³

Название экзамена	Размер файла	загрузок	Дата загрузки
Положительные целые числа
Умножение целых положительных чисел — очень просто	78 КБ	3577	3 сентября 2019 г.
Умножение целых положительных чисел — просто	143 КБ	3562	3 сентября 2019 г.
Умножение положительных целых чисел – средний	166,3 КБ	3984	3 сентября 2019 г.
Умножение положительных целых чисел – средней сложности	173,1 КБ	3242	3 сентября 2019 г.
Умножение положительных целых чисел — жесткое	561,5 КБ	2597	3 сентября 2019 г.
Умножение целых положительных чисел — очень сложно	571,8 КБ	2868	3 сентября 2019 г.
Положительные десятичные дроби
Умножение положительных десятичных дробей – очень просто	554,5 КБ	2475	3 сентября 2019 г.
Умножение положительных десятичных дробей – легко	555,5 КБ	2428	3 сентября 2019 г.
Умножение положительных десятичных дробей – средний	579.2 КБ	2282	3 сентября 2019 г.
Умножение положительных десятичных дробей – средней сложности	580,2 КБ	2066	3 сентября 2019 г.
Умножение положительных десятичных дробей – жесткое	569,5 КБ	2241	3 сентября 2019 г.
Умножение положительных десятичных дробей – очень сложно	567,2 КБ	2035	3 сентября 2019 г.
Положительные дроби
Умножение положительных дробей – очень сложно	567,2 КБ	2035	3 сентября 2019 г.
Умножение положительных дробей – очень просто	172,7 КБ	3107	3 сентября 2019 г.
Умножение положительных дробей – легко	188,9 КБ	2889	3 сентября 2019 г.
Умножение положительных дробей – среднее	577,2 КБ	2314	3 сентября 2019 г.
Умножение положительных дробей – средней жесткости	591,9 КБ	2068	3 сентября 2019 г.
Умножение положительных дробей – трудно	575,7 КБ	2080	3 сентября 2019 г.
Умножение положительных дробей – очень сложно	581 КБ	2032	3 сентября 2019 г.
Положительные смешанные числа
Умножение положительных смешанных чисел — очень просто	176,8 КБ	2281	3 сентября 2019 г.
Умножение положительных смешанных чисел – просто	209,8 КБ	2251	3 сентября 2019 г.
Умножение положительных смешанных чисел – средний	585,6 КБ	2109	3 сентября 2019 г.
Умножение положительных смешанных чисел – средний уровень сложности	592,9 КБ	1986	3 сентября 2019 г.
Умножение положительных смешанных чисел — сложно	589,3 КБ	2026	3 сентября 2019 г.
Умножение положительных смешанных чисел – очень сложно	596,6 КБ	1942	3 сентября 2019 г.
Положительные неправильные дроби
Умножение положительных неправильных дробей – очень просто	166 КБ	2015	3 сентября 2019 г.
Умножение положительных неправильных дробей – легко	169,9 КБ	2130	3 сентября 2019 г.
Умножение положительных неправильных дробей – средний	571,6 КБ	2030	3 сентября 2019 г.
Умножение положительных неправильных дробей – средней сложности	569,5 КБ	1887	3 сентября 2019 г.
Умножение положительных неправильных дробей — трудно	560,5 КБ	1865	3 сентября 2019 г.
Умножение положительных неправильных дробей – очень сложно	571,8 КБ	1921	3 сентября 2019 г.
Не положительные целые числа
Умножение целых чисел – очень просто	137,9 КБ	2656	3 сентября 2019 г.
Умножение целых чисел – легко	143,6 КБ	2772	3 сентября 2019 г.
Умножение целых чисел – средний	173,3 КБ	2727	3 сентября 2019 г.
Умножение целых чисел – средней сложности	173,5 КБ	2504	3 сентября 2019 г.
Умножение целых чисел – жесткий	565,9 КБ	2252	3 сентября 2019 г.
Умножение целых чисел — очень сложно	568 КБ	2157	3 сентября 2019 г.
Неположительные десятичные дроби
Умножение десятичных дробей – очень просто	186,6 КБ	2496	3 сентября 2019 г.
Умножение десятичных дробей – легко	187 КБ	2664	3 сентября 2019 г.
Умножение десятичных дробей – средний	578,8 КБ	2170	3 сентября 2019 г.
Умножение десятичных дробей – средней сложности	577 КБ	1949	3 сентября 2019 г.
Умножение десятичных дробей – жесткое	564,9 КБ	2088	3 сентября 2019 г.
Умножение десятичных дробей – очень сложно	567,9КБ	1960	3 сентября 2019 г.
Неположительные дроби
Умножение дробей – очень просто	179,6 КБ	2266	3 сентября 2019 г.
Умножение дробей – легко	186,7 КБ	2538	3 сентября 2019 г.
Умножение дробей – среднее	583,8 КБ	2167	3 сентября 2019 г.
Размножающие дроби – средней твердости	589 КБ	1928	3 сентября 2019 г.
Умножение дробей – жесткое	588 КБ	1829	3 сентября 2019 г.
Умножение дробей – очень сложно	594,9 КБ	1912	3 сентября 2019 г.
Неположительные смешанные числа
Умножение смешанных чисел – очень просто	192,9 КБ	1959	3 сентября 2019 г.
Умножение смешанных чисел – легко	209 КБ	2094	3 сентября 2019 г.
Умножение смешанных чисел – средний	594,7 КБ	1945	3 сентября 2019 г.
Умножение смешанных чисел – средний уровень сложности	602,2 КБ	1769	3 сентября 2019 г.
Умножение смешанных чисел – трудно	586,3 КБ	1764	3 сентября 2019 г.
Умножение смешанных чисел – очень сложно	591,3 КБ	1755	3 сентября 2019 г.
Не положительные неправильные дроби
Умножение неправильных дробей – очень просто	171,2 КБ	1824	3 сентября 2019 г.
Умножение неправильных дробей – легко	174 КБ	1865	3 сентября 2019 г.
Умножение неправильных дробей – средний	574,7 КБ	1823	3 сентября 2019 г.
Умножение неправильных дробей – средней сложности	573,9 КБ	1765	3 сентября 2019 г.
Умножение неправильных дробей – трудно	570,7 КБ	1730	3 сентября 2019 г.
Умножение неправильных дробей – очень сложно	577,4 КБ	1768	3 сентября 2019 г.

Название рабочего листа	Размер файла	загрузок	Дата загрузки
Положительный
Умножение положительных целых чисел	496,1 КБ	2972	3 сентября 2019 г.
Умножение положительных десятичных дробей	51,8 КБ	2243	3 сентября 2019 г.
Умножение положительных дробей	632,1 КБ	2043	3 сентября 2019 г.
Умножение положительных смешанных чисел	637,8 КБ	2218	3 сентября 2019 г.
Умножение положительных неправильных дробей	594,6 КБ	1790	3 сентября 2019 г.
Не положительный
Умножение целых чисел	166,8 КБ	2338	3 сентября 2019 г.
Умножение десятичных дробей	246,3 КБ	2093	3 сентября 2019 г.
Умножение дробей	393,1 КБ	2152	3 сентября 2019 г.
Умножение смешанных чисел	412,4 КБ	1940	3 сентября 2019 г.
Умножение неправильных дробей	334,1 КБ	1796	3 сентября 2019 г.

Дисплей Калькулятор:	Калькулятор без дисплея:
(-) 17 + (-) 31 ВВОД	17 (-) + 31 (-)=
Введите знак минус перед числом	Введите отрицательное число после знака

Показать калькулятор	Калькулятор без дисплея:
8.23 - (-) 1.2 ВВОД	8,23 — 1,2 (-) =
Используйте клавишу вычитания, затем введите знак минус перед числом	Используйте клавишу вычитания, затем введите знак минус после числа

Дисплей калькулятора	Калькулятор без дисплея:
(-)15 X (-)10 ВВОД	15 (-) Х 10 (-) =
Введите знак минус перед числом	Введите знак минус после числа

Показать калькулятор	Калькулятор без дисплея:
250\(\дел\)(-)10 ВВОД	250\(\дел\)10(-) =
Введите знак минус перед числом	Введите знак минус после числа

§ Деление отрицательных чисел. Деление рациональных чисел

Правила деления отрицательных чисел

Правило знаков при делении

Знак «минус» в дробях

Умножения и деление отрицательных чисел. Решение примеров.

Как правильно умножать отрицательные числа?

Основные определения

Умножение отрицательных чисел

Примеры умножения отрицательных чисел

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

Умножение положительных и отрицательных чисел

Умножение положительных и отрицательных чисел — «Семья и Школа»

Умножение и деление положительных и отрицательных чисел

Умножение отрицательных чисел

Помощь со студенческой работой на тему

Умножение чисел с противоположными знаками

Деление отрицательных чисел

Деление чисел с противоположными знаками

Умножение и деление отрицательных чисел

Отрицательные дроби.

Сложение и вычитание

Умножение и деление

Умножение положительных и отрицательных чисел

правило, примеры, умножение отрицательных чисел на положительные

Умножение отрицательных чисел

Примеры умножения отрицательных чисел

Сложение и вычитание отрицательных и положительных чисел.

Математика 10 класс

Курсы ОГЭ

Математика по Skype

Как правильно умножать отрицательные числа?

Основные определения

Примеры умножения отрицательных чисел

Умножение отрицательных дробей — Видео и стенограмма урока

Умножение отрицательных дробей

Попрактикуемся

Краткое содержание урока

Умножение и деление на целые числа (предалгебра, изучение и понимание целых чисел) — Mathplanet

Умножение и деление отрицательных чисел

Purplemath

MathHelp.

Отрицательные скобки

Упростить 6 — (3

Упростить

Рационалов (числа со знаком, включая дроби)

Рационалы (числа со знаком, включая дроби)

Упрощение выражения с помощью дроби

Результаты обучения

Знак минус в дробной части

Пример

Упрощение выражения с помощью дроби

Группировка символов

Упростите выражение с помощью дробной линейки

Пример

Пример

Умножение положительных и отрицательных чисел: 3 простых правила

Правило 1. Положительное число, умноженное на положительное, равно положительному числу.

Правило 2: Отрицательное число, умноженное на положительное, равняется отрицательному числу.

Правило 3. Отрицательное число, умноженное на отрицательное число, равняется положительному числу.

Как складывать, вычитать, умножать и делить положительные и отрицательные числа

Умножение и деление чисел с разными знаками, отрицательных и положительных чисел в 2023 году

Умножение целых чисел

Умножение чисел с разными знаками

Как умножать отрицательные числа?

Как умножать положительные числа?

Умножение нескольких целых чисел

Свойства умножения целых чисел: переместительный, сочетательный, распределительный законы

Умножение целых чисел на 0, 1 и -1

Деление целых чисел

Как правильно делить отрицательные числа?

Умножение отрицательных дробей — видео и расшифровка урока

Вы должны cСоздать учетную запись, чтобы продолжить просмотр

Зарегистрируйтесь, чтобы просмотреть этот урок

Уже зарегистрированы? Войдите здесь для доступ

Ресурсы, созданные учителями для учителей

Просто отмечаюсь. Вы все еще смотрите?

Добавить комментарий Отменить ответ