Почему делить на ноль нельзя? – статья – Корпорация Российский учебник (издательство Дрофа – Вентана)

Все математические действия равны, но некоторые равнее других

Начнём с того, что четыре арифметических действия — сложение, вычитание, умножение и деление — не являются равноправными. И разговор идёт не о порядке выполнения действий при решении какого-нибудь примера или уравнения. Нет, имеется в виду само понятие числа. И согласно ему, наиболее важными являются сложение и умножение. А уже вычитание и деление «вытекают» из них тем или иным образом.

Сложение и вычитание

Например, разберём простую операцию: «3 — 1». Что это означает? Школьник легко объяснит эту задачку: это означает, что было три предмета (например, три апельсина), один вычли, оставшееся количество предметов и есть верный ответ. Верно описано? Верно. Мы и сами объяснили бы точно так же. Но математики рассматривают процесс вычитания иначе.

Операция «3 — 1» рассматривается не с позиции вычитания, а только со стороны сложения.

Согласно этому нет никаких «три минус один», есть «какое-то неизвестное число, которое при прибавлении одного даёт три». Таким образом, простое «три минус один» превращается в уравнение с одним неизвестным: «х + 1 = 3». Причём появление уравнения изменило знак — вычитание поменялось на сложение. Осталась только одна задача — отыскать подходящее число.

Умножение и деление

Аналогичные метаморфозы происходят с таким действием, как деление. Задачу «6 : 3» математики отказываются воспринимать как некие шесть предметов, разбитых на три части. «Шесть разделить на три» не что иное, как «неизвестное число, умноженное на три, в результате чего получилось шесть»: «х · 3».

Делим на ноль

Выяснив принцип математических действий по отношению к задачам с вычитанием и делением, рассмотрим наше деление на ноль.

Задача «4 : 0» превращается в «х · 0». Получается, нам нужно найти такое число, умножение с которым даст нам 4.

Известно, что умножение на ноль всегда даёт ноль. Это уникальное свойство нуля и, собственно, его суть. Числа, умноженного на ноль и выдающего любое другое число кроме нуля, не существует. Мы пришли к противоречию, значит задача не имеет решения. Следовательно, записи «4 : 0» не соответствует никакое определённое число, а отсюда уже вытекает её бессмысленность. Поэтому, чтобы кратко подчеркнуть непродуктивность такого процесса, как деление на ноль, и говорят, что «на ноль делить нельзя».

Больше интересных материалов:

• Почему минус на минус всегда даёт плюс?
  
• Типичные ошибки учителей при проведении уроков математики в начальной школе
  
• Методическая помощь учителю математики
  
• Внеурочная деятельность по математике в начальной школе
  
• Формирование математической грамотности в начальной школе
  

А что получится, если ноль разделить на ноль?

Представим такое уравнение: «0 · x = 0». С одной стороны, выглядит вполне справедливо. Представляем вместо неизвестного числа ноль и получаем готовое решение: «0 · 0 = 0». Из этого вполне логично вывести, что «0 : 0 = 0».

Однако теперь давайте в это же уравнение с неизвестным вместо «x = 0» подставим любое другое число, например «x = 7». Получившееся выражение выглядит теперь как «0 · 7 = 0». Вроде бы, всё верно. Делаем обратную операцию и получаем «0 : 0 = 7». Но тогда, получается, что можно взять абсолютно любое число и вывести 0 : 0 = 1, 0 : 0 = 2… 0 : 0 = 145… — и так до бесконечности.

Если при любом числе х уравнение будет справедливо, то мы не имеем права выбрать лишь одно, исключив остальные. Значит, мы так и не можем ответить, какому числу соответствует выражение «0 : 0». Снова оказавшись в тупике, мы признаём, что и эта операция тоже бессмысленна. Получается, что ноль нельзя делить даже на самого себя.

Оговоримся, что в математическом анализе иногда бывают специальные условия задачи — так называемое «раскрытие неопределенности». В подобных случаях разрешается отдавать предпочтение одному из возможных решений уравнения «0 · x = 0». Однако в арифметике таких «допусков» не происходит. 

Почему нельзя в математике делить на ноль и умножать бесконечность на 0 — правило

Очень часто многие задаются вопросом, почему же нельзя использовать деление на ноль? В этой статье мы очень подробно расскажем о том, откуда появилось это правило, а также о том, какие действия можно выполнять с нолем….

Ноль можно назвать одной из самых интересных цифр. У этой цифры нет значения, она означает пустоту в прямом смысле слова. Однако, если ноль поставить рядом с какой-либо цифрой, то значение этой цифры станет больше в несколько раз.

Число очень загадочно само по себе. Его использовал еще древний народ майя. У майя ноль означал «начало», а отсчет календарных дней также начинался с нуля.

Очень интересным фактом является то, что знак ноля и знак неопределенности у них были похожи. Этим майя хотели показать, что ноль является таким же тождественным знаком, как и неопределенность.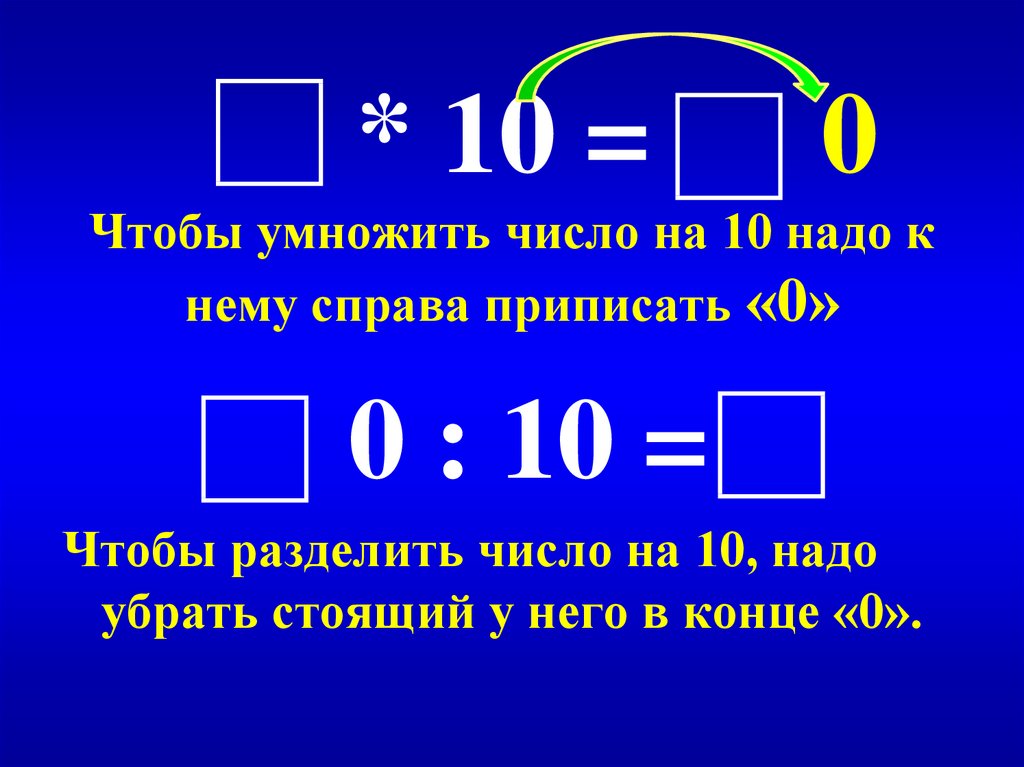 В Европе же обозначение нуля появилось сравнительно недавно.

Также многим известен запрет, связанный с нолем. Любой человек скажет, что на ноль нельзя делить. Это говорят учителя в школе, а дети обычно верят им на слово. Обычно детям либо просто не интересно это знать, либо они знают, что будет, если, услышав важный запрет, сразу же спросить «А почему нельзя делить на ноль?». Но когда становишься старше, то просыпается интерес, и хочется побольше узнать о причинах такого запрета. Однако существует разумное доказательство.

Содержание

Действия с нулем

Для начала необходимо определить, какие действия с нулем можно выполнять. Существует несколько видов действий:

• Сложение,
• Умножение,
• Вычитание,
• Деление (ноля на число),
• Возведение в степень.

Важно! Если при сложении к любому числу прибавить ноль, то это число останется прежним и не поменяет своего числового значения. То же произойдет, если от любого числа отнять ноль.

При умножении и делении все обстоит немного иначе. Если умножить любое число на ноль, то и произведение тоже станет нулевым.

Рассмотрим пример:

0*5=0

Запишем это как сложение:

0+0+0+0+0=0

Всего складываемых нолей пять, вот и получается, что

0*5=0

Попробуем один умножить на ноль. Результат также будет нулевым.

Ноль также можно разделить на любое другое число, не равное ему. В этом случае получится дробь, значение которой также будет нулевым. Это же правило действует и для отрицательных чисел. Если ноль делить на отрицательное число, то получится ноль.

0:(-5)=0

Также можно возвести любое число в нулевую степень. В таком случае получится 1. При этом важно помнить, что выражение «ноль в нулевой степени» абсолютно бессмысленно. Если попытаться возвести ноль в любую степень, то получится ноль. Пример:

04=0*0*0*0

Пользуемся правилом умножения, получаем 0.

Это интересно! Свойства натуральных логарифмов: график, основание, функции, предел, формулы и область определения

Так можно ли делить на ноль

Итак, вот мы и подошли к главному вопросу. Можно ли делить на ноль вообще? И почему же нельзя разделить число на ноль при том, что все остальные действия с нулем вполне существуют и применяются? Для ответа на этот вопрос необходимо обратиться к высшей математике.

Начнем вообще с определения понятия, что же такое ноль? Школьные учителя утверждают, что ноль-это ничто. Пустота. То есть когда ты говоришь, что у тебя 0 ручек, это значит, что у тебя совсем нет ручек.

В высшей математике понятие «ноль» более широкое. Оно вовсе не означает пустоту. Здесь ноль называют неопределенностью, так как если провести небольшое исследование, то получается, что при делении ноля на ноль мы можем в результате получить любое другое число, которое не обязательно может быть нолем.

Знаете ли вы, что те простые арифметические действия, которые вы изучали в школе не так равноправны между собой? Самыми базовыми действиями являются сложение и умножение.

Для математиков не существует понятий «деление» и «вычитание». Допустим: если от пяти отнять три, то останется два. Так выглядит вычитание. Однако, математики запишут это таким образом:

Х+3=5

Таким образом, получается, что неизвестной разностью является некое число, которое нужно прибавить к 3, чтобы получить 5. То есть, не нужно ничего вычитать, нужно просто найти подходящее число. Это правило действует для сложения.

Немного иначе дела обстоят с правилами умножения и деления. Известно, что умножение на ноль приводит к нулевому результату. Например, если 3:0=х, тогда, если перевернуть запись, получится 3*х=0. А число, которое умножалось на 0 даст ноль и в произведении. Получается, что числа, которое бы давало в произведении с нолем какую-либо величину, отличную от ноля, не существует. А значит, деление на ноль бессмысленно, то есть оно подходит к нашему правилу.

Но что будет, если попытаться разделить сам ноль на себя же? Возьмем как х некое неопределенное число. Получается уравнение 0*х=0. Его можно решить.

Если мы попробуем взять вместо х ноль, то мы получим 0:0=0. Казалось бы, логично? Но если мы попробуем вместо х взять любое другое число, например, 1, то в конечном итоге получится 0:0=1. Та же ситуация будет, если взять любое другое число и подставить его в уравнение.

В этом случае получится, что мы можем как множитель взять любое другое число. Итогом будет бесконечное множество разных чисел. Порой все же деление на 0 в высшей математике имеет смысл, но тогда обычно появляется некое условие, благодаря которому мы сможем все-таки выбрать одно подходящее число. Это действие называется «раскрытием неопределенности». В обычной же арифметике деление на ноль снова потеряет свой смысл, так как мы не сможем выбрать из множества какое-то одно число.

Важно! На ноль нельзя разделить ноль.

Ноль и бесконечность

Бесконечность очень часто можно встретить в высшей математике. Так как школьникам просто не важно знать о том, что существуют еще математические действия с бесконечностью, то и объяснить детям, почему делить на ноль нельзя, учителя как следует не могут.

Основные математические секреты ученики начинают узнавать лишь на первом курсе института. Высшая математика предоставляет большой комплекс задач, которые не имеют решения. Самыми известными задачами являются задачи с бесконечностью. Их можно решить при помощи математического анализа.

К бесконечности также можно применить элементарные математические действия: сложение, умножение на число. Обычно еще применяют вычитание и деление, но в конечном итоге они все равно сводятся к двум простейшим операциям.

Но что будет, если попытаться:

• Бесконечность умножить на ноль. По идее, если мы попробуем умножить на ноль любое число, то мы получим ноль. Но бесконечностью является неопределенное множество чисел. Так как мы не можем выбрать из этого множества одно число, то выражение ∞*0 не имеет решения и является абсолютно бессмысленным.
• Ноль делить на бесконечность. Здесь происходит та же история, что и выше. Не можем выбрать одно число, а значит не знаем на что разделить. Выражение не имеет смысла.

Важно! Бесконечность немного отличается от неопределенности! Бесконечность является одним из видов неопределенности.

Теперь попробуем бесконечность делить на нуль. Казалось бы, должна получиться неопределенность. Но если мы попробуем заменить деление умножением, то получится вполне определенный ответ.

Например: ∞/0=∞*1/0= ∞*∞ = ∞.

Получается такой математический парадокс.

Ответ, почему нельзя делить на ноль

Мысленный эксперимент, пробуем делить на ноль

Вывод

Итак, теперь нам известно, что ноль подчиняется практически всем операциям, которые производят с обычными числами, кроме одной единственной. На ноль делить нельзя только потому, что в результате получается неопределенность. Также мы узнали, как производить действия с нолем и бесконечностью. Результатом таких действий будет неопределенность.

Это интересно! Как определить определенные интегралы от нуля, константы и с доказательством

Деление на ноль — определение, деление единицы на ноль, примеры

LearnPracticeDownload

Деление на ноль с любым числом не определено. Слово «деление» означает разделение чего-либо на равные части или группы таким образом, чтобы оно было разделено поровну между всеми. Принимая во внимание, что значение нуля как числа ничто. Он ставится перед 1, это четное число, которое не является ни положительным, ни отрицательным. Давайте узнаем больше о делении на ноль и решим несколько примеров.

1.	Что такое деление на ноль?
2.	Один разделить на ноль
3.	Факты о Дивизии и Зеро
4.	Часто задаваемые вопросы о Division By Zero

Что такое деление на ноль?

Деление на ноль считается неопределенным, если ноль является знаменателем или делением и выражается как а/0, где а является числом, числителем или делимым. Другими словами, деление нуля на любое число всегда даст нам ноль, независимо от умножения или деления. Поскольку умножение и деление идут рука об руку, деление на ноль также может означать умножение на ноль. Например, 7/0 = x или 0 × x = 5. Здесь x не имеет значения или числа для завершения уравнения. Следовательно, деление на ноль любого числа неопределенно.

Единица, деленная на ноль

Единица, деленная на ноль, также считается неопределенной. По мнению математиков, любое ненулевое число, положительное или отрицательное, деленное на ноль, не определено, поскольку не имеет значения. Например, попробуем определить 1/0. Если мы разделим ненулевое число на небольшое положительное число, мы получим значение. Малое положительное число близко к нулю, но не равно нулю.

1/0,1 = 10, 1/0,01 = 100, 1/0,000001 = 1000000

Следовательно, когда мы делим единицу на все меньшие и меньшие положительные числа, мы получаем все большие и большие положительные числа. Следовательно, 1/0 = + бесконечность. Когда мы разделили отрицательные числа, близкие к нулю, мы получаем:

1/-0,1 = -10, 1/-0,01 = -100, 1/-0,000001 = -1000000

Единица делится на отрицательное число ближе к нулю приводит к другому результату, который ближе к отрицательной бесконечности.

Следовательно, 1/0 = -бесконечность. Следовательно, единица, деленная на ноль, не имеет ответа, что приводит к неопределенности.

Факты о делении и ноле

Ниже приведены некоторые факты о делении и нуле.

• Любое число, деленное на 1 (частное равно делимому), дает ответ, аналогичный делимому. Другими словами, 1 — это делитель, а частное будет равно делимому. Например: 25 ÷ 1 = 25.
• Число нельзя разделить на 0, поэтому результат не определен. Пример: 78 ÷ 0 = не определено (но 0 ÷ 78 = 0).
• Если делимое равно делителю, что означает те же числа, но не 0, то ответ всегда равен 1. Например: 36 ÷ 36 = 1.
• Ноль — это действительное число, целое число, рациональное число и целое число.
• Ноль всегда нейтрален, т. е. ноль никогда не записывается как +0 или -0.
• Степень любого числа, увеличенного на ноль, всегда равна единице.

Связанные темы

Ниже перечислены несколько интересных тем, связанных с делением на ноль. Смотри:

• Длинное деление
• Нулевое свойство умножения
• Дивизион Формула
• Деление дробей

 

Примеры деления на ноль

1. Пример 1: Если в офисе 7 ягод клубники, а в офисе никого нет, сколько клубники получит каждый в офисе?

   Решение: Дано, 7 клубник в офисе и никого вокруг. Раздавать клубнику, когда никого нет в офисе, заведомо невозможно. Кому достанется клубника? Это определенно не имеет никакого смысла, поэтому this не определено.

2. Пример 2: Что такое 0 ÷ 7?

   Решение: Ноль, разделенный на любое действительное число, кроме 0, равен нулю. Следовательно, 0 ÷ 7 = 0,

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Запишитесь на бесплатный пробный урок

Практические вопросы по разделу на ноль

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о Division By Zero

Что означает деление на ноль?

Деление на ноль означает, что при делении на ноль любого отличного от нуля, положительного или отрицательного числа результат всегда не определен. Например, 4/0 = бесконечность или неопределенность.

Можно ли разделить число на ноль?

Любое число, разделенное на ноль, считается неопределенным. Когда мы делим ноль на 1, это равно нулю, когда мы делим ноль на ноль, оно равно undefined, а когда 1 делится на ноль, оно равно undefined.

Почему деление на ноль невозможно?

Деление на ноль невозможно, так как нет однозначного ответа при делении любого числа на ноль. Следовательно, результат не определен.

Как называется деление на ноль?

В математике деление на ноль не имеет смысла, поскольку любое число, деленное на ноль, считается неопределенным. Умножение и деление идут рука об руку, и когда число умножается на ноль, результатом является сам ноль. Находясь в делении, он не определен.

Чему равно 0 при делении на 8?

Частное от 0, деленного на 8, равно 0. 0 ÷ 8 = 0. 

Скачать БЕСПЛАТНО учебные материалы

Рабочие листы на деление

Рабочие листы по математике и
наглядный учебный план

Основы алгебры — деление на ноль

Предыдущий Следующий

Деление на ноль

Давайте повторим математическое правило. Помните этот? Без деления на ноль. Ну-ну, ни за что, никогда, никогда. Не делай этого. Вы когда-нибудь задумывались, почему?

Задача на деление может быть прочитана как задача на умножение, в которой отсутствует число. «Сколько будет 24 разделить на 6?» тот же вопрос, что и «6 умножить на 24?» Оба ответа равны 4.

Давайте попробуем это с 0. Задача деления «сколько будет 24 разделить на 0?» это то же самое, что и вопрос «0 умножить на 24?» И бум, вот оно — невозможно, нет ответа, не может быть сделано, ну-у, никоим образом, никогда. Нет ничего, на что мы могли бы умножить 0, чтобы получить 24. На самом деле, нет ничего, на что мы могли бы умножить 0, чтобы получить 9.0172 любое число (кроме самого 0), потому что 0 умножить на что угодно — это просто 0. Число, деленное на 0, похоже на засасывание материи в черную дыру: оно становится неопределенным .

Этот маленький факт объясняет множество неурядиц в мире алгебры. Например, простое маленькое выражение легко-легко, если х = 2 или 81 или -2347, но если х = 0, оно растворится в луже и испарится в ничто.

Итак, теперь, когда у нас есть переменные (буквы, которые предположительно могут быть любыми числами) и дроби (деление двух чисел), нам нужно убедиться, что в знаменатели не проникают нули. Если дробь имеет 0 в знаменателе, она не определена.

Пример задачи

Какие значения x сделают неопределенными?

Когда x = 0, то знаменатель будет равен 0. Это сделает дробь неопределенной.

Пример задачи

Какие значения x сделают неопределенными?

Это немного сложнее, но ненамного. Вопрос в том, каким должно быть x , чтобы x + 1 = 0? Если мы помним наши целые числа, мы знаем, что -1 + 1 = 0. Если x = -1, то получаем в знаменателе 0 и неопределенное выражение. Проверьте это:

По сути, все, что мы делаем, это устанавливаем знаменатель равным 0, а затем находим x .

Вот в чем хитрость. Мы решили, что число мы не хотим, чтобы x было равно , никогда.