Умножение и деление алгебраических дробей. Примеры и решение

• Умножение дробей
• Возведение алгебраических дробей в степень
• Деление дробей

Умножение дробей

Чтобы умножить одну алгебраическую дробь на другую, надо умножить числитель первой дроби на числитель второй дроби (полученное произведение будет числителем результата) и отдельно умножить знаменатель первой дроби на знаменатель второй (полученное произведение будет знаменателем результата).

Правило умножения алгебраических дробей в виде формулы:

a	·	c	=	ac	,
b		d		bd

где  b≠0  и  d≠0.

Пример. Выполнить умножение алгебраических дробей:

2a2	·	a + b	.
a2 — b2		a

Решение: Перед тем, как приступать к умножению дробей, желательно разложить их числители и знаменатели на множители — это поможет сократить алгебраическую дробь, которая получится в результате:

2a2	·	a + b	=	2a2	·	a + b	=
a2 — b2		a		(a + b)(a — b)		a

=	2a2(a + b)	.
	(a + b)(a — b)a

Теперь сокращаем полученную дробь:

2a2(a + b)	=	2a	.
(a + b)(a — b)a		a — b

Чтобы умножить многочлен на алгебраическую дробь или алгебраическую дробь на многочлен, надо умножить многочлен на числитель дроби, а знаменатель оставить без изменений.

Пример. Выполнить умножение многочлена на алгебраическую дробь:

(2x + 6) ·	x — 2	.
	x + 3

Решение:

(2x + 6) ·	x — 2	=	(2x + 6)(x — 2)	.
	x + 3		x + 3

Разложим числитель на множители и сократим дробь:

(2x + 6)(x — 2)	=	2(x + 3)(x — 2)	=
x + 3		x + 3

= 2(x — 2) = 2x — 4.

Правило умножения алгебраической дроби на многочлен (или умножение многочлена на алгебраическую дробь) в виде формулы:

a ·	b	=	ab	или	b	· a	=	ab	,
	c		c		c			c

где c≠0.

Возведение алгебраических дробей в степень

Чтобы возвести в степень алгебраическую дробь, надо возвести в эту степень отдельно её числитель и отдельно знаменатель.

Правило возведения алгебраических дробей в степень в виде формулы:

(	a	)n =	an	.
	b		bn

Пример. Выполнить возведение в степень:

а) (	a2	)3 ;          б) (-	2x3	)2	.
	b		y2

Решение:

а) (	a2	)3 =	(a2)3	=	a6	;
	b		(b)3		b3

б) (-	2x3	)2 =	(2x3)2	=	4x6	.
	y2		(y2)2		y4

Посмотреть правила возведения степени в степень вы можете на странице Свойства степени.

Деление дробей

Чтобы разделить одну алгебраическую дробь на другую, надо дробь, выступающую в качестве делителя, заменить на обратную ей дробь и после этого умножить первую дробь на вторую.

Правило деления алгебраических дробей в виде формулы:

a	:	c	=	a	·	d	=	ad	.
b		d		b		c		bc

Следовательно, частное двух дробей равно произведению первой дроби и перевёрнутой второй дроби.

Пример. Выполнить деление алгебраических дробей:

ab + ac	:	ab — ac	.
bc		bc

Решение: Переворачиваем делитель и умножаем дроби по правилам умножения:

ab + ac	:	ab — ac	=	ab + ac	·	bc	=
bc		bc		bc		ab — ac

=	(ab + ac)bc	.
	bc(ab — ac)

Теперь можно приступать к сокращению полученной дроби:

(ab + ac)bc	=	ab + ac	=
bc(ab — ac)		ab — ac

=	a(b + c)	=	b + c	.
	a(b — c)		b — c

Чтобы разделить многочлен на алгебраическую дробь, надо перевернуть дробь и выполнить умножение многочлена на полученную дробь по правилам умножения.

Правило деления многочлена на алгебраическую дробь в виде формулы:

a :	b	= a ·	c	=	ac	.
	c		b		b

Пример. Выполнить деление:

6xy2 :	x	.
	y

Решение:

6xy2 :	x	= 6xy2 ·	y	= 6y3.
	y		x

Чтобы разделить алгебраическую дробь на многочлен, надо представить многочлен в виде дроби и перевернуть её, затем выполнить умножение дробей по правилам умножения.

Правило деления алгебраической дроби на многочлен в виде формулы:

a	: c =	a	:	c	=	a	·	1	=	a	.
b		b		1		b		c		bc

Пример. Выполнить деление:

2xy	: 6y.
3

Решение:

2xy	: 6y =	2xy	:	6y	=	2xy	·	1	=
3		3		1		3		6y

=	2xy	=	x	.
	18y		9

правила, свойства и примеры для 5 класса

Математика

12.11.21

8 мин.

В различных дисциплинах с физико-математическим уклоном встречается операция упрощения выражений. Иногда последние представлены в виде обыкновенных дробей.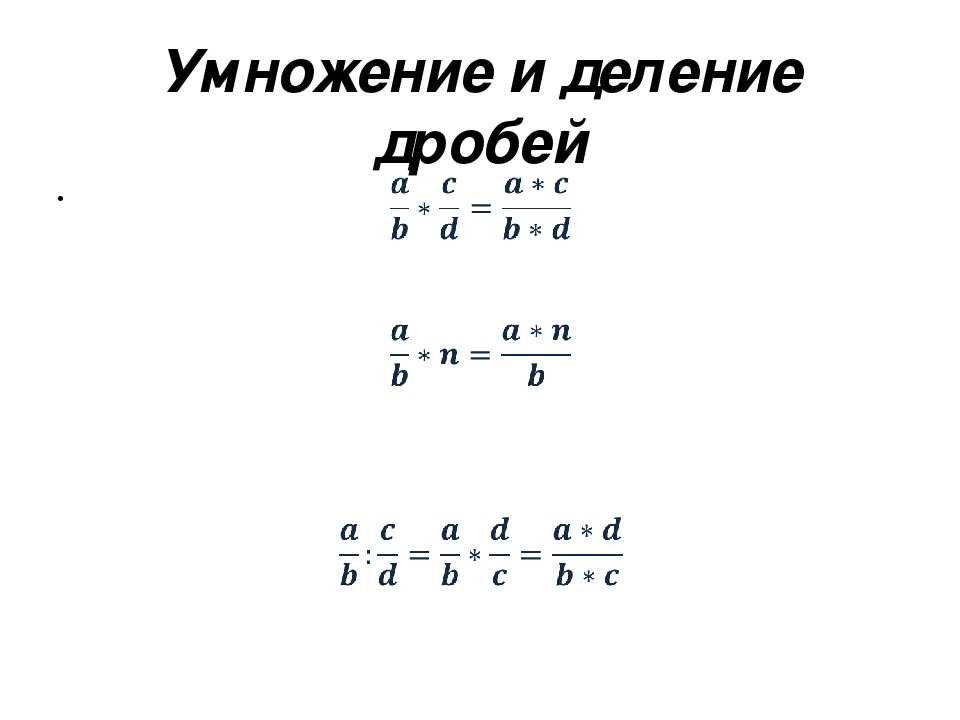 Правила деления и умножения дробных тождеств нужно знать, чтобы не совершать ошибок при вычислениях. Специалисты рекомендуют изучить теорию, а потом перейти к ее практическому применению.

Оглавление:

• Общие сведения
• Подготовительные операции
• Деление и умножение дробей

Общие сведения

Многие начинающие математики путают правила работы с обыкновенными выражениями, поскольку при делении забывают «переворачивать» делитель. Некоторые не отличают обыкновенное дробное выражение от десятичного. Кроме того, следует также знать правила деления числа на определенное значение. Итак,

дроби бывают только двух типов:

1. Обыкновенными (правильными и неправильными).
2. Десятичными (конечными и бесконечными).

Правильная — дробное выражение, у которого числитель меньше знаменателя, а у неправильного — числитель больше знаменателя (пример 2/3 и 7/3). У конечной десятичной дробной величины после запятой находится определенное количество знаков. Если же она является бесконечной, то делится на 2 типа: бесконечная периодическая (0,85 (3)) и непериодическая (1,56471238971235). Первая отличается от второй повторяющимися знаками, которые следует выделять круглыми скобками 0,(36) через определенный промежуток.

Обыкновенное дробное выражение записывается в десятичной форме. Кроме того, существует и обратное утверждение: любую десятичную дробь возможно записать в виде обыкновенной. Существует еще определенный вид дробных чисел, называющихся смешанными. Они состоят из целой части и обыкновенной дроби, т. е. 4 (½). Деление дробей в 5 классе требует некоторых подготовительных операций.

Подготовительные операции

Чтобы разделить одну дробную величину на другую, требуется произвести некоторые действия. Для этого следует руководствоваться правилом: любое смешанное число должно быть преобразовано в неправильную обыкновенную дробь. В этом случае математики рекомендуют воспользоваться следующим алгоритмом:

1. Записать величину: 12 (2/5).
2. Умножить знаменатель на целую часть, а затем прибавить числитель: 12*5+2=62.
3. Записать результат в виде неправильной дробной величины: 62/5.

Обратную операцию по преобразованию неправильной дроби в смешанное число математики рекомендуют выполнять на завершающих этапах вычисления. Выполняется конвертация по такой методике:

1. Записывается искомая величина: 62/5.
2. Выделяется целая часть при делении: 12.
3. От числителя искомого значения отнимается произведение знаменателя на величину, полученную во 2 пункте: 62−12*5=62−60=2.
4. Записывается конечный результат: 12 (2/5).

Правило деления целого числа на дробь: произвести преобразование целого в дробь деление на 1, т. е. 4=4/1. Следует также рассмотреть признаки делимости чисел. Они помогут правильно вычислять выражения и быстро сократить полученный результат.

К ним относятся:

1. На 1 делится любое число без остатка.
2. Если последняя цифра является четной, величину возможно разделить на 2.
3. Величина делится на 3, когда сумма ее цифр делится на это значение.
4. Число делится на 4, когда сумма двух крайних справа цифр можно разделить на последнее.
5. Если величина заканчивается на 5 или 0, значит, 5 является ее делителем.
6. Деление на 6 выполняется нацело в том случае, когда выполняются второе и третье правила.
7. Чтобы разделить величину на 7, нужно от произведения всех цифр, не затрагивая последнюю, отнять двойной разряд единиц. В этом случае результат должен делиться на семерку.
8. При делении на 8 нужно соблюдение второго и четвертого условий.
9. Если число делится на 9, то на нее должна делиться и сумма цифр, составляющих искомую величину.

Математики рекомендуют заготовить специальные карточки на плотной бумаге или в виде презентаций на компьютере. Для этих целей может подойти программа PowerPoint, входящая в расширенный выпуск Microsoft Office.

Описанных рекомендаций будет достаточно, чтобы выполнить деление обыкновенных дробей. Правило, которое используется при этой операции, включает в себя преобразование величин, выполнение вычислений, а затем приведение к общему виду.

Деление и умножение дробей

При делении обыкновенных дробей рекомендуется на начальных этапах использовать алгоритм. Последний не понадобится, когда учащийся выполняет операцию большое количество раз. Методика имеет следующий вид:

1. Записать 2 дроби: 3 (2/5) и 12 (2/5).
2. Преобразовать их в неправильные дробные выражения: (5*3+2)/5=17/5 и (12*5+2)/5=62/5.
3. Развернуть делитель (вторую дробь) и сменить знак деления «:» на противоположный (*), сократив на «5»: (17/5)*(5/62)=17/62.
4. Упростить результат при необходимости.

Деление целого значения на дробь выполняется по такому же алгоритму. При умножении обыкновенных дробных величин нет необходимости их переворачивать. Методика является очень простой и сводится к перемножению числителей и знаменателей, а затем результат упрощается.

Таким образом, для выполнения операций деления и умножения двух обыкновенных дробей рекомендуется изучить признаки делимости, алгоритмы и определения, а затем переходить к практике.

Не успеваете написать работу?

Заполните форму и узнайте стоимость

Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертация

Контактные данные — строго конфиденциальны!

Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.

* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности

Подтверждение

Ваша заявка принята.

Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.

Ошибка оформления заказа

Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.

Умножение и деление алгебраических дробей 8 класс онлайн-подготовка на Ростелеком Лицей

 

 

Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями

 

Урок: Умножение и деление алгебраических дробей

 

1. Правила умножения и деления обыкновенных и алгебраических дробей

 

 

Правила умножения и деления алгебраических дробей абсолютно аналогичны правилам умножения и деления обыкновенных дробей. Напомним их:

 

То есть, для того, чтобы умножить дроби, необходимо умножить их числители (это будет числитель произведения), и умножить их знаменатели (это будет знаменатель произведения).

Деление на дробь – это умножение на перевёрнутую дробь, то есть, для того, чтобы разделить две дроби, необходимо первую из них (делимое) умножить на перевёрнутую вторую (делитель).

 

2. Частные случаи применения правил умножения и деления дробей

 

 

Несмотря на простоту данных правил, многие при решении примеров по данной теме допускают ошибки в ряде частных случаев. Рассмотрим подробнее эти частные случаи:

 

Во всех этих правилах мы пользовались следующим фактом: .

 

3. Примеры умножения и деления обыкновенных дробей

 

 

Решим несколько примеров на умножение и деление обыкновенных дробей, чтобы вспомнить, как пользоваться указанными правилами.

 

Пример 1

Примечание: при сокращении дробей мы пользовались разложением числа на простые множители. Напомним, что простыми числами называются такие натуральные числа, которые делятся только на  и на само себя. Остальные числа называются составными. Число  не относится ни к простым, ни к составным. Примеры простых чисел: .

Пример 2

Рассмотрим теперь один из частных случаев с обыкновенными дробями.

Пример 3

Как видим, умножение и деление обыкновенных дробей, в случае правильного применения правил, не является сложным.

 

4. Примеры умножения и деления алгебраических дробей (простые случаи)

 

 

Рассмотрим умножение и деление алгебраических дробей.

 

Пример 4

Пример 5

Отметим, что сокращать дроби после умножения можно и даже нужно по тем же правилам, которые мы до этого рассматривали на уроках, посвящённых сокращению алгебраических дробей. Рассмотрим несколько простых примеров на частные случаи.

Пример 6

Пример 7

Рассмотрим теперь несколько более сложных примеров на умножение и деление дробей.

Пример 8

Пример 9

Пример 10

Пример 11

Пример 12

Пример 13

 

5. Примеры умножения и деления алгебраических дробей (сложные случаи)

 

 

До этого мы рассматривали дроби, в которых и числитель, и знаменатель являлись одночленами. Однако в ряде случаев необходимо перемножить или поделить дроби, числители и знаменатели которых являются многочленами. В этом случае правила остаются такими же, а для сокращения необходимо использовать формулы сокращённого умножения и вынесение за скобки.

 

Пример 14

Пример 15

Пример 16

Пример 17

Пример 18

На данном уроке мы рассмотрели правила умножения и деления алгебраических дробей, а также применение этих правил для конкретных примеров.

 

Список литературы

1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.

2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Портал для всей семьи (Источник).

2. Фестиваль педагогических идей «Открытый урок» (Источник).

3. Вся элементарная математика (Источник).

 

Домашнее задание

1. №№73-77, 80. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

2. Выполнить умножение: а), б)

3. Выполнить деление: а) , б)

4. Упростить выражение:

 

Умножение и деление дробей: примеры и методы

Джон был приглашен на день рождения Эми, и она пригласила в общей сложности 7 друзей отпраздновать свой день рождения. Чтобы получить одинаковые кусочки торта, каждый из участников должен иметь \(\frac{1}{8}\) торта. Случайно Эми уронила свой кусок пирога, поэтому Джон решил отдать ей часть своего. Он разделил свой кусок пирога на 2 и отдал половину Эми.

Можем ли мы посчитать, какая часть пирога досталась Эми в итоге? Ответ состоит в том, чтобы разделить дробь Джона на 2, то есть \(\dfrac{\dfrac{1}{8}}{2}=\dfrac{1}{16}\) торта.

В этой статье мы научимся выполнять операции умножения и деления с дробями.

Умножение и деление дробей шаг за шагом

Нас интересуют операции умножения и деления дробей. Прежде всего, давайте вспомним наши знания о дробях.

Дробь представляет часть целого . Он состоит из двух частей – числителя и знаменателя. Числитель пишется над чертой, а знаменатель — под чертой. Знаменатель не может быть равен нулю.

\(\dfrac{2}{3}, \dfrac{1}{2}, \dfrac{7}{8}, \cdots\) являются примерами дробей.

Мы знакомы с умножением и делением двух чисел. Теперь вопрос в том, как выполнять эти операции над дробями, а не над целыми числами.

Предположим, вам даны две дроби, скажем, \(\dfrac{a}{b}\) и \(\dfrac{c}{d}\), мы хотим знать, что мы подразумеваем под \(\dfrac{ a}{b}\times \dfrac{c}{d}\) и \(\dfrac{\dfrac{a}{b}}{\dfrac{c}{d}}.\)

Умножение и деление правила дробей

Правила умножения дробей

Чтобы умножить две дроби \(\dfrac{a}{b}\) и \(\dfrac{c}{d}\), необходимо перемножить числители вместе и знаменатели вместе. Таким образом. имеем

\[\dfrac{a}{b}\times \dfrac{c}{d}=\dfrac{a\times b}{c\times d}.\]

Мы, по сути, следуем следующие шаги, чтобы умножить дроби вместе.

Шаг 1. Перемножьте числители двух дробей вместе и знаменатели вместе.

Шаг 2. Разделите полученные числа, чтобы получить новую дробь.

На этом мы можем остановиться. Однако, если числитель и знаменатель новой дроби имеют общие делители, мы переходим к следующему шагу, чтобы получить простейшую форму дроби.

Шаг 3. Найдите общий делитель числителя и знаменателя новой дроби. Разделите числитель и знаменатель на этот общий множитель. Это дает простейшую форму дроби.

Перемножьте дроби \(\dfrac{3}{7}\) и \(\dfrac{5}{11}\).

Решение

Шаг 1. Перемножая числители дробей, получаем \[3\times 5=15.\]

Перемножая знаменатели дробей вместе, получаем \[7\times 11=77.\]

Шаг 2. Деление полученных чисел дает новую дробь \(\dfrac{15}{77}.\)

Так как числитель и знаменатель новой дроби не имеют общих факторов, это самая простая форма.

Умножить\(\dfrac{2}{5}\) и \(\dfrac{7}{9}\).

Решение

Перемножая числители и знаменатели, получаем

\[\dfrac{2}{5}\times \dfrac{7}{9}=\dfrac{2\times 7}{5 \times 9}=\dfrac{14}{45}.\]

Умножить \(\dfrac{5}{8}\) и \(\dfrac{2}{3}.\)

Решение

Шаг 1. Перемножая числители двух дробей вместе, мы получаем

\(5 \times 2=10.\) Точно так же, делая то же самое со знаменателями, получаем \(8\times 3=24.\)

Шаг 2. Разделив полученные числа, мы получим новую дробь \(\dfrac{10}{24}.\)

Заметим, что числитель и знаменатель новой дроби имеют общий делитель 2.

Шаг 3. Мы получаем простейшую форму этой дроби путем деления общего делителя 2 из числителя 10 и знаменателя 24. Это дает нам \(10 \divsymbol 2=5\)и \(24\divsymbol 2=12\).

Таким образом, простейшая дробь равна \(\dfrac{5}{12}.\)

Правила деления дробей

Чтобы разделить две дроби, вы по существу инвертируете дробь, на которую делите, а затем умножаете ее на первую. Таким образом, деление двух дробей вида

\[\frac{a}{b}\divsymbol\frac{c}{d}=\frac{\frac{a}{b}}{\frac{c} {d}}\]

равносильно умножению дробей \[\frac{a}{b}\times \frac{d}{c}.\] Таким образом, мы имеем

\[\frac{a }{b}\divsymbol\frac{c}{d} =\frac{a}{b}\times\frac{d}{c}. \]

Поскольку мы уже видели, как умножать две дроби, просто следуйте этим шагам отсюда.

Таким образом, мы выполняем следующие шаги для выполнения деления на дроби,

Шаг 1. Инвертируем делитель дроби – числитель становится знаменателем, а знаменатель становится числителем.

Шаг 2. После инверсии перемножьте полученные дроби вместе, используя шаги, описанные для умножения дробей.

Разделить \(\dfrac{5}{8}\) на \(\dfrac{2}{3}.\)

Решение

Шаг 1. Обратив делитель, получим \(\dfrac{3}{2}\).

Шаг 2. Теперь выполняем умножение полученных дробей,

\(\dfrac{5}{8}\) и \(\dfrac{3}{2}\), чтобы получить,

\ [\dfrac{5}{8}\times \dfrac{3}{2}=\dfrac{5\times 3}{8\times 2}=\dfrac{15}{16}.\]

Поскольку числитель и знаменатель не имеют общих делителей, это простейшая форма.

Найдите \(\dfrac{2}{5}\divsymbol \dfrac{3}{8}\).

Решение

Здесь \(\dfrac{2}{5}\) — дробь делимого, а \(\dfrac{3}{8}\) — дробь делителя.

Шаг 1. Инвертируем делитель, получаем \(\dfrac{8}{3}.\)

Шаг 2. Теперь умножаем полученные дроби,

\[\frac{2}{ 5}\divsymbol\frac{3}{8}=\frac{2}{5}\times \frac{8}{3}=\frac{2\times 8}{3\times 5} =\frac{ 16}{15}.\]

Так как числитель и знаменатель не имеют общих множителей, это самая простая форма.

При умножении или делении дроби на целое число \(a\), \(a\) может быть записано как его эквивалентная форма \(\dfrac{a}{1}\), поэтому никаких изменений в процедуре не требуется .

Найдите \(\dfrac{\dfrac{2}{5}}{3}.\)

Решение

Здесь \(\dfrac{2}{5}\) — дробь делимого, а \( 3=\dfrac{3}{1}\) — делитель дроби.

Шаг 1. Переворачиваем делитель, получаем \(\dfrac{1}{3}\).

Шаг 2. Теперь умножьте дроби, чтобы получить

\[\dfrac{2}{5}\times \dfrac{1}{3}=\dfrac{2\times 1}{5\times 3 }=\dfrac{2}{15}. \]

Так как числитель и знаменатель не имеют общих множителей, это самая простая форма.

Упростить \(\dfrac{4}{\dfrac{7}{9}}\).

Решение

Здесь \(4=\dfrac{4}{1}\) — дробь делимого, а \(\dfrac{7}{9}\) — дробь делителя.

Решение

Шаг 1. Переворачиваем делитель, получаем \(\dfrac{9}{7}\).

Шаг 2. Теперь перемножьте дроби, чтобы получить

\[\dfrac{4}{\dfrac{7}{9}}=\dfrac{4}{1}\times \dfrac{9} {7}=\dfrac{4\times 9}{1\times 7}=\dfrac{36}{7}.\]

Так как числитель и знаменатель не имеют общих множителей, это самая простая форма.

Чтобы упростить нашу работу, избегая гигантских умножений, мы можем «отменить» общие множители между числителями и знаменателями в начале, прежде чем мы перемножим члены вместе. Это изменит шаги для умножения дробей на следующие:

Шаг 1. Если какие-либо числитель и знаменатель имеют общий множитель, разделите соответствующий числитель и знаменатель на общий множитель, чтобы «сократить» общий множитель. Делайте это до тех пор, пока между числителями и знаменателями не останется общих множителей.

Шаг 2. Выполнить умножение полученных дробей.

В следующих примерах мы использовали вышеупомянутый метод.

Примеры умножения и деления дробей

До сих пор мы рассматривали примеры операций умножения и деления двух дробей. Вы можете умножать / делить несколько дробей вместе, используя те же правила, что описаны выше. Если есть цепочка из нескольких умножений и делений, вы должны сначала инвертировать члены делителя.

Упростить \(\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}\)

Решение

Здесь умножаются три дроби. Первый шаг состоит в том, чтобы умножить числители дробей вместе \(5\умножить на 18\умножить на 21\) и знаменатели вместе \(9\умножить на 13\умножить на 20.\)

Здесь мы видим, что мы получаем умножение огромных чисел. Чтобы избежать этого, мы собираемся сначала отменить общие факторы, где это возможно.

Шаг 1 . Числители 5,18,21, а знаменатели 9,13,20. Мы видим, что 9 и 18 имеют 9 в качестве общего делителя, а 5 и 20 имеют 5 в качестве делителя, таким образом, мы имеем

\[\frac{5}{9}\times\dfrac{18}{13}\times\dfrac{ 21}{20}=\dfrac{1}{1}\times\dfrac{2}{13}\times\dfrac{21}{4}.\]

Далее, мы можем упростить 2 и 4, разделив на 2, чтобы получить

\[\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}=\dfrac{1}{13} \times\dfrac{ 21}{2}.\]

Шаг 2. И окончательный ответ:

\[\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}=\dfrac{21}{13\times 2 }=\dfrac{21}{26}.\]

Упростить \[\dfrac{14}{39}\times\dfrac{12}{35}\divsymbol\dfrac{8}{13}\times\dfrac {2}{9}\]

Решение

Шаг 1. Инвертируйте дробь делителя, чтобы получить

\[\dfrac{14}{39}\times\dfrac{12}{35}\ divsymbol\dfrac{8}{13}\times\dfrac{2}{9}=\dfrac{14}{39}\times\dfrac{12}{35}\times\dfrac{13}{8}\times \dfrac{2}{9}\]

Шаг 2. Теперь попробуем привести термы к простейшему виду. Разделив 14 и 35 на 7, 13 и 39 на 13, 12 и 9 на 3, 2 и 8 на 2, получим

\[\dfrac{14}{39}\times\frac{12}{35}\ раз\dfrac{13}{8}\times\dfrac{2}{9}=\dfrac{2}{3}\times\dfrac{4}{5}\times\dfrac{1}{4}\times \dfrac{1}{3}\]

Шаг 3 . Отбросив 4, мы получим \[\dfrac{2}{3}\times\dfrac{4}{5}\times\dfrac{1}{4}\times\dfrac{1}{3}=\dfrac {2}{5}\times\dfrac{1}{5}\times \dfrac{1}{3}=\dfrac{2}{45}.\]

В следующем примере мы выполняем умножение и деление смешанных дробей.

Смешанная дробь представляет собой комбинацию целого числа и дроби. Чтобы умножить или разделить смешанные дроби, сначала преобразуйте их в неправильные дроби, а затем продолжите стандартный процесс.

Упростить

\[4\dfrac{2}{7}\times 2\dfrac{1}{3}\div \dfrac{3}{5}.\]

Решение

Преобразование смешанного дроби на неправильные дроби, получаем

\[4\dfrac{2}{7}\times 2\dfrac{1}{3}\div \frac{3}{5} = \dfrac{30}{7}\times \dfrac{7} {3} \div \dfrac{3}{5}. 3}\div \dfrac{y}{x}\) 92}. \]

Умножение и деление дробей – основные выводы

• Чтобы умножить дроби, нужно перемножить числители вместе и знаменатели вместе. Таким образом, умножение формы \( \dfrac{a}{b}\times \dfrac{c}{d}\) эквивалентно \(\dfrac{a\times c}{b\times d}.\)
• Чтобы разделить число (целое число или дробь) на дробь, мы должны сначала инвертировать делитель и применить процесс умножения к оставшейся части выражения.
• Чтобы умножить или разделить смешанные дроби, сначала преобразуйте их в неправильные дроби, а затем продолжите стандартный процесс.

Дробные показатели степени: правила умножения и деления

Обновлено 08 декабря 2020 г.

Ли Джонсон

Обучение работе с показателями степени является неотъемлемой частью любого математического образования, но, к счастью, правила их умножения и деления соответствуют правила для не дробных показателей. Первый шаг к пониманию того, как обращаться с дробными показателями, — это краткое изложение того, что они собой представляют, а затем вы можете посмотреть, как можно комбинировать показатели степени, когда они умножаются или делятся и имеют одно и то же основание. Короче говоря, вы складываете степени вместе при умножении и вычитаете один из другого при делении, при условии, что они имеют одно и то же основание.

TL;DR (слишком длинный; не читал)

Умножьте члены с показателями по общему правилу:

​ x ^a ​ + ​ 7 ​ 7 x x ^9038 9038 ​ ^{(​ a ​ + ​ b ​)}

And divide terms with exponents using the rule:

​ x ^a ​÷ ​ x ^b ​ ^{= ​ x ​ (​ а ​ – ​ б ​)}

Эти правила работают с любым выражением вместо ​ a ​ и ​ b ​, даже с дробями.

Что такое дробные показатели?

Дробные показатели степени обеспечивают компактный и полезный способ выражения квадратных, кубических и более высоких корней. Знаменатель степени говорит вам, какой корень из «базового» числа представляет термин. В таком термине, как x ^a , вы называете x основанием, а a показателем степени. Таким образом, дробный показатель говорит вам: 94

Обратить и умножить – Математика для учителей начальных классов

Дроби

Метод отсутствующих множителей — особенно хороший способ понять дробное деление. Он основан на том, что мы знаем об умножении и делении, подтверждая, что эти операции имеют одинаковые отношения независимо от того, являются ли числа целыми числами, дробями или чем-либо еще. Это имеет смысл. Но мы видели, что это не всегда работает хорошо. Например,

   

можно переписать как

   

Вы хотите спросить:

• Для числителя: . Мы можем заполнить пробел цифрой 3.
• Для знаменателя: . Мы можем заполнить пробел с помощью . (Почему это работает?)

Итак, имеем:

   

Вы узнали о дробях типа

   

еще в «Что такое дробь?» глава. Это значит, что каждому ребенку достается по 3 пирожка. Так сколько же получает отдельный ребенок (целый ребенок)? Вы можете нарисовать картинку, чтобы помочь вам понять это. Но мы также можем использовать правило ключевой дроби, чтобы помочь нам.

   

Этот процесс станет ключом к пониманию того, почему правило «перевернуть и умножить» для дробного деления действительно имеет смысл.

Пример

пироги делятся поровну между детьми. Сколько пирогов досталось каждому ребенку?

Технически мы могли бы просто записать ответ как

   

и готово! Ответ эквивалентен этой дроби, так почему бы и нет?

Есть ли способ сделать это более дружелюбным? Что ж, если мы заменим эти смешанные числа на «неправильные» дроби, это немного поможет:

   

Это немного лучше, но все еще не ясно, сколько пирога получит каждый ребенок. Давайте воспользуемся правилом ключевой фракции, чтобы сделать фракцию еще более дружелюбной.

Давайте умножим числитель и знаменатель на 3. (Почему на три?) Помните, это означает, что мы умножаем дробь на , которая является специальной формой 1, поэтому мы не меняем ее значение.

   

Теперь умножьте числитель и знаменатель на 4. (Почему четыре?)

   

Теперь мы видим, что ответ равен . Это означает, что делить пироги между детьми — то же самое, что делить 92 пирога среди 63 детей. (В обоих случаях каждый ребенок получает одинаковое количество пирога.)

 

Пример

Давайте сейчас забудем о контексте и просто сосредоточимся на вычислениях, чтобы лучше видеть, что происходит. Попробуйте это:

   

Умножение числителя и знаменателя на 5 (почему мы выбрали 5?) дает

   

Теперь умножьте числитель и знаменатель на 3 (почему мы выбрали 3?):

   

Самостоятельно

1. Каждая из приведенных ниже дробей является прекрасной дробью, но ее можно было бы записать в более простой форме. Так сделай это! Запишите каждое из них в более простой форме, следуя приведенным выше примерам.

   

 

Подумай / Соедини / Поделись

• Джессика вычислила второе упражнение выше следующим образом:

   

Верно ли ее решение или она что-то не понимает? Тщательно объясните, что происходит с ее решением, и что бы вы сделали как учитель Джессики.

• Исаак рассчитал последнее упражнение выше следующим образом:

   

Верно ли его решение или он что-то не так понял? Тщательно объясните, что происходит с его решением, и что бы вы сделали как учитель Исаака.

Возможно, вы, сами того не осознавая, только что нашли другой способ деления дробей.

Пример: 3/5 ÷ 4/7

Рассмотрим . Мы знаем, что дробь — это ответ на задачу о делении, то есть

9.0002    

Теперь мы знаем, как упростить такие уродливые дроби! Умножьте числитель и знаменатель на 5:

   

Теперь умножьте их на 7:

   

Готово! Итак,

   

 

Пример: 09.

05 ÷ 11.08

Давайте еще раз! Рассмотрим:

   

Давайте умножим числитель и знаменатель на 9 и на 11 одновременно. (Почему бы и нет?)

   

(Вы видите, что здесь произошло?)

Итак, у нас есть

   

Самостоятельно

Вычислите каждое из следующих значений, используя технику упрощения из приведенных выше примеров.

   

Рассмотрим проблему. Джанин писал(а):

   

Она остановилась, не завершив последний шаг, и воскликнула: «Деление одной дроби на другую — это то же самое, что умножение первой дроби на вторую в перевернутом виде!»

Подумай / Соедини / Поделись

Сначала проверьте каждый шаг работы Джанин здесь и убедитесь, что она права в том, что она сделала до этого момента. Затем ответьте на следующие вопросы:

• Вы понимаете, что говорит Джанин? Объясните это очень ясно.
• Разработайте с использованием метода упрощения.