Деление дробей. Правила. Примеры. — tutomath.ru репетитор по математике

Следующее действие, которое можно выполнять с дробями это деление. Выполнять деление дробей достаточно просто главное знать несколько правил деления. Разберем правила деления и рассмотрим решение примеров на данную тему.

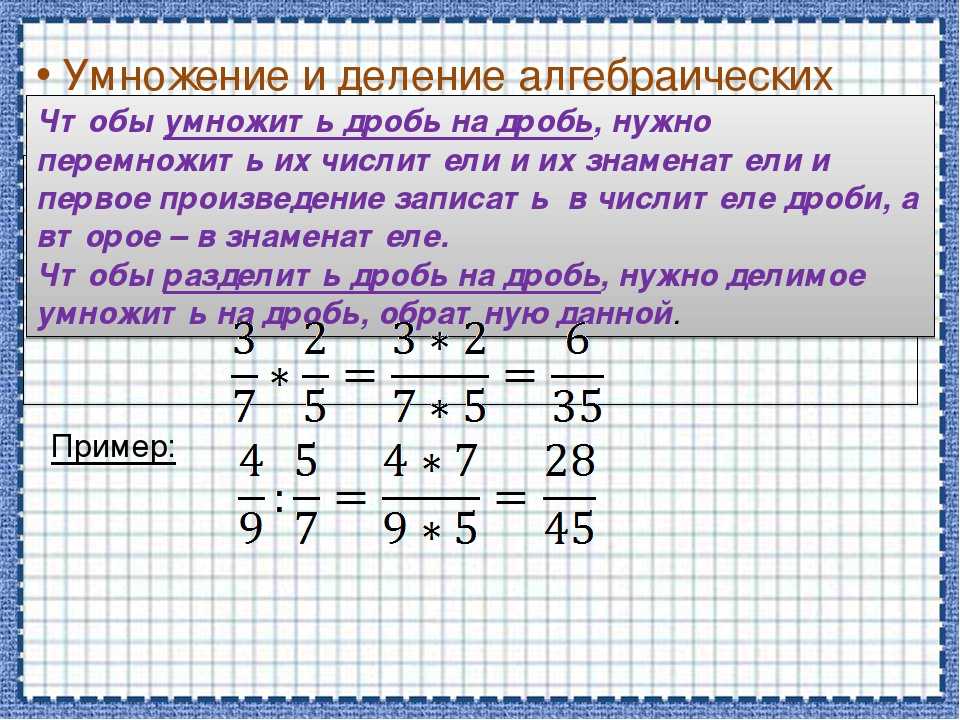
Деление дроби на дробь.

Чтобы делить дробь на дробь, нужно дробь, которая является делителем перевернуть, то есть получить обратную дробь делителю и потом выполнить умножение дробей.

\(\bf \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c}\\\)

Пример:

Выполните деление обыкновенных дробей  .

Деление дроби на число.

Чтобы разделить дробь на число, нужно знаменатель дроби умножить на число.

\(\bf \frac{a}{b} \div n = \frac{a}{b} \div \frac{n}{1} = \frac{a}{b} \times \frac{1}{n}\\\)

Рассмотрим пример:

Выполните деления дроби на натуральное число \(\frac{4}{7} \div 3\).

Как мы уже знаем, что любое число можно представить в виде дроби \(3 = \frac{3}{1} \).

\(\frac{4}{7} \div 3 = \frac{4}{7} \div \frac{3}{1} = \frac{4}{7} \times \frac{1}{3} = \frac{4 \times 1}{7 \times 3} = \frac{4}{21}\\\)

Деление числа на дробь.

Чтобы поделить число на дробь, нужно знаменатель делителя умножить на число, а числитель делителя записать в знаменатель. То есть дробь делитель перевернуть.

Рассмотрим пример:

Выполните деление числа на дробь.

Деление смешанных дробей.

Перед тем как приступить к делению смешанных дробей, их нужно перевести в неправильную дробь, а дальше выполнить деление по правилу деления дроби на дробь.

Пример:

Выполните деление смешанных дробей.

\(2\frac{3}{4} \div 3\frac{1}{6} = \frac{11}{4} \div \color{red} {\frac{19}{6}} = \frac{11}{4} \times \color{red} {\frac{6}{19}} = \frac{11 \times 6}{4 \times 19} = \frac{11 \times \color{red} {2} \times 3}{2 \times \color{red} {2} \times 19} = \frac{33}{38}\\\)

Деление числа на число.

Чтобы поделить простые числа, нужно представить их в виде дроби  и выполнить деление по правилам деления дроби на дробь.

Пример:

\(2 \div 5 = \frac{2}{1} \div \color{red} {\frac{5}{1}} = \frac{2}{1} \times \color{red} {\frac{1}{5}} = \frac{2 \times 1}{1 \times 5} = \frac{2}{5}\\\)

Примечание к теме деление дробей:
На нуль делить нельзя.

Вопросы по теме:
Как делить дроби? Как разделить дробь на дробь?
Ответ: дроби делятся так, первую дробь делимое умножаем на дробь обратную дроби делителя.

Как делить дроби с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, все дроби делятся по правилу деления дроби на дробь.

Пример №1:
Выполните деление и назовите делитель, дробь, обратную делителю: а) \(\frac{5}{9} \div \frac{8}{13}\) б) \(2\frac{4}{5} \div 1\frac{7}{8}\)

Решение:
а) \(\frac{5}{9} \div \frac{8}{13} = \frac{5}{9} \times \frac{13}{8} = \frac{65}{72}\\\\\)

\( \frac{8}{13}\) – делитель, \( \frac{13}{8}\) – обратная дробь делителя.

б) \(2\frac{4}{5} \div 1\frac{7}{8} = \frac{14}{5} \div \frac{15}{8} = \frac{14}{5} \times \frac{8}{15} = \frac{14 \times 8}{5 \times 15} = \frac{112}{75} = 1\frac{37}{75}\\\\\)

\( \frac{15}{8}\) – делитель, \( \frac{8}{15}\) – обратная дробь делителя.

Пример №2:
Вычислите деление: а) \(5 \div 1\frac{1}{4}\) б) \(9\frac{2}{3} \div 8\)

Решение:

а) \(5 \div 1\frac{1}{4} = \frac{5}{1} \div \frac{5}{4} = \frac{5}{1} \times \frac{4}{5} = \frac{\color{red} {5} \times 4}{1 \times \color{red} {5}} = \frac{4}{1} = 4 \\\\\)

б) \(9\frac{2}{3} \div 8 = \frac{29}{3} \div \frac{8}{1} = \frac{29}{3} \times \frac{1}{8} = \frac{29 \times 1}{3 \times 8} = \frac{29}{24} = 1\frac{5}{24}\\\\\)

Деление дробей — как делить дроби 🤔

Поможем понять и полюбить математику

Начать учиться

Дроби — тема в математике, которую точно нельзя пропустить. Ведь мы сталкиваемся с ними почти в каждой сфере жизни: музыка, медицина, строительство. В этой статье обсудим деление.

Понятие дроби

Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b.

Существует два формата записи:

• обыкновенный вид — 1/2 или a/b,

• десятичный вид — 0,5.

Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. В 5 классе ребята это уже знают.

Дроби бывают двух видов:

1. Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.

2. Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.

Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — .

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Основные свойства дроби

1. Дробь не имеет значения, при условии, если знаменатель равен нулю.

2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

3. Две дроби a/b и c/d называются равными, если a * d = b * c.

4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Деление дробных чисел

Деление — арифметическое действие, по которому можно узнать, сколько раз одно число содержится в другом. А еще деление — это обратное действие умножения.

Свойства деления:

1. При делении на единицу получится такое же число: a : 1 = a.

2. На ноль делить нельзя.

3. При делении нуля на что-либо получится ноль: 0 : a = 0.

4. При делении числа на само себя получится единица: a : a = 1.

5. При деления суммы на какое-либо число, можно разделить на него каждое слагаемое и сложить полученные результаты: (a + b) : c = a : c + b : c.

6. При делении разности на какое-нибудь число, можно разделить на него уменьшаемое и вычитаемое отдельно и из первого частного вычесть второе: (a — b) : c = a : c — b : c.

7. При делении произведения двух множителей на число, можно разделить на него любой из множителей и частное умножить на второй множитель: (a * b) : c = (a : c) · b = a * (b : c).

Деление обыкновенных дробей

Как делить дробь на дробь? Выполняем следующую последовательность действий:

• числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;

• знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Как делить дроби с разными знаменателями? Тут все просто: пользуемся правилами выше, поскольку на практике нам не важно, одинаковые знаменатели или нет.

Деление дроби на натуральное число

Для деления дроби на натуральное число нужно:

• представить данный делитель в виде неправильной дроби, где числитель равен этому числу, а знаменатель единица;

• произвести деление по предыдущему правилу.

Деление натурального числа на дробь

Чтобы поделить натуральное число на обыкновенную дробь нужно:

• делимое записать в виде дроби;

• умножить полученную дробь на дробь, обратную делителю, воспользовавшись алгоритмом, который мы уже разобрали выше.

Деление на смешанное число

Для деления смешанных чисел необходимо:

• представить числа в виде неправильных дробей

• выполнить деление с полученными дробями.

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

185.8K

Сложение дробей: теория и практика

К следующей статье

157.7K

Вычитание дробей

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Значение – Математика для учителей начальных классов

Дроби

Деление дробей — одна из самых сложных задач по математике в начальной школе. Вы уже привыкли к правилу: чтобы разделить на дробь, умножьте на обратную. («перевернуть и умножить»). Но спросите себя: почему это правило работает? Это действительно имеет смысл для вас? Можете ли вы объяснить, почему это имеет смысл для третьеклассника?

Мы собираемся перейти к правилу «перевернуть и умножить», но по пути мы найдем несколько более значимых способов понять деление дробей. Так что, пожалуйста, подыграйте: притворитесь, что вы еще не знаете правило «переверни и умножь», и решите задачи этой главы другими методами.

Запомните модель деления в кавычках: означает:

Сколько групп по 3 я могу найти в 18?

Мы начинаем с 18 точек (или шоколадных батончиков, или молекул) и делаем группы из 3 точек (или 3 любых других). Мы спрашиваем: сколько групп мы можем сделать?

18 точек, разделенных на группы по 3 точки. Так как групп 6, то 18 ÷ 3 = 6,

Та же идея применима, когда мы делим дроби. Например,  означает:

.

Сколько групп я могу найти в 6?

Пример: 6 ÷ 2/3

Давайте нарисуем 6 кругов и посмотрим, сколько групп мы можем найти:

Мы нашли девять одинаковых групп размера , поэтому мы заключаем, что

   

К сожалению, найти равные группы не всегда так просто. Например, задает вопрос:

Сколько групп я могу найти в ?

Пример: 3/4 ÷ 1/3

Давайте нарисуем круг и посмотрим, сколько групп мы можем найти:

На первом рисунке показан круг. На втором рисунке показаны две равные группы внутренней части , но осталось немного. Делаем вывод

   

Но сколько еще? Можем ли мы понять это точно?

Вот метод, который позволит вам выполнить вычисления точно. Мы будем использовать прямоугольные круги и разделим их на строки и столбцы на основе знаменателей делимых чисел.

Пример: 3/4 ÷ 1/3

Начните с рисования двух одинаковых прямоугольников, в каждом из которых 4 строки (от знаменателя и 3 столбца (от знаменателя ).

Оттенок первого прямоугольника (это ровно три строки) и оттенок второго прямоугольника (так что это один столбец).

Теперь спросите: сколько копий  я могу найти в ?  Ну, равно четырем меньшим квадратам.  Таким образом, мы находим группы, равные к этому:

На картинке мы можем найти:

• две группы по четыре квадрата (две группы ) и
• остался один квадрат той группы, которую мы ищем.

Делаем вывод:

   

 

Подумай / Соедини / Поделись

Используйте любой метод, описанный выше, чтобы найти следующие частные. Помните, притворитесь, что вы не знаете никакого метода деления дробей, кроме нахождения групп одинакового размера.

   

   

Подумай / Соедини / Поделись

Решите каждую из следующих задач на деление дробей методом «группы равного размера»:

   

   

Что вы заметили?

Это приводит к нашему первому методу деления дроби:

Метод общего знаменателя

Если две дроби имеют одинаковый знаменатель, то при их делении можно просто разделить числители. В символах

   

 

Подумай / Пара / Поделись

• Используйте метод общего знаменателя, чтобы найти следующие частные:

   

• Что делать, если дроби не имеют общего знаменателя? Является ли метод бесполезным, или вы можете найти способ заставить его работать? Можете ли вы решить эти проблемы?

   

Мы знаем, что всегда можем превратить задачу деления в задачу умножения с «недостающим множителем». Может ли это помочь нам вычислить дробное деление? Иногда!

Подумай / Соедини / Поделись

Для каждой задачи на деление перепишите ее как вопрос на умножение отсутствующих множителей. Затем найдите частное, используя свои знания об умножении дробей.

   

К сожалению, метод отсутствующего фактора не всегда работает так хорошо. Например,

   

можно переписать как

   

Не существует подходящего отношения целых чисел, которое, очевидно, заполняет пробел, но мы скоро вернемся к этой идее и решим ее.

Деление дробей

Деление дробей может быть немного сложным. Это единственная операция, которая требует использования , обратного . Использование обратного просто означает, что вы перевернуть дробь или перевернуть ее .

Например, , обратное число 2/3 равно 3/2 .

После того, как мы дадим вам правило деления, мы покажем вам, ПОЧЕМУ вы должны использовать обратное число в первую очередь.

А пока…

Вот правило деления

Чтобы разделить, преобразуйте процесс деления дроби в процесс умножения, выполнив следующие шаги.

1. Замените «÷» (знак деления) на «x» (знак умножения) и инвертируйте число справа от знака.
2. Умножьте числители.
3. Умножьте знаменатели.
4. При необходимости перепишите свой ответ в упрощенной или сокращенной форме

После того, как вы выполните Шаг № 1 для деления дробей, задача фактически изменится с деления на умножение .

Пример 1: Деление дробей на дроби

1/2 ÷ 1/3 = 1/2 x 3/1

1/2 x 3/1 = 3/2

Упрощенный ответ: 1 1/2

Пример 2. Деление дробей на целые числа

1/2 ÷ 5 = 1/2 ÷ 5/1

(Не забудьте преобразовать
целых чисел в дроби, СНАЧАЛА!)

1/2 ÷ 5/1 = 1/2 x 1/5

1/ 2 x 1/5 = 1/10

Пример 3: Деление целых чисел на дроби

6 ÷ 1/3 = 6/1 ÷ 1/3

(Не забудьте преобразовать
целых чисел в дроби, СНАЧАЛА!)

6/1 ÷ 1/3 = 6/1 x 3/1

6/1 x 3/1 = 18/1 = 18

Вот и все. главное, что вы должны помнить при делении, это сначала преобразовать целые числа в дроби, затем инвертировать дробь справа от знака деления и изменить знак на умножение.

«делитель» имеет некоторые других соображений  вы должны иметь в виду…

Особые примечания!

• Не забывайте инвертировать только делитель.
• Числитель или знаменатель делителя не может быть «нулем».
• Преобразование операции в умножение ПЕРЕД выполнением любых отмен.

Я обещал попробовать объяснить почему правило требует инвертировать делитель.

Вот.

Если серьезно подумать, мы делим дробь на дробь , которая образует так называемую «сложную дробь» . На самом деле это выглядит так…

При работе со сложными дробями мы сначала хотим избавиться от знаменателя (1/3) , чтобы нам было проще решить эту задачу.

Вы, наверное, помните, что любое число, умноженное на его обратное число, равно 1. И так как 1/3 x 3/1 = 1 , мы можем использовать обратное свойство 1/3, (3/1) , чтобы сделать значение знаменателя равным 1.

Вы также можете вспомнить, что что бы мы ни делали со знаменателем дроби, мы должны также делаем с его числителем, чтобы не менять общую дробь «значение».