Письменное умножение и деление

Большие числа удобно перемножать и делить письменно в столбик. Письменное умножение — это поразрядное умножение. Каждый разряд второго множителя умножается на первый множитель как одноразрядное число. В произведении поэтапного (разрядного) умножения первый разряд попадает в столбец того разряда второго множителя, на который умножают.

Правило. При умножении в столбик два множителя располагаются один под другим так, чтобы разряды чисел совпадали (находились в одном столбце). Слева ставится знак «х».

Если один из множителей или оба множителя оканчиваются нулями, то числа записываются так, чтобы значащие цифры наименьшего из разрядов находились в одном столбце. Нули переносятся в произведение и в поле записи поэтапных произведений не заносятся.

Поэтапные (разрядные) произведения складываются по разрядам и под чертой записывается результат. Слева от слагаемых произведений ставится знак «+».

Письменное умножение в столбик равноценно письменному умножению по разрядам в строку.

При письменном умножении в строку применяются сочетательный и распределительный законы умножения (сумму заменяем слагаемыми и первый множитель умножаем на каждое из слагаемых).

Пример.
1 014 * 258 = 261 612
1 014 * 258 = 1 014 * (200 + 50 + 8) = 1 014 * 200 + 1 014 * 50 + 1014 * 8 = 202 800 + 50 700 + 8 112 = 261 612

Чтобы перемножить в столбик числа, оканчивающиеся нулями, нужно их подписать друг под другом так, чтобы первая справа значащая цифра первого множителя стояла под первой справа значащей цифрой второго множителя

.

Например: 1 014 * 258 = 261 612

•      1014   — первый множитель
• Х
•        258   — второй множитель
• ———      поэтапные произведения:
•      8112   — слагаемое (первое произведение)
• + 5070    — слагаемое (второе произведение)
•   2028      — слагаемое  (третье произведение)
• ———
•   261612  — сумма (результат умножения)

Примеры записи умножении чисел, оканчивающихся нулями.

•       450
• Х
•       270
• ———
•    315       (45 * 7 = 315)
• +
•    90         (45 * 2 = 90)
• ———
•  121500

Внимание! Нули в конце множителей в поэтапном умножении не принимают участия, а сразу все нули множителей переносятся в результат вычислений.

Правильная запись:

Неправильная запись

Письменное деление многозначных натуральных чисел осуществляется и в строку, и в столбик по этапам.

Правило. При письменном делении двух натуральных чисел слева записывается делимое, а справа от него через вертикальную черту — делитель.

Под делимым в столбец записываются поэтапные произведения каждого разряда частного на делитель. После каждого поэтапного произведения проводим горизонтальную черту, под которой записывается разность делимого и произведения, которая должна быть всегда меньше делителя, если разряд частного вычислен верно.

Дополнив разность следующим разрядом делимого, принимаем это число за следующее поэтапное делимое.

Деление по этапам производим до первого разряда заданного условием делимого. Если последняя разность 0 или число, меньшее делителя, то деление натуральных чисел окончено.

Частное по разрядам (от большего к меньшему) записывается под горизонтальной чертой под делителем. В частном должно быть столько же разрядов, сколько этапов деления.

Рассмотрим пример: 12 546 : 82
Производим деление первого этапа. Множитель (1) записываем как высший разряд частного. Вычисляем разность делимого и произведения первого этапа деления (125 — 82 = 43) и дописываем к ней справа один разряд из делимого, который стоит после наименьшего разряда числа, взятого для первого этапа деления. Полученное число (434) служит делимым второго этапа

деления.

Делимое второго этапа делим на делитель (434 : 82), определяем следующий разряд в частном (5) и остаток после второго этапа деления (24). Дописываем к остатку следующий разряд делимого и выполняем третий этап деления (246 : 82). Определяем третье число в частном (3) и остаток (0).

Деление окончено после третьего этапа, следовательно, в частном — трех разрядное число (153).

Проще такое деление производить в столбик также в три этана (деление углом — это тоже поэтапное деление):

Делимое кратно 82, так как разделилось без остатка.

Правило. Если делимое и делитель умножить или разделить на одно и то же натуральное число, то их частное не изменится.

Например:
12 : 4 = 3

умножим делимое и делитель на 5, получим:
60 : 20 = 3

Например:
625 : 125 = 5
разделим делимое и делитель на 25, получим:
125 : 5 = 5

Запись опубликована в рубрике Математика с метками деление, умножение. Добавьте в закладки постоянную ссылку.

Умножение

: действительно ли порядок имеет значение?

Кое-что, что меня интересует прямо сейчас об умножении в 3-м классе…

• Когда ученики замечают, что 4 x 3 — это то же произведение, что и 3 x 4, и говорят: «Порядок не имеет значения», как вы отвечаете на этот вопрос?
• Существует ли соглашение о написании 4 групп по 3 в виде 4 x 3?
• Есть ли время, например, при переходе к делению или умножению дробей и делению, когда порядок имеет значение при решении или размышлении о контексте?

Ответы, которые у меня есть прямо сейчас на эти вопросы….

• Прямо сейчас, поскольку они только учатся умножению, я спрашиваю их, что они думают и почему.
• Я думаю, что в моем сознании есть некоторая условность, потому что картина меняется. Три корзины по 2 яблока в каждой отличаются от 2 корзин по 3 яблока в каждой. Кроме того, при чтении CCSS так кажется.
• Я все еще думаю о делении, но это наводит меня на мысль, что в этом и будет разница между делением на части и делением в кавычках. Я также думаю, что когда учащиеся начинают умножать четвертую дробь, они связывают это со своими знаниями о операциях с целыми числами, поэтому 4 x 1/2 — это 4 группы по 1/2. Это кажется важным.

Мы с учителями 3-го класса много обсуждали эти идеи. Учащиеся рисовали множество изображений точек, и некоторые твердо убеждены, что эти два выражения означают одно и то же, потому что они могут перегруппировать точки, чтобы они соответствовали обоим выражениям. Другие думают, что они другие, потому что картина меняется.

Все это кажется замечательным, но затем ученики используют это рассуждение для решения задач. Например, для такой задачи, как , есть 5 полок с 6 тыквами на каждой полке. Сколько тыкв на полках? учеников представят это как 5×6 или 6×5. Является ли это проблемой для меня, не совсем, если у них есть способ получить 30, но должен ли он быть? Я не уверена.

Я пошел в класс 3-го класса, чтобы попробовать кое-что. Я сказал им, что собираюсь рассказать им две истории, и хотел, чтобы они нарисовали картинку, представляющую историю (не картинку из художественного класса, а математическую картинку) вместе с соответствующим уравнением умножения.

1-й этаж: На стене продуктового магазина 5 полок. На каждой полке по 6 тыкв.

2-й этаж: На другой стене 6 полок с 5 тыквами на каждой полке.

Я спросил их, одинаковы ли истории, и мы, как я и ожидал, разговорились о 5×6 против 6×5 и о том, что это значит с точки зрения истории. Они говорили о 5 группах по 6, связывали переключение множителей на сложение, а затем некоторые говорили о 6 рядах по 5.

Из этой работы выяснилось много интересного…

• У некоторых учеников были разные ответы на две задачи. . Они, очевидно, не считали эти два выражения одинаковыми, потому что у них возникли проблемы с 5 группами по 6, когда они пытались считать по 6 и забыли строку.

• Одна ученица сказала, что вторая задача ей понравилась больше, потому что она могла считать до 5 легче, чем до 6.

• Учащиеся пропускают счет на 5, но добавляют 6 при нахождении 5 групп по 6. 
• Один ученик заметил разницу между 5 и 6 и понял, что удаление одной полки равнозначно добавлению тыквы в каждый из остальных рядов.

• Один ученик показал, как он использовал то, что знал об одном, чтобы поменять местами множители, чтобы упростить решение.

 

Но они продолжают спрашивать Кто из них прав? и говорю им, что у меня нет для них ответа. Я просто продолжаю спрашивать их:

Ответ тот же?

Когда вы слушаете рассказ, картинка та же самая?

После вчерашней беседы с Майклом Першаном я все еще нахожусь в странном состоянии, думая об этом, и я думаю, что он и я частично согласны с несколькими вещами (поправьте меня, если я ошибаюсь, Майкл) … Да, я думаю, что «группы» важны для контекста истории. Я хочу, чтобы учащиеся знали, что они могут найти ответ на эти типы задач путем умножения. Я хочу, чтобы учащиеся могли абстрагироваться от выражения и изменить порядок факторов, если они знают, что это облегчит решение, НО то, что я не могу прийти к четкому решению, это…

Если мы должны поощрять (или хотеть), чтобы учащиеся представляли проблему таким образом, который соответствует контексту, И если ответ положительный, то следующим образом:

Нравится:

Нравится Загрузка…

Умножение

Умножение и Отдел

 

 

Эти страницы обсуждают правила простого умножения и случая умножения II.

 

Простой Умножение

 

Есть для решения этой проблемы не предусмотрена дополнительная работа. Два варианта, что они сделали свою царапину работали над отдельным документом, либо выполняли арифметику в уме. В тексте не сказано, но я Интересно, определяли ли они простое умножение как умножение на меньшее число? больше или равно двенадцати или другому числу. Процесс для этой проблемы, кажется, 2 x 4 = 8, что дает нам цифру единиц. Чтобы получить цифру десятков, они выполнили (2 x 1) + (1 x 4) = 6. Этот метод продолжается до конца расчет. Для этого типа задач они не умножали 2 x 4684114 = 9368228, затем умножьте 10 x 4684114 = 46841140. Наконец, сложите два произведения 9368228. + 46841140 = 56209368.

 

Умножение Случай II

 

Теперь мы рассмотрим случай умножения II. Этот случай умножения аналогичен нашей стандартной форме. Разница лишь в том, что они не поставьте нули там, где значения не применяются.

 

 

Умножение Случай II Правило: «Множитель, помещаемый под единицы множителя под единицы десятки под десятками умножаются на каждый значащий множитель отдельно поместив первую цифру в каждом продукте точно под его множителем, затем добавьте несколько продуктов вместе в сумме в том виде, в каком они есть, и их сумма будет будет общий продукт»

 

 

 

 

 

 

 

Умножение Случай III и Случай IV

 

 

Эти страницы содержат процедуры умножения Case III и Case IV.

 

Умножение Случай III

 

Умножение Случай III имеет дело с числами, которые содержат нули справа либо от, либо от оба числа.

Мы видим что числа выстроены в линию, используя первую цифру каждого числа, которое делает не содержать нуля. Итак, проблема теперь становится 318 x 36, а нули просто переносятся вниз.

 

 

Для случае, когда оба числа содержат конечные нули, они выстраиваются в ряд, как показано на это изображение.

 

Умножение Пример IV Случай IV Правило: «Когда множитель является составным числом, то есть когда он получается путем умножения любых двух чисел в таблице вместе ровно сначала на одна из этих фигур и это произведение на другое и последнее произведение будет всего требуется»

 

примеры, найденные для случая IV, похоже, не следуют правилу.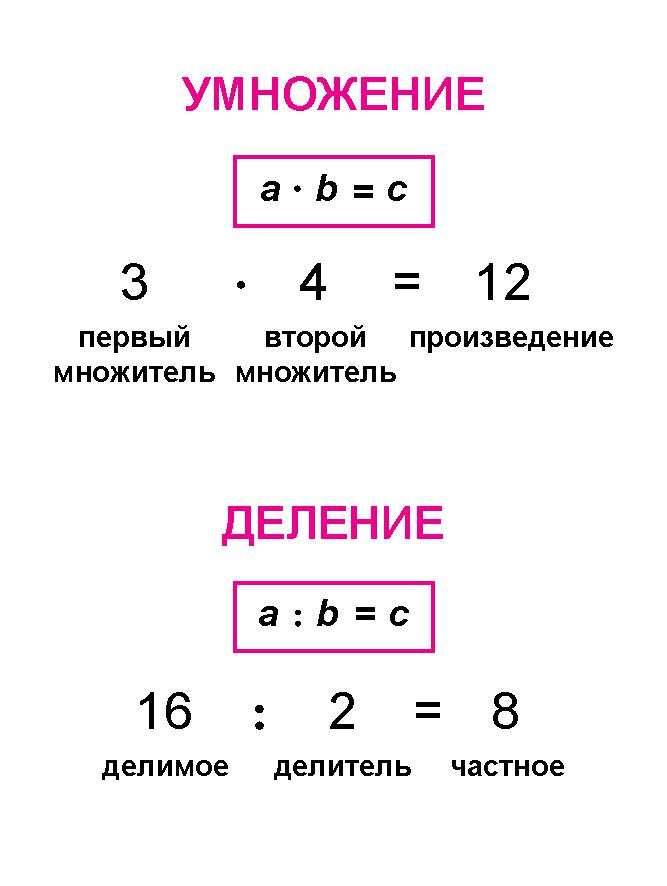 По определению правила я бы подумайте, что 615243 x 144 = 88594992 становится (615243 x 12) x 12 = 88594992.

 

Умножение Случай V и деление целых чисел Случай V

 

 

Умножение Случай V касается приложений и умножения. Эти проблемы умножают цену и количество, чтобы найти общую цену.

 

 

 

Далее мы см. деление целых чисел.

 

Подразделение Целые числа

 

 

формат для этих задач немного отличается от нашей стандартной формы. Разница в том, что частное помещается справа от дивиденда.

 

Дополнительно Метод деления

Сокращения в делении — еще один метод. Этот метод деления сравним со случаем IV умножения.

 

 

Здесь мы есть 178464  16. Это упрощается как (178464 4) 4.