Лучше, чем в столбик: новый способ перемножать большие числа
Австралийский математик нашел максимально эффективный алгоритм перемножения больших чисел. В рубрике «Техно-уик-энд» научные разработки, далекие от практики, но позволяющие лучше понять окружающий мир
Дэвид Харви, сотрудник университета Нового Южного Уэльса в Сиднее, и его французский коллега Йорис Ван дер Хэвен решили задачу, поставленную математиками еще полвека назад. Речь идет о доказательстве гипотезы Шёнхаге — Штрассена. Согласно этой гипотезе, возможен такой алгоритм перемножения целых N-значных чисел, что число шагов алгоритма с возрастанием числа не будет увеличиваться быстрее, чем N * logN.
Простейший алгоритм умножения знаком всем с начальной школы, это так называемое умножение в столбик. Чтобы перемножить два числа, надо по существу умножить каждую цифру первого числа на каждую цифру второго, а потом еще выполнить несколько сложений и расположить результаты в правильном порядке. Ключевой этап — перемножение цифр: если наши числа трехзначные, придется обратиться к таблице умножения 9 раз, а если пятизначные — 25 раз. В общем случае число таких процедур увеличивается пропорционально числу знаков в перемножаемых числах, возведенному в квадрат. И если эти числа достаточно велики, то количество шагов алгоритма становится поистине огромным.
Ключевой этап — перемножение цифр: если наши числа трехзначные, придется обратиться к таблице умножения 9 раз, а если пятизначные — 25 раз. В общем случае число таких процедур увеличивается пропорционально числу знаков в перемножаемых числах, возведенному в квадрат. И если эти числа достаточно велики, то количество шагов алгоритма становится поистине огромным.
В 1950-х годах советский математик Анатолий Карацуба обнаружил способ уменьшить сложность алгоритма умножения. В его алгоритме число шагов увеличивается не быстрее, чем N1,58 — это существенно меньше, чем N2. Впрочем, если читателю вздумается ознакомиться с алгоритмом Карацубы, он обнаружит, что при этом сам метод существенно сложнее обычного школьного умножения. Согласно оценкам, его преимущество проявляется, начиная с чисел, имеющих не менее 10 000 десятичных разрядов.
Десять лет спустя проблемой занялись два немецких математика, которые предложили еще более экономичный алгоритм — с числом шагов не больше чем N * logN * log(logN). Алгоритм Шёнхаге — Штрассена, однако, тоже не оптимален, эти же математики предположили, что возможно перемножать большие числа так, чтобы число шагов не росло быстрее чем N * logN. Однако ни предложить конкретный способ, ни даже доказать его возможность не удавалось вплоть до настоящего времени.
Алгоритм Шёнхаге — Штрассена, однако, тоже не оптимален, эти же математики предположили, что возможно перемножать большие числа так, чтобы число шагов не росло быстрее чем N * logN. Однако ни предложить конкретный способ, ни даже доказать его возможность не удавалось вплоть до настоящего времени.
Именно эту задачу и решили Харви и Ван дер Хэвен. Они предложили способ построить именно такой алгоритм.
Насколько подобные математические приемы способны ускорить реальные вычисления? По словам Харви, чтобы перемножить два числа с миллиардом десятичных знаков, современному компьютеру понадобится около месяца. Применение алгоритма Шёнхаге — Штрассена позволит уложиться в 30 секунд. Алгоритм, способ построения которого предлагает сам Харви, справится с задачей еще быстрее. Более того, математики предполагают, что это, вероятно, и есть теоретически возможный предел скорости умножения, хотя строго доказать эту гипотезу им пока не удалось. Однако если это так, данную математическую задачу можно считать окончательно решенной.
Однако если это так, данную математическую задачу можно считать окончательно решенной.
Насколько большим должно быть число, чтобы алгоритм Харви — Ван дер Хэвена дал преимущество в скорости вычисления? «Понятия не имею», — честно отвечает Харви, однако в своей статье он приводит в качестве примера умножение, дающее результат 10214857091104455251940635045059417341952. Это действительно очень большое число: во всей видимой Вселенной, к примеру, содержится всего порядка 1080 элементарных частиц.
Однако тот факт, что столь большие числа не соответствуют количеству чего бы то ни было в реальном мире, вовсе не значит, что открытие математиков бесполезно. Умножение — неотъемлемая часть других вычислительных процедур, таких как деление или извлечение корней. Данный результат окажется полезным и тем, кто намерен вычислить много-премного знаков числа пи или, к примеру, расширить список известных человечеству простых чисел.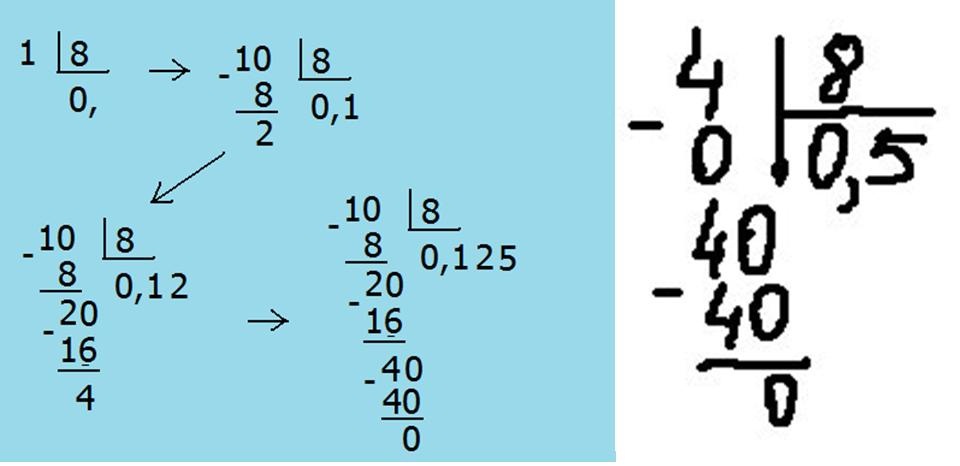
У этой работы есть еще одно интересное следствие. При обосновании преимуществ квантового компьютера нередко приводят в качестве примера алгоритмы шифрования. Эти алгоритмы часто построены на разложении очень больших чисел на множители. Квантовый алгоритм Шора справляется с этой задачей довольно легко, тогда как для классического алгоритма разложение достаточно большого числа потребует времени, сравнимого с возрастом Вселенной. Однако в этих примерах всегда неявно подразумевается, что эффективность классического алгоритма — величина, определенная раз и навсегда. Работа австралийского и французского математиков показывают, что это далеко не так. А вдруг математики будущего предложат настолько изящный классический способ разложения числа на множители, что существующие шифры легко можно будет взломать не только на квантовом, но и на классическом компьютере? Сравнение квантовых и классических алгоритмов некорректно, пока не показано, что и тот и другой действительно являются лучшими из теоретически возможных.
Остается добавить, что работа математиков пока опубликована онлайн, и их коллегам еще предстоит тщательно проверить все выкладки. Авторы выражают надежду, что они ничего не перепутали. Тем временем каждый из читателей имеет возможность самостоятельно проверить все вычисления и, возможно, найти в них ошибку.
Калькулятор больших чисел
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Калькулятор больших чисел может произвести вычисления с числами до 5000 символов.
 YНОД(X, Y)НОК(X, Y)Логарифм числа X по основанию Y
YНОД(X, Y)НОК(X, Y)Логарифм числа X по основанию YКоличество знаков после запятой в ответе
Y
Пожалуйста, опишите возникшую ошибку.
Подтвердите, что вы не робот
Иногда приходится сталкиваться с необходимостью получить более точный результат вычисления, чем дают обычные калькуляторы, используя числа большой размерности. А в таких областях как астро-физика, математика, физика, криптография и вовсе большие числа и точные вычисления неотъемлемая часть расчетов.
В данном калькуляторе вы можете использовать очень большую длину как целой, так и дробной части десятичной дроби, например, калькулятор легко вычислит частное двух таких десятичных дробей, где
X = 1943. 0034503504439681239849471035786596598658293658256982563965345876578567865487
0034503504439681239849471035786596598658293658256982563965345876578567865487
X/Y=0.000000000000000000000023097041926673822905639266089740314381321866047876906844964272495143450953422179061370419373459210608947120128674265718184908338601183316963005493117501186249246061076097373625154302811433048473915626539479629404146861726725
Примеры самых больших чисел:
Гугол = 10100 = 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
Гуголплекс = 1010100 = 1010000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Записывается как единица и гугол нулей после неё.
Гиггол = 1010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010
Числа Гугол, Гуголплекс и Гиггол, конечно очень большие, но отнюдь не самые, есть еще такие числа как: Гаггол, Бугол, Число Грэма, Траддом, Биггол, Трултом, Тругол, Квадругол, Квадрексом, Квинтугол, Губол, Бубол и другие.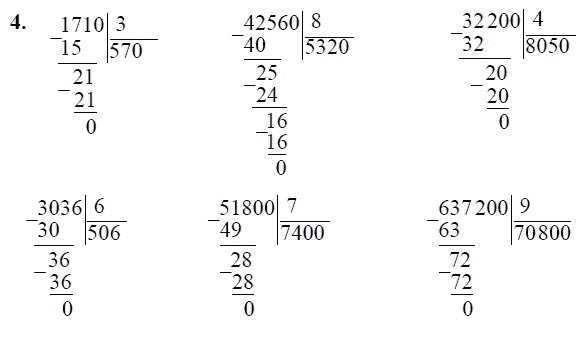
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка.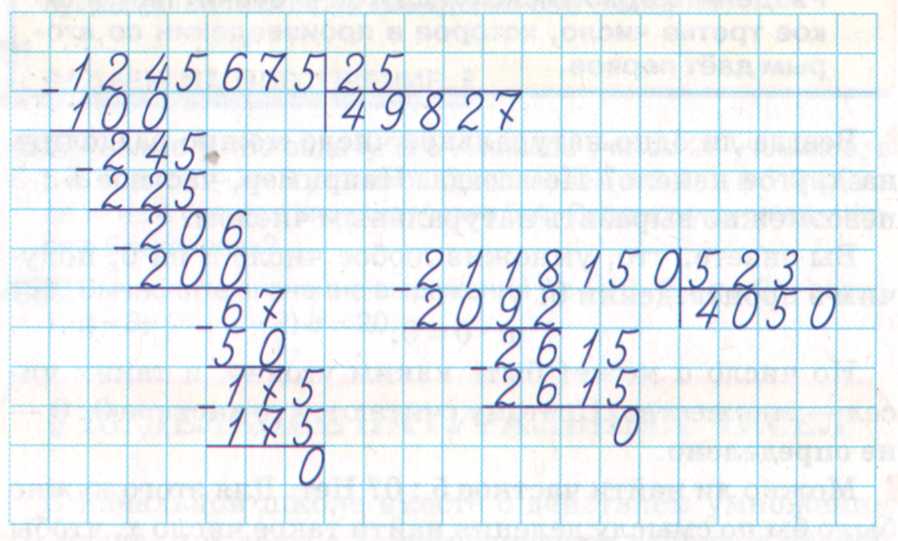 Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Введение в большие числа, значение больших чисел, примеры
Большие числа — это те числа, которые имеют большее значение, чем числа, которые мы используем в повседневной жизни. Такие числа обычно вызывают у детей чувство страха, и они часто пропускают решение задач, в которых есть большие числа. Например, 1 миллион, 1 миллиард и т. д. — это большие числа, которые используются либо для отображения численности населения страны, либо для выражения больших сумм денег на банковском счете.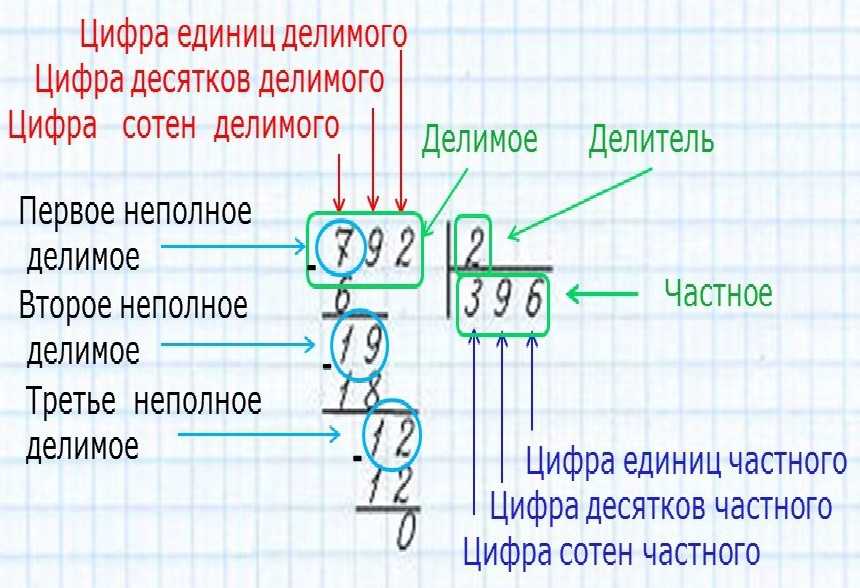
| 1. | Значение больших чисел |
| 2. | Добавление больших чисел |
| 3. | Вычитание больших чисел |
| 4. | Умножение больших чисел |
| 5. | Отдел больших чисел |
| 6. | Решенные примеры |
| 7. | Практические вопросы |
| 8. | Часто задаваемые вопросы о больших числах |
Значение больших чисел
Все учатся считать числа в очень раннем возрасте, начиная с однозначного и заканчивая семизначным. Это делается с помощью позиционной системы ценностей. Есть две системы оценки места, которым следуют — Индийская система оценки места и Международная система оценки места.
При написании больших чисел мы всегда помним о разрядной системе, чтобы гарантировать правильность написания. Согласно индийской разрядной системе, когда число записывается в стандартной форме, каждая группа цифр, разделенная запятой, называется точкой. Эти периоды называются единицами, тысячами, лакхами и так далее. Точка единиц состоит из первых трех цифр большого числа, начиная справа. Период тысяч состоит из следующих двух цифр. Период лакха состоит из следующих двух цифр и продолжается.
Согласно индийской разрядной системе, когда число записывается в стандартной форме, каждая группа цифр, разделенная запятой, называется точкой. Эти периоды называются единицами, тысячами, лакхами и так далее. Точка единиц состоит из первых трех цифр большого числа, начиная справа. Период тысяч состоит из следующих двух цифр. Период лакха состоит из следующих двух цифр и продолжается.
В соответствии с Международной системой разрядов числа также делятся на периоды. Эти периоды называются единицами, тысячами, миллионами, миллиардами и так далее. В этой системе каждый период имеет три цифры.
Давайте посмотрим на этот пример: 12 457 891. Согласно Международной системе стоимостных оценок это читается как двенадцать миллионов четыреста пятьдесят семь тысяч восемьсот девяносто один.
Некоторые другие большие числа читаются и записываются следующим образом:
1 000 000 000 = один миллиард
1 000 000 000 000 = одна тысяча миллиардов
В следующей таблице показано, как читать и записывать числа в соответствии с Международной системой разрядов.
Сложение больших чисел
Большие числа складываем так же, как работаем с другими числами. Мы располагаем числа в столбце в соответствии с значениями, которые они занимают. Процесс сложения начинается со столбца единиц, следующего столбца десятков, столбца сотен и так далее. Номера, которые необходимо перенести, помещаются в соседний столбец вместе с существующими номерами. Весь этот процесс должен выполняться до последнего столбца, где мы получаем наше окончательное число.
Пример 1: Найдите сумму следующих больших чисел: 67,34,903, 2,61,89,403 и 12,79,40,674.
Решение:
Сначала мы расставляем числа по столбцам в соответствии с их разрядностью, а затем складываем их.
Следовательно, сумма данных чисел равна 160 864 980.
Вычитание больших чисел
При вычитании больших чисел используется тот же порядок столбцов, что и при сложении. Как только числа расположены в столбцах, мы начинаем с единиц и двигаемся вперед к левой стороне. Числа заимствуются по мере необходимости с левой стороны.
Числа заимствуются по мере необходимости с левой стороны.
Пример 2: Найдите разницу между следующими большими числами: 67,89,540 и 23,78,954.
Решение:
Сначала мы расставляем числа по столбцам в соответствии с их разрядностью, а затем вычитаем их.
Следовательно, разница данных чисел составляет 4 410 586.
Умножение больших чисел
Умножение больших чисел производится так же, как и других чисел. После того, как числа размещены в столбцах, мы берем нижнее число и начинаем с числа в разряде единиц. Умножаем это число на все числа в верхней строке и пишем произведение под чертой. На следующем шаге, прежде чем мы начнем умножать следующее число, нам нужно удерживать разряд десятков, помещая ноль в разряд единиц, поэтому мы пишем ноль в разряде единиц. Затем мы повторяем процесс и берем следующее число из нижнего числа и умножаем его на все числа в верхней строке. Поместите произведение в ту же строку, где мы поставили ноль. Как только мы получим произведение обоих чисел, мы складываем их по столбцам, чтобы получить окончательный ответ.
Как только мы получим произведение обоих чисел, мы складываем их по столбцам, чтобы получить окончательный ответ.
Пример 3: Умножьте большое число 74 597 на 32.
Решение:
Следовательно, произведение заданных чисел равно 2 387 104.
Отдел больших чисел
Деление больших чисел выполняется методом длинного деления, который аналогичен всем задачам на деление. Есть делимое, которое делится на делитель, чтобы получить результат, называемый частным, а иногда и остатком. Процесс деления включает в себя полный цикл деления, вычитания и умножения.
Пример 4: Разделите большое число 1 260 257 на 37.
Решение:
Ссылки по теме:
- Поместите значение 8
- Таблица стоимости индийских мест
- Системы счисления
- Калькулятор стоимости места
Часто задаваемые вопросы о больших числах
Что означают большие числа?
Большие числа обычно представляют собой большие числа, которые не так часто используются в нашей повседневной жизни. В основном они используются при подсчете населения страны или при подсчете денег на банковском счете. Например, 1 миллион и 1 миллиард считаются большими числами.
В основном они используются при подсчете населения страны или при подсчете денег на банковском счете. Например, 1 миллион и 1 миллиард считаются большими числами.
Как мы читаем большие числа?
При чтении или записи больших чисел мы всегда начинаем слева и двигаемся вправо. Всегда лучше располагать числа в соответствии с их разрядной системой. Согласно индийской системе позиционных значений, при чтении больших чисел мы делим числа на периоды, называемые единицами, тысячами и лакхами. Например: 24,12,340 пишется и читается как двадцать четыре лакха двенадцать тысяч триста сорок. В соответствии с Международной оценочной системой периоды называются единицами, тысячами, миллионами, миллиардами и так далее. Итак, одно и то же число 2 412 340 пишется и читается как два миллиона четыреста двенадцать тысяч триста сорок.
Что такое 1000000 в больших числах?
1 000 000 читается как один миллион в соответствии с международной системой разрядов.
Является ли десятизначное число миллиардом?
Да, десятизначное число читается как миллиард.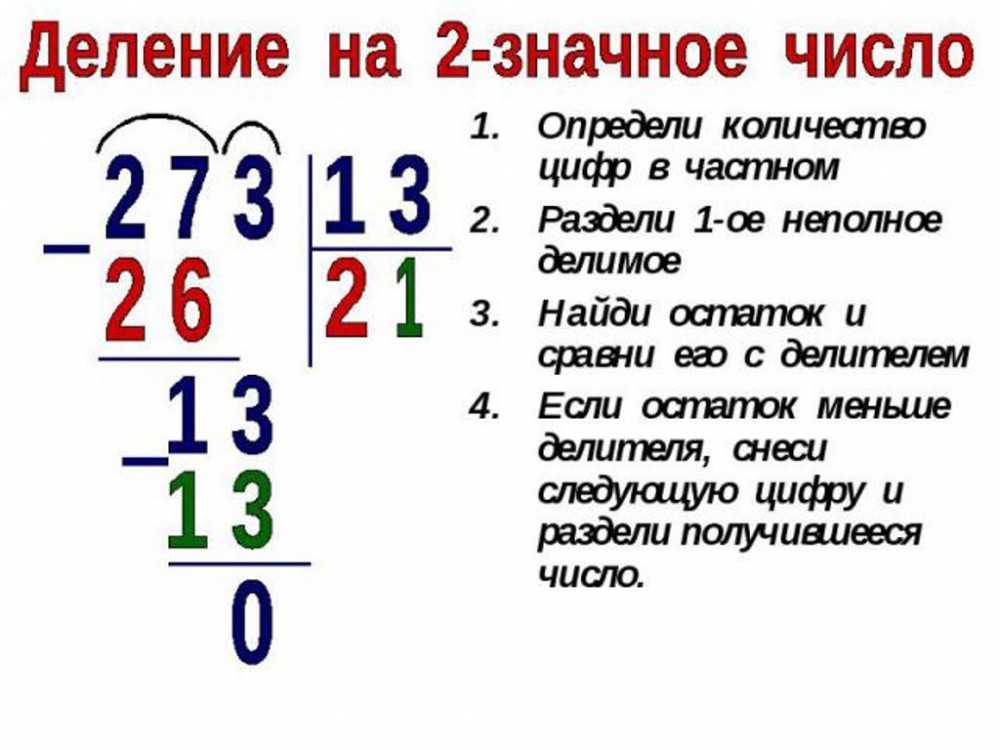 Например, 4 000 000 000 читается как четыре миллиарда.
Например, 4 000 000 000 читается как четыре миллиарда.
Как писать большие числа?
Большие числа записываются в расширенной форме с учетом соответствующих разрядов. Например, 456790 записывается как четыре лакха пятьдесят шесть тысяч семьсот девяносто в соответствии с индийской системой разрядов. По международной системе разряда то же число записывается как четыреста пятьдесят шесть тысяч семьсот девяносто.
Python 3 дает неверный результат при делении двух больших чисел?
спросил
Изменено 2 года, 10 месяцев назад
Просмотрено 3к раз
а = 15511210043330985984000000 # (25!) б = 4700 # (12!) с = 6227020800 # (13!)
При делении 5 В Python 3.x Попробуйте использовать целочисленное деление вместо деления с плавающей запятой. Ваша проблема (без использования целочисленной арифметики) была скрыта для вас Python 3.2: ans = int(a/(b*c)) или ans = int((a/b)/c) мы получаем ans равно 5200299 вместо 52003004 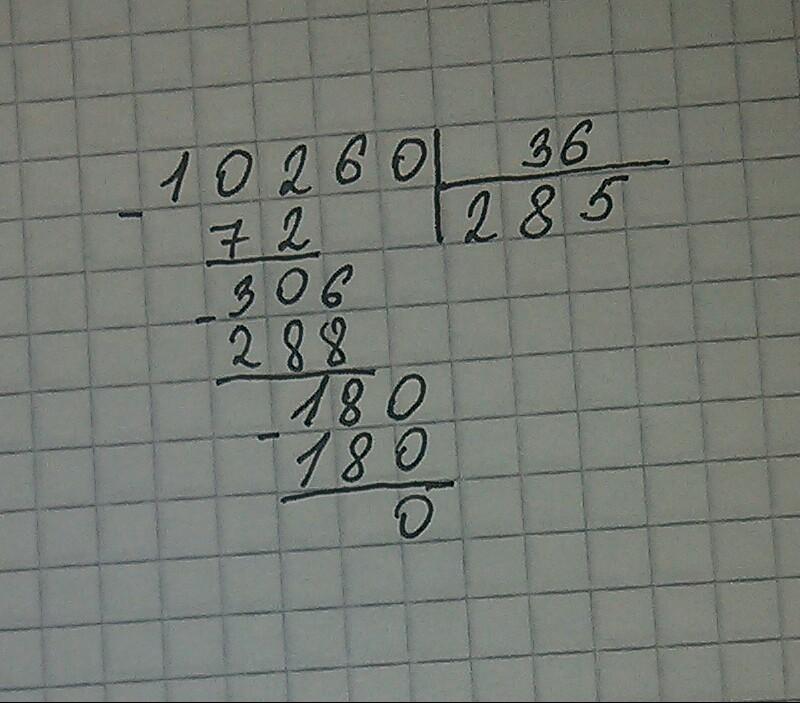 x
x/ означает деление с плавающей запятой и может давать небольшие ошибки округления. Используйте // для целочисленного деления.
анс = а // (b*c)
>>> 15511210043330985984000000 / (4700 * 6227020800)
5200299.999999999
>>> 15511210043330985984000000 // (4700 * 6227020800)
5200300
Python 3.2 (r32:88445, 20 февраля 2011 г., 21:29:02) [MSC v.1500 32 бит (Intel )] на win32
Введите «помощь», «авторское право», «кредиты» или «лицензия» для получения дополнительной информации.
>>> 15511210043330985984000000/(4700*6227020800)
5200300.0
>>> repr(15511210043330985984000000/(4700*6227020800))
'5200300.0'
>>> int(15511210043330985984000000 / (4700 * 6227020800))
5200300
Python 3.
