Решаем просто и красиво — Образовательный центр «Познание», Екатеринбург
Математика — не всегда простая и легкая наука. Сложные примеры, большие формулы – очень сложно, но даже здесь имеются свои методы, способные облегчить решение задач и примеров. Сегодня мы будем говорить о распределительном свойстве умножения относительно сложения и вычитания.
В школе нас учат, что пример, в котором содержится сразу умножение и деление, сложение и вычитание, нужно решать в несколько действий.
Например:
38 × 12+38 × 88.
Как мы видим, в данном примере три действия:
1) ×38 2) × 38 +3344
12 88_ 456_
+ 76 +304 3800
38__ _304_
4 5 6 3344
Очень долго и трудно…
Сейчас разберем данный пример с распределительным свойством относительно сложения и вычитания. С данным свойством пример решается намного легче.
С данным свойством пример решается намного легче.
Для начала, нужно вынести общий множитель за скобку.
38 × 12+38 × 88 = 38 × (12+88)
В скобках провести сложение оставшихся множителей.
(12+88) = 100
Полученную сумму умножить на вынесенный за скобку общий множитель.
38 × 100=3800
Распределительное свойство удобно применять и при вычитании.
76 × 68 – 76 × 41= 76 × (68-41) =76 × 27 = 2052
Здесь также вынесли общий множитель 76 за скобку, затем нашли разность оставшихся множителей (68-41) = 27, далее умножили общий множитель на полученную разность 76 × 27 = 2052
Сложение и вычитание может быть в одном примере.
52 × 28-52 × 15 + 52 × 31 = 52 × (28-15+31) = 52 × 44 = 2288
Данное свойство также можно применить к делению, только называться оно будет по-другому: распределительное свойство деления относительно сложения и вычитания.
Рассмотрим примеры.
93 : 3 – 27 : 3 = (93-27) : 3 = 66 : 3 = 22
160 : 20 – 80 : 20 = (160-80) : 20 = 80 : 20 = 4
81 : 9+198 : 9 = (81+198) : 9 = 279 : 9 = 3
Как мы видим, всё то же самое, единственное отличие – общий делитель всегда пишется после скобок.
Чтобы полученные знания закрепились, потратьте несколько минут и выучите 2 формулы:
Распределительное свойство деления относительно сложения и вычитания
(a ± b) : с = а: с ± b : с
Распределительное свойство умножения относительно сложения и вычитания
(a ± b) × c = a × c + b × c
Считаем в уме — Блог Ассоциации Репетиторов
Умение считать в уме – полезный навык не только в стенах школы, но и в обычной жизни. С его помощью можно почти моментально и безошибочно производить любые действия с числами без помощи калькулятора или бумаги. Сегодня будем говорить о развитии навыков устного счета, рассмотрим полезные упражнения и дадим советы.
С его помощью можно почти моментально и безошибочно производить любые действия с числами без помощи калькулятора или бумаги. Сегодня будем говорить о развитии навыков устного счета, рассмотрим полезные упражнения и дадим советы.
Плюсы устного счета
Счетным навыкам нас обучают с детства. Это элементарные операции сложения, вычитания, умножения и деления. В случае небольших чисел с ними легко справляются даже младшие школьники, но задача существенно усложняется, когда нужно произвести действие с двузначным или трехзначным числом. Однако с помощью тренировки, несложных упражнений и маленьких хитростей вполне можно подчинить данные операции быстрой умственной обработке.
Возможно, вы спросите, зачем это нужно, ведь существует такая удобная вещь, как калькулятор, а на крайний случай под рукой всегда есть бумага для осуществления вычислений. Быстрый счет в уме дает массу преимуществ:
- Экономия времени. Рассчитать стоимость покупок в магазине или кафе и проверить правильность сдачи, опередить одноклассников в решении примера или написании теста — все это возможно, если вы хорошо считаете в уме.

- Возможность обратиться к другим аспектам задачи. Зачастую задачи содержат в себе, как минимум, две стороны: чисто арифметическую (действия с числами) и интеллектуально-творческую (выбор подходящего решения для конкретной задачи, нестандартный подход для более быстрого решения и др.). Если школьник недостаточно хорошо и быстро справляется с первой стороной, то от этого страдает вторая: концентрируясь на выполнении арифметической составляющей, ребенок не задумывается над смыслом задачи, может не увидеть подвоха или более простого решения. Если же счетные операции доведены до автоматизма или просто не требуют большого количества времени, то «включается» детальное рассмотрение смысла задачи, появляется возможность применения творческого подхода к ней.
- Тренировка интеллекта. Счет в уме позволяет держать интеллект в тонусе, постоянно задействовать мыслительные процессы. Особенно это характерно для действий с большими числами, когда мы подбираем способ для максимального упрощения операции.

Упражнения с таблицами
Упражнения рассчитаны на детей любого возраста, испытывающих затруднения при выполнении операций с простыми числами (одно- и двузначными). Позволяет натренировать навыки устного счета, довести до автоматизма несложные арифметические операции.
Необходимые материалы: для выполнения упражнений понадобится сетка одно- и двузначных чисел. Пример:
Картинка из книги: Посталовский И.З. «Тренировочные таблицы для автоматизации устного счета»
В первом столбце располагаются числа, с которыми нужно выполнять действия. Во втором – ответы на эти действия. С помощью специально вырезанной закладки можно проверить правильность вычисления. Например:
Картинка из книги: Посталовский И.З. «Тренировочные таблицы для автоматизации устного счета»
Варианты упражнений:
- Последовательно сложи в уме пары чисел в сетке. Назови ответ вслух и проверь себя с помощью второго столбца и закладки.
 Задание может выполняться в свободном темпе или на время.
Задание может выполняться в свободном темпе или на время. - Последовательно выполни вычитание в уме чисел из сетки.
- Последовательно сложи в уме пары чисел в сетке. Прибавь к каждой сумме цифру 5 и назови ответ вслух.
- Последовательно сложи в уме тройки чисел в сетке.
- Последовательно со всеми числами в сетке выполни следующие действия: прибавь нижнее число, из полученной суммы вычти следующую в столбце цифру.
На основе подобных таблиц можно формировать любые задания. Сетки составляются в зависимости от модификации упражнения.
ВАЖНО! Чтобы упражнение дало результат, оно должно выполняться регулярно, до полного усвоения навыка.
Осваиваем умножение
Упражнение предназначено для детей, освоивших таблицу умножения от 1 до 10. Тренирует навык перемножения двузначного числа на однозначное.
Составляется столбик из произвольных двузначных чисел. Задание для ребенка: последовательно умножить эти числа сначала на 1, потом на 2, на 3 и т. д. Ответ произносится вслух. Выполняется до тех пор, пока ответы не запомнятся и не будет выдаваться автоматически.
д. Ответ произносится вслух. Выполняется до тех пор, пока ответы не запомнятся и не будет выдаваться автоматически.
Главное – внимание
Так что, говорите, надо решить? Источник фото
Задание: сложи последовательно числа: 3000 + 2000+ 30 + 2000 + 10 + 20 + 1000 + 10 + 1000 + 30 =
Назови ответ. Проверь себя с помощью калькулятора.
Если ответ получился верным, необходимо закрепить успех и прорешать еще несколько подобных примеров (могут составляться произвольно). Если в ответе была ошибка, нужно вернуться к последовательности чисел и исправить ее.
В чем идея: В результате сложения чисел получается сумма 9100. Но если делать это невнимательно, будет автоматически напрашиваться ответ 10000 (мозг стремится округлить сумму, сделать ответ более красивым). Поэтому очень важно сохранять контроль за своими действиями при производстве арифметических задач в несколько действий.
Возможные примеры:
3000 – 700 — 60 – 500 — 40 – 300 -20 – 100 =
100:2:2*3*2 + 50 – 100 + 200 – 30 =
1*2*3*4*3*2*1 =
26+88+13+19 =
Рекомендации по повышению внимания
Если большинство примеров решается с ошибками (НО! не связанными с умением считать в принципе), то есть смысл повысить концентрацию внимания. Для этого можно:
Для этого можно:
- Минимизировать внешние раздражители. Например, по возможности выйти в другую комнату, выключить музыку, закрыть окно и т.д. Если необходима концентрация на примере во время урока, когда нет возможности выйти и добиться полной тишины, нужно закрыть глаза и представить цифры, с которыми осуществляются действия.
- Добавить элемент состязательности. Зная, что верное и быстрое решение принесет победу над противником и/или какое-то поощрение, ученик более охотно сосредоточится на цифрах и предпримет максимум усилий в процессе вычисления.
- Устанавливать личные рекорды. Можно визуализировать все ошибки, совершенные школьником в процессе вычисления. Например, нарисовать цветок с крупными лепестками (количество лепестков = количеству решаемых примеров). Черным будет закрашено столько лепестков, сколько примеров было решено с ошибками. Задача – максимально сократить количество черных лепестков, устанавливая личные рекорды с каждой партией примеров.

Небольшие хитрости и советы для быстрого счета
Все так просто?! Источник фото
- Группировка. Последовательно складывая/вычитая несколько чисел, необходимо посмотреть, какие из них при сложении/вычитании дадут целое число: 13 и 67, 98 и 32, 49 и 11 и т.д. Сначала выполнить действия с этими цифрами, а потом перейти к остальным. Пример:7+65+43+82+64+28=(7+43)+(82+28)+65+64=50+110+124=289
- Разложение на десятки и единицы. При умножении двух двузначных чисел (например, 24 и 57) выгодно одно из них (заканчивающееся на меньшую цифру) разложить на десятки и единицы: 24 как 20 и 4. Второе число умножается сначала на десятки (57 на 20), потом на единицы (57 на 4). Затем оба значения складываются. Пример:24?57=57?20+57?4=1140+228=1368
- Умножение на 5. При умножении любого числа на 5, выгоднее сначала умножить его на 10, а потом разделить на 2.
 2=2500-4=2496
2=2500-4=2496
P.S. Данные правила могут существенно упростить устный счет, однако необходимы регулярные тренировки, чтобы в нужный момент можно было правильно воспользоваться правилом. Поэтому рекомендуется прорешать такое количество примеров на каждое из них, которое позволит автоматизировать навык. Для начала можно записывать расчеты на бумаге, постепенно сокращая количество написанного и переводя операции в мыслительный план. В первое время также рекомендуется проверять свои ответы при помощи калькулятора или стандартных вычислений в столбик.
Источник заглавной картинки
Понравилась статья? Поделитесь с друзьями:
Мудрая сова 25 сентября 2015
От общего к частному
Одна из главных причин, почему родители обращаются к репетиторам, — подготовка к школьным экзаменам.
26 февраля 2021
26 333
Дистанционка: что думают родители?
Трепет перед возможной перспективой «дистанционки» не случаен — опыт удалённого обучения для многих оказался не самым простым. Мы поговорили с родителями, чтобы узнать, что они на самом деле думают о новом формате образования.
15 февраля 2021
27 870
День дистантника
Спустя полгода обучение на дистанте уже не кажется чем-то из ряда вон выходящим. Кажется, что базовая адаптация уже случилась. Теперь, когда «дистанционку» уже освоили и учителя, и дети, самое время разобраться, чем и как в этом странном процессе могут помочь родители.
27 января 2021
25 974
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Math Symbols
| Symbol | Symbol name | Symbol Meaning | Example |
|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 |
| — | знак минус | вычитание | 1 1/2 — 2/3 |
| * | asterisk | multiplication | 2/3 * 3/4 |
| × | times sign | multiplication | 2 /3 × 5/6 |
| : | division sign | division | 1/2 : 3 |
| / | division slash | division | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
Подробнее задачи по математике »
Ключевые слова для математических операцийПервым шагом в решении задачи со словами всегда является чтение задачи. Вам нужно уметь переводить слов в математические символы, ориентируясь на ключевых слов , которые указывают на математические процедуры, необходимые для решения задачи, — как на операцию, так и на порядок выражения. Точно так же, как вы можете перевести испанский язык на английский, вы можете перевести английские слова в символы, язык математики. Многие (если не все) ключевые слова, обозначающие математические операции, являются знакомыми словами. Точно так же, как вы можете перевести испанский язык на английский, вы можете перевести английские слова в символы, язык математики. Многие (если не все) ключевые слова, обозначающие математические операции, являются знакомыми словами.Для начала вы переводите английские фразы в алгебраических выражений. Алгебраическое выражение представляет собой набор чисел, переменных , операций и символов группировки. Вы переведете неизвестное число как переменную x или n . Символы группировки обычно представляют собой набор круглых скобок, но они также могут быть наборами скобок или фигурных скобок. При переводе выражений необходимо хорошо знать основные ключевые слова, которые преобразуются в математические операции: ключевые слова сложения, ключевые слова вычитания, ключевые слова умножения и ключевые слова деления, которые рассматриваются в следующих четырех разделах. Добавление ключевых слов Вот некоторые распространенные примеры дополнительных ключевых слов:
Первые два ключевых слова (СУММА и ИТОГО) называются ведущие ключевые слова потому что они ведут выражение. Если выражение начинается с ведущих ключевых слов СУММА или ИТОГО, ведущее ключевое слово определяет соответствующее И. Затем знак плюс физически заменяет И в выражении. Пример 1: Переведите следующее: сумма пяти и числа Следующие шаги помогут вам перевести эту проблему: 1. Подчеркните слова до и после И, если они соответствуют ведущему ключевому слову СУММА ИЗ.
2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет. 3. Переведите каждое подчеркнутое выражение и замените AND знаком плюс.
Пример 2: Переведите следующее: сумма числа и минус три Используйте следующие шаги для перевода этой проблемы: 1. Ключевое слово ВСЕГО ИЗ является ведущим ключевым словом, определяющим И, поэтому подчеркните слова до и после И: «число» и «минус три».
2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет. 3. Переведите каждое подчеркнутое выражение и замените AND знаком плюс.
Пример 3: Переведите следующее: сумма семи и отрицательных четырех Переведите этот пример следующим образом: 1. Слово СУММА является ведущим ключевым словом, определяющим И, поэтому подчеркните слова до и после И: «семь» и «минус четыре».
2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет. 3. Переведите каждое подчеркнутое выражение и замените AND знаком плюс.
Напоминание: Ключевое слово AND переводится как «плюс», потому что ведущее ключевое слово SUM OF. С другими ведущими ключевыми словами (обсуждаемыми в следующих разделах) И может означать другие вещи. Также обратите внимание, что вы не упрощаете выражение и получаете «3» за ответ, потому что вы просто переводите слова в символы, а не выполняете математические операции. Два других ключевых слова в списке дополнительных ключевых слов, PLUS и INCREASED BY, могут быть правильно переведены с помощью стратегии прямого перевода . В стратегии прямого перевода вы переводите каждое слово в соответствующий ему алгебраический символ, по одному, в том же порядке, в котором они написаны, как показано в примере 4. Пример 4: Переведите следующее: число, увеличенное на двадцать четыре
Некоторые дополнительные ключевые слова, такие как ПРИБЫЛЬ, БОЛЬШЕ, УВЕЛИЧЕНИЕ и ПОВЫШЕНИЕ, обычно встречаются в задачах-рассказах, как в примере 5. Пример 5: Переведите следующую сюжетную задачу в математическое выражение о весе полузащитника: Защитный полузащитник весил двести двадцать два фунта в начале весенней тренировки. Он набрал семнадцать фунтов после четырех недель тренировок с командой.
Примечание: Не все числа, упомянутые в словесной задаче, должны быть включены в математическое выражение. Число «четыре» — это просто интересный факт, а не информация, необходимая для написания выражения о весе полузащитника. Вам также может быть интересно, почему ответ не 239 фунтов. Это потому, что вопрос просит вас перевести проблему истории в математическое выражение, а не оценивать выражение. Пример 6: Переведите следующую текстовую задачу в математическое выражение о текущей почасовой оплате кассира: Кассир в бакалейной лавке зарабатывал 6,25 доллара в час. Он получил прибавку в размере 25 центов в час.
Примечание: Почасовая оплата указана в долларах, а надбавка — в центах. Каждый раз, когда вы добавляете два числа, которые имеют единиц , убедитесь, что оба числа измеряются в одних и тех же единицах; если это не так, преобразуйте одно из чисел в те же единицы, что и другое. Измерение обоих чисел в одних и тех же единицах называется 9.0280 однородных единиц. В этом примере вы конвертируете его надбавку, 25 центов, в 0,25 доллара, поскольку его почасовая оплата измеряется в долларах, а не в центах, поэтому надбавка также должна быть в долларах. Вычитание ключевых слов Ключевые слова на вычитание также включают ведущие ключевые слова, ключевые слова, которые можно переводить по одному слову за раз, и ключевые слова, встречающиеся в задачах-рассказах.
Одно ключевое слово вычитания (РАЗНИЦА МЕЖДУ) представляет собой выражение, состоящее из двух частей, которое начинается с ведущего ключевого слова, определяющего соответствующее И. Вы можете использовать те же методы подчеркивания и обведения ключевых слов, которые показаны в предыдущем разделе, для перевода этих выражений. Пример 7: Переведите следующее: разница между четырьмя и шестью Вот как вы переводите Пример 7: 1. Поскольку ключевое слово РАЗНИЦА МЕЖДУ является ведущим ключевым словом, определяющим соответствующее И, подчеркните слова до и после И: «четыре» и «шесть».
2. 3. Переведите каждое подчеркнутое выражение и замените И знаком минус.
Примечание: И не всегда переводится как сложение. Здесь РАЗНИЦА МЕЖДУ — это ведущее ключевое слово, которое определяет, что И означает вычитание. Другие ключевые слова вычитания, такие как MINUS и DECREASED BY, используют стратегию прямого перевода. Пример 8 представляет собой задачу на вычитание слов, которая переводится по одному ключевому слову за раз в точном порядке выражения. Пример 8: Переведите следующее: двадцать четыре уменьшилось на число
В задаче на вычитание вы можете найти ключевые слова на вычитание LOSS, LESS, FEWER и TAKE AWAY, как показано в примере 9. Пример 9: Переведите следующую текстовую задачу в математическое выражение о текущей стоимости материалов на стройплощадке: Строительная компания хранила на строительной площадке материалы на сумму 1253 доллара. Компания понесла убытки в размере 300 долларов из-за ущерба, нанесенного ураганом.
Умножение ключевых слов Вот некоторые распространенные примеры ключевых слов умножения:
Для двух ключевых слов умножения, MULTIPLY и PRODUCT OF, ведущее ключевое слово определяет соответствующее BY или AND, как показано в примере 10. Пример 10: Переведите следующее: произведение семи и числа Переведите этот пример следующим образом: 1.
2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет. 3. Переведите каждое подчеркнутое выражение и замените AND знаком времени.
Примечание: Имейте в виду, что И не всегда означает сложение. Ключевое слово PRODUCT OF определяет, что И в этом выражении означает умножение. Выражение умножения, переведенное методом прямого перевода, показано в примере 11. Пример 11: Переведите следующее: число, умноженное на пятнадцать Выражение переводится как x x 15. Некоторые ключевые слова умножения, такие как DOUBLE, TWICE и TRIPLE, преобразуются в число и операцию умножения, как показано в примерах 12 и 13. Пример 12: Переведите следующее: дважды число Выражение преобразуется в 2 × x . Пример 13: Переведите следующую текстовую задачу в математическое выражение: У Дженнифер в банке было 15 долларов. За следующие две недели она удвоила свои деньги. Выражение переводится как 2 × 15. Одним из ключевых слов, указывающих на умножение, является OF. Однако в текстовых задачах вы можете увидеть более одного употребления слова «из». Единственная OF, которая указывает на умножение, — это та, которая следует за ключевым словом PERCENT, знаком процента, ключевым словом FRACTION или дробью. См. примеры 14 и 15. Пример 14: Переведите следующее: двадцать пять процентов от четырехсот долларов Выражение переводится как 0,25 × 400. Примечание: Помните, что перед умножением процент заменяется десятичной дробью. Пример 15: Переведите следующее: одна треть от двадцати семи Выражение переводится как . Ключевые слова раздела Некоторые распространенные примеры ключевых слов разделения:
Некоторым людям трудно различить ключевые слова ПРОИЗВЕДЕНИЕ ИЗ и ЧАСТНОЕ ИЗ. Вот подсказка, которая поможет вам запомнить, какое из них указывает на деление, а какое на умножение: ЧАСТНОЕ — более «сложное» слово, чем «ПРОИЗВЕД», а деление — «более сложная» операция, чем умножение. Помните: Ведущие ключевые слова определяют соответствующие И или BY для обозначения деления, обычно обозначаемого символом ÷. Пример 16: Переведите следующее: частное семи и числа 1. Поскольку ключевое слово ЧАСТНОЕ ИЗ является ведущим ключевым словом, определяющим И, подчеркните слова до и после И: «семь» и «число».
2. Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет. 3. Переведите каждое подчеркнутое выражение и замените И знаком деления.
Примечание: Здесь ключевое слово ЧАСТНОЕ определяет И для обозначения деления. Пример 17: Переведите следующее: разделите минус тридцать шесть на девять 1. Поскольку слово DIVIDE является ведущим ключевым словом, определяющим BY, подчеркните слова до и после BY: «минус тридцать шесть» и «девять».
2. Обведите ведущее ключевое слово и укажите соответствующий BY, который оно определяет. 3. Переведите каждое подчеркнутое выражение и замените BY знаком деления.
Примечание: Первое число идет в числителе при использовании дроби для обозначения деления. Число в числителе (-36) помещается внутри «дома» при использовании длинного символа деления. Некоторые ключевые слова раздела можно переводить по одному слову. Вместо этого вы просто следуете предложению и заменяете его алгебраическими обозначениями по ходу дела. Пример 18: Переведите следующее: число, разделенное на 16 Выражение переводится как . Часто в сюжетных задачах ключевым словом, указывающим на деление, является PER. Когда в сюжетной задаче требуется указать скорость транспортного средства в милях в час, настройте выражение, чтобы разделить количество миль на количество часов. Вы не только напрямую переводите «мили» ÷ «часы», но также определяете количество миль и количество часов, находя их в другом месте задачи. См. пример 19. |


 Задание может выполняться в свободном темпе или на время.
Задание может выполняться в свободном темпе или на время.
 2=2500-4=2496
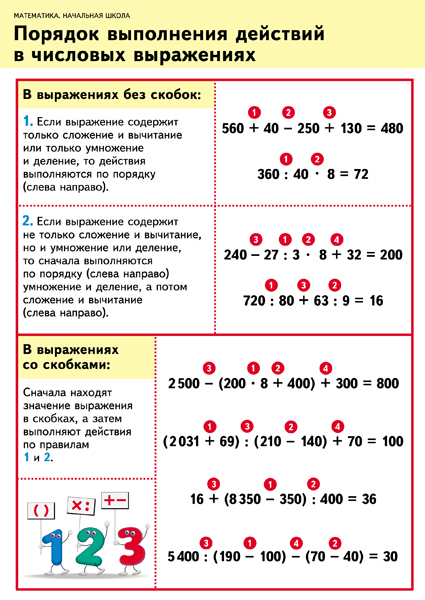
2=2500-4=2496 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Какую часть населения составляют младенцы?
Какую часть населения составляют младенцы? Двести пятьдесят два ученика переходят на 1-й уровень. Напишите в виде дроби, какая часть учеников идет в 1-й класс, а какая во 2-й класс. Сократите обе дроби до их основной формы.
Двести пятьдесят два ученика переходят на 1-й уровень. Напишите в виде дроби, какая часть учеников идет в 1-й класс, а какая во 2-й класс. Сократите обе дроби до их основной формы. Вторые два ключевых слова (ПЛЮС и УВЕЛИЧЕНИЕ НА) — это ключевые слова, которые указывают точное размещение знака плюс. Последние четыре ключевых слова встречаются в текстовых задачах и могут указывать на сложение.
Вторые два ключевых слова (ПЛЮС и УВЕЛИЧЕНИЕ НА) — это ключевые слова, которые указывают точное размещение знака плюс. Последние четыре ключевых слова встречаются в текстовых задачах и могут указывать на сложение.

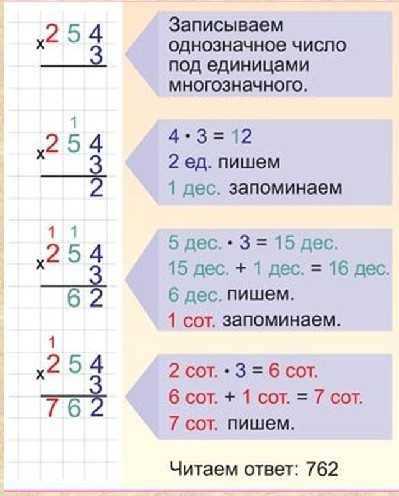
 Посмотрите на следующий список ключевых слов вычитания:
Посмотрите на следующий список ключевых слов вычитания: Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет.
Обведите ведущее ключевое слово и укажите соответствующее И, которое оно определяет. 
 Поскольку ПРОИЗВЕД ИЗ является ведущим ключевым словом, которое соответствует И, подчеркните слова до и после И: «семь» и «число».
Поскольку ПРОИЗВЕД ИЗ является ведущим ключевым словом, которое соответствует И, подчеркните слова до и после И: «семь» и «число».