Урок 36. Проверка сложения вычитанием.

Home » Сложение и вычитание в пределах первой сотни

Сложение и вычитание в пределах первой сотни

Работа над новым материалом.

В качестве подготовки к ознакомлению со способом проверки, основанным на связи между сложением и вычитанием, целесообразно включить в устные упражнения составление по образцу и решение троек примеров вида:

7 + 6 =13      9 + 5
13 — 7           …
13 — 6           …

Примеры полезно проиллюстрировать на наборном полотне.

Читаются они так: Первое слагаемое 7, второе слагаемое 6, сумма 13. Из суммы вычли первое слагаемое 7, получили второе слагаемое 6 и т. п. Детей подводят к обобщению: если из суммы вычесть одно из слагаемых, то получится другое слагаемое. Запись этих примеров на доске следует сохранить.

Полезно ставить вопросы вида: Какой пример на сложение может помочь найти разность чисел 12 — 9? 9 и 3 — это 12. Значит, 12 без 9 — это 3.

По рисунку учебника дети рассматривают и объясняют, как получены примеры, записанные вверху страницы, и читают вывод, который применяется для проверки правильности вычислений в примерах из упражнения 4, записанного на доске. Вызванный ученик, заполняя соответствующую клетку, говорит: Первое слагаемое 32, второе слагаемое 8, сумма 40. Учитель предлагает проверить, правильно ли выполнили сложение. Мы уже говорили: если из суммы вычесть одно из слагаемых, то получится другое слагаемое. Этим пользуются для проверки сложения. Если, вычтя из суммы одно из слагаемых, получили другое слагаемое, то вычисления выполнены правильно. Проверим первый пример: из суммы 40 вычтем одно из слагаемых 8. Сколько будет? (32) Получили другое слагаемое. Значит, сумму вычислили правильно.

Под руководством учителя с записью в тетради разобрать первый пример из упражнения 1.

Работа над пройденным материалом.

1. Закрепление умения выполнять вычисления в пределах 100. Прибавление по 4 (4 + 4 + 4 + 4 + 4 + 4 + 4 + 4), по 6 (6 + 6 + 6 + 6) и т. п. Такую работу можно организовать в виде игры «Счет цепочкой».

Полезно провести устное решение примеров в два действия: 100 — 86 — 7; 9 + 8 + 50 и т. п.

2. Решение задач. Под руководством учителя выяснить, каким действием решается задача из упражнения 2 и почему.

Решение задачи дети могут оформить в тетради сами.

Для самостоятельной работы можно предложить упражнение 3 с последующей проверкой, в ходе которой, если потребуется, можно схематически изобразить условие; упражнения 1 (второй и третий примеры), 4 (последние четыре колонки). Учитель поясняет, что нужно списать 4 столбика чисел из таблицы, под каждой парой слагаемых записать сумму и устно проверить, правильно ли вычислили сумму.

Каталог сайтов Всего.ру

Математика 3 класс.

Школьная программа. Учитель Ульянова Надежда Николаевна — Урок №2. Письменные приемы сложения и вычитания. Задачи в два действия

Комментарии преподавателя

На данном уроке рассмотрены отличия простой задачи от составной. Также более подробно разобраны способы решения задач в два действия. В качестве повторения объяснены письменные приемы сложения и вычитания двузначных чисел.

Источник : http://interneturok.ru/ru/school/matematika/3-klass/undefined/pismennye-priemy-slozheniya-i-vychitan…

Выполним первое задание (рис. 1).

Рис. 1. Задача

Прочитаем условие задачи. Рассмотрим предложенные схемы.

Как правильно выбрать схему задачи к первому вопросу?

Прочитаем условие задачи: длина кита от хвоста до головы – 16 м, а длина головы – на 12 м меньше. Чтобы ответить на первый вопрос задачи и узнать, какова длина головы кита, выберем схему. Рассуждаем так: больший отрезок на каждой схеме соответствует длине кита от хвоста до головы – 16 м. Меньший отрезок обозначает длину головы. По условию задачи она на 12 м меньше. Это обозначено на схеме 1 и схеме 3. Схема 2 и схема 4 не подходят для решения задачи. Значит, нам подходит схема 1, так как вопрос обозначен под коротким отрезком.

Как правильно выбрать решение задачи при ответе на первый вопрос?

Рассуждаем так: мы знаем, что длина головы на 12 м меньше, значит нужно из большего числа вычесть меньшее. Из 16 вычтем 12. Решение № 1 подходит для ответа на первый вопрос.

Правильный ответ: 16-12=4. Длина головы кита – 4 м.

Как правильно выбрать схему и решение задачи ко второму вопросу?

Чтобы ответить на второй вопрос задачи и узнать, какова общая длина кита, выберем схему. Рассуждаем так: для того чтобы узнать общую длину кита, необходимо выполнить два действия, так как сначала нужно узнать длину головы кита. Условию и вопросу задачи соответствует схема 3. Теперь выберем решение. В решении № 2 сначала предлагается узнать длину головы кита: 16-12, а затем прибавить длину кита от хвоста до головы: 16+(16-12).

Правильный ответ: 16+(16-12)=16+4=20. Общая длина кита – 20 м.

Как правильно выбрать схему и решение задачи к третьему вопросу?

Прочитаем третий вопрос: на сколько метров длиннее тело кита, чем голова? Выясним, что этот вопрос не соответствует условию задачи, так как уже из условия известно, что голова кита на 12 м меньше, чем длина туловища кита.

Сделаем вывод.

Если на схеме или краткой записи два вопроса, это составная задача, ее необходимо решать в несколько действий.

Вспомним приемы письменных вычислений сложения и вычитания.

Найдем значения данных выражений

43+12            35-21

57+23            95-65

24+67            83-26

Применим способ вычисления в столбик.

43+12

Запишем второе слагаемое под первым, начнем складывать с разряда единиц. К 3 прибавить 2 получим 5. Запишем под единицами. Затем складываем десятки. К 4 прибавить 1 получится 5. Записываем под десятками. Ответ: 55.

57+23

Записываем второе слагаемое под первым: единицы – под единицами, десятки – под десятками. Начинаем складывать с единиц. К 7 прибавить 3 получится 10. 10 – это один десяток. Цифру 0 пишем под единицами, а один десяток запоминаем. Складываем десятки. К 5 прибавить 2 получится 7 десятков, и еще прибавить один, который мы запомнили, получится 8 десятков. Записываем под десятками. Ответ: 80.

24+67

Записываем второе слагаемое под первым: единицы – под единицами, десятки – под десятками. Начинаем складывать с единиц. К 4 прибавить 7 получится 11. 11 – это один десяток и одна единица. Одну единицу пишем под единицами, а один десяток запоминаем. Складываем десятки. К 2 прибавить 6 получится 8 десятков, да еще прибавить один, который мы запомнили, получится 9 десятков. Записываем под десятками. Ответ: 91.

35-21

Записываем пример в столбик: единицы пишем под единицами, десятки – под десятками. Вычитаем с разряда единиц. Из 5 вычитаем 1, получаем 4. Пишем в разряде единиц. Из 3 десятков вычитаем 2 десятка, получаем 1 десяток. Записываем под десятками. Ответ: 14.

95-65

Записываем пример в столбик: единицы пишем под единицами, десятки – под десятками. Вычитаем с разряда единиц. Из 5 вычитаем 5, получаем 0. Пишем в разряде единиц. Из 9 десятков вычитаем 6 десятков, получаем 3 десятка. Записываем под десятками. Ответ: 30.

83-26

Записываем пример в столбик: единицы пишем под единицами, десятки – под десятками. Вычитаем с разряда единиц. Из 3 вычесть 6 нельзя. Занимаем из разряда десятков один десяток и ставим точку. Один десяток и три единицы – это 13. Из 13 вычесть 6, получится 7. Пишем под единицами. У нас осталось 7 десятков. Из 7 вычесть 2 получится 5 десятков. Записываем под десятками. Ответ: 57.

Выполним следующее задание.

Выпишем уравнения, которые решаются вычитанием, и решим их.

х — 24 = 46

72 — х = 40

с + 35 = 60

с — 35 = 60

Рассуждаем так: в первом уравнении х-24=46 неизвестно уменьшаемое. Чтобы найти уменьшаемое, нужно к значению разности прибавить вычитаемое. Значит, данное уравнение нм не подходит.

Во втором уравнении 72-х=40 неизвестно вычитаемое. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть значение разности. Значит, это уравнение решается вычитанием.

Решим его.

72 — х = 40

х = 72 — 40 = 70 + 2 — 40 = 30 + 2 = 32

х = 32

Во третьем уравнении с + 35 = 60 неизвестно слагаемое. Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое. Значит, это уравнение решается вычитанием.

Решим его.

с + 35 = 60

Выполним вычитание в столбик. Запишем единицы под единицами, десятки под десятками. Вычитаем с разряда единиц. От 0 5 нельзя отнять. Занимаем один десяток и ставим точку. Из 10 вычесть 5 получится 5. Записываем под единицами. Вычитаем десятки. Осталось 5 десятков. Из 5 вычесть 3 получится 2. Ответ: 25.

В последнем уравнении с — 35 = 60 неизвестно уменьшаемое. Чтобы найти уменьшаемое, нужно к значению разности прибавить вычитаемое. Данное уравнение решается сложением и нам не подходит.

Потренируемся в нахождении значений выражений.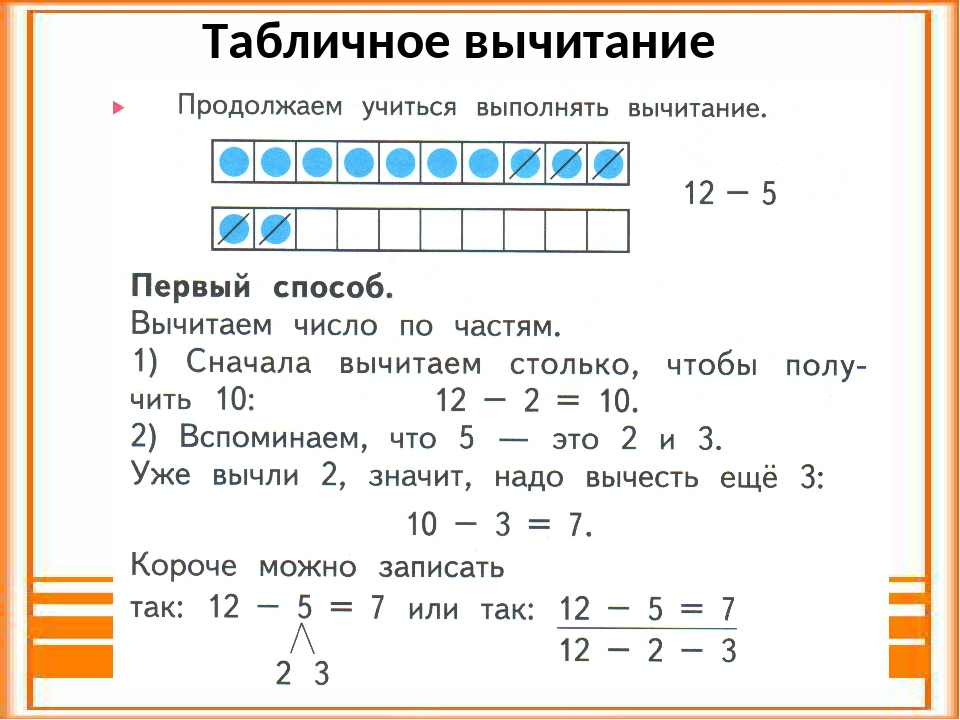

Выберем выражение, в котором сложение будет первым действием, и найдем значение этого выражения, выполняя вычисления столбиком.

70 — 56 + 16

86 — (28 + 14)

Рассуждаем так: в первом выражении, соблюдая порядок выполнения действий, необходимо выполнить сначала вычитание, потом сложение. Во втором выражении сначала выполняем действие в скобках, сложение, а затем из 86 вычтем полученный результат. Складываем числа в столбик. Записываем единицы под единицами, десятки под десятками. Вычисляем, складываем единицы: 8+4=12, 2 единицы записываем под единицами, 1 десяток запоминаем. Складываем десятки: 2+1=3, и еще один десяток получится 4 десятка, получаем 42. Теперь из 86 вычтем 42. Запишем пример в столбик: единицы под единицами, десятки под десятками. Выполним вычитание: из 6 единиц вычтем 2 единицы, получим 4 единицы, из 8 десятков вычтем 4 десятка, получим 4 десятка, ответ: 44.

Сегодня на уроке мы повторили отличия простой и составной задачи, вспомнили, как складывать и вычитать двузначные числа столбиком.

 

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Nsportal.ru (Источник).
2. Prosv.ru (Источник).
3. Do.gendocs.ru (Источник).

Файлы

Нет дополнительных материалов для этого занятия.

Представление и решение задач на сложение и вычитание

Все основные основные материалы: математические ресурсы для 1-го класса

7 диагностических тестов 180 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

Common Core: Справка по математике для 1-го класса » Операции и алгебраическое мышление » Представление и решение задач на сложение и вычитание

Большая пицца состоит из ломтиков. Если мы съедим кусочки, сколько останется?

Возможные ответы:

Правильный ответ:

Объяснение:

Это задача на вычитание, потому что мы хотим знать, сколько ломтиков останется после того, как мы съедим их. Поскольку мы едим кусочки или забираем кусочки, у нас будет меньше того, с чем мы начали.

Мы можем начать с  и считать обратно.

Сообщить об ошибке

У Эмили на тарелке черника, клубника и малина. Сколько всего кусочков фруктов у нее?

Возможные ответы:

Правильный ответ:

Объяснение:

Это задача на сложение, потому что мы хотим знать, сколько всего кусочков фруктов будет у Эмили, если мы сложим вместе чернику, клубнику и малину. Когда мы собираем вещи вместе, мы добавляем.

Мы можем начать с и считать.

Тогда мы можем подсчитать.

Сообщить об ошибке

В продуктовом магазине есть бутылки с газировкой, бутылки сока и бутылки с водой. Сколько всего бутылок у них?

Возможные ответы:

Правильный ответ:

Объяснение:

Это дополнительная проблема, потому что мы хотим знать, сколько всего бутылок было в магазине, когда мы сложили вместе бутылки сока, газировки и воды. Когда мы собираем вещи вместе, мы добавляем.

Мы можем начать с и считать.

Тогда мы можем подсчитать.

Сообщить об ошибке

Сюзи находит монеты под своим диваном, в ящике стола и на столе. Сколько всего монет у нее?

Возможные ответы:

Правильный ответ:

Объяснение:

Это задача на сложение, потому что мы хотим знать, сколько всего монет нашла Сьюзи, когда сложила все монеты вместе. Когда мы собираем вещи вместе, мы добавляем.

Мы можем начать с и считать.

Тогда мы можем подсчитать.

Сообщить об ошибке

В карнавальной игре есть медведи разных размеров в качестве призов. маленькие медведи, средние медведи и большие медведи. Сколько всего медведей в карнавальной игре?

Возможные ответы:

Правильный ответ:

Объяснение:

Это задача на сложение, потому что мы хотим знать, сколько всего медведей будет в карнавальной игре, когда мы сложим три размера вместе.

Когда мы собираем вещи вместе, мы добавляем.

Мы можем начать с и считать.

Тогда мы можем подсчитать.

Сообщить об ошибке

В автомате с жвачкой есть красные, зеленые и желтые жевательные резинки. Сколько всего жевательных резинок в автомате?

Возможные ответы:

Правильный ответ:

Объяснение:

Это задача на сложение, потому что мы хотим знать, сколько жевательных резинок получится, когда мы сложим все цвета вместе. Когда мы собираем вещи вместе, мы добавляем.

Мы можем начать с и считать.

Тогда мы можем подсчитать.

Сообщить об ошибке

Во дворе Ханны стоят три горшка с цветами. В первом горшке цветы, во втором горшке цветы, а в третьем горшке цветы. Сколько цветов во всех трех горшках?

Возможные ответы:

Правильный ответ:

Объяснение:

Это задача на сложение, потому что мы хотим знать, сколько всего цветов во всех горшках, вместе взятых. Когда мы собираем вещи вместе, мы добавляем.

Мы можем начать с и считать.

Тогда мы можем подсчитать.

Сообщить об ошибке

Во время моего хоккейного матча Джеймс забил голы в первом периоде, ни одного гола во втором периоде и голы в третьем периоде. Сколько всего голов забил Джеймс?

Возможные ответы:

Правильный ответ:

Объяснение:

Это задача на сложение, потому что мы хотим знать, сколько всего баллов было набрано, когда мы суммировали все баллы. Когда мы собираем вещи вместе, мы добавляем.

Мы можем начать с и считать.

Сообщить об ошибке

В моей корзине конфет есть присоска, шоколадные батончики и жевательные конфеты. Сколько всего конфет у меня есть?

Возможные ответы:

Правильный ответ:

Объяснение:

Это задача на сложение, потому что мы хотим знать, сколько конфет получится, если я соберу присоску, шоколад и жевательные конфеты вместе.

Когда мы собираем вещи вместе, мы добавляем.

Мы можем начать с и считать.

Тогда мы можем подсчитать.

Сообщить об ошибке

Семья Линдси собирается в отпуск. Она упаковывает сумки, ее папа упаковывает сумки, а мама упаковывает сумки. Сколько всего сумок они берут с собой в отпуск?

Возможные ответы:

Правильный ответ:

Объяснение:

Это задача на сложение, потому что мы хотим знать, сколько всего сумок в семье. Когда мы собираем вещи вместе, мы добавляем.

Мы можем начать с и считать.

Тогда мы можем подсчитать.

Сообщить об ошибке

← Предыдущая 1 2 3 Следующая →

Уведомление об авторских правах 180 практических тестов Вопрос дня Карточки Learn by Concept

Решение уравнений путем сложения или вычитания – Easy Peasy All-in-One Homeschool

Мы используем то, что математики называют обратными операциями. Обратная операция — это операция, отменяющая другую операцию. Сложение и вычитание являются операциями, обратными друг другу. Например, обратное прибавление 5 — это вычитание 5. Обратное прибавление 7 — это прибавление 7.

Найдите минутку и подумайте об этом и соотнесите это с предыдущими знаниями.

7 + 6 = 13

13 – 7 = 6

Это взаимосвязанные факты!

Теперь мы знаем, что обратные операции помогают нам решать уравнения. Как решить уравнения с помощью обратных операций?

Чтобы решить уравнения, вы должны выполнить обратные операции, чтобы получить переменную саму по себе. Помните, что сложение и вычитание являются обратными операциями. Если уравнение содержит сложение, решите его, вычитая из обеих частей, чтобы отменить сложение. Точно так же, если уравнение содержит вычитание, решите его, добавив к обеим частям, чтобы отменить вычитание.

Например. Если бы у нас было x + 5, то мы могли бы вычесть 5 и получить x сам по себе. Число плюс обратное равно 0.

10 – 10 = 0 и -7 + 7 = 0

Давайте посмотрим на определение уравнений сложения, вычитания, умножения и деления.

Решение уравнения сложения

Чтобы решить уравнение сложения, нужно вычесть одно и то же число из с каждой стороны уравнения , чтобы переменная была сама по себе на одной стороне уравнения, а ответ на другой стороне.

Две стороны равны. Думайте об этом как о балансе. Если вы отнимете что-то у одной стороны, две стороны больше не будут равными, перестанут находиться в равновесии. Но если вы отнимете одинаковую сумму от обеих сторон, они останутся равными.

Пример:

Это уравнение было 2 + 5 = 7. Мы отняли по 5 с каждой стороны и получили 2 = 2, что, конечно же, верно!

Решение уравнения на вычитание

Чтобы решить уравнение на вычитание, нужно добавить одинаковое число с каждой стороны уравнения, чтобы переменная была сама по себе на одной стороне уравнения, а ответ на другой стороне.

Это работает, потому что -10 + 10 = 0. При добавлении обратного числа число исчезает!

Надеюсь, вы заметили в определениях, что для решения использовались обратные операции.

Пример:

 

(источник)

Искать:

Задать вопрос

Пожалуйста, проверьте страницу часто задаваемых вопросов, прежде чем задавать вопрос! Группа поддержки Или найдите определенное место или группу уровня Список групп facebook

EP Gear

Большое разнообразие дизайнов и продуктов

Следите за EP на Facebook

EP на других языках

Kinderleicht Lernen

Использование EP для говорящих по-испански

Следите за блогом по электронной почте

Введите свой адрес электронной почты, чтобы следить за этим блогом и получать уведомления о новых сообщениях по электронной почте.

Адрес электронной почты:

Мои романы и книги

Истории чудес Ли – не будем бояться

Отказ от ответственности

Задания, набор ссылок, структура учебного плана и файлы, созданные этим сайтом, принадлежат этому владельцу блога и не могут быть скопированы и опубликованы на другом сайте или использованы для какой-либо коммерческой выгоды.