Что такое сочетательный закон сложения: Математические Законы

admin

Содержание

Математические Законы

Переместительный закон сложения

Начнем изучать основные законы математики со сложения натуральных чисел.

Переместительный закон сложения

От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так:

m + n = n + m

Переместительный закон сложения работает для любых чисел.

Если прибавить шестерку к двойке — получим восьмерку. И наоборот, прибавим двойку к шестерке — снова получим восьмерку. Это доказывает справедливость переместительного закона сложения.

Приведем пример с весами, которые используют продавцы в магазинах.

Если мы положим на одну чашу весов 3 килограмма конфет, а на другую — такие же 3 килограмма конфет, то стрелка весов будет на нейтральной позиции. Это говорит нам о том, что чаши действительно весят одинаково.

При этом неважно, как будут лежать конфеты, в каком порядке.

Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма. От перестановки мест конфет их сумма, то есть вес, не меняется.

Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:

Формула переместительного закона для обыкновенных дробей:


Чтобы сложить две дроби нужно сложить числители, а знаменатель оставить прежним. Вот так:


Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в онлайн-школу Skysmart.

Наши преподаватели понятно объяснят что угодно — от базовых законов математики до олимпиадных задач — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Сочетательный закон сложения

Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.

Сочетательный закон сложения: два способа


  1. Результат сложения нескольких слагаемых не зависит от порядка действий.

  2. Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.

Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.

Рассмотрим сумму из трех слагаемых:

Чтобы вычислить это выражение, можно сначала сложить числа 1 и 3 и к полученному результату прибавить 4. Чтобы было удобнее, можно сумму 1 и 3 взять в скобки — так мы поймем, что ими нужно заняться в первую очередь:

  • 1 + 3 + 4 = (1 + 3) + 4 = 5 + 4 = 8

Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:

  • 1 + 3 + 4 = 1 + (3 + 4) = 1 + 7 = 8

В обоих случаях получается один и тот же результат — что и требовалось доказать.

Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:

  • (1 + 3) + 4 = 1 + (3 + 4)
  • 8 = 8

Отразим сочетательный закон сложения с помощью переменных:

(a + b) + c = a + (b + c)

Формула сочетательного закона для обыкновенных дробей:


Например, если к сумме одной седьмой и трёх седьмых прибавить четыре седьмых, то в результате получим восемь седьмых.


Переставим скобки — к одной седьмой прибавим сумму трёх седьмых и четырех седьмых. И снова ответ будет восемь седьмых.


Значит, сочетательный закон справедлив и для обыкновенных дробей.


Переместительный закон умножения

С каждым новым правилом решать задачки по математике все интереснее.

Переместительный закон умножения

От перемены мест множителей произведение не меняется. То есть, если множимое и множитель поменять местами — их произведение никак не изменится.

Проверим, действительно ли это так. Умножим пятерку на двойку, а потом наоборот:

В обоих случаях получили один ответ — значит между выражениями 5 * 2 и 2 * 5 можно поставить знак равенства.

Переместительный закон умножения с помощью переменных выглядит так:

a * b = b * a

Сочетательный закон умножения

Рассмотрим еще один полезный закон в математике.

Сочетательный закон умножения

Если выражение состоит из нескольких сомножителей, то их произведение не зависит от порядка действий.

Другими словами, умножайте числа в любом порядке — как вам больше нравится.

Рассмотрим пример:

Это выражение можно вычислить в любом порядке. Давайте сначала перемножим числа 2 и 3, а полученный результат умножим на 4:

  • 2 * 3 = 6
  • 6 * 4 = 24
  • 2 * 3 * 4 = 24

А теперь по-другому: перемножим числа 3 и 4, а результат умножим на 2:

  • 3 * 4 = 12
  • 2 * 12 = 24
  • 2 * 3 * 4 = 24

Тот же ответ! Значит между выражениями (2 * 3) * 4 и 2 * (3 * 4) можно поставить знак равенства, так как они равны одному значению.

  • (2 * 3) * 4 = 2 * (3 * 4)
  • 6 * 4 = 2 * 12
  • 24 = 24

Для любых натуральных чисел a, b и c верно равенство:

a * b * с = (a * b) * с = a * (b * с)

Пример

Вычислить: 5 * 6 * 7 * 8.

Как решаем:

Это выражение можно вычислять в любом порядке. Вычислим слева направо:

5 * 6 = 30

30 * 7 = 210

210 * 8 = 1680

5 * 6 * 7 * 8 = 1680

Ответ: 1680

Распределительный закон умножения

Для умножения есть еще один закон — распределительный. На математике в 6 классе он звучит так:

Распределительный закон умножения

  • Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
  • Чтобы сумму чисел умножить на число, нужно каждое слагаемое отдельно умножить на число и полученные произведения сложить.

То есть при помощи распределительного закона умножения можно умножить сумму на число и число на сумму. Проверим на примере:

Сначала выполним действие в скобках:

В главном выражении (3 + 5) * 2 заменим выражение в скобках на восьмерку:

Получили ответ 16.

Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое в скобках, нужно умножить на 2, а потом сложить полученные результаты:

  • (3 + 5) * 2 = 3 * 2 + 5 * 2
  • 3 * 2 = 6
  • 5 * 2 = 10
  • 6 + 10 = 16

Отразим распределительный закон умножения с помощью переменных:

(a + b) * c = a * c + b * c

Выражение в скобках (a + b) — это множимое. Тогда переменная с — множитель, так как они соединены знаком умножения.


Из переместительного закона умножения мы знаем, что от перемены мест множимого и множителя произведение не изменится.

Если множимое (a + b) и множитель c поменять местами, то получим выражение c * (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b)

. Для такого умножения можно применять распределительный закон умножения. Переменную c можно умножить на каждое слагаемое в скобках:

c * (a + b) = c * a + c * b

 

Пример 1

Решить: 5 * (3 + 2).

Как решаем:

Умножим пятерку на каждое слагаемое в скобках и сложим полученные результаты:

5 * (3 + 2) = 5 * 3 + 5 * 2 = 15 + 10 = 25

Ответ: 25

 

Пример 2

Найти значение выражения 2 * (5 + 2).

Как решаем:

Умножим двойку на каждое слагаемое в скобках и сложим полученные результаты:

2 * (5 + 2) = 2 * 5 + 2 * 2 = 10 + 4 = 14

Ответ: 4.

Если в скобках не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. А после из полученного первого числа вычесть второе число.

 

Пример 3

Решить: 4 * (6 − 2).

Как решаем:

Умножим четверку на каждое число в скобках. Из полученного первого числа вычтем второе число:

4 * (6 − 2) = 4 * 6 − 4 * 2 = 24 − 8 = 16

Ответ: 16

Распределительный закон умножения для суммы обыкновенных дробей:


Распределительный закон умножения для разности обыкновенных дробей:


Проверим справедливость этого закона:


Посчитаем, чему равна левая часть равенства.


Теперь посчитаем, чему равна правая часть равенства.


Так мы доказали справедливость распределительного закона.

Задания для самопроверки

Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать 🙂

Задание 1. Найти значение выражения: 8 * (1 + 6).

Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).

Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).

Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).

Задание 5. Применить распределительный закон умножения: 13 * (3 + 8) + 5 * (4 + 2)

Задание 6. Какое из действий (умножение, деление, сложение или вычитание) нужно выполнить последним ((20 − 1) * 12 + 30) : 3?

Задание 7. В смартфоне 32 гб памяти. Какое количество приложений можно установить, если одно занимает 1,2 гб?

Задание 8. Верно ли равенство: 8 * 5 = 49?

 

Ответы


  1. 56;

  2. 28;

  3. 100;

  4. 81;

  5. 173;

  6. Деление;

  7. 26;

  8. Неверно.

Еще больше практики — в современной школе Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с учителем.

Приходите на бесплатный вводный урок математики и начните заниматься эффективно и в удовольствие уже завтра!

переместительный и сочетательный. Сумма нескольких слагаемых

Переместительный закон сложения

Если слагаемые поменять местами, то сумма не изменится. Это можно легко проверить, посчитав количество звёздочек, представленных на рисунке:

Можно сначала посчитать зелёные звёздочки, потом жёлтые и сложить полученные результаты, получится  9  звёздочек. Или можно сначала посчитать жёлтые звёздочки, а потом зелёные, в результате сложения жёлтых и зелёных звёздочек сумма будет опять равна  9.

Таким образом, для любых натуральных чисел  a  и  b  верно равенство:

a + b = b + a,

выражающее переместительный закон сложения:

От перестановки слагаемых сумма не меняется.

Сумма нескольких слагаемых

При сложении нескольких слагаемых действия можно выполнять в любом порядке.

Пример. Найти сумму трёх слагаемых:  5,  3  и  2.

Решение: Сумму трёх слагаемых можно найти тремя способами:

1-й способ:

5 + 3 = 8,

8 + 2 = 10.

2-й способ:

5 + 2 = 7,

7 + 3 = 10.

3-й способ:

3 + 2 = 5,

5 + 5 = 10.

Сочетательный закон сложения

Если при сложении чисел  5,  2  и  3  заменить какие-нибудь два числа их суммой, то результат сложения не измениться. Это можно легко проверить посчитав звёздочки на картинке:

Можно посчитать зелёные, синие и жёлтые звёздочки отдельно, а потом сложить полученные результаты, получим  10  звёздочек. Или можно посчитать зелёные звёздочки отдельно, а синие и жёлтые вместе и после к зелёным звёздочкам прибавить сумму синих с жёлтыми, в результате получим опять  10  звёздочек.

Из примера следует, что результат сложения не зависит от объединения слагаемых в сумму. Таким образом, для любых натуральных чисел  a,  b  и  c  верно равенство:

a + b + c = a + (b + c) = b + (a + c)

выражающее сочетательный закон сложения:

Сумма трёх и более слагаемых не изменится, если какие-нибудь из них заменить их суммой.

Основные законы сложения и умножения

a + b = b + a,

где a и b – любые числа.

Из арифметики известно, что переместительный закон верен для суммы любого числа слагаемых.

2. Сочетательный закон сложения.

Сумма нескольких слагаемых не изменится, если какую-нибудь группу рядом стоящих слагаемых заменить их суммой.

Для суммы трех слагаемых имеем:

(a + b) + c = a + (b + c).

Например, сумму 5 + 7 + 11 можно вычислить двумя способами так:

(5 + 7) + 11 = 12 + 11 = 23,
5 + (7 + 11) = 5 + 18 = 23.

Сочетательный закон справедлив для любого числа слагаемых.

Так, в сумме a + b + c + d четырех слагаемых рядом стоящие слагаемые можно как угодно объединять в группы и заменять эти слагаемые их суммой:

a + b + c + d = (a + b + c) + d = (a + b) + (c + d) =
= a + (b + c) + d = a + b + (c + d) = (a + b) + c + d.

Например, 1 + 3 + 5 + 7 = 16; мы получим то же число 16, каким бы способом ни группировали рядом стоящие слагаемые:

1 + (3 + 5) + 7 = 1 + 8 + 7 = 16,
1 + 3 + (5 + 7) = 1 + 3 + 12 = 16,
(1 + 3) + (5 + 7) = 4 + 12 = 16.

Переместительным и сочетательным законами часто пользуются при устных вычислениях, располагая числа так, чтобы легче было их сложить в уме.

Пример 1.

89 + 67 + 11.

Поменяем местами два последних слагаемых, получим:

89 + 11 + 67.

Сложить числа в этом порядке оказалось гораздо легче.

Обычно слагаемые в новом порядке не переписывают, а производят их перемещение в уме: переставив мысленно 67 и 11, сразу складывают 89 и 11 и затем прибавляют 67.

Пример 2.

.

Чтобы легче был сложить эти числа в уме, изменим порядок слагаемых так:

.

Пользуясь сочетательным законом, заключим два последних слагаемых в скобки:

.

Сложение чисел в скобках произвести легко, получим:

.

3. Переместительный закон умножения.

Произведение не изменяется от перемены порядка сомножителей:

ab = ba,

где a и b – любые числа.

Из арифметики известно, что переместительный закон верен для произведения любого числа сомножителей.

4. Сочетательный закон умножения.

Произведение нескольких сомножителей не изменится, если какую-нибудь группу рядом стоящих сомножителей заменить их произведением.

Для произведения трех сомножителей имеем:

(ab)c = a(bc).

Например, произведение трех сомножителей 5 * 3 * 4 можно вычислить так:

(5 * 3) * 4 = 15 * 4 = 60

или так:

5 * (3 * 4) = 5 * 12 = 60.

Для произведения четырех сомножителей имеем:

abcd = (abc)d = (ab)cd = a(bc)d = (ab)(cd) = a(bcd) = ab(cd).

Например, ; то же число 20 получится при любой группировке рядом стоящих сомножителей:

Применение переместительного и сочетательного законов умножения часто значительно облегчает вычисления.

Пример 1.

25 * 37 * 4.

Умножить 25 и 37 не очень легко. Переместим два последних сомножителя:

25 * 4 * 37.

Теперь умножение легко выполнить в уме.

Пример 2.

75 * 35 * 4 * 2.

Применим переместительный и сочетательный законы, запишем это выражение так:

75 * 4 * (35 * 2).

Все эти действия легко выполняются в уме.

5. Распределительный закон умножения по отношению к сложению.

Чтобы умножить сумму двух (или нескольких) чисел на какое-либо число, можно каждое слагаемое умножить на это число и результаты сложить:

(a + b)c = ac + bc.

Пример 1. Распределительный закон мы применяем, например, при умножении двузначных (и многозначных) чисел. Так, чтобы умножить 26 на 7, мы представляем 26 в виде суммы 20 + 6, умножаем 20 на 7, 6 на 7 и результаты складываем:

26 * 7 = (20 + 6) * 7 = 20 * 7 + 6 * 7 = 140 + 42 = 182.

Но иногда бывает выгоднее поступать наоборот: вместо того чтобы умножить каждое слагаемое на одно и то же число, сначала находят сумму этих слагаемых и умножают ее на данное число.

Пример 2.

87 * 28 + 13 * 28.

Представим выражение в другом виде:

(87 + 13) * 28.

Мы применили здесь распределительный закон, но только записанный в обратном порядке:

ac + bc = (a + b)c.

Теперь вычисление выполняется очень легко (устно).

Законы сложения и умножения.

Переместительный, сочетательный и распределительный законы. Они же: коммутативный, ассоциативный и дистрибутивный законы. Примерно 5 класс (10-11 лет)

 Навигация по справочнику TehTab.ru:  главная страница  / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Детский сад — 7 класс.  / / Законы сложения и умножения. Переместительный, сочетательный и распределительный законы. Они же: коммутативный, ассоциативный и дистрибутивный законы. Примерно 5 класс (10-11 лет)

Законы сложения и умножения. Переместительный, сочетательный и распределительный законы. Они же: коммутативный, ассоциативный и дистрибутивный законы.

(a+b)+c=a+(b+c) (сочетательный=ассоциативный закон сложения)
ab=ba (переместительный=коммутативный закон умножения)
(ab)c=a(bc)  (сочетательный=ассоциативный закон умножения)
a(b+c)=ab+ac (распределительный=дистрибутивный закон умножения относительно сложения)
c(a-b)=ca–cb (распределительный=дистрибутивный закон умножения относительно вычитания)



Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу.
TehTab.ru

Реклама, сотрудничество: [email protected]

 Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями.

Сочетательный закон сложения — формулировка, правило и примеры

Арифметические операции изучаются на уроках математики во втором классе. Одной из них является сложение, сочетательный закон которого позволяет значительно повысить скорость решения различных заданий. Однако не все ученики могут разобраться и досконально изучить материал. Специалисты предлагают собственную методику успешного обучения и повышения успеваемости.

Общие сведения

Сложение является одной из базовых арифметических операций в математике. Оно изучается во втором классе общеобразовательной школы. Существует всего 2 правила: переместительный и сочетательный закон сложения. Однако многие ученики часто их путают. Разобраться в этом помогут специалисты. Они разработали специальную методику, позволяющую быстро запомнить различие между ними.

Однако для изучения алгоритма нужно знать базовые термины и определения. К ним относятся:

  • Сложение — операция, направленная на увеличение числового значения на заданную величину.
  • Законы — набор правил, позволяющих оптимизировать расчетные процессы, т. е. проще посчитать какое-либо значение.

    • Сложение состоит минимум из трех элементов: двух слагаемых (одно из них увеличивается на другое) и результата. Последний называется суммой. На примере это выглядит так: 5+9=14, где 5 — I слагаемое, 9 — второй элемент-слагаемое или число, на которое нужно увеличить первое слагаемое, а 14 — их сумма.

    Переместительное правило

    Переместительное (коммутативное) правило является очень простым для понимания. Оно формулируется следующим образом: если поменять местами слагаемые, их сумма не изменится. Математическая форма записи закона выглядит следующим образом: q+w=s.

    На практическом примере правило реализуется в таком виде: 5+6=6+5=11. Последнее числовое выражение очень легко проверить. Для этого достаточно воспользоваться обыкновенным калькулятором. При сложении 5 и 6 он покажет величину, равную 11. Следует отметить, что таким образом и доказывается закон переместительного свойства сложения.

    Прием практической реализации для доказательства правил и утверждений применяется очень часто. Это и есть оптимальная методика, позволяющая выяснить работоспособность того или иного утверждения. Далее необходимо рассмотреть сочетательный закон сложения.

    Сочетательный закон

    Сочетательное правило сложения возможно применить, когда числовое выражение включает в свой состав от трех и более слагаемых. Сочетательный закон сложения во 2 классе можно сформулировать следующим образом: слагаемые, входящие в состав выражения, можно для удобства складывать в любом порядке.

    Очень часто правило называют ассоциативным свойством операции сложения. Ее математическая запись имеет такой вид: p+r+s=(p+s)+r=(s+r)+p=z. Чтобы доказать утверждение, нужно решить пример «2+9+8+1». Его специалисты рекомендуют решать по такому алгоритму:

  • Разбить на пары слагаемые: (2+8)+(9+1). Необходимо руководствоваться удобством вычислений, поскольку пару чисел «2+8» легче сложить, чем «2+9».
  • Выполнить вычисления в скобках (символах группировки) и записать результат: 10+10=20.

    • К сочетательному свойству также можно применить и переместительное (коммуникативное) правило. Этим приемом очень часто пользуются специалисты. Кроме того, по-другому ассоциативный закон называется методом группировки чисел. Далее нужно рассмотреть методику применения двух законов на практике.

    Методика применения

    Методика использования правил сложения зависит от конкретного примера. Однако специалисты рекомендуют придерживаться следующего алгоритма нахождения результатов числовых выражений:

  • Проанализировать пример и найти в нем числа, сложение которых можно произвести очень быстро.
  • Сгруппировать элементы при помощи круглых скобок (ассоциативный закон) или просто поменять их местами (переместительное свойство).
  • Вычислить значения сумм пар, находящихся в скобках.
  • Записать результат.

    • Сочетание элементов можно выполнять несколько раз, т. е. вычислить сначала одно значение, а потом опять перегруппировать выражение. Перемену мест слагаемых можно производить в несколько заходов.

    Кроме того, законы сложения можно применять не только для целых чисел, но и для дробных. Для совершенствования качества усвоения теоретического материала рекомендуется придумать примеры и решить их.

    Некоторые ученики часто путают принадлежность распределительного правила к суммации двух и более величин. Этого делать не нужно, а требуется запомнить, что у сложения только 2 закона, но не 3. Последний принадлежит только операциям деления и умножения.

    Переместительное и сочетательное свойства можно применять и для вычитания. Далее необходимо на практическом примере разобрать использование правил сложения и методику их применения.

    Пример решения

    Для закрепления теоретического материала необходимо решить следующий пример: 4+9+6+5+1+15+17+2+12+1. Находится решение по такому алгоритму:

  • Пишется пример: 4+9+6+5+1+15+17+2+12+1.
  • Переместительное свойство: 4+6+9+1+5+15+17+2+12+1.
  • Сочетательный закон: (4+6)+(9+1)+(5+15)+(17+2+1)+12.
  • Вычисление значений: 10+10+20+20+12=60+12=72.

    • Следует учитывать, что группировку элементов можно выполнять в произвольном порядке и количестве. Суть метода — достижение максимальной скорости вычислений при сложении простых элементов, позволяющих без проблем произвести расчеты.

    Если сразу выполнить расчеты сложно, рекомендуется группировать числа по количеству знаков, т. е. однозначные с однозначными, двузначные с двузначными и т. д.

    Таким образом, сочетательный и переместительный законы применяются в математике для ускорения вычислений.

    Предыдущая

    МатематикаСчётные и несчётные множества — понятие, свойства и примеры

    Следующая

    МатематикаИррациональность дроби — как правильно избавиться от знака корня в знаменателе?

    Презентация «Переместительный закон сложения»

    Слайды и текст этой онлайн презентации

    Слайд 1

    Переместительный закон сложения
    Кильчукова И.М.

    Слайд 2

    Внимательно посмотрите на выражение: 9 + 6 + 8 + 7 + 2 + 4 + 1 + 3

    Слайд 3

    Нам нужно найти его значение. Давайте это сделаем.     9 + 6 = 15 15 + 8 = 23 23 + 7 = 30 30 + 2 = 32 32 + 4 = 36 36 + 1 = 37 37 + 3 = 40

    Слайд 4

    Результат выражения 9 + 6 + 8 + 7 + 2 + 4 + 1 + 3 = 40.  Скажите, удобно ли было вычислять? Вычислять было не совсем удобно. Посмотрите еще раз на числа этого выражения. Нельзя ли их поменять местами так, чтобы вычисления были более удобными?

    Слайд 5

    Если мы перегруппируем числа по-другому:   9 + 1 + 8 + 2 + 7 + 3 + 6 + 4 = …    9 + 1 = 10  10 + 8 = 18  18 + 2 = 20  20 + 7 = 27  27 + 3 = 30  30 + 6 = 36  36 + 4 = 40 Окончательный результат выражения 9 + 1 + 8 + 2 + 7 + 3 + 6 + 4 = 40.

    Слайд 6

    Мы видим, что результаты выражений получились одинаковые.

    Слайд 7

    Слагаемые можно менять местами, если это удобно для вычислений, и значение суммы от этого не изменится.

    Слайд 8

    В математике существует закон: Переместительный закон сложения. Он гласит, что от перестановки слагаемых сумма не изменяется.

    Слайд 9

    Дядя Федор и Шарик поспорили. Шарик находил значение выражения так, как оно записано, а дядя Федор сказал, что знает другой, более удобный способ вычисления. Видите ли вы более удобный способ вычисления?

    Слайд 10

    Шарик решал выражение так, как оно записано. А дядя Федор, сказал, что знает закон, который разрешает менять слагаемые местами, и поменял местами числа 25 и 3.

    Слайд 11

    37 + 25 + 3 = 65          37 + 25 = 62                                    62  +  3 = 65 37 + 3 + 25 = 65          37  +  3 = 40                                     40 + 25 = 65
    Мы видим, что результат остался таким же, но считать стало гораздо проще.

    Слайд 12

    От перестановки мест слагаемых сумма не изменяется.

    Слайд 13

    СОЧЕТАТЕЛЬНЫЙ ЗАКОН СЛОЖЕНИЯ

    Слайд 14

    6 + (24 + 51) = 81 (к 6 прибавить сумму 24 и 51) Нет ли удобного способа для вычисления?

    Слайд 15

    Мы видим, что если прибавить 6 и 24, то мы получим круглое число. К круглому числу всегда легче что-то прибавлять. Возьмем в скобки сумму чисел 6 и 24. (6 + 24) + 51 = …  (к сумме чисел 6 и 24 прибавить 51) Вычислим значение выражения и посмотрим, изменилось ли значение выражения? 6 + 24 = 30 30 + 51 = 81 Мы видим, что значение выражения осталось прежним.

    Слайд 16

    Потренируемся еще на одном примере. (27 + 19) + 1 = 47 (к сумме чисел 27 и 19 прибавить 1)

    Слайд 17

    Какие числа удобно сгруппировать так, чтобы получился удобный способ? Вы догадались, что это числа 19 и 1. Сумму чисел 19 и 1 возьмем в скобки. 27 + (19 + 1) = …  (к 27 прибавить сумму чисел 19 и 1)

    Слайд 18

    Найдем значение этого выражения. Мы помним, что сначала выполняется действие в скобках. 19 + 1 = 20 27 + 20 = 47

    Слайд 19

    Сочетательный закон сложения: два соседних слагаемых можно заменить их суммой.

    Слайд 20

    Мы познакомились с переместительным и сочетательным законами сложения, а также узнали, как ими пользоваться для удобства вычисления.  

    Слайд 21

    Мои детки 2 «В» класса МКОУ «Гимназия № 4» Вы усвоили тему ? СПАСИБО ЗА ВНИМАНИЕ!

    Сочетательный закон сложения | World of Math

    Как Вам уже наверняка известно, в математике есть следующие законы сложения: сочетательный, переместительный, распределительный. Сегодня пришёл черёд сочетательного . 

    Сочетательный закон сложения сформулировать очень просто:

    Когда Вы складываете более двух слагаемых, Вы можете группировать их в любом удобном порядке.

    Рассмотрим на конкретном примере.

    У Кати есть 6 шоколадных конфет. А у её подруги Лены — 7 желейных конфет и 4 карамельки. Девочек попросили сосчитать, сколько конфет у них всего.

    Катя складывала так: 

    1. В первом действии прибавила к своим 6 шоколадным конфетам 7 желейных конфет Лены.
    6 + 7 = 13 (конфет)

    2. Во втором действии Катя прибавила к сумме шоколадных и желейных конфет 4 карамельки. 
    13 + 4 = 17 (конфет)

    Итого в сумме получилось 17 конфет.

    Лена же решала иначе:

    1. В первом действии она прибавила к 6 конфетам Кати 4 своих карамельки. Этот способ показался ей удобным, так как в сумме получилось круглое число.
    6 + 4 = 10 (конфет)

    2. Во втором действии Лена прибавила к 10 конфетам оставшиеся 7 желейных конфет.
    10 + 7 = 17 (конфет)

    Как и у Кати, в сумме Лена насчитала 17 конфет.

    Мы видим, что, несмотря на разные пути решения, девочки пришли к одинаковому результату. Кто из них прав или неправ? Правы обе! Более того, эту задачу возможно решить и третьим способом.

    1. В первом действии узнать, сколько всего конфет у Лены.
     7 + 4 = 11 (конфет)

    2. Во втором действии сложить все конфеты Лены с конфетами Кати.
    11 + 6 = 17 (конфет)

    Теперь Вы понимаете, как работает сочетательный закон сложения! 

    Решите задачу самостоятельно, используя все возможные способы сочетания.

    Бабушка принесла 8 яблок, 5 груш и 12 слив. Сколько всего фруктов принесла бабушка?

    Эту и другие темы Ваш ребёнок может изучить под руководством квалифицированных преподавателей онлайн-школы World of Math. Вы удивитесь, насколько интересной может быть математика!

    Попробуйте! Первое занятие абсолютно бесплатно.

    Использование принципов сложения и умножения

    Компания, занимающаяся продажей настраиваемых чехлов, предлагает чехлы для планшетов и смартфонов. Поддерживаются 3 модели планшетов и 5 поддерживаемых моделей смартфонов. Принцип сложения говорит нам, что мы можем добавить количество вариантов планшета к количеству вариантов смартфона, чтобы найти общее количество вариантов. Согласно принципу сложения, всего существует 8 вариантов, как мы можем видеть на рисунке 1.

    Рисунок 1

    Общее примечание: принцип сложения

    В соответствии с принципом сложения , если одно событие может произойти способами [latex] m [/ latex], а второе событие без общих результатов может произойти способами [latex] n [/ latex], то первое событие или второе событие может произойти [latex] m + n [/ latex] способами.

    Пример 1: Использование принципа сложения

    В меню ужина 2 вегетарианских и 5 мясных закуски. Каково общее количество вариантов первого блюда?

    Решение

    Мы можем добавить количество вегетарианских блюд к количеству вариантов мяса, чтобы найти общее количество вариантов первого блюда.

    Всего доступно 7 вариантов.

    Попробуйте 1

    Студент покупает новый компьютер. Он выбирает 3 настольных компьютера и 4 портативных компьютера.Какое общее количество компьютерных опций?

    Решение

    Использование принципа умножения

    Принцип умножения применяется, когда мы делаем более одного выбора. Предположим, мы выбираем закуску, основное блюдо и десерт. Если в меню ужина с фиксированной ценой есть 2 варианта закуски, 3 варианта основного блюда и 2 варианта десерта, имеется в общей сложности 12 возможных вариантов, по одному каждый, как показано на древовидной диаграмме на Рисунке 2.

    Возможные варианты:

    1. суп, курица, торт
    2. суп, курица, пудинг
    3. суп, рыба, торт
    4. суп, рыба, пудинг
    5. суп, стейк, торт
    6. суп, стейк, пудинг
    7. салат, курица, торт
    8. салат, курица, пудинг
    9. салат, рыба, торт
    10. салат, рыба, пудинг
    11. салат, стейк, торт
    12. салат, стейк, пудинг

    Мы также можем найти общее количество возможных обедов умножением.

    Мы также можем сделать вывод, что существует 12 возможных вариантов обеда, просто применив принцип умножения.

    Общее примечание: принцип умножения

    Согласно принципу умножения , если одно событие может произойти способами [latex] m [/ latex], а второе событие может произойти способами [latex] n [/ latex] после того, как первое событие произошло, то два события могут происходить [латексом] m \ times n [/ latex] способами. Это также известно как Фундаментальный принцип подсчета .

    Пример 1: Использование принципа умножения

    Дайан собрала 2 юбки, 4 блузки и свитер для своей деловой поездки. Ей нужно будет подобрать юбку и блузку к каждому наряду и решить, надеть ли свитер. Используйте принцип умножения, чтобы найти общее количество возможных нарядов.

    Решение

    Чтобы найти общее количество нарядов, найдите произведение количества вариантов юбки, количества вариантов блузки и количества вариантов свитера.

    Есть 16 возможных нарядов.

    Попробуй 2

    Ресторан предлагает специальный завтрак, который включает бутерброд для завтрака, гарнир и напиток. Есть 3 вида бутербродов для завтрака, 4 варианта гарнира и 5 вариантов напитков. Найдите общее количество возможных блюд на завтрак.

    Решение

    Определение, формула и практический пример

    Что такое комбинация?

    Комбинация — это математический метод, который определяет количество возможных расположений в коллекции элементов, где порядок выбора не имеет значения.В комбинациях вы можете выбирать элементы в любом порядке.

    Комбинации можно спутать с перестановками. Однако в перестановках важен порядок выбранных элементов. Например, компоновки ab и ba равны в комбинациях (рассматриваемых как одна компоновка), в то время как в перестановках компоновки различаются.

    Комбинации изучаются в комбинаторике, но также используются в различных дисциплинах, включая математику и финансы.

    Формула для комбинирования

    Математически формула для определения количества возможных расположений путем выбора только нескольких объектов из набора без повторения выражается следующим образом:

    Где:

    • n — общее количество элементов в наборе
    • k — количество выбранных объектов (порядок объектов не важен)
    • ! — факториал

    Факториал (помеченный как «!») — это произведение всех положительных целых чисел, меньших или равных числу перед знаком факториала.Например, 3! = 1 x 2 x 3 = 6.

    Обратите внимание, что формула выше может использоваться только в том случае, если объекты из набора выбраны без повторения.

    Пример комбинации

    Вы являетесь управляющим портфелем в небольшом хедж-фонде Стратегии хедж-фонда Хедж-фонд — это инвестиционный фонд, созданный аккредитованными физическими лицами и институциональными инвесторами с целью максимизации прибыли и. Вы решили создать новый фонд, который будет привлекать рисковых инвесторов.Фонд будет включать акции Налог на прирост капитала Налог на прирост капитала — это налог, взимаемый с прироста капитала или прибыли, которую физическое лицо получает от продажи активов. Налог взимается только после того, как актив был конвертирован в наличные, а не тогда, когда он все еще находится в руках инвестора. быстрорастущих компаний с высоким потенциалом роста. Ваша команда аналитиков определила акции 20 компаний, соответствующих вашему профилю.

    Поскольку это новый фонд, вы решили включить пять акций с равным весом в первоначальный портфель, а через год вы проанализируете эффективность портфеля и добавите новые акции, если фонд будет работать успешно.В настоящее время вы хотите определить количество возможных портфелей, которые вы можете создать из акций, определенных вашими аналитиками.

    Принятие инвестиционного решения является примером проблемы объединения. Поскольку вы собираетесь разработать портфель, в котором все акции будут иметь равный вес, порядок выбранных акций не влияет на портфель. Например, портфели ABC и CBA будут равны друг другу из-за схожего веса (по 33,3% каждый) каждой акции.

    Таким образом, вы можете использовать формулу комбинирования для расчета количества возможных договоренностей:

    Существует 15 504 возможных портфеля из пяти акций, которые можно создать из 20 акций, включенных в короткий список.

    Дополнительные ресурсы

    CFI предлагает программу сертификации финансового моделирования и оценки (FMVA) ™ Стать сертифицированным аналитиком финансового моделирования и оценки (FMVA) ® для тех, кто хочет вывести свою карьеру на новый уровень. Чтобы продолжать учиться и продвигаться по карьерной лестнице, вам будут полезны следующие ресурсы CFI:

    • Инвестирование: руководство для начинающихИнвестирование: руководство для начинающих Руководство CFI по инвестициям для начинающих научит вас основам инвестирования и научит их начинать.Узнайте о различных стратегиях и методах торговли, а также о различных финансовых рынках, на которые вы можете инвестировать.
    • Маржинальная торговля Маржинальная торговля Маржинальная торговля — это заимствование средств у брокера с целью инвестирования в финансовые ценные бумаги. Приобретенные акции служат залогом по ссуде. Основная причина заимствования денег — получение большего капитала для инвестирования
    • Начальная цена Страйк-цена Страйк-цена — это цена, по которой держатель опциона может реализовать опцион на покупку или продажу базовой ценной бумаги, в зависимости от
    • Типы рынков — Дилеры, брокеры, биржи Типы рынков — дилеры, брокеры, биржи Рынки включают брокеров, дилеров и биржи.Каждый рынок работает с разными торговыми механизмами, которые влияют на ликвидность и контроль. Различные типы рынков допускают разные торговые характеристики, описанные в этом руководстве.

    Правило суммы и Правило решения проблем продукта

    В этот раздел включены основные примеры и проблемы, которые подготовят вас к следующему разделу решения проблем.

    Кальвин хочет поехать в Милуоки. Он может выбрать один из 333 автобусных маршрутов или 222 поезда, чтобы отправиться из дома в центр Чикаго.Оттуда он может выбрать один из двух автобусных маршрутов или трех поездов, чтобы отправиться в Милуоки.

    На этот раз он должен купить концессию на автобус (которая позволит ему ездить только на автобусах) или концессию на поезд (которая позволит ему ездить только на поездах). Если у него есть деньги только на 111 из этих концессий, сколько у него способов добраться до Милуоки?

    Если Кальвин покупает автобусную остановку, у него есть 3 × 2 = 6 3 \ times 2 = 63 × 2 = 6 способов добраться до Милуоки.(Правило продукта)
    Если Кальвин покупает поезд в концессию, у него есть 2 × 3 = 6 2 \ times3 = 62 × 3 = 6 способов добраться до Милуоки. (Правило продукта)
    Следовательно, у него всего 6 + 6 = 12 6 + 6 = 126 + 6 = 12 способов добраться до Милуоки. (Правило суммы) □ _ \ square □

    Шесть друзей Энди, Бэнди, Кэнди, Денди, Энди и Фэнди хотят сесть в ряд в кинотеатре. Если доступно только шесть мест, сколькими способами мы можем усадить этих друзей?

    Для первого места у нас есть выбор из 6 друзей.Посадив первого человека на второе место, мы можем выбрать любого из оставшихся 5 друзей. После того, как мы рассадим второго человека на третье место, у нас будет выбор из оставшихся 4 друзей. После того, как мы рассадим третьего человека на четвертое место, мы можем выбрать любого из оставшихся 3 друзей. Посадив четвертого человека на пятое место, мы можем выбрать любого из оставшихся 2 друзей. После того, как мы рассадим пятого человека на шестое место, у нас будет выбор только из одного оставшегося друга.b2a5b, где a aa и b bb — целые числа, удовлетворяющие 0≤a≤4,0≤b≤3 0 \ leq a \ leq 4, 0 \ leq b \ leq 30≤a≤4,0≤b≤3. Есть 5 возможностей для a aa и 4 возможности для b bb, и, следовательно, всего имеется 5 × 4 = 20 5 \ times 4 = 205 × 4 = 20 (правило произведения) положительных делителей 2000. □ _ \ квадрат □

    Следующие ниже задачи познакомят вас с двумя правилами, описанными выше.

    Сколько параллелограммов образуется, когда набор из 5 параллельных прямых пересекает набор из 4 параллельных прямых?

    Детали и предположения

    • Все параллельные прямые растянуты до бесконечности.

    Отправьте свой ответ

    Если вы посчитаете способы подъема на 3 ступени, вы обнаружите, что есть 4 способа подъема на 3 ступени. Представьте себе, что ноги человека настолько длинные, что могут подниматься по 11 ступеням за раз, при этом человеку разрешается подниматься только вверх.

    Тогда найдите количество путей, по которым вы можете подняться на 11 ступенек?

    Бонус : Обобщите это на nnn шагов.

    Отправьте свой ответ

    Трое детей, каждый в сопровождении опекуна, поступают в школу.Princi хочет опросить всех 6 человек одного за другим при одном условии, что ни один ребенок не будет опрошен до его опекуна. Какими способами это можно сделать?

    Перестановка и комбинация | Репетиторы 4 You

    Перестановка : Перестановка означает расположение из вещи. Слово расположение используется, если Порядок вещей считается .

    Комбинация: Комбинация значит подборка вещей. Слово выделение используется, когда порядок вещей не имеет значения .

    Пример: Предположим, нам нужно сформировать число, состоящее из трех цифры с использованием цифр 1,2,3,4 , для формирования В этом номере цифры должны быть в порядке . В зависимости от порядок, в котором мы расставляем цифры.Это пример из Перестановка .

    Сейчас предположим, что нам нужно сделать команду из 11 игроков из 20 игроков, это пример комбинации , потому что порядок игроков в команде не повлияет в смене команды. Независимо от того, в каком порядке мы перечисляем из игроков команда останется прежней! Для будет сформирована другая команда, по крайней мере, у одного игрока будет быть измененным.

    Теперь давайте посмотрим на два основных принципы подсчета:

    Дополнение правило: если эксперимент можно провести «n» способами, & другой эксперимент можно провести «м» способами то любой из двух экспериментов можно провести в (m + n) способов.Это правило может быть распространяется на любое конечное число экспериментов.

    Пример: Предположим, в комнате 3 двери, 2 с одной стороны и 1 с другой стороны. Мужчина хочет выйти из комнаты. Очевидно, у него есть «3» варианта. Он может выйти через дверь «A» или дверь «B» или дверь ‘C’.

    Умножение Правило: Если работа может быть выполнена m способами, другая работа может быть выполнена в ‘N’ способов, то обе операции могут быть выполняется m x n способами.Его можно распространить на любую конечную количество операций.

    Пример .: Предположим, мужчина хочет зачеркнуть комната, у которой 2 двери с одной стороны и 1 дверь с другой. сайт. У него есть 2 x 1 = 2 способа для этого.

    Факториал n: продукт первых «n» натуральных чисел обозначается n !.

    п! = п (п-1) (п-2) ..3.2.1.

    Бывший.5! = 5 х 4 х 3 х 2 х 1 = 120

    Примечание 0! = 1

    Доказательство! = п, (п-1)!

    Или же (п-1)! = [n x (n-1)!] / n = n! / п

    Положив n = 1, у нас

    О! = 1! / 1

    или 0 = 1

    Перестановка

    Количество перестановок «N» разные вещи взяты «r» время определяется по формуле: —

    n P r знак равно п! / (п-р)!

    Доказательство : Допустим, у нас есть «n» разных вещей a 1 , а 2 ……, а н .

    Очевидно, что первое место может быть заполненным «n» способами. Количество вещей осталось после заполнения первое место = n-1

    Значит, второе место может быть залил (n-1) способами. Теперь количество вещей осталось после заполнение первого и второго места = n — 2

    Теперь третье место может быть залил (n-2) способами.

    Таким образом, количество способов заполнение первое место = n

    Количество способов заправки второе место = n-1

    Количество способов заправки третье место = n-2

    Количество способов заправки r-е место = n — (r-1) = n-r + 1

    Путем умножения — правило подсчета, общее количествоспособов пополнения, во-первых, второе — п-е вместе: —

    п (п-1) (п-2) ———— (п-р + 1)

    Отсюда:
    n P r = п (п-1) (п-2) ————— (п-г + 1)

    = [n (n-1) (n-2) ———- (n-r + 1)] [(n-r) (n-r-1) —— 3. 2.1.] / [(n-r) (n-r-1)] —- 3.2.1

    n P r = n! / (N-r)!

    Количество перестановок «N» разных вещей, взятых одновременно, — это выдает: —

    n P n знак равно п!

    Доказательство :
    Теперь у нас есть n объектов и n мест.

    Номер способов пополнения I места = n

    Количество способов заправки второе место = n-1

    Количество способов заправки третье место = n-2

    Количество способов заправки r-е место, т.е. последнее место = 1

    Номер способов заполнения первое, второе, — n-е место
    = n (n-1) (n-2) —— 2.1.

    n P n = n!

    Концепт.

    У нас n P r = П! / П-р

    Путь r = n, имеем: —

    n P r = n! / (н-р)

    Но n P n = п!

    Ясно возможно, только когда n! = 1

    Следовательно это доказательство того, что 0! = 1

    Примечание : Факториал отрицательного числа не определен. В выражение –3! не имеет значения.

    Примеры

    Q. Сколько разных сигналов можно подать по 5 флагам из 8-флагов разных цветов?

    Отв. Количество способов извлечения 5 флажков из 8-лепестков = 8 P 5

    = 8! / (8-5)!

    = 8 х 7 х 6 х 5 х 4 = 6720

    В. Сколько слов может быть сделано с использованием букв слова «СИМПЛЕТОН» принимать все за раз?

    Отв. В слове есть «9» разных букв «СИМПЛЕТОН»

    Номер перестановок, принимающих все буквы за раз = 9 P 9

    = 9! = 362880.

    Количество перестановок n-вещи, взятые одновременно, в которых «P» одного типа, из них ‘g’ второго типа, ‘R’ из них третьего типа, а все остальные различное вычисляется по: —

    н! / П! х д! Икс р!

    Пример: Сколько способов могут ли буквы слова «довузовской» быть согласованный?

    13! / 2! X 2! X 2!

    Количество перестановок n-вещей, взятых «r» в то время, когда каждая вещь может быть повторен r раз: = n r .

    Доказательство.

    Количество способов заправки first –place = n

    Поскольку повторение разрешено, так

    Количество способов заправки второе место = n

    Количество способов заправки третье место

    Количество способов заправки r-е место = n

    Отсюда общее количество путей в котором можно заполнить первое, второе —- r-е места

    = п х п х п ————- r факторов.

    = n r

    Пример: У ребенка 3 кармана и 4 монеты. Какими способами он может положил монеты в карман.

    Отв. Первый монету можно положить 3 способами: второй, третий и Четвертые монеты также можно положить 3 способами.

    Итак общее количество путей = 3 х 3 х 3 х 3 = 3 4 = 81

    подробнее >>>

    Менделирующие законы сложения, умножения и предсказания

    Изображение: «Замороженные образцы для анализа eDNA хранятся в морозильной камере в Центре рыболовства Среднего Запада. »От
    USFWSmidwest. Лицензия: CC BY 2.0

    .

    Фонд классической генетики

    Репродукция позволяет живым существам передавать биологические черты будущим поколениям посредством феномена наследственности. Наследственная информация передается от родителей к потомству через гены .

    Основы классической генетики заложил австрийский монах Грегор Мендель. Его работа по гибридизации растений, опубликованная в 1866 году, легла в основу генетики.Его экспериментальные выводы позже были названы «законами наследования Менделя». Эпоха классической генетики началась с повторного открытия работ Менделя в 1900 году и продолжалась до тех пор, пока Уотсон и Крик не открыли ДНК в 1953 году. Эти открытия привели к нашему нынешнему пониманию генов и их функций на молекулярном уровне.

    Первый закон Менделя

    Закон сегрегации : пара генов, то есть аллелей, отделенных друг от друга во время образования гамет. Каждая гамета несет только один аллель.

    Второй закон Менделя

    Закон независимого ассортимента : Гены различных признаков сортируются независимо во время формирования гамет.

    Применение базовой вероятности для решения генетических проблем

    Вероятность — это вероятная частота возникновения события из ряда возможных или , количественно определяющая вероятность того, что событие произойдет . Если события не происходит, вероятность равна 0; если это так, вероятность равна 1, так что вероятность того, что событие произойдет, составляет 100%.Для неопределенного события, которое может произойти, а может и не произойти, вероятность составляет от 0 до 1.

    Согласно гипотезе Менделя, передача аллеля гамете является случайной, то есть оба аллеля имеют равные шансы попасть в любую гамету. Более того, комбинация гамет после оплодотворения также случайна.

    Концепция вероятности играет важную роль в менделевской генетике из-за случайности наследственных событий. Комбинации в основном бывают одного из следующих двух типов:

    1. Взаимоисключающие
    2. Независимый

    Взаимоисключающие комбинации : Возникновение одного события означает, что другие события не произойдут, поэтому их вероятность равна нулю.

    Независимые комбинации : Вероятность того, что событие произойдет или нет, не влияет на вероятность того, что произойдет какое-либо другое событие, поэтому события независимы друг от друга.

    Два разных правила вероятности предсказывают исход как взаимоисключающих, так и независимых событий.

    Дополнительное правило

    Это правило означает, что вероятность того, что произойдет одно или другое «взаимоисключающее» событие, равна сумме вероятностей того, что произойдет отдельное событие.Правило сложения применяется только к взаимоисключающим событиям. Правило сложения применяется только к случаям «либо / или».

    Например, вероятность аллеля P (вероятность y) или аллеля p (вероятность z) равна y + z, т.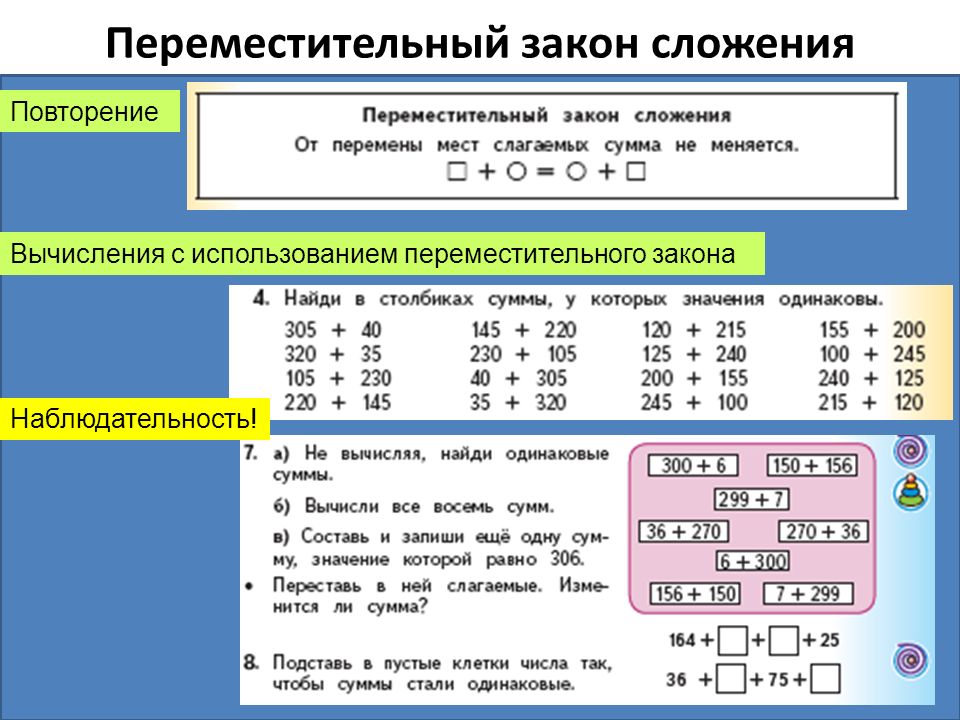 Е. ½ + ½ = 1. Правило сложения не может применяться к аллелю P и аллелю Q двух разных генов. потому что оба аллеля не исключают друг друга.

    Правило умножения

    Вероятность наступления «независимого» события равна произведению вероятности наступления каждого отдельного события.Сегрегация генов дает равное количество аллелей, которые будут сортировать независимо. Результаты таких скрещиваний предсказуемы с помощью правила умножения вероятностей. Правило умножения применяется к случаям «и… и».

    Например, предположим, что гены Pp (вероятность y) и Qq (вероятность z) осуществляют сортировку независимо. Вероятность гаметы PQ равна y * z, т.е. ½ * ½ = ¼ = 0,25

    Применение вероятности к тестовым крестам

    Фенотип можно объяснить, наблюдая за индивидом, а не за генотипом.Генотип высокого растения может быть либо гомозиготным (TT), либо гетерозиготным (Tt).

    • Гомозигота — это «чистая порода», потому что производится только один тип гамет.
    • Гетерозиготный гибрид. Он производит два разных типа гамет, т.е. половина гамет будет нести ген T, а другая половина — ген t.

    Мендель намеревался определить генотип доминирующих фенотипов растений, используя тестовые скрещивания, чтобы подтвердить обоснованность своих выводов. Он разработал систему для проверки генотипа человека, скрещивая его с человеком известного генотипа.Таким образом, особь с неизвестным генотипом по доминантному фенотипу скрещивается с гомозиготной рецессивной особью, которая выявляет неизвестный генотип .

    Квадрат Пеннета

    Площадь Пеннета названа в честь Реджинальда К. Пеннета, который открыл феномен генной связи, чтобы узнать о генетике и решении проблем. Построив квадрат Пеннета , можно просмотреть все возможные случайные события оплодотворения, а также вероятные генотипы и фенотипы . Однако применение его к шести генным проблемам и так далее может оказаться сложной задачей, поскольку это всего лишь визуальное представление возможных комбинаций.

    Тест-кросс используется для определения гомозиготности или гетерозиготности особи, то есть неизвестного генотипа. Дигибридные, тригибридные и другие громоздкие тестовые скрещивания могут быть решены с использованием правил сложения и умножения вероятностей для проверки перекрестных экспериментов.

    Вероятность предсказания скрещивания моногибридов и дигибридов

    Моногибридный кросс

    Вероятность появления гомозиготного или гетерозиготного признака в следующем поколении можно предсказать, применив правило сложения к моногибридному тест-кроссу.В следующем примере доминирующей комбинацией является (BB) для карих глаз и (bb) для рецессивного признака голубого цвета глаз. Гетерозиготный человек будет иметь карие глаза (Bb). Частоту можно рассчитать следующим образом:

    Изображение: «Квадрат Пеннета, показывающий крест BB x Bb для цвета глаз. Здесь гомозиготный доминантный кареглазый родитель и w: гетерозиготный кареглазый родитель дают 50% гомозиготных доминантных кареглазых потомков и 50% гетерозиготных кареглазых потомков. Пример, обсуждаемый в тексте, касается перекрестного теста между Bb и Bb »Purpy Pupple.Лицензия: CC BY-SA 3.0

    .

    Результаты : вероятность гомозиготы и гетерозиготы в поколении F2, если оба родителя гетерозиготны.

    • 25% потомков будут иметь гомозиготный доминантный генотип (ВВ).
    • 25% потомков будут иметь гомозиготный рецессивный генотип (bb).
    • 50% потомства будут иметь гетерозиготный генотип (Bb).

    Дигибридные и тригибридные кроссы

    Дигибридное скрещивание или тригибридное скрещивание имеет более одного рассматриваемого признака.Вероятности основаны на возможных моногибридных скрещиваниях . Дигибридное скрещивание можно легко понять, сделав два отдельных моногибридных скрещивания.

    Считается, что эти два признака наследуются независимо. Вероятность того, что семя будет зеленым или желтым, не зависит от вероятности того, что семя будет круглым или морщинистым. Однако преобладают желтые и округлые характеристики семян. Из-за независимого набора этих признаков мы можем применить правило вероятности произведения к случаю дигибридного скрещивания.

    Изображение: «Метод дигибридного кросса RrYy x RrYy» Тима ДеДжулио. Лицензия: Public Domain

    Предсказание неизвестного генотипа посредством тестового скрещивания

    Неизвестный генотип индивидуума можно предсказать с помощью метода Менделя, т.е. , создавая скрещивание гомозиготного рецессивного индивидуума и индивидуума с неизвестным генотипом, но доминантным фенотипом . Этот метод позволит выявить неизвестный генотип. Это означает важность моногибридного тестового скрещивания; он помогает обнаруживать рецессивные аллели, наносящие вред населению.

    В следующем примере коричневый цвет является доминирующим цветом глаз, а синий — рецессивным. Индивид с неизвестным генотипом с карими глазами может быть скрещен с гомозиготным рецессивным индивидом.

    Результаты можно предсказать следующим образом:

    • Если у 50% людей карие глаза и у 50% голубые глаза, то неизвестный генотип — гетерозигота (Bb).
    • Если все люди в следующем поколении имеют карие глаза, то неизвестный генотип является гомозиготным (BB).

    Ограничения законов Менделя

    Неожиданные фенотипы

    Одно из ограничений законов Менделя состоит в том, что почти все гены признаков, которые он изучал, были локализованы на разных хромосомах или на значительном расстоянии в одной и той же хромосоме; следовательно, результаты были предсказуемыми. Если проследить больше пар генов, появятся разные и неожиданные фенотипы из-за феномена кроссовера .

    Непрерывные вариации

    В естественных популяциях многие признаки, по-видимому, постоянно изменяются из-за полигенного наследования, которое возникает, когда несколько генов отвечают за одну характеристику или признак.Факторы окружающей среды, наряду с количеством генов, ответственных за один признак, вызывают огромных вариаций фенотипа признака в естественной популяции .

    Примеры таких черт включают цвет глаз, цвет кожи или рост. Количество пигмента больше в карих глазах и меньше в голубых, зеленых или серых глазах. Такие непрерывно меняющиеся черты обычно представлены колоколообразной диаграммой.

    Плейотропия

    Иногда единственный ген влияет на более чем один фенотип или признак человека, , который известен как плейотропия.Эти признаки могут быть не связаны, и аллели передаются так же, как и другие неплейотропные аллели.

    Это явление также является причиной множественных заболеваний у людей, таких как фенилкето мочевина и болезнь Марфана . При болезни Марфана хрусталик глаза, пальцы и сердце функционируют ненормально. Иногда он может быть причиной гибели эмбрионов, как показано в следующем примере.

    Изображение: «Квадрат Пеннета, иллюстрирующий летальный аллель желтой шерсти у мышей.»Пользователя Jcfidy. Лицензия: CC BY-SA 4.0

    .

    Доминирование

    Феномен доминирования применяется к диплоидным особям, у которых присутствуют по крайней мере два аллеля одного и того же гена . Однако доминирование не всегда бывает полным; время от времени оба аллеля проявляют себя, чтобы дать начало другому фенотипу. Внутренние факторы и факторы окружающей среды влияют на экспрессию генов.

    Совместное доминирование

    Ген может иметь более одной копии аллеля, т.е. более двух аллельных вариантов одного и того же гена.В этом случае фенотип также отличается от предсказанного с помощью менделизма. Если присутствует множественных аллелей и полностью выражены разные аллели , это называется совместным доминированием.

    Например, в случае групп крови аллели iA и iB для антигенов A и B являются доминантными над рецессивным аллелем i0; они полностью экспрессируются у гетерозиготных индивидуумов с группой крови AB.

    Ниже приводится пример совместного доминирования чалого крупного рогатого скота по окрасу шерсти.

    Изображение: «Эта диаграмма показывает совместное доминирование. В этом примере белый бык (WW) спаривается с красной коровой (RR), и их потомство демонстрирует совместное доминирование, выражающее как белые, так и рыжие волосы ». пользователя Hhughes15. Лицензия: CC BY-SA 4.0

    .

    Неполное доминирование

    Промежуточный фенотип у гетерозиготной особи известен как неполное доминирование. Это происходит, когда доминантный аллель не может полностью замаскировать эффект рецессивного аллеля .

    Пример: скрещиваются два растения львиный зев. У одного растения были красные цветы, а у другого — белые. Потомки имели розовые цветки, т.е. промежуточный фенотип. Это пример неполного доминирования.

    Избыточное доминирование

    Чрезмерное доминирование возникает, когда гетерозиготное потомство от двух гомозиготных родителей имеет фенотип, выходящий за пределы диапазона родителей.

    Например, скрещиваются два гомозиготных растения с длиной плода 10 см (SS) и 20 см (ss).Следующее поколение — это гетерозигота (Ss) с длиной плода 30 см.

    Влияние окружающей среды на фенотипы

    Иногда изменения экспрессии генов являются результатом изменения факторов окружающей среды, таких как температура и т. Д.

    Гималайские кролики

    Гималайские кролики имеют черные волосы на хвосте, ушах, носу и ногах. Однако волосы на туловище белые. Причиной этого явления является чувствительная к температуре экспрессия генов фермента тирозиназы .Гималайские кролики гомозиготны по мутантной форме фермента тирозиназы; он отвечает за выработку пигмента меланина, который придает волосам более темный цвет.

    Этот фермент работает только при температуре окружающей среды ниже 33 ° C (91,4 F). В области туловища хранится изрядное количество тепла, поэтому волосы на стволе кажутся светлыми. По той же причине сиамские кошки кажутся светлее летом и темнее зимой; у них есть такая же термочувствительная версия фермента тирозиназы.

    Эпистаз изменяет фенотипические соотношения

    Эпистаз определяется как взаимодействие генов в разных локусах . Экспрессия одного гена зависит от наличия определенного генотипа в других локусах. В некоторых случаях он также отвечает за полное подавление мутантного фенотипа.

    Например, гомозиготное родительское поколение белых цветков, где два аллеля отвечают за цвет цветков, подвергается перекрестному оплодотворению для получения пурпурных цветков в поколении F1.Дальнейшее скрещивание дает как белые, так и пурпурные цветки в поколении F2. Следовательно, эпистаз может изменить ожидаемые фенотипические соотношения . Появление пурпурного цвета в поколении F1 связано с взаимозависимостью ферментов в результате эпистатического явления.

    Современная генетика за гранью менделизма

    Менделирующая генетика заложила основу современной генетики и остается актуальной для многих признаков. Это хорошее введение в основные принципы генетики, но современная генетика отличается от менделевской генетики по следующим причинам:

    • Гипотеза Менделя о том, что один ген — один признак, не универсальна из-за многогенного наследования, когда многие гены контролируют один признак.
    • Независимый набор генов не применяется к тесно сцепленным генам, которые наследуются вместе из-за их расположения в непосредственной близости.
    • Из-за эпистаза предположение Менделя о том, что один ген не может влиять на другой, не применимо повсеместно.
    • Концепция Менделя о двух аллелях для одного гена больше не действует из-за появления концепции множественных аллелей.
    • Мендель предположил, что характеры могут быть либо доминирующими, либо рецессивными, но теперь мы знаем о концепциях неполного доминирования, кодоминирования и сверхдоминирования.

    перестановок и комбинаций — фундаментальный принцип подсчета (часть 2)

    Принцип умножения

    Привет. Теперь, когда у вас есть некоторое представление о подсчете связанных проблем и использовании умножения для ответа на них, я сформулирую принцип умножения немного формально:

    «Если набор объектов можно разделить на m различных типов, и каждого из этих типов можно разделить на n различных подтипов, то всего будет m x n различных типов объектов.”

    (Есть причина, по которой я выделил каждые и жирным шрифтом, потому что каждое , каждое имеет значение, и без них все будет иначе. Я вернусь к этому чуть позже.)

    Для нашего примера автомобилей мы могли бы разделить автомобили на 2 типа (седан и хэтчбек) и каждого из из них можно было бы разделить на 3 подтипа (модели), в результате чего 2 x 3 = 6 типов автомобилей.

    (Мы могли бы пойти другим путем и сначала разделить автомобили как модели, а затем разделить их на седаны и хэтчбеки.Ответ остался бы прежним: 3 х 2 = 6)

    Кроме того, каждые из этих 6 автомобилей можно разделить на 2 типа (красный и синий), что в сумме составляет 6 x 2 = 12 различных типов автомобилей.

    Правило умножения не ограничивается только классификацией объектов. Его также можно применять в разных контекстах. Рассмотрим эту проблему, например: если есть 3 разных рейса из A в B и 2 разных поезда из B в C, сколькими разными способами человек может добраться из A в C (используя только эти рейсы и поезда)?

    Вот вам все кейсы.

    Возможные маршруты — 1a, 1b, 2a, 2b, 3a и 3b — всего 6.

    Опять же, для каждый маршрут от A до B, есть 2 маршрута от B до C. И поскольку есть 3 маршрута от A до B, всего будет 3 x 2 разных маршрута.

    Другими словами, количество путей будет получено умножением количества маршрутов от A до B (3) на количество маршрутов от B до C (2), доступных для каждого маршрута от A до B: 3 х 2 = 6.

    Вот еще один способ сформулировать принцип умножения:

    «Если задача T может быть разделена на подзадачи T 1 и T 2 , которые могут быть выполнены m способами и n способами соответственно, и T будет завершена путем выполнения обоих T 1 и T 2 , то количество способов завершения Т будет mxn ”

    Давайте снова подумаем об этом примере.

    Две подзадачи T 1 и T 2 можно рассматривать как переход от A к B и переход от B к C соответственно, где T 1 может быть выполнен тремя способами, а T 2 может быть завершен 2 способами.

    Так как задача достижения от A до C будет завершена путем выполнения как T 1 , так и T 2 , поэтому количество способов достижения от A до C будет 3 x 2 = 6.

    Вот еще одна простая проблема.

    Какими способами вы можете добраться из A в D, учитывая возможные маршруты из A в B, из B в C и из C в D?

    Задача здесь — от A до D, которая будет завершена путем выполнения задач от A до B и от B до D .

    Здесь от B до D можно далее разделить на подзадачи от B до C (2 способа) и от C до D (3 способа), , обе из которых должны быть выполнены. Следовательно, количество способов добраться от B до D равно 2 x 3 = 6.

    И количество способов завершить от A до D будет 3 (от A до B) x 6 (от B до D) = 18 способов.

    Мы могли бы также напрямую записать это число как 3 (от A до B) x 2 (от B до C) x 3 (от C до D) = 18 способов.

    Краткое содержание урока

    Мы можем сформулировать принцип умножения следующим образом:

    ““ Если задача T может быть разделена на n подзадач T 1 , T 2 , T 3 ,….T n , который может быть выполнен в m 1 , m 2 , m 3 … m n способа соответственно, а T будет завершен путем выполнения каждых этих подзадач, затем количества способов завершение Т составит м 1 xm 2 xm 3 x ……. x м n ”

    На этом я остановлюсь, а в следующей части продолжу принцип сложения.

    Правило сложения для определения вероятностей

    Что такое правило сложения вероятностей?

    Правило сложения для вероятностей описывает две формулы: одна для вероятности одного из двух взаимоисключающих событий, а другая — для вероятности двух не исключающих друг друга событий.

    Первая формула — это просто сумма вероятностей двух событий. Вторая формула — это сумма вероятностей двух событий за вычетом вероятности того, что оба они произойдут.

    Ключевые выводы

    • Правило сложения для вероятностей состоит из двух правил или формул, одна из которых учитывает два взаимоисключающих события, а другая — два не исключающих друг друга события.
    • «Не исключающие друг друга» означает, что между двумя рассматриваемыми событиями существует некоторое перекрытие, и формула компенсирует это путем вычитания вероятности перекрытия P (Y и Z) из суммы вероятностей Y и Z.
    • Теоретически первая форма правила является частным случаем второй формы.

    Формулы для правил сложения вероятностей —

    Математически вероятность двух взаимоисключающих событий обозначается:

    Взаимодействие с другими людьми п ( Y или же Z ) знак равно п ( Y ) + п ( Z ) P (Y \ text {или} Z) = P (Y) + P (Z) P (Y или Z) = P (Y) + P (Z)

    Математически вероятность двух не исключающих друг друга событий обозначается следующим образом:

    Взаимодействие с другими людьми п ( Y или же Z ) знак равно п ( Y ) + п ( Z ) — п ( Y а также Z ) P (Y \ text {или} Z) = P (Y) + P (Z) — P (Y \ text {и} Z) P (Y или Z) = P (Y) + P (Z) −P (Y и Z)

    Что вам говорит правило сложения вероятностей?

    Чтобы проиллюстрировать первое правило правила сложения вероятностей, рассмотрим кубик с шестью гранями и шансами на выпадение 3 или 6.Поскольку шансы выпадения 3 равны 1 из 6, а шансы выпадения 6 также 1 из 6, вероятность выпадения 3 или 6 составляет:

    1/6 + 1/6 = 2/6 = 1/3

    Чтобы проиллюстрировать второе правило, рассмотрим класс, в котором 9 мальчиков и 11 девочек. В конце семестра 5 девочек и 4 мальчика получают оценку B. Если студент выбран случайно, каковы шансы, что он будет девочкой или четвертым? Поскольку шансы выбрать девушку составляют 11 из 20, шансы выбрать ученицу B равны 9 из 20, а шансы выбрать девушку, которая является ученицей B, составляют 5/20, шансы выбрать девушку или ученицу B находятся:

    11/20 + 9/20 — 5/20 = 15/20 = 3/4

    На самом деле два правила упрощаются до одного правила, второго.Это потому, что в первом случае вероятность двух взаимоисключающих событий равна 0. В примере с кубиком невозможно бросить одновременно 3 и 6 при одном броске одного кубика. Таким образом, эти два события исключают друг друга.

    Взаимная эксклюзивность

    Взаимоисключающие — это статистический термин, описывающий два или более событий, которые не могут совпадать.

    admin

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *