Переместительное свойство сложения – примеры (5 класс, математика)

4.3

Средняя оценка: 4.3

Всего получено оценок: 163.

4.3

Средняя оценка: 4.3

Всего получено оценок: 163.

Законы сложения настолько естественны для большей части учеников 5 класса, что они даже не замечают, когда их используют. С одной стороны это хорошо, поскольку серьезно ускоряет расчет, с другой это же мешает использовать эти свойства для решения больших примеров. Чтобы такой проблемы не возникало, поговорим о свойствах сложения и их правильном применении.

Сложение

Сложение это процесс переноса точки по числовой прямой. Каждая точка на числовой прямой соответствует какому-либо числу. Процесс вычитания или сложения это перенос этой точки. Само собой, что в процессе движения меняется значение.

Если говорить проще, то сложение можно представить, как объединение двух чисел в одно. Складываться могут любые рациональны числа: положительные и отрицательные, целые и дробные, а так же число 0.

Иррациональные числа подчиняются другим законам, просто так их сложить не получится. Но всегда можно найти приближенное значение из рациональных чисел и выполнить сложение.

Свойства сложения

У сложения всего 2 свойства: переместительное и сочетательное.

• Переместительное свойство заключается в том, что от перемены мест слагаемых сумма не меняется. И это вправду так: какая разница, в какой последовательности сложить в корзину фрукты, если их количество, в конечном счете, не изменится?
• Сочетательное свойство касается примеров с 3 и более слагаемыми. Оно говорит о том, что всегда можно выбрать два любых слагаемых, сложить их и выполнять дальнейшие действия с результатом сложения.

Переместительное свойство сложения

Первый вопрос, который нужно задавать себе, узнавая что-то новое: как это можно использовать. В математике переместительное свойство сложения отлично подходит для решения больших примеров.

Некоторые числа складывать проще других. Как правило, это десятки, пары чисел, которые образуют 10, и числа 7 и 8.

Рассмотрим несколько примеров, чтобы понять, как правильно использовать переместительное свойство сложения.

Нужно решить пример:

13+21+87+55+29+7+46+14 – сгруппируем числа так, чтобы было проще складывать.

13+21+87+55+29+7+46+14=(13+87)+(21+29)+(46+14)+(55+7) – обратите внимание, что в последней скобке собраны оставшиеся числа, которые правильно сгруппировать не удалось. Такое тоже случается, просто нужно внимательно относится к группированию, чтобы не пропустить возможность сократить время вычислений.

(13+87)+(21+29)+(46+14)+(55+7)=100+50+60+55+7=210+55+7=210+62=272

Не забывайте, что складывать можно и отрицательные числа, поэтому их можно переносить в пределах примера с сохранением знака. Главное, чтобы ученик максимально быстро решал примеры.

(19-7)+(13-9)+(17-3) – изменим компоновку примера для того, чтобы упростить решение. Сначала раскроем все скобки:

(19-7)+(13-9)+(17-3)=19-7+13-9+17-3 – теперь сгруппируем числа так, чтобы облегчить вычитание.

19-7+13-9+17-3=(19-9)+(13-3)+(17-7)=10+10+10=30 – вот так мы значительно упростили решение. При наличии определенного навыка второе действие можно сразу пропускать, сокращая время решение. Главное не терять знаки минуса.

Что мы узнали?

Мы поговорили о сложении. Узнали о свойствах сложения и рассмотрели примеры переместительного свойства сложения. Выделили, что переместительное свойство можно использовать для разности, если правильно перемещать числа со знаком минус.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Юксель Саркаров

  9/10

• Игорь Зимин

  7/10

Оценка статьи

4.3

Средняя оценка: 4.3

Всего получено оценок: 163.

---

А какая ваша оценка?

Переместительное свойство.

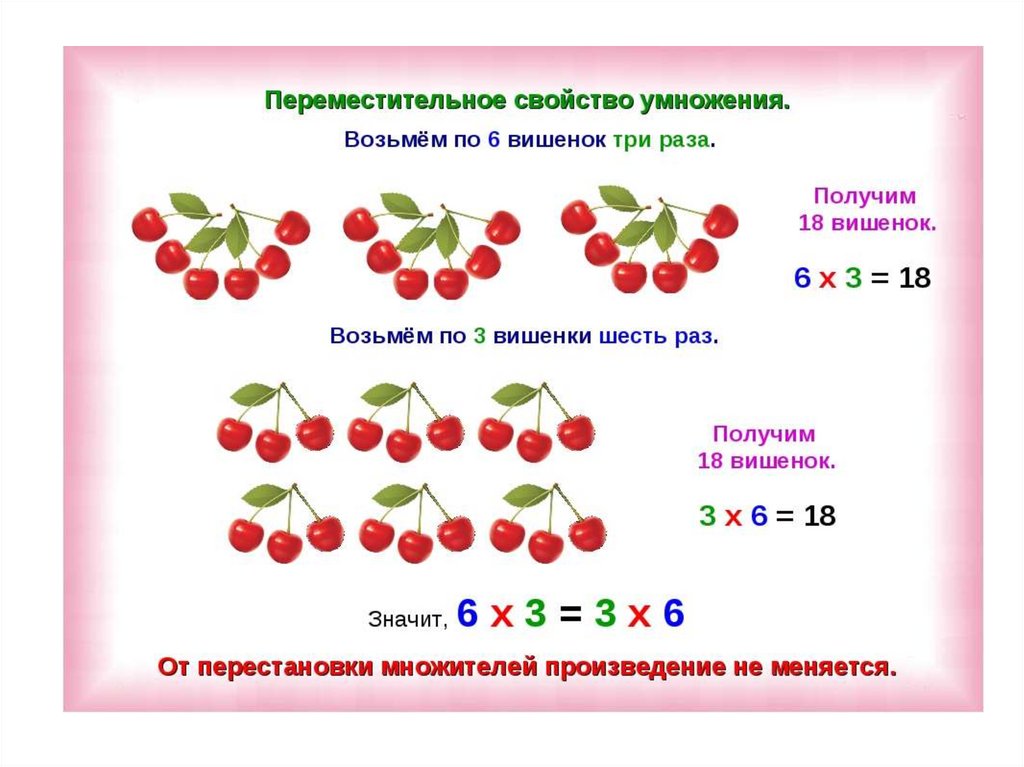
Переместительное свойство умножения.

• Альфашкола
• Статьи
• Переместительное свойство умножения

Давайте вспомним, что такое переместительное свойство умножения?  Cформулируем данный закон ниже: 

Вспомнили? Теперь рассмотрим это на примере: 

\(a*b=b*a\)

\(5*6=6*5=30\)

\(12*4=4*12=48 \)

Это свойство очень помогает при умножении в столбик:

При применении данного свойства упрощает вычисление:

\(9*5\;572=5\;572*9\)

 

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Никита Сергеевич Анохин

Репетитор по математике

Стаж (лет)

Образование:

Керченский государственный морской технологический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Любовь Сергеевна Орлова

Репетитор по математике

Стаж (лет)

Образование:

Армавирский государственный педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Ольга Анатольевна Лизогуб

Репетитор по математике

Стаж (лет)

Образование:

Мозырский государственный педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Подготовка к ОГЭ по математике
• Репетитор по химии для подготовки к ЕГЭ
• Репетитор по химии для подготовки к ОГЭ
• Подготовка к олимпиадам по физике
• Репетитор по русскому языку для подготовки к ОГЭ
• Подготовка к олимпиадам по английскому языку
• Английский язык для начинающих
• Репетитор для подготовки к ВПР по русскому языку
• Репетитор по биологии для подготовки к ЕГЭ
• Репетитор по информатике для подготовки к ОГЭ

Похожие статьи

• Чтение графика функций: парабола
• Примеры решения неравенств
• Показательные уравнения
• Как легко умножить на 0,5
• Как перевести квадратные сантиметры в квадратные миллиметры
• НИУ ВШЭ: Факультет Психологии
• Задачи на исследование функций
• Как заинтересовать ребенка читать + 20 книг для школьников всех возрастов

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Переместительное свойство — определение, примеры, формула

Переместительное свойство касается арифметических операций сложения и умножения. Это означает, что изменение порядка или положения двух чисел при их сложении или умножении не меняет конечный результат. Например, 4 + 5 дает 9, а 5 + 4 также дает 9. Порядок сложения двух чисел не влияет на сумму. Та же концепция применима и к умножению. Свойство коммутативности не выполняется для вычитания и деления, так как конечные результаты совершенно другие после изменения порядка чисел.

1.	Что такое коммутативная собственность?
2.	Коммутативное свойство сложения
3.	Коммутативное свойство умножения
4.	Коммутативное свойство против ассоциативного свойства
5.	Часто задаваемые вопросы о коммутативной собственности

Что такое коммутативное свойство?

Слово «коммутативный» происходит от слова «коммутировать», что означает передвигаться. Следовательно, свойство коммутативности связано с перемещением чисел. Таким образом, математически, если изменение порядка операндов не меняет результат арифметической операции, то эта конкретная арифметическая операция является коммутативной. Помимо этого, существуют и другие свойства чисел: ассоциативность, дистрибутивность и тождественность. Они отличаются от коммутативного свойства чисел. Кратко обсудим перестановочное свойство сложения и умножения.

Формула коммутативного свойства

Если даны два числа A и B, то формула коммутативного свойства чисел задается следующим образом:

• A + B = B + A
• А × В = В × А
• А — В ≠ В — А
• А ÷ В ≠ В ÷ А

Формула свойства коммутативности гласит, что изменение порядка двух чисел при их сложении и умножении не влияет на результат. Но при вычитании и делении любых двух действительных чисел порядок чисел важен и, следовательно, его нельзя изменить.

Коммутативное свойство сложения

Переместительное свойство сложения говорит о том, что изменение порядка слагаемых не меняет значения суммы. Если «A» и «B» — два числа, то свойство коммутативности сложения чисел может быть представлено, как показано на рисунке ниже.

Давайте возьмем пример коммутативного свойства сложения и поймем применение приведенной выше формулы. Если даны два числа 10 и 13, то 10 + 13 = 23 и 13 + 10 = 23. Следовательно, 10 + 13 = 13 + 10,

Коммутативное свойство умножения

Коммутативное свойство умножения говорит о том, что порядок, в котором мы умножаем два числа, не меняет конечного произведения. Изображение, приведенное ниже, представляет коммутативное свойство умножения двух чисел.

Если 4 и 6 числа, то 4 × 6 = 24, а 6 × 4 также равно 24. Таким образом, 4 × 6 = 6 × 4. Следовательно, свойство коммутативности выполняется для умножения чисел.

Примечание: Свойство коммутативности не выполняется для операций вычитания и деления. Возьмем в качестве примера числа 6 и 2.

• 6 — 2 = 4, но 2 — 6 = -4. Таким образом, 6 — 2 ≠ 2 — 6.
• 6 ÷ 2 = 3, но 2 ÷ 6 = 1/3. Таким образом, 6 ÷ 2 ≠ 2 ÷ 6.

Коммутативное свойство против ассоциативного свойства

Есть четыре общих свойства чисел: замкнутость, коммутативность, ассоциативность и дистрибутивность. В этом разделе мы узнаем разницу между ассоциативным и коммутативным свойством. И ассоциативное, и коммутативное свойство утверждают, что порядок чисел не влияет на результат сложения и умножения. Итак, в чем разница между ними? Давай выясним.

Посмотрите на приведенную ниже таблицу, показывающую коммутативное и ассоциативное свойства.

Коммутативное имущество	Ассоциативное свойство
Коммутативное свойство происходит от слова «коммутировать», что означает передвигаться, переключать или менять номера.	Ассоциативное свойство происходит от слова «ассоциировать», которое имеет дело с группировкой чисел.
Порядок чисел может быть изменен в случае сложения и умножения двух чисел без изменения конечного результата.	Группировка чисел может быть изменена в случае сложения и умножения трех чисел без изменения конечного результата.
Формула: А + В = В + А А × В = В × А	Формула: А + (В + С) = (А + В) + С = (А + С) + В А × (В × С) = (А × В) × С = (А × С) × В

Важные примечания:

Некоторые ключевые моменты, которые следует помнить о свойстве коммутативности, приведены ниже.

• Коммутативное свойство утверждает, что «изменение порядка операндов не меняет результат».
• Свойство коммутативности сложения: A + B = B + A.
• Свойство коммутативности умножения: A × B = B × A.

☛ Похожие темы

Ознакомьтесь с некоторыми интересными статьями, посвященными коммутативности в математике.

• Свойства натуральных чисел
• Свойства целых чисел
• Свойства рациональных чисел
• Свойства целых чисел

 

Примеры коммутативных свойств

1. Пример 1: Мать Джеки спросила его, является ли сложение двух натуральных чисел примером коммутативности. Можете ли вы помочь Джеки выяснить, является ли оно коммутативным или нет?

   Решение:

   Мы знаем, что свойство перестановочности сложения гласит, что изменение порядка слагаемых не меняет значения суммы. Если мы возьмем любые два натуральных числа, скажем, 2 и 5, то 2 + 5 = 7 = 5 + 2. Таким образом, сложение двух натуральных чисел является примером свойства коммутативности.

2. Пример 2: Найдите пропущенное значение: 132 × 121 = ___ × 132.

   Решение:

   Коммутативное свойство умножения утверждает, что если есть два числа x и y, то x × y = y × Икс. Если вы внимательно посмотрите на данное уравнение, то обнаружите, что здесь применимо свойство коммутативности. Если x = 132, а y = 121, то мы знаем, что 132 × 121 = 121 × 132.

   ∴ Недостающее число 121.

3. Пример 3: Укажите, является ли данное утверждение истинным или ложным.

   «Деление 12 на 4 удовлетворяет свойству коммутативности.»

   Решение:

   Свойство коммутативности не выполняется для операции деления. Значит, данное утверждение неверно. Давайте проверим это.
   12 ÷ 4 = 3
   4 ÷ 12 = 1/3 = 0,33
   ⇒ 12 ÷ 4 ≠ 4 ÷ 12

   ∴ Данное утверждение неверно.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по коммутативной собственности

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о коммутативном свойстве

Что такое коммутативное свойство в математике?

Свойство коммутативности гласит, что если порядок чисел поменять местами при выполнении сложения или умножения, сумма или произведение не изменится. Следует отметить, что свойство коммутативности справедливо только для сложения и умножения, но не для вычитания и деления. Например, 6 + 7 равно 13 и 7 + 6 также равно 13. Аналогично, 6 × 7 = 42 и 7 × 6 = 42.

Что такое коммутативное свойство сложения?

Согласно коммутативному свойству сложения, при сложении двух чисел в любом порядке сумма остается неизменной. Например, 3 + 9= 9 + 3 = 12.

Что такое коммутативное свойство умножения?

Согласно свойству перестановочности умножения, порядок умножения чисел не меняет произведение. Например, 4 × 5 равно 20, а 5 × 4 также равно 20. Хотя порядок чисел изменился, произведение равно 20.

Можно ли использовать переместительное свойство для вычитания и деления?

Свойство коммутативности нельзя применять для вычитания и деления, поскольку изменение порядка чисел при выполнении вычитания и деления не дает того же результата. Например, 5 — 2 равно 3, тогда как 2 — 5 не равно 3. Точно так же 10, деленное на 2, дает 5, тогда как 2, деленное на 10, не дает 5. Следовательно, коммутативное свойство не верно для вычитания и деления.

В чем разница между коммутативным и ассоциативным свойством?

Свойство перестановочности гласит, что изменение порядка двух чисел в операции сложения или умножения не меняет ни суммы, ни произведения. Коммутативное свойство сложения записывается как A + B = B + A. Коммутативное свойство умножения записывается как A × B = B × A. Ассоциативное свойство утверждает, что группировка или комбинация трех или более чисел, которые добавляются или умножение не меняет ни суммы, ни произведения. Ассоциативность сложения записывается как: (A + B) + C = A + (B + C) = (A + C) + B. Ассоциативность умножения записывается как (A × B) × C = A × (В × С) = (А × С) × В.

В чем разница между коммутативной и распределительной собственностью?

Свойство коммутативности гласит, что изменение порядка чисел в операции сложения или умножения не меняет результат. Перестановочное свойство сложения двух чисел «A» и «B» равно A + B = B + A. Распределительное свойство означает умножение числа на каждое число в скобках. Числа в скобках разделяются символом сложения или вычитания. Распределительное свойство сложения двух чисел «А», «В»: А(В + С) = АВ + АС.

Может ли коммутативное свойство иметь 3 числа?

Когда речь идет о группировке трех чисел, то это называется ассоциативным свойством, а не коммутативным свойством. Коммутативное свойство применимо к двум числам и гласит, что мы можем поменять местами эти два числа при их сложении или умножении без изменения результата.

Чем похожи коммутативные свойства сложения и умножения?

В обоих случаях, сложения и умножения, порядок чисел не влияет на сумму или произведение. Таким образом, свойство коммутативности верно для операций сложения и умножения.

Как научить коммутативному свойству сложения?

Лучший способ научить переместительному свойству сложения — это использовать предметы из реальной жизни, такие как камешки, игральные кости, семена и т. д. Дайте учащемуся 3 шарика, а затем дайте ему/ему еще 5 шариков. Попросите ее/его посчитать общее количество шариков. Затем повторите тот же процесс сначала с 5 шариками, а затем с 3 шариками. Таким образом, учащиеся будут наблюдать это свойство самостоятельно. Используйте коммутативное свойство рабочих листов сложения, чтобы проверить их понимание.

Что такое коммутативные законы?

Коммутативное право — это еще одно название коммутативного свойства, применимого к сложению и умножению. Коммутативный закон сложения гласит, что порядок сложения двух чисел не меняет суммы (A + B = B + A). Коммутативное свойство умножения гласит, что порядок умножения двух чисел не меняет произведения (A × B = B × A).

Коммутативное свойство по математике (определение и примеры)

По математике, коммутативное свойство или коммутативный закон объясняет, что порядок членов не имеет значения при выполнении арифметических операций.

Коммутативное свойство применимо только для процессов сложения и умножения. Таким образом, это означает, что мы можем изменить положение или поменять местами числа при сложении или умножении любых двух чисел. Это одно из основных свойств целых чисел.

Например: 1+2 = 2+1 и 2 x 3 = 3 x 2. 

Коммутативное свойство: А + В = В + А (дополнение) A x B = B x A    (умножение)

Что такое коммутативная собственность?

Как мы уже обсуждали во введении, в соответствии со свойством коммутативности или коммутативным законом, когда два числа складываются или умножаются вместе, изменение их положения не меняет результат.

Примеры

• 2+3 = 3+2 = 5
• 2 х 3 = 3 х 2 = 6
• 5 + 10 = 10 + 5 = 15
• 5 х 10 = 10 х 5 = 50

Итак, может быть две категории операций, которые подчиняются коммутативному свойству:

• Взаимное имущество дополнения
• Переместительное свойство умножения

История

Хотя официальное использование коммутативного свойства началось в конце XVIII века, оно было известно еще в античную эпоху.

Слово «коммутативный» происходит от французского слова «commute или commuter», что означает «переключаться» или «передвигаться», в сочетании с суффиксом «-ative» означает «склонность к». Следовательно, буквальное значение слова имеет тенденцию переключаться или перемещаться. В нем говорится, что если мы прокрутим позиции целых чисел, результат останется прежним.

Коммутативное свойство сложения

Согласно коммутативному свойству сложения, при сложении двух целых чисел ответ не изменится, даже если изменить положение чисел.

Тогда пусть A и B будут двумя целыми числами;

А + В = В + А

Примеры коммутативного свойства сложения

• 1 + 2 = 2 + 1 = 3
• 3 + 8 = 8 + 3 = 11
• 12 + 5 = 5 + 12 = 17

Коммутативное свойство умножения

В соответствии с коммутативным свойством умножения, когда мы умножаем два целых числа, ответ, который мы получаем после умножения, останется прежним, даже если целые числа поменять местами.

Тогда пусть A и B будут двумя целыми числами;

А × В = В × А

Примеры коммутативного свойства умножения

• 1 × 2 = 2 × 1 = 2
• 3 × 8 = 8 × 3 = 24
• 12 × 5 = 5 × 12 = 60

Важные факты о коммутативной собственности

• Коммутативность применима только к двум арифметическим операциям: сложению и умножению
• Изменение порядка операндов не меняет результат
• Коммутативное свойство сложения: A + B = B + A
• Коммутативное свойство умножения: A.B = B.A

Другое имущество

Другими основными свойствами сложения и умножения являются:

• Ассоциативное свойство
• Распределительная собственность

Теперь обратите внимание и на другие свойства:

Ассоциативное свойство сложения и умножения

По ассоциативному закону, независимо от того, как сгруппированы числа, можно их складывать или перемножать, ответ будет один. Другими словами, размещение скобок не имеет значения, когда речь идет о сложении или умножении.

Следовательно,

А + (В + С) = (А + В) + С A.(B.C) = (A.B).C

Примеры: 

• 1 + (2+3) = (1+2) + 3 → 6
• 3 х (4 х 2) = (3 х 4) х 2 → 24

Распределительное свойство умножения

Распределительное свойство умножения утверждает, что умножение суммы на число равносильно умножению каждого слагаемого на значение и последующему сложению произведений.

Согласно Распределительному Свойству, если a, b, c — действительные числа, то:

а х (b + с) = (а х b) + (а х с)

Пример:

• 2 х (5 + 8) = (2 х 5) + (2 х 8)
• 2 х (13) = 10 + 16
• 26 = 26

Существуют некоторые другие свойства, такие как свойство Identity, свойство замыкания, которые введены для целых чисел.

Некоммутативное свойство

Некоторые операции некоммутативны. Под некоммутативностью мы подразумеваем, что переключение порядка даст разные результаты. Математические операции, вычитание и деление, являются двумя некоммутативными операциями. В отличие от сложения, при вычитании переключение порядков членов приводит к разным ответам.

Пример: 4–3 = 1, но 3–4 = -1 – это два разных целых числа.

Кроме того, деление не следует коммутативному закону. То есть

6 ÷ 2 = 3

2 ÷ 6 = 1/3

Следовательно, 6 ÷ 2 ≠  2 ÷ 6

Решенные примеры по коммутативному свойству

Пример 1: Что из следующего подчиняется коммутативному закону?

1. 3 × 12
2. 4 + 20
3. 36 ÷ 6
4. 36 – 6
5. -3 × 4

Решение: Варианты 1, 2 и 5 следуют закону перестановки

Объяснение:

1. 3 × 12 = 36 и

       12 x 3 = 36

=> 3 х 12 = 12 х 3 (коммутативный)

2. 4 + 20 = 24 и

     20 + 4 = 24

     => 4 + 20 = 20 + 4 (коммутативный)

3. 36 ÷ 6 = 6 и

     6 ÷ 36 = 0,167

=> 36 ÷ 6 ≠ 6 ÷ 36 (некоммутативный)

4. 36 − 6 = 30 и

      6 – 36 = – 30

=> 36 – 6 ≠ 6 – 36 (не коммутативное)

5. −3 × 4 = -12 и

       4 x -3 = -12

=> -3 × 4 = 4 x -3 (коммутативное)

Q. 2: Докажите, что a+ b = b+a, если a = 10 и b = 9.

Sol: Учитывая, что a = 10 и b = 9

LHS = a+b = 10 + 9 = 19   ……(1)

RHS = b + a = 9 + 10 = 19 ……(2)

По уравнениям 1 и 2, согласно коммутативному свойству сложения, получаем;

левый = правый

Значит, доказано.

Q.3: Докажите, что A.B = B.A, если A = 4 и B = 3.

Sol: Дано, A = 4 и B = 3.

А.В = 4,3 = 12  ….. (1)

Б.А = 3,4 = 12  …..(2)

По уравнению (1) и (2), согласно коммутативному свойству умножения, мы получаем;

левый = правый

А.Б. = Б.А.

Значит, доказано.

Практические вопросы

Найдите, какое из следующих свойств является коммутативным свойством сложения и умножения.

• 3 + 4 = 4 + 3
• 10 х 7 = 7 х 10
• 8 х 9 = 9 х 8
• 6 + 4 = 4 + 6

Чтобы решить больше задач по свойствам математики, загрузите BYJU’S — The Learning App из магазина Google Play и смотрите интерактивные видеоролики.