Действия с нулём

В математике число ноль занимает особое место. Дело в том, что оно, по сути дела, означает «ничто», «пустоту», однако его значение действительно трудно переоценить. Для этого достаточно вспомнить хотя бы то, что именно с нулевой отметки начинается отсчет координат положения точки в любой системе координат.

 

Ноль широко используется в десятичных дробях для определения значений «пустых» разрядов, находящихся как до, так и после запятой. Кроме того, именно с ним связано одно из основополагающих правил арифметики, гласящее о том, что на ноль делить нельзя. Его логика, собственно говоря, проистекает из самой сути этого числа: действительно, невозможно представить, чтобы некая отличное от него значение (да и само оно – тоже) было разделено на «ничто».

Примеры вычисления

С нулем осуществляются все арифметические действия, причем в качестве его «партнеров» по ним могут использоваться целые числа, обычные и десятичные дроби, причем все они могут иметь как положительное, так и отрицательное значение. Приведем примеры их осуществления и некоторые пояснения к ним.

Сложение

При прибавлении нуля к некоторому числу (как целому, так и к дробному, как к положительному, так и к отрицательному) его значение остается абсолютно неизменным.

Пример 1

Двадцать четыре плюс ноль равняется двадцать четыре.

24 + 0 = 24

Пример 2

Семнадцать целых три восьмых плюс ноль равняется семнадцать целых три восьмых.

17

3 8

+ 0 =

17

3 8

Вычитание

При вычитании нуля из некоторого числа (целого, дробного, положительного или отрицательного) оставляет его полностью неизменным.

Пример 1

Две тысячи сто пятьдесят два минус ноль равняется две тысячи сто пятьдесят два.

2152 – 0 = 2152

Пример 2

Сорок одна целая три пятых минус ноль равняется сорок одна целая три пятых.

41

3 5

– 0 =

41

3 5

Умножение

При умножении любого числа (целого, дробного, положительного или отрицательного) на ноль получается ноль.

Пример 1

Пятьсот восемьдесят шесть умножить на ноль равняется ноль.

586 × 0 = 0

Пример 2

Ноль умножить на сто тридцать пять целых шесть седьмых равняется ноль.

0 × 135 = 0

Пример 3

Ноль умножить на ноль равняется ноль.

0 × 0 = 0

Деление

Правила деления чисел друг на друга в тех случаях, когда одно из них представляет собой ноль, различаются в зависимости от того, в какой именно роли выступает сам ноль: делимого или делителя?

В тех случаях, когда ноль представляет собой делимое, результат всегда равен ему же, причем вне зависимости от значения делителя.

Пример 1

Ноль разделить на двести шестьдесят пять равняется ноль

.

0 : 265 = 0

Пример 2

Ноль разделить на семнадцать пятьсот девяносто шестых равняется ноль.

0 :

17 596

= 0

Делить ноль на ноль согласно правилам математики нельзя. Это означает, что при совершении такой процедуры частное является неопределенным. Таким образом, теоретически оно может представлять собой абсолютно любое число.

0 : 0 = 8 ибо 8 × 0 = 0

В математике такая задача, как деление нуля на ноль, не имеет никакого смысла, поскольку ее результат представляет собой бесконечное множество. Это утверждение, однако, справедливо в том случае, если не указаны никакие дополнительные данные, которые могут повлиять на итоговый результат.

Таковые, при их наличии, должны состоять в том, чтобы указывать на степень изменения величины как делимого, так и делителя, причем еще до наступления того момента, когда они превратились в ноль. Если это определено, то такому выражению, как ноль разделить на ноль, в подавляющем большинстве случаев можно придать некий смысл.

Как раскрывать скобки в выражениях и уравнениях. Правила математики.

ГДЗ 1 класс

ГДЗ 10 класс

  

Категория: Математика

Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Этот прием носит название раскрытия скобок.

Раскрыть скобки означает избавить выражение от этих скобок.

Отдельного внимания заслуживает еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения
3−(5−7) мы получаем выражение 3−5+7. Оба этих выражения мы можем записать в виде равенства 3−(5−7)=3−5+7.

И еще один важный момент. В математике для сокращения записей принято не писать знак плюс, если он стоит в выражении или в скобках первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не +7+3, а просто 7+3, несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение (5+x) – знайте, что и перед скобкой стоит плюс, который не пишут, и перед пятеркой стоит плюс +(+5+x).

Правило раскрытия скобок при сложении

При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.

Пример. Раскрыть скобки в выражении 2 + (7 + 3) Перед скобками плюс, значит знаки перед числами в скобках не меняем.

2 + (7 + 3) = 2 + 7 + 3

Правило раскрытия скобок при вычитании

Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный. Отсутствие знака перед первым слагаемым в скобках подразумевает знак +.

Пример. Раскрыть скобки в выражении 2 − (7 + 3)

Перед скобками стоит минус, значит нужно поменять знаки перед числами из скобок. В скобках перед цифрой 7 знака нет, это значит, что семерка положительная, считается, что перед ней знак +.

2 − (7 + 3) = 2 − (+ 7 + 3)

При раскрытии скобок убираем из примера минус, который был перед скобками, и сами скобки 2 − (+ 7 + 3)  , а знаки, которые были в скобках, меняем на противоположные.

2 − (+ 7 + 3) = 2 − 7 − 3

Раскрытие скобок при умножении

Если перед скобками стоит знак умножения, то каждое число, стоящее внутри скобок, умножается на множитель, стоящий перед скобками. При этом умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.

Таким образом, сскобки в произведениях раскрываются в соответствии с распределительным свойством умножения.

Пример. 2 · (9 — 7) = 2 · 9 — 2 · 7

При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй скобки.

(2 + 3) · (4 + 5) = 2 · 4 + 2 · 5 + 3 · 4 + 3 · 5

На самом деле, нет необходимости запоминать все правила, достаточно помнить только одно, вот это: c(a−b)=ca−cb. Почему? Потому что если в него вместо c подставить единицу, получится правило (a−b)=a−b. А если подставить минус единицу, получим правило −(a−b)=−a+b. Ну, а если вместо c подставить другую скобку – можно получить последнее правило.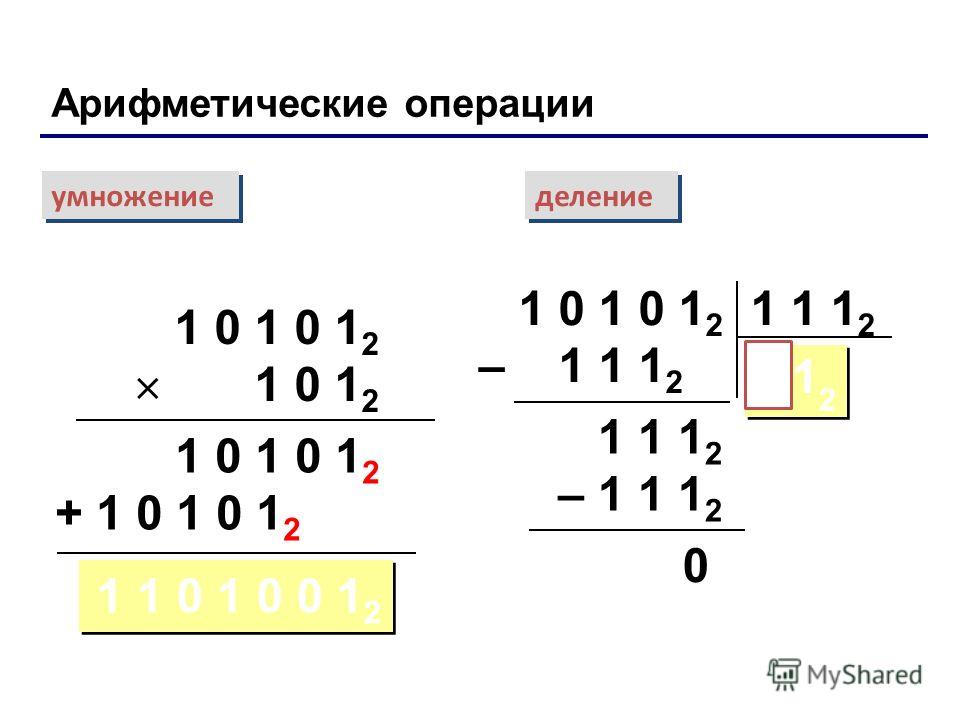

Раскрываем скобки при делении

Если после скобок стоит знак деления, то каждое число, стоящее внутри скобок, делится на делитель, стоящий после скобок, и наоборот.

Пример.  (9 + 6) : 3=9 : 3 + 6 : 3

Как раскрыть вложенные скобки

Если в выражении присутствуют вложенные скобки, то их раскрывают по порядку, начиная с внешних или внутренних.

При этом важно при раскрытии одной из скобок не трогать остальные скобки, просто переписывая их как есть. 

Пример.    12 — (a + (6 — b) — 3) = 12 — a — (6 — b) + 3 = 12 — a — 6 + b + 3 = 9 — a + b

• Назад
• Вперед

 
умножить наподелить на

 

• Уроки
• org/ListItem»> Математика

Вам может пригодиться:

Значение PEMDAS с примерами — Mashup Math

Сообщение от: Энтони Персико

В математике есть нечто, называемое порядком операций , которое является правилом для решения математических задач, которые имеют более одной операции (сложение, вычитание, умножение и т. д.). ). Изучая математику и изучая, как правильно использовать порядок операций, многие люди полагаются на общую мнемонику, известную как PEMDAS, как на средство памяти для запоминания порядка операций.

Pemdas Значение:

P = Saxesis

E = Экспоненты

M = Умножение

D = разделение

A = Добавление

S = подложка

Эти операции должны выполняться налево налево. вправо, где самая левая операция выполняется первой. Но это только общее правило для запоминания порядка операций и есть ключевые нюансы связи между умножением/делением и сложением/вычитанием, которые необходимо помнить помимо мнемоники, PEMDAS, иначе получается очень ненадежная инструмент, который часто приводит к получению неправильных ответов на, казалось бы, математические задачи. Эти ключевые нюансы выделены в разделе примеров ниже.

PEMDAS Значение: Ключевые идеи

PEMDAS существует уже давно, и многие студенты-математики учат фразу «Пожалуйста, извините, моя дорогая тетя Салли», чтобы запомнить порядок математических операций.

Тем не менее, PEMDAS не является идеальной мнемоникой для запоминания того, как правильно выполнять порядок операций , но может быть полезным инструментом, доказавшим, что вы помните несколько чрезвычайно важных нюансов:

• Всегда выполняйте скобки и /или группы первых

• После круглых скобок и группировок выполнить операции сложения и/или вычитания ( в зависимости от того, что наступит раньше слева направо)

PEMDAS Значение: Примеры

 Одно дело помнить порядок операций, и совсем другое — знать, как использовать его для правильного решения математических задач.

На самом деле, многие старожилы могут легко вспомнить фразу «Пожалуйста, извините, моя дорогая тетя Салли» спустя десятилетия после окончания школы, но понятия не имеют, что означает PEMDAS и как правильно его использовать.

 Опять же, PEMDAS полезен только как мнемоника, если вы также помните ранее упомянутые ключевые идеи и нюансы. Теперь давайте рассмотрим несколько примеров того, как правильно использовать PEMDAS для выполнения порядка операций.

PEMDAS Пример 01: (3+1) x 4

Сначала решите, что находится в скобках. В этом случае 3+1=4.

 Затем выполните умножение: 4 x 4 = 16

PEMDAS Пример 02: 92=9. Наконец, 27÷3 = 9 

.

PEMDAS Пример 03: 10 x 6 + 1

Для начала, когда нет скобок/группировок и/или показателей степени, вы можете пропустить P и E в PEMDAS.

Согласно PEMDAS, вы должны выполнить умножение/деление перед сложением/вычитанием, поэтому вы можете решить эту задачу слева направо:

 10×6 = 60 и 60 + 1 = 61

PEMDAS Пример 04: 75 — 10 x 5

Опять же, PEMDAS требует выполнения умножения/деления перед сложением/вычитанием, поэтому в этом примере; вы не выполняете операции слева направо.

В этом случае сначала выполните 10 х 5 = 50, а затем выполните 75 – 50 = 25.

PEMDAS Пример 05: 8 x 8 ÷ 16

Этот пример подчеркивает ght s, где ключевые нюансы PEMDAS имеют огромное значение. Помните, что PEMDAS требует, чтобы вы решали умножение/деление слева направо в зависимости от того, что наступит раньше.

В этом примере при движении слева направо сначала идет умножение, поэтому сначала вы должны выполнить 8 x 8 = 64.

Затем вы должны выполнить деление: 64 ÷ 16 = 4

Примечание: Если бы вы строго следовали PEMDAS, двигаясь слева направо в этом примере, вы бы получили правильный ответ, но давайте рассмотрим пример, когда деление идет первым, а умножение — вторым.

PEMDAS Пример 06: 42 ÷ 7 x 3

Чтобы правильно решить эту задачу, вы должны помнить, что ключевой нюанс значения PEMDAS заключается в том, что вы выполняете умножение/деление и сложение/вычитание на основе какая операция идет первой слева направо.

 Тот факт, что M (умножение) стоит перед D (деление) в PEMDAS, не означает, что вы всегда выполняете умножение первым.

Обратите внимание, что в этом примере есть только две операции — деление и умножение. В отличие от предыдущего примера, на этот раз сначала идет деление, поэтому вам нужно выполнить 42 ÷ 7=6 сначала, а затем 6×3=18 секунд.

Примечание: Многие учащиеся неправильно используют PEMDAS в таких примерах и сначала выполняют умножение 42 / 21 = 2. Обратите внимание, что 2 не является правильным ответом.

PEMDAS Значение: Почему это важно

 

Правильное применение порядка операций и использование PEMDAS стало очень популярным в последние годы из-за вирусных математических задач, которые появляются в социальных сетях. Такие сообщения популярны, потому что люди предполагают, что правильный способ применить порядок операций — выполнять каждую операцию слева направо. Поскольку большинство людей неправильно решают эти, казалось бы, простые математические задачи, им предлагается комментировать и делиться ими, что быстро распространяет пост и носит вирусный характер.

 

Однако, если бы люди могли помнить (A) порядок операций с использованием мнемоники, такой как PEMDAS (или еще более полезной, известной как GEMS), и (B) нюансы правильного применения порядка операций (а именно отношения между умножением/делением и сложением/вычитанием), то такие вирусные задачи можно было бы легко решить без особых споров.

 

PEMDAS Значение: Заключение

  PEMDAS является распространенным, но лишь отчасти полезным мнемоническим знаком для запоминания порядка операций в математике. PEMDAS относится к порядку операций следующим образом: скобки, возведения в степень, умножение, деление, сложение и вычитание. В то время как многие люди помнят PEMDAS, используя известную фразу «Пожалуйста, извините, моя дорогая тетя Салли», они часто забывают о важном нюансе, что умножение не выполняется автоматически перед делением, а сложение не выполняется автоматически перед вычитанием (умножение/деление и сложение/вычитание выполняются автоматически). слева направо в зависимости от того, какая операция наступит раньше). Это распространенное заблуждение обесценивает PEMDAS как надежный инструмент для запоминания и является первопричиной того, что, казалось бы, простые математические задачи становятся вирусными в социальных сетях, потому что большой процент взрослых может помнить мнемонические правила спустя десятилетия после окончания школы, но не может получить правильный ответ.

PEMDAS по-прежнему используется как стратегия для запоминания порядка операций больше из-за ностальгии и сопротивления изменениям, чем из-за того, что это самая эффективная стратегия. И хотя использование мнемотехники редко бывает хорошей стратегией для понимания математических концепций и развития навыков рассуждения, существуют гораздо лучшие альтернативы PEMDAS, включая GEMS, которые значительно надежнее.

Дополнительные бесплатные математические ресурсы для классов K-8:

1 Комментарий

Помощь по алгебре II

Студенты, нуждающиеся в помощи по алгебре II, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по Алгебре II. Имея под рукой обязательные концепции обучения и актуальные практические вопросы, вы мгновенно получите много помощи от Algebra II. Получите помощь сегодня с нашей обширной коллекцией необходимой информации об Алгебре II.

Большинство курсов алгебры II занимают важное место в обучении молодого человека. Независимо от того, следует ли курс непосредственно за его или ее первым уроком алгебры или после изучения геометрии, этот курс основывается на этих ранее полученных навыках, готовя молодого студента к дальнейшей углубленной работе по математике. Нужны ли вам лучшие репетиторы алгебры в Майами, преподаватели алгебры в Канзас-Сити или лучшие репетиторы алгебры в Оклахома-Сити, работа с профессионалом может вывести ваше обучение на новый уровень.

Когда за Алгеброй I сразу последует Алгебра II, юный ученик, скорее всего, сосредоточится на постоянном совершенствовании работы с уравнениями и их использовании, опираясь непосредственно на навыки, полученные в Алгебре I. Это потребует сосредоточения внимания на нелинейных уравнениях с одной переменной, уделяя особое внимание в частности, квадратные уравнения, но с дальнейшим вниманием к полиномам более высокого порядка в целом. Точно так же более продвинутые навыки работы с экспонентами и радикалами и их использования значительно улучшат навыки решения уравнений, которые студенты получили в ходе предыдущих курсовых работ. В дополнение к манипулированию и решению уравнений, такие студенты, вероятно, также сосредоточатся на концепциях, необходимых для оценки различных преобразований уравнений, особенно графиков квадратичных функций, абсолютных значений и других нелинейных функций. Репетиторы Varsity Tutors предлагают такие ресурсы, как бесплатные практические тесты по алгебре II, которые помогут вам в самостоятельном обучении, или вы можете подумать о репетиторах по алгебре II.

Когда Алгебра II следует за курсом геометрии, часто можно охватить гораздо больше информации, так как учащийся будет на более продвинутом уровне, чем он или она были сразу после прохождения первого курса алгебры. Проведя дополнительный год математических исследований, он или она прибудет с усиленными общими навыками, а также с пониманием ряда новых тем, относящихся к геометрии. В таком курсе Алгебры II будут преподаваться многие из вышеупомянутых навыков — различные типы манипулирования уравнениями, преобразование графиков и так далее. Однако при подготовке к тригонометрии и предварительному исчислению будет легче рассмотреть и другие темы, такие как тригонометрические тождества и конические сечения.

Всякий раз, когда в учебной программе по математике для молодых людей встречается алгебра II, это строгий и трудный курс. Отмечая важный переход в математическом обучении учащихся, курс требует от студентов повышенного объема работы и самоотверженности. Часто при прохождении этого курса молодых студентов поражает увеличение количества времени, необходимого вне занятий для закрепления навыков, приобретаемых каждый день в школе. На всех курсах математики практика может помочь изучить представленные новые темы; однако по мере того, как темы становятся все более сложными, объем требуемой работы увеличивается. В дополнение к справочному разделу по Алгебре II и урокам по Алгебре II вы также можете воспользоваться некоторыми из наших карточек по Алгебре II.

Таким образом, для достижения успеха очень важно, чтобы ученик был полностью предан своей работе. Темы, изучаемые на курсах такого рода, очень легко начинают накапливаться, оставляя студента совершенно ошеломленным за короткий промежуток времени. Бесплатная помощь по алгебре 2 от Varsity Tutors может помочь вам понять любую тему, которую вы не полностью освоили, прежде чем она начнет вызывать у вас проблемы с пониманием нового материала в вашем курсе. Наш контент по алгебре 2 разделен на конкретные темы, чтобы помочь вам точно определить область, в которой вы запутались. Нажав на одну из этих тем, вы увидите вопросы по алгебре 2, проверяющие эту концепцию, а также правильный ответ и полное объяснение. Вы можете самостоятельно работать над вопросами и проверять свои ответы или просто анализировать проблемы как правильные примеры, на которых можно смоделировать свою работу. Бесплатная справка по алгебре II от Varsity Tutors может быть особенно полезной при использовании вместе с другими нашими бесплатными ресурсами по алгебре II, включая практические тесты, диагностические тесты и карточки.