Что сначала деление или умножение: Что выполняется первым умножение или деление если оно стоит первым

Содержание

Операции c функциями — сложение, вычитание, умножение и деление

Операции c функциями

Функции можно складывать
Функции можно вычитать
Функции можно умножать
Функции можно делить
Функции могут быть составлены друг с другом

Давайте возьмем две функции
f(x) = x² and g(x) = x
Сумма этих функций:
f(x) + g(x) = x² + x

Сумма двух функций f и g определяется как f + g

Определение операций с функциями
(f + g)(x) = f(x) + g(x) Сложение
(f — g)(x) = f(x) — g(x) Вычитание
(f.g)(x) = f(x).g(x) Умножение
(f/g)(x) = f(x)/g(x) Деление

Для функции f + g, f — g, f.g, области определяются как пересечение областей f и g

Для f/g, область есть пересечение областей f и g кроме точек, где g(x) = 0

Пример
f(x) = 1 + √x — 2 and g(x) = x — 1
Тогда их сумма определяется как
(f + g)(x) = f(x) + g(x) = (1 + √x — 2) + (x — 1) = x + √x — 2

Теперь давайте сравним области первоначальных функций f и g с их суммой:

Функция	Область
f(x) = 1 + √x — 2	[2; +∞)
g(x) = x — 1	(-∞ +∞)
(f + g)(x) = x + √x — 2	[2; ∞)∩(-∞ +∞) = [2; ∞)

Пример:
Рассмотрим две функции
f(x) = 3√x and g(x) = √x
Тогда их произведение определяется как
(f.

g)(x) = f(x).g(x) = (3√x)(√x) = 3x

Обратите внимание, что

Натуральная область 3x есть (-∞; +∞)

Теперь сравним области первоначальных функций f и g, и их произведение:

Функция	Область
f(x) = 3√x	[0; +∞)
g(x) = √x	[0; +∞)
(f.g)(x) = 3x, x ≥ 0	[0; +∞) ∩ [0; +∞) = [0; +∞)

Иногда произведение двух одинаковых функций записывается как
f²(x) = f(x).f(x)
В целом, если n есть положительным целым, тогда hen
fⁿ(x) = f(x).f(x)…f(x)

Например,
sin(x).sin(x) = (sin(x))² = sin²x

Допустим, что есть две функции
f(x) = x³ и g(x) = x + 4
Если мы заменим g(x) на x в формуле для f, мы получим новую функцию, определенную
(f o g)(x) = f(g(x)) = (g(x))³ = (x + 4)³

Чтобы вычислить f(g(x)) необходимо вычислить сначала g(x) для x из области g, а тогда необходимо g(x) в области f вычислить f(g(x))

Пример:
Есть
f(x) = x² + 3 g(x) = √x
Тогда составная этих функций есть
(f o g)(x) = f(g(x)) = (g(x))² + 3 = (√x)² + 3 = x + 3

Теперь сравним областя оригинальных функций f и g, и их составную функцию

Функция	Область
f(x) = x² + 3	(-∞; +∞)
g(x) = √x	[0; +∞)
(f o g)(x) = x + 3	Все x в [0; +∞) такие, что g(x) лежит в (-∞; +∞) отсюда область is (-∞; +∞)

Рассмотрим функцию
h(x) = (x + 1)²
мы можем разбить функцию
h как
f(x) = x + 1
g(x) = x²
h(x) = g(f(x))

Примечание:
Обратите внимание, что мы можем выразить функцию как
(x² + 1)¹⁰ = [(x² + 1)²]⁵ = f(g(x))
g(x) = (x² + 1)², f(x) = x⁵
Также мы можем записать (x² + 1) = [(x² + 1)³]^10/3 = f(g(x))
g(x) = (x² + 1)³, f(x) = x^10/3

Обратите внимание, что в целом мы не можем записать
(f o g) ≠ (g o f)
Область (f o g) состоит из всех x в области g для которых g(x) в области f

3.

Умножение и деление натуральных чисел

п1. Умножение натуральных чисел и его свойства

Умножить число m на натуральное число n — значит найти сумму n слагаемых, каждое из которых равно m.

Выражение m·n и значение этого выражения называют произведением чисел m и n. Числа m и n называют множителями.

Свойства умножения:

Переместительное свойство умножения: Произведение двух чисел не изменяется при перестановке множителей: a · b = b · а
Сочетательное свойство умножения: Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель: a · (b · с) = (а · b) · c.
Свойство умножения на единицу: Сумма n слагаемых, каждое из которых равно 1, равна n: 1 · n = n.
Свойство умножения на ноль: Сумма n слагаемых, каждое из которых равно нулю, равна нулю: 0 · n = 0.

Знак умножения можно опускать: 8 · х = 8х, или а · b = ab, или a · (b + с) = a(b + с)

п2. Деление

Действие, по которому по произведению и одному из множителей находят другой множитель, называют делением.

Число, которое делят, называют делимым; число, на которое делят, называют делителем, результат деления называют частным.

Частное показывает, во сколько раз делимое больше, чем делитель.

На нуль делить нельзя!

Свойства деления:

При делении любого числа на 1 получается это же число: а : 1 = а.
При делении числа на это же число, получается единица: а : а = 1.
При делении нуля на число получается нуль: 0 : а = 0.

Чтобы найти

неизвестный множитель, надо произведение разделит на другой множитель.

5х = 45 х = 45 : 5 х = 9 Чтобы найти неизвестное делимое, надо частное умножить на делитель. х : 15 = 3 х = 3 · 15 х = 45

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

48 : х = 4 х = 48 : 4

х = 12

п3. Деление с остатком

Остаток всегда меньше делителя.

Здесь число 23 – делимое, 4 – делитель, 5 – неполное частное и 3 – остаток.

Если остаток равен нулю, то говорят, что делимое делится на делитель без остатка или, иначе, нацело.

Чтобы найти делимое a при делении с остатком, надо умножить неполное частное с на делитель b и к полученному произведению прибавить остаток d. а = с · b + d

п4. Упрощение выражений

Свойства умножения:

Распределительное свойство умножения относительно сложения: Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившиеся произведения: (а + b)с = ас + bc.
Распределительное свойство умножения относительно вычитания
: Чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе: (а — b)с = ас — bc.

3а + 7а = (3 + 7)а = 10а

Решить уравнение:

3у + 7у + 25 = 85

(3 + 7)у + 25 = 85

10у + 25 = 85

10у = 85 – 25

10у = 60

у = 60 : 10

у = 6

п5. Порядок выполнения действий

Сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел – действиями второй ступени.

Правила порядка выполнения действий:

Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку слева направо.
Если выражение содержит действия первой и второй ступени и в нем нет скобок, то сначала выполняют действия второй ступени, потом – действия первой ступени.
Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).

Каждое выражение задает программу своего вычисления. Она состоит из команд.

п6. Квадрат и куб

Произведение, в котором все множители равны друг другу, записывают короче:

а · а · а · а · а · а = а⁶

Читают: а в шестой степени. Число а называют основанием степени, число 6 – показателем степени, а выражение а⁶— называют степенью.

Произведение n и n называют квадратом числа n и обозначают n² (эн в квадрате): n² = n · n

Таблица квадратов:

n²

100

n	11	12	13	14	15	16	17	18	19	20
n²	121	144	169	196	225	256	289	324	361	400
Произведение n · n · n называют кубом числа n и обозначают n³ (эн в кубе): n³ = n · n · n Таблица кубов:
n	1	2	3	4	5	6	7	8	9	10
n³	1	8	27	64	125	216	343	512	729	1000

Первая степень числа равна самому числу.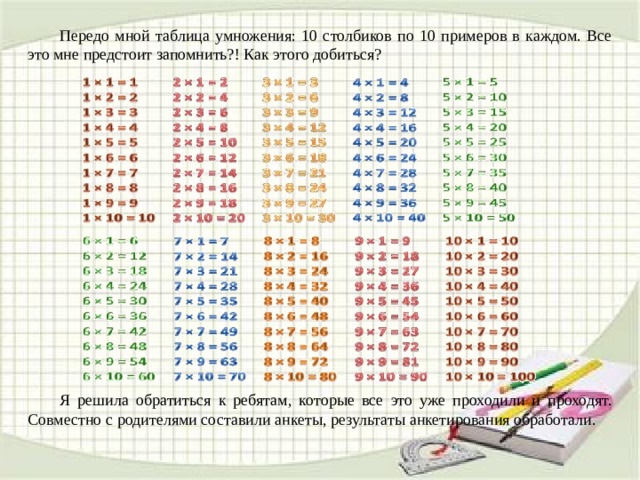

Если в числовое выражение входят степени чисел, то их значения вычисляют до выполнения остальных действий.

Почему учащиеся неправильно понимают порядок операций — Future Set Tech Camp

Многие из моих учеников средней и старшей школы помнят PEMDAS, аббревиатуру, предназначенную для представления порядка операций для вычисления математических выражений, из предыдущего класса. «Пожалуйста, извините, моя дорогая тетя Салли», — говорят они (или «Пожалуйста, съешьте мои чипсы с сальсой», — сказал мне один умный студент). «Скобки, экспоненты, умножение, деление, сложение, вычитание», — говорят они. Это здорово, правда? Эти студенты помнят порядок действий, верно? Разве PEMDAS не прекрасен?

Нет, PEMDAS , а не потрясающий. ПЕМДАС ошибается. Или, скорее, неправильное понимание многими студентами порядка выполнения операций и виной всему PEMDAS.

Давайте рассмотрим простой пример: 4 — 3 + 10 ÷ 5 × 2.

Поскольку скобки и показатели степени отсутствуют, PEMDAS заставляет многих студентов думать, что мы должны начать с оценки умножения.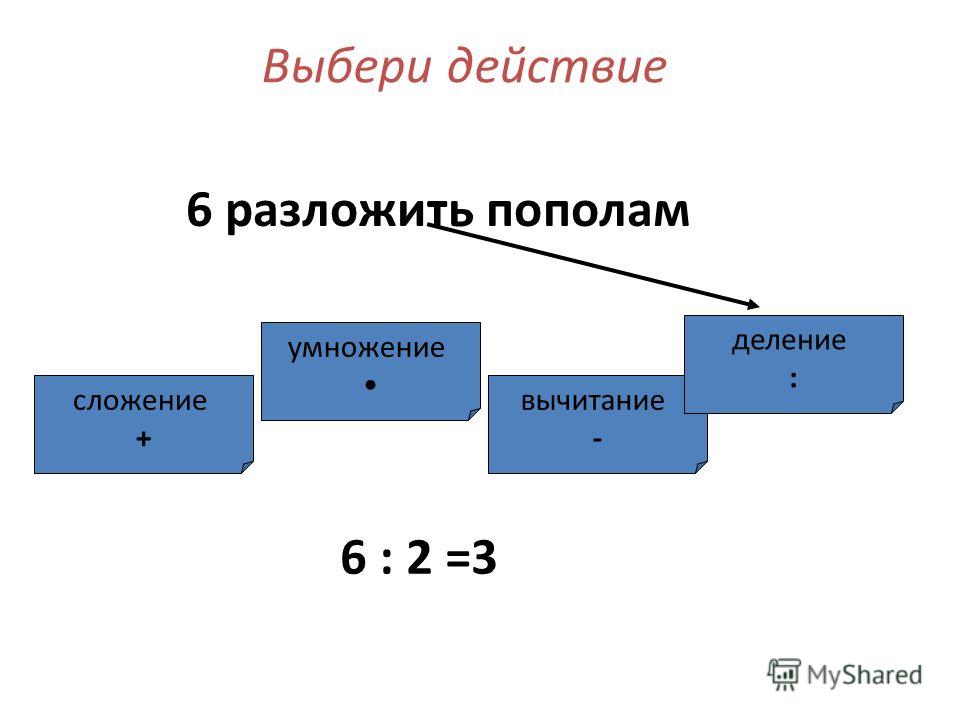 Таким образом:

4 — 3 + 10 ÷ 5 × 2 =

4 — 3 + 10 ÷ 10

Затем эти ученики перейдут к делению:

4 — 3 + 10 ÷ 10 =

4 — 3 + 1

Затем, сложение:

4 — 3 + 1 =

4 — 4

И, наконец, вычитание: 4 —

3 0

Элегантное решение! И все с помощью PEMDAS! Какое чудесное изобретение!

Или это то, что сказал бы , если бы это решение было правильным.

Для многих студентов PEMDAS подразумевает, что порядок операций состоит из шести шагов, по одному на каждую букву аббревиатуры. Фактически порядок операций состоит из четырех шагов:

Оценка операций в скобках
Оценка экспонентов
Оценка умножения и деления слева направо
Оценка и выявление слева направо
44 9007
. часть того же шага, как сложение и вычитание на следующем шаге. Давайте снова попробуем наш пример, на этот раз используя порядок операций. Так как скобок и показателей степени нет, мы начнем с третьего шага, «вычисляем умножение и деление слева направо»:
4 — 3 + 10 ÷ 5 × 2 =
4 — 3 + 2 × 2 =
4 — 3 + 4
Затем мы заканчиваем, применяя четвертый шаг: «оценить сложение и вычитание слева направо». справа”:
4 — 3 + 4 =
1 + 4 = 5
На этот раз мы пришли к правильному решению.
Я встречал слишком много студентов, которые неправильно понимали порядок операций именно таким образом. К счастью, у меня есть решение этой проблемы: вместо того, чтобы начинать урок о порядке операций с введения PEMDAS, его следует вводить только после проработки множества примеров с использованием четырехэтапного порядка операций, как это написано выше. Как только студенты приходят к понять порядок операций на практике, только тогда можно будет ввести PEMDAS, чтобы он служил по назначению: не как набор инструкций, а как мнемоническое устройство, помогающее памяти.
PEMDAS неисправен (и как мы можем это исправить)
В первую неделю преподавания раздела обсуждения «Исчисление 1» в этом семестре я решил дать учащимся предварительный расчетный лист. Его цель состояла в том, чтобы освежить их воспоминания об основах арифметики, алгебры и тригонометрии, а также посмотреть, что они запомнили из средней школы.
Удивительно, но больше всего проблем у них была с арифметической частью. Не такие вещи, как умножение и деление больших чисел в длину — этим вещам хорошо учат в наших начальных классах — но когда они столкнулись со сложной многошаговой арифметической задачей, такой как первая задача на листе, они были в тупике:
Упростить: $1+2-3\cdot 4/5+4/3\cdot 2-1$
Постепенно некоторые группы начали решать задачу. Но некоторые утверждали, что это было -16/15 долларов, другие предположили, что это было 34/15 долларов, а третьи настаивали на том, что это было -46/15 долларов. Кто был прав? И почему все они получали разные ответы, несмотря на тщательную проверку своей работы?
Ответ заключается в том, что процедура арифметического упрощения, которую изучают в начальной школе, неоднозначна и иногда неверна. В американских государственных школах учащихся учат аббревиатуре «PEMDAS», которая означает P арентез, E экспонент, M умножение, D ivision, A дополнение, S вычитание. Это называется порядком операций , который говорит вам, какие арифметические операции выполнять в первую очередь по соглашению, так что мы все согласны с тем, что должно означать приведенное выше выражение.
Но не во всех случаях PEMDAS работает должным образом. (Это уже было прекрасно продемонстрировано в нескольких видеороликах на YouTube, таких как это, но я чувствую, что было бы неплохо повторить объяснение в максимально возможном количестве мест.) Чтобы проиллюстрировать проблему, рассмотрим вычисление $6-2+3$. . Здесь мы начинаем с 6 долларов, отнимаем 2 доллара и добавляем обратно 3 доллара, так что в итоге у нас должно получиться 7 долларов. Это то, что скажет вам любой современный калькулятор (попробуйте ввести это в Google!) Но если вы будете следовать PEMDAS до буквы, он скажет вам, что сложение предшествует вычитанию, поэтому мы должны сначала добавить $2+3$, чтобы получить $5. $, а затем получаем $6-5=1$.
Еще хуже, что произойдет, если мы попытаемся сделать $6-3-2$? В итоге мы должны получить $1$, так как мы вычитаем $2$ и $3$ из $6$, и все же, если мы выберем другой порядок, в котором сначала нужно выполнить вычитание, скажем, $6-(3-2)=6-1$, мы получаем $5$. Таким образом, вычитание не может быть выполнено должным образом даже перед самим собой, и правило PEMDAS не устраняет эту двусмысленность.
У математиков есть лучшее соглашение, которое фиксирует все это. На самом деле, когда мы вычитаем , мы прибавляем отрицательное число 9.0006 : $6-2+3$ — это всего лишь $6+(-2)+3$. Это устраняет двусмысленность; сложение является коммутативным и ассоциативным, то есть независимо от того, в каком порядке мы складываем несколько вещей, ответ всегда будет одним и тем же. В этом случае мы могли либо сделать $6+(-2)=4$ и $4+3=7$, чтобы получить ответ $7$, либо мы могли сначала сделать $(-2)+3$, чтобы получить $1$ и затем добавьте это к $6$, чтобы получить $7$. Мы могли бы даже сначала добавить 6$ и 3$, чтобы получить 9$, а затем добавить -2$, и мы снова получили бы 7$. Так что теперь мы всегда получаем один и тот же ответ!
Аналогичная проблема с делением. Равны ли $4/3/2$ $4/(3/2)=8/3$ или $(4/3)/2=2/3$? PEMDAS не дает здесь однозначного ответа, и у него есть еще одна проблема: превратить $4/3\cdot 2$ в $4/(3\cdot 2)=2/3$, что опять-таки не согласуется с Google Calculator. Как и в случае с вычитанием, решение состоит в том, чтобы превратить все проблемы деления в задачи умножения : мы должны думать о делении как об умножении на обратное . Таким образом, в упражнении, которое я дал своим студентам, у нас было бы $4/3\cdot 2=4\cdot \frac{1}{3}\cdot 2=\frac{8}{3}$, и вся путаница в том, удаленный.
Чтобы закончить задачу, мы должны написать
$$\begin{eqnarray*}
1+2-3\cdot 4/5+4/3\cdot 2-1&=&1+2+(-\frac {12}{5})+\frac{8}{3}+(-1) \\
&=&2+\frac{-36+40}{15} \\
&=&\frac{34}{ 15}.
\end{eqnarray*}
$$
Единственное, что нам сейчас нужно сделать, это придумать новый акроним.