| Табличка на двери |
Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…
И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.
Вы готовы?
” (А.Франц)
(Корзина висит на доске)
Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.
Так ребёнку гораздо легче будет ориентироваться в действиях.
Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.
Так, вы, наверное, помните, что руководят порядком в выполнении действий скобки. Они показывают, что действия нужно выполнить первым. Какие существуют другие правила порядка действий? Отличается ли порядок действий в выражениях со скобками и без скобок? На эти вопросы вам предстоит найти ответы в учебнике математики 3 класса при изучении темы «Порядок выполнения действий». Вы должны обязательно потренироваться в применении изученных правил, а если понадобиться, то найти и исправить ошибки в установлении порядка действий в числовых выражениях. Помните, пожалуйста, что порядок важен в любом деле, но в математике он имеет особое значение!
действия, записанные в скобках;
Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.
Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Выбрасывай калькулятор: 17 полезных математических трюков
Собрали подборку классных математических трюков в помощь. С ними ты сможешь быстро считать в уме, не прибегая к калькулятору!
Привет!
Здесь 17 крутых математических трюков, которые полезны не только школьникам, но и взрослым.
Они помогают производить сложные вычисления в голове. Освой эти техники, и будешь решать даже те задачи, которые когда-то казались непосильными.
А после можешь пройти наш быстрый математический тест 😉
Сложение крупных чисел в голове − намного более лёгкий процесс, чем кажется. А этот метод показывает, как упростить процесс, округлив все числа до десятка. Вот пример:
644 + 238
Чтобы было проще работать, округляем каждое из чисел. Итак, 644 превращаем в 650, а 238 становится 240.
Затем складываем 650 и 240. Получается 890. Чтобы найти ответ на исходное уравнение, нужно определить, сколько мы добавили к числам, чтобы их округлить.
650 — 644 = 6 и 240 — 238 = 2
Получается, что к первому числу (644) мы добавили 6, а ко второму (238) − 2. Складываем 6 и 2 вместе, получаем 8.
Остаётся вычесть из суммы округлённых чисел (890) лишнее (8):
890 — 8 = 882
Получаем, что 644 + 238 = 882.
Это один из основных математических трюков, которые стоит знать.
Вот основное правило вычитания большого числа из 1000: раздели своё трёхзначное число на первую, вторую, третью цифру. Теперь вычти первую из 9, вторую из 9, а третью из 10. Например:
1000 — 556
Шаг 1: вычитаем 5 из 9 = 4
Шаг 2: вычитаем 5 из 9 = 4
Шаг 3: вычитаем 6 из 10 = 4
Ответ 444.
Умножая число 5 на четное число, можно быстро найти ответ. Например, 5 х 4:
Шаг 1: Берём число, которое хотим умножить на 5 и делим его пополам. В нашем случае, 4 превращаем в 2.
Шаг 2: Добавляем ноль к получившемуся числу, чтобы найти ответ. К числу 2 ставим рядом 0, получаем 20.
5 х 4 = 20
При умножении нечетного числа на 5 формула немного отличается. Например, рассмотрим 5 х 3:
Шаг 1: Вычитаем единицу из числа, которое хотим умножить на 5. В нашем случае, 3 превращаем в 2.
Шаг 2: Теперь делим получившееся число (2) пополам, получаем 1.
Ставим последнее получившееся число на первое место, а число 5, на которое мы хотели умножать изначально, приставляем рядом. Получается, рядом с 1 ставим 5, становится 15.
5 х 3 = 15
Вот быстрый способ узнать, когда число может быть равномерно разделено на эти же числа:
- 10, если число заканчивается на 0.
- 9, когда цифры складываются вместе, а сумма делится поровну на 9.
- 8, если последние три цифры делятся на 8, или число оканчивается на 000.
- 6, если при сложении чётных чисел сумма делится на 3.
- 5, если число заканчивается на 0 или 5.
- 4, если число оканчивается на 00 или двузначное число, которое делится на 4.
- 3, если при сложении цифр числа результат делится на 3.
- 2, если оно заканчивается на 0, 2, 4, 6 или 8.
Это ещё один из математических трюков, который полезен в жизни. Нужен он для умножения любого числа на 9. Вот как это работает:
Покажем на примере умножения 9 на 3.
Шаг 1: Вычитаем 1 из числа, которое умножается на 9.
3 — 1 = 2
Число 2 является первым числом в ответе на уравнение.
Шаг 2: Вычитаем получившееся число из 9.
9 — 2 = 7
Число 7 является вторым числом в ответе на уравнение.
Итого, 9 х 3 = 27.
Хитрость в умножении любого числа на 10 состоит в добавлении нуля к концу числа. Например, 62 х 10 = 620.
Существует также простой способ умножения любого двузначного числа на 11. Вот оно:
11 х 25
Возьмём двузначное число и отделим первую часть числа от второй − из 25 сделаем 2 и 5.
Теперь складываем эти два числа вместе и помещаем результат в центр, между 2 и 5:
2 (2 + 5) 5
2 7 5
Ответ: 11 х 25 = 275.
Если число в центре содержит две цифры, добавь первое число из суммы к первой цифре итогового числа, а второе оставь на месте.
Вот пример для уравнения 11 х 88:
8 (8 + 8) 8
8 (16) 8
(8 + 1) 6 8
9 6 8
Получаем ответ: 11 х 88 = 968.
Найти процент от числа может быть несколько сложно, если не подумать о способе решения, а просто считать. С этим методом всё проще. Чтобы узнать, сколько составляет 5% от 235, нужно:
Шаг 1: Переместить десятичную точку на одно значение вправо, 235 (235.0): становится 23.5.
Шаг 2: Разделить 23.5 на число 2, ответ − 11.75. Это ответ на исходное уравнение.
Используем число 35 в качестве примера:
Шаг 1: Умножим первую цифру на сумму единицы и первой цифры.
Шаг 2: В окончание поставим 25.
35 в квадрате = 3 x (3 + 1) & 25
3 x (3 + 1) = 12
12 и 25 = 1225
35 в квадрате = 1225.
Если при умножении больших чисел одно из них является четным, раздели первое число пополам, а второе умножь на 2.
Например 20 х 120:
Шаг 1: Делим 20 на 2, получаем 10. Умножаем 120 на 2, получаем 240.
Затем умножаем два ответа вместе:
10 х 240 = 2400
Ответ: 20 х 120 = 2400.
Суть метода в том, чтобы умножить числа без 0, а потом добавить нули. Рассмотрим умножение 200 на 400:
Шаг 1: Умножаем первые числа − 2 на 4:
2 х 4 = 8
Шаг 2: Ставим рядом убранные нули:
80000
200 х 400 = 80000
Это похоже на метод со сложением − здесь тоже нужно округлять. Рассмотрим его на примере выражения 97 x 96:
Округлим каждое из чисел до 100. Получим 100 и 100.
Теперь из первых 100 вычитаем первое число (97) и получаем 3, из вторых 100 вычитаем второе число (96) и получаем 4. Складываем получившиеся числа:
3 + 4 = 7
Теперь из 100 вычитаем 7: получается 93. Это будут первые две цифры итогового результата. Чтобы получить оставшиеся две цифры, нужно не сложить, а умножить 3 и 4.
Приписываем результат 12 к 93, получается 9312.
Посмотри на свои руки (в идеальном случае, должно быть 10 пальцев). Представим, что ты хочешь умножить 7 на 8.
Из 10 (как и пальцев на руках) вычти первое число (7), осталось 3. Запомни это число. Теперь вычти из 10 второе число (8), получается 2.
Теперь сложи получившиеся числа, результат (5) поставь на первое место. Затем, перемножь 3 и 2. Получится 6, цифру ставим на второе место, получается 56.
Казалось бы, как подборка математических трюков может помочь в таком серьёзном деле, как инвестирование? Может!
Если ты хочешь утроить свои инвестиции, запомни число 115. К примеру, инвестиции, которые дают 5% в год, утроятся через 23 года − 115 : 5 = 23.
Хотим посчитать 51 х 51. Возьмём одну из цифр, например, 1, к ней прибавим 25. Получается 26.
Теперь перемножим ту же цифру (1), получим 1 (01).
Соединим получившееся, 26 ставим первым числом, 01 вторым.
Получается 2601.
Найти корень из таких чисел, как 49 или 81 достаточно просто, потому что корни являются целыми числами. Но как можно найти корень с остатком? Покажем на примере числа 420.
Шаг 1: Находим ближайшее число, которое можно получить возведением в квадрат. В данном случае, это число 400, которое получают возведением в квадрат числа 20.
Шаг 2: Делим наше число (420) на корень того, ближайшего числа (20). Получаем 21.
Шаг 3: Теперь находим среднее между результатом и корнем первого числа − среднее между 21 и 20 равно 20,5.
А корень числа 420 равен 20,494. Получается, что наш ответ максимально близок.
Допустим, мы хотим узнать, чему равно 81 в квадрате.
81 х 81 = ?
Округляем число до меньшего − 80, возводим его в квадрат. Получается 6400.
Теперь к сумме дважды прибавляем округленное число − 6400 + 80 + 80, а в конце добавляем ещё один.
Получается 6560 + 1 = 6561.
Как бы ты посчитал значение выражения 32 х 125? Лучше упростить его:
32 х 125 = ?
16 х 250 = ?
8 х 500 = ?
4 х 1000 = 4000
На этом наша подборка математических трюков заканчивается. Практика этих быстрых математических приемов может помочь как в жизни, так и в работе. А ещё, может быть, пробудит интерес к математике.
Понравилась подборка математических трюков? Тебя точно заинтересует следующее:
- 12 простых советов тем, кто самостоятельно учит математику
- Математика для программистов: 7 крутых YouTube-каналов
- Математика для программиста: советы, разделы, литература
Источник: 10 математических трюков в блоге Concorida University-Portland
Расскажи, какими математическими трюками пользуешься ты?
Что делать сначала умножение или деление
Вот вам очень простой математический пример:
8 / 2(2 + 2)
Вы удивитесь, но большинство людей не смогут правильно это посчитать.
Посчитайте сами и потом смотрите правильный ответ:
В интернете много споров про такие примеры, поэтому мы решили разобраться, какие ошибки совершают чаще всего и почему многие считают неправильно. Для решения нам понадобятся три математических правила:
- То, что в скобках, выполняется в первую очередь. Если скобок несколько, они выполняются слева направо.
- При отсутствии скобок математические действия выполняются слева направо, сначала умножение и деление, потом — сложение и вычитание.
- Между множителем и скобкой (или двумя скобками) может опускаться знак умножения.
Разберём подробнее, что это значит в нашем случае.
1. То, что в скобках, выполняется в первую очередь. То есть в нашем примере, вне зависимости от чего угодно, сначала схлопнутся скобки:
8 / 2(2 + 2) → 8 / 2(4)
2. Между числом и скобкой можно опустить знак умножения.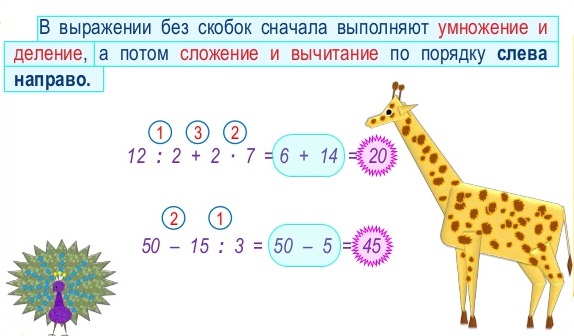
У нас перед скобкой двойка, то есть можно сделать такую замену:
3. Математические действия при отсутствии скобок выполняются слева направо: как при чтении, сначала умножение и деление, потом — сложение и вычитание. Умножение и деление имеют одинаковый приоритет. Нет такого, что сначала всегда делается умножение, затем деление, или наоборот. Со сложением и вычитанием то же самое.
Некоторые считают, что раз множители были написаны близко друг к другу (когда там стояли скобки), то оно выполняется в первую очередь, ссылаясь при этом на разные методические пособия. На самом деле это не так, и нет такого скрытого умножения, которое имеет приоритет над другим умножением или делением. Это такое же умножение, как и остальные, и оно делается в общем порядке — как и принято во всём математическом мире.
Получается, что нам сначала надо сложить 2 + 2 в скобках, потом 8 разделить на 2, и полученный результат умножить на то, что в скобках:
8 / 2 × (2 + 2) = 8 / 2 × 4 = 4 × 4 = 16
Кстати, если на айфоне записать это выражение точно так же, как в условии, телефон тоже даст правильный ответ.
А инженерный калькулятор на Windows 10 так записывать не умеет и пропускает первую двойку-множитель. Попробуйте сами 🙂
Тут в тред врываются математики и с воплями «Шустеф!» поясняют криком:
«В АЛГЕБРЕ ТОТ ЖЕ ПОРЯДОК ДЕЙСТВИЙ, ЧТО И В АРИФМЕТИКЕ, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например, a:b·c= a: (b·c)».
Этот текст из «Методики преподавания алгебры», курс лекций, Шустеф М. Ф., 1967 год. (стр. 43)
Раз в спорном примере знак умножения опущен, то спорный пример алгебраический, а значит, сначала умножаем 2 на 4, а потом 8 делим на 8!
А вот как на это отвечают те, кто действительно в теме и не ленится полностью посмотреть первоисточник:
«Для устранения недоразумений В. Л. Гончаров указывает, что предпочтительнее пользоваться в качестве знака деления чертой и ставить скобки [87].
П. С. Александров и А. Н. Колмогоров [59] предложили изменить порядок действий в арифметике и решать, например, так: 80:20×2=80:40=2 вместо обычного: 80:20×2=4×2=8. Однако это предложение не нашло поддержки».
Если апеллировать к Фриде Максовне Шустеф, то выходит, что:
- В. Л. Гончаров говорит так: «Ребята, используйте черту и ставьте скобки, чтобы ни у кого не было вопросов про приоритет».
- Если у нас всё же битва арифметики и алгебры, то, по П. С. Александрову и А. Н. Колмогорову, пример нужно решать слева направо, как обычно. Они, конечно, предложили решать такое по-другому, но научное сообщество их не поддержало.
Самое интересное, что дальше в примерах Фрида Максовна пользуется как раз правильным порядком действий, объясняя решение. Даже там, где есть умножение на скобку с опущенным знаком, она выполняет действия слева направо.
Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий.
Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Порядок вычисления простых выражений
В случае выражений без скобок порядок действий определяется однозначно:
- Все действия выполняются слева направо.
- В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Условие: вычислите, сколько будет 7 − 3 + 6 .
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
7 − 3 + 6 = 4 + 6 = 10
Ответ: 7 − 3 + 6 = 10 .
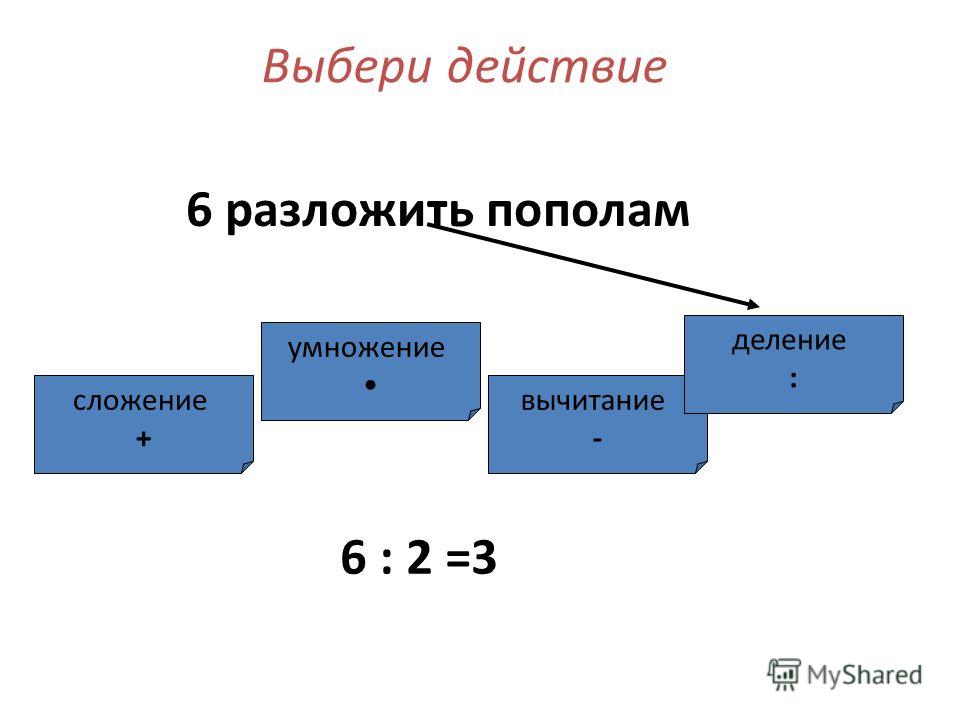
Условие: в каком порядке нужно выполнять вычисления в выражении 6 : 2 · 8 : 3 ?
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Условие: подсчитайте, сколько будет 17 − 5 · 6 : 3 − 2 + 4 : 2 .
Решение
Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:
17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7
Ответ: 17 − 5 · 6 : 3 − 2 + 4 : 2 = 7 .
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
.
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий.
В таком случае нужное правило можно записать так:
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Условие: вычислите, сколько будет 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 .
Решение
В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7 :
7 − 2 · 3 = 7 − 6 = 1
Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2
Начнем с умножения и деления, потом выполним вычитание и получим:
5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6
На этом вычисления можно закончить.
Ответ: 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 6 .
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Условие: вычислите, сколько будет 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) .
Решение
У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · ( 2 + 3 ) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .
Ответ: 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) = 28 .
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Допустим, нам надо найти, сколько будет ( 4 + ( 4 + ( 4 − 6 : 2 ) ) − 1 ) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6 : 2 = 4 − 3 = 1 , исходное выражение можно записать как ( 4 + ( 4 + 1 ) − 1 ) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению ( 4 + 5 − 1 ) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Условие: найдите, сколько будет ( 3 + 1 ) · 2 + 6 2 : 3 − 7 .
Решение
У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид ( 3 + 1 ) · 2 + 36 : 3 − 7 .
Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.
( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13
Ответ: ( 3 + 1 ) · 2 + 6 2 : 3 − 7 = 13 .
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
Наблюдение за изменением значения выражения от порядка выполнения арифметических действий
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя.
Порядок выполнения арифметических действий в выражениях без скобок
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени.
Выполняем действия слева направо по порядку (рис. 2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления – это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
Порядок выполнения арифметических действий в выражениях со скобками
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
Вычислим значение выражения.
Правило выполнения арифметических действий в выражениях без скобок и со скобками
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
Выполнение тренировочных заданий на изученное правило
Рассмотрим выражения, установим порядок действий и выполним вычисления.
Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
Узнаем, правильно ли определен порядок действий в следующих выражениях.
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
- М.
И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012. - М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
1. Определи порядок действий в данных выражениях. Найди значение выражений.
2. Определи, в каком выражении такой порядок выполнения действий:
1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
3. Составь три выражения, в которых такой порядок выполнения действий:
1. умножение; 2. сложение; 3. вычитание
1. сложение; 2. вычитание; 3. сложение
1. умножение; 2. деление; 3. сложение
Найди значение этих выражений.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Вы сначала складываете или умножаете
Порядок операций говорит вам сначала выполнить умножение и деление , работая слева направо, прежде чем выполнять сложение и вычитание.
Что будет первым: сложение или умножение?
PEMDAS («Скобки, показатели степени…») и BEDMAS также используются в США и Австралии. Возвращаясь к приведенному выше примеру, правильным ответом будет первый ответ, поскольку он следует правилам БОДМАС: деление может быть выполнено до умножения и должно быть выполнено до сложения, и 9Умножение 0003 предшествует сложению .
Почему мы умножаем перед сложением?
– Потому что умножение более эффективно, чем сложение . Мы всегда сначала делаем то, что мощнее. Любые другие идеи, чтобы добавить к этому? — Это повторяющееся добавление, чтобы мы могли перейти к более простому способу понимания.
Каков порядок математических операций?
Порядок операций правило, указывающее правильную последовательность шагов для вычисления математического выражения . Мы можем запомнить порядок, используя PEMDAS: скобки, экспоненты, умножение и деление (слева направо), сложение и вычитание (слева направо). Создано Салом Ханом.
Вы умножаете перед сложением или вычитанием?
Единственным исключением является то, что умножение и деление могут выполняться одновременно, вам разрешено делить до умножения, то же самое касается сложения и вычитания. Однако умножение и деление ДОЛЖНЫ предшествовать сложению и вычитанию . Аббревиатура PEMDAS часто используется для запоминания этого порядка.
Что такое правило сложения и умножения?
Со временем математики пришли к соглашению о наборе правил, называемых порядком операций, чтобы определить, какую операцию выполнять первой. Когда выражение включает только четыре основные операции, действуют следующие правила: Умножать и делить слева направо. Сложение и вычитание слева направо .
Правильно ли Бодмас или Пемдас?
, в то время как полная форма BODMAS — скобки, порядок, деление, умножение, сложение и вычитание. Термин PEMDAS используется в основном в США, но в Индии и Великобритании мы называем его BODMAS. Но между ними нет никакой разницы.
…
PEMDAS против BODMAS.
| P – Скобки сначала | B – Кронштейны Первые |
|---|---|
| S – Вычитание | S – Вычитание |
еще 4 строки
Каковы четыре правила математики?
Четыре основных математических правила: сложение, вычитание, умножение и деление . Q.
Каковы 5 математических правил?
Правила упорядочения в математике – BODMAS
- Скобки (части вычислений внутри скобок всегда идут первыми).
- Порядков (числа, включающие степени или квадратные корни).
- отдел.
- Умножение.
- Дополнение.
- Вычитание.
Всегда ли применяется порядок действий?
Просто, правда? Мы используем правило «порядка действий», которое выучили в детстве: «Пожалуйста, извините, моя дорогая тетя Салли», или PEMDAS, что означает скобки, показатели, умножение, деление, сложение, вычитание. * Эта удобная аббревиатура должна разрешить любой спор, но это не так, потому что это вовсе не правило.
Какая операция стоит первой в математике?
Сначала мы решаем любые операции внутри круглых или квадратных скобок . Во-вторых, мы решаем любые показатели. В-третьих, мы решаем все умножение и деление слева направо. В-четвертых, мы решаем все операции сложения и вычитания слева направо.
Как вы помните порядок действий?
Вспомните порядок действий алгебры с фразой «Пожалуйста, извините, моя дорогая тетя Салли». Этот трюк для запоминания порядка операций напоминает вам, какие шаги нужно предпринять и когда: скобки/группировка символов, экспоненты/корни, умножение, деление, сложение, вычитание (PEMDAS) .
Какой порядок математики в старшей школе?
Типичный порядок занятий по математике в старшей школе:
Алгебра 1 . Геометрия . Алгебра 2/Тригонометрия . Предварительный расчет .
Что такое правило математики?
Четыре основных математических правила: сложение, вычитание, умножение и деление .
Какое правило сложения и вычитания?
Ниже приведены правила сложения и вычитания чисел: Сложение двух положительных чисел всегда положительно . Сложение двух отрицательных чисел всегда отрицательно. Вычитание двух положительных чисел может быть как положительным, так и отрицательным.
Почему важен порядок операций?
Порядок операций важен, потому что он гарантирует, что все люди смогут прочитать и решить задачу одним и тем же способом .
Что заменило Пемдаса?
Чтобы помочь учащимся в Соединенных Штатах запомнить этот порядок операций, учителя заучивают в них аббревиатуру PEMDAS: круглые скобки, показатели степени, умножение, деление, сложение, вычитание. Другие учителя используют эквивалентную аббревиатуру 9.2/3.
Какой правильный ответ на 3 3×6 2?
Вопрос: 3 – 3 x 6 + 2. Сначала умножение: 3 – 18 + 2. Слева направо: -15 + 2 (или сначала сложение: 3 – 16) Ответ: -13 .
Каковы 5 лучших математических формул?
Вот список наиболее важных формул в каждом разделе.
…
Плоская геометрия
- Площадь треугольника: площадь = (1/2) (основание) (высота) …
- Теорема Пифагора: a²+b²=c² …
- Площадь прямоугольника: площадь = длина x ширина. …
- Площадь параллелограмма: площадь = основание x высота. …
- Площадь круга: π * r² …
- Окружность круга: длина окружности = 2π * r.
14 июля 2022 г.
Что такое базовые математические навыки?
Базовые математические навыки включают в себя вычисления сумм, размеров или других измерений . Основные понятия, такие как сложение, вычитание, умножение и деление, обеспечивают основу для изучения и использования более сложных математических понятий.
Какое правило чаще всего используется в математике?
Математические правила
Наиболее часто используемым в математике правилом является правило БОДМАС .
Какие 3 закона в математике?
Наиболее широко обсуждаемыми являются коммутативный, ассоциативный и распределительный законы .
Бодмас ошибается?
Неправильный ответ
Это был бы действительно полезный алгоритм, если бы он работал в любой ситуации, но рассмотрим гораздо более простое выражение 1 – 2 + 4 . Он не содержит скобок, степеней, деления или умножения, поэтому мы будем следовать BODMAS и делать сложение с последующим вычитанием: Это ошибка .
В чем проблема с Пемдасом?
Если вы воспринимаете PEMDAS буквально, у вас может возникнуть соблазн разделить 6 на 3, а затем 2 на 1 перед сложением. Проблема в том, что в скобках подразумевается просто потому, что задача включает сложение в числителе (вверху) и знаменателе (внизу) дроби.
Какие правила сложения?
При сложении положительного числа и положительного числа: Сложите величины. Положительный результат . При добавлении отрицательного числа и отрицательного числа: Добавьте величины. Результат отрицательный.
Как я могу выучить математику?
Итак, вот 8 простых способов запомнить математические формулы.
- Развивайте интерес к изучаемой теме. …
- Соедините свою концепцию с визуальной памятью. …
- Знание процесса математических формул. …
- Всегда решайте задачи с помощью математических формул. …
- Запишите математические формулы. …
- Наклейте написанные формулы на стену.
Другие элементы…•22 декабря 2021 г.
Какая самая сложная математика в старшей школе?
Какой самый сложный урок математики в старшей школе? В большинстве случаев вы обнаружите, что AP Calculus BC или IB Math HL — это самый сложный математический курс, предлагаемый вашей школой. Обратите внимание, что AP Calculus BC охватывает материал AP Calculus AB, но также продолжает учебную программу, рассматривая более сложные и продвинутые концепции.
Какую математику сдают 11-классники?
Обычно учащиеся 11-х классов сдают Алгебра II (если они следовали традиционной последовательности курсов: алгебра I в 9-м классе и геометрия в 10-м классе).
В каком классе сложна математика?
В третьем классе дети учатся умножать и делить числа в пределах 100, например умножать однозначные числа (6 × 9). Дети также начинают решать текстовые задачи и считать в уме. В четвертом классе понятия более сложные.
Каковы золотые правила математики?
Золотое правило математики гласит, что для любой дроби числитель и знаменатель можно умножить на одно и то же число без изменения значения дроби .
Легко ли выучить Пемдаса?
Но PEMDAS упрощает и упрощает . Итак, окончательный ответ — 317. Вы видите, как легко решить любую математическую задачу с помощью правила PEMDAS. Это правило поможет вам избежать неправильного ответа, если вы перепутаете порядок действий.
Как давно Пемдаса изучают в школах?
Первое появление явного правила PEMDAS на голландском языке находится в приложении к учебнику по алгебре для военной академии ( 1838 ), предназначенном для военных инженеров, а не для учащихся начальной школы или академических математиков.
Что означает G в Gemdas?
Очень простой способ запомнить правило GEMDAS: G —> Группировка (круглые скобки) E —-> Экспонента.
Что такое новая математика в 60-х?
Это два слова, которые до сих пор пугают учителей и школьников 1960-х: Новая математика. Это ужасное и болезненное изменение в преподавании базовой математики заставило маленьких детей размышлять над абстрактной алгеброй, модульной арифметикой, матрицами, символической логикой, булевой алгеброй и другими сверхматематическими вещами, которые им, возможно, никогда не понадобятся.
Используют ли другие страны Pemdas?
В разных странах используются разные мнемоники . В США и во Франции распространена аббревиатура PEMDAS. Это означает скобки, экспоненты, умножение/деление, сложение/вычитание. В школах PEMDAS часто расширяется до мнемоники «Пожалуйста, извините, моя дорогая тетя Салли».
Какая скобка решается первой?
В соответствии с правилом BODMAS, если выражение содержит скобки ((), {}, []) , мы должны сначала решить или упростить скобку, а затем «порядок» (это означает степени и корни и т. д.), затем деление, умножение, сложение и вычитание слева направо.
Что означает O в Bodmas?
Правило BODMAS — это аббревиатура, помогающая детям запомнить порядок операций в вычислениях. Операции — это просто разные вещи, которые мы можем делать с числами в математике. Это означает «скобки, порядок, деление, умножение, сложение, вычитание».
Кто изобрел математику?
Самые ранние свидетельства письменной математики восходят к древним шумерам , которые построили самую раннюю цивилизацию в Месопотамии. Они разработали сложную систему метрологии с 3000 г. до н.э.
Кто отец математики?
Имея длинный след изобретений и открытий, Архимед по праву считается «отцом математики». Узнайте больше о математических ресурсах в блоге BYJU’S FutureSchool и обязательно запишитесь на БЕСПЛАТНЫЙ пробный урок математики в живом формате 1:1 с выделенным инструктором.
Алгебраические выражения. Порядок операций
Навыки
в
A L G E B R A
Содержание | Дом
1
Четыре операции и их знаки
Функция скобок
«Условия» и «факторы»
Степени и показатели
Порядок операций
Раздел 2 :
Ценности и оценки
Переменные
Написание алгебраических выражений
АЛГЕБРА — ЭТО ПИСЬМЕННЫЙ НАВЫК. Это означает, что писатель решает проблему четко, эффективно и с наименьшим объемом текста. Как и любой навык — вождение автомобиля, выпечка печенья, игра на гитаре — он требует практики. Письменная практика. Тем не менее, давайте начнем.
Первое, что нужно отметить, это то, что в алгебре мы используем буквы так же, как и числа. Но буквы обозначают цифры. Мы имитируем правила арифметики буквами, потому что имеем в виду, что правило будет верным для 90 353 любых 90 354 чисел.
Вот, например, алгебраическое правило сложения дробей:
| | + | б в | = | а + б в |
Буквы a и b означают: цифры , находящиеся в числителях. Буква c означает: число в знаменателе. Правило означает:
«Какими бы ни были эти числа, добавьте числители
и запишите их сумму под общим знаменателем. »
Алгебра говорит нам, как решить любую задачу, которая выглядит как .
В конце концов, символы для чисел — 1, 2, 3 — не что иное, как письменные знаки. А так письма. Как увидит учащийся, алгебра зависит от форм, которые принимают символы. То, что вы видите выше, называется формальным правилом для сложения дробей.
Цифры — это числовые символы, а буквы — буквенные символы.
Вопрос 1. Каковы четыре арифметических действия, и
какие признаки их работы?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
| 1) | Дополнение: a + b . Знак операции + и называется знаком плюс 9.0354 . Читать a + b как « a плюс b ». |
| 1) | Например, если a представляет 3, а b представляет 4, то a + b представляет 7. |
| 2) | Вычитание: a − b . Знак операции — и называется знак минус . Читать a − b как « a минус b ». |
| 1) | Если a представляет, например, 8, а b представляет 2, то a − b представляет 6. |
3) Умножение: a · b . Читать a · b как « a умножить на b ».
Знак умножения в алгебре — это центрированная точка. Мы не используем крест умножения × ×, потому что не хотим путать его с буквой x .
Итак, если a представляет 2, а B представляет 5, затем
A · B = 2 · 5 = 10.
, 2 раза — 2 · 5, что в США означает умножение — с десятичной точкой: 2 . 5. Однако мы часто опускаем точку умножения и пишем просто ab . Читать « a , b «. Другими словами, когда между двумя буквами или между буквой и числом нет знака операции, это всегда означает умножение. 2 x означает 2 раза x .
| 4) | Подразделение: | а б | . Читать | а б | как « a разделить на b «. |
В алгебре мы используем горизонтальную черту деления. Например, если a представляет 10, а b представляет 2, то
| а б | = | 10 2 | = 5. |
«10 разделить на 2 будет 5.»
Примечание: В алгебре мы называем a + b «суммой», хотя и не называем ответа. Как увидит учащийся, в алгебре мы называем что-то просто по тому, как оно выглядит . На самом деле вы увидите, что вы делаете алгебру глазами, а дальше следует то, что вы пишете на бумаге.
Точно так же мы называем a − b разностью, ab произведением и частным.
Этот знак = конечно же знак равенства, и мы читаем это —
а = б
— как « a равно (или равно) b «.
Это означает, что число слева, которое представляет и , равно числу справа, которое представляет 9.0353 b представляет. Если мы напишем
а + б = в ,
и если a представляет 5, а b представляет 6, то c должно представлять 11.
Вопрос 2. Какова функция скобок () в алгебре?
3 + (4 + 5) 3(4 + 5)
Скобки означают, что мы должны рассматривать то, что они заключают в себе
, как одно число.
3 + (4 + 5) = 3 + 9 = 12. 3(4 + 5) = 3 · 9 = 27.
Примечание: Если между 3 и (4 + 5) нет знака операции, это означает умножение.
Задача 1. Как в алгебре написать
?а) 5 умножить на 6? 5 · 6
б) x умножить на y ? ху
| в) x разделить на y ? | x y |
г) x плюс 5 плюс x минус 2?
( х + 5) + ( х — 2)
д) x плюс 5 умножить на x минус 2?
( х + 5)( х — 2)
Задача 2. Различите следующее:
а) 8 − (3 + 2) б) 8 − 3 + 2
а) 8 – (3 + 2) = 8 – 5 = 3.
б) 8 — 3 + 2 = 5 + 2 = 7.
В а) мы рассматриваем 3 + 2 как одно число. В б) мы не делаем. Мы должны сначала вычесть 3, а затем добавить 2. (Но смотрите порядок операций ниже.)
Существует распространенное заблуждение, что скобки всегда означают умножение. Фактически, в Уроке 3 мы увидим, что мы используем круглые скобки, чтобы отделить знак операции от знака алгебры. 8 + (−2).
Вопрос 3. Условия и факторы.
Когда числа добавляются или вычитаются, они называются терминами.
Когда числа умножаются, они называются множителями.
Вот сумма четырех слагаемых: a − b + c − d .
В алгебре мы говорим о «сумме» терминов, даже если есть вычитания. Другими словами, все, что выглядит как , подобное тому, что вы видите выше, мы называем суммой.
Вот произведение четырех факторов: abcd .
Слово делитель всегда означает умножение.
И снова мы говорим о «продукте» abcd , хотя и не называем ответа.
Задача 3. Сколько в следующем выражении 90 353 членов 90 354? И сколько множителей у каждого члена?
2 а + 4 аб + 5 а ( б + с )
Есть три термина. 2 a — первый термин. Он имеет два множителя:
2 и a .
4 ab — второй член. Он имеет три множителя: 4, a и b .
И 5 a ( b + c ) — все это один термин. Он также имеет три множителя: 5, , и 9.0041 ( б + в ). Круглые скобки означают, что мы должны рассматривать все, что заключено в них, как одно число.
Степени и показатели
Когда все факторы равны — 2 · 2 · 2 · 2 — мы называем произведение степенью этого фактора. Таким образом, · называется второй степенью числа или « в квадрате». а · a · a — это третья степень числа a , или « a в кубе». аааа равно а в четвертой степени и так далее. Мы говорим, что в само по себе является первой степенью в .
Теперь вместо того, чтобы писать aaaa , мы пишем a всего один раз и ставим маленькую цифру 4:
4 (« до 4-го»)
Эта маленькая 4 называется показателем степени. Он указывает количество повторений и в качестве коэффициента.
8 3 («8 в третьей степени» или просто «8 в третьей степени») означает 8 · 8 · 8.
Задача 4. Назовите первые пять степеней числа 2. 2, 4, 8, 16, 32.
Задача 5. Прочитайте, а затем рассчитайте каждое из следующих действий.
а) 5 2 «5 во второй степени» или «5 в квадрате» = 25,9.0005
б) 2 3 «2 в третьей степени» или «2 в кубе» = 8,
.в) 10 4 «10 до четвертого» = 10 000.
г) 12 1 «12 к первому» = 12.
Однако в алгебре принято не писать показатель степени 1.
а = а 1 = 1 а .
Ученик должен быть осторожен, чтобы не перепутать 3 a , что означает 3 умножить на на , с на 3 , что означает умножить на .
| 3 а | = | a + a + a , Урок 9 арифметики |
| а 3 | = | а · и · и . |
Вопрос 4. При наличии нескольких операций
8 + 4(2 + 3) 2 − 7,
какой порядок операций?
Прежде чем ответить, отметим, что, поскольку знание естественных наук является причиной, по которой студенты должны изучать алгебру; а поскольку порядки операций появляются только в определенных формах, то на этих страницах мы представляем только те формы, с которыми учащийся может когда-либо столкнуться в реальной алгебраической практике. Знак деления ÷ никогда не используется в научных формулах, только черта деления. Крест умножения × используется только в экспоненциальной записи, поэтому учащийся никогда не увидит следующее:
3 + 6 × (5 + 3) ÷ 3 − 8.
Такая задача была бы чисто академической, т. е. упражнением ради самого себя. Это не имеет практической ценности. Это никуда не ведет.
Порядок операций следующий:
| (1) | Оцените скобки, если они есть, и если они требуют оценки. |
| (2) | Оцените степени, то есть показатели степени. |
| (3) | Умножать или делить — не важно. |
| (4) | Добавить или вычесть. |
В примерах 1 и 2 ниже мы увидим, в каком смысле мы можем прибавить или вычесть . А в примере 3 мы встретим умножение на или разделить.
Примечание: «Оценить» означает назвать и написать число.
Пример 1. 8 + 4(2 + 3) 2 − 7
Сначала оценим скобки, то есть заменим 2+3 на 5:
= 8 + 4 · 5 2 − 7
Так как теперь есть только одно число, 5, скобки писать не нужно.
Обратите внимание, что мы преобразовали один элемент, круглые скобки, и переписали все остальные.
Затем оцените показатели степени:
= 8 + 4 · 25 − 7
Теперь умножьте:
= 8 + 100 — 7
Наконец, прибавьте или вычтите , это не будет иметь значения. Если мы сначала добавим:
= 108 − 7 = 101.
Хотя если сначала вычесть:
8 + 100 — 7 = 8 + 93 = 101.
Пример 2. 100 − 60 + 3.
Первый:
100 − 60 + 3 означает ли , а не , 100 − 63.
Только при наличии скобок —
100 − (60 + 3)
— можем ли мы рассматривать 60 + 3 как одно число. При отсутствии скобок задача означает вычесть 60 из 100, затем прибавить 3:
100 — 60 + 3 = 40 + 3 = 43.
На самом деле, не имеет значения, прибавляем мы сначала или вычитаем сначала,
100 — 60 + 3 = 103 — 60 = 43.
Когда мы подойдем к числам со знаком, мы увидим, что
100 — 60 + 3 = 100 + (-60) + 3.
Порядок, в котором мы их «добавляем», значения не имеет.
| Пример 3. | 11 · 35 5 |
Нет скобок для оценки и показателей степени. Далее по порядку умножаем или делим на . Мы можем сделать и то и другое — мы получим тот же ответ. Но обычно более искусно сначала делить, потому что тогда у нас будут меньшие числа для умножения. Поэтому сначала разделим 35 на 5:
| 11 · 35 5 | = | 11 · 7 |
| = | 77. |
См.: Навыки арифметики, свойство 3 раздела.
Пример 4. ½(3 + 4)12 = ½ · 7 · 12.
порядок множителей не имеет значения: abc = bac = cab и так далее. Поэтому мы можем сначала сделать ½ · 12. То есть мы можем сначала разделить 12 на 2:
½ · 7 · 12 = 7 · 6 = 42.
(см. урок 27 арифметики, вопрос 1.)
| Пример 5. Полоса разделения. | 8 + 20 10 − 3 |
В любой задаче с делением, прежде чем мы сможем разделить, мы должны оценить верх и низ в соответствии с порядком операций. Другими словами, мы должны интерпретировать верх и низ как заключенные в круглые скобки.
| 8 + 20 10 − 3 | означает | (8 + 20) (10 − 3) | . |
Теперь действуем как обычно и сначала оцениваем скобки. Ответ: 4.
Проблема 6. Оцените каждое из следующих действий в соответствии с порядком операций.
| а) | 3 + 4 · 5 = | б) | 2 + 3 · 4 + 5 = | ||
| 3 + 20 = 23 | 2 + 12 + 5 = 19 | ||||
| в) | 4 + 5 (2 + 6) = | г) | (4 + 5) (2 + 6) = | ||
| 4 + 5 · 8 = 4 + 40 = 44 | 9 · 8 = 72 | ||||
| e) | 11 · 10 5 | е) | ½(3 + 4)8 = | ||
| 11 · 2 = 22 Сначала мы можем разделить. | ½ · 7 · 8 = 7 · 4 = 28. (½ · 8 = 4) Навыки арифметики: Урок 27, вопрос 1 | ||||
| г) | 2 + 2 · 3 2 14 − 3 · 2 2 | = | 2 + 2 · 9 14 − 3 · 4 | = | 2 + 18 14 − 12 | = | 20 2 | = | 10. |
Раздел 2 :
Ценности и оценки
Переменные
Написание алгебраических выражений
Содержание | Дом
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Круглые скобки и степени в порядке операций
Автор: Марк Зегарелли и
Обновлено: 25 апреля 2016 г. выражение имеет скобки и степени, оценивайте его в следующем порядке: содержимое скобок, степени слева направо, умножение и деление слева направо, сложение и вычитание слева направо.
Содержимое скобок
Выражение в степени (маленькое выпуклое число, обозначающее степень) группирует это выражение так же, как скобки. Оцените любое выражение с надстрочным индексом до одного числа, прежде чем оценивать мощность. Другими словами, чтобы найти 5 3–1 , вы можете представить, что 3–1 находится в скобках, что делает задачу 5 (3–1) = 5 2 = 25,
.Несколько других символов, с которыми вы можете быть знакомы, также группируют выражения вместе, как скобки. К ним относятся символ квадратного корня и столбцы абсолютных значений.
Степени слева направо
Умножение и деление слева направо
Сложение и вычитание слева направо
Примеры вопросов
Оценка (8 + 6 2 ) / (2 3 – 4).
11. Начните с оценки содержимого первого набора скобок. Внутри этого набора сначала оцените мощность, а затем выполните сложение:
(8 + 6 2 ) / (2 3 – 4)
= (8 + 36) / (2 3 – 4)
= 44 / (2 3 – 4)
Перейти к следующему набору скобок, сначала оценивая степень, а затем вычитание:
= 44 / (8 – 4) = 44 / 4
Завершите вычислением деления: 44 / 4 = 11.
Найдите значение –1 + (–20 + 3 3 ) 2 .
48. Когда все содержимое набора скобок возводится в степень, оцените, что находится внутри скобок, прежде чем оценивать степень. Внутри этого набора сначала оцените мощность, а затем дополнение:
–1 + (–20 + 3 3 ) 2 = –1 + (–20 + 27) 2 = –1 + 7 2
Далее оцениваем мощность 7 2 = 7 х 7 = 49:
= –1 + 49
Завершите вычислением сложения: –1 + 49 = 48
Практические вопросы
Найти (6 2 – 12) / (16 / 2 3 ).
Оценка –10 – (2 + 3 2 x –4).
7 2 – (3 + 3 2 / –9) 5 = ?
Что такое (10 – 1 14 x 8) 4 / 4+5
Ниже приведены ответы на практические вопросы:
(6 2 – 12) / (16 / 2 3 ) = 12.
Сосредоточившись на содержимом первого набора скобок, оцените степень, а затем вычитание:
(6 2 – 12) / (16 / 2 3 )
= (36 – 12) / (16 / 2 3 )
= 24/(16/2 3 )
Далее работайте внутри второго набора скобок, оценивая сначала степень, а затем деление:
= 24/(16/8) = 24/2
Завершить, оценив деление:
= 24 / 2 = 12
–10 – (2 + 3 2 х –4) = 24.
Ориентируясь на содержимое скобок, оцените сначала степень, затем умножение, а затем сложение:
–10 – (2 + 3 2 х –4) = –10 – (2 + 9 х – 4) = –10 – (2 + –36) = –10 – (–34)
Завершить вычислением вычитания:
–10 – (–34) = 24
7 2 – (3 + 3 2 / –9) 5 = 17.