Какие правила порядка выполнения действий в выражениях со скобками тебе известны — «Семья и Школа»

Содержание

4 класс. Математика. Выражение и его значение. Порядок выполнения действий — Выражение и его значение. Порядок выполнения действий

Комментарии преподавателя

На дан­ном уроке мы рас­смот­рим вы­ра­же­ние и его зна­че­ние, а также по­ря­док вы­пол­не­ния дей­ствий. Для на­ча­ла вспом­ним, что на­зы­ва­ют чис­ло­вым вы­ра­же­ни­ем.

Чис­ло­вое вы­ра­же­ние – за­пись, со­сто­я­щая из чисел, со­еди­нен­ных ариф­ме­ти­че­ски­ми дей­стви­я­ми.

Вы­бе­ри­те чис­ло­вые вы­ра­же­ния

1.

2.

3.

4.

5.

Вто­рая за­пись на­зы­ва­ет­ся ра­вен­ство, по­это­му она лиш­няя. Осталь­ные за­пи­си на­зы­ва­ют­ся чис­ло­вы­ми вы­ра­же­ни­я­ми. Если вы­пол­нить ука­зан­ные дей­ствия в этих чис­ло­вых вы­ра­же­ни­ях, то най­дем зна­че­ния вы­ра­же­ний.

Мы знаем че­ты­ре ариф­ме­ти­че­ских дей­ствия: сло­же­ние, вы­чи­та­ние, умно­же­ние, де­ле­ние. В одном вы­ра­же­нии можно вы­пол­нять несколь­ко дей­ствий. Чтобы найти зна­че­ние та­ко­го вы­ра­же­ния, нужно вы­пол­нять дей­ствия сле­ду­ю­щим об­ра­зом:

Пра­ви­ло 1

Если чис­ло­вое вы­ра­же­ние со­дер­жит толь­ко дей­ствия сло­же­ния и вы­чи­та­ния, то дей­ствия вы­пол­ня­ют по по­ряд­ку слева на­пра­во.

Если чис­ло­вое вы­ра­же­ние со­дер­жит толь­ко дей­ствия умно­же­ния и де­ле­ния, то дей­ствия вы­пол­ня­ют также по по­ряд­ку слева на­пра­во.

Рас­ставь­те по­ря­док дей­ствий и вы­пол­ни­те вы­чис­ле­ния:

1. 83 + 12 – 25 + 20

2. 49 : 7 ∙ 4 : 28

Ре­ше­ние:

83 + 12 – 25 + 20 = 90 (по­ря­док слева на­пра­во, так как толь­ко дей­ствия сло­же­ние и вы­чи­та­ние)

49:7 ∙ 4 : 28 = 1 (по­ря­док слева на­пра­во, так как толь­ко дей­ствия умно­же­ние и де­ле­ние)

Ответ: 1. 90; 2. 1

Пра­ви­ло 2

Если чис­ло­вое вы­ра­же­ние со­дер­жит не толь­ко сло­же­ние и вы­чи­та­ние, но и умно­же­ние с де­ле­ни­ем, то сна­ча­ла вы­пол­ня­ют умно­же­ние и де­ле­ние по по­ряд­ку слева на­пра­во, а потом сло­же­ние и вы­чи­та­ние слева на­пра­во.

За­да­ние

Рас­ставь­те по­ря­док дей­ствий и вы­пол­ни­те вы­чис­ле­ния:

1. 114 – 9 ∙ 4 : 6

2. 42 – 45 : 5 + 2 ∙ 7

Ре­ше­ние:

Ответ: 1. 108; 2. 47

Пра­ви­ло 3

Ино­гда за­пись вы­ра­же­ния со­дер­жит одну или несколь­ко пар ско­бок. В этом слу­чае сна­ча­ла на­хо­дят зна­че­ния вы­ра­же­ний в скоб­ках, а затем вы­пол­ня­ют дей­ствия по из­вест­ным нам пра­ви­лам.

За­да­ние

Рас­ставь­те по­ря­док дей­ствий и вы­пол­ни­те вы­чис­ле­ния:

1. 480 : (30 – 24) ∙ 7

2. 150 – (47 + 27 : 9)

3. (340 – 280) : (27 : 9)

Ре­ше­ние:

Ответ: 1. 560; 2. 100; 3. 20

На этом уроке мы вы­учи­ли пра­ви­ла по­ряд­ка вы­пол­не­ния дей­ствий при на­хож­де­нии зна­че­ния чис­ло­вых вы­ра­же­ний, а также под­кре­пи­ли эти зна­ния неко­то­ры­ми при­ме­ра­ми.

источник конспекта — http://interneturok.ru/ru/school/matematika/4-klass/undefined/vyrazhenie-i-ego-znachenie-poryadok-vypolneniya-deystviy

источник видео — http://www. youtube.com/watch?v=K80DkDbGW40

источник презентации — http://ppt4web.ru/nachalnaja-shkola/porjadok-vypolnenija-dejjstvijj. html

Порядок выполнения действий в примерах

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Презентация
учителя
Здравствуй, четвероклассник.
Приглашаю тебя на урок по теме «Порядок
выполнения действий ».
Сегодня тебе предстоит повторить порядок
выполнения действий в выражениях со
скобками и без скобок; совершенствовать
навык решения задач и примеров.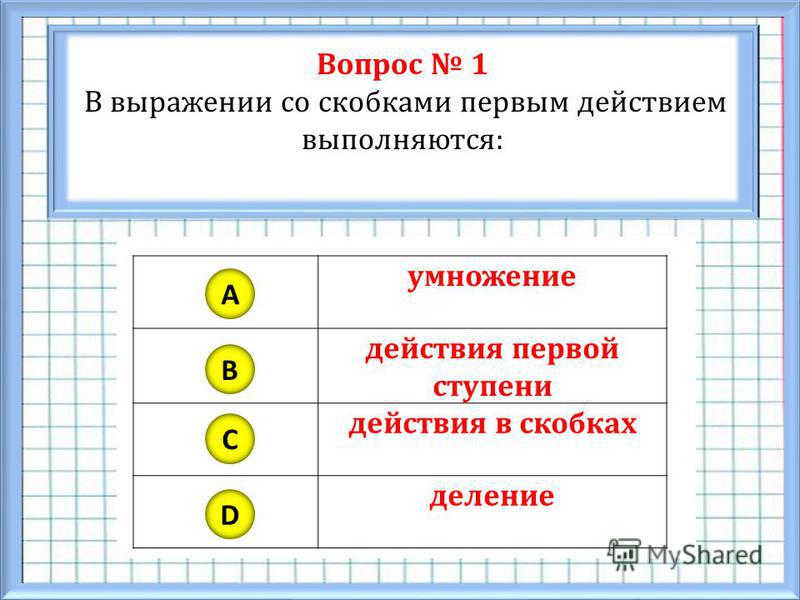
Надеюсь, что тебе понравится мое задание.
Буду рада прочитать твой ответ в строке
«комментарий».
Твой учитель.
Познакомься с содержанием
урока. Узнай, что ты сможешь
сделать на этом уроке.

3. Порядок выполнения действий.

Если тебе нужно выполнить несколько арифметических
действий (сложение, вычитание, умножение и деление), то
сначала выполняют умножение и деление по порядку слева
направо, а затем сложение и вычитание по порядку слева
направо.
Например,
В числовом выражении 4 арифметических действия:
вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над
арифметическими знаками: сначала производим деление,
потом умножение, затем вычитание и сложение.
1)15 : 3 = 5
2) 6 • 8 = 48
3) 10 — 5 = 5
4) 5 + 48 = 53
Вспомни
правило.

4. Порядок выполнения действий.

Если в выражении есть скобки, то сначала выполняют
действия в скобках, но обязательно учитывать первое и
второе правила.
Например,
Вспомни правило.
В числовом выражении 4 арифметических действия:
вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над
арифметическими знаками: сначала производим вычитание в
скобках, затем деление, потом умножение и сложение.
1) 25 — 10 = 15
2) 15 : 3 = 5
3) 6 • 8 = 48
4) 5 + 48 = 53

5. Порядок выполнения действий.

Например,
В числовом выражении 4 арифметических действия: сложение,
деление, сложение и деление.
Определим порядок действий и запишем их над
арифметическими знаками: сначала производим действия в
скобках (деление, затем сложение), затем деление, потом
сложение.
1) 12 : 4 = 3
2) 6 + 3 = 9
3) 18 : 9 = 2
4) 42 + 2 = 44

Посмотри фильм.

По ходу просмотра фильма постарайся
вспомнить материал 3 класса.
Если ты что-то не помнишь,
останавливай просмотр фильма в
непонятных местах и просматривай их
еще раз.
После просмотра фильма выполни
задания на Рабочем листе (его надо
скачать и распечатать, чтобы тебе было
удобно).
Будет здорово, если в комментариях ты
напишешь, все ли у тебя получилось.

English     Русский Правила

Числовой ряд и сложение, вычитание, умножение и деление

Авторы: Марк Зегарелли и

Обновлено: 26 марта 2016

Базовая математика и предварительная алгебра для чайников

Книга 9002 Подробнее

Числовая строка — это просто строка с числами, отмеченными через равные промежутки времени. Вы, вероятно, увидели свой первый числовой ряд, когда учились считать до десяти. Вы можете использовать этот надежный инструмент для выполнения операций Большой четверки (сложение, вычитание, умножение и деление) над относительно небольшими числами.

Числовая строка может быть полезным инструментом для сложения и вычитания небольших чисел:

Чтобы умножить на числовой прямой, начните с 0 и посчитайте первое число в задаче столько раз, сколько указано вторым числом .

Чтобы разделить на числовой прямой, сначала закройте отрезок числовой строки от 0 до первое число в задаче. Затем разделите этот отрезок поровну на количество частей, указанное вторым числом . Длина каждой части — это ответ на деление.

Примеры вопросов

1. Добавьте 6 + 7 в числовой строке.

   13. Выражение 6 + 7 означает , начиная с 6, до 7, , что приводит к 13.

2. Вычтите 12 – 4 из числовой строки.

   8. Выражение 12 — 4 означает, что начинается с 12, вниз на 4, , что приводит к 8.

3. Умножьте 2 x 5 на числовой прямой.

   10. Начиная с 0, сосчитайте двойками всего пять раз, чтобы получить 10.

4. Разделите 12 / 3 на числовой прямой.

   4. Закрасьте отрезок числовой прямой от 0 до 12. Теперь разделите этот отрезок поровну на три меньшие части. Каждая из этих частей имеет длину 4, так что это ответ на задачу.

Практические вопросы

1. Добавьте в числовую строку следующие числа:

   а. 4 + 7 = ?

   б. 9 + 8 = ?

   г. 12 + 0 = ?

   д. 4 + 6 + 1 + 5 = ?

2. Вычтите следующие числа из числовой строки:

   а. 10 – 6 = ?

   б. 14 – 9 = ?

   г. 18 – 18 = ?

   д. 9 – 3 + 7 – 2 + 1 = ?

3. Умножьте следующие числа на числовой прямой:

   а. 2 х 7 = ?

   б. 7 х 2 = ?

   г. 4 х 3 = ?

   д. 6 х 1 = ?

   эл. 6 х 0 = ?

   ф. 0 х 10 = ?

4. Разделите следующие числа на числовой прямой:

   а. 8 / 2 = ?

   б. 15/5 = ?

   г. 18/3 = ?

   д. 10/10 = ?

   эл. 7 / 1 = ?

   ф. 0 / 2 = ?

Ответы на практические вопросы следующие:

1. Добавить в числовую строку.

   а. 4 + 7 = 11 . Выражение 4 + 7 означает, что начинается с 4, до 7, , что приводит к 11.

   б. 9 + 8 = 17 . Выражение 9 + 8 означает, что начинается с 9, до 8, , что приводит к 17.

   г. 12 + 0 = 12 . Выражение 12 + 0 означает, что начинается с 12, до 0, , что приводит к 12.

   д. 4 + 6 + 1 + 5 = 16 . Выражение 4 + 6 + 1 + 5 означает, что начинается с 4, до 6, до 1, до 5, , что приводит к 16.

2. Вычесть из числовой строки.

   а. 10 – 6 = 4 . Выражение 10 – 6 означает, что начинается с 10, уменьшается на 6, , что приводит к 4.

   б. 14 – 9 = 5 . Выражение 14 – 9 означает, что начинается с 14, вниз на 9, , что приводит к 5.

   г. 18 –18 = 0 . Выражение 18 – 18 означает, что начинается с 18, уменьшается на 18, , что приводит к 0,

   д. 9 – 3 + 7 – 2 + 1 = 12 . Выражение 9 – 3 + 7 – 2 + 1 означает, что начинается с 9, вниз 3, вверх 7, вниз 2, вверх 1, , что приводит к 12.

3. Умножить на числовой прямой.

   а. 2 х 7 = 14 . Начиная с 0, посчитайте двойками семь раз, в результате чего вы получите 14.

   б. 7 х 2 = 14 . Начиная с 0, сосчитайте по семеркам всего два раза, чтобы получить 14.

   г. 4 х 3 = 12 . Начиная с 0, посчитайте по четыре в общей сложности три раза, что приведет вас к 12.

   д. 6 х 1 = 6 . Начиная с 0, сосчитайте до шести один раз, и вы получите 6.

   эл. 6 х 0 = 0 . Начиная с 0, сосчитайте по шестёрке ноль раз, и вы получите 0.

   ф. 0 х 10 = 0 . Начиная с 0, считайте нулями десять раз, что приведет к 0.

4. Разделить по числовой прямой.

   а. 8/2 = 4 . Заблокируйте отрезок числовой прямой от 0 до 8. Теперь разделите этот отрезок поровну на две меньшие части. Каждая из этих частей имеет длину 4, так что это ответ на задачу.

   б. 15/5 = 3 . Заблокируйте отрезок числовой прямой от 0 до 15. Разделите этот отрезок поровну на пять меньших частей. Каждая из этих частей имеет длину 3, так что это ответ на задачу.

   г. 18/3 = 6 . Заблокируйте отрезок числовой прямой от 0 до 18 и разделите этот отрезок поровну на три меньшие части. Каждая часть имеет длину 6, ответ на задачу.

   д. 10/10 = 1 . Заблокируйте отрезок числовой прямой от 0 до 10 и разделите этот отрезок поровну на десять меньших частей. Каждая из этих частей имеет длину 1,

   эл. 7 / 1 = 7 . Отметьте отрезок числовой прямой от 0 до 7 и разделите этот отрезок поровну на 1 часть (то есть вообще не делите). Этот кусок по-прежнему имеет длину 7.

   ф. 0 / 2 = 0 . Заблокируйте отрезок числовой прямой от 0 до 0. Длина этого отрезка равна 0, поэтому он не может быть меньше. Это показывает вам, что 0 разделить на любое число равно 0.

Об этом артикуле

Этот артикул можно найти в категории:

• Базовая математика,

Предварительное исчисление по алгебре — Зачем сначала умножать?

спросил 8 лет, 7 месяцев назад

Изменено 3 года, 8 месяцев назад

Просмотрено 15 тысяч раз

$\begingroup$

Почему мы сначала умножаем/делим, а потом складываем/вычитаем?

Я имею в виду, что меня интересует, это универсальное правило или правило, установленное человеком? Кроме того, как бы вы решили, что оперировать в первую очередь?

Например, если бы нас посетили инопланетяне, использовали бы они ту же математику? Будут ли они также сначала умножаться, а потом добавлять?

• алгебра-предварительное исчисление

$\endgroup$

6

$\begingroup$

Это всего лишь нотация , позволяющая записать одно из выражений $$(a+b)\cdot c\qquad a+(b\cdot c) $$ без круглых скобок. Можно было бы выбрать другое (или для всегда требуют круглых скобок), но подумайте, насколько сложным было бы написание, например. полиномы (если они не записаны в виде произведения линейных множителей). То же самое относится и к тому, почему $a-b-c$ означает $(a-b)-c$, а не $a-(b-c)$. В качестве альтернативы можно ввести префиксную или постфиксную (вместо инфиксной) нотацию, также известную как. (обратная) польская запись, т. е. $ab+c\cdot$ или $\cdot +abc$ по сравнению с $abc\cdot+$ или $+a\cdot bc$.

$\endgroup$

4

$\begingroup$

В дополнение к тому, что сказали другие, порядок операций также является естественным следствием перезаписи выражений, чтобы избежать двусмысленности.

Например, $3\умножить на 4+1$. Если бы все это было сложением, не было бы проблем, потому что сложение коммутативно и ассоциативно.

Композиция операций | Kotlin | CodeBasics

А что, если понадобится вычислить такое выражение: 3 + 5 — 2? Именно так мы и запишем:

println(3 + 5 - 2) // 3 + 5 - 2 => 8 - 2 => 6

Обратите внимание, что компьютер производит арифметические вычисления в правильном порядке: сначала деление и умножение, потом сложение и вычитание. Иногда этот порядок нужно изменить — об этом следующий урок.

Или другой пример:

println(2 * 4 * 5 * 10) // 2 * 4 * 5 * 10 => 8 * 5 * 10 => 40 * 10 => 400

Как видно, операции можно соединять друг с другом, получая возможность вычислять все более сложные составные выражения. Чтобы представить себе то, как происходят вычисления внутри интерпретатора, давайте разберем пример: 2 * 4 * 5 * 10.

1. Сначала вычисляется 2 * 4 и получается выражение 8 * 5 * 10.
2. Затем 8 * 5. В итоге имеем 40 * 10.
3. В конце концов происходит последнее умножение, и получается результат 400.

Операции можно соединять друг с другом, получая возможность вычислять все более сложные составные выражения.

Реализуйте программу, которая вычисляет значение выражения 8 / 2 + 5 - -3 / 2. Не вычисляйте ничего самостоятельно, ваша программа должна производить все вычисления сама.

10

Обратите внимание, что интерпретатор производит арифметические вычисления в правильном порядке: сначала деление и умножение, потом сложение и вычитание. Иногда этот порядок нужно изменить — об этом следующий урок.

Также обратите внимание на то, что в Kotlin по умолчанию используется целочисленное деление, 3 / 2 будет 1.

Упражнение не проходит проверку — что делать? 😶

Если вы зашли в тупик, то самое время задать вопрос в «Обсуждениях». Как правильно задать вопрос:

• Обязательно приложите вывод тестов, без него практически невозможно понять что не так, даже если вы покажете свой код. Программисты плохо исполняют код в голове, но по полученной ошибке почти всегда понятно, куда смотреть.

В моей среде код работает, а здесь нет 🤨

Тесты устроены таким образом, что они проверяют решение разными способами и на разных данных. Часто решение работает с одними входными данными, но не работает с другими. Чтобы разобраться с этим моментом, изучите вкладку «Тесты» и внимательно посмотрите на вывод ошибок, в котором есть подсказки.

Мой код отличается от решения учителя 🤔

Это нормально 🙆, в программировании одну задачу можно выполнить множеством способов.