Урок 2. Выражение и его значение. Порядок выполнения действий
Класс
1 класс
2 класс
- Английский язык
- Математика
3 класс
- Русский язык
- Английский язык
- Математика
4 класс
- Русский язык
- Английский язык
- Математика
5 класс
- Русский язык
- Английский язык
- Математика
- Биология
6 класс
- Русский язык
- Английский язык
- Математика
- Биология
7 класс
- Русский язык
- Английский язык
- Математика
- Биология
- Физика
- Химия
8 класс
- Русский язык
- Английский язык
- Математика
- Биология
- Физика
- Химия
9 класс
- Русский язык
- Английский язык
- Математика
- Биология
- Физика
- Химия
10 класс
- Английский язык
- Биология
- Физика
- Химия
11 класс
- Английский язык
- Биология
- Химия
4 КЛАСС
Урок 2.
 Выражение и его значение. Порядок выполнения действий
Выражение и его значение. Порядок выполнения действийПравило, определяющее порядок выполнения действий в выражениях без скобок: 1) действия выполняются по порядку слева направо, 2) причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо. Например, в числовом выражении 3 арифметических действия: сложение, вычитание и вычитание. Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо
Сначала найди сколько р. в 8 монетах.
Сначала найди сколько в одном вагоне.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое. Чтобы найти неизвестное уменьшаемое, нужно к разность прибавить вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого.
если к числу прибавить ноль, получится это же число. если к нулю прибавить число, получится это же число. если из числа вычесть ноль, получится это же число. если из числа вычесть само себя, получится ноль.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое. Чтобы найти неизвестное уменьшаемое, нужно к разность прибавить вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого.
Соотнеси пример с условием задачи.
Напишите условие задачи.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое. Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое. Чтобы найти неизвестное уменьшаемое, нужно к разность прибавить вычитаемое.Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого.
Вспомните порядок действий.
Пробуйте различные варианты.
Не забывайте про порядок действий.
Вопросники:
Вопрос:
Вопрос:
Пропуски:
Как делить со скобками, что вперед: деление или умножение, как решить 36:3 (8–6) дробь 6, правильный ответ на пример — 17 января 2023
Сможете решить правильно?
Иллюстрация: Юрий Орлов / NGS.RU
Поделиться
Минимум неделю в интернете миллионы людей ломают копья из-за простенького, на первый взгляд, примера. NGS.RU решил задачку вместе с кандидатом физико-математических наук, доцентом и преподавателем Новосибирского государственного университета Ильей Марьясовым.
Вот этот пример: 36 : 3 (8 − 6) дробь 6.
Некоторые люди готовы спорить часами, как решить этот пример
org/Person»>Фото: Александра Бруня / NGS.RUПоделиться
— Подвоха здесь особо никакого нет. У нас в математике есть соглашение о том, как у нас должны выполняться арифметические операции. Умножение и деление имеют более высокий приоритет, чем сложение и вычитание. Когда нужно изменить порядок вычисления, чтобы сложение и вычитание выполнялись раньше, то используются скобки. И еще один момент — когда появляются дроби, а дробная черта — это деление, то в этом случае оно выполняется в последнюю очередь, — объяснил Илья Марьясов
Разбираемся с числителем. По очереди идут деление, умножение, вычитание — при этом последняя операция идет в скобках. Начинаем решать слева направо.
— Поскольку деление и умножение равноправны. Сначала 36 делим на 3 и получаем 12. Потом мы должны выполнить умножение, но поскольку вычитание стоит в скобках, то сначала делаем его. Из 8 вычитаем 6 и получаем 2. Теперь делаем умножение. Мы 12 умножаем на 2 и получаем 24. Теперь делим числитель на знаменатель. То есть 24 делим на 6 и получаем 4, — объяснил специалист.
Теперь делим числитель на знаменатель. То есть 24 делим на 6 и получаем 4, — объяснил специалист.
Правильный ответ — 4.
— Как изучают математику в школе. В начальном звене вводят операции — сложение, вычитание, умножение и деление. Примерно до 6-го класса дети не знают, что существуют рациональные числа, которые записываются в виде дробной черты. Когда они вводятся, то выясняется, что операцию деления можно записать не в виде двух точек. И до самого вуза очень часто все выражения записываются, как дробное число и отдельная операция деления через две точки редко используется. Так умножение у людей фиксируется как приоритетная операция, — объяснил Илья Марьясов.
В итоге это приводит к ошибке в вычислениях.
— У людей возникает соблазн 3 умножить на 8 минус 6 (то есть на 2) и получается у них 6. Потом 36 делят на 6, получая 6. И в итоге 6 делят на 6 и выходит 1. Это неверный ответ в данном случае, — отметил математик.
Ранее в Высшей школе экономики подсчитали, что средний проходной балл ЕГЭ для поступления в вузы снизился впервые за 10 лет.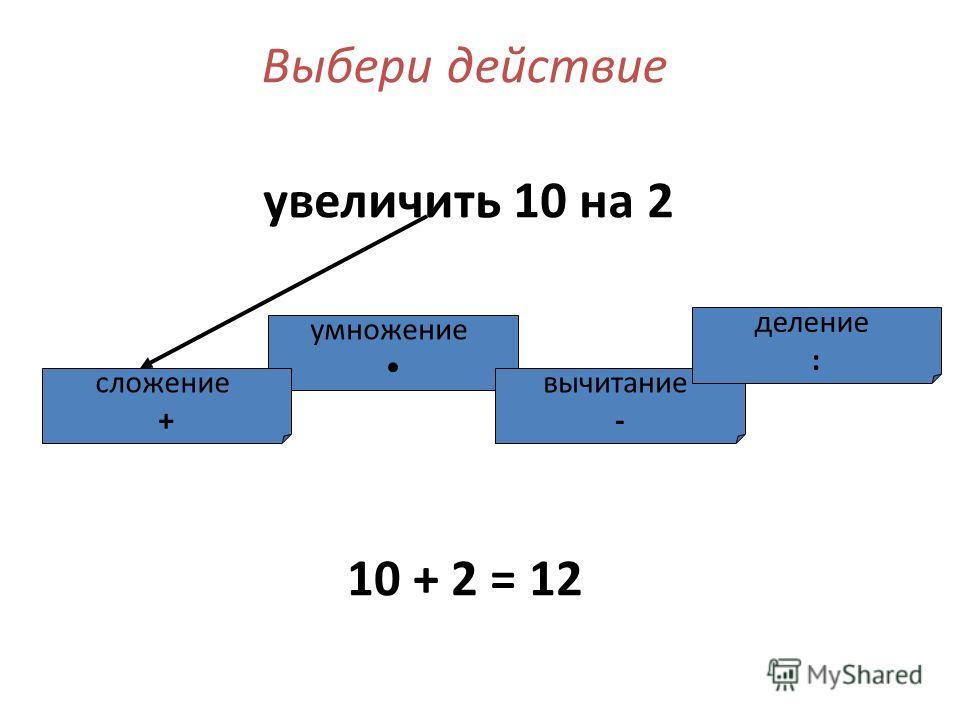 Предлагаем вам ответить на несколько вопросов (разных лет) из того самого итогового среза знаний.
Предлагаем вам ответить на несколько вопросов (разных лет) из того самого итогового среза знаний.
По теме
20 января 2023, 16:00
Один и тот же пример в разных странах решают по-разному. Как это получается?18 декабря 2022, 15:30
«Любите ли вы сплетничать?» Журналист попытался обмануть детектор лжи, и вот что обнаружил полиграф19 сентября 2022, 10:00
Это точно русский? Проверьте, сможете ли вы написать правильно все эти слова18 декабря 2022, 14:00
Русский не родной? 10 простейших слов, которые все пишут с ошибками23 февраля 2023, 17:00
Зеркальная дата 23.02.2023: что не стоит делать в этот день, чтобы не накликать беду, — советы нумеролога
Александра Бруня
Корреспондент
МатематикаРешениеПримерРазбор
- ЛАЙК13
- СМЕХ41
- УДИВЛЕНИЕ6
- ГНЕВ15
- ПЕЧАЛЬ7
Увидели опечатку? Выделите фрагмент и нажмите Ctrl+Enter
КОММЕНТАРИИ215
Читать все комментарии
Гость
Войти
Новости РЎРњР?2
Новости РЎРњР?2Базовый порядок операций (DMAS)
Введение При упрощении математических выражений, состоящих из операций одного типа, мы выполняем одну операцию за раз, как правило, начиная слева направо. Если выражение имеет более одной основной операции, вы не можете выполнять операции в том порядке, в котором они указаны. Некоторые операции должны быть выполнены раньше, чем другие. Это каждая операция имеет свой приоритет. Как правило, порядок, в котором мы последовательно выполняем операции слева направо, таков: деление, умножение, сложение, вычитание. Но когда в выражениях также используются скобки, у нас есть набор правил, определяющих приоритет операций. Давайте узнаем, как определяется это правило.
Если выражение имеет более одной основной операции, вы не можете выполнять операции в том порядке, в котором они указаны. Некоторые операции должны быть выполнены раньше, чем другие. Это каждая операция имеет свой приоритет. Как правило, порядок, в котором мы последовательно выполняем операции слева направо, таков: деление, умножение, сложение, вычитание. Но когда в выражениях также используются скобки, у нас есть набор правил, определяющих приоритет операций. Давайте узнаем, как определяется это правило.
Давайте разберемся с этим на примере.
Предположим, мы хотим найти значение 2 + 3 x 5
Есть два способа найти значение приведенного выше выражения.
В первом методе будем двигаться слева направо, решая выражение в указанном порядке. Это означает, что сначала мы найдем сумму 2 и 3. Мы получим, 2 + 3 = 5.
Теперь у нас есть 2 + 3 x 5 = 5 x 5
Теперь мы найдем произведение 5 на 5 чтобы получить ответ как 25. Следовательно, мы имеем
2 + 3 x 5 = 25 …………………………………. . ( 1 )
. ( 1 )
Теперь найдем значение этого выражения другим методом.
Сначала мы найдем значение 3 x 5 и добавим это произведение к 2. Таким образом, мы получим
3 x 5 = 15 и 15 + 2 = 17
Следовательно, теперь у нас есть
2 + 3 x 5 = 17 ………………………… ( 2 )
Из ( 1 ) и ( 2 ) мы видим, что оба полученных результата не совпадают. Это подтверждает необходимость наличия приоритета операторов, чтобы получить один и тот же ответ на данное алгебраическое выражение. Этот приоритет известен как порядок операций.
Каков основной порядок операций? Порядок операций можно определить как стандартную процедуру, которая указывает, какие вычисления следует начинать в выражении с несколькими арифметическими операциями. Без последовательного порядка операций можно допустить большие ошибки во время вычислений. Существует ряд правил, определяющих порядок операций в зависимости от задействования операторов, скобок, показателей степени и других математических символов для операций. Это правило известно как DMAS, где
Это правило известно как DMAS, где
D означает деление (÷)
M означает умножение (x)
A означает сложение (+)
S означает вычитание (–)
Давайте разберемся с правилом более подробно.
Что такое DMAS?MDAS, как определено выше, является основным порядком операций. Другими словами, он определяет порядок, в котором должны выполняться операции над числами, когда возникают ситуации, когда в выражении на две операции больше, чем две. Итак, у нас порядок операций такой –
Рассмотрим пример. Предположим, мы хотим найти значение 3 + 5 x 2.
Здесь у нас есть два оператора, а именно ( x ) и ( + ). Мы знаем, что в математике мы можем выполнять операции между двумя числами только за один раз. Если у нас есть более 2 чисел, результат первой операции используется для выполнения следующей операции. Итак, в приведенном выше примере необходимо выполнить две операции: (3 + 5) и (5 x 2). Нам нужно решить, с какой из них начать. Здесь вступает в действие правило MDAS.
Здесь вступает в действие правило MDAS.
Из этого правила видно, что умножение предшествует сложению. Поэтому сначала выполним операцию умножения. Полученный таким образом результат будет добавлен к 3. Шаги, связанные с этим процессом, будут –
3 + 5 x 2
= 3 + 10
= 13
Следовательно, 3 + 5 x 2 = 13
Рассмотрим другой пример.
Пример
Упростите следующее выражение, используя порядок операций –
6 + 5 – 4 x 2
Решение
Нам дано выражение 6 + 5 – 4 x 2
Важно отметить, что здесь задействованы три операции. Основываясь на порядке операций, умножение имеет приоритет над сложением и вычитанием, поэтому мы будем умножать первыми. Затем добавьте, а затем вычтите, так как операция сложения предшествует вычитанию слева направо.
Следовательно, мы имеем
6 + 5 – 4 x 2
= 6 + 5 – 8 (Здесь мы решили 4 x 2, что дало нам результат 8)
= Затем мы сложим 6 и 3, чтобы получить 9. Итак, у нас есть
Итак, у нас есть
6 + 5 – 8 = 11 – 8 = 3
Следовательно, 6 + 5 – 4 x 2 = 3
Использование скобок в порядке операцийМы только что узнали о приоритете основных операций сложения, вычитания, умножения и деления. В соответствии с ним порядок, в котором должны выполняться операции, — это сначала деление, затем умножение, после чего сложение и, наконец, вычитание, но иногда в сложных операциях требуется, чтобы набор операций выполнялся до другого. Например, если мы хотим, чтобы сложение выполнялось перед делением или умножением, нам нужно использовать скобки.
Скобки используются для ясности в порядке операций, в котором должны выполняться несколько операций в математическом выражении. Скобка указывает, что операции внутри нее должны выполняться до операций вне ее. Например, выражение 24 ÷ 3 x 4 обычно решается как –
24 ÷ 3 x 4
= 8 x 4 = 32
Однако, если мы хотим сначала умножить 3 и 4, а затем разделить 24 на получившееся число запишем выражение как
24 ÷ ( 3 x 4 )
Теперь, в соответствии с порядком действий, сначала разгадаем скобки, чтобы получить,
24 ÷ ( 3 x 4 )
= 24 ÷ 12
= 2
В сложных выражениях иногда необходимо иметь (внутри) в одно и то же время (одно внутри другого может сбивать с толку, поскольку чаще всего используются разные типы скобок)
Скобки Имя
( ) Круглые скобки
{ } Скобки или фигурные скобки
[ ] Скобки или квадратные скобки
Здесь важно отметить, что левая часть каждого символа скобки указывает на начало скобки, а правая часть указывает на конец скобки. При написании математических выражений, состоящих более чем из одной скобки, в самой внутренней части используются круглые скобки, за которыми следуют фигурные скобки, и эти две скобки заключаются в квадратные скобки.
При написании математических выражений, состоящих более чем из одной скобки, в самой внутренней части используются круглые скобки, за которыми следуют фигурные скобки, и эти две скобки заключаются в квадратные скобки.
Чтобы упростить выражения, включающие более одной скобки, мы будем использовать шаги, описанные ниже –
- Посмотреть, содержит ли данное выражение винкулум или нет. Если винкулум присутствует, выполните операции с красным цветом, в противном случае перейдите к следующему шагу. Винкулум — это горизонтальная линия, расположенная над выражением, чтобы показать, что все, что ниже линии, является одной группой, например, $\overline{2\: x\: 3}$.
- Теперь найдите самую внутреннюю скобку и выполните в ней операции.
- Удалите самую внутреннюю скобку, выполнив следующие действия:
- Если скобке предшествует знак плюс, удалите ее, записав ее термины как есть.
- Если скобке предшествует знак минус, измените положительный знак внутри нее на отрицательный и наоборот.

- Если между числом и символом группировки нет знака, то это означает умножение.
- Если перед некоторыми скобками стоит число, то мы умножаем число внутри скобок на число вне скобок.
- Найдите ближайшую внутреннюю скобку и выполните в ней операции. Удалите второй в направлении, используя правила, указанные в предыдущих шагах. Продолжайте этот процесс, пока не будут удалены все скобки.
Давайте разберем приведенные выше шаги на примере.
Пример
Упрощение: 37 – [ 5 + { 28 – ( 19 – 7 ) } ]
Решение
Нам дано выражение, 37 – [ 1 9 – 28 – ( 1 ) } ]
Мы будем использовать порядок операций для решения данного выражения.
Сначала мы удалим самую внутреннюю скобку, чтобы получить
37 – [ 5 + { 28 – 12 } ] …………………… [ Удаление самой внутренней скобки ( ) ]
Далее мы удалим фигурные скобки, чтобы получить
37 — [ 5 + 16 ] …………………………. [ Удаление фигурных скобок ]
Теперь мы удалим квадратные скобки, чтобы получить,
37 – 21 …………………………… [удаление квадратных скобок ]
Наконец, мы найдем разницу между 37 и 21, чтобы получить 16.
Следовательно, упрощение 37 – [ 5 + { 28 – 12 } ] приведет к 16.
Как решать выражения, используя порядок операций?Теперь, когда мы поняли, что мы подразумеваем под порядком операций, давайте узнаем о шагах, связанных с решением математических выражений с использованием порядка операций. Необходимые шаги:
- Всегда начинайте с вычисления всех выражений в круглых скобках
Прежде всего, мы должны искать удаление любых символов группировки в алгебраическом выражении. Это означает, что в верхней части списка не забывайте всегда упрощать все внутри символов группировки. Примерами символов группировки являются круглые скобки ( ), скобки и фигурные скобки { }. Для вложенных символов группировки проработайте их изнутри и снаружи.
- Упростить все показатели степени, такие как квадратные корни, квадраты, кубы и кубические корни
После удаления круглых скобок мы переходим к следующему шагу решения всех экспоненциальных значений в алгебраическом выражении. Экспоненциальные выражения, которые могут включать корневые значения, такие как квадратные корни, квадраты, кубы, кубические корни и т. д., сначала вычисляются или оцениваются перед выполнением любой из четырех основных арифметических операций, а именно: сложения, вычитания, умножения и деления.
Экспоненциальные выражения, которые могут включать корневые значения, такие как квадратные корни, квадраты, кубы, кубические корни и т. д., сначала вычисляются или оцениваются перед выполнением любой из четырех основных арифметических операций, а именно: сложения, вычитания, умножения и деления.
- Выполните умножение и деление, начиная слева направо
Затем умножьте и/или разделите слева направо перед выполнением сложения и вычитания. Это говорит нам о том, что умножение и деление имеют более высокий уровень важности, чем сложение и вычитание.
- Наконец, аналогично выполните сложение и вычитание, начиная слева направо.
Давайте разберемся на примере.
Пример Найдите значение выражения 4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 )
Решение Нам дано выражение 4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 ). Нам нужно решить ее с помощью MDAS.
Так как данное выражение содержит скобки; мы сначала решим скобки. Мы получим
Мы получим
4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 )
Теперь в скобках сначала решим секцию деления
4 ( 10 + 15 ÷ 5 x 4 – 2 × 2 )
Далее в самой скобке решим умножение, чтобы получить
4 ( 10 + 3 × 4 – 2 × 2 )
Теперь внутри скобки решим сложение, чтобы получить
4 ( 10 + 12 – 4 )
Далее в скобках складываем числа 10 и 12, а затем вычитаем из результата 4, чтобы получить
4 ( 22 – 4 )
После того, как скобка решена, подбираем число из снаружи и решить часть «Из» умножением:
= 4 × 18
= 72
Следовательно, 4 (10 + 15 ÷ 5 × 4 — 2 × 2) = 72
Используемые шаги можно табулировать как
| 888 4 | 888 4 | |||||||||||||
| 4 | ||||||||||||||
| 4 | ||||||||||||||
| 4 | ||||||||||||||
| 4 | ||||||||||||||
| Дивизион | 4 (10 + 15 ÷ 5 x 4 — 2 × 2) | |||||||||||||
| 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9 ( 10 + 3 × 4 – 2 × 2 ) | ||||||||||||||
| Addition | 4 ( 10 + 12 – 4 ) | |||||||||||||
| Subtraction | 4 ( 22 – 4 ) | |||||||||||||
| Answer | = 4 x 18 | |||||||||||||
| 72 |
Мы узнали, что в математике порядок операций помогает найти правильное значение выражения. Однако это не ограничивается задачами по математике. Порядок операций имеет значение и в повседневной жизни. Например, вы используете фиксированный порядок действий для приготовления блюда. Точно так же в химических реакциях необходимо соблюдать определенный порядок, чтобы получить желаемые результаты. Возвращаясь к математике, есть много повседневных дел, в которых используется порядок операций MDAS.
Однако это не ограничивается задачами по математике. Порядок операций имеет значение и в повседневной жизни. Например, вы используете фиксированный порядок действий для приготовления блюда. Точно так же в химических реакциях необходимо соблюдать определенный порядок, чтобы получить желаемые результаты. Возвращаясь к математике, есть много повседневных дел, в которых используется порядок операций MDAS.
Давайте разберемся на примере.
Пример
Джон покупает 2 рубашки по 8 фунтов каждая. Он также покупает джинсы за 20 фунтов стерлингов, на которые предоставляется скидка в размере 3 фунтов стерлингов. Сколько всего он платит?
Решение
Нам известно, что Джон покупает 2 рубашки по 8 фунтов каждая. Он также покупает джинсы за 20 фунтов стерлингов, на которые предоставляется скидка в размере 3 фунтов стерлингов. Нам нужно узнать, сколько Джон платит за рубашки и джинсы. Чтобы найти это, мы должны сначала разместить все значения в виде выражения. Мы получим,
Мы получим,
Цена 2 рубашек + Цена пары джинсов – Скидка = Общая стоимость, уплаченная Джоном
Следовательно,
Общая стоимость, уплаченная Джоном = 2 x 8 + 20- – 3
Здесь мы видим, что есть задействованы три операции. Основываясь на порядке операций, умножение имеет приоритет над сложением и вычитанием, поэтому мы будем умножать первыми. Затем добавьте, а затем вычтите, так как операция сложения предшествует вычитанию слева направо. Таким образом, мы получаем,
Общая стоимость, уплаченная Джоном = 16 + 20 – 3 = 36 – 3 = £ 33
Следовательно, общая стоимость, уплаченная Джоном за 2 рубашки и пару джинсов, = 33 фунта стерлингов
Теперь мы научились решать выражения, включающие более одного математического оператора. Но что, если в выражении используются скобки. Поступим ли мы так же или внесем некоторые дополнения в правило? Давайте узнаем.
Ключевые факты и сводка- Порядок операций можно определить как стандартную процедуру, которая указывает, какие вычисления следует начинать в выражении с несколькими арифметическими операциями.

- MDAS — это основной порядок операций, где MDAS, где M означает умножение (x), D означает деление (÷), A означает сложение (+), S означает вычитание (–).
- Скобки используются для ясности в порядке операций, в котором несколько операций должны выполняться в математическом выражении.
- Правила порядка операций: –
- Всегда начинайте с вычисления всех выражений в скобках
- Упростите все показатели степени, такие как квадратные корни, квадраты, куб и кубические корни.
- Выполните умножение и деление, начиная слева направо.
- Наконец, аналогично выполните сложение и вычитание, начиная слева направо.
- Скобки используются для ясности в порядке операций, в котором должны выполняться несколько операций в математическом выражении.
- При написании математических выражений, состоящих более чем из одной скобки, в самой внутренней части используются круглые скобки, за которыми следуют фигурные скобки, и эти две скобки заключаются в квадратные скобки.

Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Объединение одинаковых терминов и порядка действий
Результаты обучения
- Распознавание и объединение одинаковых терминов в выражении
- Используйте порядок операций для упрощения выражений
Несколько важных терминов, прежде чем мы начнем:
- операции/операторы: В математике мы называем такие операции, как умножение, деление, сложение и вычитание. Это глаголы математического мира, выполняющие работу с числами и переменными. Символы, используемые для обозначения операций, называются операторами, например [латекс]+{, }-{, }\times{, }\div[/latex]. Чем больше вы будете изучать математику, тем больше вы узнаете операторов.
- термин: Примерами терминов могут быть [латекс]2x[/латекс] и [латекс]-\Large\frac{3}{2}[/латекс] или [латекс]a^3[/латекс].
 Даже одиночные целые числа могут быть термином, например [latex]0[/latex]. 92b[/латекс], или [латекс]-3[/латекс] и [латекс]8[/латекс]. Если у нас есть одинаковые термины, нам разрешено добавлять (или вычитать) числа перед переменными, тогда оставьте переменные одинаковыми. Поскольку мы объединяем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный термин. Знак всегда остается с термином.
Даже одиночные целые числа могут быть термином, например [latex]0[/latex]. 92b[/латекс], или [латекс]-3[/латекс] и [латекс]8[/латекс]. Если у нас есть одинаковые термины, нам разрешено добавлять (или вычитать) числа перед переменными, тогда оставьте переменные одинаковыми. Поскольку мы объединяем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный термин. Знак всегда остается с термином.Это показано в следующих примерах:
Пример
Объедините похожие термины: [латекс]5x-2y-8x+7y[/латекс] 92+3x-1[/latex]
Показать решение
В следующем видео вам будет показан еще один пример сочетания похожих терминов. Обратите внимание, почему у вас не получается объединить в примере все три термина.
Порядок действий
Вы можете помнить или не помнить порядок действий для применения нескольких математических операций к одному выражению.
 Точно так же, как в обществе принято ездить по правой стороне дороги, порядок операций представляет собой набор соглашений, используемых для обеспечения порядка, когда вам требуется использовать несколько математических операций для одного выражения.
Точно так же, как в обществе принято ездить по правой стороне дороги, порядок операций представляет собой набор соглашений, используемых для обеспечения порядка, когда вам требуется использовать несколько математических операций для одного выражения.Порядок действий
- Сначала выполните все операции внутри группирующих символов. К символам группировки относятся круглые скобки ( ), квадратные скобки [ ], фигурные скобки { } и дроби.
- Вычисление показателей степени или квадратных корней.
- Умножение или деление слева направо.
- Сложение или вычитание слева направо.
Этот порядок операций верен для всех действительных чисел.
В следующем примере показано, как упростить выражение, содержащее как умножение, так и вычитание, используя порядок операций.
Когда вы применяете порядок операций к выражениям, которые содержат дроби, десятичные дроби и отрицательные числа, вам также нужно вспомнить, как выполнять эти вычисления.

В следующем видеоролике показано, как использовать порядок операций для упрощения выражения, содержащего умножение, деление и вычитание с элементами, содержащими дроби.
Экспоненты и квадратные корни
В этом разделе мы расширим наши навыки, применяя правила порядка операций к выражениям с экспонентами и квадратными корнями. Если в выражении есть показатели степени или квадратные корни, они должны выполняться 9{2}[/latex], [latex]7[/latex] – основание, а [latex]2[/latex] – показатель степени; показатель степени определяет, сколько раз основание умножается само на себя.)
Показатель степени представляет собой способ представления многократного умножения; порядок операций ставит его перед выполняются любые другие умножение, деление, вычитание и сложение.

В следующем видео выражение с показателями в его терминах упрощается с помощью порядка операций.
Если внутри группирующих символов есть символы группировки, расчет производится изнутри наружу. То есть сначала начните упрощение внутри самых внутренних группирующих символов.
Помните, что круглые скобки также могут использоваться для обозначения умножения. В следующем примере показаны оба варианта использования скобок — как способ представления группы, а также как способ выражения умножения.
В следующем видеоролике показано, как использовать порядок операций для упрощения выражения с помощью группировки символов, показателей степени, умножения и сложения. 9{3}}\cdot \,32[/latex]
Используйте поле ниже, чтобы записать несколько мыслей о том, как упростить это выражение с помощью дробей и символов группировки.

Показать решение
Некоторые люди используют поговорку, чтобы запомнить порядок действий. Эта поговорка называется PEMDAS или P лизинг E извините M y D ухо A unt S союзник. Первая буква каждого слова начинается с той же буквы арифметической операции.
P аренда [латекс] \displaystyle \Rightarrow [/латекс]
E xcuse [латекс] \displaystyle \Rightarrow [/латекс] E экспоненты7 M y D ухо [латекс] \displaystyle \Rightarrow [/latex] M умножение и D ivision (слева направо)
A unt S союзник [латекс] \displaystyle \Rightarrow [Rightarrow латекс] A дополнение и S вычитание (слева направо)Примечание: Несмотря на то, что в пословице умножение предшествует делению, деление может выполняться первым.


 Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого.


 Даже одиночные целые числа могут быть термином, например [latex]0[/latex]. 92b[/латекс], или [латекс]-3[/латекс] и [латекс]8[/латекс]. Если у нас есть одинаковые термины, нам разрешено добавлять (или вычитать) числа перед переменными, тогда оставьте переменные одинаковыми. Поскольку мы объединяем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный термин. Знак всегда остается с термином.
Даже одиночные целые числа могут быть термином, например [latex]0[/latex]. 92b[/латекс], или [латекс]-3[/латекс] и [латекс]8[/латекс]. Если у нас есть одинаковые термины, нам разрешено добавлять (или вычитать) числа перед переменными, тогда оставьте переменные одинаковыми. Поскольку мы объединяем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный термин. Знак всегда остается с термином. Точно так же, как в обществе принято ездить по правой стороне дороги, порядок операций представляет собой набор соглашений, используемых для обеспечения порядка, когда вам требуется использовать несколько математических операций для одного выражения.
Точно так же, как в обществе принято ездить по правой стороне дороги, порядок операций представляет собой набор соглашений, используемых для обеспечения порядка, когда вам требуется использовать несколько математических операций для одного выражения.


