Что первым делается в примере умножение или деление: Порядок выполнения действий в выражениях без скобок и со скобками — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

admin

Содержание

а, а : 1, 0 : а

Этап усвоения новых знаний

 

Ребята, вспомните, что такое умножение?
Умножение – это сложение одинаковых слагаемых
 

Замените в следующих примерах произведение суммой и запишите.

5 · 3 =
5 · 2=
5 · 1=

Проверьте себя.

5 · 3 = 5 + 5 + 5 + 5
5 · 2 = 5 + 5    
5 · 1 = ?
5 · 0 = ?
 

Удалось ли заменить сложением последние два примера?
Это особые случаи.
Нельзя взять число слагаемым один раз. Поэтому применим переместительное свойство умножения:
1 · 5 = 1 + 1 + 1 + 1 + 1 = 5

 

Кроме табличных случаев умножения и деления в математике, существуют случаи, которые называют особыми — это

математические законы, которые нужно знать: при умножении любого числа на 1, получается то число, которое умножали.   
     

В математике обозначают любое число латинской буквой а.
Запишите этот вывод формулой.
а · 1 = а
 

Запомните!
Вместо буквы а мы можем подставить любое число.
 

Рассмотрим подробно пример 5 · 0 = ?
К данному случаю можно применить переместительное свойство умножения.
0 · 5 = 0 + 0 + 0 + 0 + 0 = 0

 

Второй математический закон, который нужно сегодня запомнить:
Произведение считается равным нулю, при умножении на 0.
 

Запишите этот вывод формулой.

а · 0 = 0
 

Запомните!
Вместо буквы а,  мы можем подставить любое число.
 

Лучшему запоминанию новых случаев умножения будет способствовать создание наглядного образа.


Множитель 1 не изменяет число, его можно представить зеркальцем.
Как бы отражает второй множитель, не изменяя его.

Нуль – это шапка – невидимка. Он при умножении покрывает второй множитель и делает его невидимым.

Давайте вспомним, что такое деление.
Деление — это действие, обратное умножению.
Каждому примеру на умножение можно составить два обратных примера на деление.
Рассмотрим подробно следующие случаи деления:

а : а = ?
а : 1 = ?
0 : а = ?
 

Запишите пример 5 · 1 = ?
Проверим 5 · 1 = 5

Каждому примеру на умножение можно составить два обратных примера на деление. 
Составим и запишем.

5 : 5 = ?
Проверим 5 : 5=1

Делаем вывод:
При делении числа на то же самое число получается единица. Запишем буквенное выражение или формулу

а : а = 1
ЗАПОМНИТЕ!

 

Запишем второй пример на деление.
 5 : 1 = ?

Проверим
5 : 1 = 5

Делаем вывод:
При делении числа на 1 получается то же самое число
Запишем буквенное выражение или формулу
а : 1 = а          

      

Решим ещё один пример на деление, запишите
0 : 5 = ?….
Это значит, надо найти число, при умножении которого на 5 получится 0.
х · 5 = 0

Это будет число 0. Значит, 0 : 5 = 0…..

Делаем вывод:
При делении 0 на любое число получается 0.
Запишем буквенное выражение или формулу
0 : а = 0

 

Этап закрепления новых знаний

 

Задание 1

Выполните вычисления.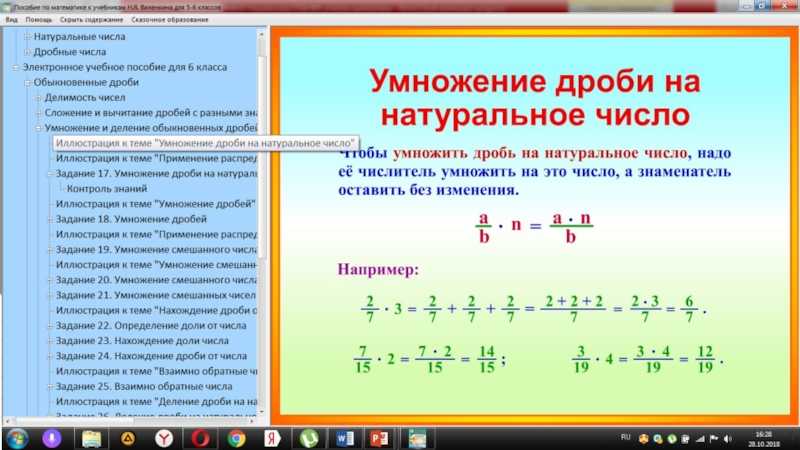

91 ∙ 1 =
64 + 0 =
18 ∙ 0 =
1 ∙ 35 =
25 + 1 =
0 ∙ 361 =
72 ∙ 0 =
54 ∙ 1 =
31 — 0 =
0 ∙ 159 =
1 ∙ 76 =
98 — 1 =

Проверьте себя и оцените свои успехи.

91 ∙ 1 = 91
64 + 0 = 64
18 ∙ 0 = 0
1 ∙ 35 = 35
25 + 1 = 26
0 ∙ 361 = 0
72 ∙ 0 = 0
54 ∙ 1 = 54
31 — 0 = 31
0 ∙ 159 = 0
1 ∙ 76 = 76
98 — 1 = 97
 

Задание 2

Найдите числовые выражения, при решении которых допущена ошибка. Запишите эти выражения, сделав вычисления правильно.

1 · 15 = 15
3 · 0 = 3
19 : 19 = 1
23 : 1 = 1
26 : 26 = 1

12 + 0 = 0
17 — 0 = 17

Проверьте себя и оцените свои успехи.

3 · 0 = 0
23 : 1 = 23
12 + 0 = 12

 

Этап подведения итогов

 

Давайте повторим:

  1. При умножении любого числа на 1 получается число, которое умножаем.
  2. При умножении любого числа на 0 получается 0.
  3. При делении числа на то же самое число получается единица.
  4. При делении числа на 1 получается то же самое число.
  5. При делении 0 на любое число получается 0.
     

Запомните! Делить на нуль нельзя!

 

Рефлексия

 

Выберите смайлик, который более всего соответствует вашему пониманию изученных сегодня на уроке правил и нарисуйте его у себя в тетради.

Спасибо за работу, вы хорошо потрудились!       

Действия какой ступени выполняются в первую очередь?

Меню раздела

Математика
Пожалуйста, оцените Оценка 1Оценка 2Оценка 3Оценка 4Оценка 5  

Ответьте на вопрос: —

Какой порядок действий при решении длинного выражения?

Порядок выполнения действий при решении выражения.

В математике последовательность выполнения действий разделена на две ступени:
к первой ступени относятся действия — сложение и вычитание, ко второй ступени — умножение и деление.
При нахождении значения выражения в первую очередь выполняются действия заключённые в скобки (если имеются), далее выполняются действия второй ступени и в последнюю очередь действия первой ступени.
Порядок действий обозначается слева направо.

Пример:

1. Слева направо обозначим действия в скобках.

2. Вернёмся к началу примера и снова продолжим слева направо обозначать теперь действия второй ступени.
Действия второй ступени — умножение и деление.

3. Вновь вернёмся к началу примера и снова продолжим слева направо обозначать теперь действия первой ступени.
Действия первой ступени — сложение и вычитание.

Всего 10 действий. Выполняем их по проставленному порядку.

Выполним действия в скобках:

18 + 8 : (27 — 25) — 2 · 8 + 4 · (6 + 4) + 16 : 8

  1. 27 — 25 = 2
  2. 6 + 4 = 10

    После выполнения действий в скобках выражение стало выглядеть так:

    18 + 8 : 2 — 2 · 8 + 4 · 10 + 16 : 8

    Теперь выполним все действия второй ступени — умножение и деление:

    18 + 8 : 2 — 2 · 8 + 4 · 10 + 16 : 8

  3. 8 : 2 = 4
  4. 2 · 8 = 16
  5. 4 · 10 = 40
  6. 16 : 8 = 2

    После выполнения действий второй ступени выражение стало выглядеть так:

    18 + 4 — 16 + 40 + 2

    Теперь выполним все действия первой ступени — сложение и вычитание:

    18 + 4 — 16 + 40 + 2

  7. 18 + 4 = 22
  8. 22 — 16 = 6
  9. 6 + 40 = 46
  10. 46 + 2 = 48

    18 + 8 : (27 — 25) — 2 · 8 + 4 · (6 + 4) + 16 : 8 = 48

Коротко:

Известные и великие математики

ученые средневековья и современности, и их вклад в мировую науку

Пафнутий Чебышёв

Русский математик и механик
Дата рождения: 16 мая 1821
Место рождения: Акатово, Боровский уезд, Калужская губерния, Российская империя
Дата смерти: 8 декабря 1894 (73 года)

Биография

Первоначальное воспитание и образование получил дома: грамоте его обучила мать Аграфена Ивановна. Арифметике, французскому языку и музыке обучала двоюродная сестра Авдотья Квинтилиановна Сухарёва. Одним из детских увлечений будущего учёного было изучение механизмов игрушек и автоматов, которые сам придумывал и изготовлял их.

В 1832 году семья переехала в Москву. В Москве с Пафнутием математикой и физикой занимался П. Н. Погорельский — один из лучших учителей Москвы, у которого в том числе учился, в пансионе Вейденгаммера, и И. С. Тургенев. Латынь Пафнутию Чебышёву преподавал в то время студент-медик, а в будущем главный врач Шереметевской больницы А. Т. Тарасенков.

Летом 1837 года Чебышёв поступил в Императорский Московский университет на вторе физико- математическе отделение философского факультета и начал изучение математики . Существенное влияние на формирование круга научных интересов молодого Чебышёва оказал его учитель — профессор прикладной математики и механики Московского университета Николай Дмитриевич Брашман. В 1841 году Пафнутий Чебышёв его окончил.

В 1846 году он успешно защитил магистерскую диссертацию «Опыт элементарного анализа теории вероятностей». В 1847 году Чебышёв был утверждён в звании адъюнкт-профессора Петербургского университета. Чтобы получить право чтения лекций в университете, он защитил ещё одну диссертацию — на тему «Об интегрировании с помощью логарифмов», после чего читал лекции по высшей алгебре, теории чисел, геометрии, теории эллиптических функций и практической механике.

В 1846 году он успешно защитил магистерскую диссертацию «Опыт элементарного анализа теории вероятностей». В 1847 году Чебышёв был утверждён в звании адъюнкт-профессора Петербургского университета. Чтобы получить право чтения лекций в университете, он защитил ещё одну диссертацию — на тему «Об интегрировании с помощью логарифмов», после чего читал лекции по высшей алгебре, теории чисел, геометрии, теории эллиптических функций и практической механике.

В 1849 году Чебышёв защитил в Петербургском университете докторскую диссертацию «Теория сравнений», после чего в 1850 году он стал профессором Петербургского университета; данную должность он занимал до 1882 года. Работая в Петербургском университете, Чебышёв близко сошёлся с профессором прикладной математики О. И. Сомовым, который тоже был учеником Н. Д. Брашмана, и эти отношения переросли в глубокую дружбу. В семейном плане Чебышёв был одинок, и это обстоятельство также способствовало его сближению с большой семьёй Сомова.

Интерес к механизмам сохранялся у Чебышёва и в зрелые годы. В 1852 году Чебышёв совершил научную командировку в Великобританию, Францию и Бельгию, в ходе которой он ознакомился с практикой зарубежного машиностроения, с музейными коллекциями машин и механизмов, с работой заводов и фабрик, а также встречался с крупнейшими математиками и механиками: О. Коши, Ж. Лиувиллем, Ж. -А. Серре, Л. Фуко, Ш. Эрмитом, Дж. Сильвестром, А. Кэли, Т. Грегори. После этого он некоторое время преподавал практическую механику в Петербургском университете и Александровском лицее.

В 1853 году академики П. Н. Фусс, В. Я. Струве, Б. С. Якоби, В. Я. Буняковский представили Чебышёва к избранию в адъюнкты Петербургской академии наук, особо отметив важность его работ в области практической механики. В том же году он был избран в адъюнкты, а в 1856 году стал экстраординарным академиком.

В 1858 году в связи с его работами по теории шарнирных параллелограммов и теории приближения функций академики В. Я. Буняковский, М. В. Остроградский, Э. Х. Ленц, Б. С. Якоби, А. Я. Купфер, О. В. Струве подписали представление к избранию Чебышёва ординарным академиком. И 1859 году Чебышёв избран ординарным академиком. Стал почётным членом Московского университета.

С 22 февраля 1860 года — ординарный профессор.

С 10 июля 1863 года — член Учёного комитета Министерства народного просвещения.

С 30 августа 1863 года — действительный статский советник.

Чем знаменит:

  • В 1840/1841 учебном году, участвуя в студенческом конкурсе Императорского Московского университета, Пафнутий Чебышёв получил серебряную медаль за работу по нахождению корней уравнения n-й степени которую написал ещё в 1838 году и сделаную на основе алгоритма Ньютона
  • Работы по теории вероятностей — изъяв из неё расплывчатые формулировки и неправомерные утверждения и превратив её в строгую математическую дисциплину
  • Работы по теории чисел
  • Работы по математическому анализу
  • Работы по прикладной математике и механике
  • Работы по «стопоходящей машины»
  • Создатель автоматического арифмометра
  • оздатель модели инвалидной коляски
  • оздатель
  • Работы по
  • Назад
  • Вперед

Если заметили ошибку, выделите фрагмент текста и нажмите Ctrl+Enter

Рейтинг: ( 0 Рейтинг )

Продырявили «Северный поток-2» Прекращение торгов долларом Застрелил дочь из ружья Изрезал ножом собственную дочь В составе России В школе № 26 отравились дети Кадыров заявил о перевыполнении плана призыва в Чечне на 254% Мальчика наградили орденом Мужества Избили, задушили и положили в ванну Все наши прежние действия покажутся детскими шалостями Обнаружили тело 14-летнего подростка Ваше место в «музее времен СССР» Питомец заразил всю семью лишаем 5 правил, как уберечь ребенка от негативного контента в интернете Сегодня Путин выступит с обращением к жителям России Школьника избили в батутном центре в Москве

Запомнить меня

Регистрация

 

Приёмы умножения и деления на 10

Урок 36.
Математика 2 класс ФГОС

На этом уроке царица Математика на материале задач знакомит с приемом умножения числа 10 и на основе переместительного свойства — с умножением на 10. Делается вывод, как надо умножать число 10 и на 10. Затем, используя знания о связи умножения и деления, царица объясняет приемы деления на 10 и с ответом 10.


Конспект урока «Приёмы умножения и деления на 10»

- Здравствуйте, ребята! Сегодня я хочу вам рассказать об очень интересных приёмах умножения и деления. Я познакомлю вас с тем как легко можно умножать и делить на число 10. Вот посмотрите на эти книжные полки:

На каждой полке стоит по 10 книг с задачами по математике. Как вы думаете, сколько всего книг стоит на этих полках? Так как книг поровну, мы можем вычисление записать действием умножения:

Ответ: всего 30 книг.

А теперь посмотрите, мне привезли новые книги с задачами, и они ещё не распакованы. Видите, лежат 10 упаковок с книгами:

В каждой из них по 3 книги. Давайте узнаем, сколько книг мне прислали?

Опять же, все упаковки одинаковые, в них по 3 книги, поэтому решение задачи записываем действием умножения:

Здесь уже вычисление при помощи действия сложения совсем неудобное.

Но ведь вы, конечно, не забыли переместительное свойство умножения? От перестановки множителей произведение не меняется. Посмотрите, в предыдущей задаче нам надо было 10 умножить на 3. А в этой — 3 умножить на 10. Множители поменялись местами, но произведение должно быть одинаковым. И значит в этой задаче тоже ответ — 30.

Ответ: всего 30 книг.

Ребята, я хочу обратить ваше внимание на результат умножения в этой задаче. Посмотрите, в нём первая цифра такая же, как первый множитель, а вторая цифра — нуль, взятый из второго множителя. Получается, что при умножении на 10 в ответе мы просто ставим первый множитель и справа приписываем к нему 0. А в предыдущей задаче первым множителем было число 10, а вторым — число 3. Здесь мы сначала записали второй множитель, число 3, и к нему справа приписали 0 из первого множителя. Ведь это так просто. Но, всё-таки, давайте проверим на других примерах. А вдруг, это — простое совпадение?

Давайте попробуем решить вот такие примеры:

Сначала 10 умножаем на 4. Поможет нам, конечно, действие сложения.

10 + 10 + 10 + 10 = 40

Получилось число 40.

Ну а второй пример мы решим, воспользовавшись переместительным свойством умножения. Мы поменяли местами множители, и теперь 4 умножаем на 10. Но при этом ответ останется прежним. Произведение чисел 4 и 10 равно 40. Посмотрите на ответы этих примеров:

При умножении чисел 4 и 10 в ответе записана цифра 4 и справа от неё — 0.

Запомните, ребята: Для того чтобы любое число умножить на 10, нужно справа от этого числа приписать 0.

Ну, а теперь давайте поговорим о делении.

Вы уже знаете, как связаны между собой действия умножения и деления. На одном из предыдущих уроков мы составляли примеры на деление на основе умножения. И вот что у нас получилось:

Я надеюсь, вы помните, что если произведение двух множителей разделить на один из них, то получится другой множитель.

А теперь давайте составим примеры на деление из решённых нами задач и примеров на умножение. Решение первой задачи выглядело так:

Вспоминаем правило: Делим произведение на первый множитель 3, получается второй множитель — 10. А теперь произведение делим на второй множитель 10, получается первый множитель — 3.

Теперь вспомним вот этот пример:

Выполняем деление:

Ну, вот и подходит к концу наша встреча. Но прежде, чем попрощаться, я ещё раз хочу напомнить вам, ребята те правила, которые помогут вам быстро и без ошибок решать задачи и примеры, в которых есть умножение на 10 и деление на 10 или с ответом 10.

·                   Для того чтобы любое число умножить на 10, нужно справа от этого числа приписать 0.

·                   Если делимое — круглое число, а делитель — однозначное число, равное числу десятков в делимом, то в частном получится 10.

·                   Если делимое — круглое число, а делитель — 10, то в частном получится однозначное число, равное числу десятков в делимом.

А я прощаюсь с вами, ребята. Но скоро мы обязательно встретимся!

Предыдущий урок 35 Связь между компонентами и результатом действия умножения

Следующий урок 37 Задачи с величинами: цена, количество, стоимость


Получите полный комплект видеоуроков, тестов и презентаций Математика 2 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Изменение результатов действий в зависимости от изменения компонентов.

Вопрос об изменении результатов арифметических действий в зависимости от изменения данных имеет большое значение: он тесно связан с постепенной подготовкой детей к усвоению понятия функции, которое играет важную роль в современной математике. С понятием функциональной зависимости ученики сталкиваются с самого начала обучения арифметике, уже в I классе при изучении таблицы сложения, где сумма чисел является функцией слагаемых. На это надо обращать внимание детей, составляя с ними таблицу сложения. Так, составив таблицу прибавления единицы к числам первого десятка

1 + 1 = 2
2 + 1 = 3
3 + 1 = 4

нужно обратить внимание детей на то, что в этой таблице результаты последовательно увеличиваются на единицу (2, 3, 4 …), и поставить это увеличение в зависимость от увеличения первого слагаемого.

Для этой же цели должна быть использована и таблица умножения. Так, составив таблицу умножения числа 3, полезно рассмотреть с учениками, как изменяются произведения в зависимости от изменения множителя:

3 х 2= 6
3 х 3= 9
3 х 4 = 12

Сравнивая, например, произведения первой и третьей строк — 6 и 12, дети заметят, что 12 больше 6 в 2 раза. Это увеличение недопоставить в связь с увеличением в 2 раза множителя: 4 больше 2 в 2 раза.

В последующих классах хорошим материалом для иллюстрации изменения произведения в зависимости от изменения данных является зависимость площади прямоугольника от длины его сторон, объема прямоугольного параллелепипеда от длины его сторон, числового значения величины от принятой единицы измерения.

Заслуживает внимания система подготовительных упражнений, разработанная доцентом Ленинградского пединститута им. Герцена М.А. Байтовой. Эта система направлена на подготовку учеников I — III классов к усвоению изменения результатов действий в зависимости от изменения компонентов. Приведем ее здесь полностью.

В нашем опыте, — пишет М. А. Бантова, — предлагались с этой целью такие пары примеров, которые позволяют предвидеть, в котором из них ответ будет больше или меньше и на сколько больше или меньше.

Приведем несколько пар примеров для каждого класса.

В I классе уже при изучении первого десятка предлагаются детям пары примеров на сложение и вычитание, до решения которых ученик устанавливает, в котором из них ответ будет больше (меньше) и почему. Вот эти пары примеров:

4 + 3 5 + 3 8 — 2 8—5

4 + 5 2 + 3 6 — 2 8 — 3

Во II классе задания усложняются. Например, к паре примеров:

30 + 14

30 + 12

Учитель предлагает такие вопросы:

В котором примере ответ больше? Почему?
На сколько больше ответ первого примера, чем второго?
Найдите ответ первого примера.
Найдите ответ второго примера, используя ответ первого.

Аналогичные вопросы ставятся к следующим парам примеров:

37 + 18   15 + 24   40 — 8   61 — 7   70 — 12    81 — 9
42 + 18   15 + 19   42 — 8   58 — 7   70 —  8     81 — 15

Во II классе даются пары примеров на умножение. До решения этих примеров учащиеся также устанавливают, в котором примере ответ больше и на сколько больше. При этом надо исходить из определения произведения как суммы одинаковых слагаемых. Так, для пары примеров 12 х 3 надо установить, в котором из них ответ 12 х 4 больше и на сколько больше. Учитель предлагает записать каждый пример в виде суммы одинаковых слагаемых:

12 х 3 = 12 + 12 + 12;

12 х 4 = 12 + 12 + 12 + 12

Теперь легко установить, на сколько ответ второго примера больше, чем первого.

Такие же вопросы ставятся к следующим парам примеров:

8 х 6 7 х 4 15 х 4 8 х 12 14 х 3
8 х 7 7 х 6 15 х 3 7 х 12 14 х 5

В III классе предлагают пары примеров, аналогичные рассмотренным, но с многозначными числами. Кроме того, в этом классе полезно предлагать задания, обратные по отношению к рассмотренным, например:

18 + П(кв) = 40
18 + П(кв) = 48

Учитель предлагает вопросы:

  1. В котором примере второе слагаемое больше и почему?
  2. На сколько больше? 
  3. Чему равно второе слагаемое в первом примере? 
  4. Найдите второе слагаемое во втором примере, используя первый пример.

Такие же вопросы ставят и при решении следующих пар примеров:

П + 140 = 380 П + 390 = 600 П -60=180
П + 140 = 320 П + 480 =600 П – 60 = 240
360 – П = 80 860 – П = 580 П – 70 = 340
360 – П =120 740 – П =580 П – 90 = 340

Приведем несколько пар примеров на умножение.

356 х 8 870 х 33 86 х 15 58 х 14 81 х 12 68 х 18
356 х 9 870 х 32 87 х 15 57 х 14 81 х 14 68 х 16

35 х 3 + 35 х 7 89 х 9 + 89 95 х 99 + 95
35 х 3 + 35 х 6 89 х 10 95 х 100 – 95
63 х 15 76 х 11 32 х 17
63 х 10 + 63 х 5 76 х 12 – 76 32 х 20 – 32 х 3.

Такого рода упражнения дают учащимся хорошую подготовку к усвоению точных формулировок, в которых находит свое выражение изменение результатов действий в зависимости от изменения данных».

В старших классах начальной школы знания учеников по этому вопросу приводят в систему: им предлагают числовые примеры, они наблюдают их, изменяют числа, сравнивают данные с результатами и делают выводы.

Приведем примеры такой работы.

При изменении суммы сначала показывается, что каждая единица, прибавленная к слагаемому, входит в сумму:

15 + 5 = 20
16 + 5 = 21

После этого рассматривается изменение суммы от прибавления к слагаемому нескольких единиц, от вычитания из одного слагаемого сначала одной, потом нескольких единиц, от одновременного увеличения одного слагаемого и уменьшения другого слагаемого на одинаковое число единиц, например:

14 + 6 = 20;
12 + 8 = 20.

Каждая пара примеров подробно разбирается и после этого делаются выводы:

  1. Если слагаемое увеличить на несколько единиц, то и сумма увеличится, на столько же единиц.
  2. Если слагаемое уменьшить на несколько единиц, то и сумма уменьшится на столько же единиц.
  3. Если одно слагаемое увеличить, а другое уменьшить на одно и то же число, то сумма не изменится.

Эти выводы применяются на практике в устных вычислениях, когда приходится одно или оба слагаемых округлять, а также при решении задач.

После выводов учащиеся и сами составляют примеры, иллюстрирующие изменение суммы в зависимости от изменения слагаемых.

Аналогичную работу проводят и по изучению изменения разности в зависимости от изменения уменьшаемого и вычитаемого. Нужно учитывать, что характер изменения разности в зависимости от изменения вычитаемого усваивается учащимися не без труда, поэтому выводы, делаемые на основе числовых примеров, надо подкреплять фактами и примерами из жизни.

Изменение произведения рассматривают в зависимости от увеличения и уменьшения сомножителей в несколько раз. Сначала рассматривают и анализируют три пары примеров, в -которых изменяется множимое:

1) 8 х 5 = 40    2) 4 х 3 = 1.2   3) 12х.2 = 24
   16 х 5 = 80      20 х 3 = 60       36 х 2 = 72

На основе рассмотрения этих примеров делается вывод:

Если множимое увеличить в несколько раз, то и произведение увеличится во столько же раз.

Дальше рассматриваются случаи изменения произведения в связи с уменьшением множимого в несколько раз:

1)10 х 4 = 40   2)12 х 6 = 72    3)24 х 2 = 48
   5 х 4 = 20          4 х 6 = 24        6 х 2 = 12

На основе наблюдения и анализа этих примеров делается вывод: если множимое уменьшить в несколько раз, то и произведение уменьшится во столько же раз.

Следующий этап работы: изменение множителя, сначала увеличение, а потом уменьшение в несколько раз — и формулировка соответствующих выводов. Выводы закрепляются путем решения вопросов и задач.

Примеры вопросов:

  1. Множимое 20, множитель 5; найти произведение. Каково будет произведение, если множимое увеличить в 3 раза? Если множитель увеличить в 4 раза?
  2. Множимое увеличено в 5 раз. Что сделается с произведением? Множитель уменьшен в 2 раза. Что сделается с произведением?

Пример задачи. Два самолета вылетели с аэродрома. Один из них пролетел 1200 км. Сколько, километров пролетел за то же время другой самолет, если его скорость была вдвое больше?

При решении этой задачи учащиеся рассуждают так: сравним скорости первого и второго самолетов. Скорость второго самолета в 2 раза больше скорости первого. Значит, множимое во втором случае в 2 раза больше множимого в первом случае. А если множимое больше в 2 раза, то и произведение, или расстояние, тоже в 2 раза больше.

Вторая задача. За несколько тетрадей ученик заплатил 36 коп. Сколько денег заплатит ученик, если купит по той же цене в 3 раза больше тетрадей? В этой задаче множитель увеличен в З раза, а значит и произведение, то есть стоимость, будет в 3 раза больше.

Изменение частного рассматривается в том же плане, как и изменение произведения. Сначала изучается изменение частного в зависимости от увеличения и уменьшения делимого. Объяснение дается на задачах, а потом и на примерах.

Задача. Обыкновенный пассажирский самолет пролетел за 4 часа 1600 км. Реактивный самолет за то же время пролетел 3200 км. Во сколько раз больше километров пролетел второй самолет, чем первый, в 1 час?

1600 км : 4 = 400
3200 км : 4 = 800

Сопоставляя обе строки, ученики устанавливают, что во второй строке делимое больше в 2 раза, поэтому и частное больше в 2 раза. Изменение частного поясняется и на примерах:

1) 15: 5= 3      2) 21 : 7 =3
    90 : 5 = 18      63 : 7 = 9

На основе анализа задачи и примеров делается вывод: Если делимое увеличить в несколько раз, то и частное увеличится во столько же раз.

Учащиеся сами составляют по 2 — 3 примера, подтверждающие это положение.

В таком плане рассматриваются задачи и примеры на уменьшение делимого и делается вывод: если делимое уменьшить в несколько раз, то и частное уменьшится во столько же раз.

Сложнее обстоит дело с изменением частного в зависимости от изменения делителя. На этом случае изменения следует остановиться более подробно, дать больше иллюстраций и жизненных примеров.

Для выяснения этой зависимости может служить следующая задача: Один мальчик разложил 12 карандашей в 2 коробки, другой— в 4 коробки. У которого мальчика в коробке карандашей будет меньше и во сколько раз? Решение этой задачи записывается в две строчки:

12 : 2 = 6
12 : 4 = 3

Выясняется, что делитель во втором примере увеличен в 2 раза, поэтому частное уменьшилось в 2 раза. Такая зависимость подтверждается и на других примерах и задачах.

Полезно проиллюстрировать это положение на чертеже: взять 2 равных отрезка в 12 см каждый и разделить первый отрезок на 3 части, а второй на 6 частей. Отсюда следует вывод: если делитель увеличить в несколько раз, то частное уменьшится во столько же раз.

На аналогичных примерах и задачах объясняется увеличение частного при уменьшении делителя.

Нетрудно видеть, что все эти упражнения являются прекрасным материалом для накопления у детей функциональных представлений и развития функционального мышления.

алгебраических выражений. Порядок операций

Навыки
в н
A L G E B R A

Содержание | Дом

1

Четыре операции и их знаки

Функция скобок

«Условия» и «факторы»

Степени и показатели

Порядок операций

Раздел 2 :

Ценности и оценки

Переменные

Написание алгебраических выражений

АЛГЕБРА — ЭТО ПИСЬМЕННЫЙ НАВЫК. Это означает, что писатель решает проблему четко, эффективно и с наименьшим объемом текста. Как и любой навык — вождение автомобиля, выпечка печенья, игра на гитаре — он требует практики. Письменная практика. Тем не менее, давайте начнем.

Первое, что нужно отметить, это то, что в алгебре мы используем буквы так же, как и числа. Но буквы обозначают цифры. Мы имитируем правила арифметики буквами, потому что имеем в виду, что правило будет верным для любые номеров.

Вот, например, алгебраическое правило сложения дробей:


  +  б
в 		  =   а + б
    в

Буквы a и b означают: цифры , находящиеся в числителях. Буква c означает: число в знаменателе. Правило означает:

«Что бы это ни было, сложите числители
и запишите их сумму над общим знаменателем.»

Алгебра говорит нам, как решить любую задачу, которая выглядит как .

В конце концов, символы для чисел — 1, 2, 3 — не что иное, как письменные знаки. А так письма. Как ученик увидит, алгебра зависит от образует , которые принимают символы. То, что вы видите выше, называется формальным правилом для сложения дробей.

Цифры — это числовые символы, а буквы — буквенные символы.

Вопрос 1.  Каковы четыре арифметических операции, и

какие признаки их работы?

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай проблему сам!

1)    Дополнение:   a + b . Знак операции + и называется знаком плюс . Читать a + b как « a плюс b ».
1)    Например, если a представляет 3, а b представляет 4, то a + b представляет 7.
2)    Вычитание:   a − b . Знак операции — и называется знаком минус . Читать a − b как « a минус b ».
1)    Если a представляет, например, 8, а b представляет 2, то a − b представляет 6.

3)   Умножение:   a ·  b . Читать a ·  b как « a  умножить на b ».

Знак умножения в алгебре — точка в центре. Мы не используем крест умножения ×, потому что не хотим перепутать его с буквой x .

Итак, если a представляет 2, а b представляет 5, то

a ·   b = 2 ·  5 = 10.

«2 умножить на 5 равно 10».

Не путайте точку в центре — 2 · 5 , которая в США означает умножение — с десятичной точкой:  2 . 5.

Однако мы часто опускаем точку умножения и пишем просто ab . Читать « a , b «. Другими словами, когда между двумя буквами или между буквой и числом нет знака операции, это всегда означает умножение. 2 x  означает 2 раза x .

4)    Подразделение:   а
б 		. Читать а
б 		 как « a разделить на b «.

В алгебре мы используем горизонтальную черту деления. Если 9Например, 0035 a  представляет 10, а b представляет 2, тогда

а
б 		 =   10
 2		   =  5.

«10 разделить на 2 будет 5.»

Примечание:  В алгебре мы называем a + b «суммой», даже если мы не называем ответ. Как увидит учащийся, мы называем что-то в алгебре просто по тому, как оно выглядит как . На самом деле вы увидите, что вы делаете алгебру глазами, а дальше следует то, что вы пишете на бумаге.

Точно так же мы называем a − b разностью, ab произведением и частным.

Этот знак = конечно же знак равенства, и мы читаем это —

=

— как « a  равно (или равно) b «.

Это означает, что число слева, которое представляет a , равно числу справа, которое представляет b . Если мы напишем

а + б = в ,

и если a представляет 5, а b  представляет 6, то c должно представлять 11.

Вопрос 2. Какова функция скобок () в алгебре?

3 + (4 + 5)       3(4 + 5)

Скобки означают, что мы должны рассматривать то, что они заключают в себе
, как одно число.

3 + (4 + 5) = 3 + 9 = 12.     3(4 + 5) = 3 ·   9 = 27.

Примечание:  Если между 3 и (4 + 5) нет знака операции, это означает умножение.

Задача 1.   Как в алгебре написать

?

а) 5 умножить на 6? 5 · 6

б)   x умножить на y ? ху

  в)   x разделить на y ? х

г) х плюс 5 плюс х минус 2?

( х + 5) + ( х — 2)

д)   х плюс 5   умножить на   x минус 2?

( х + 5)( х — 2)

Задача 2.   Различите следующее:

а)  8 – (3 + 2)         б)  8 – 3 + 2

а) 8 — (3 + 2) = 8 — 5 = 3.

б) 8 — 3 + 2 = 5 + 2 = 7.

В а) мы рассматриваем 3 + 2 как одно число. В б) мы не делаем. Мы должны сначала вычесть 3, а затем добавить 2. (Но см. порядок операций ниже.)

Существует распространенное заблуждение, что скобки всегда означают умножение. Фактически, в Уроке 3 мы увидим, что мы используем круглые скобки, чтобы отделить знак операции от знака алгебры. 8 + (−2).

Вопрос 3. Условия и факторы.

Когда числа добавляются или вычитаются, они называются терминами.

Когда числа умножаются, они называются множителями.

Вот сумма четырех слагаемых:   а − б + в − г .

В алгебре мы говорим о «сумме» терминов, даже если есть вычитания. Другими словами, все, что выглядит как то, что вы видите выше, мы называем суммой.

Вот произведение четырех множителей:   abcd .

Слово делитель всегда означает умножение.

И снова мы говорим о «продукте» abcd , хотя мы не называем ответ.

Задача 3. Сколько терминов в следующем выражении? И сколько множителей у каждого члена?

2 a + 4 ab + 5 a ( b + c )

Есть три термина. 2 a — первый термин. Он имеет два множителя:
2 и a .
4 ab — второй член. Имеет три множителя: 4, a и b .
И 5 a ( b + c ) — все это один термин. Он также имеет три множителя: 5, a и
( b + c ). Круглые скобки означают, что мы должны рассматривать все, что заключено в них, как одно число.

Степени и показатели

Когда все факторы равны — 2 · 2 · 2 · 2 — мы называем произведение степенью этого множителя. Таким образом, · называется второй степенью числа или « в квадрате». a · a · a есть третья степень числа a , или « a в кубе». аааа равно а в четвертой степени и так далее. Мы говорим, что в само по себе является первой степенью в .

Теперь вместо того, чтобы писать aaaa , мы пишем a один раз и поместите маленькую 4:

4 (« до 4″)

Эта маленькая 4 называется показателем степени. Он указывает количество повторений и в качестве коэффициента.

8 3  («8 в третьей степени» или просто «8 в третьей степени») означает 8 ·  8 ·  8.

Задача 4.   Назовите первые пять степеней числа 2. 2, 4, 8, 16, 32.

Задача 5.   Прочитайте, а затем рассчитайте каждое из следующих действий.

а) 5 2 «5 во второй степени» или «5 в квадрате» = 25,

.

б)   2 3 «2 в третьей степени» или «2 в кубе» = 8,

.

в)   10 4 «10 до четвертого» = 10 000.

г)   12 1 «12 к первому» = 12.

Однако в алгебре принято не писать показатель степени 1.

= 1 = 1 .

Учащийся должен следить за тем, чтобы не спутать 3 и , что означает 3 , умноженное на , и , с и 3 , что означает , умноженное на .

3 а = и + и + и , Урок 9арифметики
а 3 = · · .

Вопрос 4.   При наличии нескольких операций

8 + 4(2 + 3) 2 — 7,

какой порядок операций?

Прежде чем ответить, отметим, что, поскольку знание естественных наук является причиной, по которой студенты должны изучать алгебру; а поскольку порядки операций появляются только в определенных формах, то на этих страницах мы представляем только те формы, с которыми учащийся может столкнуться в реальной алгебраической практике. Знак деления ÷ никогда не используется в научных формулах, только черта деления. Крест умножения × используется только в экспоненциальной записи, поэтому учащийся никогда не увидит следующее:

3 + 6 × (5 + 3) ÷ 3 − 8.

Такая задача была бы чисто академической, т. е. упражнением ради самого себя. Это не имеет практической ценности. Это никуда не ведет.

Порядок операций следующий:

(1)   Оцените скобки, если они есть, и если они требуют оценки.
 
(2)  Оцените степени, то есть показатели степени.
 
(3) Умножать или делить — не важно.
 
(4) Добавить или вычесть.

В примерах 1 и 2 ниже мы увидим, в каком смысле мы можем прибавить или вычесть . А в примере 3 мы встретим умножение на или разделить.

Примечание:  «Оценить» означает назвать и написать число.

Пример 1.    8 + 4(2 + 3) 2 − 7

Сначала оценим скобки, то есть заменим 2+3 на 5:

= 8 + 4 ·  5 2 − 7

Так как теперь есть только одно число, 5, скобки писать не нужно.

Обратите внимание, что мы преобразовали один элемент, круглые скобки, и переписали все остальные.

Затем оцените показатели степени:

= 8 + 4 · 25 − 7

Теперь умножьте:

= 8 + 100 — 7

Наконец, прибавьте или вычтите , это не будет иметь значения. Если мы сначала добавим:

= 108 − 7 = 101,

Хотя если сначала вычесть:

8 + 100 — 7 = 8 + 93 = 101.

Пример 2.   100 − 60 + 3.

Первый:

100 − 60 + 3 означает ли , а не , 100 − 63.

Только при наличии скобок —

100 − (60 + 3)

— можем ли мы рассматривать 60 + 3 как одно число. При отсутствии скобок задача означает вычесть 60 из 100, затем прибавить 3:

100 − 60 + 3 = 40 + 3 = 43.

На самом деле не имеет значения, прибавляем мы сначала или вычитаем сначала,

100 — 60 + 3 = 103 — 60 = 43.

Когда мы подойдем к числам со знаком, мы увидим, что

100 − 60 + 3 = 100 + (−60) + 3.

Порядок, в котором мы их «добавляем», значения не имеет.

Пример 3.     11 ·  35
    5

Нет скобок для оценки и показателей степени. Далее по порядку умножаем или делим на . Мы можем сделать и то и другое — мы получим тот же ответ. Но обычно более искусно сначала делить, потому что тогда у нас будут меньшие числа для умножения. Поэтому сначала разделим 35 на 5:

11 ·  35
    5		   =   11 ·  7
    =   77.

См.: Навыки арифметики, свойство 3 раздела.

Пример 4.   ½(3 + 4)12  = ½ ·  7 ·  12.

Порядок множителей не имеет значения: abc = bac = cab и так далее. Поэтому мы можем сначала сделать ½ ·  12.  То есть мы можем сначала разделить 12 на 2:

½ ·  7 ·  12 = 7 ·  6 = 42.

(см. урок 27 арифметики, вопрос 1.)

Пример 5. Полоса разделения. 8 + 20
10 − 3

В любой задаче с делением, прежде чем мы сможем разделить, мы должны оценить верх и низ в соответствии с порядком операций. Другими словами, мы должны интерпретировать верх и низ как заключенные в круглые скобки.

8 + 20
10 − 3		    означает    (8 + 20)
(10 — 3)		 .

Теперь действуем как обычно и сначала оцениваем скобки. Ответ: 4.

Проблема 6.   Оцените каждое из следующих действий в соответствии с порядком операций.

   а)   3 + 4 · 5 =   б)   2 + 3 · 4 + 5 =
 
  3 + 20 = 23   2 + 12 + 5 = 19
 
   в)   4 + 5 (2 + 6) =   г)   (4 + 5) (2 + 6) =
 
  4 + 5 · 8 = 4 + 40 = 44       9 · 8 = 72
   e)    11 · 10
   5		   е)    ½(3 + 4)8 =
 
  11 · 2 = 22
Сначала мы можем разделить.		   ½ · 7 · 8 = 7 ·  4 = 28.
(½ ·  8 = 4) Навыки арифметики:  Урок 27, вопрос 1
   г)     2 + 2 · 3 2
14 − 3 ·  2 2  		  =  2 + 2 · 9
14 − 3 · 4		  =  2 + 18
14 − 12		  =  20
 2		  =  10.

Раздел 2 :

Ценности и оценки

Переменные

Написание алгебраических выражений

Содержание | Дом

Copyright © 2021 Лоуренс Спектор

Вопросы или комментарии?

Электронная почта:  [email protected]


Открытые учебники | Siyavula

Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.

Математика

    • Читать онлайн

    • Учебники

      • Английский

          • 7A PDF (CC-BY-ND)
          • 7B PDF (CC-BY-ND)

      • Африкаанс

          • 7A PDF (CC-BY-ND)
          • 7B PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

      • Английский

          • 8A PDF (CC-BY-ND)
          • 8B PDF (CC-BY-ND)

      • Африкаанс

          • 8A PDF (CC-BY-ND)
          • 8B PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

      • Английский

          • 9A PDF (CC-BY-ND)
          • 9B PDF (CC-BY-ND)

      • Африкаанс

          • 9A PDF (CC-BY-ND)
          • 9B PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

      • Английский

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

      • Африкаанс

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

    • Пособия для учителей

      • Английский

          • PDF (CC-BY-ND)

      • Африкаанс

          • PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

      • Английский

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

      • Африкаанс

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

    • Пособия для учителей

      • Английский

          • PDF (CC-BY-ND)

      • Африкаанс

          • PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

      • Английский

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

      • Африкаанс

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

    • Пособия для учителей

      • Английский

          • PDF (CC-BY-ND)

      • Африкаанс

          • PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

      • Английский

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

      • Африкаанс

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

    • Пособия для учителей

      • Английский

          • PDF (CC-BY-ND)

      • Африкаанс

          • PDF (CC-BY-ND)

Наука

    • Читать онлайн

    • Учебники

      • Английский

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

      • Африкаанс

          • PDF (CC-BY-ND)

    • Пособия для учителей

      • Английский

          • PDF (CC-BY-ND)

      • Африкаанс

          • PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

      • Английский

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

      • Африкаанс

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

    • Пособия для учителей

      • Английский

          • PDF (CC-BY-ND)

      • Африкаанс

          • PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

      • Английский

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

      • Африкаанс

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

    • Пособия для учителей

      • Английский

          • PDF (CC-BY-ND)

      • Африкаанс

          • PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

      • Английский

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

      • Африкаанс

          • PDF (CC-BY-ND)
          • ePUB (CC-BY-ND)
          • ePUB (CC-BY)

    • Пособия для учителей

      • Английский

          • PDF (CC-BY-ND)

      • Африкаанс

          • PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

    • Пособия для учителей

      • Английский

        • Класс 7А

          • PDF (CC-BY-ND)

        • Класс 7Б

          • PDF (CC-BY-ND)

      • Африкаанс

        • Граад 7А

          • PDF (CC-BY-ND)

        • Граад 7Б

          • PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

    • Пособия для учителей

      • Английский

        • Класс 8А

          • PDF (CC-BY-ND)

        • Класс 8Б

          • PDF (CC-BY-ND)

      • Африкаанс

        • Граад 8А

          • PDF (CC-BY-ND)

        • Граад 8Б

          • PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

    • Пособия для учителей

      • Английский

        • Класс 9А

          • PDF (CC-BY-ND)

        • Класс 9Б

          • PDF (CC-BY-ND)

      • Африкаанс

        • Граад 9А

          • PDF (CC-BY-ND)

        • Граад 9Б

          • PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

    • Пособия для учителей

      • Английский

        • Класс 4А

          • PDF (CC-BY-ND)

        • Класс 4Б

          • PDF (CC-BY-ND)

      • Африкаанс

        • Граад 4А

          • PDF (CC-BY-ND)

        • Граад 4Б

          • PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

    • Пособия для учителей

      • Английский

        • Класс 5А

          • PDF (CC-BY-ND)

        • Класс 5Б

          • PDF (CC-BY-ND)

      • Африкаанс

        • Граад 5А

          • PDF (CC-BY-ND)

        • Граад 5Б

          • PDF (CC-BY-ND)
    • Читать онлайн

    • Учебники

    • Пособия для учителей

      • Английский

        • Класс 6А

          • PDF (CC-BY-ND)

        • Класс 6Б

          • PDF (CC-BY-ND)

      • Африкаанс

        • Граад 6А

          • PDF (CC-BY-ND)

        • Граад 6Б

          • PDF (CC-BY-ND)

Лицензирование наших книг

Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:

CC-BY-ND (фирменные версии)

Вам разрешается и поощряется свободное копирование этих версий. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.

Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.

CC-BY (версии без торговой марки)

Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula.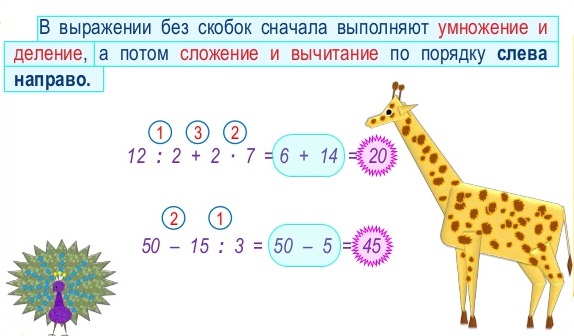 Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.

Умножение и деление рациональных чисел

В этом уроке мы познакомимся с умножением и делением рациональных чисел.

Как умножать рациональные числа

Правила умножения целых чисел верны и для рациональных чисел. Другими словами, чтобы умножать рациональные числа, вы должны уметь умножать целые числа.

Также необходимо знать основные законы умножения, такие как коммутативный закон умножения, ассоциативный закон умножения, распределительный закон умножения и закон умножения на ноль.

Пример 1. Найдите значение выражения

Это умножение рациональных чисел с разными знаками. Чтобы умножить рациональные числа с разными знаками, умножьте их модули и перед результатом поставьте знак минус.

Чтобы ясно видеть, что мы имеем дело с числами с разными знаками, заключим в скобки каждое рациональное число вместе с его знаками

Модуль

равен , а модуль . Перемножив эти модули как положительные дроби, мы получили ответ , но перед ответом поставили знак минус. Чтобы поставить этот минус перед результатом, умножение модулей производилось в скобках, а минус ставился перед результатом.

Таким образом, значение выражения

равно

Короткое решение выглядит следующим образом:

Пример 2. Найдите значение выражения  

Это умножение рациональных чисел с разными знаками. Перемножьте модули этих чисел и поставьте перед ответом минус:

Решение для этого примера можно записать в более короткой форме:

Пример 3. Найдите значение выражения

Это умножение отрицательных рациональных чисел. Чтобы умножить отрицательные рациональные числа, умножить их модули и поставить перед ответом знак плюс

Решение для этого примера можно записать в более короткой форме:

Пример 4. Найти значение выражения

Это умножение отрицательных рациональных чисел. Умножьте модули этих чисел и поставьте плюс перед ответом

Решение для этого примера можно записать в более короткой форме:

Пример 5. Найдите значение выражения

Это умножение рациональных чисел с разными знаками. Перемножьте модули этих чисел и поставьте перед ответом минус

Короткое решение будет выглядеть намного проще:

Пример 6. Найдите значение выражения

Преобразуем смешанное число

в неправильную дробь. Перепишем остальное как есть

Мы получили умножение рациональных чисел с разными знаками. Перемножьте модули этих чисел и поставьте перед ответом минус. Запись с модулями можно пропустить, чтобы не перегружать выражение

Решение для этого примера можно записать в сокращенной форме

Пример 7. Найдите значение выражения  

Это умножение рациональных чисел с разными знаками. Перемножьте модули этих чисел и поставьте перед ответом минус

Сначала ответом была неправильная дробь

, но мы извлекли из нее целую часть. Обратите внимание, что вся часть была извлечена из модуля дроби. Полученное смешанное число помещалось в круглые скобки с минусом перед ним. Это было сделано для выполнения требования правила. А правило требовало, чтобы полученному ответу предшествовал минус.

Решение для этого примера можно записать в более короткой форме:

Пример 8. Найдите значение выражения

Выражение состоит из нескольких факторов. Согласно ассоциативному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислять выражение в любом порядке.

Сначала умножаем

на

и и умножаем полученное число на оставшееся число 5. Опустим модули, чтобы не загромождать выражение.

Первое действие:

Второе действие:

Ответ: значение выражения

равно −2.

Пример 9. Найдите значение выражения:

Преобразуем смешанные числа в неправильную дробь:

Мы получили произведение отрицательных рациональных чисел. Перемножьте модули этих чисел и поставьте перед ответом плюс. Запись с модулями можно пропустить, чтобы не перегружать выражение

Пример 10. Найдите значение выражения

Выражение состоит из нескольких множителей. Согласно ассоциативному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислять выражение в любом порядке.

Поэтому посчитаем это выражение слева направо в порядке множителей. Опустим запись с модулями, чтобы не загромождать выражение

Первый акт:

Второй акт:

Третий акт:

. 11. Найдите значение выражения

Вспомните закон умножения на ноль. Этот закон гласит, что произведение равно нулю, если хотя бы один из множителей равен нулю.

В нашем примере один из множителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения

равен нулю:

Пример 12. Найдите значение выражения

Произведение равно нулю, если хотя бы один из множителей равен нулю.

В нашем примере один из множителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения

равно нулю

Пример 13. Найти значение выражения

Можно воспользоваться порядком операций и сначала вычислить выражение в скобках

и умножьте ответ на дробь .

Можно также использовать распределительный закон умножения — умножить каждое слагаемое суммы

на дробь и сложить результаты. Вот как мы будем использовать это.

Согласно порядку операций, если выражение содержит сложение и умножение, то сначала должно выполняться умножение. Поэтому в полученном новом выражении мы заключаем в скобки дроби, которые следует умножать. Таким образом, мы можем четко видеть, какие действия выполнять сначала, а какие позже:

Далее вычисляем выражение по действиям. Сначала мы рассчитываем выражения в скобках и добавляем результаты

Первый акт:

Второй акт:

Третий акт:

6.

равно

Решение для этого примера можно записать в гораздо более короткой форме. Это будет выглядеть так:

Как видите, этот пример можно решить даже в уме. Поэтому следует выработать навык анализа выражения, прежде чем приступать к его решению. Вполне вероятно, что вы сможете решить ее в уме и сэкономите массу времени и нервов. А на зачетах и ​​экзаменах, как известно, время стоит очень дорого.

Пример 14. Найдите значение выражения -4,2 × 3,2

Это умножение рациональных чисел с разными знаками. Перемножьте модули этих чисел и поставьте минус перед ответом

Обратите внимание, как умножались модули рациональных чисел. В этом случае, чтобы умножать модули рациональных чисел, нужно было уметь умножать десятичные дроби.

Пример 15. Найдите значение выражения -0,15 × 4

Это умножение рациональных чисел с разными знаками. Перемножьте модули этих чисел и поставьте перед ответом минус

Обратите внимание, как умножались модули рациональных чисел. В этом случае, чтобы перемножить модули рациональных чисел, нужно было уметь перемножать десятичное и целое число.

Пример 16. Найдите значение выражения -4,2 × (-7,5)

Это умножение отрицательных рациональных чисел. Перемножьте модули этих чисел и поставьте перед ответом плюс

Как делить рациональные числа

Деление рациональных чисел сводится к умножению одинаковых чисел. Для этого первую дробь умножают на обратную вторую дробь. Затем применяются правила умножения рациональных чисел.

Пример 1. Выполнить деление:

Умножить первую дробь на обратную вторую дробь. Обратное ко второй дроби равно

. Умножьте на нее первую дробь:

Мы получили умножение рациональных чисел с разными знаками. И мы уже умеем вычислять такие выражения. Для этого нужно перемножить модули заданных рациональных чисел и поставить перед полученным ответом минус.

Закончим этот пример до конца. Вы можете пропустить запись с модулями, чтобы не перегружать выражение

Таким образом, значением выражения

  является  

Подробное решение выглядит следующим образом:

Краткое решение можно записать следующим образом:

Пример 2. Выполнить деление  

Умножить первую дробь на обратную вторую дробь. Обратное ко второй дроби равно 9.0003

. Умножьте на нее первую дробь:

Краткое решение можно записать следующим образом:

Пример 3. Выполнить деление

Умножить первую дробь на обратную вторую дробь. Обратное ко второй дроби:

Мы получили произведение отрицательных рациональных чисел. Выполним это умножение. Запись с модулями можно пропустить, чтобы не перегружать выражение:

Пример 4. Выполнить деление

В этом случае умножьте первое число -3 на обратную дробь

.

Обратная дробь

равна . Затем применим правило умножения рациональных чисел с разными знаками:

Пример 6. Выполнить деление

Умножить первую дробь на число, обратное 4.

Число, обратное 4, является дробью 9.0003

. Умножьте на него первую дробь.

Пример 5. Выполнить деление

Умножить первую дробь на число, обратное -3

Обратное -3 является дробью

Пример значения выражения -14,4 : 1,8

Это деление рациональных чисел с разными знаками. Чтобы вычислить это выражение, разделите модуль делителя на модуль делителя и перед ответом 9 поставьте знак минус.0003

Обратите внимание, как модуль делителя был разделен на модуль делителя. В этом случае нам нужно было иметь возможность делить десятичную дробь на другую десятичную дробь.

Если нет желания работать с десятичными дробями (что бывает часто), эти десятичные дроби можно преобразовать в смешанные числа, затем можно преобразовать эти смешанные числа в неправильную дробь, а потом уже заниматься непосредственно делением.

Вычислите предыдущее выражение -14,4 : 1,8 таким образом. Превратите десятичные дроби в смешанные числа:

Теперь преобразуем эти смешанные числа в неправильную дробь:

Теперь мы можем разделить дробь

на дробь . Для этого умножьте первую дробь на дробь, обратную второй дроби:

Пример 7. Найдите значение выражения

Преобразуйте десятичную -2,06 в неправильную дробь и умножьте эту дробь на обратную вторую дробь:

Пример 8. Найдите значение выражения -7.2 : (-0.6)

Это деление отрицательных рациональных чисел. Чтобы сделать это деление, умножьте первую дробь на обратную вторую дробь.

Переместите запятую в обеих дробях на одну цифру вправо, чтобы получить деление дробный тире. Например, выражение

можно записать следующим образом:

В чем разница между выражениями

и ? На самом деле, нет никакой разницы. Эти два выражения имеют одинаковый смысл и могут быть приравнены:

В первом случае знаком деления является двоеточие и выражение записывается в одну строку. Во втором случае деление дробей пишется дробным тире. В результате получается дробь, которая называется сложной дробью 9.2217 .

При встрече с такими сложными дробями необходимо применять те же правила деления правильных дробей. Первую дробь нужно умножить на обратную вторую дробь.

Использовать такие дроби в решении крайне неудобно, поэтому можно писать их в понятной форме, используя в качестве знака деления двоеточие вместо дробной черты.

 

Например, запишем сложную дробь

в понятной форме. Для этого нам сначала нужно разобраться, где первая дробь, а где вторая дробь, потому что сделать это правильно не всегда получается. Сложные дроби могут иметь несколько дробей, которые могут сбивать с толку. Основная дробная черта, отделяющая первую дробь от второй, обычно длиннее остальных.

После определения основной дробной черты можно легко разобраться, где первая дробь, а где вторая дробь:

И тогда можно воспользоваться методом деления дробей — умножить первую дробь на обратную вторую .

Пример 2. Запишем сложную дробь

в понятной форме

Найдите главную дробную черту (она самая длинная) и убедитесь, что целое число -3 делится на обыкновенную дробь

.

А если мы по ошибке приняли вторую дробную строку за основную (более короткую), то получилось бы, что мы делим дробь

на целое число 5

В этом случае, даже если это выражение будет рассчитано правильно, задача не будет решена правильно, потому что делителем в данном случае является число -3, а делителем является дробь

.

Пример 3. Запишем многоэтажную дробь

в понятной форме

Найдите главную дробную черту (она самая длинная) и убедитесь, что дробь

делится на целое число 2

И если бы мы ошибочно приняли первую дробную строку за основную (более короткую), то получилось бы, что мы делим целое число -5 на дробь

В этом случае, даже если это выражение будет вычислено правильно, задача не будет решена правильно, потому что делитель в данном случае дробь

, а делитель — целое число 2.

Несмотря на то, что со сложными дробями неудобно работать, мы будем сталкиваться с ними очень часто, особенно при изучении высшей математики.

Естественно, для преобразования сложных дробей в понятную форму требуется дополнительное время и место. Поэтому мы можем использовать более быстрый метод. Этот способ удобен и дает готовое выражение, в котором первая дробь умножается на обратную вторую.

Этот метод реализован следующим образом:

Если дробь состоит из четырех этажей, например

, то номер первого этажа повышается до верхнего этажа. И цифра на втором этаже идет до третьего этажа. Полученные цифры следует соединить знаками умножения ( × )

В результате, минуя промежуточное обозначение

, получаем новое выражение, в котором первая дробь уже умножается на дробь, обратную второй. Это очень удобно!

Во избежание ошибок при использовании этого метода можно следовать следующему правилу:

От первого к четвертому. Со второго на третий.

Правило относится к «уровням». Фигуру с первого «уровня» следует поднять на четвертый «уровень». А фигуру со второго «уровня» надо поднять на третий «уровень».

Попробуем вычислить сложную дробь

по приведенному выше правилу.

Итак, число на первом «уровне» поднимается до четвертого «уровня», а число на втором «уровне» поднимается до третьего «уровня»

В результате обходя промежуточное обозначение

получаем новое выражение, в котором первая дробь уже умножается на дробь, обратную второй. Тогда мы можем использовать имеющиеся знания:

Пример 4. Попробуем вычислить сложную дробь

по новой схеме.

Есть только первый, второй и четвертый «уровень». Третий «уровень» отсутствует. Но мы не отходим от основной схемы: поднимаем фигуру с первого «уровня» на четвертый «уровень». А так как третий «уровень» отсутствует, то оставляем цифру на втором «уровне» как

В результате обхода промежуточной записи

имеем новое выражение, в котором первое число -3 уже умножается на дробь, обратную второму. Далее мы можем использовать имеющиеся знания:

Пример 5. Попробуем вычислить сложную дробь

по новой схеме.

Есть только второй, третий и четвертый «уровни». Первый «уровень» отсутствует. Поскольку первый «уровень» отсутствует, нам не нужно подниматься на четвертый «уровень», но мы можем поднять число со второго «уровня» на третий:

В результате, минуя промежуточное обозначение

, мы имеем новое выражение, в котором первая дробь уже умножается на число, обратное делителю. Далее мы можем использовать имеющиеся знания:

Использование переменных

Если выражение сложное и вы думаете, что оно запутает вас при решении задачи, вы можете поместить его часть в переменную и затем работать с этой переменной.

Математики часто так делают. Они разбивают сложную проблему на более простые подзадачи и решают их. Затем собирают решенные подзадачи в единое целое. Это творческий процесс, и для его изучения требуются годы напряженной практики.

Применение переменных оправдано при работе со сложными дробями. Например:

Найдите значение выражения  

Итак, в числителе есть дробное выражение, а в знаменателе — дробное выражение. Иными словами, мы снова сталкиваемся со сложной дробью, которую так не любим.

Выражение в числителе

можно записать в переменную с любым именем, например:

А вот в математике в таком случае принято называть переменные большими латинскими буквами. Не будем нарушать эту традицию, и обозначим первое выражение заглавной латинской буквой — А

А выражение в знаменателе

можно обозначить заглавной латинской буквой — В

Теперь наше исходное выражение

принимает вид . То есть мы заменили числовое выражение буквенным, предварительно введя числитель и знаменатель в переменные А и В.

Теперь мы можем вычислить отдельно значения переменной A и значение переменной B. Подставляем готовые значения в выражение

.

Найдем значение переменной A

Найдем значение переменной B

Теперь подставим их значения в основное выражение

вместо переменных A и B:

Получилась сложная дробь, в которой можно использовать схему « от первого к четвертому, от второго к третьему », то есть ту цифру, которая находится на первом «уровне», поднять до четвертый «уровень», а фигуру, которая находится на втором «уровне», поднять до третьего «уровня». Дальнейший расчет не слишком сложен:

Таким образом, значение выражения

равно -1.

Конечно, мы рассмотрели самый простой пример, но наша цель состояла в том, чтобы увидеть, как мы можем использовать переменные, чтобы упростить себе задачу и минимизировать ошибки.

Также обратите внимание, что решение для этого примера можно написать без использования переменных. Это будет выглядеть так

Это решение быстрее и короче, и в данном случае его лучше было бы написать так, но если выражение получится сложным, состоящим из нескольких параметров, скобок, корней и степеней, целесообразно вычислять его в несколько приемов, закладывая часть его выражений в переменные.

Упражнения

Задача 1. Выполните умножение:

Решение:

Показать решение

Задача 2. Выполните умножение:

Решение:

Показать решение

9216.

Решение:

Показать решение

Задача 4. Выполнить умножение:

Решение:

Показать решение

Задача 5. Выполнить умножение:

Решение:

Показать решение

Задача 6. Выполнить умножение:

Решение:

Показать решение

Задача 7. Выполните умножение:

Решение:

Покажите решение

    6666666666666. Выполнить умножение:

    Решение:

    Показать решение

    Задача 9. Выполнить деление:

    Решение:

    Показать решение

    Задача 10. Выполнение Дивизии:

    Решение:

    Show Solution

    Задача 11. Выполнение Дивизии:

    Решение:

    Показать решение

    Задача 12. Задача 13. Выполнить деление:

    Решение:

    Показать решение

    Задача 14. Выполнить разделение:

    Решение:

    Показать решение

    Задача 15. Выполнение Дивизии:

    Решение:

    Show Solution

    Задача 16. Выполнение Отделение:

    Решение:

    Показать решение

    Задача 17. Выполнение Дивизии:

    Решение:

    Показать Решение

    Задание 18. Вычислить выражение:

    Решение:

    Показать Решение

    Задание 19. Вычислить выражение:

    Решение:

    Показать решение

    Задача 20. Рассчитайте выражение:

    Решение:

    Показать решение

    Задача 21. Рассчитайте выражение:

    Решение:

    Покажите решение

    . выражение:

    Решение:

    Показать решение

    Задача 23. Запишите следующую сложную дробь через двоеточие и вычислите:

    Решение:

    Показать решение

    Задача 24. Запишите следующую сложную дробь через двоеточие и вычислите:

    Решение:

    Показать решение

    Задание 25. Запишите следующую сложную дробь через двоеточие и вычислите:

    Решение:

    3 Показать решение

    Задание 26. Используя метод « От первого к четвертому, от второго к третьему », запишите следующую дробь как умножение и вычислите:

    Решение:

    Покажите решение

    Задача 27. Используя метод « От первого к четвертому, от второго к третьему », запишите следующую дробь в виде умножения и вычислите:

    Решение:

    Покажите решение

    Задача 28. Методом « От первого к четвертому, от второго к третьему » запишите в виде умножения следующую дробь и вычислите:

    Решение:

    Показать решение

    Задача 29. Методом « От первого к четвертому, от второго к третьему » запишите в виде умножения следующую дробь и вычислите:

    Решение:

    Показать решение

    Задание 30. Найдите значение выражения:

    Решение:

    Показать решение

    Задача 31. Найти значение выражения:

    Решение:

    Показать решение

    Задача 32. 9 Найти значение выражения0003

    Решение:

    Показать решение

    Задача 33. Найти значение выражения:

    Решение:

    Показать решение

    Видео урок

    Введение в арифметику