Как делить со скобками, что вперед: деление или умножение, как решить 36:3(8–6) дробь 6, правильный ответ на пример | sterlitamak1.ru
Сможете решить правильно?
Иллюстрация: Юрий Орлов / NGS.RU
Поделиться
Минимум неделю в интернете миллионы людей ломают копья из-за простенького, на первый взгляд, примера. NGS.RU решил задачку вместе с кандидатом физико-математических наук, доцентом и преподавателем Новосибирского государственного университета Ильей Марьясовым.
Вот этот пример: 36 : 3 (8 − 6) дробь 6.
Некоторые люди готовы спорить часами, как решить этот пример
Фото: Александра Бруня / NGS.RU
Поделиться
— Подвоха здесь особо никакого нет. У нас в математике есть соглашение о том, как у нас должны выполняться арифметические операции. Умножение и деление имеют более высокий приоритет, чем сложение и вычитание. Когда нужно изменить порядок вычисления, чтобы сложение и вычитание выполнялись раньше, то используются скобки. И еще один момент — когда появляются дроби, а дробная черта — это деление, то в этом случае оно выполняется в последнюю очередь, — объяснил Илья Марьясов
Когда нужно изменить порядок вычисления, чтобы сложение и вычитание выполнялись раньше, то используются скобки. И еще один момент — когда появляются дроби, а дробная черта — это деление, то в этом случае оно выполняется в последнюю очередь, — объяснил Илья Марьясов
Разбираемся с числителем. По очереди идут деление, умножение, вычитание — при этом последняя операция идет в скобках. Начинаем решать слева направо.
— Поскольку деление и умножение равноправны. Сначала 36 делим на 3 и получаем 12. Потом мы должны выполнить умножение, но поскольку вычитание стоит в скобках, то сначала делаем его. Из 8 вычитаем 6 и получаем 2. Теперь делаем умножение. Мы 12 умножаем на 2 и получаем 24. Теперь делим числитель на знаменатель. То есть 24 делим на 6 и получаем 4, — объяснил специалист.
Правильный ответ — 4.
— Как изучают математику в школе. В начальном звене вводят операции — сложение, вычитание, умножение и деление. Примерно до 6-го класса дети не знают, что существуют рациональные числа, которые записываются в виде дробной черты. Когда они вводятся, то выясняется, что операцию деления можно записать не в виде двух точек. И до самого вуза очень часто все выражения записываются, как дробное число и отдельная операция деления через две точки редко используется. Так умножение у людей фиксируется как приоритетная операция, — объяснил Илья Марьясов.
Примерно до 6-го класса дети не знают, что существуют рациональные числа, которые записываются в виде дробной черты. Когда они вводятся, то выясняется, что операцию деления можно записать не в виде двух точек. И до самого вуза очень часто все выражения записываются, как дробное число и отдельная операция деления через две точки редко используется. Так умножение у людей фиксируется как приоритетная операция, — объяснил Илья Марьясов.
В итоге это приводит к ошибке в вычислениях.
— У людей возникает соблазн 3 умножить на 8 минус 6 (то есть на 2) и получается у них 6. Потом 36 делят на 6, получая 6. И в итоге 6 делят на 6 и выходит 1. Это неверный ответ в данном случае, — отметил математик.
Ранее в Высшей школе экономики подсчитали, что средний проходной балл ЕГЭ для поступления в вузы снизился впервые за 10 лет. Предлагаем вам ответить на несколько вопросов (разных лет) из того самого итогового среза знаний.
По теме
20 января 2023, 16:00
Один и тот же пример в разных странах решают по-разному. Как это получается?
Как это получается?18 декабря 2022, 13:30
«Любите ли вы сплетничать?» Журналист попытался обмануть детектор лжи, и вот что обнаружил полиграф19 сентября 2022, 10:00
Это точно русский? Проверьте, сможете ли вы написать правильно все эти слова18 декабря 2022, 14:00
Русский не родной? 10 простейших слов, которые все пишут с ошибками
Александра Бруня
Корреспондент
МатематикаРазборРешениеПример
- ЛАЙК0
- СМЕХ0
- УДИВЛЕНИЕ0
- ГНЕВ0
- ПЕЧАЛЬ0
Увидели опечатку? Выделите фрагмент и нажмите Ctrl+Enter
КОММЕНТАРИИ0
Что я смогу, если авторизуюсь?
Новости РЎРњР?2
Новости РЎРњР?2
Умножение3
21
перемножить в любом порядке.
Методически данное
правило имеет целью подготовить ребенка
к знакомству со способами умножения в
столбик чисел, оканчивающихся нулями,
поэтому с ним знакомятся только в
четвертом классе. Реально данное
свойство умножения позволяет
рационализировать устные вычисления
как во 2, так и в 3 классе.
Реально данное
свойство умножения позволяет
рационализировать устные вычисления
как во 2, так и в 3 классе.
Например:
Вычисли: (7 • 2) • 5 = …
В данном случае намного легче вычислить вариант
7 • (2 • 5) = 7 • 10 — 70.
Вычисли: 12 • (5 • 7) = …
8 данном случае намного легче вычислить вариант (12-5)-7 = 60-7 = 420.
Приемы вычислений
1. Умножение и деление чисел, оканчивающихся нулем: 20 • 3; 3 • 20; 60 : 3; 80 : 20
20 • 3 =… 3 • 20 =… 60:3 = …
2 дес. • 3 = 20 • 3 = 60 б дес.: 3 = 2 дес.
20 — 3 = 60 3 • 20 = 60 60: 3 = 20
Для случая 80:20
может быть использовано два способа
вычислений: тот, что использовался
в предыдущих случаях, и способ подбора
частного.
Например: 80: 20 =… 80 : 20 =…
8 дес.: 2 дес. = 4 или 20 • 4 = 80
80: 20 = 4 80: 20 = 4
В первом случае использовался прием представления двузначных десятков в виде разрядных единиц, что сводит рассматриваемый случай к табличному (8:2). Во втором случае цифра частного находится подбором и проверяется умножением. Во втором случае ребенок возможно не сразу подберет верную цифру частного, это означает, что проверка будет выполнена не один раз.
2. Прием умножения двузначного числа на однозначное: 23 • 4; 4-23
При умножении двузначного числа на однозначное актуализируются следующие знания и умения:
В случае умножения вида 4 • 23 сначала применяется перестановка множителей, а затем та же схема умножения, что и выше.
3. Прием деления
двузначного числа на однозначное: 48:3;
48:2
Прием деления
двузначного числа на однозначное: 48:3;
48:2
При делении двузначного числа на однозначное актуализируются следующие знания и умения:
В случае 48:2 = (40 + 8) : 2, а дальше аналогично предыдущему случаю. разрядные слагаемые
4. Прием деления двузначного числа на двузначное: 68 : 17
При делении двузначного числа на двузначное необходимы следующие знания и умения:
68: 17 =
Сложность последнего
приема состоит в том, что ребенок не
может сразу подобрать нужную цифру
частного и выполняет несколько проверок
подобранных цифр, что требует достаточно
сложных вычислений. Многие дети тратят
много времени на выполнение вычислений
этого вида, поскольку начинают не столько
подбирать подходящую цифру частного,
сколько перебирают все множители подряд,
начиная с двух.
1) ориентировка на последнюю цифру делимого;
2) прием округления.
Первый прием предполагает, что при подборе возможной цифры частного ребенок ориентируется на знание таблицы умножения, сразу перемножая подобранную цифру (число) и последнюю цифру делителя.
Например, 3-7 = 21. Последняя цифра числа 68 — это 8, значит нет смысла умножать 17 на 3, последняя цифра делителя все равно не совпадает. Пробуем в частном число 4 — умножаем 7 • 4 = 28. Последняя цифра совпадает, значит имеет смысл найти произведение 17 • 4.
Второй прием предполагает округление делителя и подбор цифры частного с ориентиром на округленный делитель.
Например, 68:17
делитель 17 округляется до 20. Примерная
цифра частного 3 дает при проверке
20 • 3 = 60 < 68, значит имеет смысл сразу
проверять в качестве цифры частного
4:17 • 4 = 68.
Эти приемы позволяют сократить затраты сил и времени при выполнении вычислений данного вида, но требуют хорошего знания таблицы умножения и умения округлять числа.
Целые числа, оканчивающиеся цифрами 0,1,2,3,4, округляют до ближайшего целого десятка, отбрасывая эти цифры.
Например, числа 12, 13, 14 следует округлять до 10. Числа 62, 63, 64 округляют до 60.
Целые числа, оканчивающиеся цифрами 5, 6, 7,8,9, округляют до ближайшего целого десятка в большую сторону.
Например, числа 15,16,17,18,19 округляют до 20. Числа 45,47, 49 округляют до 50.
Порядок действий в выражениях, содержащих умножение и деление
Правила порядка выполнения действий задают основные признаки выражений, на которые следует ориентироваться при вычислении их значений.
Первые правила, определяющие порядок действий в арифметических выражениях, задавали порядок действий в выражениях, содержащих действия сложения и вычитания:
1. В выражениях
без скобок, содержащих только действия
сложения и вычитания, действия выполняются
в том порядке, как они записаны: слева
направо.
В выражениях
без скобок, содержащих только действия
сложения и вычитания, действия выполняются
в том порядке, как они записаны: слева
направо.
2. Действия в скобках выполняют первыми.
3. Если выражение содержит только действия сложения, то два соседних слагаемых всегда можно заменить их суммой (сочетательное свойство сложения).
В 3 классе изучаются новые правила порядка выполнения действий в выражениях, содержащих умножение и деление:
4. В выражениях
без скобок, содержащих только умножение
и деление, действия выполняются в том
порядке, как они записаны: слева направо.
5. В выражениях без скобок умножение и деление выполняются раньше, чем сложение и вычитание.
При этом установка
на выполнение действия в скобках первым
сохраняется. Возможные случаи нарушения
этой установки были оговорены ранее.
Правила порядка выполнения действий являются общими правилами вычислений значений математических выражений (примеров), которые сохраняются на протяжении всего периода изучения математики в школе. В связи с этим формирование у ребенка четкого понимания алгоритма порядка выполнения действий является важной преемственной задачей обучения математике в начальной школе. Проблема заключается в том, что правила порядка выполнения действий являются достаточно вариативными и не всегда однозначно заданными.
Например, в выражении 48-3 + 7 + 8 следует по общей установке применять правило 1 для выражения без скобок, содержащего действия сложения и вычитания. В то же время, как вариант рациональных вычислений, можно использовать прием замены суммой части 7 + 8, поскольку после вычитания числа 3 из 48 получится 45, к чему удобно прибавить 15.
Однако подобный
разбор такого выражения в начальных
классах не предусмотрен, поскольку
есть опасения, что при неадекватном
понимании такого подхода ребенок будет
применять его в случаях вида 72 — 9 — 3 + 6. В данном случае замена выражения 3 + 6
суммой невозможна, она приведет к
неверному ответу.
В данном случае замена выражения 3 + 6
суммой невозможна, она приведет к
неверному ответу.
Большая вариативность в применении всей группы правил и вариантов правил при определении порядка действий требует значительной гибкости мышления, хорошего понимания смысла математических действий, последовательности мыслительных действий, математического «чутья» и интуиции (математики называют это «чувство числа»). Реально намного проще приучить ребенка жестко соблюдать четко установленный порядок анализа числового выражения с точки зрения тех признаков, на которые ориентировано каждое правило.
Определяя порядок действий, рассуждай так:
1) Если есть скобки, выполняю первым действие, записанное в скобках.
2) Выполняю по порядку умножение и деление.
3) Выполняю по порядку сложение и вычитание.
Данный алгоритм
задает порядок действий достаточно
однозначно, хотя и с небольшими
вариациями.
После выполнения умножения и деления в данном примере можно было сразу к 54 прибавить 6, а из 18 вычесть 9, пбсле чего результаты сложить. Технически было бы значительно легче, чем путь, обусловленный алгоритмом, возможен изначально другой порядок действий в примере:
Таким образом, вопрос о формировании умения определять порядок действий в выражениях в начальной школе определенным образом противоречит необходимости обучать ребенка способам рациональных вычислений.
Например, в случае порядок действий определен алгоритмом абсолютно однозначно, при этом требует отребенка сложнейших вычислений в уме с переходами через разряд: 42 — 7 и 35 + 8.
2 1 3
 Этот
путь вычислений противоречит установке
данного в учебнике
Этот
путь вычислений противоречит установке
данного в учебникеЧто происходит? Свойства умножения и деления
Цель
Этот модуль развивает у учащихся умение распознавать закономерности (непротиворечивость) в уравнениях, включающих умножение и деление целых чисел.
Цели достижения
NA4-8: Обобщить свойства умножения и деления целых чисел.
Разработка АО и другие учебные ресурсы
Конкретные результаты обучения
- Описать и представить переместительное свойство умножения
- Описать и представить распределительное свойство умножения, обращая внимание на разрядное значение
- Признать, что умножение и деление являются обратными операциями, и интерпретировать деление как равное деление или измерение.
- Найти отношения в разности полных квадратов, например. 7 х 7 = 49, поэтому 8 х 6 = 48.
Описание математики
Этот модуль развивает у учащихся способность распознавать закономерности (непротиворечивость) в уравнениях умножения и деления, содержащих целые числа. Образцы пар уравнений воплощают важные свойства умножения и деления, такие как коммутативность, дистрибутивность и обратное. Учащиеся учатся представлять конкретные примеры использования свойств, а затем приводить убедительные аргументы в пользу того, почему свойства сохраняются при любых обстоятельствах.
Образцы пар уравнений воплощают важные свойства умножения и деления, такие как коммутативность, дистрибутивность и обратное. Учащиеся учатся представлять конкретные примеры использования свойств, а затем приводить убедительные аргументы в пользу того, почему свойства сохраняются при любых обстоятельствах.
Важным следствием этого является то, что учащиеся учатся рассматривать переменные как обобщенные числа и выражать отношения между целыми числами при умножении и делении.
В этом разделе мы основываемся на исследованиях Деборы Шифтер и ее коллег о развитии алгебраического мышления. Шифтер работает в Центре развития образования, некоммерческой исследовательской организации в США. Ее подход состоит из нескольких шагов, которые можно связать с «возвращением назад» в модели концептуального развития Пири-Кирена, обычно используемой в новозеландских классах.
Этапы подхода следующие:
В этом разделе требования составляются с помощью наборов уравнений, включающих умножение и деление. Наборы направлены на развитие у учащихся понимания свойств умножения (коммутативность, дистрибутивность, ассоциативность, тождество и инверсия). Расширив наборы уравнений, включив в них деление, учащиеся узнают, как эти свойства сохраняются или не сохраняются при изменении операции.
Наборы направлены на развитие у учащихся понимания свойств умножения (коммутативность, дистрибутивность, ассоциативность, тождество и инверсия). Расширив наборы уравнений, включив в них деление, учащиеся узнают, как эти свойства сохраняются или не сохраняются при изменении операции.
Возможности для адаптации и дифференциации
Возможности обучения в этом модуле можно различать, предоставляя или удаляя поддержку учащихся и изменяя требования к заданиям. Сложность задач может варьироваться по-разному, включая:
- использование физических объектов для соединения числовых и операционных символов, включая равенство, с преобразованиями величин
- моделирование математических процедур (например, демонстрация умножения и деления с использованием равных множеств и массивов)
- поощрение учащихся к совместной работе в партнерстве (махи-тахи)
- предоставление доступа к калькуляторам для подтверждения ответов и переключения внимания на причины возникновения шаблонов
- , ограничивающий домен исследуемых номеров.
 Например, учащиеся могут сначала работать с фактами, которые они знают или находятся в зоне своего изучения. Выталкивание примеров за пределы известных фактов может помочь учащимся увидеть силу отношений, которые они исследуют, например. 12 х 33 легче решить, чем 4 х 99.
Например, учащиеся могут сначала работать с фактами, которые они знают или находятся в зоне своего изучения. Выталкивание примеров за пределы известных фактов может помочь учащимся увидеть силу отношений, которые они исследуют, например. 12 х 33 легче решить, чем 4 х 99. - дает полезные подсказки о «скрытых» местах в комнате
- демонстрация работ учащихся в качестве моделей для других
- , предоставляющий форматы для записи этого процесса.
Контексты для этого модуля строго математические, но используемые материалы могут быть адаптированы. Физические предметы, которые имеют значение для ваших учеников, могут быть лучше использованы, чем стандартное математическое оборудование. Например, если у вас есть большой набор ракушек для экологических исследований, вы можете использовать эти ракушки в качестве материалов. Контексты могут возникать из предпочтительных материалов. Кайтиакитанга (охрана окружающей среды) может поддерживаться поиском умных способов подсчета количества определенного животного или птицы или кусочков римурапы (водорослей), найденных на участке пляжа, или парапаре (усоногих ракушек), найденных прикрепленными к камням во время отлива. . Whānaungatanga (семейные) ценности могут включать в себя поиск справедливых и равноправных способов поделиться добытыми моллюсками. Обратите внимание, что равные доли, предполагаемые в операции разделения, не всегда соответствуют ценностям справедливого распределения.
. Whānaungatanga (семейные) ценности могут включать в себя поиск справедливых и равноправных способов поделиться добытыми моллюсками. Обратите внимание, что равные доли, предполагаемые в операции разделения, не всегда соответствуют ценностям справедливого распределения.
Словарные термины Te reo Māori, такие как ahuatanga koaro (переместительное свойство, ahuatanga tohatoha (распределительное свойство), koaro (обратное), whakawhanui (обобщения), tauwehe (фактор) и otinga (продукт) могут быть введены в этот модуль и использоваться на протяжении всего прочее математическое обучение
Требуемые ресурсы
- Квадратные плитки, соединяющие кубы
- Стоимость материалов
- Калькуляторы (дополнительно)
- Бумага с квадратной сеткой
- Копи-мастер 1
- PowerPoint 1
Упражнение
Все уроки в этом разделе проходят в той же последовательности фаз, что и на показанной диаграмме фазового подхода. Плакат с этапами предоставляется учащимся в качестве копирайтера 1. В примечаниях предлагаются возможные идеи учащихся и реакции учителей на эти ответы. Невозможно предвидеть все идеи, которые могут предложить учащиеся. Будьте гибкими в том, как вы отвечаете студентам, вместо того, чтобы сосредотачиваться на обучении представленным образцам идей и представлений.
В примечаниях предлагаются возможные идеи учащихся и реакции учителей на эти ответы. Невозможно предвидеть все идеи, которые могут предложить учащиеся. Будьте гибкими в том, как вы отвечаете студентам, вместо того, чтобы сосредотачиваться на обучении представленным образцам идей и представлений.
PowerPoint 1 содержит семь наборов уравнений, которые управляют устройством. Наборы могут стать основой недельного блока. Фазы для каждого набора уравнений описаны ниже. Наборы помечены в верхнем левом углу каждого слайда для справки.
Пары уравнений. Набор одинСлайд 1 содержит первый шаблон, на который следует обратить внимание. Образец включает коммутативное свойство, то есть a x b = b x a, с которым учащиеся должны быть знакомы. Он используется в качестве примера для ознакомления учащихся с подходом.
- Замечание регулярности
Используйте принцип «подумай, сопоставь, поделись», предложив учащимся самостоятельно рассмотреть четыре примера, определить недостающие значения, а затем поделиться своими идеями с партнером. В ходе обсуждения в классе ожидайте, что учащиеся будут выражать свои наблюдения способами, понятными другим. Студенты должны повторно выражать свои идеи, если другие не понимают, что они говорят. Возможно, вам придется напомнить учащимся, что «что-то происходит» относится ко всем четырем примерам, а не только к одному. Ожидайте ответов типа:
В ходе обсуждения в классе ожидайте, что учащиеся будут выражать свои наблюдения способами, понятными другим. Студенты должны повторно выражать свои идеи, если другие не понимают, что они говорят. Возможно, вам придется напомнить учащимся, что «что-то происходит» относится ко всем четырем примерам, а не только к одному. Ожидайте ответов типа:
С: Цифры просто перевернуты, например, 9 х 4 становится 4 х 9.
Т: Можно поконкретнее? Какие числа перевернуты?
S: Числа умножаются каждый раз.Обсуждение открывает возможность использования правильных математических терминов, таких как множитель (умножаемое число) и произведение (ответ на умножение).
S: Продукты (ответы) всегда одни и те же.
Т: Все четыре модели имеют один и тот же продукт? Что ты имеешь в виду?
СУБЪЕКТ: Нет. Продукты остаются теми же, когда факторы переворачиваются.
- Формулировка утверждения
Предложите учащимся сформулировать утверждение о том, что происходит со всеми четырьмя примерами в первом шаблоне. Сначала они могут делать это индивидуально, а затем работать в небольших группах над уточнением своих идей и способов их выражения. Поощряйте модель махи-тахи, в которой учащиеся работают совместно. Возможные идеи могут включать:
Сначала они могут делать это индивидуально, а затем работать в небольших группах над уточнением своих идей и способов их выражения. Поощряйте модель махи-тахи, в которой учащиеся работают совместно. Возможные идеи могут включать:
Если коэффициенты те же, а вы меняете их местами, продукт не меняется.
Первый фактор меняется местами со вторым фактором. Продукт тот же.Стремитесь, чтобы учащиеся выражали свои утверждения четкими, минимальными терминами, используя правильный математический язык. Например, «поворот» не так ясен, как «порядок факторов». Вы можете сравнить различные высказывания групп студентов, чтобы подчеркнуть важность такого ясного языка. Здесь можно сделать ссылки на написание объяснений (т. е. необходимость быть четкими, информативными и краткими).
- Репрезентация
На этом этапе учащиеся выбирают репрезентации, чтобы показать, почему закономерность сохраняется. Учащиеся могут выбирать физические манипуляции, такие как связывание кубов или счетчиков, рисовать диаграммы, такие как числовые линии или массивы, и использовать контексты из повседневной жизни. Предложите учащимся начать с первых двух примеров пар уравнений, а затем подумать, как одни и те же отношения могут быть обобщены на последнюю и другие подобные пары уравнений.
Предложите учащимся начать с первых двух примеров пар уравнений, а затем подумать, как одни и те же отношения могут быть обобщены на последнюю и другие подобные пары уравнений.
Примеры могут быть:- Сначала я сделал 7 x 5 из кубиков. Затем я взял по одному кубику из каждой группы из пяти кубиков, чтобы получилась группа из семи кубиков. Я обнаружил, что могу составить пять стопок по семь кубиков из семи групп по пять кубиков.
- Я нарисовал 7 x 5 в виде массива. Пятерки были колоннами. Когда я перевернул массив, семерки стали столбцами, но общее количество кубов осталось прежним.
- Сначала я сделал 7 x 5 из кубиков. Затем я взял по одному кубику из каждой группы из пяти кубиков, чтобы получилась группа из семи кубиков. Я обнаружил, что могу составить пять стопок по семь кубиков из семи групп по пять кубиков.
- Некоторые представления менее полезны, чем другие, с точки зрения понимания структуры коммутативного свойства. Например, переходы на числовой строке не показывают, как каждый элемент в наборе используется для формирования новых наборов. Учащимся важно понимать, что многократное сложение не является умножением, хотя они получают одно и то же число.
 В Новой Зеландии при обучении умножению множитель является первым множителем, а множимое — вторым множителем. В других странах учат наоборот, поэтому ожидайте, что некоторые студенты будут сбиты с толку.
В Новой Зеландии при обучении умножению множитель является первым множителем, а множимое — вторым множителем. В других странах учат наоборот, поэтому ожидайте, что некоторые студенты будут сбиты с толку. - Ваш вопрос важен для того, чтобы помочь учащимся соединить символы и другие представления.
- Объясните, где в вашем изображении находятся 7 и 5.
- Если вы начинаете с 7 x 5, почему вы можете сделать только пять подходов по семь?
- Что представляют собой 5 и 7 в 5 x 7?
- Как ваше представительство показывает, что продукт остался прежним?
- Построение аргумента
На этом этапе учащихся просят формализовать свое «замечание», создав утверждение, которое можно обобщить на все случаи. Обсуждение может начаться с конкретной пары уравнений, но должно быть расширено, чтобы описать, что происходит в целом.
S: В 7 x 5 по одному из каждых пяти составляет набор из семи. Поскольку в наборах пять, это означает, что можно составить ровно пять семерок.
Поскольку в наборах пять, это означает, что можно составить ровно пять семерок.
T: Так как же это работает с 9 x 4, 8 x 99 и 5 х 36?Это может привести к выражению свойства в общих чертах.
S: Первый множитель, умноженный на второй множитель, дает то же произведение, что и второй множитель, умноженный на первый множитель.
Т: Если бы мы дали имена первому и второму факторам, например, a и b, можно ли было бы выразить это свойство проще?Некоторые учащиеся могут экспериментировать с алгебраическими обозначениями, такими как a x b = c, поэтому b x a = c, или могут использовать символы (например, смайлики), чтобы упростить свое мышление. Обратите внимание, что это представляет исходные пары уравнений. Как правило, «а наборов b» можно реконструировать — это означает, что при взятии одного объекта из каждого набора b создаются наборы размера a. Это можно сделать b раз, в результате чего получится b x a (b наборов a).
T: Нужно ли говорить, что оба уравнения имеют ответ c? Нам нужно с?
СУБЪЕКТ: Мы могли бы просто написать a x b = b x a.
Сосредоточьтесь на классе используемых чисел, т. е. на целых числах. Предложите учащимся исследовать, выполняется ли свойство коммутативности для целых и рациональных чисел, например. Если ½ x 36 = 18, то 36 x ½ = 18.
Попросите учащихся подойти ко второму набору уравнений более независимо. Подумайте о потребностях ваших учеников — возможно, вам будет удобнее работать с небольшими группами и организовывать учащихся в небольшие группы или пары для выполнения этих заданий. С этого момента каждый набор уравнений кратко обсуждается с использованием фаз подхода.
- Замечание регулярности
Четыре уравнения применяют удвоение и деление пополам, утроение и утроение коэффициентов в первом уравнении. Эту стратегию иногда называют пропорциональной корректировкой, поскольку она лежит в основе концепции эквивалентных долей. Завершенные наборы должны быть:
8 x 3 = 24 6 x 10 = 60
4 x 6 = 24 [удвоение 3, вдвое 8] 12 x 5 = 60 [удваивание 6, вдвое 10]9 x 9 = 81 7 x 6 = 42
27 x 3 = 81 [Утроение 9, третье 9] 14 x 3 = 42 [Удвоение 7, уменьшение 6 пополам]
- Формулировка утверждения
Ожидайте, что учащиеся будут использовать фразы из своего разговорного языка, например «когда одно число удваивается, другое уменьшается вдвое». Введите важную лексику, такую как фактор (т. е. все числа, которые делят целое число на 3 и 2 без остатка, являются делителями 6) и произведение (т. е. результат, полученный при умножении чисел). Это поможет уточнить, о каких числах идет речь в формуле изобретения. Если иск ограничивается удвоением и делением пополам, обратите внимание на 9х 9 = 81 и 27 х 3 = 81. Цель состоит в том, чтобы расширить утверждение до эквивалента «один множитель делится на число, n, другой множитель умножается на n. Продукт остается постоянным (один и тот же)».
Введите важную лексику, такую как фактор (т. е. все числа, которые делят целое число на 3 и 2 без остатка, являются делителями 6) и произведение (т. е. результат, полученный при умножении чисел). Это поможет уточнить, о каких числах идет речь в формуле изобретения. Если иск ограничивается удвоением и делением пополам, обратите внимание на 9х 9 = 81 и 27 х 3 = 81. Цель состоит в том, чтобы расширить утверждение до эквивалента «один множитель делится на число, n, другой множитель умножается на n. Продукт остается постоянным (один и тот же)».
- Представление
Предполагается, что будут использоваться как физические, так и схематические представления. Представление стека кубов может выглядеть так:Диаграммы представления «наборов» могут выглядеть так:
Массивы также могут использоваться в качестве мощного представления. Первоначально кубы могли использоваться как единицы площади, что приводило к более абстрактному использованию длин сторон.

- Аргументация
Попросите учащихся обосновать, что данное количество, скажем, 24, может быть получено путем умножения двух множителей, скажем, 4 x 6. Сохраняя наше количество постоянным, один множитель можно разделить на равные части, скажем, каждое 6 делится на три равные части (3 двойки). Теперь этих частей, составляющих 24, в три раза больше. Количество частей, на которые делится фактор, является переменной величиной. Некоторым учащимся может быть удобно использовать метку, например n, для обозначения количества равных частей. Факторы и произведение также являются переменными и могут быть представлены фигурами или буквами. Хотя символическое представление на этом уровне ограничено, алгебраически отношение может быть выражено следующим образом:Предложите учащимся обобщить «отменяющий» характер обратных операций, т. е. деление на n, умножение на n. На этом уровне учащиеся продвигаются к использованию букв для представления переменных.
 Вы также можете ввести частную интерпретацию дробей, например. a÷n может быть выражено как a/ n . Умножение также может быть представлено без символа x, например. a×b может быть представлено как ab .
Вы также можете ввести частную интерпретацию дробей, например. a÷n может быть выражено как a/ n . Умножение также может быть представлено без символа x, например. a×b может быть представлено как ab .
- Замечание регулярности
Четыре уравнения применяют распределительное свойство. Это свойство часто используется при умножении многозначных чисел. Заполненные наборы должны быть:
7 x 10 = 70 5 x 20 = 100
7 x 11 = 77 [Добавление 7 x 1] 5 x 22 = 110 [добавление 5 x 2]9 x 50 = 450 6 x 100 = 600
9 x 53 = 477 [Сложение 9 x 3] 6 x 105 = 630 [Сложение 6 x 5]
- Формулировка утверждения
Ожидайте , что учащиеся будут использовать фразы из своего разговорного языка, например, «добавление стольких-то партий числа». Предложите учащимся использовать математический словарь, такой как фактор и произведение , чтобы уточнить, какие числа упоминаются в формуле изобретения. Возможно, вам придется смоделировать это для студентов. Поощряйте ясность, задавая такие вопросы, как:
Возможно, вам придется смоделировать это для студентов. Поощряйте ясность, задавая такие вопросы, как:
Знаете ли вы, насколько второй товар лучше первого? Как?
Что означает первый фактор? Что означает второй фактор?
Цель состоит в том, чтобы сформулировать утверждение примерно так: «Если ко второму множителю прибавить число, то произведение увеличится на первый множитель, умноженный на это число».
- Представление
Предполагается, что будут использоваться как физические, так и схематические представления. Поскольку в большинстве первых уравнений используются числа, кратные десяти или 100, могут быть полезны блоки позиционных значений (MAB).Диаграммы десятков и сотен могут быть схематичными, чтобы выделить важную структуру.
Массивы иллюстрируют, как первый фактор «воздействует» на второй фактор при его изменении.
- Аргументация
Попросите учащихся обосновать, что два фактора умножаются на данное произведение. Исходный продукт может быть выражен как x b. Добавление числа к b приводит к тому, что второй множитель становится b + n (n — добавляемое число). Произведение увеличивается на a x n. Учащимся важно учитывать, что происходит со всеми четырьмя наборами уравнений, поскольку n является переменной и может быть «любым числом». Учащиеся работают над выражением взаимосвязей между переменными с помощью букв и уравнений. Прогрессу можно способствовать, работая с нотациями, которые учащиеся разрабатывают сами.
Исходный продукт может быть выражен как x b. Добавление числа к b приводит к тому, что второй множитель становится b + n (n — добавляемое число). Произведение увеличивается на a x n. Учащимся важно учитывать, что происходит со всеми четырьмя наборами уравнений, поскольку n является переменной и может быть «любым числом». Учащиеся работают над выражением взаимосвязей между переменными с помощью букв и уравнений. Прогрессу можно способствовать, работая с нотациями, которые учащиеся разрабатывают сами.
Алгебраически отношение может быть выражено как:
a×b так что a×( b+n) =(a×b)+(a×n)
Умножение также может быть представлено без символа x, например a×b можно представить как ab, и ненужные скобки (из-за порядка операций) можно удалить.
аб так что а( б+н) =аб+ан
Четыре набора пар уравнений
- Замечание регулярности
Четыре уравнения используют обратную связь между умножением и делением. Это свойство используется учащимися для решения задач деления по измерению, например. «Сколько x входит в y? Завершенные наборы должны быть:
Это свойство используется учащимися для решения задач деления по измерению, например. «Сколько x входит в y? Завершенные наборы должны быть:
8 x 6 = 48 7 x 3 = 21
48 ÷ 6 = 8 [Экспрессия в разделении] 21 ÷ 3 = 7 [Экспрессия в разделении]12 x 25 = 300 68 x 9 = 612
300 ÷ 25 = 12 [выражается как деление] 612 ÷ 9= 68 [выражается как деление]
- Формулировка утверждения
Ожидается, что в естественном языке учащиеся будут использовать такие фразы, как «факторы подставляются в уравнение деления». Учащиеся могут указать, что они видят на диаграмме.Поощряйте использование математической лексики, такой как фактор и продукт , чтобы уточнить, какие числа упоминаются в формуле изобретения. Возможно, вам придется ввести термины деления, такие как делитель (число, на которое делится), частное (ответ на деление) и делимое (количество делимое). Поощряйте ясность, задавая такие вопросы, как:
Во что превращается второй множитель в уравнении деления? (делитель)
Во что превращается первый множитель в уравнении деления? (частное)
Что означает второй множитель?
Цель состоит в том, чтобы сформулировать утверждение примерно так: «Два фактора умножаются, чтобы получить продукт. Произведение, деленное на один множитель, равняется другому множителю».
Произведение, деленное на один множитель, равняется другому множителю».
- Представление
Предполагается, что будут использоваться как физические, так и схематические представления. Имейте в виду, что учащиеся могут интерпретировать деление двояко: как равное распределение (чаще всего) или как измерение. Любая интерпретация может быть использована для представления уравнений. Вот интерпретация измерения, поскольку 48 ÷ 6 рассматривается как «Сколько шестерок в 48?»Совместное представление интерпретирует 48 ÷ 6 как «48 поровну делится между шестью сторонами. Сколько получает каждая сторона?»
На схематических диаграммах, как и в массивах, коэффициенты представлены в виде длин сторон, а произведение — в виде площади. Недостающее число в уравнении может быть показано как пустая мера на диаграмме.
- Аргументация
Попросите учащихся обосновать, что если произведение a x b является произведением двух множителей a и b, то произведение можно разделить на наборы b или b наборов a. Таким образом, произведение умножения можно рассматривать как дивиденд при делении. Любой множитель может быть делителем, но другой множитель является частным.
Таким образом, произведение умножения можно рассматривать как дивиденд при делении. Любой множитель может быть делителем, но другой множитель является частным.
Постарайтесь, чтобы учащиеся согласились с тем, что факторы и произведение являются переменными, то есть они могут принимать любые значения. Произведение зависит от факторов, поэтому его всегда можно представить как a x b или ab.
Некоторые учащиеся могут использовать представление умножения с повторным сложением, например:7 x 3 означает семь наборов по три, поэтому семь наборов по три можно составить из 21.
a x b означает наборы из b, поэтому наборы из б можно сделать из аб.
- Постарайтесь отучить учащихся от повторного сложения, подкрепив более эффективные стратегии.
Пятый набор пар уравнений
- Замечание регулярности
Набор уравнений применяет пропорциональную корректировку делимого пополам и исследует влияние на частное. Это свойство может быть использовано учащимися для решения задач на деление. Завершенные наборы должны быть:
Это свойство может быть использовано учащимися для решения задач на деление. Завершенные наборы должны быть:
24 ÷ 4 = 6 40 ÷ 5 = 8
12 ÷ 4 = 3 [вдвое снижение дивидендов и коэффициента] 20 ÷ 5 = 4264 ÷ 11 = 24 72 ÷ 9= 8
132 ÷ 11 = 12 144 ÷ 9 = 16
- Формулировка утверждения
Ожидается, что в естественном языке учащиеся будут использовать такие фразы, как «деление числа вдвое уменьшает ответ пополам».
Ожидайте использования математической лексики, связанной с делением, например, делитель (число, на которое делится), частное (ответ на деление) и делимое (количество, на которое делится). Поощряйте ясность, задавая такие вопросы, как:
Что изменится в каждой паре уравнений?
Что останется прежним?
Посмотрите на уравнение четыре. Он отличается от других. Как?
Цель состоит в том, чтобы сформулировать утверждение примерно так: «Умножение или деление делимого на число при неизменном делителе приводит к умножению или делению частного на одно и то же число».
- Представление
Для моделирования отношений в парах уравнений можно использовать как равное распределение, так и интерпретацию измерения деления. Модели наборов, такие как стопки кубов, работают хорошо, но способствуют переходу к схематическим диаграммам, таким как массивы.
Обратите внимание, что четвертая пара уравнений показывает результат умножения делимого и частного на два.
- Аргументация
Ищите учащихся для обоснования, используя слова или диаграммы, а не символы. Если делитель остается прежним, то при делении делимого на число частное делится на то же число. Точно так же умножение делимого на число приводит к тому, что частное также умножается на это число.
Постарайтесь, чтобы учащиеся согласились с тем, что делимое и делитель являются переменными, то есть они могут принимать любые значения.
Имейте в виду, что некоторые учащиеся могут перевести представление многократного сложения умножения в деление следующим образом:8 x 5 означает восемь наборов по пять, что в сумме составляет 40.
 Таким образом, с половиной этого общего числа, 20, можно сделать половину меньшего. много пятерок.
Таким образом, с половиной этого общего числа, 20, можно сделать половину меньшего. много пятерок.
Если факторы рассматривать как переменные, то более общий вывод может быть «доказан» геометрически с помощью массивов.Алгебраически это может быть выражено как: «Если количество b равно ab, то a/ 2 количество b равно половине ab ( ab/ 2 ) .»
Шесть пар уравнений
- Замечание регулярности
Набор уравнений выделяет разницу квадратов. Это свойство может быть использовано учащимися для решения задач на умножение.
9 x 9 = 81 5 x 5 = 250002 20 x 20 = 400 12 x 12 = 144
21 x 19 = 399 [менее 400] 13 x 11 = 143 [один меньше 144] - Формулировка утверждения
Ожидайте , что учащиеся будут использовать фразы из своего разговорного языка, такие как «Первое уравнение имеет тот же множитель, умноженный на себя. Во втором уравнении на единицу больше и на единицу меньше, а ответ на единицу меньше». Попросите учащихся быть более конкретными в своем описании.
Во втором уравнении на единицу больше и на единицу меньше, а ответ на единицу меньше». Попросите учащихся быть более конкретными в своем описании.
Какой коэффициент увеличить на единицу?
Какой множитель уменьшить на единицу?
Верно ли это для всех четырех уравнений?
Цель состоит в том, чтобы сформулировать утверждение примерно так: «Если выбрано число, то умножение числа на единицу меньше числа на единицу больше числа равно квадрату числа меньше единицы».
- Представление
Студенты, скорее всего, будут использовать конкретные примеры, чтобы убедить других в том, как работают отношения.
- Аргументация
Массивы являются полезным представлением для «доказательства» того, что происходит с разностью полных квадратов.В общем, 2 можно пространственно преобразовать в (a-1)(a+1), удалив единицу (1 x 1) и переместив единицу (a-1), чтобы создать прямоугольник со стороной ( а-1) и (а+1).

Студенты не должны использовать алгебраическую запись на этом уровне. Учащиеся с высокими показателями могут захотеть увидеть, что трансформацию можно представить в виде:
( а-1)(а+1) = а 2 -а+ а -1 = а 2 -1
Пары уравнений, седьмой набор
Используйте седьмой набор как возможность увидеть, насколько хорошо учащиеся самостоятельно участвуют в процессе обобщения. Попросите их записывать свои утверждения, представления и аргументы удобным для них способом. Некоторые учащиеся могут предпочесть писать свои работы, в то время как другие предпочитают фиксировать свои идеи с помощью цифрового инструмента записи (например, рисунков Google).
- Замечание регулярности
Набор уравнений выделяет эквивалент деления распределительного свойства. Делимое уменьшается на кратное делителю. Это свойство используется для решения задач деления путем округления дивиденда в большую сторону, например. 76 ÷ 4, вычислив сначала 80 ÷ 4. Завершенные наборы должны быть:
76 ÷ 4, вычислив сначала 80 ÷ 4. Завершенные наборы должны быть:
80 ÷ 8 = 10 60 ÷ 5 = 12
72 ÷ 8 = 9 [один меньший набор 8] 55 ÷ 5 = 11 [один меньший набор из 5]270 ÷ 9 = 30 700 ÷ 7 = 100
261 ÷ 9 = 29 [один меньший набор из 9] 686 ÷ 7 = 98 [два меньше набора 7] - Формулировка утверждения
Ожидайте , что учащиеся будут использовать фразы из своего разговорного языка, например «первое уравнение имеет делимое, деленное на делитель. Во втором уравнении делитель в один или два раза больше делимого, поэтому частное на один или два меньше». Попросите учащихся быть более конкретными в своем описании. Диаграммы могут быть полезны.Задайте такие вопросы, как:
Покажите, как делимое уменьшается на один или два делителя.
Как это влияет на частное?
Верно ли это для всех четырех уравнений?
Утверждение с использованием математического языка может быть примерно таким: «Если делимое уменьшается на единицу, умноженную на делитель, то частное уменьшается на единицу». Обратите внимание, что четвертая пара уравнений уменьшает делимое в два раза больше делителя.
Обратите внимание, что четвертая пара уравнений уменьшает делимое в два раза больше делителя.
- Представление
Учитывая, что дивиденды кратны десяти или 100, подходящим представлением может быть блок разряда (MAB).Схематические диаграммы, как и массивы, обеспечивают более четкое представление о структуре, встречающейся в примерах.
- Аргументация
Имейте в виду, что учащиеся могут вернуться к повторному сложению умножения, чтобы убедить других в правильности своего утверждения. Подтвердите использование этой стратегии и поощряйте учащихся развивать использование «замечания регулярности». Конкретный пример может выглядеть так:
Домашняя ссылка
Уважаемая семья и whānau,
На этой неделе мы изучали свойства умножения и деления. Может ли ваш ребенок объяснить связь между умножением и делением?
Попросите ребенка показать вам некоторые из новых стратегий, которые он изучал.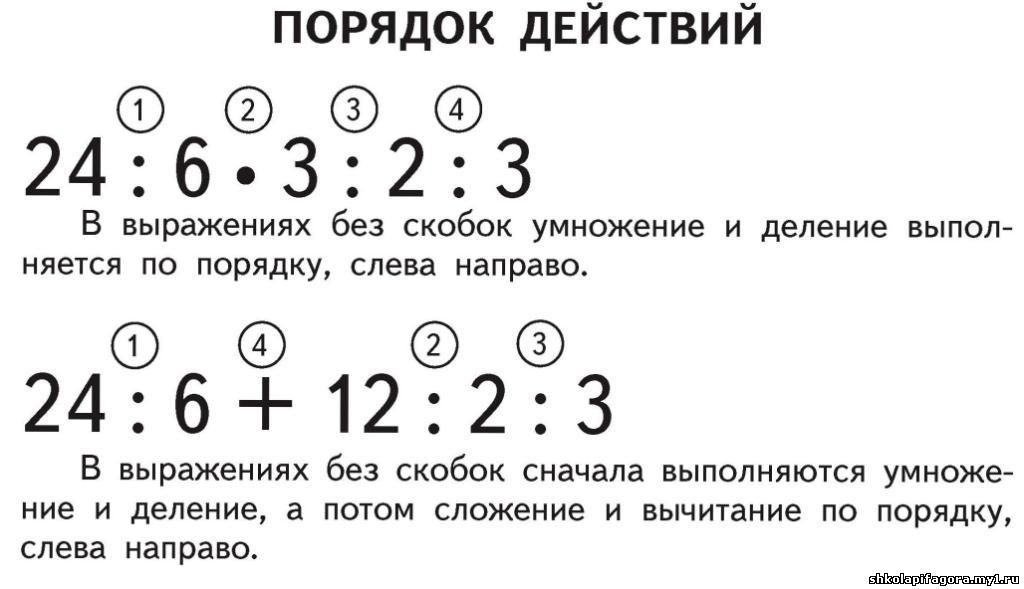
 Как это получается?
Как это получается? Например, учащиеся могут сначала работать с фактами, которые они знают или находятся в зоне своего изучения. Выталкивание примеров за пределы известных фактов может помочь учащимся увидеть силу отношений, которые они исследуют, например. 12 х 33 легче решить, чем 4 х 99.
Например, учащиеся могут сначала работать с фактами, которые они знают или находятся в зоне своего изучения. Выталкивание примеров за пределы известных фактов может помочь учащимся увидеть силу отношений, которые они исследуют, например. 12 х 33 легче решить, чем 4 х 99. В ходе обсуждения в классе ожидайте, что учащиеся будут выражать свои наблюдения способами, понятными другим. Студенты должны повторно выражать свои идеи, если другие не понимают, что они говорят. Возможно, вам придется напомнить учащимся, что «что-то происходит» относится ко всем четырем примерам, а не только к одному. Ожидайте ответов типа:
В ходе обсуждения в классе ожидайте, что учащиеся будут выражать свои наблюдения способами, понятными другим. Студенты должны повторно выражать свои идеи, если другие не понимают, что они говорят. Возможно, вам придется напомнить учащимся, что «что-то происходит» относится ко всем четырем примерам, а не только к одному. Ожидайте ответов типа:  Сначала они могут делать это индивидуально, а затем работать в небольших группах над уточнением своих идей и способов их выражения. Поощряйте модель махи-тахи, в которой учащиеся работают совместно. Возможные идеи могут включать:
Сначала они могут делать это индивидуально, а затем работать в небольших группах над уточнением своих идей и способов их выражения. Поощряйте модель махи-тахи, в которой учащиеся работают совместно. Возможные идеи могут включать:  Предложите учащимся начать с первых двух примеров пар уравнений, а затем подумать, как одни и те же отношения могут быть обобщены на последнюю и другие подобные пары уравнений.
Предложите учащимся начать с первых двух примеров пар уравнений, а затем подумать, как одни и те же отношения могут быть обобщены на последнюю и другие подобные пары уравнений.  В Новой Зеландии при обучении умножению множитель является первым множителем, а множимое — вторым множителем. В других странах учат наоборот, поэтому ожидайте, что некоторые студенты будут сбиты с толку.
В Новой Зеландии при обучении умножению множитель является первым множителем, а множимое — вторым множителем. В других странах учат наоборот, поэтому ожидайте, что некоторые студенты будут сбиты с толку. Поскольку в наборах пять, это означает, что можно составить ровно пять семерок.
Поскольку в наборах пять, это означает, что можно составить ровно пять семерок. 
 Введите важную лексику, такую как фактор (т. е. все числа, которые делят целое число на 3 и 2 без остатка, являются делителями 6) и произведение (т. е. результат, полученный при умножении чисел). Это поможет уточнить, о каких числах идет речь в формуле изобретения. Если иск ограничивается удвоением и делением пополам, обратите внимание на 9х 9 = 81 и 27 х 3 = 81. Цель состоит в том, чтобы расширить утверждение до эквивалента «один множитель делится на число, n, другой множитель умножается на n. Продукт остается постоянным (один и тот же)».
Введите важную лексику, такую как фактор (т. е. все числа, которые делят целое число на 3 и 2 без остатка, являются делителями 6) и произведение (т. е. результат, полученный при умножении чисел). Это поможет уточнить, о каких числах идет речь в формуле изобретения. Если иск ограничивается удвоением и делением пополам, обратите внимание на 9х 9 = 81 и 27 х 3 = 81. Цель состоит в том, чтобы расширить утверждение до эквивалента «один множитель делится на число, n, другой множитель умножается на n. Продукт остается постоянным (один и тот же)». 
 Вы также можете ввести частную интерпретацию дробей, например. a÷n может быть выражено как a/ n . Умножение также может быть представлено без символа x, например. a×b может быть представлено как ab .
Вы также можете ввести частную интерпретацию дробей, например. a÷n может быть выражено как a/ n . Умножение также может быть представлено без символа x, например. a×b может быть представлено как ab . Возможно, вам придется смоделировать это для студентов. Поощряйте ясность, задавая такие вопросы, как:
Возможно, вам придется смоделировать это для студентов. Поощряйте ясность, задавая такие вопросы, как:  Исходный продукт может быть выражен как x b. Добавление числа к b приводит к тому, что второй множитель становится b + n (n — добавляемое число). Произведение увеличивается на a x n. Учащимся важно учитывать, что происходит со всеми четырьмя наборами уравнений, поскольку n является переменной и может быть «любым числом». Учащиеся работают над выражением взаимосвязей между переменными с помощью букв и уравнений. Прогрессу можно способствовать, работая с нотациями, которые учащиеся разрабатывают сами.
Исходный продукт может быть выражен как x b. Добавление числа к b приводит к тому, что второй множитель становится b + n (n — добавляемое число). Произведение увеличивается на a x n. Учащимся важно учитывать, что происходит со всеми четырьмя наборами уравнений, поскольку n является переменной и может быть «любым числом». Учащиеся работают над выражением взаимосвязей между переменными с помощью букв и уравнений. Прогрессу можно способствовать, работая с нотациями, которые учащиеся разрабатывают сами. 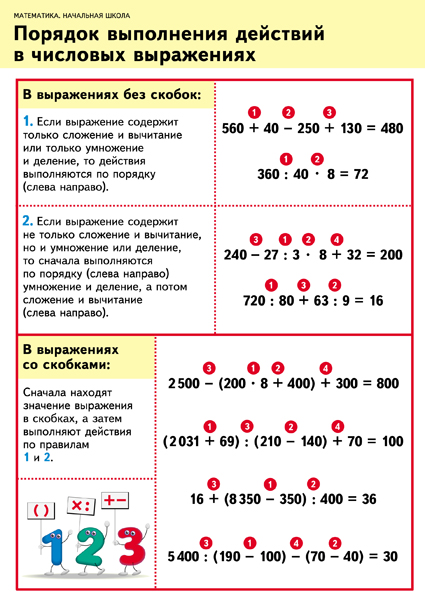 Это свойство используется учащимися для решения задач деления по измерению, например. «Сколько x входит в y? Завершенные наборы должны быть:
Это свойство используется учащимися для решения задач деления по измерению, например. «Сколько x входит в y? Завершенные наборы должны быть:  Произведение, деленное на один множитель, равняется другому множителю».
Произведение, деленное на один множитель, равняется другому множителю».  Таким образом, произведение умножения можно рассматривать как дивиденд при делении. Любой множитель может быть делителем, но другой множитель является частным.
Таким образом, произведение умножения можно рассматривать как дивиденд при делении. Любой множитель может быть делителем, но другой множитель является частным.  Это свойство может быть использовано учащимися для решения задач на деление. Завершенные наборы должны быть:
Это свойство может быть использовано учащимися для решения задач на деление. Завершенные наборы должны быть: 
 Таким образом, с половиной этого общего числа, 20, можно сделать половину меньшего. много пятерок.
Таким образом, с половиной этого общего числа, 20, можно сделать половину меньшего. много пятерок.  Во втором уравнении на единицу больше и на единицу меньше, а ответ на единицу меньше». Попросите учащихся быть более конкретными в своем описании.
Во втором уравнении на единицу больше и на единицу меньше, а ответ на единицу меньше». Попросите учащихся быть более конкретными в своем описании. 
 76 ÷ 4, вычислив сначала 80 ÷ 4. Завершенные наборы должны быть:
76 ÷ 4, вычислив сначала 80 ÷ 4. Завершенные наборы должны быть:  Обратите внимание, что четвертая пара уравнений уменьшает делимое в два раза больше делителя.
Обратите внимание, что четвертая пара уравнений уменьшает делимое в два раза больше делителя.