Что будет первым умножение или деление? – Обзоры Вики

Порядок операций можно запомнить по аббревиатуре PEMDAS, которая означает: круглые скобки, показатели степени, умножение и деление слева направо, а сложение и вычитание слева направо. Здесь нет круглых скобок или показателей степени, поэтому начните с умножения и деления слева направо.

Итак, каков порядок операций в математике? Чтобы помочь учащимся в Соединенных Штатах запомнить этот порядок операций, учителя вставляют в них аббревиатуру PEMDAS: круглые скобки, показатели, умножение, деление, сложение, вычитание.

Имеет ли значение порядок умножения и деления? Умножение и деление можно делать вместе. Другими словами, не имеет значения, выполняете ли вы сначала деление или умножение, но они должны выполняться после круглых скобок и показателей степени, а также перед сложением и вычитанием.

Дополнительно Можно ли выполнять умножение и деление в любом порядке? заказ операций говорит вам сначала выполнить умножение и деление слева направо, прежде чем выполнять сложение и вычитание. Продолжайте выполнять умножение и деление слева направо. Далее складываем и вычитаем слева направо.

Можно ли выучить деление перед умножением? дети начинают учить умножение во втором классе, и деление в третьем классе.

Каковы 5 порядка операций?

Она выступает за Круглые скобки, экспоненты, умножение / деление, сложение / вычитание. В школах PEMDAS часто расширяется до мнемоники «Пожалуйста, извините, моя дорогая тетя Салли». Канада и Новая Зеландия используют BEDMAS, что означает скобки, экспоненты, деление/умножение, сложение/вычитание.

Почему вы делаете сначала умножение и деление? Учащиеся должны были своими словами ответить на вопрос, который передает концепцию: Умножение и деление делается до сложения и вычитания чтобы преобразовать группы элементов в промежуточные итоги похожих элементов, которые можно объединить для получения общей суммы.

Что такое правило MDAS в математике? MDAS означает Умножение, деление, сложение и вычитание. Это часть Порядка операций, набора правил, определяющих последовательность упрощения математических операций. Он используется, когда выражение или уравнение имеют более одной операции.

Имеет ли деление преимущество перед умножением?

Умножение имеет тот же приоритет, что и деление, но умножение и деление имеют более высокий приоритет, чем сложение и вычитание.

Также Каковы четыре правила математики? Четыре правила математики сложение, вычитание, умножение и деление. На следующих веб-страницах вы можете узнать, как это сделать вручную (без калькулятора), а также другую важную информацию о порядке приоритета этих операций.

Что такое правило DMAS?

правило DMAS следует, когда в данной задаче присутствует несколько арифметических операций, таких как сложение, вычитание, умножение и деление. В нем говорится, что они должны выполняться в порядке деления, умножения, сложения и вычитания.

Почему студенты борются с разделением? Ребенку, которому не хватает фундаментального навыка, будет трудно разделить потому что это связано с предыдущими концепциями. Деление — это повторное вычитание и противоположность умножения. Это связано со счетом, целым и частями и пропорциональным мышлением.

Верно ли правило Бодмаса?

Его буквы обозначают скобки, порядок (значение полномочий), деление, умножение, сложение, вычитание. … Он не содержит скобок, степеней, деления или умножения, поэтому мы будем следовать BODMAS и делать сложение с последующим вычитанием: это ошибочно. Правильное значение 3.

В Бодмасе деление предшествует умножению?

PEMDAS («круглые скобки, показатели степени…») и BEDMAS также используются в США и Австралии. Возвращаясь к приведенному выше примеру, правильным ответом будет первый ответ, поскольку он следует правилам BODMAS: деление можно сделать перед умножением и должно быть сделано до сложения, а умножение предшествует сложению.

Что правильно MDAS или DMAS? Это не MDAS. На самом деле это DMAS, что означает деление, умножение, сложение и вычитание. В математике это правило соблюдается, что означает, что в уравнении или задаче порядок упрощения будет в указанном выше формате.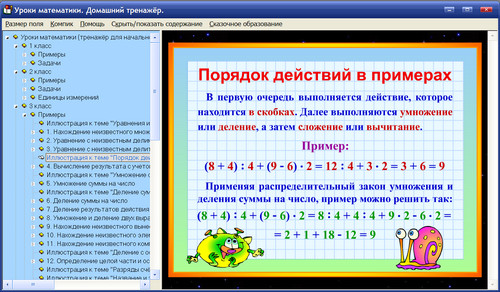

Как решить порядок действий? Порядок операций сообщает нам порядок решения шагов в выражениях с более чем одной операцией. Первый, решаем любые операции внутри скобок или скобок. Во-вторых, решаем любые показатели. В-третьих, мы решаем все умножение и деление слева направо.

Как вы оцениваете MDAS?

Чем отличается деление умножения? Умножение и деление тесно связаны между собой, поскольку деление — это обратная операция умножения. Когда мы делим, мы пытаемся разделить на равные группы, в то время как умножение предполагает объединение равных групп. … Если мы разделим этот продукт на один из множителей, то в результате получим другой множитель.

Каковы 4 порядка операций?

Порядок операций — это правило, указывающее правильную последовательность шагов для вычисления математического выражения. Мы можем запомнить порядок с помощью PEMDAS: Круглые скобки, экспоненты, умножение и деление (слева направо), сложение и вычитание (слева направо). Создал Сал Хан.

Почему умножение и деление имеют одинаковый приоритет? Сказать, что умножение и деление имеют одинаковый приоритет, значит сказать, что в выражении без скобок они оба должны выполняться до операций с более низким приоритетом, такие как сложение и вычитание, и что они оба должны выполняться после операций более высокого приоритета, таких как возведение в степень.

Какую скобку вы решите в первую очередь?

Согласно правилу BODMAS, если выражение содержит скобки ((), {}, []) мы должны сначала решить или упростить скобку, за которой следует «порядок» (что означает степени и корни и т. д.), затем деление, умножение, сложение и вычитание слева направо.

Каковы основные математические формулы? Некоторые примеры основных математических формул:

• Периметр прямоугольника = 2 (длина + ширина)
• Площадь прямоугольника = длина × ширина.
• Периметр квадрата = 4 × длина стороны.
• Площадь квадрата = длина стороны × длина стороны.
• Объем прямоугольного параллелепипеда = длина × ширина × высота.
• Прибыль = Цена продажи – Себестоимость.

Чем сложение и вычитание отличаются от умножения и деления?

Хотя операций четыре, они влекут за собой только два действия: объединение или разделение. Сложение и умножение объединяют действия и вычитание и деление являются разделяющими действиями.

Может ли MDAS быть DMSA? Это в равной степени может быть DMAS, DMSA и MDAS.. Дело в том, что умножение и деление всегда имеют более высокий приоритет, чем сложение и вычитание, за исключением скобок.

В чем разница между правилом Пемдаса и Бодмаса?

PEMDAS и BODMAS абсолютно идентичны; это разные названия одного и того же набора правил. В BODMAS вы не всегда делаете «деление перед умножением», а в PEMDAS вы не всегда делаете «умножение перед делением».

Python | Арифметические операции с числами

Последнее обновление: 23. 01.2022

Python поддерживает все распространенные арифметические операции:

• +

  Сложение двух чисел:

  print(6 + 2)  # 8

• —

  Вычитание двух чисел:

  print(6 - 2)  # 4

• *

  Умножение двух чисел:

  print(6 * 2)  # 12

• /

  Деление двух чисел:

  print(6 / 2)  # 3.0

• //

  Целочисленное деление двух чисел:

  print(7 / 2)  # 3.5
  print(7 // 2)  # 3
  

  Данная операция возвращает целочисленный результат деления, отбрасывая дробную часть

• **

  Возведение в степень:

  print(6 ** 2)  # Возводим число 6 в степень 2. Результат - 36
  

• %

  Получение остатка от деления:

  print(7 % 2)  # Получение остатка от деления числа 7 на 2.  Результат - 1
  

  В данном случае ближайшее число к 7, которое делится на 2 без остатка, это 6. Поэтому остаток от деления равен 7 — 6 = 1

При последовательном использовании нескольких арифметических операций их выполнение производится в соответствии с их приоритетом. В начале выполняются операции с большим приоритетом. Приоритеты операций в порядке убывания приведены в следующей таблице.

Операции	Направление
**	Справо налево
* / // %	Слева направо
+ —	Слева направо

Пусть у нас выполняется следующее выражение:

number = 3 + 4 * 5 ** 2 + 7
print(number)  # 110

Здесь начале выполняется возведение в степень (5 ** 2) как операция с большим приоритетом, далее результат умножается на 4 (25 * 4), затем происходит сложение (3 + 100) и далее опять идет сложение (103 + 7).

Чтобы переопределить порядок операций, можно использовать скобки:

number = (3 + 4) * (5 ** 2 + 7)
print(number)  # 224

Следует отметить, что в арифметических операциях могут принимать участие как целые, так и дробные числа. Если в одной операции участвует целое число (int) и число с плавающей точкой (float), то целое число приводится к типу float.

Арифметические операции с присвоением

Ряд специальных операций позволяют использовать присвоить результат операции первому операнду:

• +=

  Присвоение результата сложения

• -=

  Присвоение результата вычитания

• *=

  Присвоение результата умножения

• /=

  Присвоение результата от деления

• //=

  Присвоение результата целочисленного деления

• **=

  Присвоение степени числа

• %=

  Присвоение остатка от деления

Примеры операций:

number = 10
number += 5
print(number)  # 15

number -= 3
print(number)  # 12

number *= 4
print(number)  # 48

Округление и функция round

При операциях с числами типа float надо учитывать, что результат операций с ними может быть не совсем точным. Например:

first_number = 2.0001
second_number = 5
third_number = first_number / second_number
print(third_number)	# 0.40002000000000004

В данном случае мы ожидаем получить число 0.40002, однако в конце через ряд нулей появляется еще какая-то четверка. Или еще одно выражение:

print(2.0001 + 0.1)  # 2.1001000000000003

В случае выше для округления результата мы можем использовать встроенную функцию round():

first_number = 2.0001
second_number = 0.1
third_number = first_number + second_number
print(round(third_number))  # 2

В функцию round() передается число, которое надо округлить. Если в функцию передается одно число, как в примере выше, то оно округляется до целого.

Функция round() также может принимать второе число, которое указывает, сколько знаков после запятой должно содержать получаемое число:

first_number = 2.0001
second_number = 0. 1
third_number = first_number + second_number
print(round(third_number, 4))  # 2.1001

В данном случае число third_number округляется до 4 знаков после запятой.

Если в функцию передается только одно значение — только округляемое число, оно округляется то ближайшего целого

Примеры округлений:

# округление до целого числа
print(round(2.49))  # 2 - округление до ближайшего целого 2
print(round(2.51))  # 3

Однако если округляемая часть равна одинаково удалена от двух целых чисел, то округление идет к ближайшему четному:

print(round(2.5))   # 2 - ближайшее четное
print(round(3.5))   # 4 - ближайшее четное

Округление производится до ближайшего кратного 10 в степени минус округляемая часть:

# округление до двух знаков после запятой
print(round(2.554, 2))      # 2.55
print(round(2.5551, 2))      # 2.56
print(round(2.554999, 2))   # 2.55
print(round(2.
  499, 2))      # 2.5

Однако следует учитывать, что функция round() не идеальный инструмент. Например, выше при округление до целых чисел применяется правило, согласно которому, если округляемая часть одинаково удалена от двух значений, то округление производится до ближайшего четного значения. В Python в связи с тем, что десятичная часть числа не может быть точно представлена в виде числа float, то это может приводить к некоторым не совсем ожидаемым результатам. Например:

# округление до двух знаков после запятой
print(round(2.545, 2))   # 2.54
print(round(2.555, 2))   # 2.56 - округление до четного
print(round(2.565, 2))   # 2.56
print(round(2.575, 2))   # 2.58

print(round(2.655, 2))   # 2.65 - округление не до четного
print(round(2.665, 2))   # 2.67
print(round(2.675, 2))   # 2.67

Подобно о проблеме можно почитать к документации.

НазадСодержаниеВперед

Сложение и вычитание дробей

Рассмотрим непростую, но очень важную тему 5 класса по математике «сложение и вычитание дробей». Мы научимся складывать дроби как с общим, так и с разными знаменателями, разберёмся со смешанными дробями, научимся выполнять арифметические действия и с десятичными дробями.

Сложение и вычитание дробей с общим знаменателем

Допустим, по условию задания нам нужно найти сумму:

Так как в этом примере знаменатель у чисел одинаковый, это число 5, мы можем записать их под общую черту

Выполняем сложение числителей 2 и 1,  2 + 1 = 3

Тем самым получили

Найдем разность

Знаменатель у дробей общий, записываем их под одну черту и выполняем вычитание числителей 11 – 3 = 8

Получили

Тем самым вы выполнили вычитание двух дробей с общим знаменателем.

Задание для самопроверки:

Вычислите:

• ;
• ;

Сложение и вычитание дробей с разными знаменателями

Для выполнения сложения или вычитания дробей с разными знаменателями, необходимо в первую очередь найти наименьшее общее кратное (НОК) имеющихся знаменателей. НОК и есть общий знаменатель для дробей. Для этого вспомним, данную тему:

Найдем НОК (15,12). Для этого разложим каждое число на простые множители так, чтобы в конце получилась 1.

 

Подчеркнём одинаковые цифры во вторых столбцах у каждого числа.

Теперь возьмем первое число, то есть 15, и умножим его на неподчеркнутые цифры у второго числа. То есть 15 * 2 * 2, получим 60.

• Итак, теперь попробуем выполнить сложение дробей с разными знаменателями:

В первую очередь, найдем НОК знаменателей, 12 и 15.

Мы уже нашли его в предыдущем действии, НОК(12, 15) = 60

Теперь смотрим, на что нужно домножить первую дробь, чтобы ее знаменатель из 12 превратился в 60. Для этого вернемся к нахождению НОК и найдем неподчёркнутые цифры из другого столбца( смотрим на разложение числа 15), это число всего одно,  5. Мы поняли, что дополнительный множитель у первой дроби – это число 5.

Аналогично найдём дополнительный множитель для второй дроби, у второго числа 12 2 и 2 не подчёркнуты. 2*2 = 4 Следовательно дополнительный множитель для неё –  это число 4.

Получившиеся доп. множители записываем соответственно в правом верхнем углу у каждой дроби. А затем умножаем числитель дробей на этот множитель, записываем получившееся выражение уже сверху дробной функции со знаменателем 60.

Выполним необходимые действия.

В итоге мы получили дробь, которая равна сумме двух первоначальных.

• Посмотрим, как выполнять вычитание дробей с разными знаменателями, например,

Также первоначально найдем НОК, разложим знаменатели дробей 20  и 30 на простые множители.

 

Подчеркнём одинаковые цифры в двух столбцах

Домножим 20 на неподчёркнутые цифры у 30, это лишь 3.

20 * 3 =60

НОК (20,30) = 60

Значит общий знаменатель искомых дробей – 60.

Посмотрим, какой  недостающий множитель у числа 20, это цифра 3 из второго столбца.

А доп. множитель у 30 – цифра 2 из первого столбика.

Записываем дроби под общий знаменатель, при этом не забываем умножать числители на соответственный доп. множитель.

Это окончательный ответ.

Задание для самопроверки:

Сложение и вычитание десятичных дробей

Для того, чтобы научиться складывать и вычитать десятичные дроби, мы должны в первую очередь правильно их записать, запятая у второго числа должна находиться строго под запятой у первого.

Cложение десятичных дробей

Для этого суммируем цифры, находящиеся друг под другом, начиная с крайней левой. Записываем получившиеся значения под вертикальную черту. Если под одной из цифр нижняя отсутствует, как у числа 2, просто списываем эту двойку вниз.

5+2=7

1+7 = 8

Пишем ответ, оставляя запятую на прежней позиции.

Вычитание десятичных дробей

Это делается абсолютно аналогично сложению. Запишем числа друг под другом, запятая под запятой.

Начнём отнимать их верхнего числа нижнее.

5-2 = 3

1-7 невозможно вычесть, так как 1<7, поэтому занимает у предыдущей цифры 1 десяток,

1+10=11

И уже 11-7 = 4

Переходим к крайней левой цифре, так как мы у нее занимали десяток, это число ученьшилось на 1, то есть 2-1=1

Первая цифра стала равна 1

В итоге мы получили:

Не забудьте про запятую!

 Cложение десятичных дробей с разным количеством знаков после запятой

Расположим числа друг под дружкой так, чтобы запятая одной дроби находилась под запятой другой.

 

Выполним сложение, не обращая внимания на запятую.

12,75 + 7,8 = 20,55

• Рассмотрим вычитание десятичных дробей с разным количеством знаков после запятой

Снова располагаем числа друг под дружкой «запятая под запятой».

Допишем в конец второго числа нужное количество 0, так, чтобы у обоих слагаемых было одинаковое количество цифр после запятой. В нашем случае необходимо дописать всего один ноль

Вычтем из первого числа второе, запятую оставим на прежней позиции.

С 0 число начинаться не может, поэтому просто вычеркнем его.

Мы получили

Задание для самопроверки:

• 2,56 + 7, 62
• 11,7 – 3,28
• 1,11 – 1,6

        Вычитание смешанных дробей

Изучим вычитание смешанных дробей на примере:

Для начала попробуем вычесть дробные части у данных чисел

Приведем к общему знаменателю, найдя НОК (5,6)

НОК (5,6) = 5*6 = 30

Следовательно, первую дробь домножаем на 5, вторую на 6 и считаем.

Теперь вычитаем целые части

2-1=1

В итоге,

Но не всегда возможно вычесть из первой дроби вторую, например,

Пробуем выполнить вычитание дробных функций

НОК(8, 6) = 24

*Нахождение НОК чисел в предыдущее теме

Просчитать значение числителя невозможно, так как 3 < 4

Поэтому занимаем 1 у целой части первой дроби и приводим эту единицу к знаменателю 8

И снова пробуем вычитать дробные части

Теперь вычтем целые части

4 – 4 = 0

То есть целой части нет

Следовательно,

 

  Сложение смешанных дробей

Сложение смешанных дробей выполняется аналогично вычитанию.

Для этого сначала найдем сумму дробных частей. Рассмотрим пример:

Так как числитель больше знаменателя выделим целую часть:

*см. «выделение целой части»

Теперь сложим целые части:

1 + 2 = 3

Мы получили

Задание для самопроверки:

Арифметика

. Имеет ли значение порядок операций только сложения и вычитания?

Спросил 6 лет, 10 месяцев назад

Изменено 4 года, 11 месяцев назад

Просмотрено 27 тысяч раз

$\begingroup$

Спорили, можно ли выполнять сложение/вычитание в любом порядке. В частности, для следующего:

$9 — 4 + 3$

Мы оба согласны с тем, что ответ равен 8.

Я утверждаю, что, придав сложению более высокий приоритет, чем вычитанию (вместо того, чтобы иметь такой же приоритет и двигаться слева направо), вы получите 9 долларов — 4 + 3 = 9 — 7 = 2 доллара, что является неверный ответ, и поэтому важно, чтобы сложение и вычитание имели одинаковый приоритет.

Другой человек утверждает, что порядок операций не имеет значения и что их можно выполнять в любом порядке, так как если придать сложению более высокий приоритет, чем вычитанию, вы получите $9 — 4 + 3 = 9+ (-4 + 3) = 9 + — 1 = 8$, что является правильным ответом, и поэтому не имело бы значения, если бы сложение/вычитание имело разные приоритеты, а не одинаковые.

Я утверждаю, что внесение $- 4$ в скобку и последующее выполнение до $+ 3$ не было бы выполнено, если бы сложение имело более высокий приоритет. Довольно длинные дебаты можно увидеть здесь, если вы хотите их прочитать, поэтому я не перефразирую все это и не слишком предвзято отношусь к своей стороне.

Мой общий вопрос заключается в том, кто прав; имеет ли значение порядок операций только сложения и вычитания? Я готов принять ответы любой из сторон, если они объяснят причину.

• арифметика

$\endgroup$

$\begingroup$

Уточним:

$$9 — 4 + 3 \color{red}{\ne} 9 — (4 + 3) \tag{1}$$

Похоже, вы путаете, что значит группировать вместе , или связать, операции.

• Да, сложение и вычитание коммутативны : Операции можно выполнять в любом порядке.
• Да, сложение и вычитание ассоциативны : Термины могут быть сгруппированы в любом порядке перед выполнением операций.

НО , ошибка в выражении $(1)$ выше заключается в том, что термины не были сгруппированы правильно. Правильный способ связать два последних термина:

$$\begin{align*}9 — 4 + 3 &= 9 + (-4 + 3) \tag{2}\\ &=9-(4-3) \end{align*}$$

В исходном выражении $(1)$ вверху этого поста вы ввели второй знак минус.

$$\цвет{красный}{9- (4 + 3) = 9 — 4 — 3} \tag{3}$$

Итак, нет двусмысленности в том, что означает $(2)$ или $(3)$. Но они означают совершенно разные вещи. Скобки, используемые для группировки в этом примере, должны соответствовать мультипликативному свойству распределения. Если мы по желанию вставим скобки в математическое выражение, то рискуем полностью изменить результаты. Чтобы правильно сгруппировать элементы, мы должны убедиться, что наш результат передает одно и то же сообщение — тот же порядок операций.

$\endgroup$

11

$\begingroup$

Нет, они выполняются одновременно. 9 долларов — (4+3) = 9 — 7 = 2 доллара. Сложение/вычитание — это двоичная операция между двумя числами. Таким образом, когда мы говорим $a + b + c$, мы имеем в виду $a + (b + c)$ или $(a + b) + c$. Обратите внимание, что для сложения они одинаковы, поскольку + является «ассоциативным» (это определение ассоциативности). Поэтому мы просто пишем $a + b + c$, так как это однозначно. Обратите внимание, что $a — b$, по сути, является сокращением для $a + (-b)$. То же самое верно для умножения, но не для деления.

$$ (8/4)/2 = 2 / 2 = 1; \ 8/(4/2) = 8/2 = 4. $$

Вот почему у вас есть для указания порядка деления. Если рассматривать вычитание как операцию, а не как операцию, обратную сложению, то, как и в случае с делением, оно не является ассоциативным.

$\endgroup$

8

$\begingroup$

Я бы сказал, что порядок (сложения/вычитания) не имеет значения И вам не нужно повышать «приоритеты», пока вы понимаете, что вычитание — это просто сложение отрицательных чисел…

Итак, 9 — 4 + 3 — это не 9 — (4 + 3), а 9 + ( -4 + 3 ).

Помещение отрицательного знака перед скобкой означает, что вы хотите сделать все внутри отрицательным, а это не то, чего мы на самом деле хотели.

Так что просто сделайте все числом со знаком и выполняйте все процессы как сложение в том порядке, в котором вам легче всего.

$\endgroup$

$\begingroup$

Это имеет значение, потому что отражает соглашение о том, какие процедуры сначала выполняются для вычисления данного математического выражения.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

развлекательная математика — BEDMAS, где порядок сложения перед вычитанием имеет значение?

Представьте себе мир, в котором BEDMAS не существует и где необходимо указать, в каком именно порядке оцениваются операции в выражении, с помощью круглых скобок. Допустимое выражение выглядит примерно так:

$$((a + b) \times (c \div (d — e)))$$

Посмотрите на это выражение. Он имеет четыре операции и четыре набора скобок. Каждый набор скобок принадлежит ровно одной операции и наоборот.

$$\цвет{красный}(\цвет{оранжевый}(3\цвет{оранжевый}+ 5\цвет{оранжевый}) \цвет{красный}\раз \цвет{синий}(6 \цвет{синий}\ div \color{#00bf00}(9 \color{#00bf00}- 7\color{#00bf00})\color{blue})\color{red})$$

С помощью этих скобок мы точно знаем, как вычислить это выражение. Результат этого выражения равен $24$.

Теперь рассмотрим большое выражение. Что, если вы не хотите постоянно писать все эти скобки? Что делать, если вы хотите, чтобы большие выражения было легче читать? Не могли бы вы подумать о способах уменьшить количество скобок и общих символов, которые вам нужны, таким образом, чтобы результирующее выражение оставалось однозначным? Ну, математики бы. И именно поэтому существует BEDMAS.

Сначала рассмотрим выражения, в которых используется только $+$. Рассмотрим выражение $((a + b) + ((c + d) + e))$. В этом выражении достаточно круглых скобок, чтобы однозначно определить порядок операций. Но у $+$ есть замечательное свойство: для любых чисел $a, b, c$ всегда выполняется $(a+b)+c = a+(b+c)$. Это называется закон ассоциативности . Теперь, если у нас есть куча сумм сумм, мы можем просто опустить скобки между ними, потому что независимо от того, как вы их вставите, вы всегда получите один и тот же результат. Наше выражение упрощается до $a + b + c + d + e$. Отлично, мы уже избавились от многих скобок.

Теперь добавим $\times$ в бой. Закон ассоциативности выполняется и для $\times$, поэтому мы можем написать $a \times b \times c \times d \times e$ вместо $((a \times b) \times ((c \times d) \раз е))$. Теперь давайте посмотрим, что произойдет, если вы объедините $+$ и $\times$. Мы знаем, что $a + (b \times c)$ и $(a + b) \times c$ — разные выражения, поэтому мы не можем удалить скобки в обоих случаях. Но вот новый закон: мы можем переписать $(a + b) \times c$ как $(a \times c) + (b \times c)$. это закон распределения . Это означает, что мы можем написать любое выражение, используя $+$ и $\times$, как выражение, в котором вы всегда сначала выполняете все умножения, а только потом все сложения.

Как следствие, мы можем изобрести новый способ скрытия скобок. В терминах, где умножение и сложение стоят рядом друг с другом без скобок, мы соглашаемся всегда сначала выполнять умножение. Это отличный способ, потому что, когда мы его используем, мы можем написать любой термин, используя $+$ и $\times$ вообще без каких-либо круглых скобок!

Пример:

Используя закон дистрибутивности, мы можем переписать

$$(a \times (b + ((c + d) \times (e + f))))$$ в $$((a \times b) + (((a \times (c \times e)) + (a \times (c \times f))) + ((a \times (d \times e)) + (a \times ( d \times f)))))$$

Здесь много операторов, но если мы договоримся сначала сделать умножение и вспомним закон ассоциативности, то получим

$$a \times b + a \times c \times e + a \times c \times f + a \times d \times e + a \times d \times f$$

, который вообще не содержит скобок! Это не всегда было бы возможно, если бы мы оценивали слева направо или сложение перед умножением.

Теперь добавим вычитание. Во-первых, давайте вспомним, что слева от выражения стоит унарный знак минус, например, $-a$ — это сокращение для $(0-a)$. Рассмотрим член сложения и вычитания:

$$(a — (b — (c + (d — e))))$$

Используя законы $a + (b — c) = (a + b) — c$, $~a — (b + c) = (a — b) — c$ и $a — (b — c) = (a-b) + c$, мы можем переупорядочить эту последовательность операций так, чтобы скобки сдвигаются как можно дальше влево, поэтому сложение и вычитание выполняются слева направо:

$$((((a — b) + c) + d) — e)$$

Итак, давайте просто договоримся, что сложение и вычитание без скобок выполняются слева направо. Мы получаем

$$a — b + c + d — e$$

Это имеет то преимущество, что с этой записью вы фактически можете переписать вычитание как сложение отрицаний с помощью унарного $-$:

$$a + ( -b) + c + d + (-e)$$

Таким образом, этот метод делает термин намного более легким для чтения и понимания, и это позволяет нам намного легче переупорядочивать слагаемые в этой сумме.

Если мы хотим смешать умножение и вычитание, мы снова указываем, что сначала выполняется умножение.

Теперь перейдем к делению. Рассмотрим термин, смешивающий умножение и деление. Как и в случае сложения и вычитания, мы можем изменить порядок скобок так, чтобы операции выполнялись слева направо, используя совершенно аналогичные законы $a \times (b \div c) = (a \times b) \div c$ , $~a \div (b \times c) = (a \div b) \div c$ и $a \div (b \div c) = (a\div b) \times c$.

Теперь мы согласны сбрасывать круглые скобки, когда операции фактически выполняются слева направо. Итак,

$$(a \div (b \times (c \div (d \div e))))$$

становится

$$((((a \div b) \div c) \times г) \div e)$$

, которое мы записываем как $$a \div b \div c \times d \div e$$

Опять же, мы можем интерпретировать деление как умножение с обратным:

$$a \times (1 \div b) \times (1 \div c) \times d \times (1 \div e)$$

Таким образом, с этим описанием намного проще работать, например, мы можем очень легко изменить его порядок.

Когда деление смешивается со сложением или вычитанием, мы говорим, что деление всегда выполняется первым по умолчанию.

Теперь обратите внимание, что термины, использующие $\div$, не всегда могут быть записаны без круглых скобок, например, $a \div (b + c)$.

Из-за этого математики больше не используют символ $\div$. Вместо этого они используют дробную запись:

$$a \div b = \frac{a}{b}$$. Приятно то, что мы можем рисовать горизонтальную линию посередине сколь угодно долго, и что линия четко отделяет то, что находится над линией, от того, что ниже линии. Таким образом, мы можем опустить еще несколько скобок:

$$a \div (b + c) = \frac{a}{b+c}$$

Сравните это с

$$(a \div b) + c = \frac{a}{b } + c$$

Ясно, что мы видим разницу.

Таким образом, мы можем написать любой термин, используя $+$, $-$, $\times$, $\div$ совершенно без круглых скобок!

Рассмотрим термин $((a + b) \times (c \div (d — e)))$ из верхней части моего ответа. Он имеет четыре набора круглых скобок, которых мы теперь технически можем избежать, используя соответствующие обозначения и расширяя их с помощью дистрибутивного закона:

$$a \times \frac{c}{d — e} + b \times \frac{c}{d-e}$$

Обратите внимание, что это выражение обычно записывается как

$$(a + б) \times \frac{c}{d — e}$$

, так как это на самом деле легче читать и понимать. В конце концов, мы не запретили круглые скобки, мы просто придумали способы избежать их написания.

Имейте в виду, что, поскольку никто из школьников на самом деле не использует $\div$, приоритет $\times$ и $\div$ на самом деле не является общепринятым. Это означает, что нам нужно использовать круглые скобки, когда $\div$ стоит перед $\times$, чтобы люди не запутались.

Теперь мы можем, наконец, взглянуть на термин на картинке вашего вопроса:

$$6 — 1 \times 0 + 2 \div 2$$

Если мы заменим круглые скобки, используя установленные нами правила, мы получаем

$$((6 — (1 \times 0)) + (2 \div 2)) = 7$$

, что теперь должно быть совершенно однозначным.

Правила, которые мы установили, как вы уже могли догадаться, и есть БЭДМАС (или скорее БДМАС, поскольку я не говорил о возведении в степень).

Обратите внимание, что если вы просто введете данный термин в калькулятор, вы не получите того же результата, потому что калькулятор оценивает операции в том порядке, в котором они были введены, а не в порядке BEDMAS. Итак, калькулятор видит

$$((((6 — 1) \times 0) + 2) \div 2) = 1$$

, что явно является другим результатом. Так что просто помните, что калькуляторы не могут делать BEDMAS, и все готово.

Вот другое выражение:

$$24 \div 4 \times 3$$

Каков результат этого выражения? По общему соглашению мы сначала делаем деление, но опять же, технически мы должны были добавить круглые скобки, потому что соглашение не является достаточно общеизвестным. Или мы могли бы просто использовать запись дроби вместо $\div$, в этом случае мы получили бы два разных выражения:

$$\frac{24}{4}\times 3 \neq \frac{24}{4 \times 3}$$

Итак, здесь мы можем ясно видеть намеченный порядок, и все снова хорошо.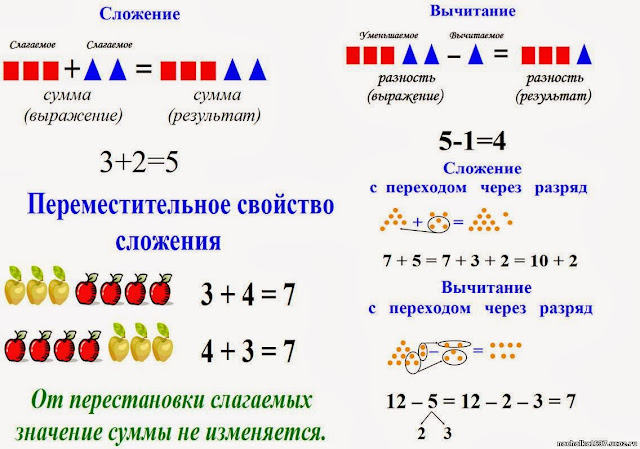

Тактильное преобразование в цифровое Часть 5: Сложение и вычитание

Это пятая статья из серии о том, как успешно обучать школьным навыкам 21 века, сочетая тактильную графику с цифровыми ресурсами. В этом посте мы обсудим использование тактильного наложения на iPad (приложение также доступно в Google Play!), чтобы представить пространственные макеты сложения и вычитания с переносом и перегруппировкой. Для сложения и вычитания учащиеся должны уметь применять технические навыки, например, уметь перетаскивать прямую линию по строкам и вниз по столбцам, чтобы складывать/вычитать правильные числа. Понимание пространственного расположения также имеет решающее значение, особенно когда речь идет о переноске или перегруппировке. Пожалуйста, ознакомьтесь с предыдущими сообщениями в этой серии, так как они обеспечивают базовые навыки, которые ведут к решению цифровых математических уравнений.

В приложении Math Melodies есть серия игр, связанных с прогрессом в математике. Игры «Сложение и вычитание математических мелодий» — это первое цифровое математическое приложение, в котором создан доступный способ перегруппировки и переноса в приложении. В этом видеоуроке Джессика демонстрирует уравнения сложения математических мелодий для продвинутого уровня первого класса. Эти задачи на сложение представлены в виде вертикальных уравнений, большинство из которых требуют переноса. Усложненные задачи на вычитание для первого класса также представлены в виде вертикальных уравнений, большинство из которых требуют перегруппировки.

Прежде чем решать эти уравнения, учащиеся должны быть знакомы с математическими фактами от 0 до 9, понимать столбцы единиц, десятков и сотен и иметь опыт проведения пальцем вверх/вниз по столбцу по прямой линии.

Примечание: базовый уровень первого класса имеет однозначные уравнения (столбец единиц с простым переносом). В то время как уравнения первого класса Advanced имеют задачи на сложение двух цифр (столбцы единиц и десятков). В видеоуроке Джессика демонстрирует продвинутый уровень первого класса, чтобы показать, как решать уравнения, которые могут быть немного сложнее.

Предварительное обучение пространственному макету

Просмотрите аналогичную задачу на сложение в версии для шрифта Брайля; обсудите столбцы единиц и десятков, где находится ответ (внизу уравнения) и где находится переносимое число (вверху числа). Подумайте о том, чтобы иметь пустые поля, чтобы указать, где вы вводите ответы и переносите числа.

Для некоторых учащихся предпочтительнее предварительное обучение навыкам с использованием тактильной графики (перед размещением графики на iPad). Как правило, этот метод используется для учащихся, которые отвлекаются на речь VoiceOver или не могут держать руки неподвижно. Для большинства учащихся знакомство с тактильным наложением на iPad предпочтительнее, так как VoiceOver предоставляет словесную информацию о том, к чему прикасается учащийся. Для многих учащихся наличие встроенной вербальной информации, доступной при использовании цифровых задач на сложение и вычитание, особенно в сочетании с тактильными наложениями, увеличивает успех учащихся в решении уравнений и создает прочные пространственные представления, необходимые для более сложных математических задач.

Первоначально сосредоточьтесь на изучении пространственного расположения всю страницу с помощью тактильной графики. Тактильная графика имеет пустые поля для уравнения, переноски и ответов «равно». Он также имеет меньшие поля с вариантами ответов, напечатанными шрифтом Брайля, в нижней части страницы и символами кнопок в правой части страницы. Это кнопки «Назад», «Выход» (выйти из игры) и «Прослушать» (параметр «Читать вслух» для учащихся, не использующих VoiceOver). Попросите ученика систематически изучить всю тактильную графику для цифрового уравнения. Чем отличается версия шрифта Брайля от тактильного наложения? Сколько рядов пустых ящиков и почему? Куда вы вводите свой ответ? Проведите пальцем вниз по столбцу единиц. Проведите пальцем вниз по столбцу десятков. Примечание. Приложение называет верхний ряд полей полями «перенос», а нижний ряд полей — полями «равно». Примечание. Тактильное наложение имеет более жирные линии вокруг полей «перенести» и «ответить», чтобы указать, что вы можете вводить числа в эти поля.

При предварительном обучении устно произнесите уравнение. (Пример: 65 + 8). Попросите ученика повторить уравнение. Если вы представляете тактильную графику на iPad, подтвердите числа в математической задаче, коснувшись самой верхней части экрана (VoiceOver снова объявит уравнение).  Куда идет первое число в пустых ячейках? Куда делся второй номер? Найдите эти числа в реальном уравнении.

Если у вашего учащегося есть хорошее представление об уравнении, спросите его/ее, что он/она обнаружит, если проведет пальцем вниз по колонке единиц? (Пример: Учащийся должен запомнить или научиться строить мысленный образ: 5, 8, квадрат «равно»). Повторите с десятками столбцов — что вы найдете? Затем подтвердите, проведя пальцем вниз по столбцу десятков. (Пример: учащийся должен запомнить или научиться строить мысленный образ: коробка «нести», 6, пусто, коробка «равно».)

Примечание для учителя: настоятельно рекомендуется, чтобы учащийся перетаскивал мышью по экрану, а не проводил пальцем вправо/влево . Свайпы вправо или влево будут перемещаться по полям слева направо. Свайп вверх или вниз НЕ перемещает столбец вверх или вниз! (Движение вверх или вниз изменит положение ротора.) При перетаскивании используйте раздельное касание, чтобы активировать поле «равно», ящик для переноски или ящик для ответов.

Примечание. В приложении меньшие поля для ответов не отображаются до тех пор, пока вы не коснетесь поля «равно». Перейдите к нужному ответу и нажмите дважды, чтобы выбрать нужный ответ. Ответ будет автоматически добавлен в выбранное поле «равно».

Навыки слушания

Когда открывается новая страница с новым уравнением, VoiceOver объявляет математическую задачу. Пример: В видеоуроке озвучена первая задача «Сколько будет 73 + 6?» Это ключевая информация! Учащийся должен мгновенно создать мысленный образ этого уравнения, запомнить числа и вернуться к этому мысленному образу при решении задачи! Учащийся должен мысленно представить вертикальное уравнение, выстроив «3» и «6» в столбце единиц и «7» в столбце десятков.

Дополнительные проблемы

После прослушивания VoiceOver, объявляющего уравнение, и создания мысленного образа вертикального уравнения, учащийся может подтвердить числа, если желает. или он/она может найти столбец с единицами и начать решать уравнение. Учащийся может подтвердить это, проведя пальцем сверху вниз по центру экрана, чтобы найти первое число (на фотографии ниже уравнение 54 + 96; с 5 в столбце десятков), затем перетащите вправо, чтобы найти столбец единиц (на в данном случае 4). Некоторым учащимся изначально необходимо подтвердить пространственное расположение , касаясь каждого отдельного числа в уравнении.  Однако это не так эффективно, как просто коснуться уравнения в верхней части страницы. Если учащемуся нужно подтвердить только числа в задаче, а не пространственное расположение, учащийся может коснуться верхней части экрана, чтобы услышать, как VoiceOver снова объявляет полное уравнение.

Примечание для учителя: попросите ученика произнести уравнение, прежде чем коснуться экрана! Если учащийся пытается решить уравнение, периодически просите его/ее назвать уравнение и шаги, которые он/она решает. Произнесение уравнения в основном помогает учащемуся думать вслух, что помогает не только учащемуся обрабатывать шаги, но и дает учителю понимание процесса мышления учащегося. При знакомстве с этим приложением часто бывает полезно смоделировать мыслительный процесс, попросив вас, учителя, произнести шаги вслух либо при моделировании процесса решения уравнения, либо при проведении/представлении учащегося в процессе в первый раз.

Решение задачи сложения

Как только учащийся твердо усвоит уравнение, решите уравнение следующим образом:

• Найдите столбец единиц (проведите пальцем сверху вниз, начиная немного правее центра), ищите конкретное число. (В примере 54 + 96 число 4.)
• Перетащите вниз, чтобы найти число, которое нужно добавить к 4. (В данном случае число 6.)
• Снова потяните вниз, чтобы найти поле «равно» в столбце единиц, и коснитесь его раздельно. Это вызывает меньшие поля для ответов в нижней части экрана.
  • Перетащите на нужный номер и разделите тап. (в данном случае ответ равен 9.) Ответ автоматически помещается в поле «равно» столбца единиц.

Если ответ требует ношения:

• Перетащите вверх, чтобы найти поле «перенос» над рядом десятков (которое в этом случае будет полем «перенос» выше с номером 5).
• Нажмите раздельно на поле «перенести» (что открывает варианты ответов в нижней части экрана).
• Найдите нужный номер в полях для ответов внизу страницы и разделите тап. (В данном примере цифра 1). Ответ автоматически помещается в поле «перенести» над столбцом десятков.

Повторяет необходимые шаги для добавления столбца десятков, а затем столбца сотен.

В видео ниже Джессика демонстрирует, как использовать тактильное наложение с задачами на сложение и вычитание в приложении Math Melody. В этой демонстрации она показывает, как носить и как брать/перегруппировывать.

Примечание редактора: процесс ношения и заимствования кажется более сложным, чем он есть на самом деле! При решении задачи шрифтом Брайля учащийся должен свернуть бумагу вверх и вниз в брайлевском писателе и выровнять головку брайлевского тиснителя, чтобы поместить переносимое число или перегруппированное число над уравнением. В цифровом формате учащийся просто проводит пальцем по нужному полю и дважды нажимает, а затем выбирает нужный ответ из вариантов внизу страницы.

Примечание редактора. В видео Джессика продемонстрировала перегруппировку вычитания в столбце единиц и завершение ответа на единицу до того, как она зачеркнула («косая черта», как это называется в приложении) столбец десятков. Часто порядок заключается в том, чтобы вычеркнуть десятки, добавить новое число в поле «перенести» над вычеркнутым числом, затем изменить число единиц, добавив исходное число в поле «единицы», затем выбрать «Добавить десять». кнопка выбора ответа. (Пример: в примере видео 63 – 15, 6 зачеркнуто, чтобы получилось 5, а 3 стало 13.)

Проблемы с вычитанием

При вводе задач на вычитание в приложении Math Melodies следуйте тем же стратегиям, перечисленным выше, для введения задач на сложение. Обязательно сравните формат Брайля с тактильным наложением на iPad! Вместо поля «перенести» над столбцом десятков теперь есть поля «перегруппировать» над столбцами десятков и единиц. Первое число в столбце десятков также имеет опцию «косая черта», что означает, что число было заимствовано.

После того, как учащийся ознакомится с тактильным наложением, пространственным расположением, решите задачу. На картинке ниже уравнение 63 – 15. Вы не можете отнять 5 от 3, поэтому вы должны позаимствовать 10 из числа в столбце десятков.

При перегруппировке найдите число в столбце десятков, у которого вы будете занимать 10.

• Вычеркните 6 в столбцах десятков, нажав на нее раздельным нажатием. (Приложение называет это «косой чертой», поскольку косая черта ставится над цифрой 6. Затем VoiceOver объявляет число (6) «заимствованным». 
• Добавьте новое число десятков над заимствованным числом. (В данном случае вы позаимствовали десять из числа 6, поэтому поставьте 5 в поле «перегруппировать» в верхней части столбца десятков. Теперь VoiceOver объявляет число (5) «перегруппировано».
• Теперь перейдите в колонку единиц и добавьте десять к исходному числу. (В этом примере вы добавите 13 в поле «перегруппировать» над столбцом единиц.
  • Перетащите в поле «перегруппировать» над ними и коснитесь раздельно.
  • Перетащите к нужному варианту ответа в нижней части экрана и коснитесь его раздельно. (В данном случае 3.)
  • Добавьте десять к числу 3, перетащив обратно в поле «перегруппировать» над единицами и разделив нажатие.
    • Перетащите к варианту ответа «Добавить десять» в нижней части экрана и нажмите раздельно. (Теперь число 13 находится в поле перегруппировки над столбцом единиц.)
• Послушайте новую проблему вычитания столбца единиц, перетащив столбец единиц вниз, начиная с поля перегруппировки. (В данном случае 13–5, поле «равно».
• Добавьте свой ответ в столбце «Единицы»: когда в поле «равно» в столбце «Единицы» нажмите раздельно.
  • Перетащите к нужному варианту ответа и разделите касание. (В этом случае вариант ответа 8.)
• При необходимости повторите шаги для столбца десятков.
• Проверьте свой ответ, выбрав кнопку «Проверить ответ», которая теперь расположена у нижнего края экрана в центре. (Примечание: на тактильном наложении кнопка проверки ответа не отображается, так как поля выбора номера ответа закрывают кнопку проверки ответа.

Тактильные накладки для сложения и вычитания

Большое спасибо Transcribe Mariners , которые пожертвовали тисненую графику для  Paths to Technology   Resource Library  и этой записи в блоге. Огромное спасибо Джессике МакДауэлл, экстраординарной фигуре TVI, за то, что поделилась своей работой по преодолению разрыва между тактильной графикой и цифровыми ресурсами!

• Дополнение Advanced Overlay pdf для PIAF/Swell
• Дополнение Advanced overlay docx для embosser
• Subtraction Advanced Overly pdf для PIAF/Swell
• Вычитание Advanced Overlay docx для тиснителя

Связанные публикации Ресурсы

• От тактильного к цифровому, часть 1: математический робот (обзор критических технических концепций, уникальных для слепых или слабовидящих учащихся, и как использовать приложение Math Robot от APH для обучения этим критическим технологическим навыкам)
• От тактильного к цифровому, часть 2: математические мелодии (представлена ​​последовательность использования моделей, тактильной графики и наложений iPad для обучения критически важным техническим навыкам, включая перетаскивание по прямой линии и применение концепций сетки к цифровой среде с помощью игры Math Melodies, Add or Удалить)
• Тактильная цифровая часть 3: Создание тактильного наложения на ходу! (Два быстрых и простых метода создания простых тактильных наложений без эмбоссера или графической машины PIAF/Swell)
• Тактильно-цифровое, часть 4: позиции в таблице (использование тактильного наложения на iPad для  представления пространственного расположения стола)
• Математические мелодии в App Store
• Математические мелодии в магазине Google Play
• Приложение «Математические мелодии»: пост 9 для юных студентов0028
• Приложение Math Melodies, часть 1: сложение (подробные видеоуроки о том, как решать цифровые математические уравнения сложения с помощью VoiceOver)

 

Прикрепленный файл(ы)

https://www.