методика выполнения операций и примеры реализации алгоритма
Математика
12.11.21
9 мин.
Одними из базовых математических операций являются умножение и деление натуральных чисел. В 5 классе они изучаются более подробно с учетом всех «тонкостей». Специалисты разработали специальные алгоритмы, позволяющие произвести расчеты без ошибок. Однако перед обучением нужно разобрать основные определения и понятия, а затем приступать к практике.
Оглавление:
- Общие сведения
- Методика умножения
- Алгоритм деления
- Примеры решений
Общие сведения
Умножением двух или нескольких чисел называется математическая операция, состоящая из множителей и результата (произведения). Следует отметить, что ее можно заменить сложением, т. е. 2*3=2+2+2=6. Иными словами, первый множитель указывает на число, а второй обозначает, какое количество раз его необходимо сложить с эквивалентным значением.
Деление — вид арифметической операции, при которой одно число (делимое) делится на другое (делитель), а их результатом является частное. Ее можно заменить вычитанием, т. е. 36/6=36−6−6−6−6−6−6=0. Следует отметить, что деление является сложным типом операции, поскольку классифицируется на два вида: без остатка и с его наличием.
Натуральные — числа, при помощи которых производится счет, т. е. 1, 2, 3, 4 и т. д. Весь числовой ряд является натуральным. Он расположен только в порядке возрастания.
Методика умножения
При умножении чисел используется специальная методика, при которой два значения записываются в столбик: единицы под единицами, десятки под десятками и т. д. Алгоритм возможно применять для многозначных величин. Он имеет следующий вид:
- Написать числовые пары одну под другой.

- Выполнить умножение единиц второго числа на первое.
- Записать результат.
- Перемножить разряд десятков с первым значением и записать его со смещением влево.
- Повторить четвертый пункт методики (нужно не забывать о постоянном смещении влево на один разряд).
- Сложить обе величины и записать окончательный результат.
Следует отметить, что для оптимизации решения примеров по математике 5 класса на умножение применяются свойства. К ним относятся следующие:
- При произведении любого натурального числа на 0 получается нулевое значение.
- Произведение двух чисел, одно из которых 1, есть другое значение, т. е. а*1=а.
- Переместительное: перемена мест сомножителей не меняет результат (mnо=mоn=nоm=nmo=omn=onm).
- Сочетательный закон: перемножать можно в любом порядке. Например, если удобно умножить 1 на 3, то можно их перемножить, а затем подключить второе значение.
- Распределительное: умножение числа на сумму двух величин эквивалентно произведению общего множителя за скобкой на первое и второе значения, а затем полученные два результата требуется сложить.
 Это свойство может быть полезно при решении уравнений.
Это свойство может быть полезно при решении уравнений.
Следует отметить, что любое из вышеописанных свойств возможно применять несколько раз. Например, можно использовать переместительное и сочетательное.
Алгоритм деления
Деление, как и умножение, выполняется по определенному алгоритму. Однако следует учитывать факт, что результат может быть целым и с остатком. В первом и во втором случае применяется аналогичный алгоритм, но существуют некоторые особенности. Методика деления натурального числа на другое значение, принадлежащего к этому типу, имеет такой вид:
- Записать делимое, а с правой стороны — делитель, отделяя их прямой чертой.
- Взять количество разрядов, соответствующих делителю.
- Подобрать множитель, а затем записать его произведение на делитель под I разрядной группой и вычислить их разность.
- Взять II разрядную группу и выполнить аналогичную операцию.
- Продолжать до того момента, пока не получится 0 или величина (остаток), которая меньше делителя.

Следует отметить, что операция деления имеет несколько особенностей. К ним относятся следующие:
- Деление на 0 невозможно. Возможно только нуль разделить на любое число. Результат при этом будет равен 0. Пример деления для 5 класса имеет такой вид: 0/8=0.
- Деление на 1 имеет эквивалентное исходное значение: 5/1=5.
После рассмотрения алгоритмов нужно перейти решению примеров на умножение и деление для 5 класса.
Примеры решений
Для примера следует разобрать задачу на перемножение чисел 25 и 25. В этом случае рекомендуется воспользоваться таким алгоритмом:
- Записать первый множитель, а под ним второй.
- Провести результирующую горизонтальную линию после величин в первом пункте.
- Поставить слева знак произведения.
- Умножить 25 на 5 (разряд единиц), а затем записать под чертой: 125.

- Перемножить 25 и 2 (десятки): 50.
- Записать величину, полученную в пятом пункте под десятками первого результата.
- Сложить величины 125+50 (смещенное влево): 625.
Следующий пример — задание на операцию деления 625 на 5. Для этого следует воспользоваться вышеописанной методикой:
- Написать делимое и делитель, разделив их вертикальной чертой.
- Рассмотреть I разряд. Он делится на 5, но с остатком: 6/5=1 (1 — остаток).
- Записать в поле результата число 1.
- Перемножить 1 и 5, записав под шестеркой: 5.
- Отделить остаток: 1.
- Перенести к 1 второй разряд: 12.
- Подобрать множитель: 5*2=10<12.
- Перемножить 5 и 2, записав результат под 12.
- Выделить остаток: 2.
- Перенести к 2 III разряд: 25.
- Осуществить деление 25 на пятерку: 25/5=5.
- Искомое частное: 125.
Следует отметить, что множитель при выполнении операции деления подбирается по такому принципу: его произведение на делитель не должно превышать значения делимого. Операция с остатком реализуется аналогично. Например, в выражении 4/3 остаток равен единице, а результат записывается следующим образом: 4/3=1 (+1). Последнее значение «(+1)» указывает на положительный остаток, т. е. 3*1+1=4.
Операция с остатком реализуется аналогично. Например, в выражении 4/3 остаток равен единице, а результат записывается следующим образом: 4/3=1 (+1). Последнее значение «(+1)» указывает на положительный остаток, т. е. 3*1+1=4.
Иногда в математической литературе можно встретить запись «(-1)», которая указывает на отрицательную величину остатка. Например, запись «11 (-1)» при делении неизвестного числа на тройку определяет исходную величину следующим образом: 3*11−1=33−1=32. Пример возможно править и в таком виде: 32/3=10 (+2)=11 (-1).
Таким образом, арифметические операции умножения и деления рекомендуется при отсутствии калькулятора выполнять в столбик, но для этого следует знать основные методики.
Не успеваете написать работу?
Заполните форму и узнайте стоимость
Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертацияКонтактные данные — строго конфиденциальны!
Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.
* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности
Подтверждение
Ваша заявка принята.
Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.
Ошибка оформления заказа
Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.
Ответ: Только для гения?? 3 – 3 х 6 + 2 = ??
Опубликовано автором WinthropDC Веселье

Даже с намеком на то, что надо запомнить порядок действий, в моем опросе люди все равно ошибались. Если вы еще не участвовали в опросе, нажмите на ссылку выше и ответьте.
Вопрос был
Правильный ответ:
- Вопрос: 3 – 3 x 6 + 2
- Первое умножение: 3 – 18 + 2
- Слева направо: -15 + 2 (или сложение сначала: 3 – 16)
- Ответ: -13
[Начать редактирование] Меня много раз спрашивали в комментариях, почему шаг 3 вычисляется только слева направо? «Разве ты не должен сначала сделать сложение?». Поэтому я добавляю этот раздел пояснений в начало статьи (он аналогичен информации в связанных связанных постах).
Порядок операций (за исключением первых двух частей Скобки/Квадратные скобки и Экспоненты/Порядки/Индексы) следующий: [DM] или [MD], за которыми следует [AS] или [SA]. Таким образом, умножение и деление можно выполнять одновременно, а затем одновременно выполнять сложение и вычитание.
Попробуйте посчитать следующие примеры слева направо:
Умножение и деление: 4 x 3 / 2 = 6 и 4 / 2 x 3 = 6 …. Порядок не имеет значения.
Сложение и вычитание: 10 – 5 + 2 = 7 и 10 + 2 – 5 = 7 …. Порядок не имеет значения.
На самом деле деление — это просто умножение обратного числа. Например: Деление на 2 равносильно умножению на 1/2.
Кроме того, вычитание — это просто сложение отрицательного числа. Например: вычитание 10 равносильно прибавлению -10.
Математика точна, и это одна из ее прелестей. Пока вы делаете это правильно, вы всегда будете получать один и тот же ответ.
Для тех из вас, кто все еще настаивает на сложении перед вычитанием:
- Вопрос: 3 – 3 x 6 + 2
- Первое умножение: 3 – 18 + 2
- Дополнение следующее: 3 – 16
- Ответ: -13 … тот же ответ, что и раньше.

Обратите внимание, что -18 + 2 это не -20, это -16. Вы не можете игнорировать знак минус перед 18.
Кроме того, 3 – 18 + 2 не равно 3 – (18 + 2) оно равно 3 – (18 -2), потому что есть минус знак перед скобками на знак 2 должен быть изменен при перемещении его внутрь скобок.
Если вы мне не верите, попробуйте решить 3 + 2 – 3 x 6 или 3 + -3 x 6 + 2, которые эквивалентны исходному уравнению.
Все числа (кроме нуля) либо положительные, либо отрицательные. Перед отрицательными числами стоит знак минус, а перед положительными — знак плюс. Но из-за лени мы обычно не пишем знак плюс, если только он не находится между двумя числами.
Итак, 3 – 3 x 6 + 2 становится +3 -3 x +6 +2 = +3 -18 +2. Теперь вы можете использовать числовую линию, чтобы закончить расчет.
Ответ по-прежнему есть и всегда будет -13.
[Конец редактирования]
Итак, что вы получите, если введете это в калькулятор (физический или в приложении)?
Это зависит от того, является ли калькулятор простым и вычисляет по мере ввода, или он умный и ожидает ввода всего уравнения и нажатия кнопки равенства.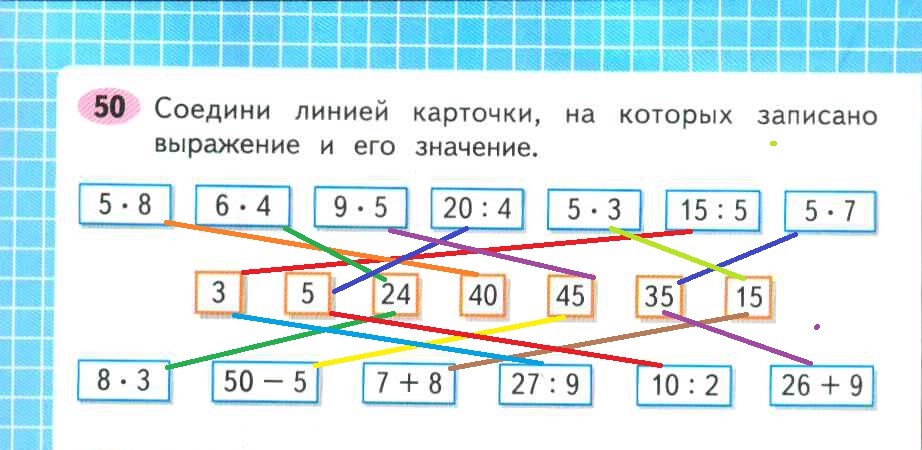
На моем телефоне с Windows 10 Mobile приложение калькулятора может работать в обоих направлениях.
В научном режиме он позволяет ввести уравнение целиком и поэтому правильно вычисляет ответ как -13, используя правила «Порядка операций» (такие же, как выше).
В стандартном режиме он вычисляет по мере ввода и поэтому неправильно дает ответ как 2. Можно думать об этом так, что он по своей сути нажимает равно каждый раз, когда вы нажимаете операционную кнопку. Это просто расчет слева направо и игнорирует правила «Порядка операций».
- 3 = 3
- 3 – 3 = 0
- 0 х 6 = 0
- 0 + 2 = 2
Если ваш калькулятор ведет себя так просто, вам придется применять правила самостоятельно. Вот кнопки, которые нужно нажать:
- 3 x 6 = MS
- 3 – МР + 2 =
Если на вашем калькуляторе есть кнопки со скобками или круглыми скобками, вы можете использовать их вместо кнопок памяти для достижения того же эффекта.
- 3 – ( 3 x 6 ) + 2
Глядя на результаты опроса из предыдущей статьи, было выбрано несколько неправильных ответов, поэтому я решил попытаться определить фактических уравнений, которые дали бы эти неправильные ответы (изменения выделены красным):
- -17 = 3 – ( 3 x 6 + 2 )
- -17 = 3 – 3 х 6 – 2
- 0 = ( 3 – 3 ) x ( 6 + 2 )
- 2 = ( 3 – 3 ) х 6 + 2
- 8 = 3 – 3 + 6 + 2
- 13 = — 3 + 3 x 6 — 2
- 17 = – 3 + 3 x 6 + 2
Надеюсь, все это имеет смысл. Вот и конец урока. 🙂
Посмотрите другие посты из этой серии:
- В тренде: Только для гениев ?? 3 – 3 х 6 + 2 = ?? С опросом и порядком работы
- Ответ: Только для гения?? 3 – 3 х 6 + 2 = ?? Эта статья
- Вывод: Только для гениев?? 3 – 3 х 6 + 2 = ?? Разбивает решение на шаги
- Последнее слово: только для гениев ?? 3 – 3 х 6 + 2 = ?? Объясняет заказ DM и AS
- Вирус: Только для гениев ?? 3 – 3 х 6 + 2 = ?? Ответ стал вирусным и пояснения
Насладись
Дэвид
03 декабря 2016 г. : В начало статьи добавлены дополнительные пояснения.
: В начало статьи добавлены дополнительные пояснения.
05 декабря 2016: Добавлена дополнительная информация о числовых строках.
Первоначально эта статья была размещена на http://www.winthropdc.com/blog.
Нравится:
Нравится Загрузка…
ВесельеВирусная математическая задача с двумя ответами разделяет Интернет
- Пользователь Твиттера @pjmdoll поделился математической задачей: 8 ÷ 2(2 + 2) = ?
- Кто-то получил 16, а кто-то 1.
- Путаница связана с различием между современной и исторической интерпретацией порядка операций.
- Правильный ответ сегодня — 16. Ответ 1 был бы правильным 100 лет назад.
- Посетите домашнюю страницу INSIDER, чтобы узнать больше.
Спасибо за регистрацию!
Получайте доступ к своим любимым темам в персонализированной ленте, пока вы в пути.
Вирусные математические уравнения, как известно, разделяют людей в Интернете. Некоторые задачи настолько ошеломляюще сложны, что кажутся невыполнимыми, даже если они предназначены для учащихся начальной школы.
Подробнее : 10 вирусных математических уравнений, которые поставили Интернет в тупик
Эта последняя вирусная проблема, которой поделился пользователь Твиттера @pjmdoll, является одним из таких уравнений.
—em ♥︎ (@pjmdolI) 28 июля 2019 г.
Уравнение: 8 ÷ 2(2 + 2) = ?
Все продолжают получать разные ответы.
—laur♏️ (@lauram_williams) 30 июля 2019 г.
—becca 10✧*.✰LILY + BARBS DAY (@spaceywhy) 30 июля 2019 г.
—maggie (@BatmanOfficial_) 29 июля 2019 г.В. Куш (@supermaddd) 29 июля 2019 г.
—Light💜 ᴮᵃⁿᵍᵗᵃⁿ ᶠᵒʳᵉᵛᵉʳ 💜 (@SakuraTsukimine) 29 июля, 2019
Вот как правильно решить 8 ÷ 2(2 + 2) = ?
Сначала добавьте числа в скобках.
8 ÷ 2(4) = ?
Теперь выполните умножение и деление слева направо.
8 ÷ 2(4) = 4(4) = 16.
Путаница вызвана различием между современной и исторической интерпретацией порядка операций, известной как PEMDAS: и дивизия (слева направо)
Похожая математическая задача стала вирусной в 2011 году, когда люди не могли прийти к единому мнению относительно ответа на 48÷2(9+3). Преш Талуокер, автор книги «Радость теории игр: введение в стратегическое мышление», объяснил полемику на своем канале YouTube MindYourDecisions и в сообщении в своем блоге.
Люди, получившие число 1 в качестве ответа на эту задачу, использовали устаревшую версию порядка операций, сначала умножая 2(4), а затем деля 8 на 8, согласно Талуокеру. Такой ответ был бы правильным 100 лет назад. Но подставив уравнение как есть в современный калькулятор, вы получите ответ 16. Чтобы получить ответ 1, вам нужно добавить еще один набор скобок.0007 Люди получают разные ответы в зависимости от того, как они применяют порядок операций. Талия Лакриц/INSIDER
Талуокер объясняет, что часть путаницы также вызвана тем, что в задаче неоднозначно указан символ деления.
«В учебниках всегда есть правильные скобки, или они объясняют, что нужно разделить», — пишет он в своем блоге.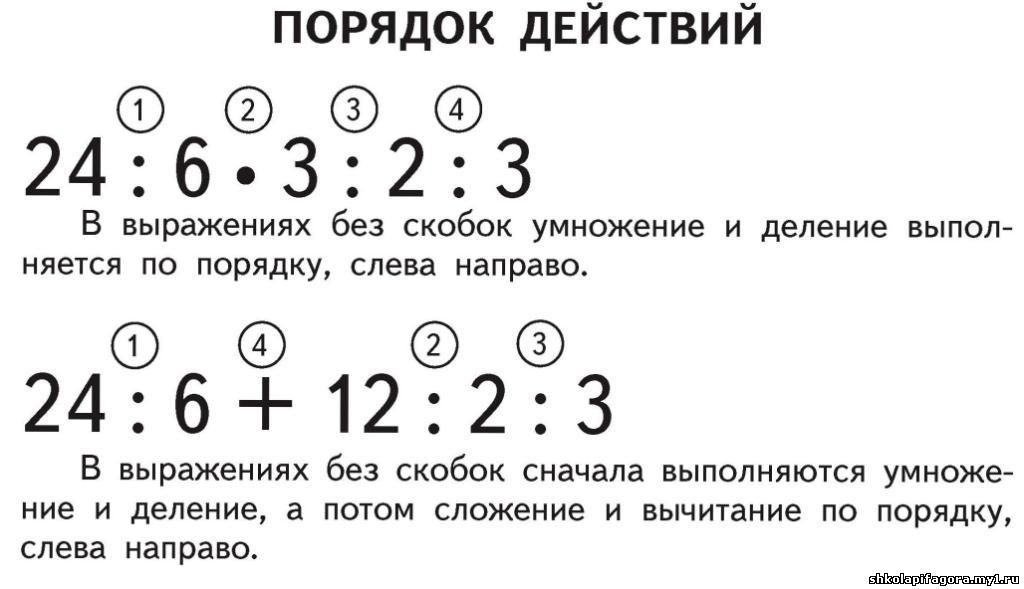

 Это свойство может быть полезно при решении уравнений.
Это свойство может быть полезно при решении уравнений.


