Как делить со скобками, что вперед: деление или умножение, как решить 36:3(8–6) дробь 6, правильный ответ на пример — 17 января 2023
Все новостиЗабрали квартиру и лишили звания: в Сочи полицейский погорел на взятках
Кто первый встал, того и паркинг: в Сочи начали борьбу с парковочными барьерами
«Нас учат заканчивать полет в аэропорту, но никак не на кукурузном поле». Интервью с легендарным пилотом Дамиром Юсуповым
Деньги взял и ушел в закат: в Сочи будут судить застройщика-мошенника
«Полиция начала применять водометы и слезоточивый газ»: россиянин приехал в отпуск в Грузию и попал в эпицентр протестов
Дороже в пять раз: прогнозируют рост цен на авиабилеты в Сочи на майские праздники
Фейка больше нет: иностранные слова попали под запрет. Проверьте, сможете ли вы заменить их на русские
У пьяного водителя отобрали права, а он вернул их, доказав, что врачи осматривали его без разрешения
Серьезное ДТП частично заблокировало выезд из тоннеля в Сочи
В Черном море между Сочи и Турцией произошло землетрясение
«Я в плену». Заключенный годами доказывает, что его подставили опера. Полицейских посадили, но его не отпускают
Заключенный годами доказывает, что его подставили опера. Полицейских посадили, но его не отпускают
Доллар по сто к концу марта? Какой максимум прочат экономисты валюте и на чем скажется этот скачок
В Израиле двое мужчин открыли стрельбу по прохожим: есть тяжелораненые
«Массированный удар возмездия» и первый памятник героям спецоперации: новости СВО за 9 марта
Экс-чиновник заперся в квартире с трехлетним сыном и начал стрелять из окна по людям — кадры с места
Сколько можно голодать? Что произойдет с организмом, если перестать есть
На 2% больше: в Сочи посчитали туристов, приехавших на праздники
«Думали, никогда не увидим ее улыбки»: девочку парализовало после укуса клеща, которого в дом принес кот
«Все были немного в шоке»: откровения многодетной мамы, которая очень мечтала о детях и родила тройню без ЭКО
Генплан стал поводом для мошенничества в Сочи
Вы точно это видели? Попробуйте вспомнить, чем закончились эти советские фильмы
Семьям военнослужащих оплатят жилье
Коварные тихие убийцы. Известный российский нефролог рассказал, почему важно проверять почки
Известный российский нефролог рассказал, почему важно проверять почки
«Так шибануло, что аж машина подпрыгнула»: как взорвался газ в читинской пятиэтажке — посмотрите на дом
Минобороны объяснило новые обстрелы Украины ответом на диверсию в Брянской области
Мужчины устроили мордобой в очереди на аттракционы в Сочи Парке
Стартовала продажа «единых» билетов из России в Абхазию через Сочи
«На миллионера обижается — представляет себя миллиардером»: на чем зарабатывает 8-летний школьник
Очереди по два часа и эвакуация с аттракциона: в Сочи отметили 8 Марта
В Сочи следователи устанавливают обстоятельства пожара, в результате которого погиб местный житель
Вкусная еда, дорогой бензин и проблемы с парковкой: россиянин рассказал, как переехал в Грецию
В Сочи начались общественные слушания по проекту нового Генплана
В Грузии отозвали законопроект об иноагентах, из-за которого в стране несколько дней шли беспорядки
В горах Сочи сноубордист спровоцировал лавину и сам попал под нее
Золотые огурцы, бриллиантовые яйца: экономисты назвали 12 продуктов, которые подорожают в скором времени
В Чите взорвался газ в многоэтажке — из-под завалов достали маленькую девочку
Выбежали в чём были. В центре Сочи дотла сгорел жилой дом
В центре Сочи дотла сгорел жилой дом
В Нижневартовске мужчина заперся с ребенком в квартире и угрожает суицидом. Что известно на данный момент
«Если тебя убьют, я заберу у тебя магазин?» Как врач-реаниматолог трижды ездил в зону спецоперации
Все новости
Сможете решить правильно?
Иллюстрация: Юрий Орлов / NGS.RU
Поделиться
Минимум неделю в интернете миллионы людей ломают копья из-за простенького, на первый взгляд, примера. NGS.RU решил задачку вместе с кандидатом физико-математических наук, доцентом и преподавателем Новосибирского государственного университета Ильей Марьясовым.
Вот этот пример: 36 : 3 (8 − 6) дробь 6.
Некоторые люди готовы спорить часами, как решить этот пример
Фото: Александра Бруня / NGS.RU
Поделиться
— Подвоха здесь особо никакого нет. У нас в математике есть соглашение о том, как у нас должны выполняться арифметические операции. Умножение и деление имеют более высокий приоритет, чем сложение и вычитание. Когда нужно изменить порядок вычисления, чтобы сложение и вычитание выполнялись раньше, то используются скобки. И еще один момент — когда появляются дроби, а дробная черта — это деление, то в этом случае оно выполняется в последнюю очередь, — объяснил Илья Марьясов
У нас в математике есть соглашение о том, как у нас должны выполняться арифметические операции. Умножение и деление имеют более высокий приоритет, чем сложение и вычитание. Когда нужно изменить порядок вычисления, чтобы сложение и вычитание выполнялись раньше, то используются скобки. И еще один момент — когда появляются дроби, а дробная черта — это деление, то в этом случае оно выполняется в последнюю очередь, — объяснил Илья Марьясов
Разбираемся с числителем. По очереди идут деление, умножение, вычитание — при этом последняя операция идет в скобках. Начинаем решать слева направо.
— Поскольку деление и умножение равноправны. Сначала 36 делим на 3 и получаем 12. Потом мы должны выполнить умножение, но поскольку вычитание стоит в скобках, то сначала делаем его. Из 8 вычитаем 6 и получаем 2. Теперь делаем умножение. Мы 12 умножаем на 2 и получаем 24. Теперь делим числитель на знаменатель. То есть 24 делим на 6 и получаем 4, — объяснил специалист.
Правильный ответ — 4.
— Как изучают математику в школе. В начальном звене вводят операции — сложение, вычитание, умножение и деление. Примерно до 6-го класса дети не знают, что существуют рациональные числа, которые записываются в виде дробной черты. Когда они вводятся, то выясняется, что операцию деления можно записать не в виде двух точек. И до самого вуза очень часто все выражения записываются, как дробное число и отдельная операция деления через две точки редко используется. Так умножение у людей фиксируется как приоритетная операция, — объяснил Илья Марьясов.
В итоге это приводит к ошибке в вычислениях.
— У людей возникает соблазн 3 умножить на 8 минус 6 (то есть на 2) и получается у них 6. Потом 36 делят на 6, получая 6. И в итоге 6 делят на 6 и выходит 1. Это неверный ответ в данном случае, — отметил математик.
Ранее в Высшей школе экономики подсчитали, что средний проходной балл ЕГЭ для поступления в вузы снизился впервые за 10 лет. Предлагаем вам ответить на несколько вопросов (разных лет) из того самого итогового среза знаний.
По теме
20 января 2023, 16:00
Один и тот же пример в разных странах решают по-разному. Как это получается?18 декабря 2022, 15:30
«Любите ли вы сплетничать?» Журналист попытался обмануть детектор лжи, и вот что обнаружил полиграф19 сентября 2022, 10:00
Это точно русский? Проверьте, сможете ли вы написать правильно все эти слова18 декабря 2022, 14:00
Русский не родной? 10 простейших слов, которые все пишут с ошибками23 февраля 2023, 17:00
Зеркальная дата 23.02.2023: что не стоит делать в этот день, чтобы не накликать беду, — советы нумеролога
Александра Бруня
Корреспондент
МатематикаРешениеПримерРазбор
- ЛАЙК0
- СМЕХ0
- УДИВЛЕНИЕ0
- ГНЕВ0
- ПЕЧАЛЬ0
Увидели опечатку? Выделите фрагмент и нажмите Ctrl+Enter
КОММЕНТАРИИ0
Гость
Войти
Новости СМИ2
Новости СМИ2
Порядок действий в математике, последовательность выполнения умножения, сложения, деления, вычитания, правила очередности арифметических действий
Главная » Мамины лайфхаки » Порядок действий в математике, последовательность выполнения умножения, сложения, деления, вычитания, правила очередности арифметических действий
Содержание
- Основные операции в математике
- Что такое действия первой и второй ступени
- Сложение и вычитание
- Умножение
- Что сначала — умножение или сложение?
- Деление
- Порядок действий без скобок
- Порядок действий со скобками
- Примеры на порядок действий 3-4 класс для тренировки
Основные операции в математике
Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).
Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).
Операции действия:
- сложение (+)
- вычитание (-)
- умножение (*)
- деление (:)
Операции отношения:
- равно (=)
- больше (>)
- меньше (<)
- больше или равно (≥)
- меньше или равно (≤)
- не равно (≠)
Сложение — операция, которая позволяет объединить два слагаемых.
Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.
Вычитание — действие, обратное сложению.
Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.
Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.
Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.
- Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.

- 3 * 4 = 3 + 3 + 3 + 3
В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.
Поэтому и множитель, и множимое называют сомножителями.
Деление — арифметическое действие обратное умножению.
Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.
В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.
Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.
Возведение степень — операция умножения числа на самого себя несколько раз.
Основание степени — число, которое повторяется сомножителем определённое количество раз.
Показатель степени — число, которое указывает, сколько раз берется одинаковый множитель.
Степенью называется число, которое получается в результате взаимодействия основания и показателя степени.
- Запись: 34 = 81, где 3 — основание степени, 4 — показатель степени, 81 — степень.
 4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня). - 2√16 = 4 — корень второй степени называется — квадратным.
При знаке квадратного корня показатель корня принято опускать: √16 = 4.
3√8 = 2 — корень третьей степени называется — кубическим.
Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Сложение и вычитание
Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.
Самое простое человеческое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.
Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.
Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.
И для этих действий придумали технику вычислений.
Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно семь. Посчитать можно на счетных палочках, камнях, рыбьих головах – результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.
Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.
Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.
Сложение столбиком − это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.
Умножение
Математики любят группировать похожие действия для упрощения расчетов. Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.
Для вычисления произведения используется такой же метод – сначала тупо заучивается таблица умножения цифр друг на друга, а потом применяется метод поразрядного умножения, что называется «в столбик».
Что сначала — умножение или сложение?
Любое математическое выражение – это фактически запись учетчика «с полей» о результатах каких-либо действий. Допустим, сбора урожая помидоров:
- 5 взрослых работников собрали по 500 помидоров каждый и выполнили норму.
- 2 школьников не ходили на уроки математики и помогали взрослым: собрали по 50 помидоров, норму не выполнили, съели 30 помидоров, надкусили и испортили еще 60 помидоров, 70 помидоров было изъято из карманов помощников.
 Зачем брали с собой их в поле – непонятно.
Зачем брали с собой их в поле – непонятно.
Все помидоры сдавали учетчику, он укладывал их по кучкам.
Запишем результат «сбора» урожая в виде выражения:
- 500 + 500 + 500 + 500 + 500 — это кучки взрослых работников;
- 50 + 50 – это кучки малолетних работников;
- 70 – изъято из карманов школьников (испорченное и надкусанное в зачет результата не идет).
Получаем пример для школы, запись учетчика результатов работы:
500 + 500 +500 +500 +500 + 50 +50 + 70 =?;
Здесь можно применить группировку: 5 кучек по 500 помидоров − это можно записать через операцию умножения: 5 ∙ 500.
Две кучки по 50 – это тоже можно записать через умножение.
И одна кучка 70 помидоров.
5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70 =?
И что делать в примере сначала − умножение или сложение? Так вот, складывать можно только помидоры. Нельзя сложить 500 помидоров и 2 кучки. Они не складываются. Поэтому сначала нужно всегда все записи привести к базовым операциям сложения, то есть в первую очередь вычислить все операции группировки-умножения. Совсем простыми словами — сначала выполняется умножение, а сложение уже потом. Если умножить 5 кучек по 500 помидоров каждая, то получится 2500 помидоров. А дальше их уже можно складывать с помидорами из других кучек.
Совсем простыми словами — сначала выполняется умножение, а сложение уже потом. Если умножить 5 кучек по 500 помидоров каждая, то получится 2500 помидоров. А дальше их уже можно складывать с помидорами из других кучек.
2500 + 100 + 70 = 2 670
При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.
Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.
Деление
Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов. Самый прямой аналог в жизни – это фасовка.
Самый прямой аналог в жизни – это фасовка.
Порядок действий без скобок
Установленный порядок арифметических действий без скобок:
- Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:
- Если выражение содержит только действия на умножение и деление, то действия выполняются в порядке следования — слева направо:
- Если в выражении присутствуют и умножение с делением, и сложение с вычитанием, то сначала выполняются умножение и деление в порядке их следования (слева направо), а затем сложение и вычитание в порядке их следования (слева направо):
Порядок действий со скобками
Если выражение содержит скобки, то сначала выполняются все действия внутри скобок, а затем все действия, находящиеся за скобками.
В числовых выражениях со скобками порядок выполнения арифметических действий такой же, как и в выражениях без скобок.
Скобки применяются для обозначения действий, которые нужно произвести раньше остальных. Скобки не влияют на порядок остальных действий в выражении, остальные действия выполняются в указанном порядке.
Скобки не влияют на порядок остальных действий в выражении, остальные действия выполняются в указанном порядке.
Примеры на порядок действий 3-4 класс для тренировки
Рассмотрим выражения, установим порядок действий и выполним вычисления.
Будем действовать по правилу. В выражении 43 – (20 – 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 – (20 – 7) +15 =43 – 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 – 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 – 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении.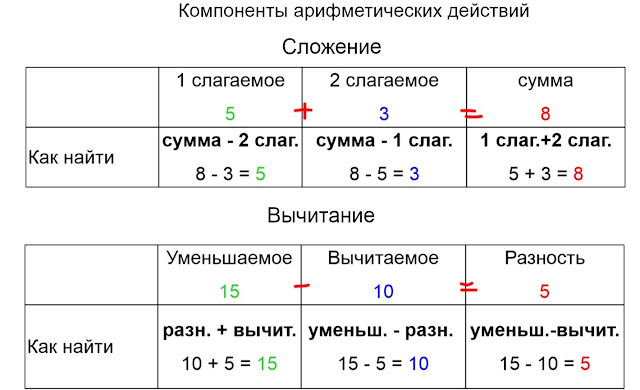 То есть первое действие – умножение, второе – деление, третье – вычитание.
То есть первое действие – умножение, второе – деление, третье – вычитание.
Узнаем, правильно ли определен порядок действий в следующих выражениях.
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.
 : «Просвещение», 2012.
: «Просвещение», 2012. - М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
Определи порядок действий в данных выражениях. Найди значение выражений.
***
Определи, в каком выражении такой порядок выполнения действий:
- умножение;
- деление;.
- сложение;
- вычитание;
- сложение.
Найди значение данного выражения.
***
Составь три выражения, в которых такой порядок выполнения действий:
- умножение; 2.
 сложение; 3. вычитание
сложение; 3. вычитание - сложение; 2. вычитание; 3. сложение
- умножение; 2. деление; 3. сложение
Найди значение этих выражений.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.
Если производить действия в порядке их записи.
Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.
Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:
Чтобы не загромождать чрезмерно записи, условились не писать скобок:
- в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны;
- в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.

При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:
- сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
- затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.
Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 – 9 = 1
Сначала выполняем действия в скобках:
16 – 2 · 7 + 4 = 16 – 14 + 4 = 6
2 + 5 = 7
Теперь выполняем остающиеся действия:
9 + 16 : 4 – 2 · 6 + 6 · 7 =
= 9 + 4 – 12 + 42 =
= 43
Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки. Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные [].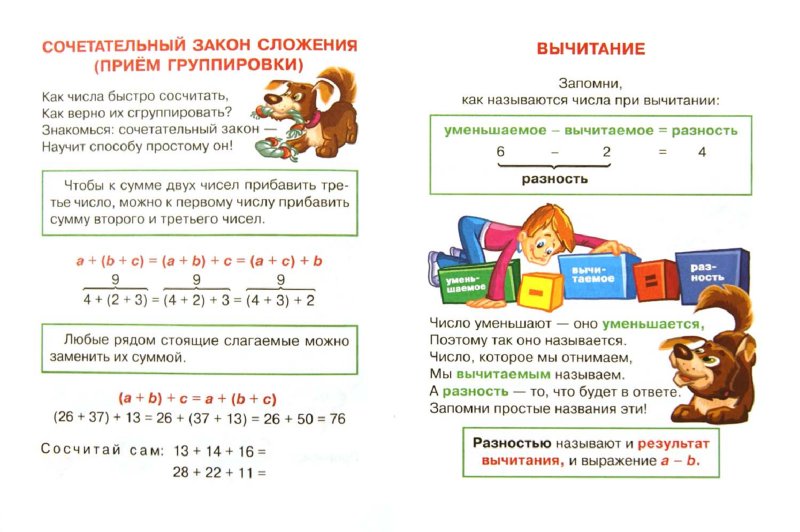 Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Выполняем действия в круглых скобках, имеем:
8 – 6 = 2
10 – 2 · 3 = 10 – 6 = 4
действия в квадратных скобках дают:
14 – 3 · 2 = 8
выполняя остающиеся действия скобках находим:
5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29
Порядок действий:
30 – 20 = 10
35 – 10 = 25
100 – 25 = 75
75 · 2 = 150
Расставь порядок действий. Найди значение выражения:
- (12 – 0 : 4) : 3 – (7 — 7)*45 + (36 : 6) : (15 : 15)
- 36 : (12 – 6 : 20 – (0 *5 + 3) – (7 * 8) : 14 : 4
- (3 + 27 : 3) * 5 – 60 * 3 : 90 + 8 * (7 – 7) : 4
- (630 : 7 + 4 * 9) : (5 + 5 : 5) + (8 – 8) : (35 * 7 + 49)
- 5 * (48 : 6 + 2 : 2) – 280 : 20 * 3 + (50 – 32) : 9
- 8040 : 6 + (109004 – 76048) : 7
- (64000 : 80 * 3 + 600) : 15 – (3200 * 100) : 2000
- 240400 – (5796 + 1803200 : 400) * 8
- 345 * (250 * 125) * (8 * 400)
- 56432 : 8 * 50 – (223956 + 882630 : 9)
- (62456715 + 548185) : 700 – 300 * 80450 : 5000
- 80 – (17 * 4) : (20 – 380 : 20) + 90 * 40 : 120
- (1000 – 999) * 40 – 0 : 24 + 360 : (16 * 5 + 280 : 7)
- (600000 – 538704) * 500 : 300
- 280 : (60 : 15) – (25 + 3 * 8) : 7 + 3 * (720 : 80)
- (250 * 840 – 145 * 1008) : 60
- (1000 – 832) * 715 : 30 + (104402 – 58842 : 7)
Источники
- https://skysmart.
 ru/articles/mathematic/poryadok-dejstvij-v-matematike
ru/articles/mathematic/poryadok-dejstvij-v-matematike - https://Zaochnik.com/spravochnik/matematika/vyrazhenija/porjadok-vypolnenija-dejstvij/
- https://1Ku.ru/obrazovanie/62562-chto-snachala-slozhenie-ili-umnozhenie-pravila-porjadok-vypolnenija-dejstvija-i-rekomendacii/
- https://izamorfix.ru/matematika/arifmetika/poryadok_deystviy.html
- https://koncpekt.ru/nachalnye-klassy/rabochie-programmy/matematika-4-klass/5032-primery-na-poryadok-deystviy-so-skobkami-po-matematike-dlya-3-4-klassa.html
развлекательная математика — BEDMAS, где порядок сложения перед вычитанием имеет значение?
Представьте себе мир, в котором BEDMAS не существует и где необходимо указать, в каком именно порядке оцениваются операции в выражении, с помощью круглых скобок. Правильное выражение выглядит примерно так:
$$((a + b) \times (c \div (d — e)))$$
Посмотрите на это выражение. Он имеет четыре операции и четыре набора скобок. Каждый набор скобок принадлежит ровно одной операции и наоборот.
$$\цвет{красный}(\цвет{оранжевый}(3\цвет{оранжевый}+ 5\цвет{оранжевый}) \цвет{красный}\раз \цвет{синий}(6 \цвет{синий}\ div \color{#00bf00}(9 \color{#00bf00}- 7\color{#00bf00})\color{blue})\color{red})$$
С помощью этих скобок мы точно знаем, как вычислить это выражение. Результат этого выражения равен $24$.
Теперь рассмотрим большое выражение. Что, если вы не хотите постоянно писать все эти скобки? Что делать, если вы хотите, чтобы большие выражения было легче читать? Не могли бы вы подумать о способах уменьшить количество скобок и общих символов, которые вам нужны, таким образом, чтобы результирующее выражение оставалось однозначным? Ну, математики бы. И именно поэтому существует BEDMAS.
Сначала рассмотрим выражения, в которых используется только $+$. Рассмотрим выражение $((a + b) + ((c + d) + e))$. В этом выражении достаточно круглых скобок, чтобы однозначно определить порядок операций. Но у $+$ есть замечательное свойство: для любых чисел $a, b, c$ всегда выполняется $(a+b)+c = a+(b+c)$. Это называется законом ассоциативности . Теперь, если у нас есть куча сумм сумм, мы можем просто опустить скобки между ними, потому что независимо от того, как вы их вставите, вы всегда получите один и тот же результат. Наше выражение упрощается до $a + b + c + d + e$. Отлично, мы уже избавились от многих скобок.
Это называется законом ассоциативности . Теперь, если у нас есть куча сумм сумм, мы можем просто опустить скобки между ними, потому что независимо от того, как вы их вставите, вы всегда получите один и тот же результат. Наше выражение упрощается до $a + b + c + d + e$. Отлично, мы уже избавились от многих скобок.
Теперь добавим $\times$ в бой. Закон ассоциативности выполняется и для $\times$, поэтому мы можем написать $a \times b \times c \times d \times e$ вместо $((a \times b) \times ((c \times d) \раз е))$. Теперь давайте посмотрим, что произойдет, если вы объедините $+$ и $\times$. Мы знаем, что $a + (b \times c)$ и $(a + b) \times c$ — разные выражения, поэтому мы не можем удалить скобки в обоих случаях. Но вот новый закон: мы можем переписать $(a + b) \times c$ как $(a \times c) + (b \times c)$. это закон распределения . Это означает, что мы можем написать любое выражение, используя $+$ и $\times$, как выражение, в котором вы всегда сначала выполняете все умножения, а только потом все сложения.
Как следствие, мы можем изобрести новый способ скрытия скобок. В терминах, где умножение и сложение стоят рядом друг с другом без скобок, мы соглашаемся всегда сначала выполнять умножение. Это отличный способ, потому что, когда мы его используем, мы можем написать любой термин, используя $+$ и $\times$ вообще без каких-либо круглых скобок!
Пример:
Используя закон дистрибутивности, мы можем переписать
$$(a \times (b + ((c + d) \times (e + f))))$$ в $$((a \times b) + (((a \times (c \times e)) + (a \times (c \times f))) + ((a \times (d \times e)) + (a \times ( d \times f)))))$$
Здесь много операторов, но если мы договоримся сначала сделать умножение и вспомним закон ассоциативности, то получим
$$a \times b + a \times c \times e + a \times c \times f + a \times d \times e + a \times d \times f$$
, который вообще не содержит скобок! Это не всегда было бы возможно, если бы мы оценивали слева направо или сложение перед умножением.
Теперь добавим вычитание. Во-первых, давайте вспомним, что слева от выражения стоит унарный знак минус, например, $-a$ — это сокращение для $(0-a)$. Рассмотрим член сложения и вычитания:
Во-первых, давайте вспомним, что слева от выражения стоит унарный знак минус, например, $-a$ — это сокращение для $(0-a)$. Рассмотрим член сложения и вычитания:
$$(a — (b — (c + (d — e))))$$
Используя законы $a + (b — c) = (a + b) — c$, $~a — (b + c) = (a — b) — c$ и $a — (b — c) = (a-b) + c$, мы можем переупорядочить эту последовательность операций так, чтобы скобки сдвигаются как можно дальше влево, поэтому сложение и вычитание выполняются слева направо:
$$((((a — b) + c) + d) — e)$$
Итак, давайте просто договоримся, что сложение и вычитание без скобок выполняются слева направо. Мы получаем
$$a — b + c + d — e$$
Это имеет то преимущество, что с этой записью вы фактически можете переписать вычитание как сложение отрицаний с помощью унарного $-$:
$$a + ( -b) + c + d + (-e)$$
Таким образом, этот метод делает термин намного более легким для чтения и понимания, и это позволяет нам намного легче переупорядочивать слагаемые в этой сумме.
Если мы хотим смешать умножение и вычитание, мы снова указываем, что сначала выполняется умножение.
Теперь перейдем к делению. Рассмотрим термин, смешивающий умножение и деление. Как и в случае сложения и вычитания, мы можем изменить порядок скобок так, чтобы операции выполнялись слева направо, используя совершенно аналогичные законы $a \times (b \div c) = (a \times b) \div c$ , $~a \div (b \times c) = (a \div b) \div c$ и $a \div (b \div c) = (a\div b) \times c$.
Теперь мы согласны сбрасывать круглые скобки, когда операции фактически выполняются слева направо. Итак,
$$(a \div (b \times (c \div (d \div e))))$$
становится
$$((((a \div b) \div c) \times г) \div e)$$
, которое мы записываем как $$a \div b \div c \times d \div e$$
Опять же, мы можем интерпретировать деление как умножение с обратным:
$$a \times (1 \div b) \times (1 \div c) \times d \times (1 \div e)$$
Таким образом, с этим описанием намного проще работать, например, мы можем очень легко изменить его порядок.
Когда деление смешивается со сложением или вычитанием, мы говорим, что деление всегда выполняется первым по умолчанию.
Теперь обратите внимание, что термины, использующие $\div$, не всегда могут быть записаны без круглых скобок, например, $a \div (b + c)$.
Из-за этого математики больше не используют символ $\div$. Вместо этого они используют дробную запись:
$$a \div b = \frac{a}{b}$$. Приятно то, что мы можем рисовать горизонтальную линию посередине сколь угодно долго, и что линия четко отделяет то, что находится над линией, от того, что ниже линии. Таким образом, мы можем опустить еще несколько скобок:
$$a \div (b + c) = \frac{a}{b+c}$$
Сравните это с
$$(a \div b) + c = \frac{a}{b } + c$$
Ясно, что мы видим разницу.
Таким образом, мы можем написать любой терм, используя $+$, $-$, $\times$, $\div$ совершенно без круглых скобок!
Рассмотрим термин $((a + b) \times (c \div (d — e)))$ из начала моего ответа. Он имеет четыре набора круглых скобок, которых мы теперь технически можем избежать, используя соответствующие обозначения и расширяя их с помощью дистрибутивного закона:
Он имеет четыре набора круглых скобок, которых мы теперь технически можем избежать, используя соответствующие обозначения и расширяя их с помощью дистрибутивного закона:
$$a \times \frac{c}{d — e} + b \times \frac{c}{d-e}$$
Обратите внимание, что это выражение обычно записывается как
$$(a + б) \times \frac{c}{d — e}$$
, так как это на самом деле легче читать и понимать. В конце концов, мы не запретили круглые скобки, мы просто придумали способы избежать их написания.
Теперь имейте в виду, что, поскольку никто из школьников на самом деле не использует $\div$, приоритет $\times$ и $\div$ на самом деле не является общепринятым. Это означает, что нам нужно использовать круглые скобки, когда $\div$ стоит перед $\times$, чтобы люди не запутались.
Теперь мы можем, наконец, взглянуть на термин на картинке вашего вопроса:
$$6 — 1 \times 0 + 2 \div 2$$
Если мы заменим круглые скобки, используя установленные нами правила, мы получаем
$$((6 — (1 \times 0)) + (2 \div 2)) = 7$$
, что теперь должно быть совершенно однозначным.
Правила, которые мы установили, как вы уже, наверное, догадались, и есть БЭДМАС (или, скорее, БДМАС, поскольку я не говорил о возведении в степень).
Обратите внимание, что если вы просто введете данный термин в калькулятор, вы не получите того же результата, потому что калькулятор оценивает операции в том порядке, в котором они были введены, а не в порядке BEDMAS. Итак, калькулятор видит
$$((((6 — 1) \times 0) + 2) \div 2) = 1$$
, что явно является другим результатом. Так что просто помните, что калькуляторы не могут делать BEDMAS, и все готово.
Вот другое выражение:
$$24 \div 4 \times 3$$
Каков результат этого выражения? По общему соглашению мы сначала делаем деление, но опять же, технически мы должны были добавить круглые скобки, потому что соглашение не является достаточно общеизвестным. Или мы могли бы просто использовать запись дроби вместо $\div$, в этом случае мы получили бы два разных выражения:
$$\frac{24}{4}\times 3 \neq \frac{24}{4 \times 3}$$
Итак, здесь мы можем ясно видеть предполагаемый порядок, и все снова хорошо.
Сложение и вычитание: когда дети учатся
Сложение и вычитание — это первые математические операции, которые изучают дети. Но это не происходит сразу. Обучение сложению и вычитанию обычно происходит небольшими шагами между детским садом и четвертым классом.
Узнайте больше о том, когда у детей развивается этот навык.
Когда дети учатся складывать и вычитать?
Обучение сложению и вычитанию начинается с обучения счету. Для некоторых детей обучение счету начинается в детском саду или дошкольном учреждении. Но это не значит, что к тому времени дети уже умеют складывать или вычитать. Вот как обычно выглядит обучение детей сложению и вычитанию:
Изучите темы, выбранные нашими экспертами
Математика
В детском саду: Дети считают в прямом и обратном порядке, начиная и заканчивая нулем. Дети также начинают учиться соединять однозначные числа и сравнивать суммы, чтобы увидеть разницу.
В первом классе: Дети соединяют однозначные и двузначные числа для сложения. Они также вычитают однозначные числа и десятки.
Во втором классе: Дети работают над более сложным сложением и вычитанием. Они также начинают учиться перегруппировке или «заимствованию».
К четвертому классу: Обычно дети понимают, как складывать и вычитать многозначные числа, не используя предметы и картинки для моделирования. Они тоже могут перегруппироваться.
Когда дети переходят в четвертый класс и еще не умеют складывать и вычитать, не используя предметы и картинки, это не обязательно означает наличие проблемы. Дети развиваются с разной скоростью. Но если они борются и отстают, важно выяснить, почему.
Почему у некоторых детей возникают проблемы со сложением и вычитанием
Детям может быть трудно изучать математику по разным причинам. Обычный — это проблемы с набором навыков, которые являются более базовыми, чем счет, сложение и вычитание. Эти навыки известны как чувство числа.
Эти навыки известны как чувство числа.
Проблемы с концентрацией внимания также могут затруднить изучение сложения и вычитания. Узнайте больше о том, что может вызвать проблемы с математикой.
Способы помочь детям научиться сложению и вычитанию
Практика сложения и вычитания может помочь улучшить эти навыки. Но это не должно быть похоже на работу. Вот несколько интересных занятий:
Визуализируйте это. Используйте Cheerios или сушеные бобы для счета. Перемещение их — отличный способ для детей понять, как работают математические операции.
Сделайте это искусством. Предложите детям использовать цветные карандаши или фломастеры, чтобы показать, как выглядит математическая операция.
Играйте в математические настольные игры. В таких играх, как Connect Four, используются такие концепции, как подсчет и определение последовательности. Вот еще идеи для настольных игр.
Основные выводы
К четвертому классу большинство детей понимают, как складывать и вычитать.


 4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня). Зачем брали с собой их в поле – непонятно.
Зачем брали с собой их в поле – непонятно. : «Просвещение», 2012.
: «Просвещение», 2012.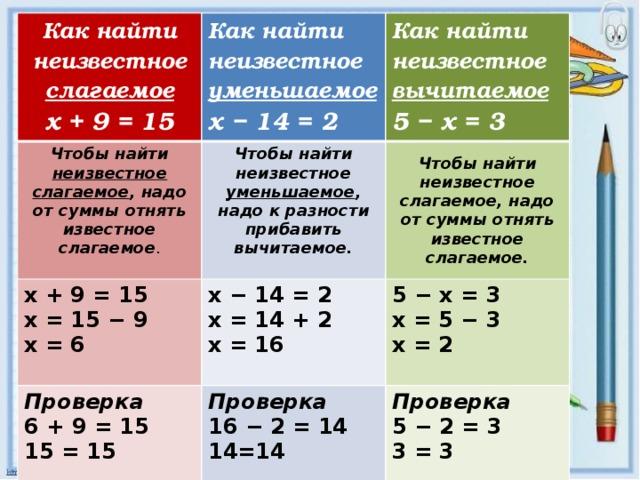 сложение; 3. вычитание
сложение; 3. вычитание
 ru/articles/mathematic/poryadok-dejstvij-v-matematike
ru/articles/mathematic/poryadok-dejstvij-v-matematike