Математика урок 3 класс — начальные классы, уроки

Математика

Тема: Порядок выполнения арифметических действий со скобками и без скобок.

Цель: Познакомить с правилом порядка выполнения действий в выражениях, содержащих арифметические действия со скобками и без них;

 — совершенствовать вычислительные навыки;

— развивать

— воспитание доброжелательности, самостоятельности, аккуратности при работе в тетради.

Ход занятия

1.Организационный момент

2.Актуализация опорных знаний

– арифметический диктант + самопроверка

1. Произведение чисел 5 и 4 2.

2. Частное чисел 24 и 3

3. Первое слагаемое 40 и второе слагаемое 40, найдите сумму

4. Уменьшаемое 25, вычитаемое 20, чему равна разность

 – Чтобы записать примеры, какие арифметические знаки использовали? / повторение арифметических знаков и их обозначение /.

А ещё есть скобки / показ /. Кто догадался, чем сегодня мы будем заниматься на уроке? / ответы учеников /.

3.Сообщение темы и цели урока

Существуют правила порядка выполнения арифметических действий, которые надо строго соблюдать

4. Усвоение материала

№1Определи порядок действий

37+12:6 27+6-3 12:6*3 (6+10):2+5

5*2+4:2 54-14-7 18:9*5 50+(98-90)*2

Правило

1.Сначала выполни действие в скобках

2.Затем * или : по порядку

3.Потом + или – по порядку

№1(б) Исправь ошибки

5. Физ.минутка

6. Закрепление материала

Работа по учебнику/ стр. 44 № 2

№3 Задачи

Красных роз 8р.по4кус.

Белых роз 23кус.

Всего-?роз

(8*4)+23=55роз

Лиственных д.-179с.

Хвойных д.-186с.

Высадили-?с.

Осталось -145с.

(179+186)-145=220с.

7.Повторение

№4 Реши уравнения

— Какие компоненты неизвестны?

-Как найти множитель? Делимое? Делитель?

Х*5=10 Х:6=2 14:Х=7 8*Х=16

Х=10:5 Х=2*6 Х=14:7 Х=16:8

Х=2 Х=12 Х=2 Х=2

2*5=10 12:6=2 14:2=7 8*2=16

Работа в парах

№6 Расставь скобки так, чтобы равенства были верными

(3+5)*4=32 (3+5)*4-2=30

3+(5*4)=23 3+5*(4-2)=13

Взаимопроверка

8. Итог урока

— Что узнали нового?

9.Задание на дом №2 (3,4 строчки)стр.44

3+5*4=32 3+5*4-2=30

3+5*4=23 3+5*4-2=13

3+5*4=32 3+5*4-2=30

3+5*4=23 3+5*4-2=13

3+5*4=32 3+5*4-2=30

3+5*4=23 3+5*4-2=13

3+5*4=32 3+5*4-2=30

3+5*4=23 3+5*4-2=13

ПРИЛОЖЕНИЕ

Задание № 1 / на голубом листе /

700 + 200 – 600 =

200 + 80 + 120 =

300 – 200 – 50 =

90 – 40 + 500 =

Задание №2 / на ярко – жёлтом листе /

( 98 – 8 ) – 50 =

100 + ( 4 + 6 ) =

( 1 + 9 ) – 5 =

50 – ( 25 – 20 ) =

Задание № 3 / на розовом листе /

24 : 4 : 1 =

8 × 0 × 7 =

10 : 2 × 5 =

7 × 3 : 21 =

Задание № 4 / на бледно- зелёном листе /

25 : ( 1 × 5 ) =

( 6 × 3 ) : 18 =

24 : ( 12 : 3 ) =

( 9 × 4 ) × 1 =

Задание № 5 / на оранжевом листе /

5 × 2 + 60 =

42 – 4 : 2 =

60 : 1 – 12 × 0 =

20 : 4 + 5 × 3 =

Задание № 6 / на белом листе /

( 15 + 35) : 5 =

8 × ( 9 – 4 ) =

( 2 + 8 ) × 3 – 20 =

( 5 + 5 ) : ( 11 – 1 ) =

ОСУД « Порядок действий в выражениях, содержащих 4 арифметических действия и скобки » 3 класс

ЕСЛИ В ВЫРАЖЕНИИ

ТОЛЬКО

+ и —

ЕСЛИ В ВЫРАЖЕНИИ

ТОЛЬКО * и :

ЕСЛИ В ВЫРАЖЕНИИ

+ и — , * и :

ЕСЛИ В ВЫРАЖЕНИИ

ОДНА ИЛИ НЕСКОЛЬКО ( )

все действия по порядку

все действия по порядку

1. * или :

по порядку

1.сначала действия

в скобках

2.+ или –

по порядку

2.* или : по порядку

3.+ или – по порядку

КГУ « ОШ № 2 акимата города Шахтинка »

ТЕМА:

« Порядок выполнения арифметических действий

в числовых выражениях без скобок и со скобками,

состоящими из 2-3 действий »

Урок математики по теме «Порядок выполнения действий в выражениях без скобок и со скобками». 3-й класс

Разделы: Начальная школа

Ход урока

I. Оргмомент (звучит песня “Дважды два четыре”). СЛАЙД

Презентация.

— Ребята, кто из вас любит математику? Почему вы её любите? Математику любят наши знакомые Миша и Маша, ученики 3 класса. Сегодня они как всегда с нами на уроке.

“Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели

. ” (А. Маркушевич)

СЛАЙД “Математику уже затем изучать нужно, что она ум в порядок приводит”

Михаил Васильевич Ломоносов, русский учёный, энциклопедист, поэт.

II. Устная работа.

1. Повторение табличных случаев умножения и деления. Работа в группах с использованием ноутбуков.

— Как вы считаете, какое задание, выполняемое нами на каждом уроке приводит наш ум в порядок? (повторение таблицы умножения и деления)

— Проверим, чья группа первая справится с этим заданием. Если вы ошибаетесь в ответе, вас компьютер возвращает к началу теста, и вы выполняете задание заново.

— Прекрасное начало урока! Рада, что вы все справились с заданием!

2. Игра “Да или нет”

— Поиграем в игру “Да или нет”. Если вы согласны с моим высказыванием, то показываете “Да” (скрещенные пальчики), если не согласны – “Нет” ( один указательный пальчик). Договорились?

— При умножении любого числа на 1 получается 1 (да).

— При умножении любого числа на 1, получается 1 (да).

— Чтобы разделить на 10, достаточно дописать 0 (нет, отбросить).

— Умножать на 0 нельзя (нет, можно).

— Чтобы найти делимое, нужно значение частного умножить на делитель (да).

— Чтобы найти неизвестный множитель, нужно значение произведения умножить на известный множитель (нет, разделить).

— В выражениях без скобок все действия выполняются по порядку слева направо (нет, сначала умножение и деление, потом вычитание и сложение).

— С каждым уроком у вас получается всё лучше! Просто замечательно!

3. Логические упражнения.

Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным. 

(Б. Паскаль) Предлагаю выполнить логические задания. Вы готовы?

— Какие два числа, если их перемножить, дают такой же результат, что и при их сложении? (2 и 2)

— Из-под забора видно 6 пар лошадиных ног. Сколько этих животных во дворе? (3)

— Петух, стоя на одной ноге весит 5кг. Сколько он будет весить, стоя на двух ногах? (5кг)

— На руках 10 пальцев. Сколько пальцев на 6 руках? (30)

— У родителей 6 сыновей. Каждый имеет сестру. Сколько всего детей в семье? (7)

— Сколько хвостов у семи котов?

— Сколько носов у двух псов?

— Сколько ушей у 5 малышей?

— Ребята, именно такой работы я и ждала от вас: вы были активны, внимательны, сообразительны.

III. Актуализация знаний.

“Чтобы переварить знания, надо поглощать их с аппетитом.”

 (А.Франц)

— Вы готовы поглощать их с аппетитом? Тогда внимание!

— Посмотрите, пожалуйста, внимательно на доску. Как вы считаете, какое задание предполагается? (Указать арифметические действия, которые выполняются в заданном порядке)

— Проговорите правило, которое подходит к данной схеме.

В выражениях без скобок, содержащих только сложение и вычитание – действия I ступени, или умножение и вычитание – действия II ступени, действия выполняются в том порядке, как они записаны : слева направо.

В выражениях без скобок сначала выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание.

В выражениях со скобками сначала вычисляют значения выражений в скобках. Затем по порядку слева направо выполняется умножение или деление.

— Озвучьте тему нашего урока. (“Порядок выполнения действий в выражениях со скобками и без скобок”)

— Просто умницы, ловко справились, умело.

VI. Целеполагание.

— Ребята, как вы считаете, достаточно ли хорошо отработана нами тема “Порядок выполнения действий в выражениях”?

— На что нам сегодня необходимо обратить внимание? Над чем поработать? (Упражняться в нахождении значений выражений, содержащий действия разных ступеней со скобками и без них. Познакомиться с видами выражений, в которых можно допустить ошибки)

— И в этом разобрались. Я думаю, достаточно поставленных задач на сегодняшний урок.

V. Постановка проблемной ситуации. Работа в группах. (карточки)

— Ребята, послушайте, пожалуйста, что говорил французский математик Д. Пойя: “Лучший способ изучить что-либо — это открыть самому”. Вы готовы к открытиям?

СЛАЙД— Даны выражения, посмотрите, как справились с заданием Маша и Миша.

— Кто выполнил задание верно: Маша или Миша? (ответы детей)

— К кому из наших друзей можно отнести следующее высказывание Р. Декарта “Мало иметь хороший ум, главное – хорошо его применять? (К Мише, потому что он ошибся)

— Какие ошибки допущены Мишей?

СЛАЙД — Давайте проверим!

— Я знала, что это задание вам было под силу!

VII. Разрешение проблемной ситуации.

СЛАЙД — В данной ситуации кто является КП – “кислой парочкой”? (Миша и выражения)

— Как разрешить проблему?

(Миша должен САМ найти значения выражений

— Какие у него есть для этого ресурсы? (Память, чтобы запомнить правило, старание, тренировка, учебник,

Выражения САМИ должны быть решены, для этого ресурсы: Маша, учитель, родители)

— Какое ИКР вы бы выбрали? Почему?

— А если Миша воспользуется ИКР2? Это будет хорошо или плохо, давайте поиграем!

Игра “Хорошо-плохо”

— Если за него выполнят задание, то будет хорошо, потому что. ..(ему не нужно будет долго сидеть за уроками, не нужно будет думать, у него появится свободное время…)

— Если за него выполнят задание, то будет плохо…(сам не научится решать, не будет трудолюбивым, не усвоит тему, будут проблемы в учёбе…)

“Величие человека — в его способности мыслить.” (Б. Паскаль)

— Ребята, у вас получилось лучше, чем я могла бы подумать!

— А ещё вам предлагается новый способ записи решения. В чём он заключается? (Нужно выписывать все действия ниже данного выражения)

— Вот в этом мы сейчас с вами и поупражняемся.

VIII. Нахождение значений выражений. (№228) – у доски 3 выражения.

“Счет и вычисления — основа порядка в голове.” (Песталоцци)

IX. Самостоятельная работа № 228, 3 выражения.

— Я горжусь вами, что вам удалось выполнить задание почти без ошибок.

X. Решение задачи №227.

“Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их. ” (Д.Пойа)

У всех учащихся второго класса 39 ручек. У шести учеников по одной ручке, у пяти по три, а у остальных по две. Сколько учеников имеют по две ручки? Маша записала решение этой задачи выраженим так: 39-1 * 6+3 * 5. Миша – так: 39-(1 * 6+3 * 5) Кто прав: Миша или Маша?

— Прочитайте установку и ответьте на вопрос. Кто прав Миша или Маша?

— Самостоятельно запишите решение задачи и ответ.

— Назовите ответ.

СЛАЙД — Давайте проверим!

— Поздравляю, это правильный ответ!

XI. Работа по алгоритму.

— Что такое алгоритм? (Порядок выполнения действий)

СЛАЙД — Выполните действия по алгоритму.

— “Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.”, говорил М.В. Остроградский. Вот и мы сейчас вспомним то, что изучали на уроках информатики.

— Какая фигура получилась? (прямоугольник)

— Ниже начертите фигуру, площадь которой в 6 раз больше.

— Что примите за единичный отрезок? (2 клетки)

— Вы на верном пути!

СЛАЙД — Из скольких мерок состоит ваша фигура?

— Внимание на слайд! Вас ждёт сюрприз, если правильно найдёте значения выражений.

XII. Нахождение значений выражений. (СЛАЙД)

— Именно этого мы с вами и ждали! (на слайде появляется фото класса)

XIII. Итог урока.

— Выполнили ли мы поставленные цели урока? Что планировали? Всё ли у нас получилось? Над чем необходимо поработать?

— Вы сегодня просто умнички, много сделали. Работать с вами просто радость!

XIV. Рефлексия.

— Оцените работу вашей группы, насколько успешно работали, аргументируйте свой выбор (карточки с цифрами).

XV. Домашнее задание.

— Что необходимо закрепить дома? (порядок выполнения действий в сложных выражениях) № 234 (1 столбик), №230.

— “Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.” (М.И. Калинин)

Муниципальное бюджетное  общеобразовательное учреждение

Целинная средняя общеобразовательная школа № 14 Урок математики 2 класс

Тема: « Порядок выполнения действий. Скобки УМК «Школа России»

   Автор : учитель начальных классов  Котюшева В.Н

Цели: познакомить с порядком выполнения действий при вычислениях; учить находить значения выражений со скобками; развивать умение решать текстовые задачи и задачи логического характера; совершенствовать вычислительные навыки.

УУД:

Познавательные :учащиеся научатся соблюдать порядок действий при вычислениях; находить значения выражений, содержащих скобки;

Регулятивные: использовать графические модели при решении задач;

Коммуникативные: слушать собеседника и вести диалог;

Личностные: оценивать себя и товарищей.

        Ход урока:

1. Мотивация (самоопределение) к учебной деятельности.

Прозвенел звонок и смолк-

Начинается урок.

Вы за парты тихо сели,

На меня все посмотрели.

Пожелайте успехов глазами

И вперёд за новыми знаниями!

 

— Работать сегодня мы будем коллективно и в парах. Вспомните правила работы в парах.(Прислушиваться к мнению соседа, работать дружно, помогать друг другу)

В конце урока каждый из вас оценит свою работу.

 

1. Актуализация и фиксирование индивидуального затруднения в пробном действии.

(На доске записаны примеры.)

20-9+8=19

20-9+8=3  

-Рассмотрите примеры. Сравните. Чем они похожи? Чем отличаются?

-Какое равенство верно? (Первое.)

— Как выполняли действия?  (Сначала выполнили вычитание, а потом сложение.)

— В каком порядке нужно выполнить действия во втором равенстве, чтобы оно стало верным? (Сначала сложить 9 и 3, а затем из 20 вычесть их сумму. )

3. Выявление места и причины затруднения.

— Мы поняли, как нужно решать эти примеры. А как показать это другим?

— Чего мы не знаем?  (Как показать, в каком порядке нужно выполнять действия в некоторых примерах.)

 

1. Построение проекта выхода из затруднения (тема, цель, задачи, план, способ, средство)

— О чём сейчас говорили?  (О порядке выполнения действий.)

— Какая тема урока?  (Порядок выполнения действий.)

-Какова цель нашего урока? (Научиться обозначать в записи порядок действий.)

5.Поиск решения проблемы.

-Посмотрите, чем отличаются столбики примеров?

8-3+4=9                      8-(3+4)=1

18-8+9=19                  18-(8+9)=1

20-5+3=18                  20-(5+3)=12

(В первом столбике нет скобок, а во втором есть.)

— Зачем же они нужны?

-Как выполняли действия в первом столбике? (По порядку. )

-Как будем выполнять действия во втором столбике, чтобы получить эти значения выражений? (Сначала выполним действие в скобках.)

-Сравните порядок выполнения действий в первом и во втором столбиках. Что вы можете сказать? ( В первом столбике мы выполняли действия по порядку, а во втором  сначала в скобках.)

-Что нам поможет указать на порядок выполнения действий?  (Скобки.)

-Сформулируйте правило, как правильно выполнять действия в выражениях со скобками. (Сначала выполняются действия в скобках, а потом по порядку)

Первичное закрепление с проговариванием во внешней речи

— Мы получили новое знание. Проверим, правильно ли мы сделали выводы.

Сравним наше новое знание с научным в учебнике. Прочитайте на с.38 выделенное в рамочку.

-Попробуем применить наше новое знание на практике.

№ 1 (с. 38).

(Коллективное выполнение с комментированием.)

Физкультминутка

 

1. Самостоятельная  работа в парах  с самопроверкой по эталону.

№2 (с. 38).

-Решите первый пример. Проверьте, получим ли мы нужный результат, если вычисления будем выполнять по порядку. (Не получим.)

-Измените порядок действий. Какое действие выполним первым? (Сложение.)

-Вычислите. Получился ли у вас нужный результат? (Да.)

—Поставьте скобки.

(Остальные примеры  разбираются аналогично.  Следует обра­тить  внимание учащихся на то, что, если скобки не меняют порядок  действий,  их можно не ставить.)

1. Включение в систему знаний повторение.

№3 (с. 38).

(Один ученик выполняет на доске с комментированием,  остальные— в тетрадях.)

№4 (с. 38).

-Рассмотрите рисунок.

( Составьте задачу по первому решению. (В лодке плыли 5 де­тей и 1 взрослый. Сколько всего человек плыло в лодке ?)

( Составьте задачу по второму решению. (В лодке было 6 че­ловек. На берег вышли 2 человека. Сколько человек осталось и лодке?)

Можно ли задачи назвать обратными? (Нет.)

-Решите задачи.

(Ученик, решивший задачу первым, записывает решение и ответ на доске. Проверка. Тем, кто справится с заданием быстрее других, дополнительно можно предложить составить ко второй задаче обратные задачи.)

№5 (с. 39).

(Самостоятельное выполнение. Проверка по образцу на ли сточке, который находится у учителя.)

8. Рефлексия.

— Итак, над какой темой мы работали? Удалось ли решить поставленную задачу?

— В чём испытывали трудности?

(«Проверь себя» (учебник, с.39). Самостоятельное выполнение. Коллективная проверка. Самооценивание.

— Я поздравляю Вас, вы поднялись ещё на одну ступеньку знаний вверх Молодцы. Спасибо за урок.

9.Домашнее задание (по выбору).

 

 

 

 

 

Калькулятор онлайн по действиям.

Порядок выполнения действий в выражениях без скобок и со скобками

И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .

В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.

Навигация по странице.

Сначала умножение и деление, затем сложение и вычитание

В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :

• действия выполняются по порядку слева направо,
• причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.

Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.

Пример.

Выполните действия 7−3+6 .

Решение.

Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .

Кратко решение можно записать так: 7−3+6=4+6=10 .

Ответ:

7−3+6=10 .

Пример.

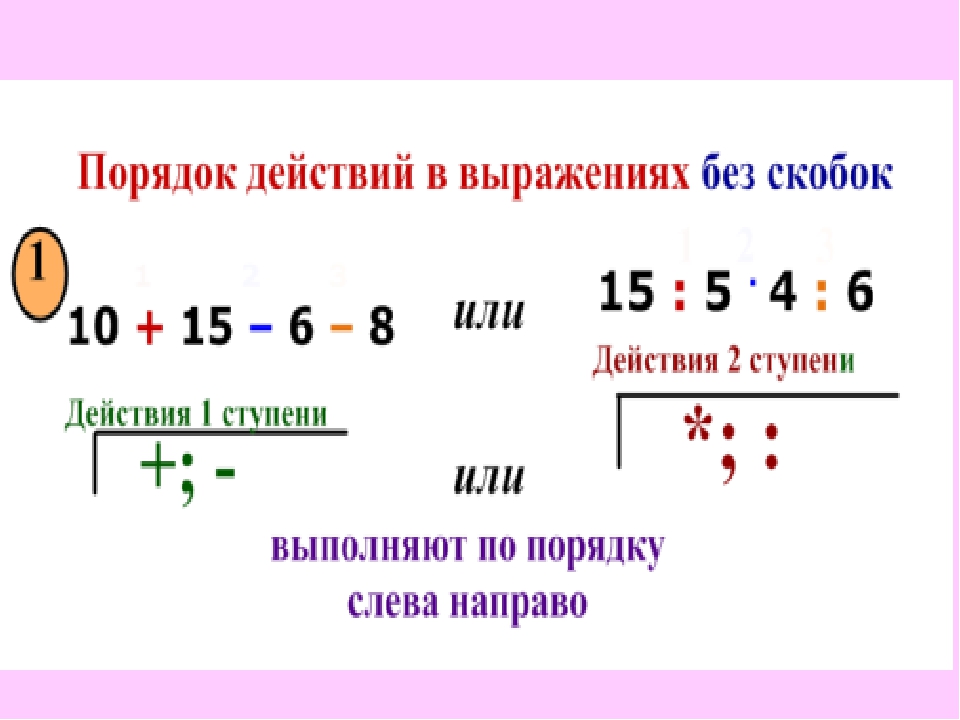
Укажите порядок выполнения действий в выражении 6:2·8:3 .

Решение.

Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.

Ответ:

Сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.

Пример.

Вычислите значение выражения 17−5·6:3−2+4:2 .

Решение.

Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .

Ответ:

17−5·6:3−2+4:2=7 .

На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .

Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.

Действия первой и второй ступени

В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.

Определение.

Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .

В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).

Порядок выполнения арифметических действий в выражениях со скобками

Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Пример.

Выполните указанные действия 5+(7−2·3)·(6−4):2 .

Решение.

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .

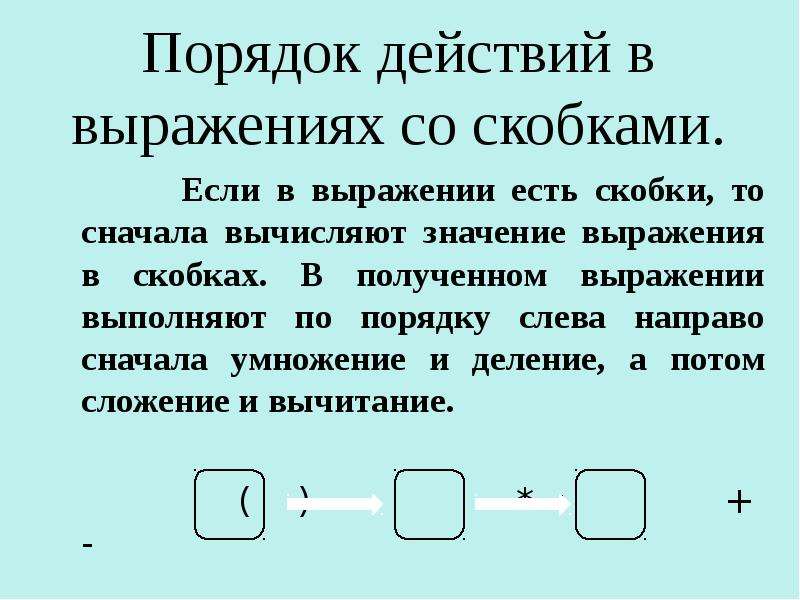
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .

Ответ:

5+(7−2·3)·(6−4):2=6 .

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Пример.

Выполните действия в выражении 4+(3+1+4·(2+3)) .

Решение.

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .

Ответ:

4+(3+1+4·(2+3))=28 .

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .

Бесплатная программа ЛовиОтвет — функциональный калькулятор для решения примеров и уравнений. В программе Лови Ответ происходит автоматическое решение математических примеров и уравнений с выводом действий и этапов их решения.

Для чего нужна такая программа? Программа Лови Ответ — это своего рода математический решебник, который выводит ответ, с пошаговым решением выполненного задания.

Программа Лови Ответ будет интересна школьникам и их родителям. С помощью этой программы родители могут проверять домашние задания, которые выполнил учащийся. Также школьники и студенты могут решать примеры и уравнения при помощи этого математического калькулятора.

Взрослые, которые уже не помнят многого из школьного курса, а также учащиеся смогут при помощи данной программы, быстро решить математический пример любой степени сложности.

В программе ЛовиОтвет можно будет выполнять такие математические действия:

• Совершать действия с натуральными числами.
• Производить действия с дробями (десятичными, обыкновенными, смешанными).
• В программе можно будет упрощать выражения, производить действия с многочленами.
• Решать линейные и квадратные уравнения.

Примеры и уравнения будут решены в программе Лови Ответ пошагово, с последовательными действиями. Визуально, в окне программы, вы увидите решение примера или уравнения. Ответ и пошаговые действия для его решения, будут записаны на своеобразном тетрадном листе. Все этапы решения можно будет записывать в программе в столбик.

Скачать программу ЛовиОтвет можно с официального сайта производителя. Программа доступна для работы на компьютерах с операционной системой Windows. Есть версии программы для устройств на операционной системе Android, для Aplle устройств (iPad, iPhone/iPod), для мобильных телефонов (java, java-mini).

Лови Ответ скачать

После загрузки, вам можно будет установить программу на свой компьютер.

Установка программы Лови Ответ

Запустите процесс установки программы LoviOtvet на своем компьютере.

При установке программы будьте внимательны! Снимите флажки в тех пунктах, где вам предложат установить дополнительные программы, для того, чтобы не устанавливать на свой компьютер постороннее программное обеспечение.

По завершению установки программы на компьютер, будет открыто главное окно программы ЛовиОтвет.

Обзор программы Лови Ответ

В верхней части окна программы расположены кнопки меню для управления программой.

С помощью кнопки меню «Правка» вы можете скопировать решение на свой компьютер, выбрав необходимый вариант копирования из контекстного меню. Из меню «Настройки» вы можете выбрать размер листа, клеток, очистить историю. Здесь вы можете изменить цвет отображения окна программы, передвинув в нужное место ползунок, по шкале цвета.

Под панелью меню расположено поле, в которое вводится задание.

В левой части окна расположены кнопки и переключатели для ввода данных. Здесь находится основная и дополнительная панель.

Дополнительную панель можно будет скрыть с помощью кнопки «Скрыть дополнительную панель». Отсюда, в случае необходимости, вы можете изменить размер листа и размер клеток в рабочей области.

Остальную часть окна программы занимает рабочая область, в которой будет отображено решение задания.

Для решения примера, с помощью соответствующих кнопок введите выражение, а затем нажмите на кнопку «Ответ». Решение можно будет выводить в нескольких вариантах: стандартное решение, обыкновенные дроби, решение «в столбик».

После клика по треугольнику в крайней правой части поля, в котором вводится пример или уравнение, откроется дополнительное поле, в котором будут отображена история расчетов. В этом поле можно будет очистить историю расчетов.

Подробнее о том, как пользоваться математическим калькулятором, можно будет прочитать на официальном сайте производителя программы ЛовиОтвет, на странице сайта «Как пользоваться».

Лови Ответ онлайн

Производитель запустил онлайн версию программы ЛовиОтвет, которая доступна по такому адресу: https://calc.loviotvet.ru/ .

По заявлению производителя, версия Лови Ответ онлайн менее функциональна, чем программа, которая устанавливается на компьютер или мобильное устройство. Но, все равно, онлайн калькулятор может быть полезен в некоторых случаях, для выполнения решения поставленных задач.

Выводы статьи

Бесплатная программа Лови Ответ — математический решебник и калькулятор, который помогает школьникам, студентам и родителям выполнять или проверять решение примеров и уравнений любой степени сложности.

ЛовиОтвет — программа для решения примеров и уравнений (видео)

На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.

В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.

А в математике обязательно ли выполнять арифметические действия в определенном порядке?

Давайте проверим

Сравним выражения:
8-3+4 и 8-3+4

Видим, что оба выражения совершенно одинаковы.

Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий

В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.

Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.

Видим, что значения выражений получаются разные.

Сделаем вывод: порядок выполнения арифметических действий менять нельзя .

Узнаем правило выполнения арифметических действий в выражениях без скобок.

Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.

Потренируемся.

Рассмотрим выражение

В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .

Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий

Рассмотрим второе выражение

В этом выражении имеются только действия умножения и деления — это действия второй ступени.

Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий

В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Рассмотрим выражение.

Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.

Вычислим значение выражения.

18:2-2*3+12:3=9-6+4=3+4=7

В каком порядке выполняются арифметические действия, если в выражении имеются скобки?

Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.

Рассмотрим выражение.

30 + 6 * (13 — 9)

Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.

30 + 6 * (13 — 9)

Вычислим значение выражения.

30+6*(13-9)=30+6*4=30+24=54

Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?

Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:

1. действия, записанные в скобках;

2. умножение и деление;

3. сложение и вычитание.

Схема поможет запомнить это несложное правило (рис. 4).

Рис. 4. Порядок действий

Потренируемся.

Рассмотрим выражения, установим порядок действий и выполним вычисления.

43 — (20 — 7) +15

32 + 9 * (19 — 16)

Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.

2*9-18:3=18-6=12

Узнаем, правильно ли определен порядок действий в следующих выражениях.

37 + 9 — 6: 2 * 3 =

18: (11 — 5) + 47=

7 * 3 — (16 + 4)=

Рассуждаем так.

37 + 9 — 6: 2 * 3 =

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие — деление, второе — умножение. Третье действие должно быть сложение, четвертое — вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37

Продолжаем рассуждать.

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

18:(11-5)+47=18:6+47=3+47=50

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

7*3-(16+4)=7*3-20=21-20=1

Выполним задание.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого — вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.

1. Festival.1september.ru ().
2. Sosnovoborsk-soobchestva.ru ().
3. Openclass.ru ().

Домашнее задание

1. Определи порядок действий в данных выражениях. Найди значение выражений.

2. Определи, в каком выражении такой порядок выполнения действий:

1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.

3. Составь три выражения, в которых такой порядок выполнения действий:

1. умножение; 2. сложение; 3. вычитание

1. сложение; 2. вычитание; 3. сложение

1. умножение; 2. деление; 3. сложение

Найди значение этих выражений.

Примеры с дробями – один из основных элементов математики. Существует много разных типов уравнений с дробями. Ниже приведена подробная инструкция по решению примеров такого типа.

Как решать примеры с дробями – общие правила

Для решения примеров с дробями любых типов, будь то сложение, вычитание, умножение или деление, необходимо знать основные правила:

• Для того чтобы сложить дробные выражения с одинаковым знаменателем (знаменатель – число, находящееся в нижней части дроби, числитель – в верхней), нужно сложить их числители, а знаменатель оставить тем же.
• Для того чтобы вычесть от одного дробного выражения второе (с одинаковым знаменателем), нужно вычесть их числители, а знаменатель оставить тем же.
• Для того чтобы сложить или вычесть дробные выражения с разными знаменателями, нужно найти наименьший общий знаменатель.
• Для того чтобы найти дробное произведение, нужно перемножить числители и знаменатели, при этом, если есть возможность, сократить.
• Для того чтобы разделить дробь на дробь, нужно умножить первую дробь на перевернутую вторую.

Как решать примеры с дробями – практика

Правило 1, пример 1:

Вычислить 3/4 +1/4.

Согласно правилу 1, если у дробей двух (или больше) одинаковый знаменатель, нужно просто сложить их числители. Получим: 3/4 + 1/4 = 4/4. Если у дроби числитель и знаменатель одинаковы, такая дробь будет равна 1.

Ответ: 3/4 + 1/4 = 4/4 = 1.

Правило 2, пример 1:

Вычислить: 3/4 – 1/4

Пользуясь правилом номер 2, для решения этого уравнения нужно от 3 отнять 1, а знаменатель оставить тем же. Получаем 2/4. Так как два 2 и 4 можно сократить, сокращаем и получаем 1/2.

Ответ: 3/4 – 1/4 = 2/4 = 1/2.

Правило 3, Пример 1

Вычислить: 3/4 + 1/6

Решение: Пользуясь 3-м правилом, находим наименьший общий знаменатель. Наименьшим общим знаменателем называется такое число, которое делится на знаменатели всех дробных выражений примера. Таким образом, нам нужно найти такое минимальное число, которое будет делиться и на 4, и на 6. Таким числом является 12. Записываем в качестве знаменателя 12. 12 делим на знаменатель первой дроби, получаем 3, умножаем на 3, записываем в числителе 3*3 и знак +. 12 делим на знаменатель второй дроби, получаем 2, 2 умножаем на 1, записываем в числителе 2*1. Итак, получилась новая дробь со знаменателем, равным 12 и числителем, равным 3*3+2*1=11. 11/12.

Ответ: 11/12

Правило 3, Пример 2:

Вычислить 3/4 – 1/6. Этот пример очень схож с предыдущим. Проделываем все те же действия, но в числителе вместо знака +, пишем знак минус. Получаем: 3*3-2*1/12 = 9-2/12 = 7/12.

Ответ: 7/12

Правило 4, Пример 1:

Вычислить: 3/4 * 1/4

Пользуясь четвертым правилом, умножаем знаменатель первой дроби на знаменатель второй и числитель первой дроби на числитель второй. 3*1/4*4 = 3/16.

Ответ: 3/16

Правило 4, Пример 2:

Вычислить 2/5 * 10/4.

Данную дробь можно сократить. В случае произведения сокращаются числитель первой дроби и знаменатель второй и числитель второй дроби и знаменатель первой.

2 сокращается с 4. 10 сокращается с 5. получаем 1 * 2/2 = 1*1 = 1.

Ответ: 2/5 * 10/4 = 1

Правило 5, Пример 1:

Вычислить: 3/4: 5/6

Пользуясь 5-м правилом, получим: 3/4: 5/6 = 3/4 * 6/5. Сокращаем дробь по принципу предыдущего примера и получаем 9/10.

Ответ: 9/10.

Как решать примеры с дробями – дробные уравнения

Дробными уравнениями называются примеры, где в знаменателе есть неизвестное. Для того чтобы решить такое уравнение нужно пользоваться определенными правилами.

Рассмотрим пример:

Решить уравнение 15/3x+5 = 3

Вспомним, нельзя делить на ноль, т.е. значение знаменателя не должно равняться нулю. При решении таких примеров, это нужно обязательно указывать. Для этого существует ОДЗ (область допустимых значений).

Таким образом, 3x+5 ≠ 0.
Отсюда: 3x ≠ 5.
x ≠ 5/3

При x = 5/3 уравнение просто не имеет решения.

Указав ОДЗ, наилучшим способом решить данное уравнение будет избавиться от дробей. Для это сначала представим все не дробные значения в виде дроби, в данном случае число 3. Получим: 15/(3x+5) = 3/1. Чтобы избавиться от дроби нужно умножить каждую из них на наименьший общий знаменатель. В данном случае таковым будет (3x+5)*1. Последовательность действий:

1. Умножаем 15/(3x+5) на (3x+5)*1 = 15*(3x+5).
2. Раскрываем скобки: 15*(3x+5) = 45x + 75.
3. То же самое проделываем с правой частью уравнения: 3*(3x+5) = 9x + 15.
4. Приравниваем левую и правую часть: 45x + 75 = 9x +15
5. Переносим иксы влево, числа вправо: 36x = – 50
6. Находим x: x = -50/36.
7. Сокращаем: -50/36 = -25/18

Ответ: ОДЗ x ≠ 5/3 . x = -25/18.

Как решать примеры с дробями – дробные неравенства

Дробные неравенства по типу (3x-5)/(2-x)≥0 решаются при помощи числовой оси. Рассмотрим данный пример.

Последовательность действий:

• Приравниваем числитель и знаменатель к нулю: 1. 3x-5=0 => 3x=5 => x=5/3
  2. 2-x=0 => x=2
• Чертим числовую ось, расписывая на ней получившиеся значения.
• Под значение рисуем кружок. Кружок бывает двух типов – заполненный и пустой. Заполненный кружок означает, что данное значение входит в ареал решений. Пустой круг говорит о том, что данное значение не входит в ареал решений.
• Так как знаменатель не может быть равным нулю, под 2-ой будет пустой круг.

• Чтобы определить знаки, подставляем в уравнение любое число больше двух, например 3. (3*3-5)/(2-3)= -4. значение отрицательное, значит над областью после двойки пишем минус. Затем подставляем вместо икса любое значение интервала от 5/3 до 2, например 1. Значение опять отрицательное. Пишем минус. То же самое повторяем с областью, находящейся до 5/3. Подставляем любое число, меньшее чем 5/3, например 1. Опять минус.

• Так как нас интересуют значения икса, при котором выражение будет больше или равно 0, а таких значений нет (везде минусы), это неравенство не имеет решения, то есть x = Ø (пустое множество).

Ответ: x = Ø

Данный калькулятор пытается оценить сложность вычисления без калькулятора (на листочке) задач с использованием арифметических операций сложения, вычитания, умножения и деления.
Калькулятор определяет количество элементарных операций в примере, дает условную сложность выраженную в миллисекундах, требуемых для вычисления примера. Сложность складывается из суммы элементарных операций, помноженных на коэффициент сложности (время в миллисекундах, требуемое для выполнение операции). Расшифровка элементарных операций дается в таблице в нижней части калькулятора.

Результат вычисления

Количество элементарных операций

Сложность (время вычисления)

Расшифровка операций с указанием сложности.
++ сложность 200, увеличение на единицу, например, при умножении 2003000 — будет одно умножение 2 3 и 5 раз выполнится подсчет нулей
+ сложность 500, элементарное сложение например 5+4
— сложность 500, элементарное вычитание, например 3-2
* сложность 1000, элементарное умножение, например 2*2
/ сложность 1000, деление — операция деления сводится к последовательном выполнении операций умножения и вычитания, при этом мы прикидываем всякий раз какой множитель необходимо выбрать, чтобы произведение получилось чуть меньше или равно текущего делимого. Эта элементарная операция подсчитывается в данной колонке. Необходимые умножения и вычитания подсчитываются дополнительно.
0+ сложность 100, сложение с нулем — частный случай выделен отдельно, так как это более простая операция чем сложение.
0 сложность 100, подстановка нулей
°+ сложность 700, сложение с переносом единицы, например 16+7 — содержит две операции — элементарное сложение и перенос единицы в следующий разряд.
=0 сложность 200, сокращение — операции вычитания равных величин, например 100-100
°- сложность 600, заем единицы при вычитании, например при вычитании 11-9 будет выполнен один заем и одна операция вычитания.
** сложность 400, повторное умножение. часто случается, что при выполнении элементарных (и не только) операций умножения выполняются одни и те же операции. Например 2533 будет содержать два элементарных умножения и один повтор, мы просто можем переписать результат умножения 25 3 еще один раз.
*0 сложность 100, частный случай умножения на ноль
*1 сложность 200, частный случай умножения на единицу
°* сложность 700, перенос при умножении, например 234 — два элементарных умножения плюс один перенос (1) при умножении 3 4
+- сложность 300, смена знака
сложность 500, перестановка вычитаемых, выполняется если мы пытаемся вычесть из меньшего большее
. сложность 500, операций с плавающей точкой

Рассмотрим вычисление сложности на примере (4567+987-8354)*32/25:
Пример содержит все четыре арифметических операции.

Сначала выполняется сложение 4567+987=5554

Как видим, в этом примере имеется три элементарных сложения: 7+7, 6+8, 5+9, при выполнении каждого из которых осуществляется перенос единицы в старший разряд.

Затем вычитание 5554-8354=-2800

Так как из меньшего вычитается большее число, результат получается отрицательным, перед вычитанием выполняется перестановка операндов. Первые два разряда 5,4 сокращаются, затем при вычислении 3-5 осуществляется элементарное вычитание с займом единицы, затем просто вычитание 8-1-5=2.

Третьим действием выполняем умножение -2800*32=-89600

Так как первый множитель заканчивается нулями, выполняем подсчет их количества, чтобы в конце умножения приписать нули к результату. Затем умножаем 2832. При умножении на 3 8 и 28 выполняется перенос в след. разряд. 2 2 и 2*3 — просто элементарные умножения. Итого 4 элементарных умножения, 2 переноса, 2 подсчета.

Последнее действие — деление -89600/25=-3584

На каждом шаге деления осуществляется подбор множителя таким образом, чтобы произведение его на делитель было близко к числу, составляемому первыми разрядами текущего остатка от деления. Эта операция засчитывается как элементарное деление, после чего выполняется умножение и вычитание, сложность которых рассчитывается по аналогии с предыдущими шагами.
В частности при делении первых разрядов (86) на 25 выбираем множитель = 3. Далее производится умножение 25*3-75, далее вычитание 89-75=14.
Итого при вычислении 89600/25 имеем: 4 деления и 4 вычитания, 8 произведений, 3 сокращения, два умножения с переносом, при умножении с переносом осуществляется одно сложение.

В конечном итоге в ходе вычисления всего примера произведено 52 элементарные операции — с учетом обозначенных весовых коэффициентов, общая сложность составляет 28500. Таким образом для решения данного примера понадобится примерно полминуты (28.5 секунды).

P.S. Все временные оценки и сам алгоритм вычисления сложности сделаны на основе субъективных предположений автора, комментарии и замечания приветствуются.

6/2(2+1)= Как решается этот проклятый пример: denis_demakhin — LiveJournal

Уже давно я увлечен этим примером:

Делал по нему опросы

И сейчас попробую обосновать мою новую точку зрения, которая теперь выглядит так:

Дело в том, что между алгеброй и арифметикой есть разница в порядке действий:

Теперь понятно, почему инженерный калькулятор показывает ответ: 1.

Он не сломался. Он алгебраический.

Алгебраический калькулятор считает по правилам алгебры.

Осталось понять, алгебраический это пример или арифметический. От этого будет зависеть ответ.

Букв в примере нет, однако, в нем есть пропущенный знак умножения перед скобкой:

Случаи возможного пропуска знака умножения:

1. Между буквенными множителями;


2. Между числовым и буквенным множителем;


3. Между множителем и скобкой;


4. Между выражениями в скобках.

Тут подходит только правило №3. И тогда пропущенный знак умножения равносилен скобкам, то есть 2(2+1) = (2*(2+1)), следуя правилам из скана выше.

И получается, что если выражение (2+1) заменить на икс, то написание 6/2Х читается как «шесть, разделить на два икса».

Тогда ответ: 1.

Но почему тогда самая умная штука на Земле — Гугл-поисковик считает, что ответ 9?

Потому что и Гугл и смартфон считают по арифметическим правилам.

Но вот тут есть тонкий момент. Арифметические правила должны, по-правильному то, действовать при указании знака умножения. Так, как я написал здесь:

Тут уже нет оснований применять правила алгебры, в которых пропущенный знак умножения считается неразрывным. И ответ получается: 9.

Вывод:

Всё зависит от того, алгебра это или арифметика.

Еще интересные штуки:

Задачи, ломающие мозг (с ответами, спрятанными под спойлер)

Тренировка ума развивальщика предприятий

Подписывайся, мыслитель!

Выполнение математических операций в Go с помощью операторов

Введение

Числа используются повсюду в программировании. Они используются для представления таких вещей, как размеры экрана, географическое местоположение, денежные средства и баллы, количество времени, передаваемого в видео, расположение игровых аватаров, отображение цветов через присвоение числовых кодов и т. д.

Эффективное выполнение математических операций в программировании является важным навыком, который необходимо развивать, поскольку вы очень часто будете работать с числами. Хотя понимание математических операций на высоком уровне может помочь вам стать более профессиональным программистом, это не является обязательным условием. Если у вас нет опыта работы с математическими операциями, попробуйте посмотреть на математику как на инструмент, с помощью которого вы можете добиться того, чего хотите, и как на способ улучшить ваше логическое мышление.

Мы будем работать с двумя наиболее используемыми типами данных Go, int и float:

• Int — это целое число, которое может быть положительным, отрицательным или 0 (… -1,0, 1…).
• Float — вещественные числа с десятичными дробями, например, 9,0 или -2,25.

В этом обучающем руководстве мы изучим операторы, которые мы можем использовать с числовыми типами данных в Go.

Операторы

Оператор — это символ или функция, указывающая операцию. Например, в математике значок плюс или + — это оператор сложения.

В Go мы увидим несколько похожих операторов, которые взяты из математики. Однако другие операторы, которые мы будем использовать, принадлежат только к компьютерному программированию.

Здесь вы можете найти таблицу с математическими операторами в Go. Мы рассмотрим все эти операторы в рамках данного руководства.

Операция	Что возвращает
x + y	Сумма x и y
x - y	Разница между x и y
-x	Изменение знака x
+x	Тождественность x
x * y	Произведение x и y
x / y	Результат деления x на y
x % y	Остаток деления x на y

Также мы рассмотрим составные операторы присваивания, включая += и *=, которые совмещают арифметический оператор с оператором =.

Сложение и вычитание

В Go операторы сложения и вычитания работают так же, как и в математике. По сути, вы можете использовать язык программирования Go как калькулятор.

Давайте рассмотрим несколько примеров, начиная с целых чисел:

fmt.Println(1 + 5)

Output
6

Вместо передачи целых чисел прямо в оператор fmt.Println мы можем инициализировать переменные для хранения целочисленных значений, используя следующий синтаксис:

a := 88
b := 103

fmt.Println(a + b)

Output
191

Поскольку целые числа могут быть как положительными, так и отрицательными (как и 0), мы можем добавить отрицательное число к положительному:

c := -36
d := 25

fmt.Println(c + d)

Output
-11

Сложение будет работать аналогичным образом для чисел с плавающей точкой:

e := 5.5
f := 2.5

fmt.Println(e + f)

Output
8

Поскольку мы складывали два числа с типом float, Go возвращает float с дробной частью. Однако, поскольку в этом случае десятичная часть равна 0, fmt.Println опускает десятичную часть. Чтобы надлежащим образом настроить формат вывода, мы будем использовать fmt.Printf​​​ с %.2f для форматирования числа с двумя знаками после запятой, как это показано в данном примере:

fmt.Printf("%.2f", e + f)

Output
8.00

Синтаксис для вычитания аналогичен сложению, кроме того, что мы изменяем оператор со знака плюс (+) на знак минус (-):

g := 75.67
h := 32.0

fmt.Println(g - h)

Output
43.67

В Go мы можем использовать операторы только для одинаковых типов данных. Мы не можем складывать int и float64:

i := 7
j := 7.0
fmt.Println(i + j)

Output
i + j (mismatched types int and float64)

При попытке использовать операторы с типами данных, не являющимися одинаковыми, вы получите ошибку компиляции.

Унарные арифметические операторы

Унарные математические выражения включают только один компонент или элемент. В Go мы можем использовать знаки плюс и минус как один элемент со значением, в частности, для возврата тождественности значения (+) или изменения знака значения (-).

Хотя обычно это не используется, значок плюс указывает тождественность значения. Мы можем использовать знак плюс с положительными значениями:

i := 3.3
fmt.Println(+i)

Output
3.3

Когда мы используем знак плюс с отрицательным значением, он будет возвращать тождественность этого значения, а в данном случае это будет отрицательное значение:

j := -19
fmt.Println(+j)

Output
-19

При отрицательном значении знак плюс возвращает то же самое отрицательное значение.

Знак минус, однако, изменяет знак значения. Поэтому при передаче положительного значения мы обнаружим, что знак минус, который идет перед значением, будет возвращать отрицательное значение:

k := 3.3
fmt.Println(-k)

Output
-3.3

Также, когда мы используем унарный минус с отрицательным значением, будет возвращаться положительное значение:

j := -19
fmt.Println(-j)

Output
19

Унарные арифметические операции со знаком плюс и знаком минус возвращают либо тождественность значения в случае +i или значение с противоположным знаком в случае -i​​​.

Умножение и деление

Как и сложение и вычитание, умножение и деление будут выглядеть примерно так, как в математике. Знак, который мы используем в Go для умножения — это *, а знак, который мы используем для деления — это /.

Здесь приведен пример выполнения умножения в Go двух чисел с плавающей запятой:

k := 100.2
l := 10.2

fmt.Println(k * l)

Output
1022.04

В Go деление имеет разные характеристики в зависимости от типа числового значения, на которое мы делим.

Если мы делим целые числа, оператор / Go выполняет обычное деление, где для целой части x возвращаемое число — это самое большое число, которое меньше или равно x.

Если вы запустите следующий пример с делением 80 / 6, вы получите 13 в качестве результата, а типом данных будет int:

package main

import (
    "fmt"
)

func main() {
    m := 80
    n := 6

    fmt.Println(m / n)
}

Output
13

Если желаемый результат вывода — float, вы должны явно преобразовывать значения, прежде чем выполнять деление.

Вы можете сделать это, обернув желаемый тип float32()​​​ или float64() вокруг ваших значений:

package main

import (
    "fmt"
)

func main() {
    s := 80
    t := 6
    r := float64(s) / float64(t)
    fmt.Println(r)
}

Output
13.333333333333334

Модуль

Оператор % — это модуль, который возвращает остаток, а не целую часть после деления. Это полезно для получения чисел, умножающихся на одно и то же число.

Давайте рассмотрим пример модуля:

o := 85
p := 15

fmt.Println(o % p)

Output
10

Например, 85 при делении на 15 возвращает целое число 5 с остатком 10. Наша программа возвращает значение 10, поскольку оператор модуля возвращает остаток от деления.

Для выполнения вычисления модуля с типом данных float64 вы будете использовать функцию Mod из пакета math:

package main

import (
    "fmt"
    "math"
)

func main() {
    q := 36.0
    r := 8.0

    s := math.Mod(q, r)

    fmt.Println(s)
}

Output
4

Приоритет операций

В Go, как и в математике, мы должны помнить, что операторы будут оцениваться по порядку приоритета, а не в порядке слева направо или справа налево.

Если мы рассмотрим следующее математическое выражение:

u = 10 + 10 * 5

Мы можем прочитать его слева направо, но сначала будет выполняться умножение, так что если бы мы выводили u, то получили бы следующее значение:

Output
60

Это объясняется тем, что 10 * 5 дает 50, а затем мы добавляем 10 для получения 60 в качестве результата.

Если же мы хотим добавить значение 10 к 10, а затем умножить сумму на 5, нужно использовать скобки в Go, как это делается в математике:

u := (10 + 10) * 5
fmt.Println(u)

Output
100

Одним из способов, с помощью которого можно запомнить порядок операций, является акроним PEMDAS:

Порядок	Символ	Значение
1	P	Parentheses (скобки)
2	E	Exponent (степень)
3	M	Multiplication (умножение)
4	D	Division (деление)
5	A	Addition (сложение)
6	S	Subtraction (вычитание)

Вы можете быть знакомы с другим акронимом для порядка операций, например, BEDMAS или BODMAS. Какой бы акроним вам ни подошел, попробуйте держать его в уме, когда вы будете выполнять математические операции в Go, чтобы получить результаты, которые вы ожидаете.

Операторы присвоения

Самый распространенный оператор присвоения — это тот, который вы уже использовали: знак равенства =. Оператор присвоения = присваивает значение справа переменной слева. Например, v = 23 присваивает значение 23 переменной v.

При программировании обычно используются составные операторы присвоения, выполняющие операцию со значением переменной, а затем присваивают новое полученное значение этой переменной. Эти составные операторы объединяют арифметические операторы с опертором =. Поэтому для сложения мы соединим + и = для получения составного оператора +=. Давайте посмотрим, как это выглядит:

w := 5
w += 1
fmt.Println(w)

Output
6

Во-первых, мы зададим переменную w равной 5, а затем используем составной оператор += для добавления нужного числа переменной слева, а затем присвоим результат переменной w.

Составные операторы присвоения используются в циклах for, которые вы используете, когда хотите повторить процесс несколько раз:

package main

import "fmt"

func main() {

    values := []int{0, 1, 2, 3, 4, 5, 6}

    for _, x := range values {

        w := x

        w *= 2

        fmt.Println(w)
    }

}

Output
0
2
4
6
8
10
12

Используя цикл for для прохождения по срезу values, вы можете автоматизировать процесс для оператора *=, который умножает переменную w на число 2, а затем присваивает результат переменной w.

Go имеет составной оператор присвоения для каждого из арифметических операторов, описанных в этом обучающем руководстве.

Чтобы добавить, а затем присвоить значение:

y += 1

Чтобы вычесть, а затем присвоить значение:

y -= 1

Чтобы умножить, а затем присвоить значение:

y *= 2

Чтобы разделить, а затем присвоить значение:

y /= 3

Чтобы вернуть остаток, а затем присвоить значение:

y %= 3

Составные операторы присвоения могут быть полезными, когда нужно инкрементировать или декрементировать значение, или при необходимости автоматизировать определенные процессы в вашей программе.

Заключение

В этом обучающем руководстве мы познакомились с множеством операторов, которые вы будете использовать с целыми числами или числами с плавающей точкой. Вы можете узнать больше о разных типах данных в статьях Знакомство с типами данных в Go и Конвертация типов данных.

PEMDAS Значение, объясненное примерами — Mashup Math

PEMDAS Значение: почему это важно

Правильное применение порядка операций и использование PEMDAS стало очень популярным в последние годы из-за вирусных математических проблем, которые появляются в социальных сетях. Такие сообщения популярны, потому что люди предполагают, что правильный способ применения порядка операций — выполнять каждую операцию слева направо. Поскольку большинство людей неправильно понимают эти, казалось бы, простые математические задачи, их поощряют комментировать и делиться, что быстро приводит к вирусному распространению сообщения.

Однако, если бы люди могли помнить (A) порядок операций с использованием мнемоники, такой как PEMDAS (или даже более полезной, известной как GEMS), и (B) нюансы для правильного применения порядка операций (а именно отношения между умножением / делением и сложением / вычитанием), то подобные вирусные проблемы можно было бы легко решить без особых разногласий.

PEMDAS Значение: Заключение

PEMDAS — распространенная, но в некоторой степени полезная мнемоника для запоминания порядка операций в математике.PEMDAS относится к следующему порядку операций: круглые скобки, экспоненты, умножение, деление, сложение и вычитание. Хотя многие люди помнят PEMDAS, используя знаменитую фразу «Пожалуйста, извините мою дорогую тетю Салли», они часто забывают важный нюанс: умножение не выполняется автоматически перед делением, а сложение не выполняется автоматически перед вычитанием (выполняется умножение / деление и сложение / вычитание слева направо в зависимости от того, какая операция наступит раньше).Это распространенное заблуждение обесценивает PEMDAS как надежный инструмент памяти и является основной причиной, по-видимому, простых математических задач, которые становятся вирусными в социальных сетях, потому что большой процент взрослых может вспомнить мнемонику спустя десятилетия после начальной школы, но не может получить правильный ответ.

PEMDAS сохранил свою популярность как стратегию запоминания порядка действий больше из-за ностальгии и сопротивления изменениям, чем из-за того, что это самая эффективная стратегия. И хотя использование мнемоники редко бывает хорошей стратегией для понимания математических концепций и развития навыков рассуждения, существуют гораздо лучшие альтернативы PEMDAS, включая GEMS, которые значительно более надежны.

Каков порядок операций в математике? — Определение и примеры — Урок математики [видео 2021 года]

Порядок действий Шаги

Шаги, которые мы используем для решения любого математического выражения:

1. Упростите все скобки . Это включает в себя все формы группирующих символов, такие как скобки и фигурные скобки, в дополнение к круглым скобкам.
2. Упростить все показатели .
3. Упростите все умножение и деление слева направо .Упрощая умножение и деление, работайте слева направо.
4. Упростите все сложение и вычитание слева направо . Опять же, упрощая сложение и вычитание, работайте слева направо.

Следуя этому порядку, мы все сможем решить проблему и получить одно и то же решение.

PEMDAS

После объяснения всех этих правил моей тете Салли, она кажется немного ошеломленной. Однако у меня есть ярлык, чтобы помочь ей запомнить эти шаги.Он называется PEMDAS .

Это означает:

P — Скобки

E — Экспоненты

M — Умножение

D — Раздел

A — Сложение

S — Вычитание Помните, что шаги для умножения и деления — это один шаг. Мы выполняем все операции умножения и деления за один шаг слева направо. Умножение не всегда предшествует делению; они обрабатываются в том порядке, в котором они появляются.Это также верно для сложения и вычитания. Они обрабатываются одинаково слева направо. Для меня простой способ запомнить эти шаги — это запомнить фразу Пожалуйста, извините мою дорогую тетю Салли , где:

P — Круглые скобки — Пожалуйста,

E — Экспоненты — Excuse

M — Умножение — Мой

D — Отдел — Уважаемый

A — Дополнение — Тетя

S — Вычитание — Салли

Примеры

Давайте покажем тете Салли, как порядок операций помогает нам решать проблемы.Я хочу показать тете Салли проблему из моей домашней работы сегодня вечером. Задача 3 + [6 (11 + 1 — 4)] ÷ 8 x 2. Помните, что для решения этой задачи мы будем следовать порядку действий. Давайте подумаем о PEMDAS.

Первым шагом к решению этой проблемы является работа с буквой P (круглые скобки). В этой задаче использовались как круглые, так и квадратные скобки. Нам нужно будет начать внутри скобок и работать, пока мы не заполним все символы группировки. Кроме того, работая внутри символов группировки, мы должны соблюдать оставшийся порядок.Для начала нам нужно будет сложить 11 + 1, а затем вычесть 4, что составляет 8. Теперь мы все еще должны работать внутри скобок, 6 умножить на 8 равно 48.

Следующая буква в нашем аббревиатуре — E для экспонент. Поскольку экспонентов нет, продолжаем. Следующий шаг — упростить M и D (умножение и деление) слева направо. Поскольку деление на самом деле стоит на первом месте, мы работаем с ним слева направо. Сначала мы разделим 48 ÷ 8, что составляет 6. В нашей задаче все еще существует умножение, поэтому теперь нам нужно будет умножить 6 на 2, что равно 12.Остается только один шаг — AS (сложение и вычитание). В этой задаче осталось только одно: 3 плюс 12, что равно 15. Итак, как вы видите, тетя Салли, ответ на эту проблему будет 15.

Давайте вместе займемся другой задачей. Решаем 20-4 + 52/5.

Шаг 1: проверьте, нет ли скобок, поэтому мы можем перейти к шагу 2.

Шаг 2: Далее идут экспоненты, и у нас есть показатель степени в 52, который упрощается до 25. Это меняет задачу, чтобы выглядеть как 20 — 4 + 25/5.

Шаг 3: Умножения нет, поэтому мы можем перейти к следующему шагу — делению.

Шаг 4: Работа по разделению, которую нам нужно выполнить, составляет 25/5, что составляет 5. Теперь проблема выглядит как 20 — 4 + 5.

Шаг 5: Далее идет сложение, и у нас есть -4 + 5, что составляет 1. Задача упрощается до 20 + 1, и это дает нам окончательный ответ 21.

Как гласит старая пословица, практика ведет к совершенству, поэтому давайте рассмотрим другой пример проблемы и решим ее.

Следующая задача — (6-5 x 2) 2 / (3 + 7).

Шаг 1: Нам нужно выполнить работу в двух скобках. В круглых скобках числителя указано вычитание и умножение. PEMDAS говорит нам сначала сделать умножение. Это дает нам (6-10) 2. Теперь мы можем вычесть эти значения и получить (-4) 2, что равно 16. Это наш числитель. Круглые скобки знаменателя — это сложение, которое дает 10. Теперь задача упрощается до 16/10, что составляет 1,6.

Поскольку у нас это очень хорошо получается, мы сделаем еще одну задачу, чтобы продемонстрировать наши новые навыки!

Новая задача: 16-4 x 2 + 3 / (17-42) x 32.

Шаг 1. Видны ли скобки? Да! Давайте сначала решим это. В круглых скобках 42, то есть 16. Завершение математических расчетов внутри скобок дает нам 17 — 16 = 1. Теперь задача выглядит как 16 — 4 x 2 + 3/1 x 32.

Шаг 2: Степень больше не существует. , поэтому мы можем перейти к шагу 3.

Шаг 3: Следующий шаг — умножение. У нас есть -4 x 2 и 3 x 32. Таким образом, задача выглядит как 16 — 8 + 96.

Шаг 4: Окончательный вид задачи — 16 — 8 + 96, и ответ — 104.

Теперь давайте рассмотрим то, что мы узнали.

Резюме урока

Порядок операций — это порядок, в котором мы складываем, вычитаем, умножаем или делим для решения проблемы. Шаги, которые мы используем для решения любого математического выражения:

1. Упростите все скобки . Сюда входят все формы символов группировки, такие как скобки, фигурные скобки и круглые скобки.
2. Упростить все показатели .
3. Упростите все умножение и деление слева направо .Упрощая умножение и деление, убедитесь, что вы работаете слева направо.
4. Упростите все сложение и вычитание слева направо . Опять же, упрощая сложение и вычитание, работайте слева направо.

Для меня полезный способ запомнить этот порядок: Пожалуйста, извините, дорогая тетя Салли , что означает:

P — Круглые скобки

E — Экспоненты

M — Умножение

D — Раздел

A — Сложение

S — Вычитание

Помните, что умножение и деление включаются в один и тот же шаг и упрощаются слева направо.То же самое и для сложения и вычитания.

Результаты обучения

После этого урока вы сможете:

• Перечислить шаги, входящие в порядок операций для решения математических выражений
• Найдите аббревиатуру, которая поможет запомнить порядок операций
• Применить порядок операций для решения математического выражения

Порядок операций — предварительная алгебра

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

4.2 — Арифметические вычисления с использованием арифметических операторов

Следующий пример содержит вычисление, иллюстрирующее стандартный порядок операций. Предположим, инструктор по статистике вычисляет итоговую оценку, взвешивая средний балл за экзамен на 0.6, оценка проекта 0,2, а итоговый экзамен 0,2. Следующая программа SAS показывает, как преподаватель (неправильно) вычисляет финальных оценок учащихся:

  марки DATA;
имя входа $ 1-15 e1 e2 e3 e4 p1 f1;
финал = 0,6 * e1 + e2 + e3 + e4 / 4 + 0,2 * p1 + 0,2 * f1;
ДАТАЛИНЫ;
Александр Смит 78 82 86 69 97 80
Джон Саймон 88 72 86. 100 85
Патрисия Джонс 98 92 92 99 99 93
Джек Бенедикт 54 63 71 49 82 69
Рене Портер 100 62 88 74 98 92
;
ЗАПУСТИТЬ;

Данные PROC PRINT = оценки;
имя переменной e1 e2 e3 e4 p1 f1 final;
ЗАПУСТИТЬ;  

Ну да ладно, значит, инструктор должен придерживаться статистики, а не математики.Как вы можете видеть в заявлении о назначении, инструктор пытается указать SAS усреднить четыре оценки за экзамен, сложив их и разделив на 4, а затем умножив результат на 0,6. Посмотрим, что делает вместо этого SAS. Запустите и запустите программу SAS и просмотрите вывод, чтобы увидеть, сможете ли вы выяснить, что SAS сделала, скажем, для первого ученика Александра Смита. Если вы все еще не уверены, еще раз просмотрите правила порядка выполнения операций. Правила говорят нам, что сначала SAS:

• дает оценку 78 за первый экзамен Александра и умножает ее на 0.6, чтобы получить 46,8
• берет четвертый балл Александра 69 за экзамен и делит его на 4, чтобы получить 17,25
• берет оценку за проект Александра 97 и умножает ее на 0,2, чтобы получить 19,4
• берет итоговую оценку Александра 80 за экзамен и умножает ее на 0,2, чтобы получить 16,0

Затем SAS выполняет все сложение:

  46,8 + 82 + 86 + 17,25 + 19,4 + 16,0  

, чтобы получить его окончательный результат 267,45. Возможно, это окончательная оценка, которую хочет Александр, но это все равно в корне неверно.Давайте посмотрим, сможем ли мы помочь настроить инструктор по статистике, воспользовавшись тем последним правилом, которое гласит, что операции в круглых скобках выполняются первыми.

Каков приоритет арифметических операторов? — Aristides S. Bouras

Арифметические операторы следуют тем же правилам приоритета, что и в математике, а именно: возведение в степень выполняется первым (если возможно), затем выполняется умножение и деление, последними выполняются сложение и вычитание. *, /, \, Мод +, —

Python

Высший приоритет Младший приоритет	Арифметические операторы
	**
	*, /, //,%
	+, —

Когда умножение и деление существуют в одном выражении, и поскольку оба имеют одинаковый приоритет, они выполняются слева направо (так же, как вы читаете), что означает, что выражение

6/3 * 2

эквивалентно 4 (деление выполняется перед умножением).

Если вы хотите, однако, чтобы умножение выполнялось перед делением, вы можете использовать круглые скобки для изменения приоритета, то есть:

6 / (3 * 2)

, что эквивалентно

Примечание: Компьютерные программы можно писать с помощью текстового редактора вашего компьютера, но имейте в виду, что дроби нельзя записывать в форме или. Забудь это! В текстовом редакторе нет редактора формул! Все дроби должны быть записаны в одной строке.Например, он должен быть записан как 6/3 и должен быть записан как (4 * x + 5) / 6 .

Порядок операций можно резюмировать следующим образом:

1. Любые операции, заключенные в круглые скобки, выполняются первыми.
2. Далее выполняются любые возведения в степень (доступные в Visual Basic и Python).
3. Затем все операции умножения и деления выполняются слева направо.
4. В конце концов, любые операции сложения и вычитания выполняются слева направо.

Итак, в выражении (20 + 3) + 12 + 8/4 * 3

операции выполняются следующим образом:

1. 20 прибавляем к 3, в результате получаем 23.
2. 8 делится на 4, что дает результат 2. Затем этот результат умножается на 3, что дает результат 6.
3. 23 прибавляется к 12, что дает результат 35. Затем этот результат прибавляется к 6, давая окончательный результат 41.

Далее следует та же последовательность операций, представленная в более наглядном виде.

открытых учебников | Сиявула

Математика

Наука

• • Читать онлайн

  • Учебники

    • Английский

      • Класс 7A

      • Марка 7Б

      • 7 класс (A и B вместе)

    • Африкаанс

      • Граад 7А

      • Граад 7Б

      • Граад 7 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • Марка 8A

      • Марка 8Б

      • Оценка 8 (вместе A и B)

    • Африкаанс

      • Граад 8А

      • Граад 8Б

      • Граад 8 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • Марка 9А

      • Марка 9Б

      • 9 класс (A и B вместе)

    • Африкаанс

      • Граад 9А

      • Граад 9Б

      • Граад 9 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • Класс 4A

      • Класс 4Б

      • Класс 4 (вместе A и B)

    • Африкаанс

      • Граад 4А

      • Граад 4Б

      • Граад 4 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • Марка 5A

      • Марка 5Б

      • Оценка 5 (вместе A и B)

    • Африкаанс

      • Граад 5А

      • Граад 5Б

      • Граад 5 (A en B saam)

  • Пособия для учителя

• • Читать онлайн

  • Учебники

    • Английский

      • Марка 6A

      • Марка 6Б

      • 6 класс (A и B вместе)

    • Африкаанс

      • Граад 6А

      • Граад 6Б

      • Граад 6 (A en B saam)

  • Пособия для учителя

Наша книга лицензионная

Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:

CC-BY-ND (фирменные версии)

Вам разрешается и поощряется свободное копирование этих версий.Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.

Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.

CC-BY (безымянные версии)

Эти небрендированные версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula.