Конспект по математике

Предмет: Математика Урок: 88		Школа:
Дата:		ФИО учителя: Мамаева А.М.
Класс: 3		Количество присутствующих:	Количество отсутствующих:
Раздел (сквозная тема):		Раздел 3A – Внетабличное умножение и деление.
Тема урока:		Закрепление устных приёмов умножения и деления. Графика.
Цели обучения, которым посвящен урок:		3. 1.2.7 — выполнять устно внетабличное умножение и деление в случаях вида: 17·5, 96:6, 75:15, 84:4 3.1.2.9 — применять правила деления суммы и произведения на однозначное число, умножение суммы на число при устном выполнении умножения и деления чисел в пределах 100 3.2.2.2 — решать простейшие уравнения, содержащие действия умножения и деления; уравнения сложной структуры видах· (25:5)=60; (24·3):х=6;х: (17·2)=2;k+124 : 4 = 465
Развитие навыков:		1.2Операции над числами 2.1 Числовые и буквенные выражения 2.2 Равенства и неравенства. Уравнения
Предполагаемый результат:		Все учащиеся смогут: выполнять устно умножение и деление внетабличных случаях вида: 17 · 5; 96 : 6; 75 : 15; 84 : 4; применять правила деления суммы и произведения на однозначное число, умножение суммы на число при устном выполнении умножения и деления чисел в пределах 100. Большинство учащихся смогут: объяснять правила деления суммы и произведения на однозначное число, умножение суммы на число при устном выполнении умножения и деления чисел в пределах 100. Некоторые учащиеся смогут: группировать случаи устного умножения и деления во внетабличных случаях вида: 17 · 5; 96 : 6; 75 : 15; 84 :4.
Языковая цель		Учащиеся могут: объяснять правила деления суммы и произведения на однозначное число, умножение суммы на число при устном выполнении умножения и деления чисел в пределах 100. Предметная лексика и терминология: Правило умножения и деления суммы на число, подбор частного. Серия полезных фраз для диалога/письма Обсуждение: Объясните, какое правило лежит в основе конкретного приема: деление суммы и произведения на однозначное число, умножение суммы на число при устном выполнении умножения и деления чисел в пределах 100. Как вы считаете, для чего нужно знать правила и свойства действий? Как выполнить проверку своих вычислений?
		Письмо: Запишите вычисления и их проверку
Материал прошедших уроков:		Приемы внетабличного умножения и деления
Ход урока:
Этапы урока	Запланированная деятельность на уроке			Ресурсы
0-3 мин	Мотивация Педагог показывает графические рисунки. Вовлекает детей в беседу о таком виде изобразительного искусства. Графика (др. греч. γρᾰφικός письменный, от др.греч. γράφ ω – записывать, писать) – вид изобразительного искусства, использующий в качестве основных изобразительных средств линии, штрихи, пятна и точки. Цвет также может применяться, но, в отличие от живописи, здесь он традиционно играет вспомогательную роль. В современной графике цвет может быть не менее важен, чем в живописи. При работе в графике обычно используют один или два цвета, кроме основного черного или красно-коричневого цвета сангины, можно использовать белый, в особенности на тонированной бумаге. Но при работе пастелью может использоваться вся цветовая палитра, как в живописи; согласно современной музейной классификации, работа пастелью на бумаге тоже относится к графике. Кроме контурной линии, в графическом искусстве широко используются штрих и пятно, также контрастирующие с белой (а в иных случаях также цветной, черной, или реже – фактурной) поверхностью бумаги – главной основой для графических работ. Сочетанием тех же средств могут создаваться тональные нюансы. Наиболее общий отличительный признак графики – особое отношение изображаемого предмета к пространству, роль которого в значительной мере выполняет фон бумаги (по выражению советского мастера графики В. А. Фаворского, – «воздух белого листа»). В графике, в частности, в гравюрах, может использоваться большое число цветов (при создании некоторых гравюр может использоваться более десятка печатных форм, каждая из которых «добавляет» свой цвет).
Середина урока 4-6 мин 7-11 мин 12-29 мин 31-37 мин	Актуализация. На этом уроке можно провести математический диктант «Да – нет» с проверкой. • Произведение 29 и 3 равно 87. • Число 5 увеличили в 19 раз. Получили 85. • Сумму 17 и 5 увеличили в 4 раза. Получили 98. • Одну седьмую часть от 56 увеличили в 12 раз. Получили 96. • Первый множитель равен одной пятой от 25, второй множитель равен 11. Тогда произведение равно 55. • Произведение 12 и 8 меньше 100. • Разность 570 и 370 увеличили в 4 раза. Получили 900. • Делимое равно 720, делитель равен разности 20 и 11. Тогда частное равно 9. • Первый множитель равен сумме чисел 37 и 4. Второй множитель равен 2. Тогда произведение равно 82. «Найди лишнее слово». Далее педагог предлагает выполнить задание №2 (а, б) в учебнике. В каждом из этих пунктов примеры подобраны на применение одного из свойств действий. Поэтому комментирование решений позволит выявить, что за свойство лежит в основе. Параллельно с комментированием педагог на доске вывешивает буквенные записи свойств. Постановка цели (проблемная ситуация). Для каждого случая внетабличного умножения и деления предлагает восстановить алгоритм. Например, для случая 25·3 1. Прочитать каждый шаг алгоритма. 2. Составить алгоритм. 3. Объяснить выполнение шагов алгоритма. Шаги предлагает на карточках: Карточка 1. Сложите полученные произведения. Запишите ответ. Разложите число на сумму разрядных слагаемых. Умножьте на это число поразрядно. Карточка 2. Разложите число на сумму разрядных слагаемых. Умножьте на это число поразрядно. Полученные произведения сложите. Запишите ответ. Для всех остальных случаев надо построить алгоритм на сегодняшнем уроке. Проверяет, все ли усвоили. Самостоятельная работа. Предлагает выполнить задание №3 в учебнике. После сравнения с эталоном (решенными уже примерами) составляет план коррекции. Коррекция затруднений Педагог проверяет правильность выполнения. – У кого возникли затруднения? – В каком месте вы допустили ошибку? – В чем причина допущенной ошибки? – Те, у кого не возникло затруднений в самостоятельной работе, сформулируйте цель вашей деятельности. (Выполнить дополнительные задания). – Какова дальнейшая цель работы у тех, кто выявил затруднения? (Исправить ошибки). – Используем алгоритм исправления ошибок. – Каждый проговаривает свою учебную задачу. Работа над ранее изученным Педагог дает задания индивидуально, в зависимости от уровня продвижения ребенка. Предлагает выполнить задание №6. Рассматривая вычисления в первой строчке, делается вывод, что при умножении 111на однозначное число, количество сотен, десятков и единиц равно этому числу. Предлагает выполнить задание №8. Для решения задачи составляется граф.Пять точек соединяются попарно. Получается из одной точки проводим 4 линии. 5∙4=20 Второй способ. Рассуждаем: каждый отдал по 4 фотографии. Друзей 5 значит 4∙5=20 Педагог предлагает задание в тетради с критериями оценивания. Предлагает в тетради решить и проверить простые уравнения, содержащие изученные приемы. х :5=19 750:х=5 23·х=69 Я могу:  решить простое уравнение на умножение и деление;  выполнить устно умножение и деление;  выполнить проверку. Составь вопросы по теме урока. В каждом уроке нового или закрепления учащиеся составляют вопросы. Это позволит помочь провести рефлексию усвоения темы. Со словами, приведенными в учебнике надо составить вопросы. Можно использовать прием: ромашка или кубик Блума.			Учебник Тетрадь Учебник Тетрадь Учебник Тетрадь
Конец урока 38-40 мин	Рефлексия. Определяет домашнее задание с учетом индивидуальных трудностей детей. – Какие задачи мы ставили перед собой в начале урока? – Удалось ли достичь этих задач? – Возникали у вас затруднения? – Вы смогли их преодолеть? – Чем интересен был сегодняшний урок? Предлагает оценить свою работу при помощи линейки успеха.			Самооценивание

Читать онлайн «Репетитор по математике. Арифметика», М. Л. Фартушняк – Литрес

Дизайнер обложки М. Л. Фартушняк

© М. Л. Фартушняк, 2021

© М. Л. Фартушняк, дизайн обложки, 2021

ISBN 978-5-0053-3834-1

Создано в интеллектуальной издательской системе Ridero

Введение или как работать с этой книгой

1. Почему репетитор? Название возникло сразу. Не потому, что подобных названий почти нет. Судите сами, это ведь не учебник, где весь учебный материал подаётся от более простого к сложному. В учебнике существует тенденция перескакивания с одной темы на другую, а потом возвращение к уже более сложными заданиям. В репетиторе такого нет. Если вы начали изучать какую-то тему, то изучаете её от начала и до конца. Кроме этого, в репетиторе теоретический материал подан в самом необходимом минимальном объёме без каких-либо доказательств и выведения формул. Это также и не справочник, где существует множество формул, определений, таблиц, где много теоретического материала, но почти нет практического применения теоретических знаний. Цель же репетитора – обучение практическим навыкам решения разнообразных математических задач. Наиболее похож репетитор на практикум, там тоже большое внимание уделяется практическим занятиям, но в отличие от практикума, где почти нет теоретического материала, в репетиторе он присутствует. Кроме этого, в данном учебном пособии есть тестовые задания, которые, как правило, отсутствуют в учебниках, справочниках, практикумах.

2. Кому прежде всего будет полезна эта книга? Репетитор ориентирован на основные задания, которые могут встретиться на экзаменах по математике. Поэтому данное пособие прежде всего станет незаменимым помощником именно для учащихся средней школы. Она также может быть применима и учителями, и выпускниками средних школ, и даже абитуриентами, а так же тем, кто хочет повысить свою математическую грамотность и научиться решать типовые математические задачи. Автор отдаёт себе отчёт в том, что никакое учебное пособие не заменит реального живого репетитора, который сможет подкорректировать и направить свои усилия на те разделы математики, в которых ученик разбирается не совсем хорошо.

Увы, книга лишена такой возможности. Она может служить только дополнением к занятиям с реальным репетитором. Однако репетитор стоит немалых денег и не у всех есть возможность его нанять. Поэтому данное учебное пособие является хоть и неполной, но альтернативой. Ещё будучи учителем в школе, автор обратил внимание, что овладеть основными математическими навыками может практически любой человек. Есть только небольшой процент людей, которые не могут этого сделать по разным объективным причинам. Остальные не знают математику и не умеют решать математические задачи потому что, или не хотят, или не хватает времени, или просто в жизни это может не пригодится, или лень заниматься каждый день. Таким людям я не рекомендую открывать репетитор. Вы не добьётесь желаемого результата и будете винить во всем автора. А для тех, кто решил серьёзно заняться изучением математики – добро пожаловать на страницы этого пособия. Если хотя бы половине этих людей репетитор поможет, автор будет считать, что его труд не был напрасным.

3. Чем же репетитор отличается от других учебных пособий? Прежде всего простотой подачи материала. Автор общается с обучаемым и указывает на характерные ошибки, которые могут встретиться при решении задач. В репетиторе показано решение типовых задач, а также задач повышенной трудности. Каждая задача или пример решается досконально с пояснениями, что позволяет усвоить базовые навыки даже людям, которые считали, что математика не для них.

4. О структуре данной книги. Вся книга поделена на темы. В каждой теме есть необходимый минимум теоретического материала, примеры решения задач. В конце каждого раздела даются два тестовых задания и задачи для самостоятельного решения.

Поговорим отдельно о каждой из этих составляющих.

Теоретический материал. Как было уже сказано ранее, это тот необходимый минимум, без которого невозможно обойтись при решении заданий. Если формула выведена крупным шрифтом – её необходимо запомнить. Тоже самое касается формулировок и прочих элементов теории. Таких обязательных элементов для запоминания в книге немного. Обучение построено по американской системе, где от учащегося не требуется зазубривание теоретического материала, а предпочтение отдаётся только навыкам его применения на практике. Поэтому, при самостоятельном решении задач автор разрешает пользоваться формулами. Запоминание формул произойдёт автоматически при практическом их применении. В конце книги собран и изложен в кратком виде весь теоретический материал. Им вы можете пользоваться при решении задач. Это не значит, что теоретический материал можно совсем не изучать или изучить бегло. Как я уже сказал, в конце каждой темы есть тестовые задания и без базовых знаний теоретического материала, вы вряд ли сможете их пройти.

Примеры решения задач. В репетиторе рассмотрены решения как базовых типовых задач, так и задач повышенной сложности. Все задания взяты из разных источников: учебных пособий, экзаменационных работ и т. д. Автор уважает авторские права других, поэтому в конце книги дан список использованной литературы. Как было сказано выше, все примеры решения задач приведены с подробными пояснениями.

Тестовые задания. К каждой теме предложено два тестовых задания. Каждое тестовое задание включает 32 вопроса с четырьмя вариантами ответов, один из которых является правильным. Оценивание тестовых заданий производится по 12-ти бальной системе. Чтобы не путаться, привожу перевод 12-ти бальной системы в пятибальную.

12 баллов – оценка 5+

11 баллов – 5

10 баллов – 5-

9 баллов – 4+

8 баллов – 4

7 баллов – 4-

6 баллов – 3+

5 баллов – 3

4 балла – 3-

3 балла – 2+

2 балла – 2

1 балл – 2 —

Я надеюсь, что последние шесть строчек вам не понадобятся при оценивании тестовых заданий. Только все должно быть по честному. Помните, если вы будете не объективны, то в первую очередь обманите сами себя.

Теперь, как оценивать тестовые задания. За каждое правильное тестовое задание начисляется 1 балл.

Если вы набрали 31—32 балла, то это 12 баллов по 12-ти бальной системе оценивания.

29 —30 – 11 баллов

27 – 28 – 10 баллов

25 – 26 – 9 баллов

23 – 24 – 8 баллов

21 – 22 – 7 баллов

19 – 20 – 6 баллов

17 – 18 – 5 баллов

15 – 16 – 4 балла

Если вы набрали меньше 15 баллов, то вам следует вернуться к изучению теоретического материала, а потом пройти тест заново.

Продолжительность тестирования – 45 минут. Выделите для тестирования отдельный день. Берите чистый лист бумаги и вперёд. Тесты это не только интересно, но и познавательно. Желательно пройти все предложенные тесты (но не в один день), в конце книги имеются ответы на тестовые задания для проверки. Не стоит в них заглядывать раньше времени.

Задачи для самостоятельного решения. Автор сознательно не выделял какими-то знаками задания повышенной сложности и считает, что такое приём способствует более спокойному решению задач без излишнего волнения и стресса. В процессе решения вы сами сможете понять, сложна для вас данная задача или нет. Притом сложность задачи – это субъективная оценка. Некоторые с лёгкостью могут решать подобные задачи, а вот более простые в нашем понимании могут вызвать затруднение. Если вы поняли, что можете приступать к решению задач, то не медлите. Каких-то ограничений по количеству решаемых задач в день нет. Когда поняли, что устали, то занятие можно прекратить, но хотя бы 30 – 40 минут в день вы должны уделять решению задач. Это не обязательно делать изо дня в день. Через какое-то время можно сделать себе 1- 2-х дневный перерыв. Но с отдыхом не затягивайте. Почувствовав, что немного отдохнули и есть свободное время, приступайте снова к решению задач. Автор рекомендует решить все задачи, которые есть в разделе для самостоятельного решения. Решив какую-то задачу, загляните в раздел ответы и, убедившись, что вы все решили правильно, продолжайте дальше. Если ваш ответ не совпадает с ответом в конце книги, рекомендуется ещё раз пройтись по своему решению и выявить ошибки. Если вы их не обнаружили, то загляните в раздел « Указания к решению задач». Он находится после раздела ответов.

Прочитав указания к решению задач (они есть ко всем задачам), снова приступайте к решению сложной для вас задачи. К задачам для самостоятельного решения есть полные и подробные решения, которые находятся в соответствующем разделе. Но это последний раздел, в который вам следует заглянуть. Это в том случае, когда задача не решается без посторонней помощи. Не злоупотребляйте этим разделом, иначе вы так никогда и не научитесь решать математические задачи. Постарайтесь ограничиться только разделом «Указания к решению задач». Этого бывает достаточно, чтобы понять свою проблему и попытаться её искоренить.

В конце книги, как я уже сказал, находится справочный раздел, ответы к тестовым заданиям, ответы к задачам для самостоятельного решения, указания к решению задач, решение задач. Кроме этого, там же находится список использованной литературы. Структура книги максимально удобна для использования.

Кроме этого, в конце книги  будет предложена итоговая контрольная работа из 8 заданий (2 варианта).

Выбирайте любой вариант и приступайте к решению. Время решения контрольной работы полтора часа. Только когда решены все задания контрольной работы, можно заглянуть в ответы и оценить свои знания. Если из 8 заданий вы решили полностью правильно 5-6, то можете себя поздравить. Вы не зря потратили время, работая с этой книгой.  Пользоваться справочными материалами при решении контрольной работы не рекомендуется, как и другими учебниками и учебными пособиями. Разрешается использовать только калькулятор.

 

Автор будет благодарен за любые замечания и обнаруженные неточности и ошибки при написании этого пособия. А также будет рад любому мнению и практическим советам от учителей и преподавателей математики по улучшению данной книги.

Примечание: некоторые понятия, изложенные в этом пособии (например,

бесконечная периодическая дробь, среднее геометрическое и др.) не относятся к разделу «Арифметика», но они введены здесь для целостности восприятия.

Арифметика

Арифметика – базовая дисциплина для овладения более сложной составляющей математики – алгебры. Без навыков решения арифметических задач невозможно выучить алгебру и геометрию. Это нижний фундамент и основа грандиозного сооружения под названием математика. Очень часто на экзаменах по математике учащиеся делают именно арифметические ошибки, которые в итоге снижают им общий балл. Обидно? Конечно. А всё из-за того, что некоторые игнорируют учебный материал, изучаемый в пятом-щестом классе средней школы и считают его чем-то несерьёзным и ненужным. Это заблуждение.

Понятно, что для многих содержимое этой книги известно, но для целостности восприятия я всё-таки рекомендую вам ознакомиться с предложенными темами, решить типовые задачи и ответить на тестовые задания. Это совсем несложно и поэтому на него вы потратите минимум времени, но зато, поверьте мне, в дальнейшем вам будет намного проще осваивать более сложный материал. Итак, вперёд, друзья мои! Время не ждёт.

Тема 1

Числа, цифры, арифметические действия, порядок действий, скобки

Само название «арифметика» происходит от греческого слова означающего «число». Само число – это простейшие понятие, его можно пояснить лишь предметным образом. По мере развития человечества возникла необходимость счета людей, животных, предметов домашнего обихода и прочих вещей. Так возникла количественная оценка предметов. Многие задают вопрос, чем же число отличается от цифры? Цифра – это письменный знак, изображающий число. Сейчас, в основном, мы пользуемся арабской системой записи чисел. И совсем не задумываемся, написав цифру 2, мы отлично понимаем, что это цифра больше, чем цифра 1 и меньше, чем цифра 3. Арабская система исчисления – десятичная. Это означает, что названия всех чисел образованы из названий чисел первого десятка и чисел 10, 100, 1000.

Например, 17 (семнадцать – семь на (сверху) десять), 50 (пятьдесят – пять десятков), 400 (четыреста – четыре сотни). Особняком стоит 90 (девяносто),образованное по другому принципу (девять до ста) и число 40 (сорок) – единственное исключение.

У разных народов были разные системы нумерации. До наших дней дошла ещё римская нумерация чисел. Но она очень неудобна при операциях сложения, умножения и так далее, поэтому в математике не используется. Для желающих познакомиться более детально с римской нумерацией чисел, добро пожаловать в дополнительный раздел. Но мы не будем сейчас на этом останавливаться. Следует заметить, не все числа, которыми мы сейчас пользуемся, возникли одновременно. Первыми числами, которыми пользовался человек, были натуральные числа, обозначаемые буквой N. Именно, они возникли первыми при счёте предметов. Натуральные числа начинаются с единицы и продолжаются до бесконечности. Примеры таких чисел довольно просты: на улице 18 домов, в коробке 12 карандашей, в библиотеке 5432 экземпляра книг, в городе проживает 252 196 жителей. Далее возникла необходимость ввести число 0, ведь при вычитании одинаковых натуральных чисел получалось «нечто», не имеющее материального обоснования. Перед тем как появилась необходимость введения отрицательных чисел для обозначения этого «ничего» ввели число 0. По мере дальнейшего совершенствования человеческих отношений, развития науки и техники возникла необходимость в отрицательных числах. Натуральные числа, противоположные к ним и 0 составили множество целых чисел Z. Потом возникли дробные числа. О дробных числах мы поговорим подробнее в соответствующей теме. Целые и дробные числа составляют множество рациональных чисел Q. Если к множеству рациональных чисел добавить иррациональные числа, мы получим множество действительных чисел R. Для наглядности составлена такая таблица. (табл.1)

Для удобства чтения и запоминания больших чисел их разбивают на классы. Справа отделяют три цифры (первый класс), потом ещё три цифры (второй класс) и т. д. Между собой классы отделяются небольшим пробелом. Первый класс даёт число единиц, второй – число тысяч, третий – миллионов. Каждая из цифр класса наз. его разрядом, счёт разрядов также идёт справа. Числа в первом классе справа налево: единицы, десятки, сотни, во втором классе соответственно: тысячи, десятки тысяч, сотни тысяч. В третьем классе: миллионы, десятки миллионов, сотни миллионов. Единица четвёртого класса называется миллиардом, пятого триллионом. Существует единица и для 6, 7, 8 и т. д. классов, но мы их рассматривать не будем. А теперь поупражняемся.

Таблица 1

35 461 298 читается так: 35 миллионов 461 тысяча 298.

Не следует бояться больших чисел, число 12 021 306 200 025 имеет 5 классов, поэтому читается таким образом: 12 триллионов 21 миллиард 306 миллионов 200 тысяч 25.

Теперь перейдём непосредственно к арифметическим действиям. Мы не будем давать здесь определений арифметических действий, они известны всем. Итак, арифметические действия – это сложение, вычитание, умножение и деление, а также возведение в степень и извлечение корня. Степени и корни изучаются в курсе алгебры и мы их рассматривать не будем. Здесь приведём примеры основных арифметических действий:

Сложение.

8 +5 = 13. Здесь 8 и 5 – слагаемые, 13 – сумма.

Вычитание.

15 – 8 = 7. Здесь 15 – уменьшаемое, 8 – вычитаемое, 7 – разность.

Умножение.

6 × 5 = 30. Здесь 6 – множимое, 5 – множитель, 30 – произведение.

Деление.

30 ÷ 6 = 5. Здесь 30 – делимое, 6 – делитель, 5 – частное.

Эти термины нам понадобятся в дальнейшем.

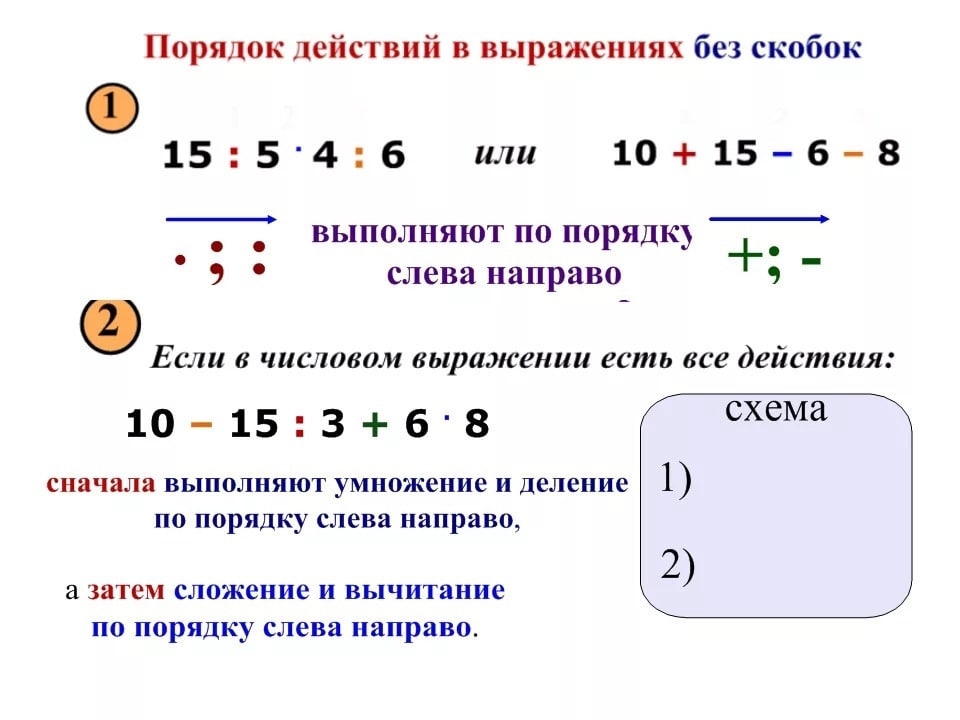
Важнейшим понятием арифметики есть порядок действий. При вычислениях им нельзя игнорировать. Поэтому 4—2+1 будет равно трём если проводить действия в порядке их записи. Если же сначала сложить 2+1 и вычесть полученную сумму из 4, то получим совсем другой ответ, которой равен единице. Чтобы указать в каком порядке нужно выполнять действия пользуются скобками. Действие, заключённое в скобки, выполняется раньше других. Таким образом, порядок действий при вычислениях:

1. Сначала выполняются действия, заключённые в скобки. Умножение и деление делается в порядке их следования, но раньше, чем сложение и вычитание.

2. Затем выполняются оставшиеся действия, причём опять умножение и деление делается в порядке их следования, но раньше сложения и вычитания.

Рассмотрим пару примеров: (2+4) ×5.

Сначала вычисляем действие в скобках 2+4 = 6, далее следует умножение на 5:

6×5 = 30.

Это простой пример. Рассмотрим более сложный:

9+16:4—2 × (16—2×7+4) +6 × (2+5)

Сначала выполняем действия в скобках, не забывая о том, что умножение и деление идёт впереди сложения и вычитания.

Первая скобка: 2 × 7 = 14, 16 – 14 = 2, 2 +4 = 6.

Вторая скобка: 2 +5 = 7.

Наш пример примет вид: 9 +16: 4 – 2 × 6 +6 × 7. Теперь выполняем операции умножения и деления в порядке их следования:

16: 4 = 4, 2 × 6 = 12, 6 × 7 = 42.

И окончательно, выполняем операции сложения и вычитания в порядке их следования. Имеем 9 +4 – 12 +42 = 43.

Иногда приходится заключать скобки в скобки, поэтому пользуются ещё и квадратными скобками.

Порядок действий: сначала выполняются в круглых скобках, потом в квадратных, а потом все остальные действия. Например,

5+2× [14—3× (8—6)] +32: (10—2×3)

Выполняем действия в круглых скобках, имеем:

8 – 6 = 2, 10 – 2 × 3 = 10 – 6 = 4

Действия в квадратных скобках дают: 14 – 3 × 2 = 8

Выполняя оставшиеся действия, имеем:

5 +2 × 8 +32: 4 = 5 +16 +8 = 29.

А теперь немного отвлечёмся. Сейчас в соц. сетях некоторые пользователи придумывает такое развлечение, они выкладывают простой арифметический пример и просят других пользователей дать правильный ответ. Вот, например,

10:2 (4—2).

Наиболее часто встречающиеся ответы 10 и 2.5. Вы уже немного продвинулись в арифметике и поэтому для вас не составит труда дать правильный ответ. Это число 10. 70％ пользователей дают правильный ответ на эту арифметическую задачу. И это, я считаю, неплохо. А теперь на этом примере рассмотрим характерные ошибки, которые делают остальные 30％.

Наиболее существенная ошибка. Простой арифметический пример пытаются решить алгебраическими методами, в частности раскрывая скобки (об этом методе поговорим в дальнейшем), тем самым нарушая порядок действий. Сразу замечу, алгебра и арифметика – это две разные дисциплины. В арифметике, в отличие от алгебры, основная функция скобки – обозначение приоритета очерёдности действий. Каких только определений не придумывается для этого ошибочного решения: коэффициент скобки, действия на скобку и т.  д. Если вы таким образом решите данный пример, то получите 2.5. Внимание: неправильное решение.

10: (2×4 – 2×2) =10: (8—4) = 10:4 = 2.5

Другие пользователи помнят, что сначала выполняется действие в скобках, но потом делает характерную ошибку: они умножают двойку на то, что получилось в скобках, а потом уже выполняют деление. Запомните, никакого приоритета умножение перед делением не имеет, поэтому все оставшиеся действия делаются слева направо в порядке их написания. Если вы сделаете ошибку такого рода получите снова 2.5. Внимание: неправильное решение.

10:2×2 = 10:4 = 2.5.

Я не представляю, какие дебаты могли возникнуть, если был бы выложен более сложный арифметический пример. Часть тех, что делают ошибку утверждают, что их так учили и 30—50 лет назад этот пример решался именно так. Замечу, что арифметика – древняя наука и те правила, которые сложились ещё много веков назад действуют и по сей день. Интересно, что те, кто правильно решает данный пример не настолько агрессивны, как те, что решают его неправильно. В чём природа такого явления нужно спросить у психологов. Ещё одно ошибочное утверждение, некоторые доказывают, что правильных ответов может быть два и более. Это заблуждение, арифметика – точная наука и у любого задания есть единственно верный ответ (в отличие, кстати, от алгебры).

О единственно верном ответе есть отличный видеоролик, снятый американскими кинематографистами. Впрочем, смысл этого ролика немного в другом, я попытаюсь пересказать его содержание, но рекомендую вам самим посмотреть его. Достаточно в поисковой строке набрать 2+2=22 или название ролика «Альтернативная математика». В начале учительница пытается объяснить мальчику, что два плюс два равняется четырём, а не 22, как тот написал в тесте. Беседа с ребёнком ничего не даёт и тогда учительница приглашает родителей мальчика. Родители в недоумении и заявляют, что учитель не имеет права навязывать школьнику своё мнение, если ребёнок считает что два плюс два равняется 22, значит нужно согласится с его мнением. Дальше история становится ещё абсурдней. Директор школы настаивает на том, чтобы учительница извинилась перед родителями, т.к своим поведением она мешает школьникам мыслить самостоятельно и навязывает свои догмы. Дальше – больше, перед образовательным учреждением ученики выходят с плакатами на площадь, а учительницу вызывают на комиссию с требованием признать, что существует несколько правильных ответов. Учительница возражает: «Есть только один правильный ответ». В конце-концов учительница отстаивает свою точку зрения. Директор вызывает учительницу и перед журналистами и телевизионщиками говорит: « Нам придётся вас уволить, вы получите 4000. 2.000 за прошлый месяц и 2.000 за текущий. И тут учительница иронично замечает: « Не верно, это 22000». На этом ролик заканчивается. На самом деле он не о том что, математика – точная наука, здесь больше критика в сторону толерантного образования США. На самом деле создатели ролика немного ошиблись, т.к 2000 +2000 = 2 000 2 000,т.е 20 миллионов 2 тысячи, если считать по правилам альтернативной математики.

Мы пользуемся десятичной системой исчисления, это связано, скорее всего, с тем, что у нас на руках 10 пальцев. В компьютерных системах применяется двоичная система исчисления, а также восьмеричная и шестнадцатеричная. Кроме этого может существовать пятеричная, двенадцатеричная и какие угодно другие системы исчисления. Запись одного и того же числа в разных системах исчисления будет иной, чем в привычной нам десятичной системе. Кому это интересно, добро пожаловать в дополнительный раздел.

Начало Умножение и деление НАБОР

Ищете отличный способ ввести умножение и деление? Этот пакет идеально подходит для использования в дистанционном обучении, поскольку он позволяет учащимся работать независимо, а также имеет ссылку на Google Classroom.

ПРИМЕЧАНИЕ. В этом ресурсе теперь есть задания Google Classroom, что делает его идеальным для цифрового дистанционного обучения и дистанционного обучения! Ссылки см. на 3-й странице каждого PDF-файла!

В комплекте: 9 шт. 0003

Начало Умножения: Полностью переработано к новому учебному году!!! Этот блок идеально подходит для ознакомления ваших студентов с умножением. Он начинается с разрешения учащимся рисовать картинки, а затем переходит к словесным задачам. Дается практика умножения на 2,3,4 и 5. Это можно использовать в обычном учебном классе или в классе специального образования. Его можно использовать для дополнительной практики, RTI или дифференцированного обучения. В комплект входят:

• 3 страницы для рисования изображений для умножения на 2

• 3 страницы для рисования картинок для умножения на 3

• 3 страницы для рисования картинок для умножения на 4

• 3 страницы для рисования картинок для умножения на 5

• 3 страницы для рисования картинок для умножения на 2,3 ,4,5

• Рисунок рисунков для оценки умножения

• 2 страницы для умножения на 2

• 2 страницы для умножения на 3

• 2 страницы для умножения на 4

• 2 страницы для умножения на 5

• 2 страницы для умножения на 2,3,4,5

• Задачи Word для оценки умножения

• Набор из 24 карточек с заданиями

• Предложения по выполнению модуля и использованию карточек с заданиями

• Ключ ответа

9 0002 Начало Дивизия: Полностью переработана к новому учебному году!!! Этот модуль идеально подходит для ознакомления ваших учеников с дивизией! Он начинается с разрешения учащимся рисовать картинки, а затем переходит к словесным задачам. Дается практика деления на 2,3,4 и 5. Это можно использовать в обычном классе или в классе специального образования. Его можно использовать для дополнительной практики, RTI или дифференцированного обучения. В этот блок входят:

• Использование счетчиков для деления на 2

• Деление на 2 с использованием рисунков – 2 страницы

• Задания на деление на 2 – 2 страницы

• Использование счетчиков для деления на 3

• Деление на 3 с использованием изображений – 2 страницы

• Словесные задачи на деление на 3 – 2 страницы

• Использование счетчиков для деления на 4

• Деление на 4 с использованием картинок – 2 страницы

• Word задачи на деление на 4 – 2 страницы

• Использование Счетчики для деления на 5

• Деление на 5 с использованием рисунков – 2 страницы

• Задания на деление на 5 – 2 страницы

• Использование счетчиков для деления на 2,3,4 и 5

• Деление на 2,3,4, & 5 Использование иллюстраций – 2 страницы

• Задачи на деление на 2, 3, 4 и 5 – 2 страницы

• Оценка задач – 2 страницы

• Набор из 24 карточек с заданиями и листом ответов

• Предложения для использования данного устройства

• Клавиша ответа

Не уверены, что это для вас? Загрузите ПРЕДВАРИТЕЛЬНУЮ ПРОСМОТР для бесплатного образца!

Полное руководство по обучению умножению и делению

Умножение и деление являются основными математическими навыками для старших классов начальной школы. В этом посте я собрал для вас БЕСПЛАТНЫЕ уроки, ключевые навыки, якорные таблицы, рекомендации по книгам и несколько дифференцированных упражнений для обучения умножению и делению.

Скачайте все, что вам нужно — бесплатно!

Это бесплатное руководство в формате PDF позволит вам иметь под рукой все ресурсы, необходимые для обучения умножению и делению.

Критические элементы при обучении навыкам умножения и деления

Поскольку при обучении умножению и делению необходимо охватить множество стратегий, в PDF-файл включен этот контрольный список, чтобы вы могли охватить все на своих уроках.

Последовательность уроков по умножению

Обратите внимание: эта последовательность навыков идеально подходит для учащихся 3-го класса и старше и предполагает, что учащиеся имеют минимальное представление о массивах и равных группах.

Визуализация умножения

Я всегда начинаю урок умножения с практического ознакомления с концепцией умножения. Я даю своим ученикам большую горсть ластиков (забавные формы из долларового пятна) или любые другие манипуляции. Я даю им либо кратное 2, либо 5, в зависимости от уровня моих учеников. Я прошу их посчитать, сколько у них всего. Обычно они начинают считать по одному, но всегда есть несколько человек, которые начинают разделять их на группы для подсчета – обычно группы по 10 человек. думать за всех нас. Затем я прошу всех своих учеников найти другой способ сгруппировать ластики, чтобы их было легче считать. Дайте им время изучить, и они часто будут придумывать различные группы. Именно тогда я начинаю использовать словоблудие вроде: «О, я вижу, у тебя 7 групп по 5. Давайте пропустим счет на 5, чтобы узнать, сколько всего у вас есть. Я записываю все их различные группы (пока без символа умножения). Каждый год студенты замечали, что это умножение (из-за их предшествующих знаний), и указывали на это группе, но если бы они этого не делали, я бы вводил это на этом этапе.

Удивительный сон Аманды Бин (партнерская ссылка Amazon) — одна из моих самых любимых книг, посвященных умножению. Я читаю эту книгу своему классу, а затем изменяю упражнения в конце книги в качестве вводных уроков, основываясь на уровне навыков ваших учеников и их предшествующих знаниях. Даже если вы не учите уроки в конце книги, не пропускайте эту книгу! Это закладывает такую ​​прекрасную основу!

Способы отображения умножения

На этом этапе мы начинаем изучать все различные способы отображения и моделирования умножения. Я начинаю с повторных добавлений/пропусков, считая . Здесь я начинаю подчеркивать, что вы можете заменить знак умножения на «группы», чтобы лучше помнить, что именно показывает умножение. Затем я перехожу к равных групп . Затем до прыжков по числовой строке и, наконец, по массивам . ( Раньше я начинал с массивов, но я обнаружил, что это немного более абстрактно для студентов, и теперь подождите, пока они сначала не усвоят другие концепции . ) После того, как мы установили эти стратегии для демонстрации умножения, я представляю таблицу фактов умножения. Я также создаю якорную диаграмму «Способы показать умножение» по мере того, как мы учимся.

Пока мы изучаем различные способы отображения умножения, я предлагаю им собрать свои стратегии в мини-книгу для справки (обычно я использую небольшие книжки, которые можно купить в долларовом магазине). Так как это часто происходит в октябре месяце, обычно мы делаем тему Хэллоуина, но вы можете выбрать любую тему. Я настоятельно рекомендую вам, чтобы учащиеся рисовали стратегии в своих книгах или использовали наклейки, чтобы показать различные стратегии и группировки. Вы можете узнайте больше об этих справочниках в моем Instagram «умножение» под номером .

Свойства умножения

После того, как мы получили четкое представление о различных способах отображения умножения, мы приступаем к рассмотрению свойств умножения. Тождество и нулевое свойство обычно берут только быстрый урок. Переместительное свойство и ассоциативное свойство занимают около дня. Распределительное свойство требует гораздо больше времени и занимает несколько дней, чтобы по-настоящему понять и освоить его, и я считаю, что студенты, которые хорошо разбираются в массивах, лучше всего справляются с этим навыком. Хотя это сложный навык, когда учащиеся развивают истинное понимание этого, их концептуальное понимание умножения значительно возрастает!

Советы по свойству распределения: Лучший способ, которым я пользовался, чтобы показать свойство распределения, — это использование массивов и миллиметровой бумаги, как показано на моей якорной диаграмме свойств умножения. Вы также можете использовать блок сотен с основанием 10 и разделить его несколькими способами с помощью сухостираемого маркера.

Свойства Совет для освоения: Я создал этот ресурс Мастера умножения , чтобы помочь своим ученикам освоить СПОСОБЫ показывать умножение и СВОЙСТВА умножения. Он стал абсолютно важным компонентом моего устройства умножения, и благодаря его использованию я добился значительных успехов в понимании и запоминании математических фактов.

Множители и множители

Хотя этот ресурс посвящен вводным навыкам умножения, здесь я хотел бы представить множители и множители. Вы можете узнать больше об обучении факторам и множителям здесь .

Умножение на числа, кратные 10 и 100

Это такой увлекательный и доступный урок! Я учу своих студентов находить основной факт, подсчитывать количество нулей в ваших множителях и присоединять количество нулей к их произведению. Мы широко моделируем, ПОЧЕМУ это работает, что вы можете l заработайте больше в этом посте .

Многозначное умножение

После этого я начинаю обучать стратегиям многозначного умножения .

Последовательность уроков Teaching Division

Пожалуйста, обратите внимание: эта последовательность навыков идеально подходит для 3-го класса и старше и предполагает интенсивное знакомство с понятиями умножения и овладение ими.

Визуализация деления

Мы начинаем исследование деления так же, как мы начинаем исследование умножения. Я объединяю своих учеников в группы и даю им небольшую горсть ластиков. Я прошу их разделить или разделить их поровну между каждым человеком в их группе. Как только они разделятся, я прошу их посмотреть на группы, которые они сформировали. Затем я прошу их использовать свои навыки умножения, чтобы вычислить, сколько всего ластиков у них есть. Обычно в этот момент у них появляется блеск в глазах и они начинают осознавать связь между умножением и делением! Как только они нашли свою сумму, я записываю число и спрашиваю их, на сколько групп оно было разделено/разделено. Наконец, я спрашиваю их, сколько человек в каждой группе.

The Doorbell Rang (партнерская ссылка Amazon) — это ВЕЛИКОЛЕПНАЯ книга для ознакомления с делением и равными долями, а также с идеей семейства фактов с умножением и делением.

Умножение или деление?

Как только учащиеся получат общее представление о делении, я приостанавливаю обучение стратегиям деления и прошу их подумать о связях и различиях между умножением и делением. Я использую свои карточек с заданиями на умножение ИЛИ деление и предложите учащимся попрактиковаться в определении того, какая операция подходит для заданных сценариев. Это также прекрасное время, чтобы научить делению в кавычках против партитивного деления на .

Способы показать деление

На этом этапе мы начинаем изучать все различные способы показа и моделирования деления. Мы обсудим: использование массива , повторного вычитания, создание равных групп , с использованием числовой прямой , создание ленточной диаграммы и использование факт семейства .

Свойства деления

Для деления я преподаю студентам следующие основные концепции свойств:

• При делении нуля на число частное равно нулю.
• Любое число, деленное на единицу, и есть само число.
• Если мы разделим число само на себя, то в частном будет единица. (Не относится к нулю)
• Мы не можем разделить число на ноль.

Обратные операции

Обучение умножению и делению как обратным операциям имеет решающее значение для развития концептуального понимания деления и помогает учащимся усвоить математические факты. Мы создаем эту интерактивную якорную диаграмму вместе.

Интерпретация остатков

После того, как они освоят деление, я учу студентов интерпретации остатков. Они уже встречались с остатками до этого урока, но им ЛЮБИТ «тайну» выяснения того, что представляет собой остаток. Я включил несколько документов, включающих «Напоминания об остатках», которым я учу своих студентов. Вот различные способы использования остатков:

• Использовать остаток — Это происходит, когда остаток на самом деле является ответом.
• Округление в большую сторону — Когда вы используете остаток, чтобы округлить свой ответ. Частное — это не ваш ответ, но оно на единицу больше, потому что у вас есть остаток. (Например: когда вы распределяете детей по машинам, чтобы поехать в летний лагерь. Вы не можете просто оставить двух учеников, поэтому вам нужно добавить еще одну машину, чтобы перевезти всех)
• Игнорировать — Иногда мы игнорируем остаток. Обычно это происходит, когда мы находим действительно равные группы.
• Разделите остаток на дробь или десятичные дроби — Я МОГУ немного рассказать своим ученикам об этом варианте, особенно ученикам, готовым к этой информации, но в целом я не учу этому четырехклассников, поскольку это начинает запутывать их понимание.

Длинное деление

После этого я начинаю преподавать стратегии длинного деления до 4-го класса. Этот пост в блоге о подразделении наполнен советами .

Освоение математических фактов об умножении и делении

Вот несколько моих любимых способов закрепить математические факты. PDF включает в себя еще несколько!

Мой любимый математический факт

Знаю, это звучит глупо, но у меня есть любимый математический факт! Это 6 x 6 = 36, и каждый ученик, которого я когда-либо преподавал, знает этот забавный факт обо мне. Естественно, я встраиваю его в свою практику по математике и предлагаю своим ученикам выбрать любимый математический факт. Я распечатываю его на этикетке и позволяю им носить его, чтобы с гордостью показать свой любимый математический факт БЕЗ ответа… Затем мы играем в игру, в которой мы ходим и говорим: «Привет! Ваш любимый математический факт: 6 x 6 равно 36!» Это круто!

Run a Row

Мои ученики ОБОЖАЮТ практиковать свои математические факты в этой веселой эстафете! Дети выстраиваются в две линии и должны соревноваться в стиле эстафеты, чтобы правильно установить все факты. Числа 1-12 находятся на стороне доски каждой команды, а затем у них есть число (в данном случае это было +7, но вы можете очень легко адаптировать его к другим операциям), которое нужно сложить или умножить на каждое число. ТАК легко адаптироваться к сложению, вычитанию и умножению! Вы можете посмотреть видео этой игры в действии здесь.

Практика ментальной арифметики

Каждое занятие по математике я начинаю с быстрого 2-3-минутного чтения карточек ментальной математики. Я даю учащимся ВЕРБАЛЬНУЮ многошаговую задачу, которую они должны решить. Использование этих карточек с математическими задачами в уме упрощает подготовку.

Дополнительные практические занятия по умножению и делению

После обширного обучения умножению и делению, вот несколько дополнительных способов отработки наших навыков.

Флипбуки

Я создал эти флипбуки с умножением как способ закрепить наше обучение и как альтернатива интерактивным занятиям со складывающимися блокнотами. Левая часть предназначена для обучения и повторения концепции, а правая — для отработки навыков. У нас есть целый раздел в нашей папке для них, так что они могут вернуться и ссылаться на них в течение всего года.

Отправляйтесь на экскурсию по массивам

Это всегда нравится моим ученикам, и я часто задаю его в качестве домашнего задания! Отправьте учащихся в магазин, чтобы они нашли все предметы, расставленные рядами (печенье, пончики, сосиски, витрины и т.  д.). Попросите их сфотографироваться и принести их обратно в класс. Нет времени на экскурсию? Без проблем! Просто пусть они используют предметы повседневного обихода для создания массивов, соответствующих выражениям. Щелкните здесь, чтобы получить бесплатный шаблон домашних массивов .

Карнавал с заданиями на умножение и деление

Существует СТОЛЬКО разных навыков, свойств и стратегий для практики с умножением и делением, что мы тратим на операции около двух месяцев! В течение этих двух месяцев я всегда сосредотачиваюсь на том, чтобы позволить моим ученикам взаимодействовать с этими навыками различными способами. За годы работы я создал десятков карточек задач, которые отрабатывают ВСЕ свойства и стратегии . Они являются основным продуктом в моем классе. Я использую их:

• Для разминки всей группы
• Играть в SCOOT всем классом
• В небольших группах, самостоятельно или со мной
• На охоте за мусором в комнате или снаружи
• Для обзора в стиле Jeopardy

Списки книг по умножению и делению

Я создал партнерский список Amazon из моих любимых иллюстрированных книг по умножению и делению .