Числа от 1 до 100. Сложение и вычитание. Математика 3 класс.
Задачи для 3 класса
- Математические диктанты
- Комбинаторные задачи
- Нестандартные задачи
- Множество и его элементы
- Способы задания множеств
- Пустое множество
- Диаграмма Венна
- Диаграмма Венна. Часть 2
- Подмножество
- Множество. Задачи
- Скорость, время, расстояние
Числа от 1 до 100
- Сложение и вычитание
- Буквенные выражения
- Единицы длины
Контрольные работы
- Умножение и деление
- Итоговая контрольная работа
- 1 четверть
- 2 четверть
- Контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Контрольная работа 1
- Итоговые контрольные работы 3 класс
- Контрольная работа 1
Тесты. 3 класс.
3 класс.
- Тесты по математике 3 класс
- Табличное умножение и деление чисел
- Особые случаи умножения и деления
Примеры, уравнения
- Примеры
- Уравнения
- Кроссворды
Страница >> 1 2
Задание 1.
Прочитай числа: 4, 16, 8, 32, 43, 6, 25, 93.
Сколько в каждом из них единиц и десятков?
Решение:
- 1) 4 — 4 единицы.
- 2) 16 — 1 десяток, 6 единиц.
- 3) 8 — 8 единиц.
- 4) 32 — 3 десятка 2 единицы.
- 5) 43 — 4 десятка 3 единицы.
- 6) 6 — 6 единиц.
- 7) 25 — 2 десятка, 5 единиц.
- 8) 93 — 9 десятков, 3 единицы.
Задание 2.
- 1) Увеличь на 1 числа: 8, 28, 38, 98.

- 2) Уменьши на 1 числа: 40, 50, 75, 90.
Решение:
- 1) 9, 29, 39, 99.
- 2) 39, 49, 74, 89.
Задание 3
Реши примеры, объясняя свои вычисления.
- 9 + 1 + 5
- 5 + 5 + 8
- 13 — 3 — 4
- 17 — 7 — 1
- 6 + 4 + 5
- 7 + 3 + 7
- 14 — 4 — 6
- 16 — 6 — 2
Решение:
- 9 + 1 + 5 = 15 (9 + 1 = 10, 10 + 5 = 15)
- 5 + 5 + 8 = 18 (5 + 5 = 10, 10 + 8 = 18)
- 13 — 3 — 4 = 6 (13 — 3 = 10, 10 — 4 = 6)
- 17 — 7 — 1 = 9 (17 — 7 = 10, 10 — 1 = 9)
- 6 + 4 + 5 = 15 (6 + 4 = 10, 10 + 5 = 15)
- 7 + 3 + 7 = 17 (7 + 3 = 10, 10 + 7 = 17)
- 14 — 4 — 6 = 4 (14 — 4 = 10, 10 — 6 = 4)
- 16 — 6 — 2 = 8 (16 — 6 = 10, 10 — 2 = 8)
Задание 4.

Реши примеры, объясняя свои вычисления.
Решение:
5. Реши примеры.
| 98 + 2 | 10 + 7 | 8 + 6 | 12 — 4 | 7 + 0 |
| 30 — 1 | 28 — 8 | 9 + 5 | 16 — 8 | 6 — 0 |
| 70 — 30 | 9 + 60 | 3 + 9 | 15 — 7 | 14 — 4 |
| 30 + 70 | 96 — 90 | 7 + 4 | 13 — 4 | 12 — 5 |
Решение:
98 + 2 = 100 10 + 7 = 17 8 + 6 = 14 12 — 4 = 8 7 + 0 = 7 30 — 1 = 31 28 — 8 = 20 9 + 5 = 14 16 — 8 = 8 6 — 0 = 6 70 — 30 = 40 9 + 60 = 69 3 + 9 = 12 15 — 7 = 8 14 — 4 = 10 30 + 70 = 100 96 — 90 = 6 7 + 4 = 11 13 — 4 = 9 12 — 5 = 7
6.
 Реши примеры, обозначая порядок действий.
Реши примеры, обозначая порядок действий.| 46 + 11 — 8 | 50 — 39 + 18 |
| 85 — 24 + 9 | 19 + 80 — 3 |
| 100 — (34 + 26) | 44 + 36 — 20 |
| 80 — (42 — 12) | 50 — (30 — 2) |
| 62 + 38 — 8 | 50 + (30 + 2) |
| 62 + (38 — 8) | 50 — 30 + 2 |
| 80 — 42 +12 | 70 — (12 + 3) |
7. Реши примеры, записывая только ответы.
Решение:
- )
Простые задачи
- Задачи на умножение
- Задачи на деление по содержанию и на равные части
- Задачи на 1 действие
Составные задачи
- Задачи на нахождение суммы
- Задачи на нахождение уменьшаемого, вычитаемого, разности
- Задачи на 2 действия
- Задачи на 3 действия
- Задачи на разностное и кратное сравнение
«Числа от 1 до 100.
 Сложение и вычитание»
Сложение и вычитание»Цель урока: совершенствование вычислительных навыков и умений решать задачи.
Задачи:
Образовательные:
1. Повторить и закрепить умения:
- решать простые задачи;
- составные задачи выражением;
- сравнивать именованные числа;
2. Проверить степень усвоения умений решать примеры и задачи изученных видов.
Развивающие:
- Развивать логическое мышление учащихся;
- Обогащать словарный запас учащихся предметной терминологией.
Воспитательные:
- Воспитывать взаимопомощь.
- Воспитывать самостоятельность.
Ход урока
I. Организационный момент.
Организационный момент.
II. Постановка целей урока.
— Ребята, тема урока сегодня «Закрепление изученного материала. Сложение и вычитание в пределах 100». (Презентация. Слайд 1)
Давайте вспомним, чему мы учились последнее время на уроках математики и поставим цели. (Презентация. Слайд 2)
Какие умения мы будем закреплять?
Закрепить умения:
- решать примеры;
- решать простые задачи;
- решать составные задачи выражением;
- читать и записывать выражения со скобками;
- сравнивать именованные числа;
- развивать логическое мышление
III. Устный счёт.
— Сегодня к нам на урок пришёл сказочный герой. Давайте угадаем, кто это. Для этого нужно решить примеры, и тогда откроется его имя.
Дети решают примеры с последующей проверкой. (Презентация. Слайд 3)
| 9 + 7 | 30 + 4 | |||||
| 60 + 20 | 70 – 1 | |||||
| 12 – 7 | 28 – 20 | |||||
| 96 + 1 | 8 + 6 |
— Расположите ответы в соответствии с буквами в таблице. Прочитайте имя сказочного героя, который пришёл к нас сегодня на урок.
Прочитайте имя сказочного героя, который пришёл к нас сегодня на урок.
— Сказочного героя зовут Буратино.
— Как называется сказка, кто её автор? (Презентация. Слайд 4)
Буратино узнал, что в нашей школе проводится неделя математики. Оказывается, в нашем классе находится царство Математики, а в нём есть бесценный клад. Кто его найдёт, тот станет самым мудрым из мудрых. Чтобы его найти, необходимо уметь считать, решать задачи. Буратино пришёл к нам научиться этому, чтобы вместе с вами попасть в Царство Математики. Поможем Буратино?
1-е задание.
— Запишите числа (результаты выражений) в порядке возрастания.
5, 8, 14, 16, 34, 69, 80, 97. (Презентация. Слайд 5)
2-е задание.
Представьте в виде суммы разрядных слагаемых числа 16, 34, 97. (Презентация. Слайд 6)
(Презентация. Слайд 6)
- 16 = 10 + 6
- 34 = 30 + 4
- 97 = 90 + 7
IV. Чтение, запись и решение выражений.
— Ребята, вспомните, как звали в сказке девочку с голубыми волосами? (Мальвина)
— А самую грустную куклу? (Пьеро) (Презентация. Слайд 7)
Пьеро читал Мальвине стихи:
Мы сидим на кочке,
Где растут цветочки,
Жёлтые, приятные,
Очень ароматные.
Давайте поможем Пьеро собрать букет для Мальвины. Для этого надо прочитать выражения и найти их значения. (Презентация. Слайды 8,9)
- 80 + (11 – 4)
- (45 – 40) + 8
- (20 + 5) + 1
- 60 – (19 – 9)
- (67 – 7) – 20
V. Решение задач.
Решение задач.
1. Рассмотрите краткую запись и скажите, кто живёт в пруду черепахи Тортилы? (Презентация. Слайд 10)
Составьте задачу по краткой записи.
Можно ли сразу узнать, сколько жуков было в пруду? Почему?
Расскажите план решения задачи.
Самостоятельное решение. Проверка. (Презентация. Слайд 11)
2. Задача. (Презентация. Слайд 12)
В харчевне «Трёх пескарей» лиса Алиса и кот Базилио заказали одного жареного барашка, одного гусёнка, парочку голубей, шесть штук жирных карасей, а мелкой сырой рыбы на закуску столько, сколько жирных карасей. Сколько всего съели лиса Алиса и кот Базилио?
1 + 1 + 2 + 6 + 6 = 16 (Презентация. Слайд 13)
3. Решение ребусов.
Коварные Лиса Алиса и кот Базилио обманом привели Буратино на поле чудес. (Презентация. Слайд 14)
(Презентация. Слайд 14)
Чтобы пройти его, необходимо решить ребусы. 100ляр; ви3на; по2л; 7я Р1а (Презентация. Слайд 15)
VI. Музыкальная физкультминутка. (Дети исполняют танец под музыку из кинофильма «Приключения Буратино»)
VII Решение составной задачи
— Рассмотрите рисунок, назовите героев сказки «Золотой ключик, или приключения Буратино». Дуремар (Презентация. Слайд 16) , Карабас Барабас (Презентация. Слайд 17)
— Дуремар продаёт Карабасу пиявок. Составьте по краткой записи задачу. (Презентация. Слайд 18)
Поймал – 10 п.
Продал – утром – 6 п., вечером – 2 п.
Осталось — ?
— Решите задачу выражением.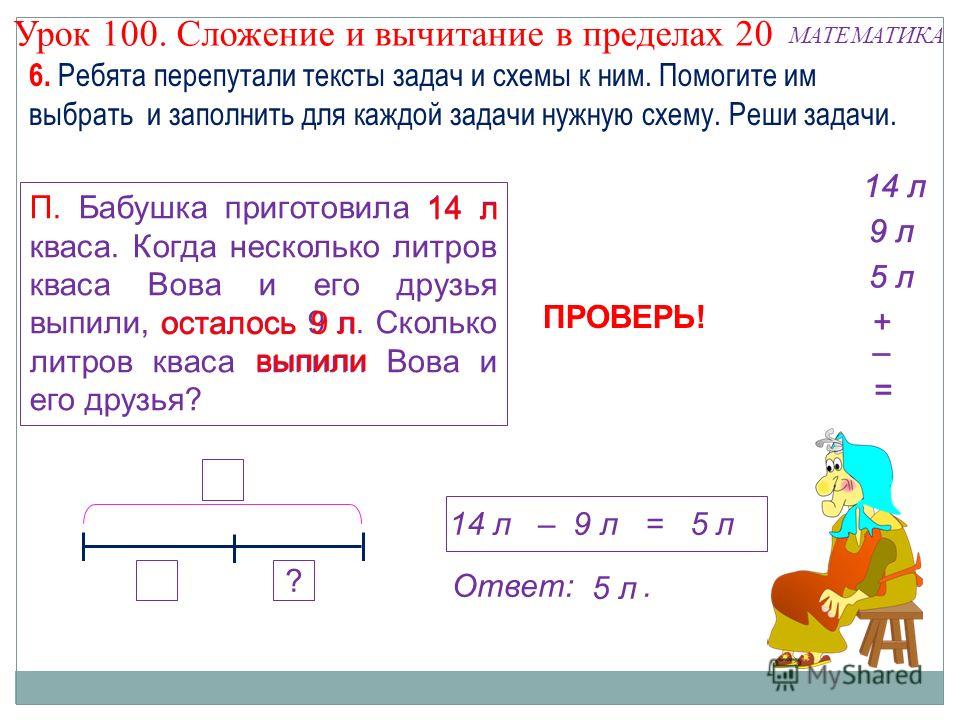
(10 – 6 – 2 = 2), (10 – (6 +2)) (Презентация. Слайд 19)
-Что вы знаете о пиявках?
Подготовленный ученик рассказывает материал о пиявках, об их применении в медицине. (Презентация. Слайды 20,21)
VIII. Решение задач на логическое мышление.
— Ребята, вспомните, кто подарил шарманщику Карло говорящее полено? (столяр Джузеппе) (Презентация. Слайд 22)
Работа со словом столяр
— Слово столяр произносится с ударением на второй слог.
— Как вы понимаете значение слова столяр?
Подготовленный ученик рассказывает о значении слова «столяр» (Презентация. Слайд 23)
Столяр – это ремесленник по столярной работе, по чистой отделке деревянных вещей, по внутренней отделке комнат и деревянной утвари.
Задача. (Презентация. Слайд 24)
Столяр Джузеппе распилил бревно на три части. Сколько распилов сделал столяр? (2)
Задача. (Презентация. Слайд 25)
От дощечки прямоугольной формы столяр отпилил 1 угол. Сколько углов стало? (5)
IX. Сравнение именованных чисел.
Диктует Мальвина стихи и загадки, (Презентация. Слайд 26)
Спешит Буратино урок преподать.
Смотри, сколько клякс насажал он в тетрадки,
И что тут написано, надо понять!
| 20 см * 2 дм 5 см | 45мм * 5 | см 60 мин * 1ч |
— Как вы думаете, что надо поставить вместо клякс? (Знаки >, >. =) (Презентация. Слайды 27,28)
=) (Презентация. Слайды 27,28)
X. Решение задачи.
— Вспомните страшный бой на опушке леса. (Презентация. Слайд 29)
Буратино позвал на помощь деревянным человечкам зверей, птиц, насекомых. На его зов откликнулись 8 стрижей, 1 коршун, 7 жаб, семейство ежей – сам ёж, ежиха, 2 ежовы тётки и 5 маленьких ежат. Сколько всего животных откликнулось на зов Буратино?
(8 + 1 + 7 + 1 + 1 + 2 + 5 = 25) (Слайд 30)
XI. Самостоятельная работа учащихся ( решение примеров по вариантам) (Презентация. Слайд 31)
| I вариант | II вариант | |||
|---|---|---|---|---|
| 23-20 | 64-4 | |||
| 40+6 | 50 + 2 | |||
| 81-1 | 9+8 | |||
| 12-4 | 36-1 | |||
| 75+1 | 13-9 | |||
| 9+7 | 27+1 |
XII. Подведение итогов урока, оценивание, рефлексия.
Подведение итогов урока, оценивание, рефлексия.
— Итак, ребята, все задания вы хорошо выполнили. Я думаю, что Буратино многому научился у вас. Кто выполнил поставленные цели?
Проанализируйте свою работу на уроке, закончив предложения: (Презентация. Слайд 32)
- Я узнал…
- Я научился…
- Было интересно…
- Было трудно…
Звучит волшебная музыка, появляется Царство Математики. (Презентация. Слайд 33)
Мы вместе с Буратино попадаем в Царство Математики. Ваше путешествие по дорогам математики только начинается. Пройдя все дороги, вы станете самыми мудрыми из мудрых. А знания — это и есть бесценный клад!
Дети рассказывают стихи:
(Презентация. Слайд 34)
Не случайно математике такой почёт,
Это ей дано давать ответы,
Как хороший выполнить расчёт
Для постройки здания, ракеты.
Есть о математике молва,
Что она в порядок ум приводит.
Потому хорошие слова
Часто говорят о ней в народе.
Ты нам, математика, даёшь
Для победы трудностей закалку.
Учится с тобою молодёжь
Развивать и волю, и смекалку.
И за то, что в творческом труде
Выручаешь в трудные моменты,
Мы сегодня искренне тебе
Посылаем гром аплодисментов!
Тема: Повторение. Числа от 1 до 100. Сложение и вычитание. | План-конспект урока по математике (2 класс) на тему:
Тема: Повторение. Числа от 1 до 100. Сложение и вычитание.
Цель урока: закрепить знания обучающихся, полученные на предыдущих уроках
Задачи:
1. Образовательные:
- совершенствовать навыки обучающихся устно складывать и вычитать в пределах 100,
- решать задачи в одно и два действия,
- умение преобразовывать единицы длины.

2. Воспитательные:
- воспитывать аккуратность, умение работать в коллективе,
- воспитывать бережное отношение к природе.
3. Развивающие:
- развивать познавательный интерес к окружающему миру,
- развивать внимание, память, мышление.
Ход урока.
I. Орг. момент
Долгожданный дан звонок –
Начинается урок.
Каждый день – всегда, везде,
На занятиях, в игре,
Смело, чётко говорим
И тихонечко сидим.
II. Актуализация знаний
Проблема и постановка цели урока:
Посмотрите на доску и решите примеры
9+7 = 16 – Н
15-7 = 8 – Е
11-5 = 6 – С
10+9 = 19 – Ь
8-4 = 4 – О
Расположите карточки с числами в порядке возрастания, и вы узнаете, кто к нам пришел сегодня на урок. (Осень) – Какие сезонные изменения происходят в осеннем лесу с деревьями? – Листопад
— Листья, каких деревьев не изменяют окраску? – Ели
-Сегодня мы проверим и закрепим то, что прошли на прошлых уроках. Сегодня мы отправимся в путешествие по осеннему лесу.
Сегодня мы отправимся в путешествие по осеннему лесу.
Начинаем урок с устного счёта:
1) Посчитайте от 1 до 20, от 1 до 20 через 1
2) Посчитайте десятками до 100 и обратно. Молодцы!
3) -Перед вами задания на листочке.
Обведите правильный ответ. Сколько будет если:
1. -Увеличить на 10 число 90 (100)
2.- 7 уменьшить на 2 (5)
3.- Первое слагаемое 9, второе слагаемое 6, найдите сумму чисел (6)
4.- Из 10 вычесть 6 (4)
5.-Найди сумму чисел 30 и 20 (50)
6.- Какое число предшествует числу 5? (4)
7.- число, следующее за числом 18 (19)
8.- уменьшаемое 12 вычитаемое 6 найдите разность (6)
4. Веселые задачки:
1. Ёжик по лесу шёл,
На обед грибы нашёл:
Два — под берёзой,
Один у осины.
Сколько их будет
В плетёной корзине? – 3
2. Белка сушит на верёвке
Два грибка и три морковки.
Прибежал хорёк, утащил грибок.
Съел зайчонок две морковки.
Что осталось на верёвке? — 1 гриб, 1морковка
3. Я нашел в дупле у белки
Я нашел в дупле у белки
Пять лесных орешков мелких.
Вот ещё один лежит,
Мхом заботливо укрыт.
Ну и белка! Вот хозяйка!
Все орешки посчитай-ка. – 6
4. Шесть грибов нашел Вадим,
А потом ещё один.
Вы ответьте на вопрос:
Сколько он грибов принес? – 7
5. Я вошел в теннисный бор
И увидел мухомор,
Два опенка,
Два сморчка,
Три масленка,
Два строчка:
У кого ответ готов:
Сколько я нашёл грибов? – 10
На слайде геометрические фигуры.
-Какие геометрические фигуры вы видите на экране?
— Сколько треугольников?
— Сколько квадратов?
— Сколько кругов?
-Каких фигур меньше, на сколько? Каких фигур больше на сколько?
— Ребята, посмотрите какие необычные математические ёлочки приготовила для вас Осень.
Ёлочки состав числа. Числа 13 (9,4; 8,5; 7,6), 14 (, 15
Откройте тетрадь и запишите число, классная работа.
Мы продолжаем наше путешествие по осеннему лесу. На опушке леса растет три молодых клена. Они никак не меняют цвет своих листьев. Давайте поможем осени одеть клёны в осенний наряд.
Они никак не меняют цвет своих листьев. Давайте поможем осени одеть клёны в осенний наряд.
— Запишите в тетрадь только ответы.
- запишите сумму чисел 6 и 5 (11)
- запишите разность чисел 13 и 7 (6)
- запишите число, которое больше 14 на 2
- запишите число, в котором три десятка и 6 единиц (36)
- первое слагаемое 9, второе слагаемое 3, найдите сумму (12)
- запишите число, которое меньше 8 на 5 (3)
-Возьмите карандаш и подчеркните все однозначные числа.
Молодцы! первый клен одели.
2 клен.
Вставьте пропущенные числа, что бы равенства были верными.
20 + ? = 23 ? + 7 = 47
52 — ? = 50 ? – 20 = 4
Молодцы второй клен одели!3
3 клен. >,
1 дм * 10 см. 96к. * 1 р.
Молодцы третий клен одели!
Физкультминутка
Продолжаем наше путешествие. Осталось последнее дерево, которое мы покрасим в осенние цвета. Это дуб. Осень приготовила для вас задачу. Посмотрите на экран.
Посмотрите на экран.
— Первая белка собрала 10 желудей, вторая на 6 желудей больше. Сколько желудей собрала вторая белка?
О ком говориться в задаче? Что собирали белки? Что известно в задаче?
Каким действием будем решать задачу? (Сложением)
У доски 1 ребенок: 1 – 10 ж.
2 — ? на 6> чем 10+6=16 ж ответ.
Как изменить вопрос к задаче, что бы задача решалась в два действия?
— сколько желудей собрали белки?
Измените задачу так, чтобы задача решалась вычитанием.
— первая белка собрала 10 желудей, вторая на 6 желудей меньше. Сколько желудей у второй белки?
Итог:
Кто у нас был в гостях?
Что повторили?
Рефлексия – светофор!
Д.З. стр. 47, № 1, №6
Контрольная работа за 1 четверть по теме « Числа от 1 до 100. Сложение и вычитание. Решение задач»
2 класс
Задачи: проверить умение выполнять сложение и вычитание в изученных случаях; решать выражения со скобками, решать составные задачи.
Планируемые образовательные результаты:
Личностные: имеют мотивацию к учебной деятельности; стремятся развивать внимание, память, логическое мышление, смекалку, навыки счета, аккуратность; проявляют самостоятельность, личную ответственность.
Предметные: знают, устную и письменную нумерацию чисел в пределах 100; отличительные особенности задачи; умеют: складывать и вычитать двузначные числа в случаях вида: 36 + 2, 36 + 20, 36 – 2, 36 – 20, 26 + 4, 30 – 7, 60 – 24, 26 + 7; решать задачи и выражения изученных видов.
Метапредметные (критерии сформированности/оценки компонентов УУД): регулятивные: формулируют учебную задачу урока; планируют, контролируют и оценивают собственную деятельность, вносят корректировки, если это необходимо; способны к мобилизации волевых усилий; познавательные: формулируют познавательную цель; создают алгоритм деятельности; строят логическую цепочку рассуждений, устанавливают причинно-следственные связи; коммуникативные: умеют слушать, слышать и понимать партнеров по речевому высказыванию.
Методы и формы обучения: письменного контроля и самоконтроля; индивидуальная.
Основные понятия и термины: увеличить, уменьшить, сложение, вычитание, сумма, разность, прибавить, вычесть, задача, составная задача, выражение,
Вариант 1
1.Реши задачу.
Маша использовала для поделок 7 шишек, а желудей – на 5 больше. Сколько шишек и желудей использовала Маша?
2. Найди значения выражений. В выражениях со скобками укажите порядок действий:
60 – 21 = 70 – 20 = 32 + 8 =
55 – 20 = 39 – 2 = 79 – (30 + 10) =
46 + 2 = 77 + 3 = 54 + (13 – 7) =
3.Сравни:
10 см … 1 м 56 см … 6 дм 5 см
4.Вставь вместо звёздочек знаки «+» или « — », чтобы записи были верными:
36 * 4 * 8 = 32 23 * 40 * 7 = 70
5*. Вставь в «окошки» числа так, чтобы
Вставь в «окошки» числа так, чтобы
равенство сохранилось;
знак равенства изменился на знак «>».
52 + … = 52 + …
Сделай две записи.
Вариант 2
1.Реши задачу.
Лена очистила 13 картофелин, а её сестра на 6 картофелин меньше. Сколько картофелин очистили обе девочки?
2.Найди значения выражений. В выражениях со скобками укажите порядок действий:
70 – 23 = 80 – 30 = 46 + 4 =
53 – 20 = 50 – 9 = 63 – (15 + 8) =
55 + 3 = 95 + 5 = 48 + (10 – 20) =
3.Сравни:
10 дм … 1 м 89 см … 9 дм 8 см
4.Вставь вместо звёздочек знаки «+» или «-», чтобы записи были верными:
23 * 7 * 5 = 25 18 * 50 * 8 = 60
5*. Вставь в «окошки» числа так, чтобы
Вставь в «окошки» числа так, чтобы
равенство сохранилось;
знак равенства изменился на знак «>».
41 + … = 41 + …
Сделай две записи.
Проверим и оценим свои достижения
Тест
Вариант 1.
Выберите правильный ответ
Задание | Варианты ответов |
1.Укажи число, в котором 7дес.8ед. | 87 78 98 |
2.На сколько 4дес. больше, чем 4 ед? | На: 36 8 44 |
3.Укажи число, которое на 6 меньше, чем 50 | 56 44 54 |
4.К какому числу надо прибавить 10, чтобы получить 48? | 58 47 38 |
5. | 20 100 30 |
6.Какое число увеличили на 6, если получили 60? | 66 54 55 |
7. Какое число надо вычесть из 74, чтобы получить 4? | 70 4 78 |
8.Какие цифры надо записать в указанном порядке в окошки равенства 7__ — 3 __= __7 | 1 и 4 0 и 6 2 и 5 |
9. Первое слагаемое 20. Второе слагаемое 5.Чему равно значение суммы | 55 15 25 |
10.На сколько 80 больше, чем 60 | На: 2 20 40 |
Тест
Вариант 2.
Задание | Варианты ответов |
1.Укажи число, в котором 8 дес. и 7 ед | 87 78 98 |
2.На сколько 6 единиц меньше, чем 6 дес. ? | На: 12 66 54 |
3.Укажи число, которое на 7 больше, чем 33. | 40 26 39 |
4.Из какого числа надо вычесть 10, чтобы получить 54? | 34 64 74 |
5.Первое слагаемое 60, второе 40. Укажи значение суммы | 100 30 20 |
6.Какое число уменьшили на 9, если получили 80? | 89 88 71 |
7. | 100 92 98 |
8.Какие цифры надо записать в указанном порядке в окошки равенства 5__- __2 =__8 | 6 и 5 0 и 4 4 и 8 |
9. Первое слагаемое 6. Второе слагаемое 50.Чему равно значение суммы | 44 56 65 |
10. На сколько 60 больше, чем 20 | 40 4 20 |
Ключ Вариант 1 | Ключ Вариант 2 |
1. 78 | 1. 87 |
2. на 36 | 2. на 54 |
3. | 3. 40 |
4. 38 | 4. 64 |
5. 20 | 5. 100 |
6. 54 | 6. 89 |
7. 70 | 7. 92 |
8. 2 и 5 | 8. 0 и 4 |
9. 25 | 9. 56 |
10. на 20 | 10. 40 |
Источник:учебник «Математика», УМК «Школа России», 2 класс Москва «Просвещение» 2012г. Авторы:М.И.Моро, М.А.Бантова, Г.В.Бельтюкова, С.И.Волкова.
404 Страница не найдена | Образование голышмановского района
- ГЛАВНАЯ
- Структура
- НОВОСТИ
- Учредительные документы
- Объявления
- Региональный центр «Новое поколение»
- История
- Родителям
- Советы родителям школьника
- Как выбрать школьную форму
- Горячая линия» по вопросам профилактики инфекций, передающихся клещами
- Об актированных днях
- Меры социальной поддержки, предоставляемые семьям с детьми органами социальной защиты населения
- ПАМЯТКА для получения ежемесячной выплаты в связи с рождением (усыновлением) первого ребёнка
- Меры социальной поддержки, предоставляемые семьям с детьми органами социальной защиты населения 2018
- Отцы, защитите своих детей! (безопасность 0+)
- Открытое окно — опасность для ребенка
- «Скоро в школу»
- Дошкольное образование
- «Горячая Линия» по вопросам организации дошкольного образования
- Дошкольное образование в нацпроектах
- Родителям
- Об утверждении Порядка учета детей на территории Голышмановского городского округа
- Приказ Минобрнауки России от 13.
 01.2014 N 8 «Об утверждении примерной формы договора об образовании по образовательным программам дошкольного образования» (Зарегистрировано в Минюсте России 27.03.2014 N 31757)
01.2014 N 8 «Об утверждении примерной формы договора об образовании по образовательным программам дошкольного образования» (Зарегистрировано в Минюсте России 27.03.2014 N 31757) - ПРИКАЗ от 27 июня 2017 г. N 602 ОБ УТВЕРЖДЕНИИ ПОРЯДКА РАССЛЕДОВАНИЯ И УЧЕТА НЕСЧАСТНЫХ СЛУЧАЕВ С ОБУЧАЮЩИМИСЯ ВО ВРЕМЯ ПРЕБЫВАНИЯ В ОРГАНИЗАЦИИ, ОСУЩЕСТВЛЯЮЩЕЙ ОБРАЗОВАТЕЛЬНУЮ ДЕЯТЕЛЬНОСТЬ
- Об установлении родительской платы за содержание детей в дошкольных образовательных учреждениях
- Постановление №955 от 31.12. 2019 «Об утверждении Порядка распределения средств, предоставляемых в целях частичного возмещения расходов учреждений, реализующих образовательную программу дошкольного образования, на осуществление присмотра и ухода за детьми
- Об организации зачисления детей в образовательные учреждения, реализующие основную образовательную программу дошкольного образования
- О внесении изменений и дополнений в постановление Администрации Голышмановского муниципального района от 30.
 06.2015 № 874 (в редакции от 18.05.2016 № 606)
06.2015 № 874 (в редакции от 18.05.2016 № 606) - Приказ О закреплении образовательных учреждений за конкретными территориями Голыгимановского городского округа №21 от 20.01.20
- Aдминистративный регламент предоставления муниципальной услуги «Прием заявлений, постановка на учет и зачисление детей в образовательные учреждения, реализующие основную образовательную программу дошкольного образования (детские сады)»
- Постановление от 12.10.2021 № 996 Об утверждении муниципальной программы «Основные направления развития системы образования Голышмановского городского округа» на 2022-2024 годы
- МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПРОВЕДЕНИЮ ОЦЕНКИ КАЧЕСТВА ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ УСЛОВИЙ
- Общее образование
- О проведении мониторинга качества подготовки обучающихся в 2021-2022 учебном году
- Публичный отчет Голышмановский городской округ 2020
- Об утверждении муниципальной программы «Основные направления развития системы образования в Голышмановском городском округе» на 2021-2023 годы
- Постановление ГГО Губернаторская елка 2021
- Положение о проведении Губернаторской елки
- Положение о проведении Губернаторской елки
- ПМПК
- О ПМПК
- Положение о ПМПК
- Основные направления деятельности ТПМПК
- Выбор маршрута
- Порядок осуществления обследования
- Консультации
- Запись на обследование
- Документы на ПМПК
- Вопрос — ответ
- ПМПС
- Состав ПМПС
- Положение о ПМПС 2019
- Направления работы ПМПС
- Консультации
- Защита прав детей
- Конвенция о правах ребенка
- Федеральный закон «Об основах профилактики безнадзорности и правонарушений несовершеннолетних» № 120-ФЗ от 24.
 06.1999г.
06.1999г.
- Организация питания
- НОРМАТИВНО-ПРАВОВАЯ ДОКУМЕНТАЦИЯ
- ГОРЯЧАЯ ЛИНИЯ ПО ПИТАНИЮ
- ИНФОРМАЦИЯ ДЛЯ РОДИТЕЛЕЙ
- Организация летнего отдыха
- Распоряжение № 1124-рп от 10.12.2021 г Об организации детской оздоровительной кампании в Тюменской области в 2022 году
- Реестр организации отдыха детей и их оздоровления Голышмановского городского округа на 2022г
- Постановление № 989 от 11.10.2021г Об утверждении муниципальной программы «Организация отдыха, оздоровления и занятости несовершеннолетних в Голышмановском городском округе» на 2022-2024 годы
- Постановление № 1372 30.12.2021 Об организации отдыха, оздоровления населения и занятости несовершеннолетних в Голышмановском городском округе в 2022 году
- Приказ №35 от 08.04.2022 Об организации отдыха,оздоровления и занятости детей и подростков в 2022 году
- Постановление №517 от 17.05.2022 Об утверждении Положения о порядке и условиях внесения родительской платы на организацию отдыха и оздоровления детей в лагерях с дневным пребыванием на территории Голышмановско
- Постановление №476 от 04.
 05.2022
05.2022 - Постановление № 523 от 17.05.2022
- Постановление №524 от 17.05.2022
- Постановление №594 от 01.06.2022
- ПРОФСОЮЗ
- Горячая линия
- ФГОС НОО ОВЗ
- НОРМАТИВНО-ПРАВОВАЯ БАЗА
- Всероссийская олимпиада школьников
- Ссылки на сайты ВсОШ
- Всероссийская олимпиада школьников 2021-2022
- Всероссийская олимпиада школьников 2020-2021
- Всероссийская олимпиада школьников 2019-2020
- «Точка опоры»
- Консультационные пункты
- Куда обратиться
- Кураторы проекта
- Навигатор для родителей
- Наши консультанты
- О проекте
- Реализация проекта в ОО ГГО
- Родительская школа
- Обратная связь
- Здоровье
- НОРМАТИВНО-ПРАВОВАЯ ДОКУМЕНТАЦИЯ
- Рекомендации по организации работы ОУ
- ИНФОРМАЦИЯ ДЛЯ РОДИТЕЛЕЙ
- Банк успешных практик
- ВНЕУРОЧНАЯ ДЕЯТЕЛЬНОСТЬ
- ДОШКОЛЬНОЕ ОБРАЗОВАНИЕ
- КЛАССНЫЙ РУКОВОДИТЕЛЬ
- МАТЕМАТИКА
- МАТЕРИАЛЫ ТЬЮТОРСКИХ СЕМИНАРОВ ПО ПОДГОТОВКЕ К ЕГЭ, ОГЭ
- МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ СТАЖИРОВОЧНОЙ ПЛОЩАДКИ ПО СОВЕРШЕНСТВОВАНИЮ МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ
- НАЧАЛЬНЫЕ КЛАССЫ
- ОДАРЕННЫЕ И ТАЛАНТЛИВЫЕ ДЕТИ
- РУССКИЙ ЯЗЫК И ЛИТЕРАТУРА
- Оценка механизмов управления качеством образования
- 1.
 Образовательные результаты
Образовательные результаты - 2. Образовательная деятельность
- 1.
- МКУ «Центр развития образования»
- Структура
- Учредительные документы
- Антикоррупционная деятельность
- Консультационно-методическое обеспечение введения ФГОС НОО и ФГОС ООО
- ФГОС НОО
- ФГОС ООО
Министерство просвещения Российской Федерации
Департамент образования и науки Тюменской области
ТОГИРРО
РОССИЙСКОЕ ОБРАЗОВАНИЕ ФЕДЕРАЛЬНЫЙ ПОРТАЛ
Федеральные государственные образовательные стандарты
ФЕДЕРАЛЬНЫЙ ЦЕНТР ИНФОРМАЦИОННО-ОБРАЗОВАТЕЛЬНЫХ РЕСУРСОВ
ОФИЦИАЛЬНЫЙ ИНФОРМАЦИОННЫЙ ПОРТАЛ ЕДИНОГО ГОСУДАРСТВЕННОГО ЭКЗАМЕНА
ЕГЭ.RU
Портал государственных и муниципальных услуг в сфере образования Тюменской области
Детские сады Тюменской области
Единое окно доступа к образовательным ресурсам
Электронная школа Тюменской области
Официальный интернет-портал правовой информации
Темы Контрольных работ «Шаги к пятёрке по математике»
1 КЛАСС
ПОДГОТОВКА К ИЗУЧЕНИЮ ЧИСЕЛ
Счёт предметов. Сравнение групп предметов.
Сравнение групп предметов.
ПРОСТРАНСТВЕННЫЕ И ВРЕМЕННЫЕ ПРЕДСТАВЛЕНИЯ
Местоположение предметов. Временные представления.
ЧИСЛА И ЦИФРЫ ОТ 1 до 10
Образование, обозначение, названия, чтение и запись чисел. Сравнение чисел. Сложение и вычитание чисел. Свойства нуля.
ГЕОМЕТРИЧЕСКИЕ ОБЪЕКТЫ И ВЕЛИЧИНЫ
Длина. Отношения длиннее, короче, одинаковые по длине. Единица длины сантиметр. Точка. Кривая линия. Прямая линия. Отрезок. Луч. Ломаная линия. Многоугольник.
ЧИСЛА ОТ 1 ДО 10. СЛОЖЕНИЕ И ВЫЧИТАНИЕ
Сложение и вычитание вида ?± 1,? ± 2, ?± 3, ?± 4 Переместительное свойство сложения. Таблица сложения. Вычитание. Вычитание в случаях вида 6 -?, 7 — ?, 8 -?, 9 -?, 10 -?.
ТЕКСТОВЫЕ ЗАДАЧИ
Решение задач на увеличение (уменьшение) числа на несколько единиц. Составление задач по рисунку, по решению. Решение задач на разностное сравнение чисел. Текстовая задача: дополнение условия недостающими данными или вопросом, решение задач.
ИЗМЕРЕНИЕ ВЕЛИЧИН
Единица массы: килограмм. Единица вместимости: литр. Единица длины дециметр. Соотношение между дециметром и сантиметром.
ЧИСЛА ОТ 11 ДО 20
Нумерация. Сложение и вычитание чисел. Текстовые задачи в 2 действия. Сложение однозначных чисел с переходом через десяток. Вычитание с переходом через десяток
2 КЛАСС
ЧИСЛА ОТ 1 ДО 100. Нумерация
Повторение: числа от 1 до 20. Нумерация. Замена двузначного числа суммой разрядных слагаемых. Сложение и вычитание вида 30 + 5, 35? 5, 35 – 30.
ЕДИНИЦЫ ИЗМЕРЕНИЯ
Миллиметр. Метр. Таблица единиц длины. Рубль. Копейка. Соотношения между ними. Время. Единицы времени: час, минута. Соотношение 1 ч = 60 мин.
ГЕОМЕТРИЧЕСКИЕ ОБЪЕКТЫ И ВЕЛИЧИНЫ
Сумма и разность отрезков. Длина ломаной. Периметр многоугольника.
ЧИСЛОВОЕ ВЫРАЖЕНИЕ
Порядок выполнения действий в числовых выражениях. Скобки. Сравнение числовых выражений.
Выражения с переменной вида а + 12, b? 15, 48? c. Уравнения. Решение задач. Запись решения задачи выражением. Решение и составление задач, обратных заданной.
Уравнения. Решение задач. Запись решения задачи выражением. Решение и составление задач, обратных заданной.
ЧИСЛА ОТ 1 ДО 100. СЛОЖЕНИЕ И ВЫЧИТАНИЕ
Письменные приёмы сложения и вычитания двузначных чисел без перехода через десяток. Письменные приёмы сложения и вычитания двузначных чисел с переходом через десяток. Сочетательное свойство сложения. Применение свойств для вычислений. Проверка сложения и вычитания.
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ
Угол. Виды углов (прямой, тупой, острый). Прямоугольник. Периметр прямоугольника. Квадрат.
ЧИСЛА ОТ 1 ДО 100. УМНОЖЕНИЕ И ДЕЛЕНИЕ
Умножение. Свойства умножения. Текстовые задачи, раскрывающие смысл действия умножение. Деление. Задачи, раскрывающие смысл действия деление. Табличное умножение и деление. Умножение и деление. Приём умножения и деления на число 10. Задачи на нахождение третьего слагаемого. Умножение числа 2 и на 3. Деление на 2 и на 3. Задачи с величинами: цена, количество, стоимость.
3 КЛАСС
ЧИСЛА ОТ 1 ДО 100. ПОВТОРЕНИЕ
ПОВТОРЕНИЕ
Повторение изученного. Решение уравнений.
ТАБЛИЧНОЕ УМНОЖЕНИЕ И ДЕЛЕНИЕ
Повторение. Порядок выполнения действий в выражениях со скобками и без скобок. Таблицы умножения и деления с числами 4, 5, 6, 7, 8 и 9.
ЗАВИСИМОСТИ МЕЖДУ ПРОПОРЦИОНАЛЬНЫМИ ВЕЛИЧИНАМИ
Зависимости между величинами, характеризующими процессы купли-продажи: цена, количество, стоимость. Масса одного предмета, количество предметов, масса всех предметов. Расход ткани на один предмет, количество предметов, расход ткани на все предметы. Текстовые задачи на увеличение (уменьшение) числа в несколько раз, на кратное сравнение чисел.
ПЛОЩАДЬ
Способы сравнения фигур по площади. Единицы площади: квадратный сантиметр, квадратный дециметр, квадратный метр. Площадь прямоугольника.
ДОЛИ
Доли и сравнение долей. Задачи на нахождение доли целого и целого по его доле.
ВНЕТАБЛИЧНОЕ УМНОЖЕНИЕ И ДЕЛЕНИЕ
Приёмы умножения. Умножение суммы на число. Приёмы деления. Деление суммы на число. Проверка умножения делением. Деление с остатком.
Приёмы деления. Деление суммы на число. Проверка умножения делением. Деление с остатком.
ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ
Выражения с двумя переменными, вычисление их значений. Решение задач на нахождение четвёртого пропорционального.
ЧИСЛА ОТ 1 ДО 1000.
Нумерация. Последовательность чисел. Увеличение и уменьшение числа в 10 раз, в 100 раз. Замена трёхзначного числа суммой разрядных слагаемых. Сравнение трёхзначных чисел.
ЧИСЛА ОТ 1 ДО 1000. СЛОЖЕНИЕ И ВЫЧИТАНИЕ
Устное сложение и вычитание. Письменное сложение и вычитание.
ЧИСЛА ОТ 1 ДО 1000. УМНОЖЕНИЕ И ДЕЛЕНИЕ
Приём письменного умножения и деления на однозначное число. Проверка деления умножением. Знакомство с калькулятором.
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ
Обозначение геометрических фигур буквами. Круг. Окружность. Виды треугольников: разносторонний, равнобедренный, равносторонний, прямоугольный, тупоугольный, остроугольный.
ВЕЛИЧИНЫ
Единицы массы: килограмм, грамм. Соотношение между ними. Единицы времени: год, месяц, сутки
Соотношение между ними. Единицы времени: год, месяц, сутки
4 КЛАСС
ЧИСЛА ОТ 1 ДО 1000. ПОВТОРЕНИЕ
Нумерация. Четыре арифметических действия.
РАБОТА С ИНФОРМАЦИЕЙ
Столбчатые диаграммы. Чтение и составление столбчатых диаграмм.
ЧИСЛА, КОТОРЫЕ БОЛЬШЕ 1000
Класс единиц и класс тысяч. Представление многозначных чисел в виде суммы разрядных слагаемых.
Сравнение многозначных чисел. Выделение в числе общего количества единиц любого разряда. Класс миллионов. Класс миллиардов.
ВЕЛИЧИНЫ
Единица длины километр. Таблица единиц длины. Единицы площади. Определение площади с помощью палетки. Масса. Единицы массы: центнер, тонна. Время. Единицы времени: секунда, век. Решение задач на определение начала, продолжительности и конца события. Сложение и вычитание значений величин.
СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ
Алгоритмы устного и письменного сложения и вычитания многозначных чисел. Решение уравнений. Нахождение нескольких долей целого. Решение задач.
Нахождение нескольких долей целого. Решение задач.
УМНОЖЕНИЕ И ДЕЛЕНИЕ МНОГОЗНАЧНОГО ЧИСЛА НА ОДНОЗНАЧНОЕ
Алгоритм письменного умножения многозначного числа на однозначное. Алгоритм письменного деления многозначного числа на однозначное. Решение уравнений. Решение текстовых задач на пропорциональное деление. Умножение числа на произведение. Деление числа на произведение. Деление с остатком на 10, 100, 1000. Умножение числа на сумму.
СКОРОСТЬ. ВРЕМЯ. РАССТОЯНИЕ
Зависимости между величинами: скорость, время, расстояние. Решение задач с величинами: скорость, время, расстояние. Задачи на одновременное встречное движение. Решение задач на одновременное движение в противоположных направлениях.
УМНОЖЕНИЕ И ДЕЛЕНИЕ МНОГОЗНАЧНОГО ЧИСЛА НА ДВУЗНАЧНОЕ И ТРЁХЗНАЧНОЕ ЧИСЛО
Алгоритм письменного деления многозначного числа на двузначное число. Деление на трёхзначные числа. Проверка умножения делением и деления умножением.
ГЕОМЕТРИЧЕСКИЕ ПРОСТРАНСТВЕННЫЕ ФИГУРЫ
Куб. Параллелепипед. Пирамида. Цилиндр. Шар. Конус.
Параллелепипед. Пирамида. Цилиндр. Шар. Конус.
Методы сложения чисел от 1 до 100 – BetterExplained
Существует популярная история о том, что у Гаусса, выдающегося математика, был ленивый учитель. Так называемый воспитатель хотел занять детей, чтобы он мог вздремнуть; он попросил класс сложить числа от 1 до 100.
Гаусс подошел со своим ответом: 5050. Так скоро? Учитель заподозрил обман, но нет. Сложение вручную было для лохов, и Гаусс нашел формулу, позволяющую обойти проблему:
Давайте поделимся несколькими объяснениями этого результата и действительно поймем его интуитивно. Для этих примеров мы добавим 1 к 10, а затем посмотрим, как это применимо к 1 к 100 (или 1 к любому числу).
Техника 1: Парные номера
Парные номера — распространенный подход к этой проблеме. Вместо того, чтобы записывать все числа в один столбец, давайте обернем числа так:
1 2 3 4 5 10 9 8 7 6
Возникает интересный паттерн: сумма каждого столбца равна 11 . По мере увеличения верхней строки нижняя строка уменьшается, поэтому сумма остается прежней.
По мере увеличения верхней строки нижняя строка уменьшается, поэтому сумма остается прежней.
Поскольку 1 находится в паре с 10 (наше n), мы можем сказать, что в каждом столбце есть (n+1). А сколько у нас пар? Итак, у нас есть 2 равных строки, у нас должно быть n/2 пар.
, что является формулой выше.
Подождите, а как насчет нечетного количества предметов?
Ах, я рад, что вы подняли эту тему. Что, если мы сложим числа от 1 до 9? У нас нет четного количества предметов, которые можно соединить. Многие объяснения просто дадут объяснение выше и остановятся на этом. я не буду.
Складываем числа от 1 до 9, но вместо того, чтобы начинать с 1, давайте считать с 0:
0 1 2 3 4 9 8 7 6 5
Считая от 0, мы получаем «дополнительный элемент» (всего 10), поэтому у нас может быть четное количество строк. Однако наша формула будет выглядеть немного иначе.
Обратите внимание, что сумма каждого столбца равна n (а не n+1, как раньше), поскольку 0 и 9 сгруппированы. И вместо того, чтобы иметь ровно n элементов в 2 строках (всего n/2 пар), у нас есть n + 1 элемент в 2 строках (всего (n + 1)/2 пар). Если вы подставите эти числа, вы получите:
И вместо того, чтобы иметь ровно n элементов в 2 строках (всего n/2 пар), у нас есть n + 1 элемент в 2 строках (всего (n + 1)/2 пар). Если вы подставите эти числа, вы получите:
, что является той же формулой, что и раньше. Меня всегда раздражало, что одна и та же формула работает и для нечетных, и для четных чисел — дробь не получится? Да, вы получаете ту же формулу, но по другим причинам.
Способ 2: Использование двух рядов
Описанный выше метод работает, но вы по-разному обрабатываете нечетные и четные числа. Разве нет лучшего способа? Да.
Вместо того, чтобы зацикливать числа, давайте запишем их в два ряда:
1 2 3 4 5 6 7 8 910 10 9 8 7 6 5 4 3 2 1
Обратите внимание, что у нас есть 10 пар, и каждая пара в сумме дает 10+1.
Сумма всех приведенных выше чисел равна
Но нам нужна сумма только одной строки, а не обеих. Итак, мы делим приведенную выше формулу на 2 и получаем:
Вот это круто (настолько круто, насколько могут быть ряды чисел). Это работает для нечетного или четного количества предметов одинаково!
Это работает для нечетного или четного количества предметов одинаково!
Техника 3: Создание прямоугольника
Недавно я наткнулся на другое объяснение, свежий подход к старому объяснению спаривания. Разные объяснения работают лучше для разных людей, и мне это нравится больше.
Вместо того, чтобы писать числа, представьте, что у нас есть бобы. Мы хотим добавить 1 боб к 2 бобам, к 3 бобам… вплоть до 5 бобов.
х х х х х х х х х х х х х х х
Конечно, мы могли бы использовать 10 или 100 бобов, но с 5 вы поняли идею. Как нам посчитать количество бобов в нашей пирамиде?
Ну, сумма явно 1 + 2 + 3 + 4 + 5. Но давайте посмотрим на это по-другому. Допустим, мы зеркально отразим нашу пирамиду (я буду использовать «о» для отраженных бобов), а затем опрокинем ее:
х о х о о о о о х х о о х х о о о о х х х о о о => х х х о о о х х х х о о о о х х х х о о х х х х х о о о о о х х х х х х о
Круто, да? Если вам интересно, действительно ли это совпадает, то это так. Взгляните на нижний ряд правильной пирамиды с 5′x (и 1°). В следующем ряду пирамиды на 1 x меньше (всего 4) и на 1 больше (всего 2), чтобы заполнить пробел. Так же, как и в паре, одна сторона увеличивается, а другая уменьшается.
Взгляните на нижний ряд правильной пирамиды с 5′x (и 1°). В следующем ряду пирамиды на 1 x меньше (всего 4) и на 1 больше (всего 2), чтобы заполнить пробел. Так же, как и в паре, одна сторона увеличивается, а другая уменьшается.
Теперь пояснение: сколько у нас всего бобов? Ну, это просто площадь прямоугольника.
У нас есть n строк (количество строк в пирамиде мы не меняли), а ширина нашей коллекции (n + 1) единиц, так как 1 «о» стоит в паре со всеми «иксами».
Обратите внимание, что на этот раз нам все равно, будет ли n нечетным или четным — формула общей площади работает просто отлично. Если n нечетно, у нас будет четное количество элементов (n+1) в каждой строке.
Но, конечно, нам не нужна общая площадь (количество иксов и ноликов), нам нужно только количество иксов. Поскольку мы удвоили x, чтобы получить o, x сами по себе составляют лишь половину общей площади:
И мы вернулись к нашей первоначальной формуле. Опять же, количество x в пирамиде = 1 + 2 + 3 + 4 + 5 или сумма от 1 до n.
Техника 4: Усреднение
Все мы знаем, что
среднее = сумма / количество элементов
, что мы можем преобразовать в
сумма = среднее * количество элементов
Чтобы получить среднее значение, обратите внимание, что все числа распределены поровну. Для каждого большого числа на другом конце есть маленькое число. Давайте посмотрим на небольшой набор:
1 2 3
Среднее значение равно 2. 2 уже находится посередине, а 1 и 3 «сокращаются», поэтому их среднее значение равно 2.
Для четного числа предметов
1 2 3 4
среднее между 2 и 3 — это 2,5. Несмотря на то, что у нас есть дробное среднее, это нормально — поскольку у нас есть даже элементов, когда мы умножаем среднее значение на количество, эта уродливая дробь исчезнет.
Обратите внимание, что в обоих случаях 1 находится по одну сторону от среднего, а N одинаково далеко по другую. Таким образом, мы можем сказать, что среднее значение всего набора на самом деле является средним значением 1 и n: (1 + n)/2.
Таким образом, мы можем сказать, что среднее значение всего набора на самом деле является средним значением 1 и n: (1 + n)/2.
Подставляем это в нашу формулу
И вуаля! У нас есть четвертый способ думать о нашей формуле.
Так почему же это полезно?
Три причины:
1) Быстрое сложение чисел может быть полезным для оценки. Обратите внимание, что формула расширяется до этого:
Допустим, вы хотите сложить числа от 1 до 1000: предположим, вы получаете 1 дополнительного посетителя на свой сайт каждый день — сколько всего посетителей будет через 1000 дней? Так как тысяча в квадрате = 1 миллион, мы получаем миллионов / 2 + 1000/2 = 500 500 .
2) Эта концепция сложения чисел от 1 до N проявляется и в других местах, например, при вычислении вероятности парадокса дня рождения. Твердое понимание этой формулы поможет вашему пониманию во многих областях.
3) Самое главное, этот пример показывает, что есть много способов понять формулу. Может быть, вам нравится метод сопряжения, может быть, вы предпочитаете технику прямоугольника, или, может быть, есть другое объяснение, которое вам подходит. Не отказывайтесь от , если вы не понимаете — попробуйте найти другое объяснение, которое работает. Счастливая математика.
Может быть, вам нравится метод сопряжения, может быть, вы предпочитаете технику прямоугольника, или, может быть, есть другое объяснение, которое вам подходит. Не отказывайтесь от , если вы не понимаете — попробуйте найти другое объяснение, которое работает. Счастливая математика.
Кстати, есть более подробная информация об истории этой истории и возможной технике, которую использовал Гаусс.
Вариации
Вместо 1 до n, как насчет 5 до n?
Начните с обычной формулы (1 + 2 + 3 + … + n = n * (n + 1) / 2) и вычтите ненужную часть (1 + 2 + 3 + 4 = 4 * (4 + 1) / 2 = 10).
Сумма для 5 + 6 + 7 + 8 + … n = [n * (n + 1) / 2] – 10
И для любого начального числа a:
Сумма от a до n = [n * (n + 1) / 2] – [(a - 1) * a / 2]
Мы хотим избавиться от всех чисел от 1 до — 1.
Как насчет четных чисел, таких как 2 + 4 + 6 + 8 + … + n?
Просто удвойте обычную формулу.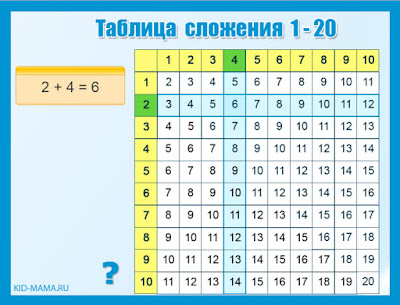 Чтобы сложить четные числа от 2 до 50, найдите 1 + 2 + 3 + 4 … + 25 и удвойте его:
Чтобы сложить четные числа от 2 до 50, найдите 1 + 2 + 3 + 4 … + 25 и удвойте его:
Сумма 2 + 4 + 6 + … + n = 2 * (1 + 2 + 3 + … + n/ 2) = 2 * п/2 * (п/2 + 1) / 2 = п/2 * (п/2 + 1)
Итак, чтобы получить четные числа от 2 до 50, нужно сделать 25 * (25 + 1) = 650
Как насчет нечетных чисел, например 1 + 3 + 5 + 7 + … + n?
Это то же самое, что и четная формула, за исключением того, что каждое число на 1 меньше своего аналога (у нас есть 1 вместо 2, 3 вместо 4 и т. д.). Получаем следующее по величине четное число (n + 1) и убираем лишнее (n + 1)/2 «-1″ предметов:
Сумма 1 + 3 + 5 + 7 + … + n = [(n + 1)/2 * ((n + 1)/2 + 1)] – [(n + 1) / 2]
Чтобы добавить 1 + 3 + 5 + … 13, возьмите следующее наибольшее четное (n + 1 = 14) и выполните
[14/2 * (14/2 + 1)] – 7 = 7 * 8 – 7 = 56 – 7 = 49
Комбинации: четы и смещения
Допустим, вам нужны четы из 50 + 52 + 54 + 56 + … 100. Найдите все четы
Найдите все четы
2 + 4 + 6 + … + 100 = 50 * 51
и вычесть ненужные
2 + 4 + 6 + … 48 = 24 * 25
Итак, сумма из 50 + 52 + … 100 = (50 * 51) – (24 * 25) = 1950
Фу! Надеюсь это поможет.
Рубиновые умники: вы можете проверить это, используя
(50..100).select {|x| х % 2 == 0 }.inject(:+)
1950 г.
Специалисты по Javascript, сделайте это:
[...Array(51).keys()].map(x => x + 50).filter(x => x % 2 == 0).reduce(( х, у) => х + у) 1950 г. // Примечание: имеется 51 число от 50 до 100 включительно. Забор!
Другие сообщения из этой серии
- Методы сложения чисел от 1 до 100
- Переосмысление арифметики: визуальное руководство
- Quick Insight: интуитивное значение подразделения
- Quick Insight: вычитание отрицательных чисел
- Удивительные закономерности в квадратных числах (1, 4, 9, 16…)
- Развлечение с модульной арифметикой
- Учимся считать (избегая проблемы с ограждением)
- Причудливое введение в системы счисления
- Еще один взгляд на простые числа
- Интуиция для золотого сечения
- Различные интерпретации числа ноль
Натуральные числа от 1 до 100 |Сумма натуральных чисел от 1 до 100
Натуральные числа от 1 до 100 — это набор первых 100 натуральных чисел, где 1 — натуральное число, а 100 — самое большое. Натуральные числа, являющиеся частью системы счисления, включают в себя все положительные целые числа от 1 до бесконечности. Их также называют счетными числами, так как они не включают ноль или отрицательные числа. Набор натуральных чисел — это классификация под большим набором действительных чисел, включающим только положительные целые числа, но не ноль, дроби, десятичные дроби и отрицательные числа.
Натуральные числа, являющиеся частью системы счисления, включают в себя все положительные целые числа от 1 до бесконечности. Их также называют счетными числами, так как они не включают ноль или отрицательные числа. Набор натуральных чисел — это классификация под большим набором действительных чисел, включающим только положительные целые числа, но не ноль, дроби, десятичные дроби и отрицательные числа.
В этой статье давайте изучим натуральные числа от 1 до 100 и найдем их сумму с помощью формулы и решенных примеров.
| 1. | Натуральные числа от 1 до 100 Таблица |
| 2. | Сумма натуральных чисел от 1 до 100 |
| 3. | Примеры натуральных чисел от 1 до 100 |
| 4. | Практические вопросы по натуральным числам от 1 до 100 |
| 5. | Часто задаваемые вопросы о натуральных числах от 1 до 100 |
Натуральные числа от 1 до 100 Таблица
Таблица натуральных чисел от 1 до 100 поможет вам перечислить все натуральные числа от 1 до 100. Итак, 100 — последнее натуральное число в списке натуральных чисел от 1 до 100. Это делается с помощью простая формула, в которой мы добавляем 1 к предыдущему числу, чтобы получить следующее число. Другими словами, это все последовательные числа от 1 до 100. 1 — наименьшее натуральное число в списке.
Итак, 100 — последнее натуральное число в списке натуральных чисел от 1 до 100. Это делается с помощью простая формула, в которой мы добавляем 1 к предыдущему числу, чтобы получить следующее число. Другими словами, это все последовательные числа от 1 до 100. 1 — наименьшее натуральное число в списке.
Сумма натуральных чисел от 1 до 100
Натуральные числа от 1 до 100 можно записать как 1, 2, 3, 4,5…….100 — это арифметическая прогрессия (А.П). Сумма всех натуральных чисел от 1 до 100 может быть рассчитана по формуле S = n/2[2a + (n − 1) × d], где n — общее количество натуральных чисел от 1 до 100, d — разница между двумя последовательными терминами, а первый термин. Всего существует 100 натуральных чисел, поэтому n = 100,9.0003
Таким образом, a = 1, d = 1 и n = 100
Вычислим сумму натуральных чисел от 1 до 100
Сумма A.P,
S = n/2[2a + (n − 1 ) × d]
S = 100/2[2 + (100 – 1) × 1]
S = 50 [2 + 99]
S = 5050
Следовательно, сумма натуральных чисел от 1 до 100 равно 5050.
Важные примечания:
- 1 — наименьшее натуральное число.
- Всего существует 100 натуральных чисел от 1 до 100.
- Натуральные числа считают числа только начиная с 1.
- Сумма натуральных чисел от 1 до 100 равна 5050.
Темы, связанные с натуральными числами от 1 до 100
Ознакомьтесь со статьями, посвященными концепции натуральных чисел от 1 до 100.
- Нечетные числа
- Четные числа
- Четные и нечетные числа
- Целые числа
Часто задаваемые вопросы о натуральных числах от 1 до 100
Какие натуральные числа от 1 до 100?
Натуральные числа от 1 до 100 — это все те числа в этом диапазоне, которые представляют собой все последовательные числа, начинающиеся от 1 до 100. Натуральные числа от 1 до 100 — это 1, 2, 3, 4, 5, 6, 7, 8. , 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33 , 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58 , 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94 , 95, 96, 97, 98, 99 и 100.
Как найти сумму натуральных чисел от 1 до 100?
Сумма всех натуральных чисел от 1 до 100 равна 5050. Общее количество натуральных чисел в этом диапазоне равно 100. Таким образом, применяя это значение в формуле: S = n/2[2a + (n − 1) × d] получаем S=5050.
Какое среднее значение натуральных чисел от 1 до 100?
Среднее значение натуральных чисел от 1 до 100 равно 100. Оно рассчитывается по формуле среднего, которая гласит, что Среднее = Сумма всех значений/Общее количество значений. Здесь сумма значений равна 5050, а общее количество натуральных чисел от 1 до 100 равно 100. Значит, среднее = 5050/100 = 50,5. Следовательно, 50,5 — это среднее натуральных чисел от 1 до 100.
Какое самое большое натуральное число в списке натуральных чисел от 1 до 100?
100 — наибольшее натуральное число в списке натуральных чисел от 1 до 100. Следующим натуральным числом будет 101, которое больше 100. Итак, 100 — наибольшее натуральное число в списке четных чисел от 1 до 100.
Какая формула для нахождения суммы натуральных чисел от 1 до 100?
Список натуральных чисел от 1 до 100 хорошо организован в виде арифметической последовательности. Таким образом, мы можем просто использовать формулу суммы n членов арифметической прогрессии, то есть S = n/2[2a + (n − 1) × d], чтобы вычислить формулу суммы натуральных чисел.
поместите знаки плюс/минус между цифрами
Начните с последовательности ненулевых цифр 123456789. Задача состоит в том, чтобы поставить плюс или минус знаки между ними так, что результатом описанной арифметической операции будет 100.
Мы получили один ответ
12 + 3 — 4 + 5 + 67 + 8 + 9 = 100
и предположил, что существует как минимум еще один. Я не утверждаю, что провел исчерпывающий поиск, но кажется, что есть больше, чем просто два ответа. Один из них
123 + 4 — 5 + 67 — 89 = 100
Я уверен, что там как минимум еще один. Хотите найти?
Есть острое наблюдение, что в двух приведенных выше примерах по крайней мере одна из операций — вычитание. И это также верно для всех аддитивных (тех, в которых разрешены только операции сложения и вычитания) приведенных ниже примеров. На самом деле невозможно избежать вычитания, даже если цифры идут в произвольном порядке. Чтобы понять почему, полезно вспомнить понятие цифровых корней.
И это также верно для всех аддитивных (тех, в которых разрешены только операции сложения и вычитания) приведенных ниже примеров. На самом деле невозможно избежать вычитания, даже если цифры идут в произвольном порядке. Чтобы понять почему, полезно вспомнить понятие цифровых корней.
Вы можете разрешить любые операции, кроме сложения и вычитания. Это приводит к совершенно новому набору проблем с числами, имеющими дробные части. Варианты включают установку целей, отличных от 100. Вот, например, представление единицы, в которой используются все десять цифр:
. 1 = 148/296 + 35/70
Есть много способов весело провести время, решая арифметические задачи. Один из способов — попытаться представить числа ограниченными средствами. Например, я могу представить 100 пятью тройками как 100 = 33×3 + 3/3. Удивительно, как много чисел можно представить таким образом.
В 1960-х годах очень популярным стал другой вид числовых головоломок. Криптарифмы — это головоломки, полученные
когда цифры в числовых расчетах заменены буквами. Обычно различаются
буквы обозначают разные цифры. Звезды заменяют любую цифру и не связаны друг с другом.
Обычно различаются
буквы обозначают разные цифры. Звезды заменяют любую цифру и не связаны друг с другом.
Я получил следующее письмо из Бельгии:
От: Gui et Nicole RULMONT
Дата: вторник, 22 апреля 1997 г., 17:02:44 +0200
Уважаемый Cut-the-Knot,
Сначала извините за мой английский. Я бельгиец, и меня очень заинтересовал ваш сайт!
Вы писали в «Веселье с цифрами»: Начните с последовательности ненулевых цифр 123456789. Задача состоит в том, чтобы расставить между ними знаки плюс или минус так, чтобы результатом описанной арифметической операции было 100.
Несколько лет назад я нашел во французском журнале Science et Vie 11 решений:
1 + 2 + 34 — 5 + 67 — 8 + 9 = 100
12 + 3 — 4 + 5 + 67 + 8 + 9= 100
123 — 4 — 5 — 6 — 7 + 8 — 9 = 100
123 + 4 — 5 + 67 — 89 = 100
123 + 45 — 67 + 8 — 9 = 100
123 — 45 — 67 + 89 = 100
12 — 3 — 4 + 5 — 6 + 7 + 89 = 100
12 + 3 + 4 + 5 — 6 — 7 + 89 = 100
1 + 23 — 4 + 5 + 6 + 78 — 9 = 100
1 + 23 — 4 + 56 + 7 + 8 + 9 = 100
1 + 2 + 3 — 4 + 5 + 6 + 78 + 9 = 100
Если мы поставим «-» перед 1, у нас будет еще одно решение:
-1 + 2-3 + 4 + 5 + 6 + 78 + 9 = 100
Использование «. » десятичное разделение Я нашел другое решение:
» десятичное разделение Я нашел другое решение:
1 + 2,3 — 4 + 5 + 6,7 + 89 = 100 (моё решение)
А как насчет 987654321? Есть 15 решений, сказал Science et Vie :
98 — 76 + 54 + 3 + 21 = 100
9 — 8 + 76 + 54 — 32 + 1 = 100
98 + 7 + 6 — 5 — 4 — 3 + 2 — 1 = 100
98 — 7 — 6 — 5 — 4 + 3 + 21 = 100
9 — 8 + 76 — 5 + 4 + 3 + 21 = 100
98 — 7 + 6 + 5 + 4 — 3 — 2 — 1 = 100
98 + 7 — 6 + 5 — 4 + 3 — 2 — 1 = 100
98 + 7 — 6 + 5 — 4 — 3 + 2 + 1 = 100
98 — 7 + 6 + 5 — 4 + 3 — 2 + 1 = 100
98 — 7 + 6 — 5 + 4 + 3 + 2 — 1 = 100
98 + 7 — 6 — 5 + 4 + 3 — 2 + 1 = 100
98 — 7 — 6 + 5 + 4 + 3 + 2 + 1 = 100
9 + 8 + 76 + 5 + 4 — 3 + 2 — 1 = 100
9 + 8 + 76 + 5 — 4 + 3 + 2 + 1 = 100
9 — 8 + 7 + 65 — 4 + 32 — 1 = 100
Напишите знак «-«, три решения:
-9 + 8 + 76 + 5-4 + 3 + 21 = 100
-9 + 8 + 7 + 65 — 4 + 32 + 1 = 100
-9-8 + 76 — 5 + 43 + 2 + 1 = 100
С десятичной точкой:>
9 + 87,6 + 5,4 — 3 + 2 — 1 = 100 (моё решение)
Если «перетасовать» цифры, то есть много решений. Я нашел некоторые, когда
Я был молод, например:
Я нашел некоторые, когда
Я был молод, например:
91 + 7,68 + 5,32 — 4 = 100
98,3 + 6,4 — 5,7 + 2 — 1 = 100
538 + 7 — 429 — 13 = 100
(8×9,125) + 37 — 6 — 4 = 100 и т.д. и т.п.. ..
очень интересуюсь криптарифмами и собираю их. Вы хотите получить французские криптарифмы? Знаете ли вы неанглийские криптарифмы? Спасибо!
Gui et Nicole Rulmont
Энтони Лезар отмечает, что решение 1 + 2 + 3 — 4 + 5 + 6 + 78 + 9 = 100 можно немного изменить без изменения результата: 1! + 2! + 3 — 4 + 5 + 6 + 78 + 9 = 100.
Примечание : Существует целая куча страниц, предлагающих практические задачи такого рода. Кроме того, Inder Jeet Taneja собрал фантастическую коллекцию различных последовательных представлений чисел от 1 до 11111.
|Контакты| |Главная страница| |Содержание| |Ты знал?| |Алгебра|
Copyright © 1996-2018 Александр Богомольный
Сложение и вычитание с использованием разрядных значений
- Учебные ресурсы
- 1-й класс
Обучение сложению и вычитанию основных навыков, первый класс : 1. НБТ.4. Ниже мы показываем два видеоролика, демонстрирующих этот стандарт. Затем мы даем разбивку по конкретным шагам в видеороликах, которые помогут вам провести урок.
НБТ.4. Ниже мы показываем два видеоролика, демонстрирующих этот стандарт. Затем мы даем разбивку по конкретным шагам в видеороликах, которые помогут вам провести урок.
Предварительное обучение
Ваши учащиеся должны уметь считать от 1 до 100, используя единицы и десятки, начиная с любого числа. Они также должны уметь читать, писать и представлять объекты, используя числа от 0 до 20 (K.CC.1-3).
Future Learnings
Позже, понимание значений разрядов позволит вашим учащимся пропускать счет в пределах 1000 (считая до 5, 10 и 100). Они также смогут читать и записывать числа, используя «цифры с основанием десять, названия чисел и расширенную форму» (2.NBT.1-3).
Общий базовый стандарт: 1.NBT.4 — Сложение в пределах 100 однозначных и двузначных чисел, кратных 10; использовать конкретные модели, рисунки и стратегии, основанные на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием
Учащиеся, понимающие этот принцип, могут:
- Использовать физические модели, рисунки и т.
 д. для объяснения сложения в пределах 100, добавляя однозначное и двузначное число.
д. для объяснения сложения в пределах 100, добавляя однозначное и двузначное число. - Используйте физические модели, чертежи и т. д., чтобы объяснить сложение в пределах 100, добавляя двузначное число и число, кратное десяти.
- Используйте физические модели, рисунки и т. д., чтобы объяснить сложение в пределах 100 путем сложения двух двузначных чисел.
- Разложите оба слагаемых, используя частичные суммы, чтобы сложить их в пределах 100.
- Разложите одно слагаемое, используя частичные суммы, чтобы сложить в пределах 100.
- Объясните, почему при сложении чисел иногда получается «новая десятка».
2 видео, которые помогут вам преподавать стандарт Common Core: 1.NBT.4
Ниже мы приводим два видео с разбивкой по ним, которые помогут вам обучать своих учеников этому стандарту.
Видео 1: Различные методы сложения больших чисел
youtube.com/embed/ZSQxc8MEJLI» title=»Adding within 100 (1.NBT.4)»>В этом видео показаны три различных способа сложения двух больших чисел. Девушка на видео сбита с толку, потому что сначала она не знает, как решить 43 + 21. Затем она вспоминает 3 разных метода, которым она научилась в школе, как решать такие типы задач.
Первый метод использует блоки для решения уравнения.
- Сначала разбейте числа на 10 и 1.
а. На видео показаны числа 43 и 21 в виде блоков, разбитых на группы по 10 и 1. - Сложите две десятки вместе.
а. 40 + 20. - Сложите две единицы вместе.
а. 3 + 1. - Затем объедините их, чтобы получить общее количество: 64.
Следующий пример следует той же схеме, но без вспомогательных блоков.
- 40 + 20 = 60.
- 3 + 1 = 4.
- 60 + 4 = 64.
В последнем примере для решения уравнения используется числовая прямая.
- Начните с 43 (большее число) в числовой строке.

- Затем добавьте 20 на 10 сек.
а. Одну 10, чтобы получить 53, и еще 10, чтобы получить 63. - Тогда остается только еще одно число: 1.
a. 63 + 1 = 64.
Видео заканчивается напоминанием учащимся, что они могут складывать большие числа, разбивая их на десятки и единицы и используя числовую прямую.
Видео 2. Добавление больших чисел в столбцы
Видео начинается с краткого обзора разрядных значений и того, что они собой представляют: «Разрядное значение показывает позицию цифры в числе». Например, если в числе 6 десятков и 2 единицы, то это число равно 62.
Затем Боддл объясняет, что разрядные значения могут использоваться для упрощения сложения и вычитания. Затем в видео представлено несколько примеров, чтобы учащиеся могли увидеть, как работает эта концепция.
- В уравнении 23 + 5 учащиеся могут выстроить их в столбец.
а. Убедитесь, что значения мест выровнены.
б. 1s над 1s и 10s над 10s. - Начните с добавления цифр в разряде 1.
а. 3 + 5 = 8. - Затем добавьте цифры в разряде десятков.
а. Так как 2 стоит одна на десятках, приведите ее к сумме.
б. Или подумайте об этом как 2 + 0 = 2. - 23 + 5 = 28.
Затем видео приводит другой пример: 35 + 7. Оно демонстрирует, как учащиеся могут решить уравнение сложения, которое переводит новое число в 10-е место.
- Запишите уравнение в столбик.
- Добавьте значения в разряде 1.
а. 5 + 7 = 12. - Затем видео напоминает учащимся, что на одно разрядное значение можно записать только 1 число.
- Записано только 2 из 12, и оно стоит на 1 месте.
- 1 идет сверху 3, так как они обе на десятках.
- 1 и 3 складываются вместе.
- Ответ равен 42, поэтому 35 + 7 = 42.

Хотите больше практики?
Предложите своим учащимся дополнительную практику в соответствии со стандартами с помощью Boddle Learning. Boddle включает в себя вопросы, связанные со сравнением и измерением длин, а также награждение монетами и играми для ваших учеников, чтобы они были вовлечены. Нажмите здесь, чтобы зарегистрироваться в Boddle Learning и создать свое первое задание сегодня.
*Информация о стандартах взята из Учебного пособия по математике Департамента государственного образования штата Нью-Мексико и с веб-сайта Common Core.
Сложение и вычитание в 1-м классе (возраст 5–6 лет)
В 1-м классе ваш ребенок начнет читать, писать и понимать математические идеи, используя сложение (+), вычитание (–) и равенство (= ) знаки. Они будут практиковаться в счете и начнут решать простые словесные задачи.
Ключевые слова в этом разделе — эквивалентность и числовые связи.
Чему научится ваш ребенок
Ознакомьтесь с требованиями Национальной учебной программы к сложению и вычитанию в 1-м классе (возраст 5–6 лет):
Понимать и использовать сложение (+), вычитание (–) и равенство (=) знаки
Ваш ребенок поймет сложение, вычитание и идею эквивалентности. Они также смогут использовать символы «+», «–» и «=» для записи вычислений и смогут понять задачи, в которых используются эти символы.
Они также смогут использовать символы «+», «–» и «=» для записи вычислений и смогут понять задачи, в которых используются эти символы.
Они поймут, что сложение означает нахождение суммы двух или более наборов объектов или чисел. Сначала они посчитают все предметы в двух группах. Например:
Если у вашего ребенка есть группа из 2 предметов и еще одна группа из 3 предметов, он будет считать каждый предмет в обеих группах: 1, 2, 3, 4, 5.
Затем они перейдут к подсчету. Это означает, что не всегда начиная с 1, а начиная с одного из чисел в расчете. Например:
Если у вашего ребенка есть группа из 2 предметов и еще одна группа из 3 предметов, он может начать с 2 предметов и рассчитывать, что найдет сумму: 3, 4, 5.
Ваш ребенок начнет понимать, что быстрее считать от большего числа в сумме. Например, для групп из 2 и 3 объектов они начнут с группы из 3 и будут рассчитывать еще на 2, чтобы найти общее количество.
Ваш ребенок также будет знать, что вычитание означает удаление, чтобы узнать, сколько осталось. Объекты очень полезны для демонстрации того, как это работает. Для начала вашего ребенка можно познакомить с вычитанием как с различием. например, «4 – 1» может быть прочитано как «В чем разница между 4 и 1?».
Your child will be expected to use language such as put together , add , altogether , total , take away , distance between , difference between , more than and меньше при сложении и вычитании.
Использование числовых связей и связанных с ними фактов вычитания до 20
Ваш ребенок будет составлять и использовать числовые связи до 20. Числовые связи – это разные способы составления чисел. Например, количество связей с 4 равно:
4 и 0
3 и 1
2 и 2
1 и 3
0 и 4
Ваш ребенок выучит пары чисел, которые составляют 10, и будет использовать свое понимание, чтобы вычислить пары чисел, которые составляют 20.
Ожидается, что ваш ребенок также будет знать соответствующие факты вычитания до 20. Например :
Если 9 + 7 = 16 …
Тогда 16 – 7 = 9 и 16 – 9 = 7.
Ваш ребенок также будет знать, что добавление нуля к числу означает, что оно не изменится.
Складывать и вычитать однозначные и двузначные числа до 20
Ваш ребенок будет складывать и вычитать числа, используя предметы, рисуя диаграммы и записывая вычисления.
Ожидается, что ваш ребенок будет складывать и вычитать однозначные и двузначные числа с ответами от 0 до 20. Например, 27 – 11 = 16.
Решайте одношаговые задачи и задачи с пропущенными числами
Ваш ребенок будет решать простые задачи на сложение и вычитание (включая текстовые задачи). Например:
6 + 4 = ?
Если я куплю 6 яблок и 4 апельсина, сколько всего фруктов у меня будет?
Ваш ребенок будет использовать ряд предметов, рисунков, диаграмм и символов для решения задач на сложение и вычитание. Они также будут решать проблемы с пропущенными числами, связанные с сложением и вычитанием, например, 7 = ? – 9.
Они также будут решать проблемы с пропущенными числами, связанные с сложением и вычитанием, например, 7 = ? – 9.
Как помочь дома
Существует множество способов помочь ребенку научиться складывать и вычитать. Вот лишь несколько идей:
1. Сыграйте в игру «Пары фактов о числах»
Ваш ребенок должен знать ряд фактов о числах, включая сложение и вычитание. Числовые факты — это факты, которые мы знаем сразу, без необходимости вычислять, например, 2 + 2 = 4.
Например, для будущего обучения вашего ребенка очень важно, чтобы он мог вспомнить различные способы, которыми мы можем разделить (перерыв друг от друга) цифры от 1 до 10. Вы можете помочь им учиться, играя вместе в Number Facts Pairs !
- Напишите числа от 1 до 10 два раза, сделав 20 отдельных карточек с числами.
- Переверните карты лицевой стороной вниз и выберите одну наугад. Это число, которое вы собираетесь попытаться сделать.
- Теперь по очереди собирайте карты.
 Складывайте каждую карту, которую вы подбираете, пока не дойдете до целевого числа. Если вы зашли слишком высоко, вы можете использовать свой ход, чтобы положить обратно одну из карт, которые вы взяли, лицевой стороной вниз.
Складывайте каждую карту, которую вы подбираете, пока не дойдете до целевого числа. Если вы зашли слишком высоко, вы можете использовать свой ход, чтобы положить обратно одну из карт, которые вы взяли, лицевой стороной вниз. - Когда игрок достигает заданного числа, он выигрывает!
Есть много забавных вариантов игры, которые вы можете попробовать. Почему бы не добавить более высокие цифры или не посмотреть, сколько целей вы сможете достичь за две минуты?
2. Сосредоточьтесь на вычитании
Ожидается, что ваш ребенок будет знать факты вычитания до 10. Он начнет с вычитания единицы из набора объектов и заметит, что набор уменьшился в размере. Поощряйте ребенка связывать вычитание с отнятием, показывая ему, как это работает в повседневных ситуациях.
Например, если у вашего ребенка есть горсть изюма, спросите его, сколько у него есть. Когда они съедят одну, спросите их, сколько у них осталось. У них больше изюма или меньше изюма? Что будет, если съесть два изюма одновременно? Использование реальных объектов или рисунков и удаление тех, которые вы хотите вычесть, помогает вашему ребенку визуализировать, что на самом деле означает вычитание.
3. Играйте в игры с костями
Существует множество способов побудить ребенка решать практические задачи на сложение и вычитание. Все, что вам нужно, это две игральные кости.
В школе их учат, что сложение — это когда мы складываем две группы объектов вместе или когда у нас есть начальная сумма, а затем мы добавляем к ней больше, создавая общее увеличение. Вы можете сыграть в игру, в которой каждый игрок бросает два кубика и должен найти сумму. Победителем становится игрок, набравший наибольшую сумму.
Вы можете использовать подобные игры для вычитания. Например:
Начните с заданного количества предметов, скажем, 12. Затем по очереди бросайте шестигранный кубик.
Первый игрок, выбрасывающий кубик, вычитает число, указанное на кубике, из 12 предметов и вычисляет, сколько у него осталось. Они забирают объекты, которые они вычитали.
Следующий игрок бросает кубик и отбирает свой номер из оставшейся стопки предметов.
Игра продолжается до тех пор, пока все объекты не будут удалены. Игрок с наибольшим количеством предметов в конце игры становится победителем.
Вы можете попросить ребенка записывать вычисления для каждого броска игральной кости, например, 12 – 3 = 9..
Наконец, почему бы не поиграть в настольные игры с двумя кубиками? Они дают прекрасную возможность практиковать числовые связи, а также обучать другим полезным навыкам, таким как счет и ожидание своей очереди.
4. Сосредоточьтесь на счете
Помогите ребенку попрактиковаться в сложении, комбинируя два или более набора предметов. Например, если у вас есть 4 виноградины, а у вашего ребенка 7 виноградин, попросите их узнать, сколько всего виноградин. Ваш ребенок может пересчитать каждую виноградину по одной, чтобы найти общее количество.
Чтобы убедиться, что они точно считают каждую виноградинку, попросите ребенка расположить ягоды в ряд. Ваш ребенок может начать решать сложение, «рассчитывая на». В этом методе ребенок может начать с 4 виноградин, а затем посчитать еще 7, чтобы найти общее количество, то есть 5, 6, 7, 8, 9, 10, 11. Затем вы можете помочь своему ребенку записать, что он сделал. используя символы, т. е. 4 + 7 = 11.
В этом методе ребенок может начать с 4 виноградин, а затем посчитать еще 7, чтобы найти общее количество, то есть 5, 6, 7, 8, 9, 10, 11. Затем вы можете помочь своему ребенку записать, что он сделал. используя символы, т. е. 4 + 7 = 11.
Если вашему ребенку нравится собирать наклейки, спросите его, сколько у него уже есть. Затем спросите их, сколько у них было бы, если бы вы дали им еще 2. Это побудит их начать «рассчитывать» от первоначальной суммы, чтобы решить проблему сложения, что намного быстрее, чем считать каждую наклейку!
5. Вычитание как различие
Скорее всего, вашего ребенка учат вычитанию как «разнице». Например:
’10 – 8’ можно также рассматривать как «В чем разница между 10 и 8?»
Используйте предметы, чтобы помочь вашему ребенку понять концепцию различия. Почему бы не попросить вашего ребенка рассортировать свои игрушки по группам, а затем посмотреть, сможет ли он определить, в каких группах больше или меньше предметов? Затем вы можете попросить их сравнить две группы.
Чем отличается количество мягких игрушек вашего ребенка от количества твердых игрушек? Как насчет разницы между их красными игрушками и их синими игрушками? Размещение двух групп рядом друг с другом в линию — это хороший способ быстро определить разницу между ними.
Поощряйте ребенка записывать свои мысли в виде вычитания. Например:
Если у них есть 6 красных игрушек и 2 синих игрушки, то разница равна 4. Это можно записать как 6 – 2 = 4.
Обучение сложению и вычитанию чисел до 20
Это вторая часть из четырех статей, посвященных обучению сложению и вычитанию на начальных уровнях. Другие части этой серии, посвященные другим диапазонам чисел, можно найти по следующим ссылкам:
- Стратегии обучения сложению и вычитанию — часть 1: числа до 10
- Стратегии обучения сложению и вычитанию — часть 2: числа до 20 (этот пост)
- Стратегии обучения сложению и вычитанию. Часть 3. Числа до 100
- Стратегии обучения сложению и вычитанию.
 Часть 4. Числа до 1000
Часть 4. Числа до 1000
. сложение и вычитание в пределах однозначных чисел до 10. На этой неделе мы поговорим о проблемах, с которыми сталкиваются молодые учащиеся, когда они расширяют свое обучение числам в пределах 20.
Сложение и вычитание до 20 — это уникальная веха, потому что это дети впервые знакомятся с такими понятиями, как расстановка ценностей и перегруппировка. Многие полагаются на счет для сложения и вычитания в пределах 20. Хотя это совершенно нормально для младших школьников, их также следует познакомить с такими понятиями, как составление десяти, разложение десяти и получение фактов. Это будет иметь большое значение для создания прочного фундамента в числовом смысле.
Давайте рассмотрим несколько областей, в которых учащиеся часто сталкиваются с трудностями при сложении и вычитании в пределах 20.
A. Разрядное значение для десятков и единиц
Первым препятствием, с которым сталкиваются дети, обычно является представление о разрядном значении. Когда им дается 12 единиц для счета, расположенных в 1 группе по десять и 2 единицы, многие дети начинают считать с первой цифры 1, 2, 3,…. Они часто не видят, что 12 на самом деле равно 10 + 2. Это может привести к трудностям при сложении и вычитании, а часто и к тому, что отличает учащихся с высокими достижениями от учащихся ниже среднего, как можно увидеть в последующих абзацах.
Когда им дается 12 единиц для счета, расположенных в 1 группе по десять и 2 единицы, многие дети начинают считать с первой цифры 1, 2, 3,…. Они часто не видят, что 12 на самом деле равно 10 + 2. Это может привести к трудностям при сложении и вычитании, а часто и к тому, что отличает учащихся с высокими достижениями от учащихся ниже среднего, как можно увидеть в последующих абзацах.
Интересно, что у детей из некоторых азиатских семей в нашем классе с этим меньше проблем. Это может быть связано со структурой некоторых азиатских языков. Например, китайское слово для 11 — «десять-один», для 12 — «десять-два», для 22 — «два-десять-два» и т. д. Благодаря интуитивному ощущению позиционного значения это преимущество может быть перенесено. к сложению, где 22 + 25 = «два десятка два» + «два десятка пять» = «четыре десятка семь».
B. Дополнение
B1. Добавление в пределах 20 без перегруппировки
На примере 12 + 3 можно разложить 12 на 10 и 2, а затем отдельно сложить десятки и единицы.
Для детей этого возраста (первого класса) нет ничего плохого (и не редкого) в расчете на получение ответа, то есть на 13, …, 15. Опять же, мы должны поощрять детей гибко использовать числа. Исследования показали, что учащиеся, достигшие высоких результатов, — это те, кто понял, что числа можно гибко разбивать на части и снова складывать.
Б2. Сложение в пределах 20 с перегруппировкой
1. Сложение путем составления десятки
Это еще одно препятствие для юных учащихся. Например,
4 + 8 = 4 + 6 + 2 = 10 + 2 = 12
Чтобы получить 10 из 4, нам нужно разложить 8 на 6 и 2, чтобы 4 + 6 = 10.
Из нашего Опыт показывает, что многие дети не умеют решать задачи 4 + 8 с помощью манипулятивных средств (Конкрет). У них также нет проблем с разбиением 8 на 6 и 2. Однако, столкнувшись с математическим уравнением 4+8 (Аннотация), многие теряются и не знают, с чего начать.
Затем мы попробовали подход Concrete->Pictorial->Abstract, при котором графическое представление вводится перед математическим уравнением (Abstract). Благодаря нашим наблюдениям мы поняли, что этот подход работает лучше всего, когда Конкретное представление как можно теснее связано с Графическим представлением.
Благодаря нашим наблюдениям мы поняли, что этот подход работает лучше всего, когда Конкретное представление как можно теснее связано с Графическим представлением.
В приведенном ниже примере мы используем магнитные ластики для представления разложения числа 8. Под числовыми связями написаны слова «сделать десять» и «остальные», чтобы аккуратно обозначить части. Это похоже на обозначение наших числовых связей на «часть», «часть» и «целое» для наших начинающих студентов в нашем предыдущем блоге о сложении и вычитании в пределах 10.
Затем мы пытаемся как можно ближе связать это конкретное представление с нашим изобразительным представлением, заменяя магнитные ластики цифрами. Ученикам в нашем классе нравится переход от конкретных к графическим представлениям, которые так тесно связаны между собой, когда они могут помещать манипулятивные средства в числовые связи и передавать свои знания в письменной форме на своих рабочих листах!
Некоторые будут сомневаться в важности этого, когда ответ можно легко получить путем подсчета. Однако мы обнаружили, что детям с развитым чувством числа легче справляться с большими числами в младших классах. Это распространяется не только на сложение и вычитание, но и на умножение и деление дробей и десятичных дробей.
Однако мы обнаружили, что детям с развитым чувством числа легче справляться с большими числами в младших классах. Это распространяется не только на сложение и вычитание, но и на умножение и деление дробей и десятичных дробей.
2. Сложение путем создания эквивалентных, но более простых сумм
(i) Использование двойных чисел
По некоторым причинам дети с большей готовностью воспринимают вещи, которые встречаются в парах. Мы заметили, что для маленьких детей, которые впервые учатся складывать, концепция двойников более интуитивно понятна, чем другие. Например, учить 6 + 6 намного проще, чем 6 + 7.
Первый шаг — познакомить учащихся с двойниками. Это можно сделать, пропуская счет. то есть 6+6=12, 7+7=14, 8+8=16, 9+9 = 18, а 10+10 = 20.
Второй шаг — ввести производные факты, основанные на этих двойниках.
Например,
7 + 8 на 1 больше, чем 7 + 7,
, поэтому 7 + 8 на 1 больше, чем 14. + 6 на 1 меньше 14.
(ii) Составление десятков
Мы можем ввести производные факты, основанные на делении десятков, т. е. для чисел, близких к 10, сначала составить 10, а затем считать в обратном порядке. Например,
е. для чисел, близких к 10, сначала составить 10, а затем считать в обратном порядке. Например,
6 + 9 = 6 + 10 – 1
Профессор Джо Боалер в своей книге «При чем здесь математика?» рассказывает о важности производных ответов и о том, как беглый подход, в отличие от метода механического запоминания, позволяет учащимся развивать более осмысленные математические знания. опыт. Она также говорит о том, как это сильное чувство числа распространяется на более поздние годы, где исследования показали, что если дети могут легко идентифицировать эти эквивалентные выражения раньше, они, как правило, преуспевают в более поздние годы.
«Исследователи обнаружили, что дети в возрастной группе 8+ выше среднего рассчитывали на 9процентов случаев они использовали известные факты в 61 проценте случаев. В той же возрастной группе учащиеся с показателями ниже среднего считали все 22 % времени, считали 72 % времени, использовали известные факты 6 % времени и никогда не использовали производные факты.
Именно это отсутствие производных фактов было решающим фактором их низких достижений».
«Из своих открытий исследователи сделали два важных вывода. Одна из них заключалась в том, что малоуспевающих часто считают медленными учениками, хотя на самом деле они не учатся медленно одним и тем же вещам. Скорее, они изучают разные математики. Во-вторых, математика, которую изучают плохо успевающие, является более сложным предметом. «От профессора Джо Боулер в ее книге «При чем тут математика?».
Примечание. При вычислении 7 + 6
- Подсчитано все относится к счету от 1.
- Подсчитано относится к счету от 8,
- Известный факт относится к 7 + 7 = 14
- 8 Производное до 7 + 6 на единицу меньше, чем 7 + 7.
3. Сложение трех чисел в пределах 20
Для этого есть два случая: (i) два числа составляют десять или (ii) два числа не составляют десять.
(i) Когда два числа составляют десять,
У учащихся обычно не возникает проблем с этим, особенно когда два числа, составляющие десять, расположены рядом друг с другом. Благодаря нашим исследованиям мы знаем, что учащиеся лучше учатся, когда жесты рук вводятся в обучение в классе. Мы сделали шаг вперед и ввели жесты руками в наш конкретно-графический-абстрактный подход и обнаружили, что наши ученики могут очень хорошо применять эти новые знания.
Благодаря нашим исследованиям мы знаем, что учащиеся лучше учатся, когда жесты рук вводятся в обучение в классе. Мы сделали шаг вперед и ввели жесты руками в наш конкретно-графический-абстрактный подход и обнаружили, что наши ученики могут очень хорошо применять эти новые знания.
Например, при сложении 6 + 4 + 2 учащихся просят сделать V-образный жест пальцами под 6 и 4, метафорически группируя их. Затем им можно сказать, чтобы они нарисовали числовую связь под этими двумя числами, чтобы получилось десять. Результатом является абстрактное представление 10 + 2 = 12.
Для чисел, которые не находятся рядом друг с другом, можно использовать тот же метод, когда учащиеся делают V-точку пальцами под два числа, которые составляют десять, и нарисуйте числовую связь под этими двумя числами.
(ii) Если ни одно из чисел не дает сразу десять,
В этом случае учащиеся должны разложить одно из чисел так, чтобы один из компонентов мог составить 10 с другим числом.
Например, в 5 + 6 + 7 разложите 6 на 5 и 1.
Так как это новинка и часто проблема для первоклассников, многие учащиеся полагаются на обратный счет. По нашему опыту мы видим, что, хотя многие первоклассники могут не «поймать» с первого раза, важно прививать эту гибкость с раннего возраста, чтобы показать им, что счет — не единственный метод. Как упомянула Джо Боалер, «ученики, достигшие высоких результатов, были теми, кто понял, что числа можно гибко разбивать на части и снова собирать. Проблема неуспевающих детей заключалась просто в том, что они не научились этому».
Примечание. Есть интересная статья «От действия к абстракции: использование рук для изучения математики», опубликованная онлайн-изданием Psychological Science. Чтобы узнать больше о том, как жестикуляция может помочь в математической эквивалентности, прочитайте эту статью, опубликованную Яном Ингмайром из Чикагского университета.
C. Вычитание
C1. Вычитание в пределах 20 без перегруппировки
Подобно сложению в пределах 20, учащиеся должны быть знакомы с разрядными значениями и разложением двузначного числа на десятки и единицы. Они должны знать, что при вычитании двузначных чисел вычитаются десятки и десятки, единицы и единицы. Отличный пример приведен в книге профессора Джо Боалер «При чем тут математика?» где дети ниже среднего, когда им давали задачу 16–13, начинали с числа 16 и отсчитывали до 13 чисел (16-15-14-13-12-11-10-9).-8-7-6-5-4-3). «Когнитивная сложность этой задачи огромна, и количество ошибок огромно. Дети выше среднего не делали этого».
Они должны знать, что при вычитании двузначных чисел вычитаются десятки и десятки, единицы и единицы. Отличный пример приведен в книге профессора Джо Боалер «При чем тут математика?» где дети ниже среднего, когда им давали задачу 16–13, начинали с числа 16 и отсчитывали до 13 чисел (16-15-14-13-12-11-10-9).-8-7-6-5-4-3). «Когнитивная сложность этой задачи огромна, и количество ошибок огромно. Дети выше среднего не делали этого».
С2. Вычитание в пределах 20 с перегруппировкой
Вычитание в пределах 20 – еще одна важная тема для обсуждения на данном этапе. По нашему опыту, помимо счета, есть еще три метода, которым вычитание обычно преподается в школах.
1. Вычитание путем разложения до десяти
Это еще одно сложное понятие для некоторых детей. Например,
По нашим наблюдениям, у детей нет проблем с пониманием этой концепции, когда им предъявляются конкретные манипуляции, например с 12 штуками магнитных кубиков на белой доске, но с трудом переносят это на бумагу, т. е. не могут найти связь между конкретным и изобразительным изображением.
е. не могут найти связь между конкретным и изобразительным изображением.
Опять же, чтобы помочь учащимся перейти от конкретной визуализации к изобразительной, мы делаем конкретный пример похожим на установленную числовую связь. Это похоже на настройку бетона на изображение при добавлении десяти.
2. Вычитание путем удаления единиц из десяти
Это еще одна популярная стратегия, описанная во многих учебниках. Однако, благодаря нашему опыту в классе, мы обнаружили, что многие из наших студентов испытывают трудности с этой стратегией, что привело нас к нашей недавней записи в блоге «Вычитание в пределах 20 — стоимость рабочей памяти». Поразмыслив, мы обнаружили, что студенты обычно находят «разложение на десять» менее утомительным, и это может быть связано с меньшими требованиями к рабочей памяти.
Здесь приведен пример метода «Вычитание единиц из десяти». В этом методе, поскольку невозможно отнять 7 от 2, учащийся сначала отнимает 7 от 10. Затем учащийся прибавляет оставшиеся 3 к 2.
3. Вычитание путем понимания вычитания как проблемы неизвестного сложения
6 + ____ = 11
При решении этих типов задач мы находим полезным связать числовые связи с семейством числовых фактов. Поработав некоторое время с этими задачами на отсутствующие слагаемые, учащиеся познакомятся с семейством чисел 6+5=11, 5+6=11, 11-6=5, 11-5=6 и узнают, что
11 – 6 = 5,
Другой способ — снова использовать производные факты. Например,
6 + 6 = 12, поэтому 12 – 6 = 6
и
12 – 6 = 6, поэтому 12 – 5 = 7
Заключение
Мы надеемся, что вы найдете это обсуждение обучения «сложению и вычитание для чисел до 20” полезно. На следующей неделе мы поговорим о типичных проблемах, возникающих при обучении сложению и вычитанию чисел в пределах 100.
Подробнее об обучении сложению и вычитанию:
- Стратегии обучения сложению и вычитанию – Часть 1: Числа до 10
- Стратегии обучения сложению и вычитанию – Часть 2: Числа до 20 (этот пост)
- Стратегии обучения сложению и вычитанию – Часть 3: Числа до 100
- Стратегии обучения сложению и вычитанию.


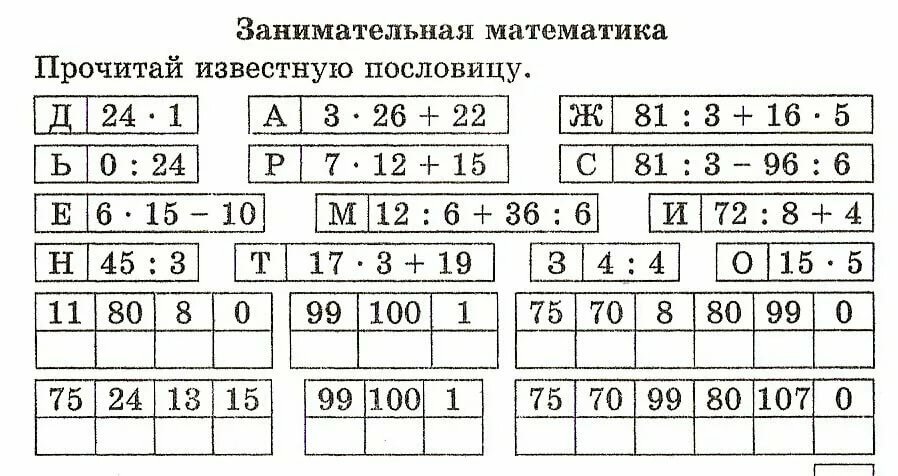

 Уменьшаемое 60, вычитаемое 40. Укажи значение разности.
Уменьшаемое 60, вычитаемое 40. Укажи значение разности. Какое число надо прибавить к числу 4, чтобы получить 96?
Какое число надо прибавить к числу 4, чтобы получить 96? 44
44 01.2014 N 8 «Об утверждении примерной формы договора об образовании по образовательным программам дошкольного образования» (Зарегистрировано в Минюсте России 27.03.2014 N 31757)
01.2014 N 8 «Об утверждении примерной формы договора об образовании по образовательным программам дошкольного образования» (Зарегистрировано в Минюсте России 27.03.2014 N 31757) 06.2015 № 874 (в редакции от 18.05.2016 № 606)
06.2015 № 874 (в редакции от 18.05.2016 № 606) 06.1999г.
06.1999г. 05.2022
05.2022 Образовательные результаты
Образовательные результаты д. для объяснения сложения в пределах 100, добавляя однозначное и двузначное число.
д. для объяснения сложения в пределах 100, добавляя однозначное и двузначное число.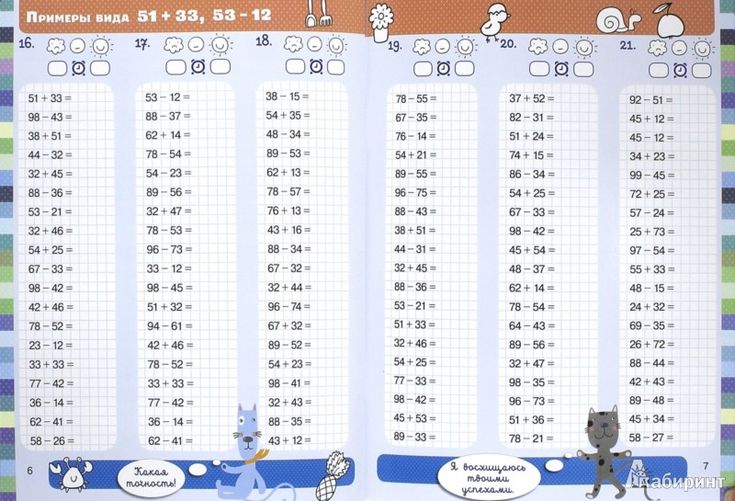

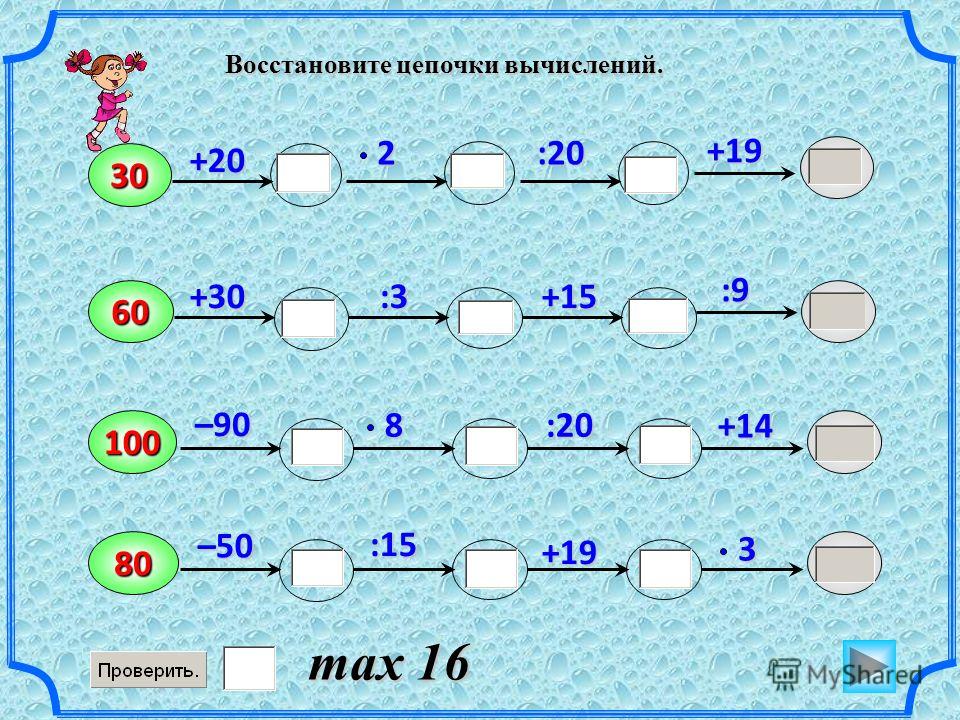 Складывайте каждую карту, которую вы подбираете, пока не дойдете до целевого числа. Если вы зашли слишком высоко, вы можете использовать свой ход, чтобы положить обратно одну из карт, которые вы взяли, лицевой стороной вниз.
Складывайте каждую карту, которую вы подбираете, пока не дойдете до целевого числа. Если вы зашли слишком высоко, вы можете использовать свой ход, чтобы положить обратно одну из карт, которые вы взяли, лицевой стороной вниз. Игра продолжается до тех пор, пока все объекты не будут удалены. Игрок с наибольшим количеством предметов в конце игры становится победителем.
Игра продолжается до тех пор, пока все объекты не будут удалены. Игрок с наибольшим количеством предметов в конце игры становится победителем. Часть 4. Числа до 1000
Часть 4. Числа до 1000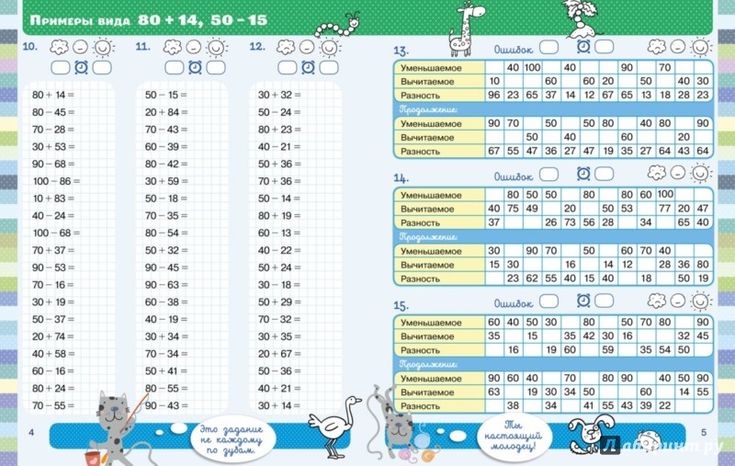 Именно это отсутствие производных фактов было решающим фактором их низких достижений».
Именно это отсутствие производных фактов было решающим фактором их низких достижений».