Умножение на 5 | Таблица умножения

    На этой странице представлены примеры, описывающие умножение на 5 и умножение числа 5, деление, некоторые способы произношения и записи, таблица умножения на 5 без ответов, в конце статьи — картинки для скачивания, с помощью которых можно распечатать часть таблицы.

Умножение на 5:
1 x 5 = 5
2 x 5 = 10
3 x 5 = 15
4 x 5 = 20
5 x 5 = 25
6 x 5 = 30
7 x 5 = 35
8 x 5 = 40
9 x 5 = 45
10 x 5 = 50

Первый вариант произношения:
1 x 5 = 5 (1 умножить на 5, равно 5)
2 x 5 = 10 (2 умножить на 5, равно 10)
3 x 5 = 15 (3 умножить на 5, равно 15)
4 x 5 = 20 (4 умножить на 5, равно 20)
5 x 5 = 25 (5 умножить на 5, равно 25)
6 x 5 = 30 (6 умножить на 5, равно 30)
7 x 5 = 35 (7 умножить на 5, равно 35)
8 x 5 = 40 (8 умножить на 5, равно 40)
9 x 5 = 45 (9 умножить на 5, равно 45)
10 x 5 = 50 (10 умножить на 5, равно 50)

Второй вариант произношения:
1 x 5 = 5 ( по 1 взять 5 раз, получится 5)

2 x 5 = 10 ( по 2 взять 5 раз, получится 10)
3 x 5 = 15 ( по 3 взять 5 раз, получится 15)
4 x 5 = 20 ( по 4 взять 5 раз, получится 20)
5 x 5 = 25 ( по 5 взять 5 раз, получится 25)
6 x 5 = 30 ( по 6 взять 5 раз, получится 30)
7 x 5 = 35 ( по 7 взять 5 раз, получится 35)
8 x 5 = 40 ( по 8 взять 5 раз, получится 40)
9 x 5 = 45 ( по 9 взять 5 раз, получится 45)
10 x 5 = 50 ( по 10 взять 5 раз, получится 50)

От перемены мест множителей значение произведения не меняется, поэтому, зная результаты умножения на 5, можно легко найти результаты умножения числа 5. В качестве знака умножения в разных источниках используют разные символы. Выше был показан пример с (x), в этот раз сделаем запись с помощью приподнятой точки ( ∙ )

Умножение числа 5:

5 ∙ 1 = 5
5 ∙ 2 = 10
5 ∙ 3 = 15
5 ∙ 4 = 20
5 ∙ 5 = 25
5 ∙ 6 = 30
5 ∙ 7 = 35
5 ∙ 8 = 40
5 ∙ 9 = 45
5 ∙ 10 = 50

Варианты произношения:
5 ∙ 1 = 5 (по 5 взять 1 раз, получится 5)
5 ∙ 2 = 10 (по 5 взять 2 раза, получится 10)
5 ∙ 3 = 15 (по 5 взять 3 раза, получится 15)
5 ∙ 4 = 20 (по 5 взять 4 раза, получится 20)
5 ∙ 5 = 25 (по 5 взять 5 раз, получится 25)
5 ∙ 6 = 30 (по 5 взять 6 раз, получится 30)
5 ∙ 7 = 35 (по 5 взять 7 раз, получится 35)
5 ∙ 8 = 40 (по 5 взять 8 раз, получится 40)
5 ∙ 9 = 45 (по 5 взять 9 раз, получится 45)
5 ∙ 10 = 50 (по 5 взять 10 раз, получится 50)

5 ∙ 1 = 5 (5 умножить на 1, равно 5)
5 ∙ 2 = 10 (5 умножить на 2, равно 10)
5 ∙ 3 = 15 (5 умножить на 3, равно 15)
5 ∙ 4 = 20 (5 умножить на 4, равно 20)
5 ∙ 5 = 25 (5 умножить на 5, равно 25)
5 ∙ 6 = 30 (5 умножить на 6, равно 30)
5 ∙ 7 = 35 (5 умножить на 7, равно 35)
5 ∙ 8 = 40 (5 умножить на 8, равно 40)
5 ∙ 9 = 45 (5 умножить на 9, равно 45)
5 ∙ 10 = 50 (5 умножить на 10, равно 50)

Деление на 5:

5 ÷ 5 = 1
10 ÷ 5 = 2

15 ÷ 5 = 3
20 ÷ 5 = 4
25 ÷ 5 = 5
30 ÷ 5 = 6
35 ÷ 5 = 7
40 ÷ 5 = 8
45 ÷ 5 = 9
50 ÷ 5 = 10

5 ÷ 5 = 1 (5 разделить на 5, равно 1)
10 ÷ 5 = 2 (10 разделить на 5, равно 2)
15 ÷ 5 = 3 (15 разделить на 5, равно 3)
20 ÷ 5 = 4 (20 разделить на 5, равно 4)
25 ÷ 5 = 5 (25 разделить на 5, равно 5)
30 ÷ 5 = 6 (30 разделить на 5, равно 6)
35 ÷ 5 = 7 (35 разделить на 5, равно 7)
40 ÷ 5 = 8 (40 разделить на 5, равно 8)
45 ÷ 5 = 9 (45 разделить на 5, равно 9)
50 ÷ 5 = 10 (50 разделить на 5, равно 10)

Картинка: 

Деление.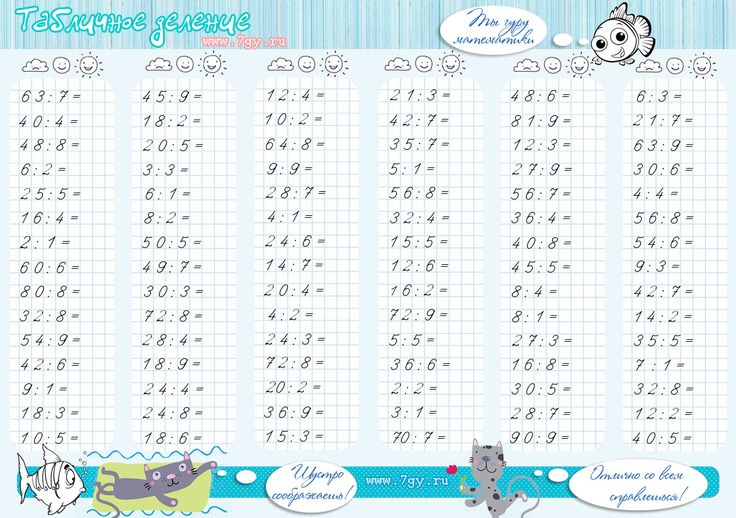 Картинка: 

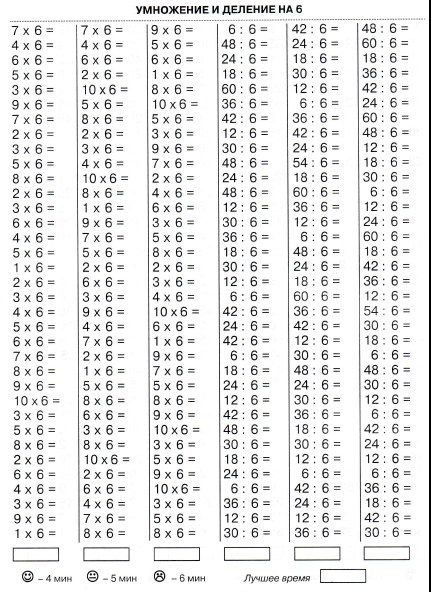
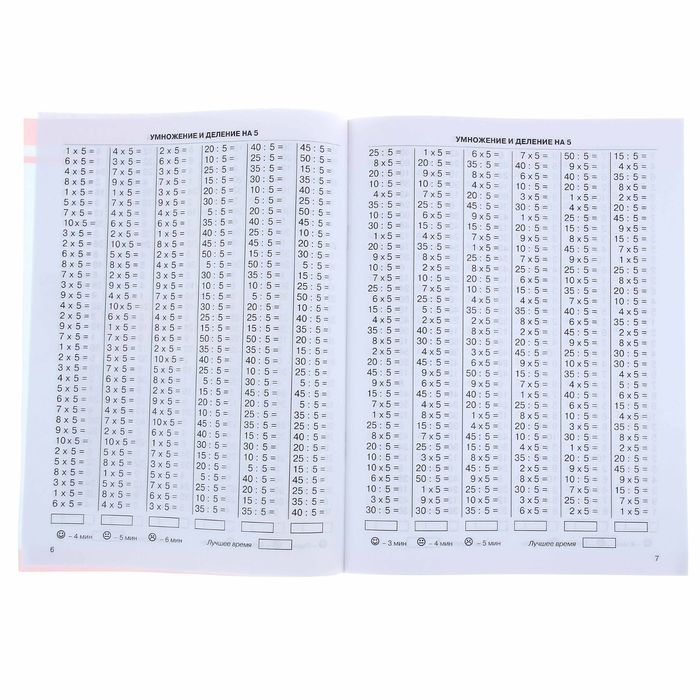
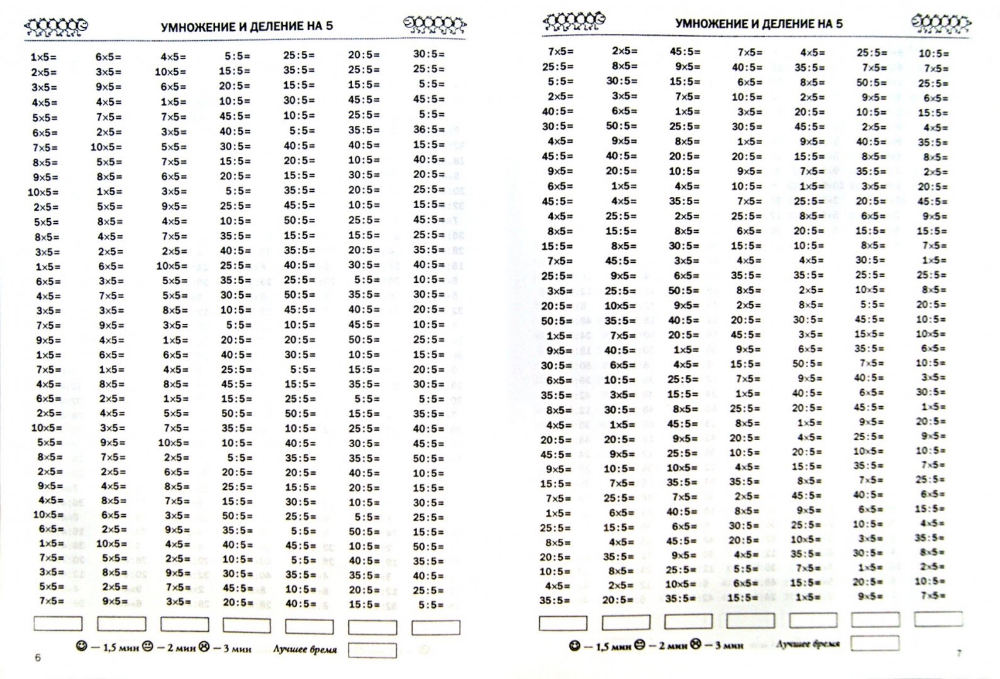
Таблица умножения и деления на 5 без ответов (по порядку и вразброс):

1 ∙ 5 =	7 ∙ 5 =	5 ÷ 5 =	30 ÷ 5 =
2 ∙ 5 =	6 ∙ 5 =	10 ÷ 5 =	25 ÷ 5 =
3 ∙ 5 =	1 ∙ 5 =	15 ÷ 5 =	35 ÷ 5 =
4 ∙ 5 =	4 ∙ 5 =	20 ÷ 5 =	10 ÷ 5 =
5 ∙ 5 =	2 ∙ 5 =	25 ÷ 5 =	15 ÷ 5 =
6 ∙ 5 =	3 ∙ 5 =	30 ÷ 5 =	20 ÷ 5 =
7 ∙ 5 =	10 ∙ 5 =	35 ÷ 5 =	50 ÷ 5 =
8 ∙ 5 =	5 ∙ 5 =	40 ÷ 5 =	40 ÷ 5 =
9 ∙ 5 =	9 ∙ 5 =	45 ÷ 5 =	45 ÷ 5 =
10 ∙ 5 =	8 ∙ 5 =	50 ÷ 5 =	5 ÷ 5 =

Способы записи таблицы умножения на 5:

x	Приподнятая точка	*	Знак не указан
1 x 5 = 5	1 ∙ 5 = 5	1 * 5 = 5	1 __ 5 = 5
2 x 5 = 10	2 ∙ 5 = 10	2 * 5 = 10	2 __ 5 = 10
3 x 5 = 15	3 ∙ 5 = 15	3 * 5 = 15	3 __ 5 = 15
4 x 5 = 20	4 ∙ 5 = 20	4 * 5 = 20	4 __ 5 = 20
5 x 5 = 25	5 ∙ 5 = 25	5 * 5 = 25	5 __ 5 = 25
6 x 5 = 30	6 ∙ 5 = 30	6 * 5 = 30	6 __ 5 = 30
7 x 5 = 35	7 ∙ 5 = 35	7 * 5 = 35	7 __ 5 = 35
8 x 5 = 40	8 ∙ 5 = 40	8 * 5 = 40	8 __ 5 = 40
9 x 5 = 45	9 ∙ 5 = 45	9 * 5 = 45	9 __ 5 = 45
10 x 5 = 50	10 ∙ 5 = 50	10 * 5 = 50	10 __ 5 = 50

Способы записи таблицы деления на 5:

/	:	÷	Знак не указан
5 / 5 = 1	5 : 5 = 1	5 ÷ 5 = 1	5 __ 5 = 1
10 / 5 = 2	10 : 5 = 2	10 ÷ 5 = 2	10 __ 5 = 2
15 / 5 = 3	15 : 5 = 3	15 ÷ 5 = 3	15 __ 5 = 3
20 / 5 = 4	20 : 5 = 4	20 ÷ 5 = 4	20 __ 5 = 4
25 / 5 = 5	25 : 5 = 5	25 ÷ 5 = 5	25 __ 5 = 5
30 / 5 = 6	30 : 5 = 6	30 ÷ 5 = 6	30 __ 5 = 6
35 / 5 = 7	35 : 5 = 7	35 ÷ 5 = 7	35 __ 5 = 7
40 / 5 = 8	40 : 5 = 8	40 ÷ 5 = 8	40 __ 5 = 8
45 / 5 = 9	45 : 5 = 9	45 ÷ 5 = 9	45 __ 5 = 9
50 / 5 = 10	50 : 5 = 10	50 ÷ 5 = 10	50 __ 5 = 10

Умножение на:

‹ Умножение на 4 Вверх Умножение на 6 ›

Умножение десятичных дробей — примеры, правила как умножать в 5 классе

Десятичные дроби — хитрый зверек, но только не для нас. В этой статье научимся умножать десятичные дроби, чтобы решать задачки на контрольной в 5 классе и старше легко и быстро.

Записывайтесь на онлайн-фестиваль для родителей SmartFest!

Ждём вас 8 октября в 13:00. Вместе с педагогами, психологами и другими экспертами в образовании и воспитании ответим на главные вопросы мам и пап.

Бесплатный урок по математике

Записаться

Понятие десятичной дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

• обыкновенный вид — ½ или a/b,

• десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

Вернемся к обыкновенным дробям позже, а сейчас обсудим десятичные дроби. Их знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,8

• 7,42

• 9,932

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Свойства десятичных дробей

Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то она равна нулю.

• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д.

• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Как записать десятичную дробь

Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.

Пример 1. Перевести обыкновенную дробь в десятичную.

Как решаем:

1. Знаменатель равен 10 — это один ноль.

2. Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.

3. В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.

Ответ:

Пример 2. Перевести в десятичную дробь.

Как решаем:

1. Знаменатель равен 1000 — это три нуля.

2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.

3. Так как в числителе только две цифры, то на пустующие места пишем нули.

4. В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.

Ответ:

Учёба без слёз (бесплатный гайд для родителей)

Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.

Как читать десятичную дробь

Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно.

Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:

Сколько цифр после запятой?	Читается, как
одна цифра — десятых;	1,3 — одна целая, три десятых;
две цифры — сотых	2,22 — две целых, двадцать две сотых;
три цифры — тысячных;	23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных;
четыре цифры — десятитысячных;	0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных;
и т.д.

Сохраняй наглядную картинку, чтобы быстрее запомнить.

Свойства умножения

С десятичными дробями можно производить те же действия, что и с любыми другими числами: складывать и вычитать, делить и умножать. В этом блоке узнаем, как умножать дроби.

Свойства умножения десятичных дробей

Переместительное свойство умножения — от перестановки мест множителей произведение не изменяется. ab = ba Сочетательное свойство умножения — чтобы умножить число на произведение двух чисел, нужно сначала умножить его на первый множитель, затем полученное произведение умножить на второй множитель. (ab)c = a(bc) Распределительное свойство умножения относительно сложения — чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить. a(b + c) = ab + ac Распределительное свойство умножения относительно вычитания — чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе. a(b — c) = ab — ac

Умножение десятичных дробей друг на друга можно упростить и просто умножить натуральные числа. Главное — правильно поставить запятую в ответе.

Если в задаче даны десятичные дроби с разными знаками — используем правило умножения отрицательных чисел. Как быстро запомнить:

«−−»	минус на минус дает плюс
«−+»	минус на плюс дает минус
«+−»	плюс на минус дает минус
«++»	плюс на плюс дает плюс

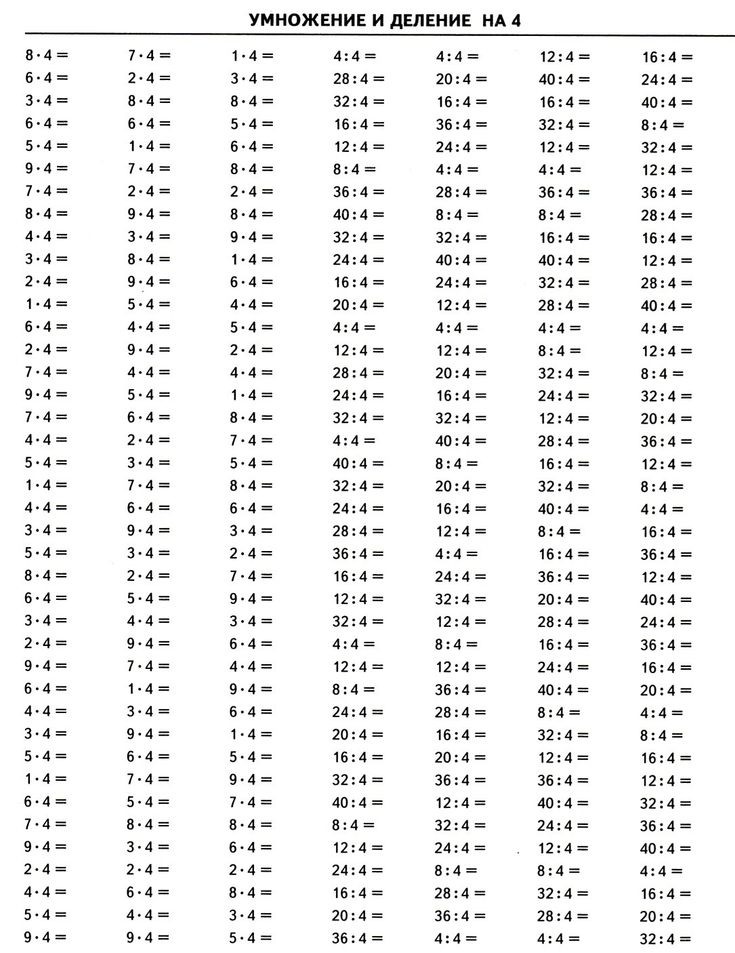
Числа с единицей и нулями (10, 100, 1000 и т. д.) называются разрядными единицами, так как цифра 1 — единственная значимая цифра в числе и от ее местоположения зависит количественное значение числа. Важно запомнить правила для умножения и деления на разрядную единицу:

• Чтобы умножить число на разрядную единицу, достаточно к числу справа дописать столько нулей, сколько их содержит разрядная единица.

• Чтобы разделить число на разрядную единицу, достаточно от числа справа отбросить столько нулей, сколько их содержит разрядная единица.

Как умножать десятичные дроби в столбик

Чтобы перемножить десятичные дроби нужно сделать три шага:

1. Записать десятичные дроби в столбик и умножить друг на друга, как обыкновенные числа.

2. Посчитать количество знаков после запятой у каждой дроби. Сложить их количество.

3. Полученное количество знаков отсчитать справа налево и поставить запятую.

Пример: умножить 3, 11 на 0,01.

Как решаем:

1. Запишем дроби в столбик и умножим их, как будто у нас нет никаких запятых:

   Получаем: 311 ∗ 001 = 311.

2. Считаем общее количество цифр после запятой у обеих дробей — в нашем примере их четыре (по две на каждую).

3. Берем число, которое получилось после умножения и отсчитываем справа налево 4 знака. Но у нас получилось всего три цифры, а не четыре. Значит добавляем перед ними один ноль и вуаля — четыре цифры после запятой готовы

Ответ: 3,11 ∗ 0,01 = 0,0311.

Примеры умножения десятичных дробей столбиком:

Как умножать десятичные дроби на натуральные числа

Умножение десятичных дробей на обычные числа происходит так же, как и умножение между десятичными дробями. Чтобы считать быстрее, умножайте их в столбик по правилам выше. А вот и примерчики!

Пример 1. Умножить десятичную дробь 2,27 на целое число 15.

Как решаем:

умножить столбиком данные числа и отделить два знака запятой.

Ответ: 15 ∗ 2,27 = 34,05.

Пример 2. Умножить 11 на 0,005.

Как решаем:

умножить столбиком данные числа и отделить три знака запятой.

Ответ: 11 ∗ 0,005 = 0,055.

Пример 3. Умножить 0,1557.. на 3.

Как решаем:

1. Округлить бесконечную дробь:

   0,1557..≈ 0,156

2. 0,156 * 3 ≈ 0,468.

Ответ: 0,1557.. ∗ 3 ≈ 0,468.

Как умножать десятичные дроби на 10, 100, 1000

Чтобы умножить десятичную дробь на 10, 100, 1000, нужно просто перенести запятую в дроби вправо на столько знаков, сколько нулей стоит во втором множителе. Лишние нули слева можно отбросить. А если цифр не хватает — дописываем нули.

Примеры:

• 1,15 ∗ 10 = 11,5;

• 22,345 ∗ 100 = 2 234,5;

• 8,99 ∗ 1 000 = 8 990;

• 0,54678 ∗ 10 000 = 5467,8;

• 0,07 ∗ 1 000 = 70;

• 0,00033 ∗ 100 = 0,033.

Как умножать десятичные дроби на 0,1, 0,01, 0,001

Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001, нужно перенести запятую в дроби влево на столько знаков, сколько нулей стоит перед единицей. Ноль целых — тоже считаем. Если цифр не хватает — просто дописываем дополнительный ноль — один или несколько — после запятой.

Примеры:

• 34,9 ∗ 0,1 = 3,49;

• 1,8 ∗ 0,1 = 0,18;

• 145,7 ∗ 0,01 = 1,457;

• 9655,1 ∗ 0,001 = 9,6551;

• 11,9 ∗ 0,0001 = 0,00119.

Как умножить десятичную дробь на обыкновенную

Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.

Пример 1. Умножить  на 0,9.

Как решаем:

1. Записать 0,9 в виде обыкновенной дроби:

2. Умножить числа по правилам

Ответ:

Пример 2.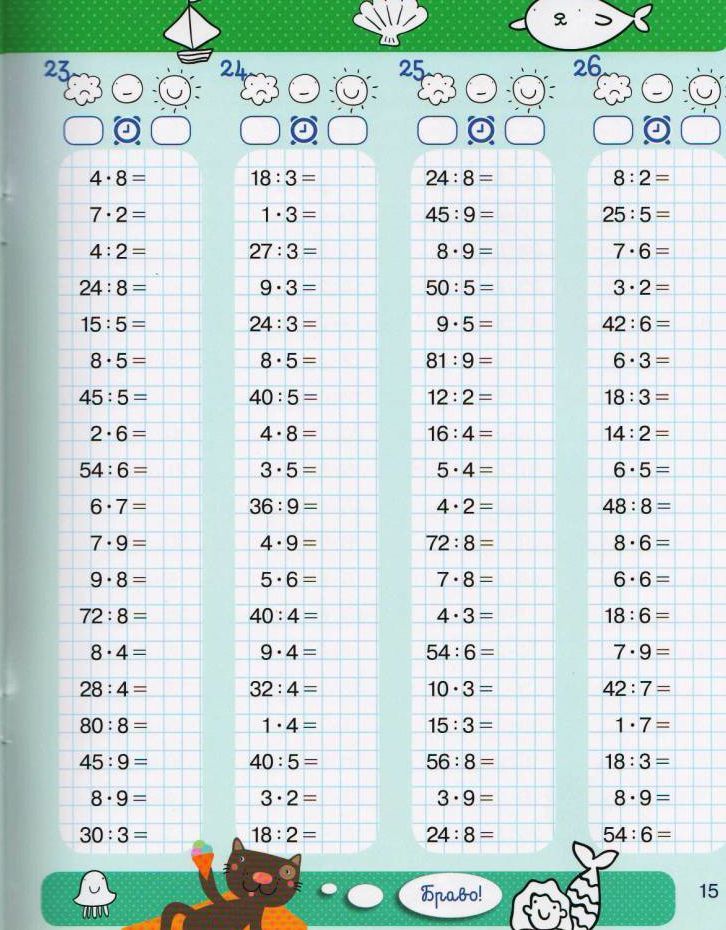 Умножить 0,18 на .

Как решаем:

1. Записать в виде десятичной дроби:

2. Произвести умножение в столбик или при помощи калькулятора:

Ответ:

 

Шпаргалки по математике родителей

Все формулы по математике под рукой

Примеры онлайн на умножение однозначных чисел

Примеры онлайн на умножение однозначных чисел

ПримерОнлайн.ru

Генератор примеров по математике 1-3 класс

При изучении таблицы умножения важно выработать навык автоматического счёта, чтобы ученик не задумывался над каждым примером, а выдавал ответ «автоматически». При этом у учителя обычно возникают проблемы с фантазией – как выбрать цифры из разных сегментов таблицы умножения. В этом поможет тренажёр — неповторяющиеся примеры на умножение позволяют сгенерировать сколько угодно неповторяющихся примеров на умножение однозначных чисел.

Онлайн примеры для закрепления таблицы умнождения позволяют вывести неповторяющийся набор примеров для устного счёта.

 



Настройка генератора примеров



Файл для печати В файле 1234567891012152025303540455060708090100 стр. Скачать: файл заданий, файл ответов

Свой формат страницы Выводить 153050100200300500 примеров Распечатать страницу

Интерактивные примеры Выводить 153050100200300500 примеров Показать страницу

Образец примеров

7 * 9

4 * 6

8 * 9

7 * 3

8 * 9

3 * 6

2 * 9

9 * 5

7 * 7

6 * 2

7 * 7

4 * 3

7 * 6

8 * 9

4 * 5

3 * 7

5 * 9

2 * 7

7 * 3

4 * 7

6 * 6

2 * 8

6 * 3

9 * 5

7 * 7

3 * 3

4 * 6

2 * 9

6 * 7

4 * 5

3 * 7

9 * 6

8 * 5

5 * 9

8 * 7

2 * 5

3 * 8

4 * 9

8 * 2

7 * 8

4 * 6

3 * 9

6 * 4

2 * 8

3 * 5

7 * 8

5 * 9

7 * 8

4 * 6

9 * 5

3 * 3

4 * 6

5 * 9

9 * 7

5 * 8

8 * 6

7 * 4

2 * 6

3 * 7

9 * 5

8 * 7

2 * 8

4 * 6

5 * 8

2 * 9

9 * 5

5 * 6

9 * 9

2 * 5

7 * 8

5 * 2

2 * 4

3 * 5

5 * 8

3 * 7

5 * 4

6 * 8

7 * 7

2 * 9

3 * 6

7 * 7

8 * 4

7 * 5

4 * 6

9 * 8

7 * 3

9 * 9

5 * 4

4 * 8

8 * 7

6 * 5

9 * 4

2 * 9

6 * 5

3 * 2

4 * 8

7 * 4

5 * 2

6 * 8

5 * 3

7 * 4

5 * 7

6 * 2

7 * 6

4 * 8

5 * 7

8 * 3

2 * 6

3 * 2

4 * 4

5 * 8

4 * 5

5 * 6

8 * 7

7 * 9

4 * 5

3 * 9

5 * 7

7 * 3

9 * 4

3 * 8

7 * 2

5 * 3

9 * 5

4 * 2

2 * 7

3 * 6

2 * 2

4 * 4

5 * 2

9 * 4

6 * 8

2 * 9

3 * 3

6 * 8

4 * 5

6 * 4

9 * 9

3 * 3

2 * 5

4 * 6

2 * 9

5 * 6

6 * 9

9 * 5

4 * 3

7 * 9

9 * 2

8 * 6

2 * 3

7 * 7

5 * 6

8 * 2

3 * 5

2 * 9

8 * 5

2 * 6

3 * 2

7 * 6

6 * 2

7 * 6

4 * 8

6 * 5

9 * 9

3 * 8

8 * 6

5 * 2

7 * 3

6 * 5

2 * 6

6 * 4

4 * 3

6 * 5

9 * 9

8 * 7

9 * 6

2 * 4

4 * 8

3 * 7

4 * 3

2 * 2

4 * 6

2 * 3

3 * 7

5 * 6

8 * 7

4 * 5

5 * 7

2 * 8

8 * 3

7 * 7

5 * 3

7 * 4

8 * 7

2 * 9

4 * 8

5 * 4

8 * 9

3 * 8

7 * 7

3 * 6

7 * 4

2 * 5

3 * 2

4 * 9

7 * 5

3 * 7

5 * 6

9 * 9

7 * 5

9 * 8

2 * 7

7 * 6

5 * 7

4 * 4

2 * 2

8 * 6

9 * 9

4 * 6

8 * 7

5 * 2

6 * 6

4 * 7

6 * 4

7 * 5

5 * 7

8 * 8

4 * 7

2 * 5

5 * 4

2 * 3

5 * 8

8 * 7

3 * 2

2 * 3

7 * 9

5 * 4

6 * 6

2 * 2

3 * 6

8 * 2

7 * 8

6 * 7

2 * 3

7 * 7

6 * 3

9 * 4

8 * 3

9 * 2

8 * 4

4 * 3

5 * 8

6 * 2

4 * 3

9 * 5

5 * 7

4 * 9

8 * 3

3 * 5

8 * 8

6 * 9

8 * 8

7 * 9

2 * 4

7 * 7

3 * 6

6 * 7

7 * 4

2 * 6

4 * 3

6 * 4

7 * 2

4 * 5

7 * 9

3 * 3

2 * 2

7 * 6

3 * 7

2 * 9

7 * 2

4 * 4

6 * 5

4 * 7

5 * 8

2 * 5

5 * 8

3 * 4

7 * 9

3 * 7

4 * 6

9 * 8

6 * 5

3 * 2

2 * 9

6 * 7

9 * 3

8 * 5

2 * 3

9 * 4

8 * 3

9 * 5

4 * 4

9 * 2

6 * 8

5 * 6

4 * 4

9 * 6

2 * 3

5 * 4

4 * 9

8 * 7

7 * 2

4 * 8

6 * 5

4 * 4

2 * 2

9 * 6

6 * 3

4 * 5

8 * 2

7 * 5

5 * 8

9 * 5

6 * 7

8 * 3

7 * 2

4 * 3

9 * 7

8 * 3

3 * 2

2 * 6

3 * 4

2 * 2

6 * 4

2 * 5

5 * 7

6 * 8

8 * 4

9 * 3

3 * 6

2 * 8

3 * 6

2 * 5

7 * 7

6 * 5

3 * 4

5 * 6

7 * 7

8 * 4

7 * 2

9 * 3

3 * 7

7 * 3

5 * 9

3 * 3

2 * 2

3 * 3

7 * 4

5 * 8

2 * 3

4 * 4

6 * 9

9 * 5

6 * 3

9 * 2

4 * 7

3 * 2

9 * 4

7 * 8

2 * 9

8 * 2

2 * 7

9 * 9

7 * 6

4 * 2

2 * 9

4 * 4

7 * 2

5 * 6

9 * 9

5 * 2

7 * 6

9 * 8

4 * 9

7 * 8

4 * 5

5 * 6

8 * 5

3 * 2

6 * 3

2 * 2

7 * 4

3 * 8

8 * 5

3 * 6

9 * 7

3 * 3

7 * 9

2 * 8

8 * 9

4 * 4

6 * 2

5 * 3

9 * 7

8 * 5

9 * 2

8 * 3

2 * 6

8 * 9

4 * 3

8 * 6

6 * 8

3 * 4

6 * 8

3 * 4

2 * 3

4 * 2

8 * 3

4 * 2

7 * 6

8 * 8

5 * 3

9 * 9

2 * 2

4 * 9

5 * 2

7 * 8

9 * 2

2 * 7

6 * 9

3 * 4

9 * 7

2 * 2

9 * 6

4 * 7

2 * 8

6 * 2

2 * 3

8 * 9

2 * 8

4 * 2

3 * 3

7 * 7

5 * 4

7 * 2

2 * 3

3 * 5

6 * 2

9 * 4

6 * 2

9 * 9

6 * 4

7 * 9

5 * 2

6 * 4

7 * 5

9 * 3

5 * 4

2 * 7

4 * 8

3 * 9

9 * 4

8 * 5

9 * 7

7 * 4

4 * 2

3 * 4

4 * 2

7 * 4

2 * 7

3 * 9

7 * 2

9 * 4

2 * 3

5 * 6

9 * 2

4 * 7

9 * 6

6 * 3

9 * 7

6 * 3

2 * 2

5 * 4

3 * 2

7 * 5

9 * 2

5 * 7

6 * 5

5 * 2

3 * 3

5 * 9

9 * 5

4 * 2

6 * 5

2 * 6

5 * 5

9 * 9

3 * 4

 

Умножение по основанию пять

Умножение по основанию пять может быть сложной задачей. Тем не менее, я постараюсь разбить информацию на этапы, чтобы ее было легко понять и освоить.

Это похоже на умножение чисел по основанию 10. Однако, поскольку мы не привыкли делать это по основанию 5, это может показаться сложным.

Запланируйте потратить некоторое время на чтение этого урока об умножении по основанию пять несколько раз.

Во-первых, узнайте разницу между значением разряда по основанию 5 и значением разряда по основанию 10.

Разницу показываю двумя числами: 48573 и 13412 ₅

Для 48573 5 стоит в разряде сотен и это означает, что их 5 сотен и это означает, что есть 4 двадцати пяти

Самое сложное понятие с умножением в основе пять состоит в том, чтобы освоить, как переносить числа.

Внимательно изучите следующие два умножения. Тот, что справа, — это умножение по основанию пять.

Пример умножения по основанию пять

8 6 4       ×    3 6    _____________

3 4 3 5       ×    2 4 5    ______________

5 3 2        8 6 4     ×    3 6   __________    5 1 8 4	3 3 2        3 4 3 5     ×    2 4 5   ___________    3 0 3 2 5
Шаг 1: 6 × 4 = 24. 24 = 10 + 10 + 4 Вам нужно нести 2 десятка. Запишите 4 вместо единиц. Перенесите 2 десятки, поставив 2 на разряде десятков (показано красным)	Шаг 1: 4 × 3 = 12. 12 = 5 + 5 + 2 Вам нужно нести 2 пятерки. Запишите 2 вместо единиц. Пронести 2 пятерки, поставив 2 на место пятерок (показано красным)
Шаг 2: 6 × 6 = 36. 36 + 2 = 38 десяти. = 100 + 100 + 100 + 8 десятков Вам нужно нести 3 сотни. Запишите 8 в разряде десятков и перенесите 3 сотни, поставив 3 в разряде сотен (показано зеленым)	Шаг 2: 4 × 4 = 16. 16 + 2 = 18 пятерок 18 пятерок = 5 пятерок + 5 пятерок + 5 пятерок + 3 пятерки = 25 + 25 + 25 + 15 + 5 + 5 + 3 пятерки Вам нужно нести 3 двадцатипятки. Запишите 3 на месте пятерок и перенесите 3 двадцатипятки, поставив 3 на месте двадцати пяти (показано зеленым цветом)
Шаг 3: 6 × 8 = 48. 48 + 3 = 51 сотня 51 сотня = 10 сот + 10 сот + 10 сот + 10 сот + 10 сот + 1 сотня = 1000 + 1000 + 1000 + 1000 + 1000 + 100 = 1000 + 1000 + 1000 + 1000 + 1000 + 1 сотня Вам нужно нести 5 тысяч. Запишите 1 в разряде сотен и перенесите 5 тысяч, поставив 5 в разряде тысяч (показано черным) Запишите 5 в разряде тысяч	Шаг 3: 4 × 3 = 12. 12 + 3 = 15 двадцать пять 15 двадцать пять = 5 двадцать пять + 5 двадцать пять + 5 двадцать пять + 0 двадцать пять = 125 + 125 + 125 + 0 = 125 + 125 + 125 + 0 двадцать пять Вам нужно нести 3 сто двадцать пять. Запишите 0 в разряде двадцать пять и перенесите 3 сто двадцать пять, поставив 3 в разряде сто двадцать пять (показано черным) Запишите 3 в разряде сто двадцать пять. Обратите внимание снова на 0 в разряде двадцати пяти.

2 1 1            8 6 4            ×  3 0   ________________    2 5 9 2 0	1 1 1             3 4 3 5              × 2 0 5    _______________     1 2 4 1 0 2 5
Шаг 4: 3 × 4 = 12 десятков. 12 десятков = 10 десятков + 2 десятка = 100 + 2 десятка Перенесите 1 сотню, поставив 1 в разряде сотен (показано красным) Запишите 2 в разряде десятков. Поскольку на месте единиц ничего нет, просто поставьте 0.	Шаг 4: 2 × 3 = 6 пятерок. 6 пятерок = 5 пятерок + 1 пятерка = 25 + 1 пятерка Перенесите 1 двадцать пять, поставив 1 на место двадцати пяти (показано красным) Запишите 1 на место пятерок. Поскольку на месте единиц ничего нет, просто поставьте 0.
Шаг 5: 3 × 6 = 18 сотен. 18 сотен + 1 сотня = 19 сотен 19 сотен = 10 сотен + 9 сотен = 1000 + 9 сотен Запишите 9 в разряде сотен и перенесите 1 тысячу, поставив 1 в разряде тысяч (показано зеленым цветом)	Шаг 5: 2 × 4 = 8 двадцать пять. 8 двадцати пяти + 1 двадцать пять = 9 двадцати пяти 9 двадцати пяти = 5 двадцати пяти + 4 двадцати пяти = 125 + 4 двадцати пяти Запишите 4 в двадцать пятерки и перенесите 1 сто двадцать пять, поставив 1 на сто двадцать пятом месте (показано зеленым)
Шаг 6: 3 × 8 = 24 тысячи. 24 тысячи + 1 тысяча = 25 тысяч. 25 тысяч = 10 тысяч + 10 тысяч + 5 тысяч. разряд десяти тысяч (показан черным цветом) Опустите двойку в разряд десяти тысяч	Шаг 6: 2 × 3 = 6 сто двадцать пять. 6 сто двадцать пять + 1 сто двадцать пять = 7 сто двадцать пять 7 сто двадцать пять = 5 сто двадцать пять + 2 сто двадцать пять = 625 + 2 сто двадцать пять Запишите 2 на месте сто двадцать пять и перенесите 1 шестьсот двадцать пять, поставив 1 на шестьсот двадцать пятом месте (показано черным цветом)

Просто добавьте сейчас. Возможно, вам придется повторить сложение по основанию пять еще до того, как вы начнете этот урок об умножении по основанию пять.

Сложение результатов по основанию десяти.

  1 1 1
       5 1 8 4
   2 5 9 2 0
  __________________
   3 1 1 0 4

Сложение результатов по основанию пять.

  1
       3 0 3 2
   1 2 4 1 0
  ______________
   2 0 4 4 2

Опять же, довольно сложно выполнить умножение по основанию пять. Я рекомендую вам не торопиться при чтении этого урока. Не сдавайся!

1. Задачи на диаграмму Венна

   5 октября, 22 10:58

   Эти словесные задачи с диаграммами Венна покажут вам, как использовать диаграммы Венна для решения задач, связанных со счетом.

   Подробнее

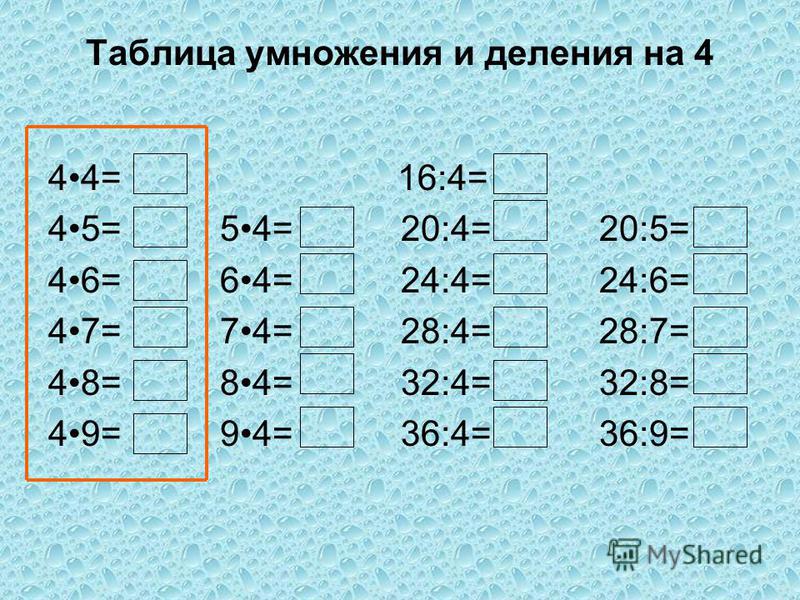
Таблицы умножения 4-х и 5-значных чисел

Как умножать 4- и 5-значные значения: Пример №1: Найдите произведение 3769 и 2. Перегруппировка чисел в четыре шага. Во-первых, поместите числа в таблицу значений разряда. Шаг № 1: Умножьте единицы — 2 × 9 (единицы) = 18 (единицы). Таким образом, перегруппируйте 18 (единиц) = 1 (десятки) + 8 (единиц). Шаг № 2: Умножьте десятки. 2 (десятки) × 6 (десятки) = 12 (десятки). 12 (десятков) + перенесенная 1 (десятки) = 13 (десятки). Перегруппировка 13 (десятков) = 1 сотня + 3 (десятка). Шаг № 3: Умножьте сотни. 2 ×7=14 (сотни). Итак, 14 (сотни) + перенесенная 1 (сотня) = 15 (тысячи).

Таким образом, перегруппируйте 15 (сотни) = 1 (тысячи) + 5 (сотни). Шаг № 4: Умножьте тысячи. 2 (тысячи) × 2 (тысячи) = 6 (тысячи). Теперь 6 (тысяч) + перенесенная 1 (тысячи) = 7 (тысячи). Таким образом, 3769× 2 = 7 538 (произведение) Пример № 2: Найдите произведение 34 654 и 3. Поместите числа в таблицы стоимостных значений. Умножьте 4 × 3 = 12. Запишите 2 в один столбец и перенесите 1 в столбцы десятков. Затем умножьте десятки 5 × 3 = 15 и 1 + 15 = 16. Таким образом, запишите 6 в столбце десятков и перенесите 1 в столбец сотен. Далее, 6 × 3 = 18 и 18 + 1 = 19. Таким образом, запишите 9 в столбце сотен и перенесите 1 в столбце тысяч. Далее, 4 × 3 = 12 и 12 + 1 = 13. Таким образом, напишите 3 в столбце тысяч и перенесите в столбец десяти тысяч. Наконец, 3 × 3 = 9и 9 + 1 = 10. Таким образом, запишите 0 в столбце тысяч и 1 в столбце разрядов. Таким образом, продукт = 34 654 × 3 = 1,03 962

При работе с очень большими числами запятые и, в частности, внимание к запятым — это огромная разница. Я часто предпочитаю писать числа намного больше, когда я умножаю и храню значения в столбцах. Это делает его ясным и легким для просмотра. Быстрый трюк, который вы можете сделать при работе с двумя большими четными числами, — это разделить первое число пополам и удвоить второе число. Это облегчает работу и действительно работает. Эти рабочие листы объясняют, как выполнять умножение, используя четырех- и пятизначные числа. Работа с большими числами потребует от вас пространства для письма, чтобы у вас было место для заметок.

Получите бесплатные рабочие листы в свой почтовый ящик!

---

Нажмите кнопки, чтобы распечатать каждый рабочий лист и ключ ответа.

1. Начните с произведения 3 из-под разряда. 2. Возьми произведение 1 из-под разряда десятков. Поставьте 0 в колонке единиц. В примере показан X. 3. Произведение 2 возьми из-под разряда сотен. Поставьте 0 в столбце единиц и десятков. В примере показан ХХ. 4. Возьмите произведение 1 из разряда тысяч.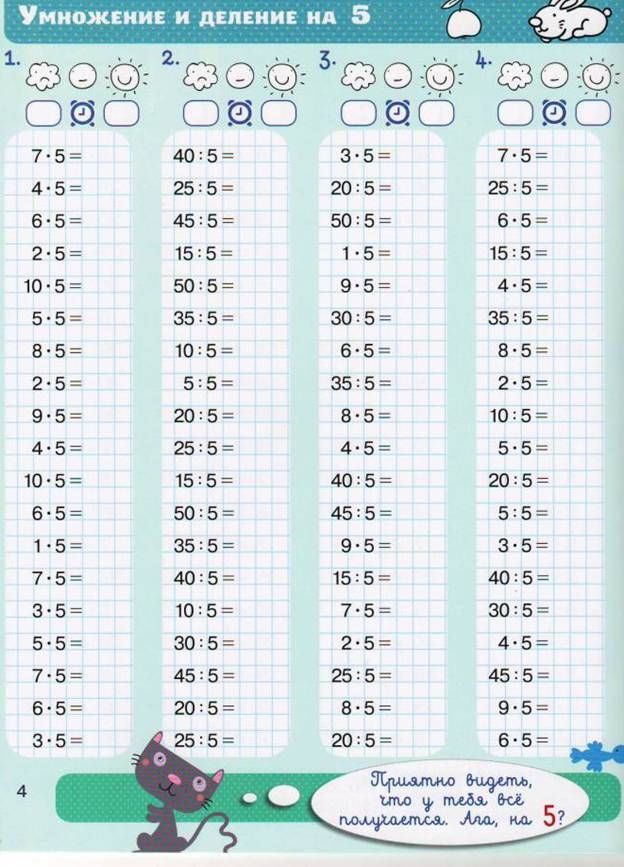 Поставьте 0 в столбце единиц, десятков и сотен. В примере показано XXX. 5. Добавьте все эти продукты. 6. Требуемый продукт = 41547676.

Учащиеся найдут произведение четырех- и пятизначных чисел на четырехзначные. Дано десять задач.

Этот практический лист имеет хороший жирный шрифт для вашей работы. Дано десять задач.

Концепция умножения 12421 и 12131 изучена и полностью описана для вас. 1. Начать с произведения 1 из-под единиц место. 2. Возьми произведение 3 из-под разряда десятков. Поставьте 0 в колонке единиц. В примере показан X. 3. Возьмите произведение 1 из-под разряда сотен. Поставьте 0 в столбце единиц и десятков. В примере показан ХХ. 4. Возьмите произведение 2 из-под тысячи место. Поставьте 0 в единицах, десятках и сотнях столбец. В примере показано XXX. 5. Возьмите произведение 1 из-под десяти тысяч место. Поставьте 0 в единицах, десятках, сотнях и тысяч столбец. В примере показано XXX. 6. Добавьте все эти продукты. 7. Требуемый продукт = 162 810 151

Учащиеся продемонстрируют свою способность решать подобные задачи.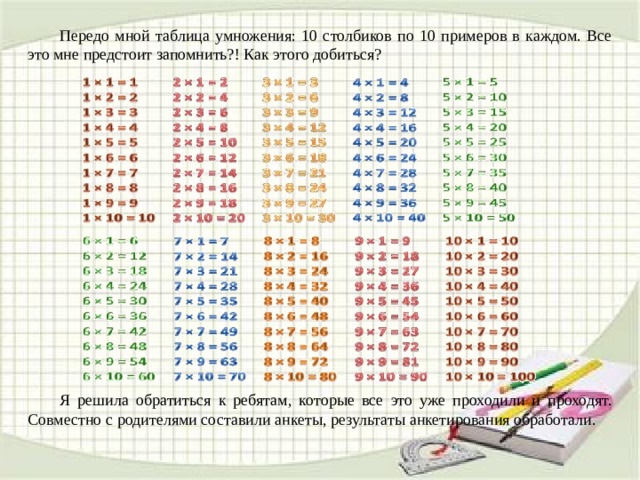 Дано десять задач.

Учащиеся будут практиковаться в умножении четырех- и пятизначных чисел на четырехзначные числа. Предлагаются три задачи, а также место, где учащиеся могут скопировать правильный ответ, когда он будет дан.

Полное пошаговое руководство по нахождению произведения: 54623 и 19356. Шаг 1: Умножьте цифру в разряде единиц (6) на 54632. Шаг 2: Добавьте «x» вместо единиц. Умножьте цифра в разряде десятков (5) с 54632. Шаг 3: Добавьте «x» в разряде единиц и десятков. Умножить цифра в разряде сотен (3) с 54632. Шаг 4: Добавьте «x» к единицам, десяткам и сотням. место. Умножьте цифру на тысячи место (9) с 54632. Шаг 5: Добавьте «x» к единицам, десяткам, сотням тысяч место. Умножьте цифру на разряд десяти тысяч (1) с 54632.

Учащиеся повторят все концепции и навыки, связанные с этими формами умножения. Решается примерная задача и предлагаются две практические задачи.

Учащиеся выполнят серию вычислений по умножению четырех- и пятизначных чисел. Дано десять задач.

Обязательно выровняйте значения мест, чтобы вы могли отслеживать, куда это идет. Дано десять задач.

Используйте этот рабочий лист как еще один набор упражнений для этого навыка. Предлагается восемь задач.

Хороший способ повторить или разобрать концепцию умножения пятизначных чисел. Предлагаются три задачи.

Задачи на умножение — Математика с мамой

Опубликовано от Математика с мамой

Задачи на умножение

ExampleVideoQuestionsLesson

Share to Google Classroom

ExampleVideoQuestionsLesson

Отправить в Google Classroom

• Есть 3 стола и за каждым столом 6 детей.
• Дети в равных группах по 6 человек.
• Есть 3 группы.
• У нас есть 3 лота по 6, которые мы можем записать как умножение.
• 3 × 6 = 18, значит, у нас 18 детей.
• Мы умножили количество групп на количество в каждой группе, чтобы найти общее количество.

Когда у нас есть равные группы с одинаковым числом, мы умножаем, чтобы найти общее количество.

• В каждой коробке по 6 яиц, а у меня 5 коробок.
• У меня 5 партий по 6 яиц.
• Когда у нас одинаковое количество в каждой группе, мы имеем умножение.
• Мы умножаем количество групп на количество в каждой группе, чтобы найти общее количество.
• У нас есть 5 групп по 6 и 5 × 6 = 30.
• Всего 30 яиц.

Как определить проблемы с умножением слов

Когда у нас есть равные группы одинакового количества, мы можем использовать умножение, чтобы найти общее количество.

Количество групп, умноженное на сумму в каждой группе, дает нам общее количество.

Лучший способ определить проблему с умножением слов — полностью прочитать вопрос и попытаться понять контекст.

Если у нас есть несколько групп с одинаковым количеством элементов, и нам нужно общее количество, то у нас есть проблема умножения.

Ключевые слова могут помочь определить умножение. Некоторые ключевые слова умножения:

• Партии
• Группы
• Каждый
• Всего
• Всего
• Всего

Однако эти ключевые слова являются лишь ключом к умножению, и мы всегда должны проверять контекст вопроса. Например, такие слова, как «в целом» и «во всем», могут вместо этого указывать на сложение.

Простые задачи на умножение слов

Чтобы решить задачи на умножение слов, выполните следующие действия:

1. Определите числа в вопросе.
2. Определите, какое из этих чисел говорит нам, сколько их в каждой группе.
3. Определите, какое из этих чисел говорит нам о количестве групп.
4. Умножьте эти два числа, используя таблицу умножения или длинное умножение.

В этих примерах мы рассмотрим простые задачи на умножение слов, в которых нет большого абзаца текста, а числа для умножения будут меньше 12.

В этом вопросе «Есть 3 стола и 6 детей на 9».0070 на каждую таблицу ». Нас спрашивают: «Сколько всего детей?»

У нас по 6 детей за каждым столом, поэтому в каждой группе по 6 человек.

У нас 3 стола, поэтому 3 группы детей.

Нас просят об итогах. Чтобы найти сумму, мы умножаем количество групп на сумму в каждой группе.

У нас есть 3 группы по 6 человек или 3 партии по 6 детей.

Слово «много» можно заменить знаком умножения.

3 × 6 = 18, значит, всего 18 детей.

Пока у нас одинаковое число в каждой группе, мы можем умножить, чтобы увидеть, сколько их всего. У нас было по 6 детей на каждом столе.

Слова каждое и в сумме вместе в этом вопросе могли бы дать нам ключ к тому, что у нас могло быть умножение.

При обучении задачам на умножение очень важно понимать контекст. Для этого мы пытаемся представить, что на самом деле происходит в реальной жизни.

Предложите детям нарисовать ситуацию или смоделировать ее с помощью кубиков или фишек.

В этих примерах мы нарисовали ситуацию, чтобы помочь визуализировать то, что происходит.

В следующем примере: «В коробке 6 яиц. У меня 5 коробок. Сколько яиц в числе всего ?»

В каждой группе по 6 яиц.

У нас есть 5 коробок, поэтому 5 лотов по 6.

У нас одинаковое количество элементов в каждой группе, поэтому, чтобы найти общее количество, мы умножаем количество групп на количество элементов в каждой группе.

У нас есть 5 коробок по 6 или 5 партий по 6 яиц.

5 × 6 = 30, значит, всего в 5 коробках 30 яиц.

Мы могли бы умножить в этой словесной задаче, потому что в каждой коробке было одинаковое количество яиц.

Опять же, при объяснении этих задач на умножение слов полезно нарисовать или смоделировать ситуацию, если ее трудно осмыслить.

Здесь вместо того, чтобы рисовать коробки для яиц, вы можете нарисовать круг, обозначающий каждое яйцо, или использовать 5 стопок по 6 жетонов.

В этом примере: «В мешках 10 ягод, а всего 6 мешков.