Умножение на 5 | Таблица умножения

    На этой странице представлены примеры, описывающие умножение на 5 и умножение числа 5, деление, некоторые способы произношения и записи, таблица умножения на 5 без ответов, в конце статьи — картинки для скачивания, с помощью которых можно распечатать часть таблицы.

Умножение на 5:
1 x 5 = 5
2 x 5 = 10
3 x 5 = 15
4 x 5 = 20
5 x 5 = 25
6 x 5 = 30
7 x 5 = 35
8 x 5 = 40
9 x 5 = 45
10 x 5 = 50

Первый вариант произношения:
1 x 5 = 5 (1 умножить на 5, равно 5)
2 x 5 = 10 (2 умножить на 5, равно 10)
3 x 5 = 15 (3 умножить на 5, равно 15)
4 x 5 = 20 (4 умножить на 5, равно 20)
5 x 5 = 25 (5 умножить на 5, равно 25)
6 x 5 = 30 (6 умножить на 5, равно 30)
7 x 5 = 35 (7 умножить на 5, равно 35)
8 x 5 = 40 (8 умножить на 5, равно 40)
9 x 5 = 45 (9 умножить на 5, равно 45)
10 x 5 = 50 (10 умножить на 5, равно 50)

Второй вариант произношения:
1 x 5 = 5 ( по 1 взять 5 раз, получится 5)

2 x 5 = 10 ( по 2 взять 5 раз, получится 10)
3 x 5 = 15 ( по 3 взять 5 раз, получится 15)
4 x 5 = 20 ( по 4 взять 5 раз, получится 20)
5 x 5 = 25 ( по 5 взять 5 раз, получится 25)
6 x 5 = 30 ( по 6 взять 5 раз, получится 30)
7 x 5 = 35 ( по 7 взять 5 раз, получится 35)
8 x 5 = 40 ( по 8 взять 5 раз, получится 40)
9 x 5 = 45 ( по 9 взять 5 раз, получится 45)
10 x 5 = 50 ( по 10 взять 5 раз, получится 50)

От перемены мест множителей значение произведения не меняется, поэтому, зная результаты умножения на 5, можно легко найти результаты умножения числа 5. В качестве знака умножения в разных источниках используют разные символы. Выше был показан пример с (x), в этот раз сделаем запись с помощью приподнятой точки ( ∙ )

Умножение числа 5:

5 ∙ 1 = 5
5 ∙ 2 = 10
5 ∙ 3 = 15
5 ∙ 4 = 20
5 ∙ 5 = 25
5 ∙ 6 = 30
5 ∙ 7 = 35
5 ∙ 8 = 40
5 ∙ 9 = 45
5 ∙ 10 = 50

Варианты произношения:
5 ∙ 1 = 5 (по 5 взять 1 раз, получится 5)
5 ∙ 2 = 10 (по 5 взять 2 раза, получится 10)
5 ∙ 3 = 15 (по 5 взять 3 раза, получится 15)
5 ∙ 4 = 20 (по 5 взять 4 раза, получится 20)
5 ∙ 5 = 25 (по 5 взять 5 раз, получится 25)
5 ∙ 6 = 30 (по 5 взять 6 раз, получится 30)
5 ∙ 7 = 35 (по 5 взять 7 раз, получится 35)
5 ∙ 8 = 40 (по 5 взять 8 раз, получится 40)
5 ∙ 9 = 45 (по 5 взять 9 раз, получится 45)
5 ∙ 10 = 50 (по 5 взять 10 раз, получится 50)

5 ∙ 1 = 5 (5 умножить на 1, равно 5)
5 ∙ 2 = 10 (5 умножить на 2, равно 10)
5 ∙ 3 = 15 (5 умножить на 3, равно 15)
5 ∙ 4 = 20 (5 умножить на 4, равно 20)
5 ∙ 5 = 25 (5 умножить на 5, равно 25)
5 ∙ 6 = 30 (5 умножить на 6, равно 30)
5 ∙ 7 = 35 (5 умножить на 7, равно 35)
5 ∙ 8 = 40 (5 умножить на 8, равно 40)
5 ∙ 9 = 45 (5 умножить на 9, равно 45)
5 ∙ 10 = 50 (5 умножить на 10, равно 50)

Деление на 5:

5 ÷ 5 = 1
10 ÷ 5 = 2

15 ÷ 5 = 3
20 ÷ 5 = 4
25 ÷ 5 = 5
30 ÷ 5 = 6
35 ÷ 5 = 7
40 ÷ 5 = 8
45 ÷ 5 = 9
50 ÷ 5 = 10

5 ÷ 5 = 1 (5 разделить на 5, равно 1)
10 ÷ 5 = 2 (10 разделить на 5, равно 2)
15 ÷ 5 = 3 (15 разделить на 5, равно 3)
20 ÷ 5 = 4 (20 разделить на 5, равно 4)
25 ÷ 5 = 5 (25 разделить на 5, равно 5)
30 ÷ 5 = 6 (30 разделить на 5, равно 6)
35 ÷ 5 = 7 (35 разделить на 5, равно 7)
40 ÷ 5 = 8 (40 разделить на 5, равно 8)
45 ÷ 5 = 9 (45 разделить на 5, равно 9)
50 ÷ 5 = 10 (50 разделить на 5, равно 10)

Картинка: 

Деление. Картинка: 

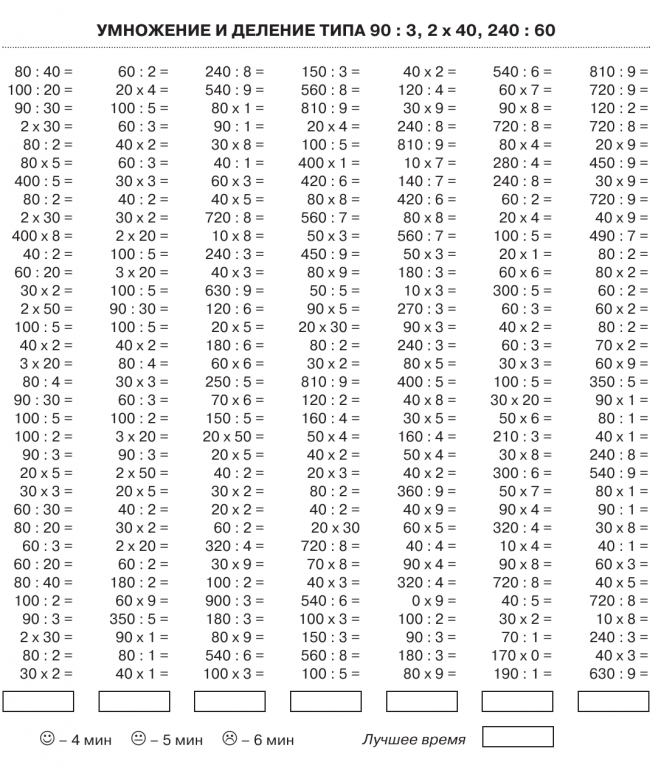
Таблица умножения и деления на 5 без ответов (по порядку и вразброс):

1 ∙ 5 =	7 ∙ 5 =	5 ÷ 5 =	30 ÷ 5 =
2 ∙ 5 =	6 ∙ 5 =	10 ÷ 5 =	25 ÷ 5 =
3 ∙ 5 =	1 ∙ 5 =	15 ÷ 5 =	35 ÷ 5 =
4 ∙ 5 =	4 ∙ 5 =	20 ÷ 5 =	10 ÷ 5 =
5 ∙ 5 =	2 ∙ 5 =	25 ÷ 5 =	15 ÷ 5 =
6 ∙ 5 =	3 ∙ 5 =	30 ÷ 5 =	20 ÷ 5 =
7 ∙ 5 =	10 ∙ 5 =	35 ÷ 5 =	50 ÷ 5 =
8 ∙ 5 =	5 ∙ 5 =	40 ÷ 5 =	40 ÷ 5 =
9 ∙ 5 =	9 ∙ 5 =	45 ÷ 5 =	45 ÷ 5 =
10 ∙ 5 =	8 ∙ 5 =	50 ÷ 5 =	5 ÷ 5 =

Способы записи таблицы умножения на 5:

x	Приподнятая точка	*	Знак не указан
1 x 5 = 5	1 ∙ 5 = 5	1 * 5 = 5	1 __ 5 = 5
2 x 5 = 10	2 ∙ 5 = 10	2 * 5 = 10	2 __ 5 = 10
3 x 5 = 15	3 ∙ 5 = 15	3 * 5 = 15	3 __ 5 = 15
4 x 5 = 20	4 ∙ 5 = 20	4 * 5 = 20	4 __ 5 = 20
5 x 5 = 25	5 ∙ 5 = 25	5 * 5 = 25	5 __ 5 = 25
6 x 5 = 30	6 ∙ 5 = 30	6 * 5 = 30	6 __ 5 = 30
7 x 5 = 35	7 ∙ 5 = 35	7 * 5 = 35	7 __ 5 = 35
8 x 5 = 40	8 ∙ 5 = 40	8 * 5 = 40	8 __ 5 = 40
9 x 5 = 45	9 ∙ 5 = 45	9 * 5 = 45	9 __ 5 = 45
10 x 5 = 50	10 ∙ 5 = 50	10 * 5 = 50	10 __ 5 = 50

Способы записи таблицы деления на 5:

/	:	÷	Знак не указан
5 / 5 = 1	5 : 5 = 1	5 ÷ 5 = 1	5 __ 5 = 1
10 / 5 = 2	10 : 5 = 2	10 ÷ 5 = 2	10 __ 5 = 2
15 / 5 = 3	15 : 5 = 3	15 ÷ 5 = 3	15 __ 5 = 3
20 / 5 = 4	20 : 5 = 4	20 ÷ 5 = 4	20 __ 5 = 4
25 / 5 = 5	25 : 5 = 5	25 ÷ 5 = 5	25 __ 5 = 5
30 / 5 = 6	30 : 5 = 6	30 ÷ 5 = 6	30 __ 5 = 6
35 / 5 = 7	35 : 5 = 7	35 ÷ 5 = 7	35 __ 5 = 7
40 / 5 = 8	40 : 5 = 8	40 ÷ 5 = 8	40 __ 5 = 8
45 / 5 = 9	45 : 5 = 9	45 ÷ 5 = 9	45 __ 5 = 9
50 / 5 = 10	50 : 5 = 10	50 ÷ 5 = 10	50 __ 5 = 10

Умножение на:

‹ Умножение на 4 Вверх Умножение на 6 ›

Умножение на 2,5.

Умножение дробей на целое число.

• Альфашкола
• Статьи
• Как быстро умножить число на 2,5

Для того чтобы быстро умножить на \(2,5\) надо разложить число в виде суммы \(2\) и \(0,5\). Существует правило быстрого умножения на \(2,5\):

 

Пример 1.  Умножьте \(16\) на \(2,5\).

Решение: \(16*2,5=16*2+\frac{16}{2}=32+8=40\)

Ответ: \(40\).

---

Пример 2.  Умножьте \(\frac{3}{5}\) на \(2,5\).

Решение: \(\frac{3}{5}*2,5=\frac{3*2}{5}+\frac{3}{5*2}=\frac{6}{5}+\frac{3}{10}=\frac{12}{10}+\frac{3}{10}=\frac{15}{10}=1,5\)

Ответ: \(1,5\).

---

Пример 3.  Умножьте \(52\) на \(2,5\).

Решение: \(52*2,5=52*2+\frac{52}{2}=104+26=130\)

Ответ: \(130\).

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Любовь Сергеевна Орлова

Репетитор по математике

Стаж (лет)

Образование:

Армавирский государственный педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Евгений Борисович Царенков

Репетитор по математике

Стаж (лет)

Образование:

Брестский государственный университет им. А.С. Пушкина

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Вадим Вадимович Козлов

Репетитор по математике

Стаж (лет)

Образование:

Брянский государственный технический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Репетитор по алгебре
• Подготовка к олимпиадам по химии
• Репетитор для подготовки к ЕГЭ по физике
• Подготовка к олимпиадам по физике
• Репетитор для подготовки к сочинению ЕГЭ по русскому
• Репетитор по английскому языку для подготовки к ОГЭ
• Подготовка к олимпиадам по английскому языку
• Репетитор для подготовки к ОГЭ по истории
• Репетитор для подготовки к ВПР по английскому языку
• Репетитор по биологии для подготовки к ЕГЭ

Похожие статьи

• Хорда. Свойства хорды
• Объем куба
• Площадь сектора окружности
• Как перевести граммы в килограммы?
• Как записать комплексное число в алгебраической и тригонометрической форме
• Как решать задание №21 из ОГЭ по математике
• Учимся решать задачи с прикладным содержанием
• Переход в другую школу: как помочь ребенку справиться со стрессом и влиться в коллектив

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Умножение по основанию пять

Умножение по основанию пять может быть сложной задачей. Тем не менее, я постараюсь разбить информацию на этапы, чтобы ее было легко понять и освоить.

Это похоже на умножение чисел по основанию 10. Однако, поскольку мы не привыкли делать это по основанию 5, это может показаться сложным.

Запланируйте потратить некоторое время на чтение этого урока об умножении по основанию пять несколько раз.

Во-первых, узнайте разницу между значением разряда по основанию 5 и значением разряда по основанию 10.

Разницу показываю двумя числами: 48573 и 13412 ₅

Для 48573 5 стоит в разряде сотен и это означает, что их 5 сотен и это означает, что есть 4 двадцати пяти

Самое сложное понятие с умножением в основе пять состоит в том, чтобы освоить, как переносить числа.

Внимательно изучите следующие два умножения. Тот, что справа, — это умножение по основанию пять.

Пример умножения по основанию пять

8 6 4       ×    3 6    _____________

3 4 3 5       ×    2 4 5    ______________

5 3 2        8 6 4     ×    3 6   __________    5 1 8 4	3 3 2        3 4 3 5     ×    2 4 5   ___________    3 0 3 2 5
Шаг 1: 6 × 4 = 24. 24 = 10 + 10 + 4 Вам нужно нести 2 десятка. Запишите 4 вместо единиц. Перенесите 2 десятки, поставив 2 на разряде десятков (показано красным)	Шаг 1: 4 × 3 = 12. 12 = 5 + 5 + 2 Вам нужно нести 2 пятерки. Запишите 2 вместо единиц. Пронести 2 пятерки, поставив 2 на место пятерок (показано красным)
Шаг 2: 6 × 6 = 36. 36 + 2 = 38 TENS 38 TENS = 10 TENS + 10 TENS + 10 TENS + 8 TENS = 100 + 100 + 100 + = 100 + 100 + 100 + 8 десятков Вам нужно нести 3 сотни. Запишите 8 в разряде десятков и перенесите 3 сотни, поставив 3 в разряде сотен (показано зеленым)	Шаг 2: 4 × 4 = 16. 16 + 2 = 18 пятерок 18 пятерок = 5 пятерок + 5 пятерок + 5 пятерок + 3 пятерки = 25 + 25 + 25 + 15 + 5 + 5 + 3 пятерки Вам нужно нести 3 двадцатипятки. Запишите 3 на месте пятерок и перенесите 3 двадцатипятки, поставив 3 на месте двадцати пяти (показано зеленым цветом)
Шаг 3: 6 × 8 = 48. 48 + 3 = 51 сотня 51 сотня = 10 сот + 10 сот + 10 сот + 10 сот + 10 сот + 1 сотня = 1000 + 1000 + 1000 + 1000 + 1000 + 100 = 1000 + 1000 + 1000 + 1000 + 1000 + 1 сотня Вам нужно нести 5 тысяч. Запишите 1 в разряде сотен и перенесите 5 тысяч, поставив 5 в разряде тысяч (показано черным) Запишите 5 в разряде тысяч	Шаг 3: 4 × 3 = 12. 12 + 3 = 15 двадцать пять 15 двадцать пять = 5 двадцать пять + 5 двадцать пять + 5 двадцать пять + 0 двадцать пять = 125 + 125 + 125 + 0 = 125 + 125 + 125 + 0 двадцать пять Вам нужно нести 3 сто двадцать пять. Запишите 0 в разряде двадцать пять и перенесите 3 сто двадцать пять, поставив 3 в разряде сто двадцать пять (показано черным) Запишите 3 в разряде сто двадцать пять. Обратите внимание снова на 0 в разряде двадцати пяти.

2 1 1            8 6 4            ×  3 0   ________________    2 5 9 2 0	1 1 1             3 4 3 5              × 2 0 5    _______________     1 2 4 1 0 2 5
Шаг 4: 3 × 4 = 12 десятков. 12 десятков = 10 десятков + 2 десятка = 100 + 2 десятка Перенесите 1 сотню, поставив 1 в разряде сотен (показано красным) Запишите 2 в разряде десятков. Поскольку на месте единиц ничего нет, просто поставьте 0.	Шаг 4: 2 × 3 = 6 пятерок. 6 пятерок = 5 пятерок + 1 пятерка = 25 + 1 пятерка Перенесите 1 двадцать пять, поставив 1 на место двадцати пяти (показано красным) Запишите 1 на место пятерок. Поскольку на месте единиц ничего нет, просто поставьте 0.
Шаг 5: 3 × 6 = 18 сотен. 18 сотен + 1 сотня = 19 сотен 19 сотен = 10 сотен + 9 сотен = 1000 + 9 сотен Запишите 9 в разряде сотен и перенесите 1 тысячу, поставив 1 в разряде тысяч (показано зеленым цветом)	Шаг 5: 2 × 4 = 8 двадцать пять. 8 двадцати пяти + 1 двадцать пять = 9 двадцати пяти 9 двадцати пяти = 5 двадцати пяти + 4 двадцати пяти = 125 + 4 двадцати пяти Запишите 4 в двадцать пятерки и перенесите 1 сто двадцать пять, поставив 1 на сто двадцать пятом месте (показано зеленым)
Шаг 6: 3 × 8 = 24 тысячи. 24 тысячи + 1 тысяча = 25 тысяч. 25 тысяч = 10 тысяч + 10 тысяч + 5 тысяч. разряд десяти тысяч (показан черным цветом) Опустите двойку в разряд десяти тысяч	Шаг 6: 2 × 3 = 6 сто двадцать пять. 6 сто двадцать пять + 1 сто двадцать пять = 7 сто двадцать пять 7 сто двадцать пять = 5 сто двадцать пять + 2 сто двадцать пять = 625 + 2 сто двадцать пять Запишите 2 на месте сто двадцать пять и перенесите 1 шестьсот двадцать пять, поставив 1 на шестьсот двадцать пятом месте (показано черным цветом)

Просто добавьте сейчас.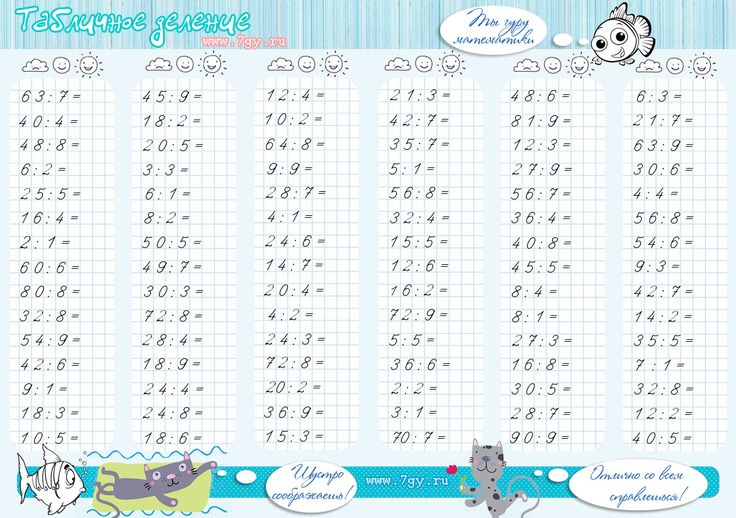 Возможно, вам придется повторить сложение по основанию пять еще до того, как вы начнете этот урок об умножении по основанию пять.

Сложение результатов по основанию десяти.

  1 1 1
       5 1 8 4
   2 5 9 2 0
  __________________
   3 1 1 0 4

Сложение результатов по основанию пять.

  1
       3 0 3 2
   1 2 4 1 0
  ______________
   2 0 4 4 2

Опять же, довольно сложно выполнить умножение по основанию пять. Я рекомендую вам не торопиться при чтении этого урока. Не сдавайся!

1. Рациональные числа — определение и примеры

   15, 23 марта 07:45

   Чтобы узнать о рациональных числах, написать их десятичное представление и распознать рациональные числа, которые повторяют десятичные дроби и завершают десятичные дроби.

   Подробнее

2. Площадь трапеции – определение, формула и примеры

   13, 23 марта 07:52

   Узнайте, как получить площадь трапеции, используя прямоугольник и треугольник, формулу, а также когда высота трапеции отсутствует.

   Подробнее

Определение, длинное умножение, свойства, решенные примеры

В математике умножение — это метод нахождения произведения двух или более чисел. Это одна из основных арифметических операций, которые мы используем в повседневной жизни. Основное применение мы можем видеть в таблицах умножения.

В арифметике умножение двух чисел представляет собой многократное сложение одного числа по отношению к другому. Эти числа могут быть целыми числами, натуральными числами, целыми числами, дробями и т. д. Если m умножается на n, то это означает, что либо m добавляется к самому себе «n» раз, либо наоборот.

Умножение (обозначаемое как « × ») в математике — это математическая операция, помимо сложения, вычитания и деления. Учащиеся сами изучают четыре основных арифметических действия в своих начальных классах. Здесь мы научимся решать задачи на умножение простым и быстрым способом.

Содержание: Определение умножения Символ умножения Формула умножения Свойства умножения Замкнутое свойство умножения Коммутативное свойство умножения Ассоциативное свойство умножения Распределительное свойство умножения Идентификационное свойство умножения Нулевое свойство умножения Правила умножения Знаки умножения Таблица умножения Умножение дробей Умножение десятичных дробей Трюки с умножением Решенные проблемы Часто задаваемые вопросы

Что такое умножение?

Умножение — это процесс вычисления произведения двух или более чисел. Умножение чисел, скажем, «а» и «б», выражается как «а», умноженное на «б».

В математике основным объяснением умножения является многократное сложение числа по отношению к другому числу.

Например, если мы умножаем 2 на 3, это означает, что 3 прибавляется к самому себе два раза, то есть 3 + 3 = 6. Это простая техника умножения чисел для детей.

Примеры умножения

См. еще несколько примеров умножения здесь:

• Умножение 3 на 3 = 3 x 3 = 9
• Умножение 4 на 4 = 4 + 4 + 4 + 4 = 16
• Умножение 5 на 5 = 5 + 5 + 5 + 5 + 5 = 25
• Умножение 10 х 10 = 100
• Умножение 8 на 9 = 8 x 9 = 72

Символ умножения

Символ умножения обозначается знаком креста (×), а также иногда точкой (.).

Примеры:

• 3 × 11 = 33
• 5 × 9 = 45
• 8 × 2 × 10 = 160
• (9).(10) = 90
• (7).(8) = 56

Формула умножения

Формула умножения:

Множитель × множимое = Произведение

• Множимое — это общее количество объектов в каждой группе
• Множитель – это количество одинаковых групп
• Произведение является результатом умножения множителя на множимое

Пример: если множитель = 5 и множимое = 8, то произведение равно:

Продукт = 5 х 8 = 40

Свойства умножения

Свойства умножения:

• Свойство закрытия
• Коммуникативное имущество
• Ассоциативное свойство
• Распределительное имущество
• Идентификационное свойство
• Нулевое свойство

Замкнутое свойство умножения

Согласно свойству замыкания умножения,

• Произведение двух целых чисел равно целому числу (-4 x 3 = -12)
• Произведение двух дробей представляет собой дробь или целое число (1/2 x 2 = 1)

Коммутативное свойство умножения

Свойство коммутативности умножения утверждает, что если A и B — любые два целых числа, то:

А × В = В × А

Например: 2 × 3 = 3 × 2 = 6

Ассоциативное свойство умножения

Согласно ассоциативному свойству умножения, если A, B и C — любые три целых числа, то:

А × (В × С) = (А × В) × С

Например: 2 × (3 × 4) = (2 × 3) × 4 = 24

Распределительное свойство умножения

Согласно распределительному свойству умножения, если A, B и C — любые три целых числа, то:

А × (В + С) = (А × В) + (А × С)

Например: 4 × (2 + 3) = 4 × 2 + 4 × 3 → 20

Идентификационное свойство умножения

Согласно тождественному свойству умножения, если мы умножаем любое значение на 1, то его значение остается неизменным, так что;

А × 1 = А

Например:

• 12 × 1 = 12
• -3 × 1 = -3

Нулевое свойство умножения

Нулевое свойство умножения гласит, что любое число, умноженное на 0, равно только нулю.

А × 0 = 0

где A — любое целое число.

Например: 9 × 0 = 0

Правила умножения (Как умножать)

Существуют различные правила умножения чисел. Они:

• Умножение двух целых чисел является целым числом
• Любое число, умноженное на 0, равно 0
• Любое число, умноженное на 1, равно исходному числу
• Если целое число умножается на число, кратное 10, то такое же количество нулей добавляется в конце исходного числа. Пример: 4 × 1000 = 4000
• Порядок чисел не имеет значения при умножении. Пример: 2 × 3 × 4 × 5 = 5 × 4 × 3 × 2 = 3 × 2 × 4 × 5 = 120

Знаки умножения

Когда два или более числа умножаются с разными знаками (+ и -), то выходной результат меняется в соответствии с приведенными ниже правилами знаков:

С.№.	Эксплуатация	Результат
1.	(+ve) × (+ve)	+ ве
2.	(+ve) × (-ve)	-ве
3.	(-ve) × (+ve)	-ве
4.	(-ve) × (-ve)	+ ве

Описание:

• При умножении двух положительных целых чисел результат положительный
• При перемножении одного положительного целого числа и одного отрицательного целого числа или наоборот результат будет отрицательным
• При умножении двух отрицательных целых чисел получается положительное целое число

Факты:

Умножение четных чисел отрицательных целых чисел всегда положительно. (-) × (-) × (-) × (-) = (+)

Таблица умножения

Ниже приведена таблица умножения чисел от 1 до 10 по строкам и столбцам. С помощью этих таблиц мы можем легко и быстро найти произведение двух чисел от 1 до 10.

×	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

Умножение дробей

При умножении двух или более дробей числители и знаменатели перемножаются, так что:

(а/б) × (в/г) = (а×в)/(б×г)

• Пример 1: Умножьте ¾ и 5/2.

(¾) × (5/2)

= (3×5)/(4×2)

= 15/8

• Пример 2: умножение 4/7 и 21/2

(4/7) × (21/2)

= 2 × 3

= 6

Умножение десятичных дробей

Метод нахождения произведения десятичных дробей такой же, как умножение целых чисел. Здесь нам нужно позаботиться о позиции десятичной дроби (.) после умножения. Давайте разберемся на примере.

• Пример 1: Найдите произведение 1.2 и 3.

Сол: 1,2 × 3 = 3,6

• Пример 2: умножение 4,2 на 1,5

Сол: Давайте умножим 4,2 и 1,5, удалив здесь десятичные дроби и считая их целыми числами. Следовательно,

42 × 15

= 630

Теперь, если мы вернем десятичную запятую, то произведение двух десятичных чисел будет иметь до двух десятичных разрядов справа налево, так что;

4,2 × 1,5 = 6,30

Трюки с умножением

Умножение однозначных чисел — простая задача. Но умножение двух или более цифр может быть трудной и трудоемкой задачей. Вот несколько приемов умножения, которые учащиеся могут запомнить, находя произведение.

• Умножать числа можно в любом порядке. (3 х 4 = 4 х 3)
• При умножении числа на число, кратное 10, просто поставьте число нулей, кратное 10, рядом с множителем (например, 6 x 100 = 600)
• Если необходимо умножить три числа, сначала умножьте меньшие числа для быстрого вычисления, а затем умножьте на третье число
• Если при умножении участвуют двузначные или трехзначные числа, то запишите такие числа в развернутом виде и затем умножьте. (Например: 45 х 9 = (40 + 5) х 9 = 40 х 9 + 5 х 9 = 360 + 45 = 405)
• Следуйте правилу знаков, указанному в предыдущем разделе

Умножение Статьи по теме

• Трюки с умножением
• Таблица умножения
• Умножение и деление целых чисел
• Умножение алгебраических выражений
• Умножение многочленов
• Двоичное умножение
• Факторы и множители
• Умножение матриц
• Свойства умножения целых чисел

Задачи на умножение

Вопрос 1: Если у Шикхи 10 корзин и в каждой корзине 5 яблок. Затем найдите общее количество яблок у Шихи.

солов: количество корзин у Шихи = 10

Количество яблок в каждой корзине = 5

Общее количество яблок = (Количество корзин) × (Количество яблок в каждой корзине)

= 10 × 5 = 50

Следовательно, у Шихи 50 яблок.

Q.2: Сэм приносит с рынка 3 коробки конфет. Если в каждой коробке 50 конфет, то сколько всего конфет у него было?

Решение: Количество ящиков = 3

Количество конфет в каждой коробке = 50

Общее количество конфет = 3 x 50 = 150

Значит, у Сэма 150 шоколадок.

Q.3: Найдите произведение 13,99 × 10000.

Сол: 13,99 × 10000

= 139900,00

= 139900

Практические вопросы по умножению

Студенты могут практиковать эти суммы умножения здесь:

1. Найти: 45 × 10
2. Умножить 1,2 × 90
3. Найти 8 × 11
4. Найдите произведение 10 и 78
5. Найдите произведение 900 и 70
6. Найти 0,5 × 100

Часто задаваемые вопросы по умножению

Что такое умножение в математике?

Умножение — это арифметическая операция, при которой мы находим произведение двух или более чисел.