Колонка INdEX 140/500 | Cytiva
Оценка колонки
Эффективность колонки зависит от того, насколько хорошо она упакована. Плохо набитая колонка приводит к неравномерному потоку, что приводит к расширению зоны и снижению разрешения. Таким образом, важно иметь метод, с помощью которого можно было бы протестировать колонку до того, как она будет введена в эксплуатацию. Такой метод должен быть простым, количественным и не должен вводить загрязняющие вещества. Преимущество также в том, что тот же метод можно использовать для контроля производительности колонки в течение всего срока ее службы, чтобы можно было легко определить, когда следует повторно наполнить или заменить среду.
Избегайте методов, в которых используются окрашенные соединения, такие как синий декстран. Они не соответствуют вышеуказанным критериям и не могут использоваться со средами для ионообменной и аффинной хроматографии.
Опыт показал, что наилучший метод выражения эффективности колонны – это высота, эквивалентная теоретической тарелке, HETP, уменьшенное число тарелок, h, и коэффициент асимметрии пика, A 
Эти значения можно легко определить, нанеся на колонку раствор NaCl или ацетона (см. ниже).
Важно, чтобы колонка была должным образом уравновешена ( > 2 объема колонки) перед оценкой упаковки. В идеале запустите три тестовых прогона, чтобы увидеть, стабильны ли значения. Если первоначальный плохой результат улучшится во время более позднего теста, причина может заключаться в том, что колонка не была должным образом уравновешена. Чтобы убедиться, что слой стабилен, запустите колонку при давлении набивки 70% на 20 часов и снова проверьте ее.
Учтите, что скачки давления могут привести к плохой упаковке (растрескиванию). В этом случае установите воздушную ловушку и клапан сброса давления между насосом и колонкой. Найдите предохранительный клапан между воздушной ловушкой и колонкой.
Выбор тестового образца для колонок
Наиболее подходящим материалом для тестирования колонок, конечно же, является образец, который должен быть запущен в приложении, но это не всегда практично или экономично.
В качестве альтернативы, раствор NaCl или ацетона даст хорошее представление о качестве заполнения колонки. Элюат контролируют путем измерения проводимости или УФ-поглощения, и полученный профиль элюирования используется для расчета значения HETP.Преимущества использования NaCl заключаются в том, что он легко доступен и может безопасно использоваться для тестирования всех колонок. Одним из недостатков является то, что NaCl может взаимодействовать с матрицей среды, особенно с ионообменными матрицами, и, таким образом, давать ошибочные результаты.
Ацетон, напротив, не взаимодействует с матрицей и обнаруживается по поглощению в УФ-диапазоне при 280 нм. Кроме того, вы можете увеличить концентрацию текущего буфера в 10 раз и использовать его в качестве тестового раствора.
На приведенном ниже рисунке показана УФ-кривая для ацетона в типичном применении колонки BPG и приведены расчетные значения HETP и As.
Расчет HETP
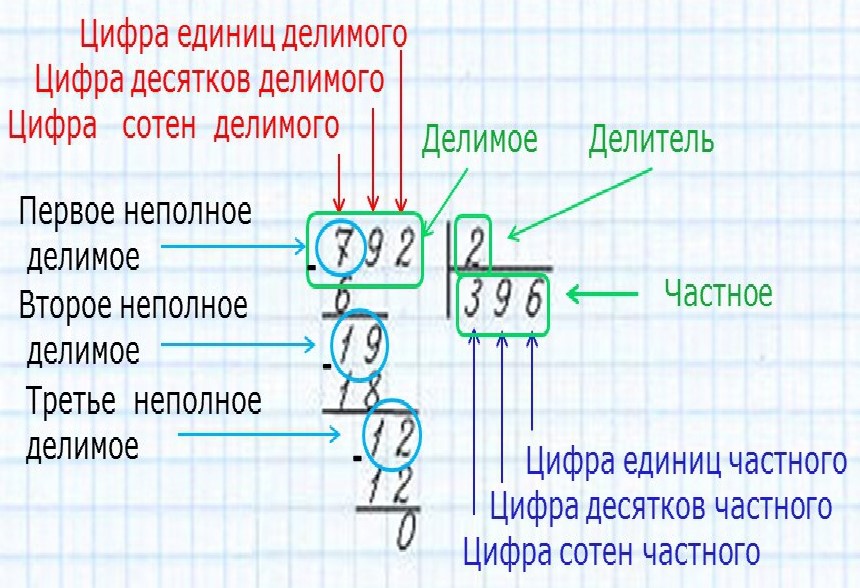
Объем пробы должен составлять примерно 1% от общего объема слоя, а концентрация 1,0% об.
/об. NaCl или эквивалент при использовании более сильного буфера. В качестве альтернативы используйте 1,0% об./об. ацетона. Скорость потока должна быть от 10 до 30 см/ч в зависимости от размера гранул хроматографической среды. Высокая скорость потока может быть использована для маленьких шариков, тогда как большие шарики допускают только низкую скорость потока. Во избежание разбавления пробы наносите ее как можно ближе к входу колонки. Если в систему включена ловушка для воздуха, не используйте ее во время нанесения пробы, чтобы избежать обратного смешивания. Рассчитайте значение HETP по кривой проводимости (или УФ) следующим образом:
HETP, проще говоря, выражается как:
HETP = L/N
где
L = высота слоя (см)
N = количество теоретических тарелок.
N определяется по уравнению:
N = 5,54 (V e /W h ) 2
где
V e = объем элюирования (мл)
ч W половина высоты (мл)
V e измеряется как объем, прошедший через колонку до пикового максимума.
Вт ч измеряется как ширина пика на половине высоты пика.
В примере на рисунке значение HETP можно рассчитать по хроматограмме следующим образом:
| В и (мл) | Ш В (мл) | Н | Н/м | НЕТР см | |
| Ацетон | 18800 | 900 | 2417 | 4203 | 0,024 |
Колонки с хорошей набивкой имеют низкие значения HETP. Однако сравнивать можно только колонки, заполненные одним и тем же типом среды и протестированные в одинаковых условиях.
Как правило, хорошее значение HETP примерно в два-четыре раза больше среднего диаметра гранул рассматриваемой среды, при условии, что образец не взаимодействует со средой.
На практике корреляцию между HETP и производительностью колонки может оценить только оператор колонки. Как только это будет установлено, можно установить стандарт для оценки приемлемости насадки колонки.
Например, оператор колонки может знать из опыта, что колонка, заполненная гель-фильтрационной средой Sephadex G-25 со значениями HETP выше 0,05 см, не обеспечивает требуемого разделения. Следовательно, оператор установит это значение как максимально допустимое, т.е. минимально допустимое качество.
Уменьшенный номер тарелки
Определение сокращенного номера тарелки: h = HETP/dp
h = уменьшенный номер тарелки
HETP = описанная выше высота, эквивалентная теоретической тарелке
dp = средний диаметр частиц хроматографической среды
уменьшенное число тарелок должно быть в 2-4 раза больше среднего диаметра частиц гранул хроматографической среды.
Расчет коэффициента асимметрии пика
Коэффициент асимметрии пика должен быть как можно ближе к 1, а форма пика должна быть максимально симметричной. Обычно это имеет место для гель-фильтрационных сред, но для некоторых ионообменных и аффинных сред форма может быть асимметричной из-за взаимодействия со средой.
Изменение формы пика обычно является первым признаком износа колонки.
Коэффициент асимметрии пика, A s , рассчитывается по приведенному выше графику:
A s = b/a
, где
a = расстояние от вершины пика до 10% высоты пика на восходящей стороне пик
b = расстояние от вершины пика до 10% высоты пика на нисходящей части пика
Примечание: Измерение значений HETP, h и As — лучший способ оценить состояние насадочной колонки. Упакованная колонка может хорошо выглядеть, но для оптимальной производительности ее все же необходимо переупаковать. Всегда проверяйте колонку после упаковки и регулярно между запусками, чтобы обеспечить наилучшую производительность.
4.4.3 Расчет режима
Содержание
Текст начинается
Тематическая навигация
- 4 Исследование данных
- 4.4 Меры центральной тенденции
- 4.
4.1 Вычисление среднего - 4.4.2 Расчет медианы
- 4.4.3 Расчет режима
- 4.
- 4.4 Меры центральной тенденции
4.1 Вычисление среднегоКогда мода уникальна, это значение, которое чаще всего встречается в наборе данных, и его можно использовать в качестве меры центральной тенденции, как медиана и среднее значение. Но иногда режима нет или есть несколько режимов.
Не существует режима, при котором все наблюдаемые значения встречаются в наборе данных одинаковое количество раз. Существует более одного режима, когда самая высокая частота наблюдалась для более чем одного значения в наборе данных. В обоих этих случаях режим нельзя использовать для определения центра распределения.
Этот режим можно использовать для суммирования категориальных переменных, тогда как среднее значение и медиану можно вычислить только для числовых переменных. В этом состоит основное преимущество моды как меры центральной тенденции.
Вот несколько примеров расчета режима для дискретных переменных.
Пример 1 – Количество очков во время хоккейного турнира
Во время хоккейного турнира Одри набрала 7, 5, 0, 7, 8, 5, 5, 4, 1 и 5 очков в 10 играх. После суммирования данных в частотной таблице можно легко увидеть, что мода равна 5, поскольку это значение встречается в наборе данных чаще всего (4 раза). Моду можно считать мерой центральной тенденции для этого набора данных, потому что она уникальна.
| Количество набранных баллов | Частота (количество игр) |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 4 | 1 |
| 5 | 4 |
| 7 | 2 |
| 8 | 1 |
Пример 2. Количество очков в 12 баскетбольных матчах
В баскетбольном сезоне, состоявшем из 12 игр, Марко набрал 14, 14, 15, 16, 14, 16, 16, 18, 14, 16, 16 и 14 очков. После суммирования данных в таблице частот вы можете увидеть, что в этом наборе данных есть две моды: 14 и 16.
Оба значения встречаются в наборе данных 5 раз, и 5 — это самая высокая наблюдаемая частота. Моду нельзя использовать в качестве меры центральной тенденции, потому что существует более одной моды. Это бимодальное распределение.
| Количество набранных баллов | Частота (количество игр) |
|---|---|
| 14 | 5 |
| 15 | 1 |
| 16 | 5 |
| 18 | 1 |
Пример 3.
Количество тачдаунов в течение футбольного сезона Следующий набор данных представляет количество тачдаунов, забитых Джеромом в школьном футбольном сезоне: 0, 0, 1, 0, 0, 2, 3, 1, 0, 1, 2, 3, 1, 0. Давайте сравните среднее, медиану и моду.
Сумма всех значений равна 14, и имеется 14 точек данных. Это дает среднее значение 1. Поскольку число значений четное, медиана является средним значением между точкой данных ранга 7 и точкой данных ранга 8 после упорядочения набора данных в порядке возрастания.
| Ранг | Количество приземлений |
|---|---|
| 1 | 0 |
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 0 |
| 6 | 1 |
| 7 | 1 |
| 8 | 1 |
| 9 | 1 |
| 10 | 1 |
| 11 | 2 |
| 12 | 2 |
| 13 | 3 |
| 14 | 3 |
Следовательно, медиана равна 1.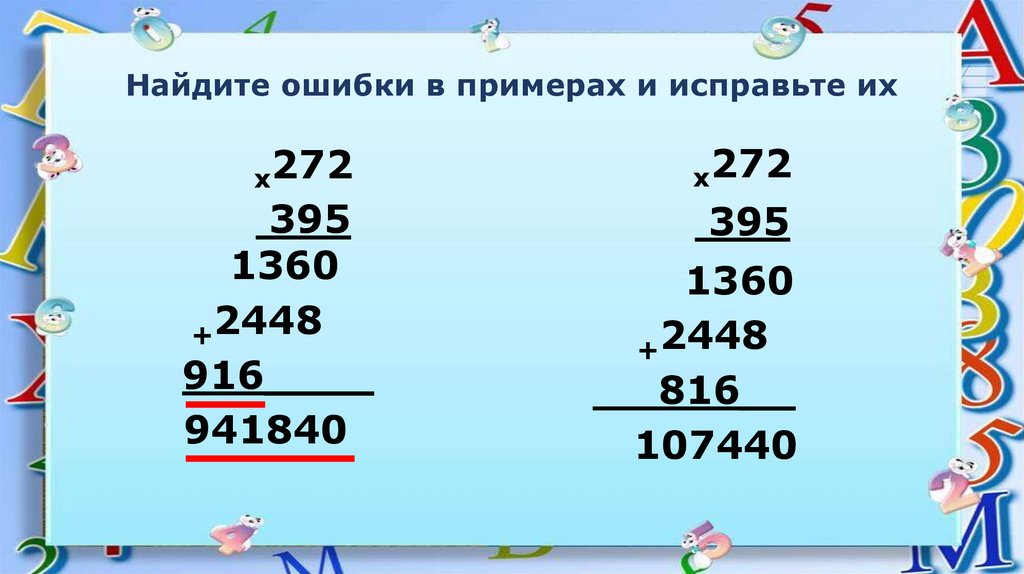
После суммирования данных в частотной таблице можно увидеть, что мода равна 0, поскольку это значение встречается чаще всего (6 раз).
| Количество приземлений | Частота |
|---|---|
| 0 | 6 |
| 1 | 4 |
| 2 | 2 |
| 3 | 2 |
Таким образом, в этом примере среднее значение равно 1, медиана равна 1, а мода равна 0.
Этот режим не так часто используется для непрерывных переменных, потому что с этим типом переменной вполне вероятно, что ни одно значение не будет появляться более одного раза. Например, если вы спросите 20 человек об их личном доходе за предыдущий год, возможно, у многих из них будут очень близкие суммы дохода, но вы никогда не получите точно такое же значение для двух человек. В таком случае полезно сгруппировать значения во взаимоисключающие интервалы и визуализировать результаты с помощью гистограммы для определения интервала модального класса.
Пример 4. Рост людей на арене во время баскетбольного матча
Нас интересует рост людей, находящихся на арене во время баскетбольного матча. В таблице 4.4.3.5 представлено количество людей для 20-сантиметровых интервалов роста.
| Высота (в сантиметрах) | Частота (количество человек) |
|---|---|
| от 20 до 39 | 42 |
| от 40 до 59 | 105 |
| от 60 до 79 | 176 |
| от 80 до 99 | 230 |
| от 100 до 119 | 214 |
| 120 до 139 | 168 |
| от 140 до 159 | 363 |
| от 160 до 179 | 480 |
| от 180 до 200 | 170 |
| от 200 до 219 | 11 |
Информация сгруппирована по высоте (в сантиметрах) (отображается в виде заголовков строк), частоте (количество людей) (отображается в виде заголовков столбцов). На диаграмме 4.
4.3.1 этот набор данных представлен в виде гистограммы.
Данные, представленные в этой таблице, являются данными из таблицы 4.4.3.5.
Глядя на таблицу и гистограмму, вы можете легко определить интервал модального класса от 160 до 179 сантиметров, частота которого равна 480. Вы также можете видеть, что по мере уменьшения высоты от этого интервала частота также уменьшается для интервала от 140 до 179 сантиметров. 159 сантиметров (363) и продолжает уменьшаться от 120 до 139 сантиметров (168), прежде чем начать увеличиваться, пока высота не достигнет 80-99 сантиметров (230).
Для категориальных или дискретных переменных множественные моды — это значения, которые достигают одной и той же частоты: самой высокой из наблюдаемых. Для непрерывных переменных все пики распределения можно считать модами, даже если они не имеют одинаковой частоты. Распределение для этого примера является бимодальным, с основной модой, соответствующей интервалу модального класса от 160 до 179.