Книга «Математика: Десяток. Состав числа. 1 класс и дошкольники» из жанра Рабочие тетради, прописи, альбомы
Математика: Десяток. Состав числа. 1 класс и дошкольники
| Автор: Узорова О.В.
Жанр: Рабочие тетради, прописи, альбомы
Издательство: Клевер-Медиа-Групп
Год: 2014 Количество страниц: 16
Формат:
PDF (0.80 МБ) Дата загрузки: 19 марта 20172015-12-23 Скачать с нашего сайта Скачать в два клика
| |||
| Аннотация Тетрадь для многоразового использования «Математика. | |||
| Комментарии
| |||
Книги Узорова О.
|
«3000 примеров по математике. 1 класс. Счёт в пределах десятка. Состав числа» Узорова Ольга Васильевна, Нефедова Елена Алексеевна — описание книги | 3000 примеров для начальной школы
Алматы
Алтайский край
Альметьевск
Ангарск
Астрахань
Белгород
Благовещенск
Братск
Брянск
Владивосток
Волгоград
Воронеж
Грозный
Губкин
Екатеринбург
Забайкальский край
Ивановская область
Иркутск
Кабардино-Балкарская Республика
Калужская
Кемерово
Кемеровская область
Киров
Краснодарский край
Красноярск
Красноярский край
Курск
Липецк
Лиски
Москва
Московская область
Нижегородская область
Нижний Новгород
Нижний Тагил
Новосибирск
Нур-Султан
Омск
Оренбург
Оренбургская область
Орловская область
Пенза
Пермь
Республика Адыгея
Республика Башкортостан
Республика Бурятия
Республика Крым
Республика Мордовия
Республика Северная Осетия — Алания
Республика Татарстан
Республика Тыва
Республика Хакасия
Россошь
Ростов-на-Дону
Ростовская область
Рязань
Самара
Самарская область
Саратов
Саратовская область
Севастополь
Смоленск
Ставрополь
Ставропольский край
Старый Оскол
Тамбов
Тверь
Томск
Тула
Тулун
Тульская область
Тюмень
Ульяновск
Ульяновская область
Хабаровск
Ханты-Мансийский автономный округ
Челябинск
Челябинская область
Чувашская Республика
Энгельс
Ямало-Ненецкий автономный округ
Ярославль
Ярославская область
ОТКРЫТЫЙ УРОК ПО МАТЕМАТИКЕ В 1 КЛАССЕ Тема: «Состав числа 9,10»
ЗАНЯТИЕ 2.
 Ход занятия
Ход занятияЗАНЯТИЕ 2 Тема: РАЗВИВАЕМ ИНТЕЛЛЕКТ Цели: 1. закрепление знаний о правилах поведения в школе; 2. развитие представления о признаках предмета; 3. развитие внимания, аналитического восприятия, мышления;
ПодробнееМ А Т Е М А Т И К А В Ш К О Л Е
Тесты по математике по учебнику М. И. Моро для 1 класса. 1 и 2 четверти Тесты по математике для 1 класса, 1 четверть Тест 1 Вариант I 1. На рисунке изображены круги и квадраты. Закрась синим цветом фигуры,
ПодробнееОткрытый урок по математике во 2 классе
МОУ Большебыковская средняя общеобразовательная школа Открытый урок по математике во 2 классе Тема: «Повторение и обобщение изученного во 2 классе» «Путешествие в сказку» Подготовила учитель начальных
ПодробнееОткрытый урок по математике во 2 классе
МКС(К) ОУ для обучающихся воспитанников с ограниченными возможностями здоровья Старогородковской специальной (коррекционной) общеобразовательной школы-интерната VIII вида им.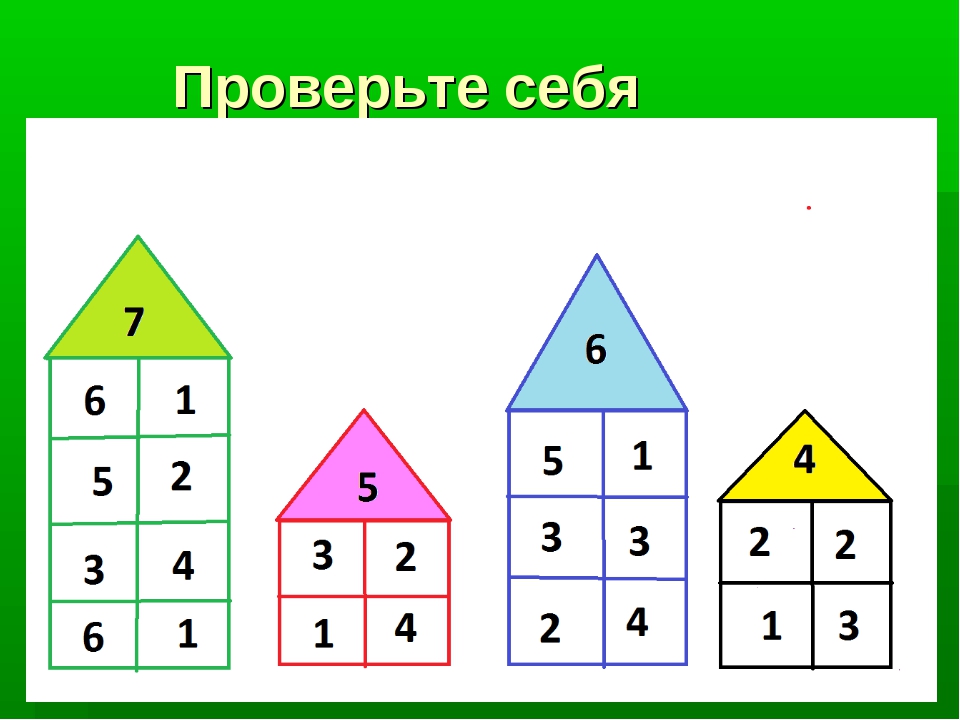 Заслуженного учителя РФ Фурагиной
Заслуженного учителя РФ Фурагиной
КОНСПЕКТ ОТКРЫТОГО ПРОСМОТРА ПО
Муниципальное бюджетное дошкольное образовательное учреждение Детский сад 23 КОНСПЕКТ ОТКРЫТОГО ПРОСМОТРА ПО ПОЗНАВАТЕЛЬНОМУ РАЗВИТИЮ (ФОРМИРОВАНИЕ ЭЛЕМЕНТАРНЫХ МАТЕМАТИЧЕСКИХ ПРЕДСТАВЛЕНИЙ) Подготовила
ПодробнееСоставление и заучивания.
Урок математики в 1-м классе «Прибавить и вычесть 2» Составление и заучивания. Тема: «Прибавить и вычесть 2.Составления и заучивание таблиц» Цель урока: составление и заучивание таблиц+-2: -повторить приёмы
ПодробнееПлан-конспект урока математики во 2 классе
Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа 8» города Торжка Тверской области План-конспект урока математики во 2 классе По теме «Буквенные выражения». Подготовила
Подготовила
7* : :2 31 4*
Открытый урок математики в 3в классе Тема: «Умножение числа на произведение» урок закрепления материала Цели урока: Образовательные: Обобщить материал по темам «Умножение многозначных чисел на однозначное»,
ПодробнееТехнологическая карта урока
Технологическая карта урока Учебный предмет: математика Класс: 1 Школа: МАОУ СОШ 36 г. Тамбова Учитель: Ковалева Татьяна Михайловна УМК: Образовательная система «Школа 2100» Тема урока Цель урока Планируемый
ПодробнееЭтапы, время 1 Орг. момент
ОТКРЫТЫЙ УРОК ПО МАТЕМАТИКЕ Тема: «Деление» Цели: — познакомить с понятием деление; — рассмотреть простые задачи на деление (на части и по содержанию) и сравнить их решения; — установить связь между действиями
ПодробнееУрок по математике в 1 классе
МБОУ «Стрелецкая средняя общеобразовательная школа» Красногвардейского района Белгородской области Урок по математике в 1 классе Подготовила учитель начальных классов Чернякова Нина Петровна 2010 год.
ПодробнееТема: «Название чисел при умножении.»
Муниципальное общеобразовательное учреждение Падовская средняя общеобразовательная школа Урок математики во 2 классе Тема: «Название чисел при умножении.» Учитель: Носкова О.Н 2010 год Тема: «Название
Подробнее8 1 (1 ) , 2 ( 7) 10 2 (1 ) — 10
3.1.Конспект урока (в таблице). III. Содержательная часть: Деятельность учителя с указанием Деятельность ученика номера слайда (при наличии презентации) Этап 1 урока Организационный момент. 3 мин Цель
ПодробнееТема: «Больше. Меньше. Столько же»
Технологическая карта урока по математике 1 класс «Планета знаний» Тема: «Больше. Меньше. Столько же» Галецкая Виктория Александровна ГБОУ гимназия 426 учитель начальных классов Тема: «Больше. Меньше.
Подробнее«Путешествие в страну математики»
1 «Путешествие в страну математики» Бинарный урок ГБСКОУ школа 657 Приморского района Санкт — Петербурга учитель Грачева О.Л. дефектолог Соломаха Л.В. Санкт Петербург 2013-2014 2 Тема: «Путешествие в страну
ПодробнееКОНСПЕКТ УРОКА ПО МАТЕМАТИКЕ ВО 2 КЛАССЕ
227 Рубанова Н Ю Учитель начальных классов КОНСПЕКТ УРОК ПО МТЕМТИКЕ ВО 2 КЛССЕ Тема: «Систематизация умений, необходимых для решения текстовых задач» Цели урока Главная цель урока: систематизировать умения
ПодробнееТема: Равнобедренные треугольники.
Конспект урока по учебнику И. И. Аргинской «Математика. 2 класс» (1-4) Учитель Шульженко Ольга Игоревна г. Москва ГБОУ «Школа с углублённым изучением иностранных языков 1900» Тема: Равнобедренные треугольники.
ПодробнееГБОУ школа интернат 1 ст. Елизаветинской
ГБОУ школа интернат 1 ст. Елизаветинской Открытый урок русского языка в 3 классе по теме: «Однокоренные слова». Провела учитель логопед Антошкина Н.А. 25.11.2015г. Цели: Познавательные: учить ориентироваться
ПодробнееТехнологическая карта урока
Технологическая карта урока Приложение 2. Тема: Конкретный смысл действия умножения. Тип урока: урок первичного предъявления знаний Цель: создать условия для организации совместной деятельности учащихся
Подробнее«Число и цифра 8» (1 класс)
государственное бюджетное специальное (коррекционное) образовательное учреждение для обучающихся, воспитанников с ограниченными возможностями здоровья общеобразовательная школа 9 VIII вида г. Туапсе Краснодарского
ПодробнееОбъединение «Школа детства»
МБУДО ЦДТ «Феникс» Объединение «Школа детства» Дополнительная общеобразовательная программа по формированию математических представлений у детей дошкольного возраста «Считалочка» (третий год обучения).
ПодробнееКонспект практического занятия
МКДОУ ЦРР — д/c 10 «Сказка» Конспект практического занятия (для родительского собрания) в старшей группе 4 «Белочка» Подготовила: О.В.Воробьёва — воспитатель 1 кат. Дата проведения: март 2016г. Форма проведения:
ПодробнееКонспект урока математики в 1 классе.
Конспект урока математики в 1 классе. Учебник «Математика». Авторы Т.Е.Демидова, С. А. Козлова. Тема урока: «Число 8. Цифра 8» Составила конспект учитель МАОУ «СОШ 96» Оборина Светлана Геннадьевна Основные
ПодробнееДата: Класс: 1-А
Дата: 26.02.2014 Класс: 1-А Тема. Упражнения на усвоение названий компонентов при сложении и вычитании. Сравнение выражений и чисел. Подготовительные упражнения к решению задач в два действия. Измерение
ПодробнееКак работать с пособием
Как работать с пособием Уважаемые взрослые! Предлагаемое пособие рассчитано на совместную работу воспитателей, педагогов и родителей с дошкольниками, готовящимися к школьному обучению. Первоначальной задачей
Подробнее1 десяток. Состав числа 10
Цели урока.
1. Закрепить знание состава числа 10. Совершенствовать умения:
а) выполнять задания, требующие знание состава числа 10;
б) записывать выражения по рисунку или соотносить предложенные с рисунком;
в) выполнять группировку;
г) выявлять закономерности;
д) отмечать изменения.
2. Развивать внимание, память, логическое мышление, воображение, математическую речь.
3. Воспитывать интерес к предмету, аккуратность, чувство товарищества и взаимопомощи.
Оборудование: рисунок к загадке, модель капельки, карточки с числами, геометрические фигуры-маленькие и большие квадраты разного цвета, рисунок “волшебного колеса”, стопка тетрадей, перфокарты, капелька для каждого ученика.
Ход урока
I. Организация учащихся на работу
У: Какое время года?
Д: Весна.
У: Что изменилось в природе?
Д: Тает снег, солнце греет сильнее, на улице становится тепло.
У: Отгадайте загадку:
Растёт она вниз головой,
Не летом растёт, а зимой.
На солнце её припечёт,
Заплачет она и умрёт. (Сосулька)
У: Что значит заплачет?
Д: Капают капли.
Рисунок 1
У: Каждая упавшая капля пахнет весной, она не простая и предлагает вам задание. Если мы быстро и правильно выполним задание, то эта капля попадает в ручеёк знаний (пока что ещё маленький).
Рисунок 2
II. Чистописание (1-ая капелька)
У: Разгадайте правило, по которому составлен ряд чисел, и продолжите его (только однозначные числа)
4, 6, 5, 7, 6, …, …, …, …
Д: 4, 6, 5, 7, 6, 8, 7, 9, 8 (фронтальная проверка).
У: Уменьшите каждое число в ряду на 3.
На обратной стороне доски даны ответы (самопроверка).
1, 3, 2, 4, 3, 5, 4, 6, 5,
У: Мы справились с заданием, и первая капелька попадает в ручеёк знаний (капельку помещаем в ручеёк).
III. Устный счёт (2-ая капелька)
1) У: На доске даны карточки с числами 1-9. Я говорю задание, вы должны подумать и выбрать карточку с нужным ответом:
- на сколько число 8 больше числа 4?
- на сколько число 7 меньше числа 9?
- число 9 уменьшить на 3;
- число 2 увеличить на 1;
- чему равна сумма чисел 2 и 5?
- чему равна разность чисел 7 и 6?
Д: 4, 2, 6, 3, 7, 1 (фронтальная проверка).
2) У: Вставьте вместо точек числа, чтобы получились верные записи. Использовать только числа, полученные в первом задании
… + …=… — …
… — …=… — …
… + …=… + …
Задание выполняется самостоятельно в тетрадях, затем проверяется у доски. Рассматриваются все варианты ответов.
У: Мы справились с заданием, и вторая капелька попадает в ручеёк знаний (капельку помещаем в ручеёк).
IV. Подготовка к работе (3-я капелька)
У: Назовите числа, которые нужно вставить в «окошки».
Рисунок 3
Учащиеся называют числа, выходят к доске и переворачивают карточки:
3, 9, 5, 1, 6, 10
У: Назовите лишнее число.
Д: 10.
У: Почему?
Д: Двузначное, один десяток.
У: Какую задачу урока ставим? Зачем?
Д: Повторение и закрепление состава числа 10, чтобы потом легко и быстро выполнять сложение и вычитание.
Сообщение темы и задач урока.
У: Мы справились с заданием, и третья капелька попадает в ручеёк знаний (капельку помещаем в ручеёк).
V. Повторение.
1) 4-ая капелька.
У: У меня в стопке тетради. Сколько их?
Д: 5 (считают).
У: Я добавила еще несколько. Сколько стало?
Д: 10 (считают).
У: Сколько я добавила тетрадей?
Д: 5.
У: Как получили 10?
Д: 5 + 5=10.
Выражение записывается на доске и в тетради.
2) 5-ая капелька.
Даны фигуры. Назовите их.
Рисунок 4
У: По какому признаку нужно разбить все фигуры на две группы, чтобы это соответствовало выражению 5 + 5?
Д: По цвету.
Ученик у доски делит фигуры по цвету на две группы.
У: По какому ещё признаку можно разбить фигуры?
Д: По размеру.
Ученик у доски делит фигуры по размеру на две группы и записывает выражение 6+4=10, 4+6=10. Дети записывают в тетрадь.
3) Физкультминутка “Хомка”.
Хомка-хомка, хомячок,
Полосатенький бочок.
Хомка раненько встаёт,
Щёки моет, шейку трёт.
Подметает хомка хатку
И выходит на зарядку.
Раз, два, три, четыре, пять!
Хомка хочет сильным стать. (Дети имитируют все движения хомячка.)
4) 6-ая капелька.
Игра «Волшебное колесо»
Рисунок 5
У: Расположите числа от 1 до 9 так, чтобы в любом направлении по прямой линии получилось в сумме 10.
Ученики выходят к доске и записывают пары чисел.
У: А теперь напишем новые выражения на доске и в тетради: 1+9=10; 9+1=10; 2+8=10; 8+2=10; 3+7=10; 7+3=10.
Прочитайте все выражения (записи в тетради).
У: Мы справились с этими заданиями, поэтому все капельки попадают в ручеёк знаний.
5) 7-ая капелька.
Работа по учебнику Н.Б.Истоминой. Страница 125 № 291 (работа в парах).
У: Рассмотрите каждую пару рисунков. Что происходит?
Д: Количество кругов увеличивается.
1-ая пара объясняет: число красных кругов увеличили на 2, стало 10 (8+2)
2-ая пара – число жёлтых кругов увеличили на 4, получили 10 (6+4)
3-я пара — число зелёных кругов увеличили на 5, получили 10 (5+5)
4-ая пара — число синих кругов увеличили на 3, получили 10 (7+3)
У: Какого случая не хватает?
Д: 9+1=10
6) 8-ая капелька.
Работа в тетради на печатной основе (ТПО). Страница 37 №79. Первое задание выполняется с объяснением.
У: В треугольнике 4 круга. Какой цифрой записали это число?
Д: 4.
У: Сколько надо дорисовать кругов до 1 десятка?
Д: 6.
У: Сколько всего кругов?
Д: 10. Для записи этого числа используем две цифры: 1 и 0.
Дальше задание выполняется самостоятельно. После выполнения – проверка.
У: Мы справились с заданием, и эти капельки тоже попадают в ручеёк знаний.
7) 9-ая капелька.
Работа с перфокартами.
У: У вас на столе перфокарта, с помощью которой я проверю, как вы усвоили состав числа 10. А опускать капельку в ручеёк или нет, я решу после проверки выполненной работы.
Рисунок 6
VI. Итог.
У: Что повторили на уроке? Какие задания больше понравились?
На столе у каждого маленькая капелька. Если вы уверены, что хорошо знаете состав числа 10, не затруднялись при выполнении заданий, то ваша капелька попадает в “ручеёк знаний”. Если кто-то не уверен в себе, пусть ваша капелька пока останется с вами. И когда вы убедитесь в своих знаниях, вы опустите капельку в ручеёк. Может быть это будет завтра.
Дети выходят к доске и опускают свою капельку в “ручеёк знаний” (в конверт).
Список литературы:
- Истомина Н.Б. Математика: учебник для 1 класса общеобразовательных учреждений / Н.Б. Истомина. – 10-е изд. – Смоленск: Ассоциация XXI век, 2010. – 176 с.
- Истомина Н.Б., Редько З.Б. Математика: тетрадь к учебнику для 1 класса общеобразовательных учреждений. В 2 ч. Ч.2. / Н.Б. Истомина. – 13-е изд. – Смоленск: Ассоциация XXI век, 2010. – 64 с.
- Бугримова Т.А. Математика. 1 класс: Поурочные планы (по учебнику Н.Б. Истоминой) / Т.А. Бугримова. – Волгоград: Учитель, 2004. – 287 с.
Тема:Число 10. Состав числа 10. | Презентация к уроку по математике (1 класс) на тему:
Открытый урок по математике
Тема: «Число 10. Состав числа 10».
Цели урока: рассмотреть состав числа 10, его графическое изображение; формировать умения анализировать и решать задачи на нахождение части и целого; закреплять изученные приемы решения уравнений и текстовых задач; развивать речь, память, внимание, логическое мышление.
Планируемые результаты: учащиеся научаться читать и записывать число 10; работать в паре; формулировать выводы; использовать полученные знания в повседневной жизни.
Оборудование: карточки с цифрами от 0 до 9; круги (черные и белые)
Ход урока
- Организационный момент (слайд 1,2)
Ну-ка, проверь, дружок,
Ты готов начать урок?
Все ль на месте,
Все ль в порядке?
Все ли правильно сидят
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку пять!
- Актуализация знаний.
- Логическая задача (слайд 3)
Во дворе гуляли куры и собаки. Мальчик посчитал их лапы, получилось 10 лап. Сколько могло быть кур и сколько собак? (1 собака и 3 курицы или 2 собаки и 1 курица)
- Математический диктант (слайд 4)
- Какое число на 6 единиц больше 2? (8)
- Разложите число 8 на сумму двух одинаковых слагаемых. (4 и 4)
- Какое число на 2 меньше 7? (5)
- Какое число предшествует числу 7? (6)
- Первое слагаемое 3, второе слагаемое 6. Найдите сумму. (9)
- Найдите разность чисел 6 и 5.
— Откройте тетради и запишите число, классная работа.
- Самоопределение к деятельности (слайд 5)
— Посмотрите на числовой ряд. Какое число при счете идет перед числом 8? (7)
— Сравните число 8 с предыдущим числом (8 больше 7)
— Какое число при счете следует за числом 8? (9)
— Как это записать? (8+1=9)
— Какое число идет при счете за числом 9? (10)
— Кто может назвать тему урока? (число 10) (слайд 6)
(слайд 7)
— – Что мы будем делать на уроке?
– Чему должны научиться?
— Чем необычно это число? (оно состоит из двух цифр)
Число 10 двузначное. Числа от 1 до 9 однозначные, так как состоят из одной цифры.
Нолик мне терять нельзя,
Без него исчезну я,
Стану тощей единицей,
Буду плакать я и злиться!
IV. Работа по теме урока
- Знакомство с числом 10
— В повседневной жизни вы встречали число 10? И где?
— Чего у человека 10 (10 пальцев на руках и ногах)
За девятью идет десятка.
Ты это знаешь? Молодец!
Сочти все пальцы по порядку,
И счету нашему конец.
Это интересно (слайд 8)
Поскольку у человека десять пальцев, десяток издревле использовался как укрупненная единица счета. Число 10 являлось в древности символом гармонии и полноты. Десяток стал основой десятичной системы счета, которую используют во всем мире. С этим связано и обозначение числа десять: 1д и 0е стали записывать короче – просто 10. В римской нумерации обозначение числа 10 напоминает две ладони, составленные вместе: Х. (слайд 9)
Круглый ноль такой хорошенький,
Но не значит ничегошеньки!
Если ж слева, рядом с ним,
Единицу поместим,
Он побольше станет весить,
Потому что это – десять.
(Отрывок из стихотворения С.Я. Маршака «Веселый счет»)
— Рассмотрите числовой отрезок на доске. Где находится число 10 в числовом отрезке? (после 9)
— Как получили число 10 (к 9 прибавили 1)
— Посмотрите на модель числа 10. (слайд 8)
— Как расположены 10 точек? (в виде треугольника)
— Число 10 называют треугольным числом.
Работа в паре
— У вас на партах лежат круги. Выложите эти круги в виде треугольника. Сложите черные и белые круги, результат запишите на листиках. Проверим, что у вас получилось.
— Можно ли теперь определить состав числа 10? (да, можно)
— На доске домик числа 10, давайте его заполним.
Запись числа 10 в рабочей тетради
-Чем число 10 отличается от остальных чисел числового ряда? (оно состоит из 2 цифр 1 и 0)
— Сейчас мы с вами пропишем число 10. Так как число 10 двузначное, для его записи требуется 2 клетки. (слайд 9)
V. Физкультминутка
Встали, сели, сели, встали
И друг друга не задели.
Мы немножко отдохнем
И опять считать начнем!
Выше руки! Шире плечи!
Раз, два, три! Дыши ровней!
От зарядки станешь крепче,
Станешь крепче и сильней!
— Спасибо, ребята. А теперь тихо сели за свои парты. Мы продолжим наш урок.
VI. Закрепление изученного материала
Работа по учебнику
№ 4, стр. 26, рабочей тетради сложение и вычитание с помощью числового отрезка
— Назовите свои ответы. У всех так получилось?
— Откройте учебники на стр. 40 №3. (решить 2 уравнения)
— Перед вами уравнения. Один решает у доски, а остальные в тетради.
— Чем в уравнении является х? (часть \ целое)
№ 7 стр.41 (а)
Задача
(Анализ задачи)
— Прочитайте задачу.
— Что известно в задаче? (Что у Васи было 4 тетради. Он купил еще 6 тетрадей)
— Что нужно найти? (Сколько тетрадей стало у Васи?)
— Начертите схему к задаче.
— Чтобы ответить на вопрос, что мы должны сделать? (сложить количество тетрадей.)
— Что неизвестно: часть или целое? (целое, чтобы его найти, нужно сложить части)
— Находим. Эта задача простая или составная (Простая)
VII. Упражнения для развития навыков письма
Пальчиковая гимнастика
Пальцы делают зарядку
Чтобы меньше уставать
А потом они в тетрадке
Будут циферки писать!
(Сжимать и разжимать пальцы)
— В рабочей тетради выполним задание №7 (в)
— Что известно в задаче?
— Что нужно найти?
— Что неизвестно: часть или целое?
(Если позволяет время №2, №4, №5)
VIII. Рефлексия
Нарисуйте на полях тетради: зелёный кружок– у вас всё получилось, на уроке всё было понятно; жёлтый кружок – не всё было понятно, не всё получилось; красный кружок – требовалось помощь учителя.
Продолжи фразу: Я сегодня узнал…
Я научился…
Я запомнил…
Какой у меня номер? Дифференциация в К-1
В своей книге Как дети учат понятия чисел * Кэти Ричардсон посвятила целую главу составлению и разложению чисел. Вас может удивить название главы: «Сложение и вычитание: части чисел». Эта цитата прекрасно подводит итог:
«Если основные факты должны быть основополагающими, они должны основываться на понимании состава и разложения чисел.”
* Этот пост содержит партнерские ссылки, что просто означает, что когда вы используете мою ссылку и покупаете продукт, я получаю небольшую комиссию. Никаких дополнительных затрат с вашей стороны не взимается, и я ссылаюсь только на книги и продукты, которые я лично использую и рекомендую.
И CCSSM, и Texas TEKS имеют ряд стандартов для детского сада и 1-го класса, относящихся к составлению и разложению чисел, как показано в этой таблице.
Одна важная особенность стандартов, которую часто упускают из виду, заключается в том, что они описывают уровень конкретной или графической поддержки, которую должен получить ученик.Обратите внимание, что K.OA.3, например, утверждает, что учащиеся должны использовать «объекты или рисунки» и записывать разложение с помощью «рисунка или уравнения». В этом стандарте вы слышите каждую фазу в конкретной, репрезентативной, абстрактной (CRA) последовательности инструкций. Обратите внимание на то, как конкретное и графическое связаны с абстрактным (уравнением), чтобы помочь учащимся установить эту важную связь. Стремление учеников к абстрактному или чисто символическому обучению — это верный путь к катастрофе, и это признано в стандартах.
Составление и разложение чисел является настолько важным компонентом числового восприятия, что оно должно составлять основную часть обучения в детском саду и в первом классе. Ричардсон заявляет, : «По мере того, как дети выучивают комбинации, составляющие числа до 10, они достигнут точки, в которой они так хорошо знают части, что могут определить недостающую часть, зная сумму и одну часть». Другими словами, студентам нужно много попрактиковаться в составлении чисел, работая с различными комбинациями каждого числа, прежде чем они смогут разложить числа или найти недостающую часть.В вашем наборе обучающих приемов вы захотите найти самые разные упражнения, чтобы попрактиковаться в составлении и разложении чисел. Эти сообщения в блоге дадут вам идеи для занятий, а также бесплатные подарки, которые вы можете использовать на этой неделе!
- Встряхивание и разлив
- Математик Сделай десять
- Сделай 5 иди и рыбачь
- В пещере
Для всех этих заданий важно понимать, что учащиеся должны освоить комбинации одного числа, прежде чем переходить к следующему.Для ребенка бесполезно практиковаться в составлении и разложении 6, если он не знает комбинаций для 5. Вот тут и проявляется дифференциация. Ричардсон описывает использование «скрытой оценки» для определения беглости ребенка с каждым числом. Чтобы определить, знает ли ребенок все комбинации для 3, попросите ребенка отсчитать 3 фишки или связать кубики. Спрячьте некоторые счетчики и покажите некоторые, попросив учащегося определить, сколько из них скрыто. Например, скройте 1 счетчик и покажите 2. «Если у меня 3 счетчика и 2 отображаются, сколько скрыто?» Продолжайте эту процедуру для каждой комбинации для 3 (скрыть 3, показать 0; скрыть 2, показать 1; скрыть 0, показать 3).Если ученик может назвать все недостающие части для 3, попробуйте комбинации для 4. Когда ученик больше не может легко назвать недостающие части, , что , становится ее номером. Используйте регистрационный лист , чтобы отслеживать номер каждого учащегося, чтобы вы могли различать действия, такие как описанные выше, в зависимости от потребностей каждого учащегося. Например, на этой неделе все ученики могут использовать Shake and Spill на рабочем месте, но каждый ребенок использует свое собственное целевое число. Каждые несколько недель «проверяйте» своих учеников, чтобы определить, готовы ли они перейти к новому номеру.Карточки с отсутствующими деталями — полезный инструмент для периодической оценки.
Может показаться сложным проводить дифференциацию по количеству учащихся, но хорошая новость заключается в том, что несколько увлекательных занятий имеют большое значение. Постоянное чередование занятий поддерживает высокий уровень вовлеченности и позволяет удовлетворить потребности каждого ученика без большой подготовительной работы. Чтобы узнать о других интересных занятиях, ознакомьтесь с Building Number Sense: Games and Activities to Practice Combinations для 10 или этих других сообщений блога , помеченных ключевым словом «compose.”
Decomposing Math Center Activities — Жизнь детского учителя
Здравствуйте! Я пишу, чтобы поделиться разложением математического центра действия, которые вы можете использовать, чтобы укрепить идеи разложения. Продолжайте читать, чтобы взять халява в конце этого сообщения в блоге.
Раньше я разделял действия по декомпозиции. Я люблю учить разложению! Это сложная концепция, но есть ТОННА действий, которые вы можете использовать, чтобы научить этому навыку учащихся начальной школы.
Что разлагается?
Декомпозиция — это разбиение числа на части. Студенты привыкли работать с целыми числами (используя объекты для получения 5) и теперь узнают, что числа можно разбить на части (2 и 3 такие же, как 5). Они будут раскладывать числа, рисуя и используя предметы. Некоторые студенты будут готовы писать уравнения, но когда мы впервые узнаем о разложении, они используют слова, чтобы объяснить свое мышление.
Студенты должны разбирать числа в пределах 10, находить число, равное 10, и решать задачи со словами путем разложения.Цель состоит в том, чтобы развить у учащихся понимание чисел, например научить их гибкости.
Работающие стратегии
Вот несколько стратегий, которые вы можете использовать, чтобы помочь своим ученикам разложить:
- Обучайте их языку, моделируя — покажите студентам, как разложить число, моделируя, как это сделать. Думайте вслух, раскладывая число. Предложите студентам поделиться тем, что они замечают или что их смущает, и используйте это время как возможность прояснить любые недопонимания.Некоторые новые словарные слова, которые вы хотите использовать при моделировании декомпозиции, — это декомпозиция, соединение и , разделение .
- Предоставьте учащимся многочисленные возможности и различные средства выражения своего мышления. Позвольте им рисовать картинки, разыгрывать их, используя все тело и пальцы, а также предметы.
- Научите студентов использовать инструменты обучения, такие как s part-part-who le, числовые связи и десять кадров , чтобы моделировать, как разложить числа.
Действия по разложению номеров
Вот несколько упражнений, которые предоставляют учащимся значимые возможности для разложения чисел.
Покажи это 3 пути
Студенты выбирают карточку с номером. Они раскладывают число кубиками, разбивая кубики на 2 части. Они пишут уравнение или числовое предложение и рисуют картинку.
Сдвинуть и разложить
Ученики помещают 5 или 10 фишек или предметов в кружки.Попросите учащихся сдвинуть несколько фишек в верхний и нижний прямоугольники. Они пишут, как раскладывают число в виде уравнения или числового предложения.
Мат частично-частично-весь
Учащиеся выбирают число и разлагают его, используя коврик «частично-частично-целое».
Количество облигаций
После того, как они выберут число, учащиеся раскладывают это число, используя числовую связь.
Giant Number Bond
Иногда больше может быть лучше! Студенты могут разложить число, используя большое число, и написать, как они разложили число на столе (или листе записи!)
Перевернуть и разложить
Эта игра так весело! Учащиеся переворачивают карточку и используют рамку из десяти, чтобы показать, сколько еще предметов им нужно сделать 10.
Они также практикуют изготовление 5.
Постройте и запишите недостающее число
Учащиеся выбирают уравнение и решают пропущенное число с помощью десятичной рамки.
Сделай это тремя способами
Это мероприятие произвело на моих учеников большой успех! Мои ученики всегда больше всего волнуют самые простые игры! Учащиеся выбирают целевое число и раскладывают его 3 способами. Вы можете попросить их использовать предметы или нарисовать картинку. Затем они написали предложение или уравнение, чтобы показать, как они разложили число.
Пазлов!
Мои ученики любят головоломки! Это отличная партнерская игра, которая заставит ваших учеников поговорить о разложении. Они выбирают уравнение и сопоставляют его под правильным номером.
Решить и закрыть
Это отличная игра, которая помогает ученикам задуматься о различных способах разложения числа. Они выбирают домино, складывают числа, чтобы найти сумму, и закрывают ответ на игровом поле.
Вращай и решай
Моим ученикам нравится эта практическая игра! Тем более, что я купил пластиковые спиннеры, и им больше не нужно пользоваться карандашом и скрепкой (их волнуют мелочи!).Они вращают вертушку, вычисляют, сколько еще им нужно, чтобы получить 10, и закрывают рамку из десяти, отображающую это число на игровом поле.
Сделайте 10!
Ученики пересчитывают монеты в копилке и с помощью рамки из десяти показывают, сколько еще им нужно, чтобы заработать 10.
Коврик для разговоров по математике
Это отличное задание, которое поможет студентам развить словарный запас для разложения чисел. Я преподаю английский как второй язык, и это упражнение помогло мне видеть и произносить «части» и «целые» числа.Студенты выбирают числовую связь и моделируют ее, используя коврик «часть-часть-весь». Затем они пишут, как разложили число, и делятся своей работой с партнером.
Действуй!
Есть 3 Действуй! слово проблемные коврики. Учащиеся разыгрывают словесные задачи с помощью предметов и записывают их разложение, записывая уравнение или числовое предложение.
Сделайте 5! Настольная игра
Это игра для двоих. Один ученик переворачивает карточку и говорит, показывают ли пальцы, как можно набрать 5 или нет.Если это способ сделать 5, они передвигают пешку на одну позицию вверх. Они продолжают играть, пока не дойдут до конца.
Уф! Это много разлагающих игр!
Щелкните изображение ниже, чтобы получить Slide and Decompose:
Вы хотите, чтобы все задания математического центра разлагались? Нажмите на изображение ниже, чтобы купить в моем магазине TpT!
Какие еще действия по декомпозиции вы использовали в своей инструкции? Дайте мне знать в разделе комментариев ниже.
Любовь,
Тройник.
Составление и разложение чисел для сложения и вычитания
У ваших учеников есть трудности с составлением и разложением чисел при сложении и вычитании ? Мои ученики борются с тем, чтобы разбить число на части и использовать его части для вычислений. Такой способ восприятия чисел требует огромной практики и тяжелой работы!
Старые фразы, такие как заимствование и перенос, больше не используются в Common Core.Они не имеют никакого значения, связанного с математическим мышлением, поэтому я думаю, что хорошо, что мы их не используем. Точно так же запоминаются запоминающиеся фразы и стихи, но мне интересно, насколько студенты понимают и могут объяснить, что происходит в процессе.
Моя цель — научить моих учеников понять, как работают числа , как числа можно разбить на части и собрать вместе по-разному . Я хочу, чтобы они гибко думали о числах и применяли эту гибкость к сложению и вычитанию.
В начале года мы начали с разложения и составления меньших чисел, чтобы получить 10. Используя факты +8 и +9, мы посмотрели, как составление 10 может помочь нам в решении проблем.
Хотя я дал студентам стратегию, потребовалось много практики, чтобы помочь им понять преимущества ее использования вместо того, чтобы считать на пальцах. Я создал пакет математических станций, сосредоточенных вокруг использования 10s для сложения (+9 и +8) . С этого началось наше путешествие по разложению чисел.
Позже в том же году, когда мы перешли к сложению больших чисел, мы снова пересмотрели стратегию make 10 для сложения чисел, но работали над добавлением десятков и получением 100 для сложения.
Одна из стратегий, которая хорошо сработала для учащихся, заключалась в том, чтобы они рисовали палочки, обозначающие количество десятков в каждом числе, а затем считали и вычеркивали каждую палочку по мере их подсчета. Когда ученик набирал 100 очков, он останавливался и писал 100, затем начинал заново и считал оставшиеся палочки.
Благодаря этому упражнению ученики начали видеть «понятные числа» и понимать, как использовать 100 при сложении.
Еще один ресурс, который мы использовали в этом году, — «Разборка числовых головоломок».Это помогло студентам понять, что 44 равно 40 + 4, что также равно 30 + 14 и 30 + 10 + 4. Не все мои дети сделали прыжок, чтобы увидеть, как все эти числа связаны и как разложить числа. У нас еще немало работы осталось!
В ноябре мы использовали числовые головоломки, и зимой я снова вытащил их, чтобы обсудить с несколькими моими учениками, которым нужно еще немного укрепить их.
Последнее, что я сделал в последнее время, — это выдавал учащимся рамки предложений при вычитании.Пару недель назад я перехожу с написания горизонтальной задачи на задание ученикам вертикального вычитания. Они не знали, что делать! Им было так тяжело!
Мое решение заключалось в том, чтобы дать студентам рамки предложений. Я начал с простых, например: «Их недостаточно, чтобы вычесть _____ единиц. Вам не нужно / не нужно разбирать десятку. Сейчас их ___ десятков и ___ единиц ».
Честно говоря, я бы не стал предлагать студенту разлагать десять, чтобы вычесть 4, но нам нужно было попрактиковаться в концепции с меньшими числами, прежде чем переходить к большим числам.
Разобрать десятку представляет собой набор фреймов предложений и заданий типа scoot, в которых учащиеся смотрят, нужно ли им разложить десять, прежде чем решать задачи.
Мы также использовали числовые линии, и я попросил студентов нарисовать блоки с основанием 10. Мои ученики добились наибольшего успеха, используя числовые линии и считая от вычитаемого.
У меня есть набор заданий по математике, где студенты практикуют вычитание, используя различные стратегии и инструменты. Эти упражнения действительно заставляют учащихся задуматься о математике и научиться гибко обращаться с числами.
Как развить концептуальное понимание составления и разложения чисел в классе? Как вы помогаете студентам гибко думать о числах? Я хотел бы услышать больше идей!
Если вы преподаете во втором классе, вам могут понравиться несколько страниц из некоторых моих двузначных продуктов сложения и вычитания. Я собрал этот PDF-файл с ресурсами в качестве выборки из нескольких различных продуктов, которые действительно подчеркивают всю работу, которую мы делаем в нашем классе для углубленной разработки этих стратегий.
Различные компоненты сэмплера могут использоваться всей группой или небольшой группой и идеально подходят для того, чтобы помочь вашим ученикам мыслить нестандартно, когда дело доходит до решения сложения и вычитания многозначных чисел.
Возможно, вас заинтересует. . .
Ценность преподавательского места для первоклассников
Разрядное значение: значение, присвоенное каждому разряду в числовом значении, в зависимости от основания системы счисления. Это не совсем то определение, которое доступно и полезно учителю начальных классов! Конечно, нам нужно преподавать эту важную концепцию нашим студентам-математикам как основу нашей системы обозначений и, что, возможно, более важно, как основу их будущего изучения математики.Эти молодые студенты когнитивно готовы изучать, понимать и целенаправленно использовать идею позиционной ценности. Благодаря этому модулю сами учителя начальных классов получат более полное понимание ценности места как реального жизненного навыка и впоследствии будут использовать стратегии и уроки для своих учеников, чтобы получить тот же результат. Ключевые идеи этого раздела заимствованы из сингапурской математической программы, неизменно успешного подхода к обучению учащихся начальной школы.
Как учитель первого класса в отдельном классе в Нью-Хейвене, в моем классе 26 учеников шести и семи лет, а иногда и восьмилетний.Наш район / магнитная среда — это благоприятная среда, когда ученики приходят в школу каждый день из разных домашних обстоятельств и с разницей в академическом уровне. В результате этих переменных у детей разный уровень базовых знаний и жизненного опыта. Класс представляет собой смесь разных этнических групп, экономических слоев, а также сильных и слабых социальных и эмоциональных факторов.
В течение последних двух лет в нашем школьном округе апробируются новые учебные программы по элементарной математике.Моя школа, в частности, работала с двумя разными математическими программами, обе в первые годы обучения. Первый год — это математические выражения, опубликованные Houghton Mifflin и разработанные Детским исследовательским проектом по математическим мирам. Вторая, выпущенная в этом году, — это ThinkMath, опубликованная Harcourt и разработанная Education Development Center, Inc через Национальный научный фонд. Каждая из этих двух пилотных программ представляет разные стратегии по основам математики. Трудно предсказать, как ученики будут работать в будущих классах, имея эти два разных подхода в первом и втором классах.Мы продолжаем работу над ThinkMath в следующем году, что обеспечит некоторую последовательность. Включив этот модуль в нашу учебную программу по математике, я надеюсь эффективно научить студентов концепции места, которая, безусловно, является важным навыком, независимо от того, какого издателя мы наконец определим для округа!
Обязанностью каждого учителя математики начальной школы является эффективное использование требуемой учебной программы по математике, в конечном итоге направляя своих учеников через последовательный путь концепций и практики.Выбор «концептуальных путей» определяется и оформляется авторами и издателями каждой учебной программы. Нам, как профессионалам, даются определенные ресурсы, которые могут нам помочь. Они принимают форму руководств для учителей, повышения квалификации, групповых встреч и занятий по планированию. Эти ресурсы необходимы для успеха учебного года для каждого из нас и учебного года для студентов. Конкретные стратегии обучения и концепции математики в рамках учебной программы должны быть усвоены и полностью поняты учителями, использующими ее.
В результате принятия закона «Ни одного отстающего ребенка» штаты стремятся повысить успеваемость по математике, чтобы затем улучшить результаты государственного тестирования, которое должно проводиться каждый год с третьего по восьмой класс. Из-за стремления добиться успеха в достижении этой цели школьные округа обращаются к новым учебникам, совершенствуют технологии и находят способы подготовить учащихся к достижению более высоких результатов. В настоящее время многие школы и учителя испытывают то же, что и наш округ — пробуют несколько вариантов.Переменная, на которую не обращают внимания, — это сами учителя. Хорошие учителя должны лежать в основе прочного математического образования.
Эффективное преподавание математики зависит от твердого понимания материала. Учителя должны уметь заниматься математикой, которую они преподают, но этого недостаточно для преподавания. Эффективное обучение требует понимания основного смысла и обоснования идей и процедур, которые необходимо преподавать, а также способности устанавливать связи между темами.Знания педагогического содержания, знание того, как преподавать концепцию или предмет, должны быть согласованы со знанием предмета, чтобы создать продуктивный опыт обучения для ученика. Вместе они позволяют понять ответы учащихся и определить цель урока.
Статья Хилла, Болла и Шиллинга о знаниях педагогического содержания предполагает, что, хотя знания учителей о содержании и учащихся не всегда легко измерить, из первоначального исследования видно, что новости хорошие.Учителя в этом исследовании продемонстрировали знакомство с математическим мышлением учащихся, например, предсказывая типичные ошибки учащихся. Понимание того, как думают ученики, отличается от чистого содержания или педагогических знаний и показывает навыки учителя и понимание, необходимые для успешного обучения и роста учеников. Поскольку учителя видят работу учеников, слышат утверждения учеников и видят, как ученики решают проблемы, они постоянно думают о том, что делают ученики и как они думают. Разработка инструкций и мотивация студентов к обучению — это потенциальные положительные результаты этих уникальных знаний. 1
У меня двоякое намерение и цель при написании этой учебной программы. Первоначально подразделение будет сосредоточено на расширении концептуальных знаний о числовой стоимости и порядке величины. Эта первая цель позволит более успешно выполнить вторую задачу, которая состоит в том, чтобы затем первоклассники развили с помощью математических упражнений концепцию ценности места. Этот блок охватывает двухзначные числа и заканчивается первым трехзначным числом в нашей системе счисления, 100. Основная цель для этих студентов — узнать, что двузначное число состоит из определенного количества десятков и определенного количества единиц. .Ключевой принцип оценки, который следует усвоить, заключается в том, что десятки больше, чем единицы, и, в частности, если даны два числа, то с большей цифрой десятков больше. Основная идея этой концепции — это то, что обозначает цифра в определенном месте. Это приведет к следующему уровню инструкций, который складывает и вычитает двузначные числа.
Этот блок будет использовать месяцы до 100 -го дня учебного года для подготовки к празднованию этого дня. В начальных классах по всей стране стало стандартной практикой отмечать 100 -й день школы.Конечно, это монументально не только как число, но и как ориентир для учителей и учеников, поскольку продолжительность обучения в общеобразовательной школе составляет 180 дней. Это, конечно, может стать веселым, захватывающим, ожидаемым днем активности, практики и подкрепления.
Чтобы добиться успеха в этом вопросе, предметные знания учителя о ценности места помогут обеспечить более глубокое понимание для учеников. Ценность места кажется достаточно простой концепцией и, безусловно, встречается в наших учебниках для первого класса или рабочих тетрадях с руководствами по языку для учителей.Так должно быть, что мы готовы и готовы учить. Однако недостаточно знать как, нужно знать почему. Как учитель очень маленьких детей, моя задача — дать им прочную и полную основу, которую можно использовать на уроках математики и на протяжении всего обучения. На самом деле это слишком важно, чтобы не заметить и пролететь быстро и неподготовленно.
В широко распространенном сравнении мировых математических навыков, Trends in International Mathematics and Science Study, Сингапур постоянно занимает первое место среди участников.Сингапур — процветающая, многокультурная, многоязычная страна с 4 ½ миллиона человек, чьи четвертые и восьмые классы достигли этого статуса. 2 В сингапурской системе математики мирового класса есть компоненты качества, согласованные с целью подготовки учащихся, которые в совершенстве изучают математику. Эти компоненты включают в себя в высшей степени логичную национальную систему математики Сингапура, математически богатые проблемные учебники, сложные экзамены по математике и высококвалифицированных учителей математики, чья педагогика сосредоточена на обучении до совершенства . 3
Начинающие математики часто испытывают трудности с пониманием абстрактных математических понятий. Учащимся первого и старшего классов необходимо наглядное представление математических идей. Числа — это идеи. Стратегия четких иллюстраций для представления идеи и закрепления навыков является важной частью этой учебной программы. Поскольку шестилетний-семилетний ребенок не достиг абстрактного мышления и не имел достаточного относительного опыта, событие или опыт должны быть визуальными, слуховыми и / или тактильными.Это кажется более ясным и, возможно, более логичным при обсуждении грамотности, помогающей связывать слова с изображениями, например: «Кот на дереве». Студент будет читать предложение, глядя на иллюстрацию, показывающую то же самое. Мы должны признать, что это в равной степени применимо даже к математике.
Сингапурские иллюстрации демонстрируют подход от конкретного к живописному к абстрактному. Такой подход позволяет студентам начать осмысленное изучение математики, понимая математические концепции до того, как изучать «правила» или формулы.Например, текст для первого класса в Сингапуре начинается с пустого прямоугольника и числа и слова, обозначающих «ноль». Ниже находится прямоугольник с одним роботом внутри, а также число и слово, обозначающие «один». Затем прямоугольник с двумя куклами, цифрой и словом «двое» и так далее. Страница очень наглядная, но относится к чему-то очень конкретному. Рядом с картинками — точки. Начиная с числа шесть (представленного шестью ананасами), точки расположены в два ряда, так что шесть представлены как один ряд из пяти точек и второй ряд с одной точкой. 4
Обучение мастерству — еще один ключевой компонент этого подхода. Темы подробно освещены и преподаются в совершенстве. Сразу после обучения новым концепциям ученики занимаются разнообразными математически сложными задачами, чтобы обеспечить их глубокое понимание. «Сингапурская математика» предназначена для развития математических мыслителей, проводя учащихся по составным частям задачи, прежде чем просить их решить проблему целиком. Убедившись, что учащиеся действительно понимают, это позволит им добиться большего успеха при введении новых концепций.
«В сингапурских текстах не особо много говорится о концепциях, но они представлены в правильной и экономичной форме», — сказал Роджер Хоу, профессор математики Йельского университета. «Он обеспечивает основу для очень упорядоченного и систематического концептуального понимания арифметики и математики». 5
Эта учебная программа будет охватывать введение числового значения после того, как будут освоены навыки подготовки к математике, включая заучивание числовых имен до 10 (и их порядковый номер) и использование этих чисел для подсчета количеств, развитие навыков и навыков с числами, практика с числами, произнесение чисел, их запись и чтение с последующим простым сложением и вычитанием, или, как говорит язык этого блока, составление и разложение чисел до 10.
Сохранение узкого диапазона будет важным для овладения этим навыком. Студентам необходимо будет использовать предыдущие знания, чтобы подготовиться к пониманию числовой ценности. Умение составлять и разлагать десятку существенно помогает в обучении сложению и вычитанию в пределах 20.
Я бы охарактеризовал это как скорее концептуальную единицу, чем процедурную учебную программу. Классные занятия будут включать математические факты до 20 или сложение с составлением и вычитанием с разложением в пределах 20, работу с манипуляторами и, в конечном итоге, использование этих концептуальных знаний при работе с двузначными числами, превышающими 20.Из-за тесной связи между этим модулем и сингапурским математическим подходом стратегии в этом модуле будут отражать их. Цель здесь — способствовать прочному изучению этой темы в логическом и последовательном порядке.
Начнем с того, что цифры в разных местах имеют разное значение или обозначают разные значения. Когда учащиеся изучают регулярное сложение и вычитание, разрядное значение становится для них более значимым, поскольку они должны выстраивать цифры с одинаковым разрядным значением. После этого, изучая сложение с составлением и вычитание с разложением, учащиеся изучают идею составления и разложения на единицу более высокого значения.Состав и декомпозиция единицы являются важными аспектами концепции места. Студентам важно знать, что разряд — это математическое понятие, а не метка столбцов для выстраивания цифр.
Одна из стратегий обучения студентов — заставить их думать о сложении, когда они выполняют вычитание, обратную операцию. Это поможет облегчить их концептуальное обучение. Это дает представление о плавном движении между этими двумя операциями.Обратные операции — один из основных принципов, лежащих в основе отношений между операциями математики.
Составление и разложение — это другой способ обучения сложению и вычитанию. Эти два термина позволяют студентам понять, что числа могут идти вместе и расходиться. Сложение с переносом называется сложением с составлением — вычитание с перегруппировкой называется вычитанием с разложением. Состав и декомпозиция единицы являются важными аспектами концепции места.Цель состоит в том, чтобы подчеркнуть, что 1 десятка состоит из 10 единиц и может быть разложена на 10 единиц. 6
Учащиеся должны иметь четкое представление о ставке для составления единицы более высокой ценности, чтобы они могли лучше понять, почему единица более высокой ценности разлагается на 10 единиц более низкой ценности.
Четкое понимание концепции на порядок повысит эффективность преподавания этого раздела в классе. Этот уровень информации слишком сложен для младших классов начальной школы, но наличие этих базовых концептуальных знаний соответствует философии истинного понимания перед преподаванием.Поскольку учащиеся находятся на разных уровнях, подготовка к дальнейшему объяснению этой концепции дает ребенку возможность понять более полно.
Порядки величины обычно используются для очень приблизительных сравнений. Если два числа отличаются на один порядок, одно примерно в десять раз больше другого. Если они различаются на два порядка, они различаются примерно в разы http://en.wikipedia.org/wiki/100_%28number%29 100. Два числа одного порядка величины имеют примерно одинаковый масштаб: большее значение меньше чем в десять раз меньшее значение.
Например, предположим, что средний рост человека составляет около 1,7 метра (около 5 футов 7 дюймов). Для простоты округлим 1,7 метра до ближайшей степени 10, которая составляет 10 0 м. (или 1 м). Это не означает, что средний рост человека составляет всего 1 метр, а скорее средний рост ближе к 1 метру (или 10 0 метра), чем к 10 метрам (или 10 ). 1 метра). Точно так же, округляя высоту муравья, которая составляет примерно 8 x 10 — 4 метра, до ближайшей степени десяти дает 10 — 3 метра.Другими словами, высота муравья составляет 10 — 3 метра. Теперь, если мы сравним рост человека (10 0 метра) с высотой муравья (10 — 3 метра), мы получим соотношение рост человека / рост муравья = 10 0 /10 — 3 = 10 0 — ( — 3 ) = 10 3 = 1000.Человек примерно в 1000 раз (или в 10 3 раза) выше муравья. Другими словами, человек на 3 порядка (3 степени 10) выше муравья.
Наша общая десятичная система представляет собой очень сложный метод эффективной записи целых чисел. Он использует всего 10 символов (цифры: 0,1,2,3,4,5,6,7,8,9), расположенных в тщательно структурированные группы, для выражения любого целого числа. Кроме того, он делает это с впечатляющей экономией. Чтобы выразить общую численность населения мира, потребуется всего лишь десятизначное число, для записи которого потребуется всего несколько секунд.
Это введение и объяснение из эссе доктора Хоу о значении места дает пример концепции порядка величины. Как он поясняет в этом эссе, первое, что нужно знать о десятичной системе счисления, — это то, что десятичное выражение числа неявно разбивает число на сумму чисел особого типа.
7 452 = 7 000 + 400 + 50 + 2
Это называется развернутой формой. Хотя это не первый навык, важно построить концептуальные знания определенного порядка.Ограничение знаний по предмету узким кругом ограничивает способность учителя продвигать концептуальное обучение своих учеников. Знание важности этого базового навыка улучшит способность учащихся понимать, почему, а не как.
Слагаемые в развернутой форме числа — разрядные компоненты числа. Каждый компонент разряда представляет собой цифру (возможно, 0), умноженную на степень 10:
.7000 = 7 × 1000 = 7 × (10 × 10 × 10) = 7 × 10 3
400 = 4 × 100 = 4 × (10 × 10) = 4 × 10 2
50 = 5 × 10 = 5 × 10 1
2 = 2 × 1 = 2 × 10 0
Одноразрядное число — это цифра, умноженная на номинал.
Порядок величины также может быть описан как количество нулевых цифр, используемых для записи номинала, или как количество цифр меньше, чем общее количество используемых цифр. Под порядком величины (ненулевого) числового значения мы подразумеваем порядок величины его номинала. Наконец, порядок величины десятичного числа определяется как порядок его наибольшей (ненулевой) составляющей разряда. Таким образом, 7 452 имеет порядок величины 3, такой же, как его самый большой десятичный компонент, 7000; а 400, 50 и 2 имеют порядки 2, 1 и 0 соответственно. 7
В рамках этой единицы работы с двузначными числами следует помнить важный принцип: двузначное число — это столько десятков и столько единиц, например, 47 — это четыре десятки и семь единиц. Затем добавление десятков и единиц должно стать естественным с помощью руководства и обсуждения. Опять же важна логическая последовательность. Перед представлением двузначного сложения важно установить принцип «сделать десять». Используя модель сингапурской математики, сложение фактов — это не просто список для запоминания, а возможность начать понимать структуру системы счисления.Акцент делается на процессе преобразования десяти единиц в 10, когда сумма цифр больше 10, и на разложении 10 обратно на единицы в соответствующих задачах на вычитание.
И, как говорилось ранее, вычитание должно быть связано со сложением до тех пор, пока учащиеся не подумают об этом как об отмене сложения. Помня, что семьи (или в этой учебной программе числовые связи) не ограничиваются однозначными числами. Этот процесс связывания задач на вычитание с задачами на сложение помогает учащимся понять смысл вычитания.
Числовые связи похожи на семейства фактов, но не представлены в виде уравнения. Студентов необходимо научить определять части в целом. Следует использовать примеры с легко идентифицируемыми характеристиками, такими как размер или цвет, чтобы учащийся мог легко разделить целое на две части. Счетные элементы, вырезы с картинками и карточки с картинками можно использовать для представления ярких и разнообразных примеров для студентов, чтобы они могли практиковаться в определении частей и весь.
Идея представления числовых связей состоит в том, чтобы использовать картинки, чтобы выразить, что одно большое число состоит из двух меньших чисел и что вам нужно сделать большое число, начинающееся с одного из маленьких чисел, и другое маленькое число.Уравнения, которые выражают то, что говорит связь чисел, будут семейством фактов. Опять же, это навык, который вводится графически перед использованием чисел. Примером для начинающих студентов может быть изображение 5 яблок, 3 маленьких и 2 больших. Затем учеников попросят рассказать историю о картине. Есть 5 яблок; 2 большие; 3 маленькие.
Подсчет и сравнение
Учащиеся научатся считать, читать и писать в пределах 20. Двузначные числа в пределах 20 вводятся как 1 десятка, а дополнительные 20 — как 2 десятки.Чтобы подсчитать такие объекты, как вырезки из картинок, ученики сначала составляют 10, затем они могут рассчитывать от 10. Числовые карточки используются, чтобы помочь студенту распознать цифру, представляющую число в пределах 20. В то же время соответствующее числовое слово может быть написанным, чтобы помочь учащимся связать числовое слово с символическим представлением.
Когда ученики познакомятся с числами в пределах 20, они также научатся считать в обратном порядке в пределах 20. Это поможет им вспомнить числовую последовательность в пределах 20, что, в свою очередь, поможет при сравнении чисел в пределах 20.
Студенты сначала знакомятся с сравнением количества объектов, таких как животные и счетчики, между двумя или более наборами перед абстрактным сравнением чисел. Во время сравнений они будут использовать термины больше, больше, меньше и меньше.
Сложение и вычитание
Студенты научатся складывать, сделав 10 вначале. Для демонстрации этого метода используются вырезы из рисунков. Затем используются числовые связи, чтобы показать символическую форму сложения, которая помогает ученику перейти к сложению без наглядных пособий.
При вычитании учеников сначала учат группировать объекты по единицам и десяткам, прежде чем выполнять действие по удалению желаемого количества объектов во время вычитания. Они считают оставшиеся предметы, чтобы найти ответ на вычитание. Числовые связи используются снова, чтобы отобразить символическую форму вычитания и показать, что удаление может иметь место до десяти или единиц.
Подсчет
Как и при обучении счету до 10 и 20, учащиеся сначала научатся читать и писать числовые символы и числовые слова для чисел до 40.Вырезки из изображений снова используются для отображения количества, в то время как числовые символы и числовые слова обучаются вместе с количеством.
Студентов постепенно учат считать до 40. Сначала их учат считать до 30, а затем до 40, сделав сначала десять. Используя вырезки из картинок и карточки с цифрами, учащиеся научатся распознавать логический рекламный шаблон, согласно которому счет свыше 20 совпадает с шаблоном счета свыше 30.
Студенты будут изучать числовую последовательность и понятие «больше и меньше, чем» с помощью заданий, включающих поиск числа 1, 2 или 3 больше или меньше заданного числа.Поняв эти концепции, учащиеся смогут с легкостью сравнивать числа и располагать заданный набор чисел в порядке возрастания или убывания.
Сложение и вычитание
Поскольку учащиеся научились интерпретировать двузначное число в терминах десятков и единиц, это лучше подготовило их к сложению и вычитанию с переименованием и без него.
Студентам сначала представлены примеры сложения и вычитания без переименования.Сложение и вычитание без переименования можно продемонстрировать с помощью комбинации вырезок из изображений и числовых связей. Используя вырезки из картинок, учащимся показывают, что такое сложение и вычитание происходит внутри объектов, не сгруппированных в группу из десяти, и что нет никаких изменений в объектах, сгруппированных в группы из десяти. Связи с соответствующими числами используются, чтобы показать, что происходит на абстрактном уровне. Показано, что сложение и вычитание влияют на число в разряде единиц, в то время как число в разряде десятков не изменяется.Обратное происходит при сложении и вычитании десяти.
Студенты также научатся применять метод сложения и вычитания с учетом и обратным отсчетом для сложения или вычитания 1, 2 или 3 из заданного числа для чисел до 40.
При показе сложения с переименованием с использованием прямоугольных вырезов учащиеся должны научиться складывать 10, чтобы получить ответ. С помощью вычитания учащиеся узнают, что им нужно вычесть из десяти, чтобы получить ответ.Демонстрации сложения и вычитания с переименованием включают использование прямоугольных вырезов, прежде чем перейти к их демонстрации на абстрактном уровне с использованием числовых связей.
Десятки и единицы
Теперь учащиеся научатся считать, читать и записывать целые числа до 100. Сначала им будут представлены десятки, то есть 50, 60, числовые символы и числовые слова. Затем, используя счетные предметы и числовые карточки, учащиеся увидят, что они могут считать десятками и единицами, и написать соответствующие числовые символы.Они также должны уметь делать обратное, то есть определять, сколько десятков и единиц в данном двузначном числе.
Оценка
Учащиеся научатся оценивать количество предмета в контейнере, сравнивая пропорцию неизвестного количества с известным количеством в другом контейнере того же типа. Этот метод оценки полезен для количеств, которые различаются примерно на десять или кратны десяти.
Чтобы студенты могли прийти к разумным оценкам, им необходимо испытать различные сценарии, требующие оценки, например, количество предметов, которые могут храниться в контейнерах различных размеров.Это необходимо для развития таких навыков, как суждение о размере предмета и контейнера и составление разумных оценок.
Урок первый
Задача: учащиеся будут считать в пределах 20, составляя (наращивая) 10, а также читая и записывая цифры от 11 до 20 и соответствующие им числовые слова.
Материалы: магнитные вырезки для прикрепления к классной доске, учебники для студентов
Процедура: Покажите набор вырезанных изображений, например яблок или цветов.Убедитесь, что вырезов меньше десяти. Попросите ученика подсчитать количество вырезов. Добавляйте вырезки для картинок один за другим, пока общее количество не станет десять. Каждый раз, когда добавляется картинка, попросите учащегося назвать сумму. Добавьте еще один вырез прямо под первым вырезом, показывая один ряд из 10 и еще один. Попросите учащихся сказать «одиннадцать». Напишите на доске числовое слово «одиннадцать» и цифру «11». Попросите учащихся скопировать числовое слово и число в свои тетради. Укажите учащимся, что одиннадцать написано как «11», чтобы показать «десять и один» как строку из десяти пунктов и еще один пункт.Пример будет выглядеть так:
одиннадцать
11
Добавьте еще один вырез во втором ряду, аккуратно ниже второго выреза в первом ряду. Попросите учащихся сказать «двенадцать» и написать числовое слово и цифру. Напомните им, что для двенадцати есть один ряд из десяти и два дополнительных элемента.
Продолжайте добавлять вырезки изображений один за другим, пока общее количество не станет 20. Каждый раз записывайте число, как числовое слово, так и как число. Попросите учащихся произнести числовое слово вслух, а также записать числовое слово и цифру в своих тетрадях.Когда будет 20, объясните, что этот символ означает «две десятки и ничего», как видно из двух рядов по десять элементов.
Покажите набор вырезок с картинками с общим количеством от 10 до 20. Попросите учащихся сосчитать до суммы один за другим, правильно произнося числовое слово. Повторите это с разным количеством вырезов.
Напишите на доске число от 10 до 20. Попросите учащихся нарисовать в своих тетрадях одинаковое количество точек. Попросите их нарисовать группу из десяти человек, а затем лишних в отдельной группе.Повторите это с разными числами.
Покажите набор вырезок из картинок, случайным образом распределенных на доске. Попросите одного ученика подойти к доске, чтобы выбрать 10 фигурок и сложить их в аккуратный ряд. Попросите другого ученика сделать вырезы один за другим из оставшихся вырезов. Попросите учащегося использовать вырезы, чтобы сформировать еще один ряд, при этом подсчитывая новую сумму, начиная с 10, один за другим. Когда они закончат, пусть они произнесут название номера. Напишите цифру и спросите, о чем нам говорит 1? О чем нам говорит (число в разряде единиц)? Спросите, слышат ли они части числа в имени.То есть слышат ли они «десять» в «четырнадцати»? (Звучит немного иначе, не так ли? Но если задуматься, то можно услышать «десять». А еще четыре?
Повторите этот процесс, используя различное количество вырезок изображения. В конце выделите этот метод выделения сначала 10 объектов, а затем отсчитайте от 10.
Урок второй
Задача: учащиеся сложат два однозначных числа, используя стратегию «составить десять».
Материалы: магнитные карточки-вырезки для классной доски
Процедура: Отобразите набор из 10 вырезок для изображений.Попросите учащихся пересчитать их. Добавьте 2 выреза для картинок под первый набор. Попросите учащегося подсчитать количество добавленных элементов. Обращаясь к двум числам, напишите вопрос на доске: 10 + 2 =?. Попросите учащихся узнать ответ, подсчитав общее количество элементов. Затем попросите их написать законченное предложение-добавление в своих тетрадях.
10 + 2 =?
10 + 2 = 12
Отобразите на доске две группы вырезок с изображениями.Попросите учащихся подсчитать количество элементов в каждой группе. (6, 7)
Ссылаясь на два числа, напишите вопрос на доске: 6 + 7 =?. Попросите учащихся найти общую сумму, подсчитав предметы. (13) Предложите другой способ подсчета, чтобы получить общее количество предметов. Попросите учащихся сосчитать только второй кластер, начиная с одного, больше, чем количество элементов в первом кластере. (7, 8, 9, 10, 11, 12, 13) Попросите учащихся написать законченное дополнительное предложение в своей тетради.
6 + 7 =?
6 + 7 = 13
Повторите процесс подсчета, начиная со следующего числа, на этот раз перемещая элементы по одному в другой кластер по мере их подсчета, пока общая сумма не станет 10.
Попросите учащихся подсчитать количество предметов, оставшихся во второй группе. (3) Затем объясните, что общее количество теперь можно определить, прибавив 10 к сумме, оставшейся во втором кластере. Попросите учащихся сказать: 6 + 7 = 13 то же самое, что 10 + 3.
Урок третий
Задача: учащиеся отсчитают до 40, сделав сначала десятки. Они будут читать и писать числовые символы от 21 до 40 и соответствующие числовые слова.
Материалы: карточки с магнитными вырезками для классной доски, карточки с номерами 20, 30, 40 и 1-9
Процедура: Отобразите 16 вырезок изображений. Попросите учащихся пересчитать их Добавляйте вырезы один за другим, пока общее количество не станет 20. Это превратится в два ряда по десять картинок вырезов. Каждый раз попросите учащихся назвать текущую сумму.Напомните учащимся, что у номеров с 11 по 19 есть особые имена. Напишите числа на доске в столбик. Позовите учащегося к доске и попросите его написать числовое слово рядом с каждым из них.
20
двадцать
Добавьте еще один вырез. Скажите студентам, что их всего двадцать один. Попросите учащихся произнести вслух двадцать один. Покажите ученикам, что это 2 десятка и еще 1. Теперь покажите карточки с цифрами для двадцати одного, совместив карточку с цифрами для двадцати с карточкой с номером для одного.Напишите на доске цифру 21 и соответствующее числовое слово.
21 двадцать один
Попросите учащихся скопировать цифру 21 в своих тетрадях и написать рядом с ней «двадцать один». Объясните: мы ставим тире между «двадцатью» и «одним», чтобы показать связь между двумя словами. Так мы пишем числа больше двадцати.
Добавьте еще один вырез на дисплей. Скажите студентам, что их всего двадцать два. Попросите студентов произнести вслух двадцать два.Напишите на доске цифру 22 и покажите соответствующую карточку с числовыми словами. Попросите учащихся скопировать цифру 22 в свои тетради и написать рядом с ней двадцать два.
Продолжайте этот процесс добавления вырезов один за другим, пока общее количество не станет 29, записывая числа и числовые слова, чтобы сформировать четкую последовательность, чтобы учащиеся могли видеть узор. Теперь запишите числа с 21 по 29 в столбец. Попросите учащихся назвать числовые слова и написать их рядом с каждым соответствующим числом.Попросите учащихся таким же образом скопировать их в свои тетради.
Эта же процедура будет использоваться при вводе чисел от 31 до 40.
Урок четвертый
Задача: учащиеся добавят однозначное число к двузначному без переименования.
Материалы: цифровые карточки или меловая доска
Процедура: Отобразите 23 карточки с картинками в кластере. Попросите учеников их пересчитать. Отобразите пять вырезов в другом кластере. Попросите учеников тоже их посчитать.Напишите на доске дополнительное предложение.
23 + 5 =?
Разложите первый набор вырезов на два ряда по десять штук в каждом и поместите оставшиеся три выреза в третий ряд. Добавьте второй набор вырезов в третий ряд. Попросите учащегося подсчитать элементы в первых двух рядах и убедиться, что каждая строка содержит десять элементов. Затем попросите их подсчитать количество вырезов в третьей строке и найти общую сумму в этой строке.
Изобразите ситуацию, используя числовую связь.Предложите учащимся сказать 23: это 2 десятка и 3 единицы. Затем предложите ученикам сказать: 23 плюс 5 — это 2 десятки, а 3 единицы плюс 5 единиц.
Напишите предложение сложения для единиц. Попросите учащихся дать ответ (8) без счета. Используя ответ, измените числовую связь.
3 + 5 =?
Напишите соответствующее предложение сложения и завершите числовую связь. Предложите учащимся сказать: 23 плюс 5 равно 20 плюс 8 единиц.
20 + 8 = 28
Объясните процесс сложения на этом иллюстрированном примере
Повторите процесс для других пар двузначных и однозначных чисел. Убедитесь, что общая сумма меньше 40, а сумма единиц меньше 10.
Урок пятый
Задача: учащиеся будут считать по десяткам, считать в пределах 100, составляя десятки, а также читать и писать числовые символы и числовые слова. Они смогут сказать, сколько десятков и единиц составляют данное двузначное число.
Материалы: 10 связок по 10 соломинок, основа десять блоков, фишки (бусины, бобы, пуговицы)
Процедура: Покажите студентам связки соломинок. Попросите 10 учеников подсчитать, сколько соломинок в каждой связке. Обратите внимание на то, что количество соломинок в каждой связке одинаково; то есть они равные группы. Следовательно, посчитав пучки, мы можем узнать, сколько в них отдельных соломинок. Спросите студентов, могут ли они подумать, как это можно сделать. Затем укажите (даже если они есть), что мы можем считать соломинки десятками, потому что в каждой связке по десять соломинок.Запишите список цифр следующим образом:
1 десять = 10 десять
2 десятки = 20 двадцать
3 десятка = 30 тридцать
4 десятка = 40 сорок
5 десятков = 50 пятьдесят
6 десятков = 60 шестьдесят
7 десятков = 70 семьдесят
8 десятков = 80 восемьдесят
9 десятков = 90 девяносто
10 десятков = 100 сто
Покажите ученикам основу из десяти стержней (10 шт.) И снова попросите их подсчитать, сколько в каждой стержне.Покажите студентам три стержня и спросите, сколько всего. Предложите ученикам считать десятками. Повторите это упражнение, используя другое количество стержней (до 10).
1. Heather C.Hill, et al. «Распаковка знаний педагогического содержания: концептуализация и измерение предметных знаний учителей учащихся».
2. Митчелл Лансберг. «В Лос-Анджелесе сингапурская математика имеет дополнительную ценность»
3. Элизабет Витт, главный редактор. Чему Соединенные Штаты могут научиться у сингапурской математической системы мирового класса (и чему Сингапур может научиться у Соединенных Штатов): исследовательское исследование,
4. Сингапур Начальная математика , 1A.
5. Митчелл Лансберг. «В Лос-Анджелесе сингапурская математика имеет дополнительную ценность
6. Liping Ma. Знание и преподавание элементарной математики: понимание учителями фундаментальной математики в Китае и США., 9-10.
7. Роджер Хоу, Серьезное отношение к ценности: арифметика, оценка и алгебра.
Болдридж, Скотт и Томас Паркер. Начальная математика для учителей . Септон Эш Паблишерс
Карпентер, Томас П. и др. Детская математика: познавательно управляемое обучение. Портсмут, Нью-Хэмпшир: Hinemann, 1999.
Эта книга описывает развитие понимания детьми основных представлений о числах.Авторы предлагают подробное объяснение и многочисленные примеры решения задач и вычислительных процессов, которые практически все дети используют для развития своего числового мышления. Они также описывают, как можно организовать классы, чтобы способствовать такому развитию.
Гарлик, Барри. «Лабиринтный подход к математике Education Next Spring 2005 Vol 4 No. 2 http://www.hoover.org/publications/ednext/3220616.html
Автор, обучая студентов математике, со своей точки зрения обнаруживает некоторые основные проблемы в текущих учебных программах по математике.
Гарлик, Барри. «Чудо-математика» Education Next , осень 2006 г., том 6, № 4, http://www.hoover.org/publications/ednext/3853357.html
Автор обсуждает метод Сингапурской математики, используемый в пригороде США, округе Монтгомери, штат Мэриленд.
Хилл, Хизер К., Дебора Лёвенберг Болл и Стефан Г. Шиллинг. «Распаковка знаний педагогического содержания: концептуализация и измерение тематических знаний учителей учащихся», Журнал исследований в области математического образования, Vol.39, №4, июль 2008 г.
В этой статье описывается попытка концептуализировать и разработать меры совокупного знания учителей о содержании и учащихся.
Хоу, Роджер, Серьезное отношение к ценности: арифметика, оценка и алгебра. http://www.maa.org/pmet/resources/PlaceValue_RV1.pdf
млн лет назад, Липин. Знание и преподавание элементарной математики: понимание учителями фундаментальной математики в Китае и США. Махва, Нью-Джерси: Издательство Лоуренса Эрлбаума, 1999.
Эта книга описывает природу и развитие «глубокого понимания фундаментальной математики», которое необходимо учителям начальной математики, чтобы стать опытными учителями математики, и предлагает, почему такие педагогические знания гораздо более распространены в Китае, чем в Соединенных Штатах, несмотря на тот факт, что китайский язык учителя имеют менее формальное образование, чем их коллеги из США.
Сингапур Начальная математика. Сингапур: Times Media Private Limited, 2003.
Яркие и простые учебники и рабочие тетради, предназначенные для обучения в классе.
ThinkMath! . Центр развития образования, Харкорт, 2008.
Лансберг, Митчелл. «В Лос-Анджелесе сингапурская математика имеет дополнительную ценность», Los Angeles Times , 9 марта 2008 г., http://articles.latimes.com/2008/mar/09/local/me-math9
Вайнштейн, Лавенси и Джон А.Адамс, Предположение: решение мировых проблем на оборотной стороне салфетки для коктейлей. Princeton University Press. 2008.
Витт, Элизабет, главный редактор. Чему Соединенные Штаты могут научиться у сингапурской математической системы мирового класса (и чему Сингапур может научиться у Соединенных Штатов): исследовательское исследование, Алан Гинзбург, Стивен Лейнванд, Терри Анстром, Элизабет Поллок http: //www.air. org / новости / документы / Сингапур
Base Ten Blocks — это набор из единичных кубов, стержней (10 штук), плоских частей (10 стержней) и куба (10 плоскостей).Полезно использовать те, которые могут отображаться спереди класса, либо с диапроектора, либо те, которые можно наклеить на доску. Вы также можете их рисовать, но ученики должны быть знакомы с конкретными предметами.
Счетные предметы, такие как счетчик, пуговицы, кубики, карандаши
Соломинки или палочки для поделок, которые можно складывать в десятки штук с помощью ленты или резиновых лент
Карточки с картинками и вырезки из картинок — В этом модуле используются цветные идентичные вырезки из картинок для демонстрации групп из десяти человек.Предлагаются вырезы из плотной бумаги с изображениями предметов (фруктов, фигур) или картинки из журналов или газет.
Карточки с цифрами — Большие карточки для отображения на доске чисел 10, 20, 30, 40, 50, 60, 70, 80, 90 и от 1 до 9. Карточки с единицами должны соответствовать цифре 0 на поле. десятки карт.
Составление и разложение чисел в дошкольном и детском саду
Составление и разложение чисел — это математический навык, который следует ввести в Pre-K и дополнительно развить в детском саду.Он включает в себя помощь детям в разбивке чисел на части. Ребенок, который умеет составлять и раскладывать числа, понимает, что 2 и 3 вместе составляют 5. Они также будут знать, что 5 можно разбить на 1 и 4. Когда дети привыкают к однозначным числам (0-9), они становятся готовы перейти к двузначным и, в конечном итоге, к трехзначным числам — что называется объединением!
Лучший способ познакомить маленьких детей с составлением и разложением чисел — это начать с простых наглядных изображений, которыми они могут манипулировать.У меня есть три простые идеи, которые вы можете попробовать.
Для этого упражнения требуются пластиковые тарелки с разделами, цветная лента, карточки с номерами (или стикеры) и манипуляторы по вашему выбору.
С помощью цветной ленты разделите пластину на одну большую и две меньшие области. Дети должны поместить карточку с цифрой в самую большую часть тарелки, отсчитать количество манипуляций и поместить их в большую часть тарелки с цифрой.
Затем детям нужно разделить свои манипуляторы на две меньшие части, чтобы представить число, разбитое на части.
Повторите этот процесс, показывая различные способы создания числа.
Используйте пластиковые бусинки, средства для чистки труб, малярную ленту и маркер, чтобы сделать браслеты с цифрами.
Поместите определенное количество бусинок на устройство для очистки труб и соедините концы, скручивая их, чтобы получился браслет в форме круга. После того, как концы будут скручены, оберните кусок ленты вокруг скрученной части. Оставьте немного свисающей ленты, чтобы записать количество бусинок, на которых размещен браслет.
Браслеты позволяют детям видеть все количество и количество, разбитое на две части, когда бусинки разделены по-разному.
К этому занятию также есть дополнение, чтобы дети могли представить свое мышление. Это важный навык, которым дети извлекут пользу и будут использовать по мере приближения к математике в старших классах.
Эта первая версия предназначена для Pre-K. Дети будут представлять, как разбиваются числа в зависимости от того, как выглядит их браслет.
Вторая версия предназначена для детского сада. Дети будут представлять, как числа разбиты в зависимости от того, как выглядит их браслет, а также добавят числовое предложение под ним.
Загрузить коврики
С бусинами, очистителем для труб и стаканчиками из пенопласта вы можете легко создать эти наглядные пособия, чтобы дети попрактиковались в составлении и разложении чисел и количеств!
Напишите число на лицевой стороне чашки, затем отсчитайте то же количество бусинок, которое вы написали на чашке.Разрежьте устройство для чистки труб пополам и проделайте отверстия в верхней части чашки.
Нанижите бусины на устройство для очистки труб и поместите концы устройства для очистки труб в отверстия в верхней части чашки.
И так же, как ваша чашка превратилась в отличный математический инструмент!
Каждая из этих идей дает детям возможность видеть числа как части и манипулировать ими! Попробуйте один или попробуйте все три! 😉
Удачной компоновки и декомпозиции!
Журналов по математике для первого класса
В начале учебного года я поделился постом о том, как приучить учеников начать работу с журналами по математике.Я надеюсь, что вы пробовали намочить ноги журналами, или, может быть, вы пытались это сделать и просто проверяете новую идею или две!
Я начал использовать математические журналы как часть моей управляемой математической ротации три года назад в середине года! Это был такой замечательный опыт!
У меня были сомнения, как студенты отреагируют на ежедневную работу в математическом дневнике. Я знал, что повседневные дела, которые я выполняю, должны им понравиться. Все мы знаем, что средний класс первого класса состоит из учеников, которые начинают как мастеров оригами, так и тех, у кого проблемы с пространством.Я определенно та девочка, которая поднимала руку в поисках помощи, когда дело касалось складывания бумаги в школе. По этой причине я хотел, чтобы все было просто!
Чтобы облегчить жизнь как учителю, так и ученику, я создал образец дневника для каждого занятия. Это меня спасает, потому что дает пример макета прямо в классе. Это также помогает ученикам увидеть, как должны выглядеть складки. Для начала я сокращаю задания, а ученики работают только над их складыванием и правильным расположением.По мере того, как ученики становятся лучше в этом, я выполняю все меньше и меньше резки. Большую часть года студенты могут справиться со всем самостоятельно.
Пара уловок, которые помогут вам, — это разбросать задания на цветной бумаге. Студенты влюбляются в свои математические журналы и начинают сильно гордиться своими шедеврами. В первый год, когда я ввел занятия в математическом журнале, мои студенты МОЛИЛИ меня поторопиться и перейти к занятиям в математическом журнале. Мне пришлось стереть шок с лица, потому что я думал, что это будет борьба, а не любимый поворот !!
На самом деле, все действия выполняются не на цветной бумаге, но я старался делать это в максимально возможной степени.У меня есть маленький друг по имени Astrobrights, который очень помог мне в этом! Мои студенты ОБОЖАЮТ листать свои красочные, заполненные работой журналы. Я получаю большую часть своих статей об Astrobrights на Amazon. (партнерская ссылка) Я люблю запасаться этими разнообразными наборами для математических журналов.
Не все действия нужно раскрашивать. Студенты также могут использовать цветные карандаши для выполнения заданий. В этом задании ниже я прошу студентов раскрасить две части снеговика, которые составляют десять. Затем внутри клапана пишут числовое предложение и решают задачу на сложение.
Когда дело доходит до заданий, которые склеиваются после того, как они были решены, как, например, приведенное ниже, я отрезаю их в сторону. Таким образом, я могу сделать аналогичный пример с камерой для документов, не выдавая никаких ответов.
Еще один небольшой совет — держите свои любимые пустые графические органайзеры или мыслящие карты в корзине занятий в математическом журнале. Когда у вас есть концепция, которая поддается графическому органайзеру, вы можете взять ее и начать!
Некоторые занятия в конечном итоге во многом напоминают занятия по математике.Если есть способ включить ваши манипуляторы в журнальную деятельность, студенты всегда оценят это!
Если вы хотите получать более одного набора за раз, вы можете получить семестровый пакет!
Меня спросили, совпадают ли ежемесячные журналы и ежемесячные математические центры с единицами управляемой математики. Ответ ДА!
Я твердо верю, что ученики первого класса должны независимо работать над уже усвоенными концепциями.Я не хочу, чтобы мои ученики работали независимо над концепцией, которую я все еще предлагаю. Эти ежемесячные журнальные пакеты содержат обзор ранее изученных концепций, а также предоставляют практику с текущими концепциями!
Во время нашего блока математики, после мини-урока в группе, ученики поочередно выполняют 5 заданий по математике. Математический журнал — одно из пяти занятий.
Как вы пользуетесь математическими журналами? Готовы ли вы попробовать?
10 советов по развитию математических навыков в первом классе
В этом возрасте математика должна быть интересной и полезной.Играйте в эти игры и воспользуйтесь возможностью, чтобы показать своему 6-летнему ребенку, как математика вписывается в повседневную жизнь.
Одноклассник по математике
Повторное начало школы может вызвать у вашего ребенка нервную дрожь. Успокойте своего первоклассника, превратив его новый класс в решаемую проблему. Спросите: «Сколько девочек в классе? Сколько мальчиков? Сколько всего? Были ли сегодня дети? » Вычтите отсутствующее число из общей суммы. Использование предметов для представления каждого одноклассника помогает вашему ребенку в математическом мышлении.
Я думаю о числе…
Детям этого возраста не нужно просто считать и вычислять, им нужно чувствовать числа. Эта простая игра поможет: придумайте число от 1 до 120 (начните с меньшего диапазона в первый раз, когда вы играете) и попросите ребенка угадать, что это такое. Дайте ей подсказки, например «выше» или «ниже», чтобы помочь ей угадать ваше число. (Эта игра также подготовит вашего ребенка к Price Is Right .)
Изобразите эти угощения на графике!
В этот Хэллоуин превратите конфетное сокровище первоклассника в урок построения графиков.Попросите ребенка разложить конфеты по стопкам («Сникерс», «Баттерфингеры» и т. Д.) И пересчитать их. Затем нарисуйте гистограмму, показывающую пять лучших собранных угощений. Спросите: «Какие конфеты появляются чаще всего? Реже всего? У вас есть такое же количество угощений? » Попробуйте этот лист с конфетами, чтобы подсластить горшок.
Часы с циферблатом и стрелками!
Этой зимой сделайте своего первоклассника своим официальным хронометристом. Начните с того, что регулярно спрашивайте у ребенка время, уделяя особое внимание полным часам и полчаса.Попросите ребенка записать время в цифровом формате и нарисовать его на аналоговых часах. Затем попросите их нарисовать и написать, сколько времени будет через полчаса. Эти тематические рабочие листы тоже помогут!
10, 20, 30…
У вас есть банка с монетами? Используйте эти монеты, чтобы помочь первокласснику понять, как считать до 100 по единицам и десяткам. Попросите ребенка отсчитать 100 пенсов (или что у вас есть). Затем попросите ребенка разделить пенни на группы по 10. Пусть ваш ребенок посчитает пенни за вас по 10 шилл.Хвалите их (и дайте им дезинфицирующее средство для рук). Затем попробуйте эту таблицу добавления монет, чтобы укрепить финансовую смекалку вашего ребенка.
Чистая одежда и данные
Сортировка белья в этом возрасте — не только развлечение, но и ускорение обучения математике. Используйте его, чтобы помочь вашему ребенку систематизировать, категоризировать и считать. Сопоставьте носки, посчитайте пары и определите количество отдельных носков и пар носков. Разделите одежду на цветовые категории или по тому, куда она идет. Задавайте вопросы, чтобы ваш ребенок интерпретировал данные, например: «Кому нужно идти в магазин за футболками?» Можно практиковать несколько навыков, если вы добровольно получите помощь в том, что когда-нибудь станет рутинной работой.
Помощь на кухне
Первый шаг в дробь для вашего первоклассника сейчас. Они могут лучше понимать половинки и четверти — и что каждая часть равна! — «помогая» вам на кухне. Попросите их сказать вам, где разрезать пиццу, чтобы сделать половинки, а затем четвертинки. Пусть они поделятся с вами половиной ломтика сыра или четвертью апельсина. Посмотрите, понимают ли они, что разделение чего-либо на две части не обязательно означает разделение чего-либо пополам.
Математические сказки: использование историй для практики арифметики
Дети любят математические рассказы, в которых есть они и их друзья! Представьте сценарий, который включает два или три количества, например, у Лоры было 5 карандашей, у соседки Уолли 3, а у двоюродной сестры Меган было 7. Спросите: «Если вы трое сложите все свои карандаши, сколько у вас будет? На сколько карандашей у Лоры больше, чем у Уолли? Затем попросите ребенка составить истории сложения и вычитания, в которых участвуют они сами и их друзья.
Значение за цифрами
К настоящему времени ваш первоклассник узнает, что наша система счисления основана на группах по 10.
 1 класс и дошкольники. Десяток. Состав числа. Более 500 примеров для вычисления» может стать одной из первых обучающих тетрадей для вашего ребенка. Ориентирована тетрадь на детей 4-7 лет, готовящихся к школе, и на первоклассников. Тетрадь содержит игровые задания и более 500 примеров на вычисление. Тетрадь – многоразовая: каждая страничка имеет специальное покрытие, на котором можно писать фломастером, а затем всё стереть … И делать это еще и еще раз, пока состав числа 10 не будет ребёнком полностью усвоен, а счёт не станет безошибочным и не дойдет до автоматизма.
1 класс и дошкольники. Десяток. Состав числа. Более 500 примеров для вычисления» может стать одной из первых обучающих тетрадей для вашего ребенка. Ориентирована тетрадь на детей 4-7 лет, готовящихся к школе, и на первоклассников. Тетрадь содержит игровые задания и более 500 примеров на вычисление. Тетрадь – многоразовая: каждая страничка имеет специальное покрытие, на котором можно писать фломастером, а затем всё стереть … И делать это еще и еще раз, пока состав числа 10 не будет ребёнком полностью усвоен, а счёт не станет безошибочным и не дойдет до автоматизма. В.
В. 1 класс. 49 проверочных работ в одной тетрадке» ориентирована на детей 6-8 лет, учащихся в первом классе. В данное пособие включены именно те слова и задания, которые всегда встречаются в контрольных работах, мониторингах и проверочных текстах по русскому языку в 1 классе. В этой тетрадке отрабатываются следующие темы: • заглавная буква в словах • слоги и ударения • перенос слов • сочетания ЖИ-ШИ • сочетания ЧА-ЩА • сочетания ЧУ-ЩУ • безударные гласные в корне слова, проверяемые ударением • парные согласные • Ь — показатель мягкости согласного • предложение. Удобная подача материала позволит вам экономить драгоценное время, как на уроке, так и при проверке задания. Тетрадка станет для вас незаменимым помощником на весь учебный год – в ней дети могут писать и стирать написанное, что даст вам возможность возвращаться к одному и тому же материалу столько раз, сколько нужно: сначала при разборе нового материала, а затем для закрепления – в течение всего учебного года. И вы добьетесь 100% грамотности!
1 класс. 49 проверочных работ в одной тетрадке» ориентирована на детей 6-8 лет, учащихся в первом классе. В данное пособие включены именно те слова и задания, которые всегда встречаются в контрольных работах, мониторингах и проверочных текстах по русскому языку в 1 классе. В этой тетрадке отрабатываются следующие темы: • заглавная буква в словах • слоги и ударения • перенос слов • сочетания ЖИ-ШИ • сочетания ЧА-ЩА • сочетания ЧУ-ЩУ • безударные гласные в корне слова, проверяемые ударением • парные согласные • Ь — показатель мягкости согласного • предложение. Удобная подача материала позволит вам экономить драгоценное время, как на уроке, так и при проверке задания. Тетрадка станет для вас незаменимым помощником на весь учебный год – в ней дети могут писать и стирать написанное, что даст вам возможность возвращаться к одному и тому же материалу столько раз, сколько нужно: сначала при разборе нового материала, а затем для закрепления – в течение всего учебного года. И вы добьетесь 100% грамотности! 3 класс. 48 проверочных работ в одной тетрадке» ориентирована на детей 8-10 лет, учащихся в третьем классе. В данное пособие включены именно те слова и задания, которые всегда встречаются в контрольных работах, мониторингах и проверочных текстах по русскому языку в 3 классе. Удобная подача материала позволит вам экономить драгоценное время, как на уроке, так и при проверке задания. Тетрадка станет для вас незаменимым помощником на весь учебный год – в ней дети могут писать и стирать написанное, что даст вам возможность возвращаться к одному и тому же материалу столько раз, сколько нужно: сначала при разборе нового материала, а затем для закрепления – в течение всего учебного года. И вы добьетесь 100% грамотности!
3 класс. 48 проверочных работ в одной тетрадке» ориентирована на детей 8-10 лет, учащихся в третьем классе. В данное пособие включены именно те слова и задания, которые всегда встречаются в контрольных работах, мониторингах и проверочных текстах по русскому языку в 3 классе. Удобная подача материала позволит вам экономить драгоценное время, как на уроке, так и при проверке задания. Тетрадка станет для вас незаменимым помощником на весь учебный год – в ней дети могут писать и стирать написанное, что даст вам возможность возвращаться к одному и тому же материалу столько раз, сколько нужно: сначала при разборе нового материала, а затем для закрепления – в течение всего учебного года. И вы добьетесь 100% грамотности! 4 класс. 48 проверочных работ в одной тетрадке» ориентирована на детей 9-11 лет, учащихся в третьем классе. В данное пособие включены именно те слова и задания, которые всегда встречаются в контрольных работах, мониторингах и проверочных текстах по русскому языку в 4 классе. Удобная подача материала позволит вам экономить драгоценное время, как на уроке, так и при проверке задания. Тетрадка станет для вас незаменимым помощником на весь учебный год – в ней дети могут писать и стирать написанное, что даст вам возможность возвращаться к одному и тому же материалу столько раз, сколько нужно: сначала при разборе нового материала, а затем для закрепления – в течение всего учебного года. И вы добьетесь 100% грамотности!
4 класс. 48 проверочных работ в одной тетрадке» ориентирована на детей 9-11 лет, учащихся в третьем классе. В данное пособие включены именно те слова и задания, которые всегда встречаются в контрольных работах, мониторингах и проверочных текстах по русскому языку в 4 классе. Удобная подача материала позволит вам экономить драгоценное время, как на уроке, так и при проверке задания. Тетрадка станет для вас незаменимым помощником на весь учебный год – в ней дети могут писать и стирать написанное, что даст вам возможность возвращаться к одному и тому же материалу столько раз, сколько нужно: сначала при разборе нового материала, а затем для закрепления – в течение всего учебного года. И вы добьетесь 100% грамотности! 1 класс. Сложение и вычитание в пределах 10. 1200 примеров для вычисления» может стать одной из первых обучающих тетрадей для вашего ребенка. Ориентирована тетрадь на детей 6-7 лет, готовящихся к школе, и на первоклассников. Как отучить ребенка считать на пальцах? Для этого необходимо научить его быстро складывать и вычитать в уме. Этот навык можно развить только решением многочисленных примеров. Разнообразие подачи примеров в новой многоразовой тетради «Математика. 1 класс. СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕДЕЛАХ 10» не даст малышу соскучиться и поможет ему легче ориентироваться и быть успешным в разнообразных формах контрольных, проверочных работ и мониторингов, проводимых в 1 классе. Цель нашей тетради: доведение до автоматизма навыка счета в пределах 10 при помощи игры. А прекрасных результатов можно достичь уже за неделю, занимаясь с ребенком всего по 5–10 минут ежедневно.
1 класс. Сложение и вычитание в пределах 10. 1200 примеров для вычисления» может стать одной из первых обучающих тетрадей для вашего ребенка. Ориентирована тетрадь на детей 6-7 лет, готовящихся к школе, и на первоклассников. Как отучить ребенка считать на пальцах? Для этого необходимо научить его быстро складывать и вычитать в уме. Этот навык можно развить только решением многочисленных примеров. Разнообразие подачи примеров в новой многоразовой тетради «Математика. 1 класс. СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕДЕЛАХ 10» не даст малышу соскучиться и поможет ему легче ориентироваться и быть успешным в разнообразных формах контрольных, проверочных работ и мониторингов, проводимых в 1 классе. Цель нашей тетради: доведение до автоматизма навыка счета в пределах 10 при помощи игры. А прекрасных результатов можно достичь уже за неделю, занимаясь с ребенком всего по 5–10 минут ежедневно.
 2-3 класс. СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕДЕЛАХ 100. Более 900 примеров для вычисления» охватывает все виды примеров на сложение и вычитание в пределах 100, которые ваш ребенок будет изучать в начальной школе. Тема «Сотня» — одна из базовых в 1-4 классах. Важно не только научиться решать примеры без ошибок, но и решать их за определенное время. Можно сказать, что ребенок научился считать, если навык счета доведен до автоматизма. В конце занятий, ребенок сможет раскрасить забавных зверюшек, что поможет ему отдохнуть и закончить обучение в прекрасном настроении.
2-3 класс. СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕДЕЛАХ 100. Более 900 примеров для вычисления» охватывает все виды примеров на сложение и вычитание в пределах 100, которые ваш ребенок будет изучать в начальной школе. Тема «Сотня» — одна из базовых в 1-4 классах. Важно не только научиться решать примеры без ошибок, но и решать их за определенное время. Можно сказать, что ребенок научился считать, если навык счета доведен до автоматизма. В конце занятий, ребенок сможет раскрасить забавных зверюшек, что поможет ему отдохнуть и закончить обучение в прекрасном настроении. Впервые же в школьную программу таблица умножения была введена в Англии в конце Средних веков. Примеры в тетради для многоразового использования «Математика. 2-3 классы. ТАБЛИЧНОЕ УМНОЖЕНИЕ И ДЕЛЕНИЕ. Более 800 примеров для вычисления» нужно решать на время. Хороший результат — 1 столбик без ошибок — за 1,5—2 минуты, таблицу — за 2—3 минуты. Если заниматься каждый день по 5–10 минут, через неделю решение примеров доводится до автоматизма.
Впервые же в школьную программу таблица умножения была введена в Англии в конце Средних веков. Примеры в тетради для многоразового использования «Математика. 2-3 классы. ТАБЛИЧНОЕ УМНОЖЕНИЕ И ДЕЛЕНИЕ. Более 800 примеров для вычисления» нужно решать на время. Хороший результат — 1 столбик без ошибок — за 1,5—2 минуты, таблицу — за 2—3 минуты. Если заниматься каждый день по 5–10 минут, через неделю решение примеров доводится до автоматизма. 2-3 классы. ТАБЛИЧНОЕ УМНОЖЕНИЕ И ДЕЛЕНИЕ. Более 800 примеров для вычисления» • Тетрадь для многоразового использования «Математика. 2-3 класс. СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕДЕЛАХ 100. Более 900 примеров для вычисления» • Тетрадь для многоразового использования «Русский язык. 2 класс. 48 проверочных работ в одной тетрадке» • Учебник для отличника. 2 класс.
2-3 классы. ТАБЛИЧНОЕ УМНОЖЕНИЕ И ДЕЛЕНИЕ. Более 800 примеров для вычисления» • Тетрадь для многоразового использования «Математика. 2-3 класс. СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕДЕЛАХ 100. Более 900 примеров для вычисления» • Тетрадь для многоразового использования «Русский язык. 2 класс. 48 проверочных работ в одной тетрадке» • Учебник для отличника. 2 класс. 2-3 класс. СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕДЕЛАХ 100. Более 900 примеров для вычисления» • Тетрадь для многоразового использования «Русский язык. 3 класс. Контрольные работы. 48 проверочных работ в одной тетрадке» • Учебник для отличника. 3 класс.
2-3 класс. СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕДЕЛАХ 100. Более 900 примеров для вычисления» • Тетрадь для многоразового использования «Русский язык. 3 класс. Контрольные работы. 48 проверочных работ в одной тетрадке» • Учебник для отличника. 3 класс.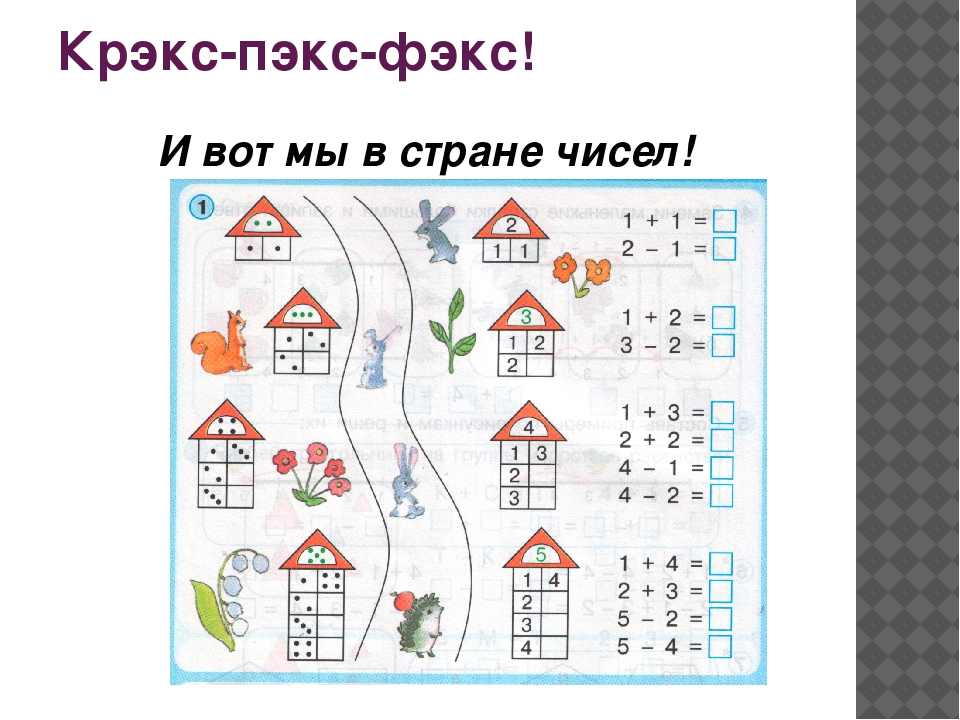 4 класс.
4 класс. Систематическое выполнение этих заданий развивает логическое и математическое мышление, сообразительность, укрепляет память и внимание. По усмотрению учителя цепочки примеров можно использовать как для олимпиадных работ и заданий повышенной сложности, так и для повторения и закрепления изученной темы. Для лучшего усвоения материала рекомендуется решать по десять примеров в день. Пособие можно использовать на уроках математики и для самостоятельной работы дома.
Систематическое выполнение этих заданий развивает логическое и математическое мышление, сообразительность, укрепляет память и внимание. По усмотрению учителя цепочки примеров можно использовать как для олимпиадных работ и заданий повышенной сложности, так и для повторения и закрепления изученной темы. Для лучшего усвоения материала рекомендуется решать по десять примеров в день. Пособие можно использовать на уроках математики и для самостоятельной работы дома. Когда в столбике встречается много переводов в более мелкие единицы (например, для получения более точного ответа часы и минуты необходимо перевести в секунды), время решения одного примера увеличивается до 10-12 секунд. В этом случае можно говорить, что навык счета доведен до автоматизма. На каждой странице приведены 3-4 столбика в среднем по 50 примеров. Если ученик решает столбик за 4-6 минут, это свидетельствует о хорошем уровне подготовки. На целую страницу у него должно уходить не более 30 минут. Чтобы достичь отличных результатов, каждый день следует решать по одной странице. Пособие может быть использовано на уроках математики, а также для самостоятельной работы дома.
Когда в столбике встречается много переводов в более мелкие единицы (например, для получения более точного ответа часы и минуты необходимо перевести в секунды), время решения одного примера увеличивается до 10-12 секунд. В этом случае можно говорить, что навык счета доведен до автоматизма. На каждой странице приведены 3-4 столбика в среднем по 50 примеров. Если ученик решает столбик за 4-6 минут, это свидетельствует о хорошем уровне подготовки. На целую страницу у него должно уходить не более 30 минут. Чтобы достичь отличных результатов, каждый день следует решать по одной странице. Пособие может быть использовано на уроках математики, а также для самостоятельной работы дома. Малыш с увлечением решит весёлые задачки и при этом, сам того не замечая, освоит важные логические операции: обобщение, исключение, причинно-следственные связи. Задания также помогут ребёнку морально подготовиться к школе: приучат к аккуратности и собранности.
Малыш с увлечением решит весёлые задачки и при этом, сам того не замечая, освоит важные логические операции: обобщение, исключение, причинно-следственные связи. Задания также помогут ребёнку морально подготовиться к школе: приучат к аккуратности и собранности. Для проверки знаний учащихся и самопроверки даны ответы ко всем заданиям. Они расположены так, что при необходимости учителя или родители могут их легко удалить. Пособие можно использовать для коллективной и индивидуальной работы в классе, а также для работы дома.
Для проверки знаний учащихся и самопроверки даны ответы ко всем заданиям. Они расположены так, что при необходимости учителя или родители могут их легко удалить. Пособие можно использовать для коллективной и индивидуальной работы в классе, а также для работы дома. Ваш ребёнок скоро пойдёт в школу, он уже умеет читать и пробует самостоятельно писать. Значит, пора начинать учить правила. «Но это же трудно и скучно!» — скажете вы. Только не с книгой известных учителей-практиков начальной школы Е. Нефёдовой и О. Узоровой! Эта книга позволит ребёнку стать грамотным и подготовиться к школе весело и увлекательно. Юных читателей и писателей ждут увлекательные задания, поиск ответов на интересные вопросы, весёлые переменки с наклейками и рисунками для раскрашивания.»
Ваш ребёнок скоро пойдёт в школу, он уже умеет читать и пробует самостоятельно писать. Значит, пора начинать учить правила. «Но это же трудно и скучно!» — скажете вы. Только не с книгой известных учителей-практиков начальной школы Е. Нефёдовой и О. Узоровой! Эта книга позволит ребёнку стать грамотным и подготовиться к школе весело и увлекательно. Юных читателей и писателей ждут увлекательные задания, поиск ответов на интересные вопросы, весёлые переменки с наклейками и рисунками для раскрашивания.»