Умножение дробей. — tutomath.ru репетитор по математике

Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.

Умножение обыкновенной дроби на дробь.

Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.

\(\bf \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\\\)

Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.

\( \frac{6}{7} \times \frac{2}{3} = \frac{6 \times 2}{7 \times 3} = \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\)

Дробь \( \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\) сократили на 3.

Умножение дроби на число.

Для начала вспомним правило, любое число можно представить в виде дроби \( \bf n = \frac{n}{1}\) .

Воспользуемся этим правилом при умножении.

\(5 \times \frac{4}{7} = \frac{5}{1} \times \frac{4}{7} = \frac{5 \times 4}{1 \times 7} = \frac{20}{7} = 2\frac{6}{7}\\\)

Неправильную дробь \(\frac{20}{7} = \frac{14 + 6}{7} = \frac{14}{7} + \frac{6}{7} = 2 + \frac{6}{7}= 2\frac{6}{7}\\\) перевели в смешанную дробь.

Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:

\(\frac{2}{5} \times 3 = \frac{2 \times 3}{5} = \frac{6}{5} = 1\frac{1}{5}\\\\\) \(\bf \frac{a}{b} \times c = \frac{a \times c}{b}\\\)

Умножение смешанных дробей.

Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.

Пример:
\(2\frac{1}{4} \times 3\frac{5}{6} = \frac{9}{4} \times \frac{23}{6} = \frac{9 \times 23}{4 \times 6} = \frac{3 \times \color{red} {3} \times 23}{4 \times 2 \times \color{red} {3}} = \frac{69}{8} = 8\frac{5}{8}\\\)

Умножение взаимно обратных дробей и чисел.

Дробь \(\bf \frac{a}{b}\) является обратной для дроби \(\bf \frac{b}{a}\), при условии a≠0,b≠0.
Дроби \(\bf \frac{a}{b}\) и \(\bf \frac{b}{a}\) называются взаимно обратными дробями. Произведение взаимно обратных дробей равно 1.
\(\bf \frac{a}{b} \times \frac{b}{a} = 1 \\\)

Пример:
\(\frac{5}{9} \times \frac{9}{5} = \frac{45}{45} = 1\\\)

Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.

Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.

Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.

Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.

Пример №1:
Вычислите произведение: а) \(\frac{8}{9} \times \frac{7}{11}\) б) \(\frac{2}{15} \times \frac{10}{13}\)

Решение:
а) \(\frac{8}{9} \times \frac{7}{11} = \frac{8 \times 7}{9 \times 11} = \frac{56}{99}\\\\\)
б) \(\frac{2}{15} \times \frac{10}{13} = \frac{2 \times 10}{15 \times 13} = \frac{2 \times 2 \times \color{red} {5}}{3 \times \color{red} {5} \times 13} = \frac{4}{39}\)

Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac{17}{23}\) б) \(\frac{2}{3} \times 11\)

Решение:
а) \(3 \times \frac{17}{23} = \frac{3}{1} \times \frac{17}{23} = \frac{3 \times 17}{1 \times 23} = \frac{51}{23} = 2\frac{5}{23}\\\\\)
б) \(\frac{2}{3} \times 11 = \frac{2}{3} \times \frac{11}{1} = \frac{2 \times 11}{3 \times 1} = \frac{22}{3} = 7\frac{1}{3}\)

Пример №3:
Напишите число обратное дроби \(\frac{1}{3}\)?
Ответ: \(\frac{3}{1} = 3\)

Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac{104}{215} \times \frac{215}{104}\)

Решение:
а) \(\frac{104}{215} \times \frac{215}{104} = 1\)

Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?

Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.

б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac{3}{3}\) , обратная ей дробь равна \(\frac{3}{3}\). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.

в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac{3}{1}\), то обратная ей дробь будет \(\frac{1}{3}\). Дробь \(\frac{1}{3}\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac{1}{1} = \frac{1}{1} = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.

Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac{4}{5}\) б) \(1\frac{1}{4} \times 3\frac{2}{7}\)

Решение:
а) \(4 \times 2\frac{4}{5} = \frac{4}{1} \times \frac{14}{5} = \frac{56}{5} = 11\frac{1}{5}\\\\ \)
б) \(1\frac{1}{4} \times 3\frac{2}{7} = \frac{5}{4} \times \frac{23}{7} = \frac{115}{28} = 4\frac{3}{7}\)

Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?

Рассмотрим на примере. Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.

Конспект урока по математике в 6 классе по теме: «Умножение дробей».

6 класс Математика

Учитель : Сейдаметова Г. К.

18.12.2020 г.

Урок № 74

ТЕМА: «Умножение дробей»

Тип урока: урок комплексного применения знаний и умений (урок закрепления).

Продолжительность урока: 45 минут.

Методы обучения: словесный, наглядный, практический, проблемный.

Цели:

Образовательная: обобщение и систематизация знаний учащихся, закрепление и совершенствование навыков умножения обыкновенных дробей любого знака.

Развивающая: развитие навыков самоконтроля и самооценки достигнутых знаний и умений, интереса к математике.

Воспитательная: воспитание внимательности, активности, самостоятельности и ответственности, потребности вести здоровый образ жизни, поддерживать на высоком уровне общую работоспособность для успешного учения.

Формируемые результаты:

Предметные: формировать умение умножать обыкновенные дроби любого знака.

Личностные: формировать интерес к изучению темы и желание применять приобретенные знания и умения, формировать умение работать в коллективе и находить согласованные решения; формировать учебную мотивацию, адекватную самооценку.

Метапредметные: формировать умение определять способы действий в рамках предложенных условий; осуществлять анализ объектов; ставить новые учебные задачи и осуществлять действия для реализации замысла; планировать в сотрудничестве с учителем и самостоятельно свои действия для решения задачи; аргументировать свою позицию и координировать её с позициями партнеров в совместной деятельности.

Познавательные УУД:

• формирование навыков умножения дробей произвольных знаков с разными знаменателями;

• применять полученные знания при решении задач.

Коммуникативные УУД:

• воспитание любви к математике, коллективизм, уважение друг к другу, умение слушать, дисциплинированность, самостоятельность мышления.

Регулятивные УУД:

• понимание учебной задачи урока,

• осуществление решения учебной задачи под руководством учителя,

• определение цели учебного задания, контролирование своих действий в процессе его выполнения.

Образовательные технологии, используемые на уроке:

• информационно-коммуникационная;

• проблемно-диалоговая технология; 

• здоровьесберегающая технология (физкультминутка, создание позитивного эмоционального настроя на работу всех учеников в ходе урока; организация различных форм деятельности учащихся, организация урока с учетом временного восприятия и усвоения учебного материала).

Формы работы учащихся: групповая, фронтальная, индивидуальная.

Методы обучения:

словесные – беседа, рассказ;

наглядные – демонстрация презентации;

практические – решение задач, практическая работа

Необходимое оборудование и материалы для урока: компьютер, мультимедийный проектор, раздаточный материал, электронное приложение к учебнику.

ХОД УРОКА:

1. Организационный этап.

Приветствие, проверка готовности к уроку, организация внимания детей.

Учитель начинает со слов приветствия:

Наш урок пора начать.

Пришло время вычислять.

И на трудные вопросы.

Вы ответ сумейте дать.

Ребята, я рада приветствовать Вас на уроке математики.

На ваших столах лежат листы самооценки. Подпишите их. А теперь пожалуйста на листах самооценки отметьте галочкой смайлик, который соответствует вашему настроению, с которым вы пришли на урок.

Открываем тетради, записываем число, классная работа.

1. Проверка домашнего задания.

Скажите пожалуйста, все ли выполнили домашнее задание?

У кого-то возникли вопросы по домашнему заданию?

Хорошо, я обязательно проверю ваши работы.

1. Мотивация учебной деятельности. Постановка цели и задач урока.

«Человек подобен дроби, числитель которой есть то, что человек представляет собой, а знаменатель – то, что он думает о себе. Чем большего человек о себе мнения, тем больше знаменатель, а значит, тем меньше дробь»

Л.Н.Толстой

Это слова Л. Н. Толстова – одного из наиболее известных русских писателей и мыслителей.

Задумайтесь над этими словами… Я хочу, чтобы мы с вами были подобны дроби, у которой числитель будет больше…

С чем сравнивал Л. Н. Толстой человека? (С дробью)

Скажите, правила выполнения какого арифметического действия с дробями мы изучили на прошлом уроке? (Правила умножения дробей)

Итак, как Вы думаете какой будет наша тема сегодня? (Умножение дробей)

Запишите тему урока. («Умножение дробей»)

Итак, мы с вами знаем правила – теорию как умножать дроби. Теперь нам нужно научиться эти правила ………? (закреплять, применять)

Значит какой будет наша цель на уроке? (Учащиеся формулируют цели урока)

4. Актуализация знаний.

Понятие дроби мы широко используем в повседневной жизни. Во многих профессиях без них невозможно обойтись. При изучении большинства школьных предметов требуется знание дробей. Вместе с тем, нам известно, что действия с дробями производить не так-то просто. Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка “попасть в дроби”, что означает попасть в трудное положение.

Чтобы реже оказываться в таких ситуациях, мы продолжаем изучать действия с дробями или рациональными числами.

Начнём с разминки. Пожалуйста, посмотрите на экран,

Задание 1: Даны дроби:

Выпишите правильные дроби :

Выпишите неправильные дроби:

Выделите целую часть неправильной дроби:

Назовите равные дроби:

Каждая верно определенная дробь – 1 балл.

(в листах самооценки те, кто получил более 7 баллов ставят 1 балл)

Устный опрос:

Чтобы умножить две дроби надо числитель умножить на числитель, результат записать в числитель, а знаменатель умножить на знаменатель, результат записать в знаменатель.

;

Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменений.

;

Положительное, т.к. при умножении минуса на минус — получается плюс.

Минус – т.к. если один из двух множителей отрицательный, то и произведение будет отрицательным.

Для того, чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения.

(в листах самооценки те, кто верно ответил на вопрос ставят 1 балл)

5. Закрепление материала.

№ 1 Ребята, вы любите животных? Сейчас мы с вами решим математическую цепочку и узнаем интересный факт из их жизни.

1. Какой кошке поклонялись древние индейцы? Гепард Ягуар Рысь *2 * *4

№2 Выполнить умножение (задания из ВПР):

а) б)

в) г)

д) _е)

ж) ()² = з)

Физминутка.

Мы с вами активно работаем, поэтому нужно немного отдохнуть. Я хочу, чтобы вы все встали. Сейчас на экране будут появляться примеры на произведение чисел с разными знаками. Вы должны увидев пример определить какой знак будет иметь их произведение. Если в ответе будет знак «минус» — то вы должны хлопнуть в ладоши опустив руки вниз, если же в ответе будет знак «плюс» — то вы должны сделать хлопок над головой.

Все поняли? Готовы? Выполняем задания активно и весело!

№3 Игра «Найди пару».

Установите соответствие между парами дробей и их произведением

№4 Заполните пропуски в таблице.

(в листах самооценки те, кто решил пример у доски ставят 1 балл)

6. Применение знаний в новой ситуации (проверочная работа).

У Вас на столах лежат карточки с заданиями разных цветов. Решив правильно синюю карточку, вы сможете набрать 2 балла, а зеленую — 1 балл. Эти баллы вы занесете в лист самооценки. Ваша задача выбрать себе карточку по своим возможностям и решить предложенные в ней задания.

1 балл

2 балла

(в листах самооценки те, кто верно решил зеленую карточку ставят 1 балл, кто верно решил синюю карточку – 2 балла)

7. Информация о домашнем задании.

Ребята, запишите домашнее задание.

Повторить правила умножения дробей — п. 3.5,

Решить №№ 529, 540 (а, б, д, ж), 546 (б, г*)

1. Подведение итогов урока. Рефлексия.

Наш урок подходит к концу, значит нам пора подвести итоги.

Чему вы научились на этом уроке?

Какие задания выполняли?

Что понравилось больше?

Достигли ли мы с вами поставленной цели?

Итак, ребята, сегодня на уроке мы с вами закрепили правила умножения дробей, вспомнили как сокращать дроби, как переводить смешанную дробь в неправильную и наоборот.

Заполните листы самооценки и подсчитайте свои оценки за урок.

А также отметьте галочкой смайлик, который соответствует вашему настроению в конце нашего урока.

Выставление оценок за урок.

На этом наш урок окончен! Спасибо за работу! Вы молодцы! Хорошего дня!

6

Как умножать дроби — ACT Math

• Войти
• Биографии репетитора
• Подготовка к тесту

  СРЕДНЯЯ ШКОЛА

  • ACT Репетиторство
  • SAT Репетиторство
  • Репетиторство PSAT
  • ASPIRE Репетиторство
  • ШСАТ Репетиторство
  • Репетиторство STAAR

  ВЫСШАЯ ШКОЛА

  • Репетиторство MCAT
  • Репетиторство GRE
  • Репетиторство по LSAT
  • Репетиторство по GMAT

  К-8

  • Репетиторство AIMS
  • Репетиторство по HSPT
  • Репетиторство ISEE
  • Репетиторство ISAT
  • Репетиторство по SSAT
  • Репетиторство STAAR

  Поиск 50+ тестов

• Академическое обучение

  репетиторство по математике

  • Алгебра
  • Исчисление
  • Элементарная математика
  • Геометрия
  • Предварительный расчет
  • Статистика
  • Тригонометрия

  репетиторство по естественным наукам

  • Анатомия
  • Биология
  • Химия
  • Физика
  • Физиология

  иностранные языки

  • французский
  • немецкий
  • Латинский
  • Китайский мандарин
  • Испанский

  начальное обучение

  • Чтение
  • Акустика
  • Элементарная математика

  прочие

  • Бухгалтерия
  • Информатика
  • Экономика
  • Английский
  • Финансы
  • История
  • Письмо
  • Лето

  Поиск по 350+ темам

• О
  • Обзор видео
  • Процесс выбора наставника
  • Онлайн-репетиторство
  • Мобильное обучение
  • Мгновенное обучение
  • Как мы работаем
  • Наша гарантия
  • Влияние репетиторства
  • Обзоры и отзывы
  • Освещение в СМИ
  • О преподавателях университета

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Все математические ресурсы ACT

14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept

ACT Math Help » Арифметика » Фракции » Операции и дроби » Как умножать дроби

Какое значение делает уравнение верным?

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем просто перекрестить, умножить, чтобы получить , и разделить на 8, чтобы найти .

Сообщить об ошибке

Упростите следующее выражение;

Возможные ответы:

Правильный ответ:

Объяснение:

Умножьте числители  2 x 6 x 4 = 48. Затем умножьте знаменатели 3 x 8 x 12 = 288.  Ответ: 48/288. Чтобы упростить, разделите и числитель, и знаменатель на 48, чтобы получить 1/6.

 

Сообщить об ошибке

Оценить –3 ^–2  * 2 ^–3 .

Возможные ответы:

Правильный ответ:

Объяснение:

Поскольку показатели степени отрицательны, мы можем преобразовать –3 ^–2    до ¹ / ₉ и 2 ^–3   до ¹ / ₈ .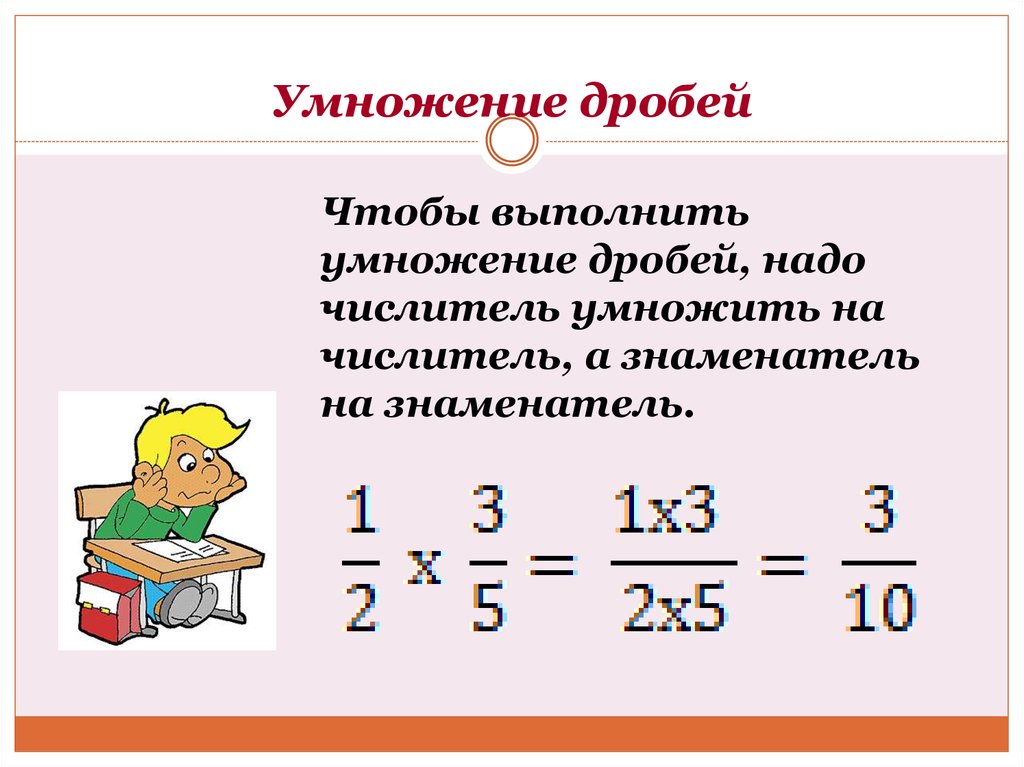

Затем мы умножаем прямо сверху и снизу, что дает вам ¹ / ₇₂ .

Сообщить об ошибке

Упростите следующее в одну дробь

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы перемножить дроби, нужно перемножить весь числитель и весь знаменатель вместе. Однако, прежде чем мы это сделаем, мы можем отменить что-нибудь из знаменателя с чем-нибудь в числителе.

шесть отменов с 12

5 отмены с 25

Умножьте все это и получите

Отчет о ошибке

Уведомление о сообщении

. Висконсин-Мэдисон, бакалавр искусств, математика. Главный кампус Университета Южной Флориды, магистр искусств, прем…

Просмотр ACT Math Tutors

Laci
Сертифицированный репетитор

Университет Говарда, бакалавр наук, биология, общие.

Просмотр ACT Math Tutors

Rajshree
Сертифицированный репетитор

Мумбайский университет, бакалавр электротехники.

Все математические ресурсы ACT

14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept

Как умножать дроби | Математика 4 класса

Дроби говорят нам о частях целого.

Верхнее число числитель . Он показывает количество деталей, которые у вас есть.

Нижнее число знаменатель . Он показывает общее количество частей, на которые делится целое.

Давайте воспользуемся моделью площадей , чтобы увидеть, как выглядит 3/4.

Модели площадей дробей

Модель площадей представляет собой фигуру, разделенную на равные части. Он показывает, как выглядит дробь.

Давайте покажем 3/4 , используя модель площади.

Наш знаменатель равен 4, поэтому мы разделили нашу фигуру на 4 равные части.

Мы затеняем 3 из этих частей, потому что наш числитель равен 3.

Наша модель площади для 3/4 завершена.

Теперь давайте научимся умножать дроби на примере.

Умножьте 3/4 на 2/5.

Умножение дробей с использованием моделей площадей

Когда мы умножаем 3/4 на 2/5 , мы на самом деле находим 3/4 от 2/5 .

Нарисуем модель площади 2/5.

Есть 5 частей. Две части заштрихованы:

Мы использовали вертикальных линий выше.

Теперь давайте нарисуем модель площади для другой дроби, 3/4, на этот раз используя горизонтальных линий .

Нарисуем прямоугольник и разделим его на 4 равные части. Затем мы заштриховываем 3 из 4 частей:

Когда мы умножаем эти две дроби, мы накладываем модель площади для 3/4 на модель площади для 2/5. Перекрывающаяся часть — ваш ответ!

Сколько заштрихованных частей перекрываются? 🧐

Да, 6 частей перекрываются.

6 — это числитель

нашего ответа.