+, -, =. «Прибавить», «вычесть», «получится»
Урок 8. Математика 1 класс
Вместе с нашими героями дети узнают, едят ли птицы кофейные зерна, а заодно и познакомятся с новыми знаками «+», «-», «=». Научатся писать эти знаки, складывать и вычитать.
Конспект урока «Знаки: +, -, =. «Прибавить», «вычесть», «получится»»
— Ежик, ну что ты там видишь?
— Пока ничего. Теперь вижу. Один воробей прилетел. Сейчас зернышки клевать будет.
— А вот ещё один прилетел.
— Ну и сколько всего?
— Один да один, будет два.
— Ёжик, а ты знаешь, что в математике лучше говорить не один да один, а к одному прибавить один. А записывается это с помощью специального знака, который называется «плюс».
Смотри
плюс состоит
из двух палочек, которые пересекаются посередине. Он используется для того,
чтобы что-то сложить. Например: сложим яблоки. Два яблока плюс два яблока получится
четыре яблока. А записать это можно так: два плюс два получится 4. В этом
случае мы выполняем действие сложения, а числа при этом складываем.
Например: сложим яблоки. Два яблока плюс два яблока получится
четыре яблока. А записать это можно так: два плюс два получится 4. В этом
случае мы выполняем действие сложения, а числа при этом складываем.
Вообще знак плюс и слова прибавить или сложить играют очень важную роль не только в математике, но и в жизни. Например: мы купили в магазине три конфеты и одну булочку. Так вот, чтобы посчитать сколько покупок мы сделали надо все сложить. А в математике можно записать и сказать так: три конфеты плюс одна булочка получится четыре покупки, или к трем прибавить один равно четыре.
— А я ещё я вспомнил, что можно сказать так, чтобы посчитать сколько покупок, надо сложить числа 3 и один и получится тоже четыре.
А сейчас мы с тобой будем учиться писать знак плюс. Как я уже сказала, он состоит из двух палочек, которые пересекаются.
— Так просто. Я тоже хочу написать.
— А давай ты раскрасишь
клеточки таким образом, чтобы получился знак плюс.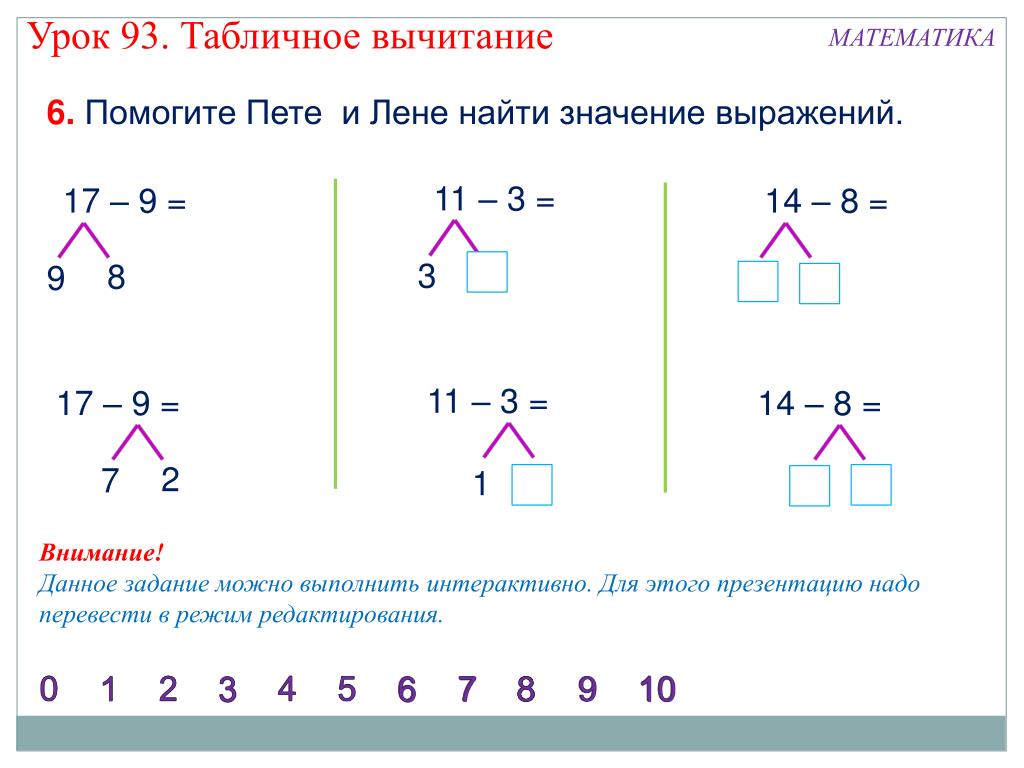
— Давай. Вот готово.
— Молодец, совершенно верно. Ежик, а давай посмотрим, склевали воробьи зерна или нет?
— Давай. Ой, кажется один воробей улетел. И даже зерна не склевал.
— Точно.
— Белочка, у нас осталось воробьёв два без одного.
— Ежик, вообще-то, лучше говорить, не два без одного, а два минус один получится один.
Например. На пенёчке сидели 2 воробья. Один улетел, а один воробей остался. В математике можно записать и сказать так: два минус один, или из двух вычесть один.
— Так что получается мы опять какое-то действие выполнили.
— Да, мы выполнили действие вычитания, а записать это можно с помощью знака минус.
— Минус, ничего себе.
— Да, минус. Смотри, минус состоит из одной палочки, и записывается очень просто. Вот так.
— Белочка, а давай я опять раскрашу клеточки, только так, чтобы получился знак
минус.
— Ну давай.
— Все верно. Минус тоже очень важен. Он используется, для того чтобы что-то отнять. Например: вот у меня две банки с вареньем. Я одну дала тебе, а у меня тоже осталась одна. В математике это можно записать так: два минус один получится один. В этом случае мы выполнили действие вычитание, и из большего числа вычли меньшее.
А еще в математике придумали слово «получится» тоже обозначать специальным знаком, который называется равно. Этот знак состоит из двух палочек, которые пишутся друг под другом. Вот так.
— Ну вот Ёжик, теперь мы знаем такие важные математические знаки, как «плюс», «минус», «равно».
— Белочка, что-то я уже все знаки перепутал. И забыл когда, какой знак пишется.
— Ну
давай повторим. Знак плюс пишется,
если нам надо что-то сложить, т.е
сделать больше, чем есть. Например: два яблока полюс одно яблоко равно три
яблока.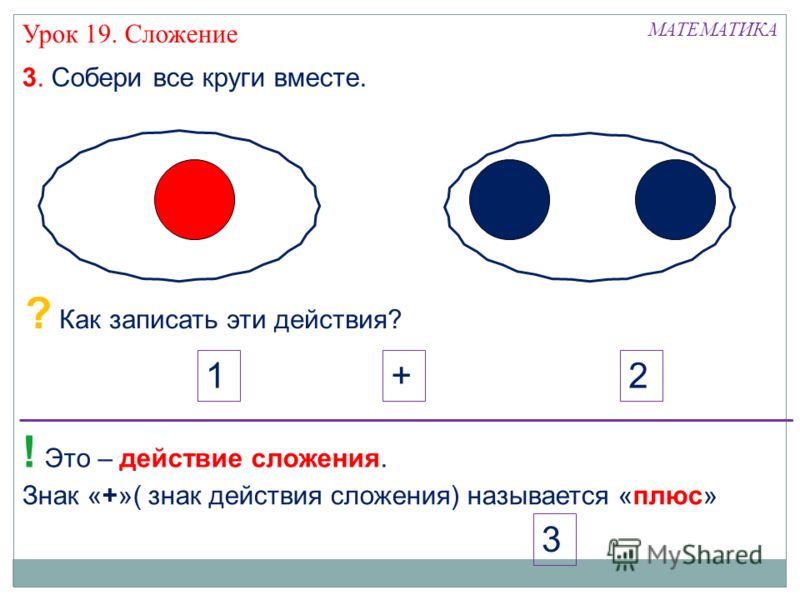 В этом случае мы выполняем действие сложение, а числа складываем.
Вместо слово получится мы говорим равно и записываем
знаком равно.
В этом случае мы выполняем действие сложение, а числа складываем.
Вместо слово получится мы говорим равно и записываем
знаком равно.
— Знак минус пишется, если нам надо из большего числа вычесть меньшее. Например, из двух яблок нам надо вычесть одно получится одно. А записать это можно так: два минус один, получится один. В этом случае мы выполнили действие вычитание, а числа вычли. Вместо слово получится мы тоже говорим равно и записываем знаком равно.
— Ну что. Теперь ты все запомнил?
— Конечно. Белочка, что-то птицы наши зернышки не склевали.
— Так ведь это кофейные зерна, из которых кофе варят. И птицы их не едят. Эх ёжик. Завтра надо опять зёрнышки насыпать, только другие.
Предыдущий урок 7 Число и цифра 3
Следующий урок 9 Число и цифра 4
Получите полный комплект видеоуроков, тестов и презентаций Математика 1 класс
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Урок математики в 1-м классе по теме «Знаки «+», «–», «=» прибавить, вычесть, получится.
 Числа 1, 2, 3″
Числа 1, 2, 3″Первоклассник идет в школу. Ведущей
деятельностью становится учение. Первый год
обучения проходит в детском саду. Уроки ведёт
учитель, внеучебную деятельность осуществляет
воспитатель. У детей хорошее настроение. Они
полны желания учиться. Это желание надо
поддерживать. Уроки проводятся в игровой форме.
Это и уроки-сказки, уроки-путешествия, уроки на
основе стихотворений, уроки на основе песен и т.д.
На этих уроках учебный материал даётся детям в
интересной форме. Задания даются от имени
сказочных персонажей. При выполнении таких
заданий учащиеся овладевают программными
знаниями и умениями. А такие уроки носят как
познавательный, так и воспитательный характер.
Учащиеся преодолевают трудности, помогая тем или
иным героям, они переживают вместе с ними, учатся
правилам общения. На уроках можно загадывать
загадки, читать занимательные стихи, отгадывать
кроссворды и ребусы, сочинять сказки.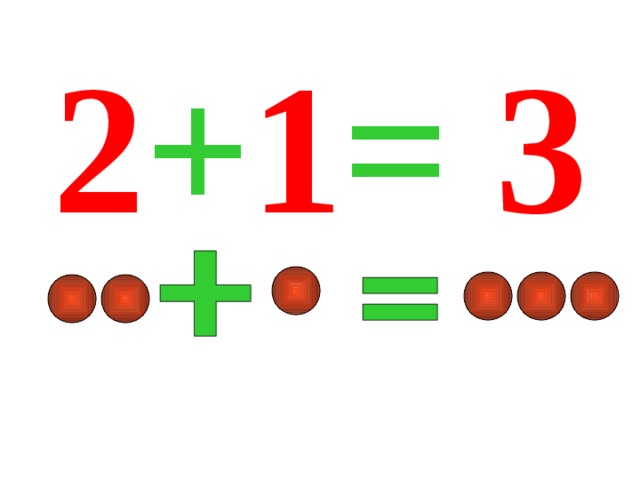
Очень хорошо об игре и уроке сказал В.А.Сухомлинский: “Учение – труд, и его нельзя превращать в игру. Но нельзя и поставить китайскую стену между трудом и игрой. Игра занимает важное место в жизни ребёнка. Для него игра – это самое серьёзное дело. В игре раскрывается перед детьми мир, раскрываются творческие способности личности. Игра – это огромное светлое окно, через которое в духовный мир ребёнка вливается живительный поток представлений… В игре дети смеются, переживают, страдают”.
Первоклассники – это мечтатели, фантазёры и они сами порой подсказывают учителю моменты игры. Они ещё верят в чудеса и невероятные истории. Дети сами приносят сказки, по которым им хотелось бы совершить добрые дела и поступки. Главное, чтобы всё это помогло им получить знания, без которых невозможно дальнейшее обучение.
Урок математики, проведённый в первом классе.
Тема: Числа1,2,3. Знаки “+”, “-”, “=”.
Знаки “+”, “-”, “=”.
Цели:
- Продолжить работу над нумерацией чисел 1, 2, 3.
- Познакомить детей со знаками “ + ”, “ — ”, “ = ”; с записью и чтением примеров.
Ход урока
Организационный момент.
Ну-ка, проверь, дружок,
Ты готов начать урок?
Всё ль на месте,
Всё ль в порядке,
Ручка, книжки и тетрадка?
(Садитесь).
Все ли правильно сидят?
Все ль внимательно глядят?
Все ль готовы слушать?
Начинаем наш урок.
Разминка.
Сегодня мы отправимся в замок математических знаков. Каких, мы узнаем позже. Путь наш будет долгим.
На первой полянке нас встречает добрый Дракоша, а в руках у него конвертик с заданием. Давайте его прочитаем.
(Читаем задание).
Дракоша предлагает нам разминку и устные
упражнения.
Задание Дракоши.
- Что наступает после осени?
- Назови осенние месяцы?
- Назови пять имён девочек?
- Назови крупное рогатое животное, которое даёт молоко?
- Кто от дедушки ушёл? Кто от бабушки ушёл?
2. Назови числа от 1 до 10 по порядку.
— Сосчитай от 5до8, от 2до 9, от 8до5,от4до7.
И вот мы попадаем на полянку. Какая она красивая на ней мы передохнём!
III.Физкультминутка.
Раз, два — выше голова,
Три, четыре – руки шире,
Пять, шесть – тихо сесть,
Семь, восемь – лень отбросим.
IV.Работа над темой урока.
Наш путь продолжается. Отгадайте загадку.
Загадка о лесе:
Весной весёлый,
Летом холодный,
Осенью умирает,
Весной оживает.
А посмотрите, в какой удивительный лес мы
попали. А сколько в нём грибов?
А сколько в нём грибов?
Ежик уже насобирал целую корзинку грибов. Давайте и мы пособираем грибы. Вот у нас есть корзиночка. Алина, иди к доске. Найди и положи в корзиночку 2 гриба, а потом ещё один. Сколько всего грибов стало?
Сколько было грибов сначала? Поставьте цифру на доске. Сколько ещё грибов нашла Алина? Обозначьте цифрой. Сколько грибов стало в корзинке? Обозначьте цифрой. Теперь посмотрим, как это можно записать.
(На доске: 2 +1=3).
А навстречу Алине попадается Миша. Он очень расстроен. Алина собрала все грибы. Не расстраивайся, Миша. На тебе гриб. Сколько грибов в корзине осталось? Кто может выложить запись на доске.
(На доске: 3 – 1=2).
Вот мы и подошли к замку. Но не вижу я его жителей.
Давайте поиграем в игру “День и ночь”.
( В замке появляются знаки “ + ” , “ — ”, “ = ”).
Назовите, ребята, знаки, которые живут в замке.
IV.Закрепление.
1. Работа в тетради.
А знаки предлагают нам написать их в тетради. Откройте тетради на стр.7.
— Нарисуй столько морковок или яблок, или грибочков, сколько указано цифрами.
— Рассмотри образец.
-Выполни запись по точкам. Допиши до конца строчки.
2. Игра “Собери листочки”.
А сейчас давайте поиграем. Ой! Кто-то с шумом мчится. Кто же это? Вы слышите шум?
Отгадайте загадку:
Бабусю знает целый свет,
Ей от роду лишь триста лет.
Там, на неведомых дорожках,
Дом её на курьих ножках.
Да,это Баба-Яга, которую мы первого сентября взяли в школу учиться.
Принесла она нам конвертик. Посмотрим, что в нём. Но сначала отгадаем загадку:
Осенью кружатся.
На землю ложатся,
С земли не встают и тут изгнивают.
(Листья).
Задание Бабы-Яги.
В конвертике, ребята, осенние листочки и
задание.
(Девочки, возьмите жёлтые листочки, а мальчики – зелёные).
Что написано на листочках.
(У девочек стоит знак “ + ”, а у мальчиков знак “ — ”, а теперь положите,
девочки, свои листочки и возьмите оранжевые. Что на них написано? Знак “+”. Все вместе мы называемся как? Класс.)
3.Путь наш подходит к концу. Но есть ещё очень интересные стихи о знаках. Послушайте их.
Если с ветром дождь сложить
И размытые дороги,
То мы можем получить
Осень мокрую в итоге.
И снежинок кутерьма,
Плюс лыжня да плюс морозы,
Получается зима-
В белом инее берёзы.
А сложи-ка ручеёк,
И подснежник, и скворечник.
Что получится, дружок?
Угадал…Весна, конечно!
Ну, а что ещё осталось,
Летом солнечным назвалось.
(М. Геллер).
(Вывешиваются картинки, на которых нарисовано
то, о чём говорится в стихотворении).
О каком знаке идёт речь в стихотворении?
Проходила наша Таня
С малышами вычитанье.
Вычитанное как понять?
Надо, что – нибудь отнять.
У Аришки — орешки,
У Маришки – матрёшку,
У Андрюшки – новый мяч.
Во дворе и вой и плач.
Получился ответ:
Игрушки есть – подружек нет.
(А.Стройло)
О каком знаке идёт речь в стихотворении? Можно ли поступать, как Таня? Почему?
V. Итог урока.
Урок наш подходит к концу. Я вам сейчас буду показывать знаки, а вы их называйте. (Показываю знаки, ребята называют их).
Молодцы, ребята!
Вот опять звенит звонок и кончается урок!
Литература.
1. В.В.Волина “Праздник числа”. Москва. АСТ ПРЕСС. 1996г.
Сложение и вычитание: Введение в сложение
Урок 1: Введение в сложение
Что такое сложение?
Дополнение — это способ собрать вещи воедино. Когда вы добавляете две суммы, вы считаете их вместе, как одну большую сумму. Добавление происходит все время в реальной жизни.
Когда вы добавляете две суммы, вы считаете их вместе, как одну большую сумму. Добавление происходит все время в реальной жизни.
Например, если у этого кролика есть дети…
Например, если у этого кролика есть дети… она добавляет своей семье.
Мы можем подсчитать количество кроликов, чтобы узнать их количество.
Мы можем подсчитать количество кроликов, чтобы узнать их количество.
Мы можем подсчитать количество кроликов, чтобы узнать их количество.
Мы можем подсчитать количество кроликов, чтобы узнать их количество.
Всего 4 крольчихи. Если у вас 1 крольчиха и 3 крольчихи, всего у вас 4 крольчихи.
Что, если бы было еще четыре кроликов?
Как видите, если у вас есть 4 кроликов и вы добавите еще 4 , то всего у вас будет 8 кроликов. Вы можете написать это так:
Вы можете написать это так:
4 + 4 = 8
4 + 4 = 8 — это математическое уравнение . Вы можете прочитать это так: Четыре плюс четыре равно восьми. Математическое уравнение в основном представляет собой математическое предложение . Он использует цифры и символы вместо слов. Когда мы записываем уравнения со сложением, мы используем два символа: + и = .
Знак плюс ( + ) означает, что две вещи складываются вместе. Вот почему мы поместили его между кроликами — у нас было 4 кролика и добавилось еще 4.
Другой символ в нашем уравнении: равно знак ( = ). Когда вы видите знак равенства в уравнении, это означает, что на два больше, чем на 9.0007 равно или эквивалентно . Эквивалентные вещи не всегда выглядят или кажутся совершенно одинаковыми, но они означают одно и то же.
Например, когда вы видите знакомого, вы можете сказать несколько вещей:
Эти слова не совсем похожи, но означают одно и то же. Это все способы приветствовать кого-то.
В математике знак равенства показывает, что два числа или выражения означают одно и то же , даже если они могут выглядеть по-разному. Помните наших кроликов? Поскольку всего было 8 кроликов, мы написали 8 справа от знака равенства.
Видите, как каждая сторона означает 8? Слева 8 кроликов, а справа цифра 8. Обе стороны равны .
Попробуйте!
Заполните пропуски, чтобы завершить уравнения.
Запись выражений
На последней странице мы рассмотрели некоторые математические выражения. Выражения полезны, так как они могут помочь вам отслеживать суммы, которые вы добавляете.
Любую задачу на сложение можно превратить в письменное выражение. Например, скажите, что вы планировали пригласить на ужин троих друзей.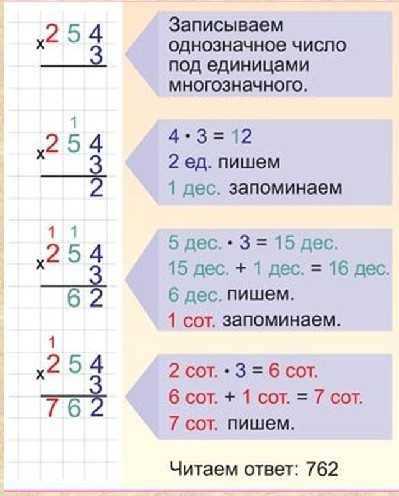 В последнюю минуту вы приглашаете еще двоих. Чтобы получить общее количество друзей, которые приходят к вам домой, вы можете написать следующее выражение:
В последнюю минуту вы приглашаете еще двоих. Чтобы получить общее количество друзей, которые приходят к вам домой, вы можете написать следующее выражение:
3 + 2
Это выражение представляет собой еще один способ описать ситуацию: три друзей плюс еще два приходить на ужин.
Попробуй!
Запишите эти ситуации в виде математических выражений. Пока не решайте проблемы — просто установите их.
Вы съели три куска пиццы на обед. За ужином вы съели еще два :
Вы уже прождали пять минут, чтобы обратиться к врачу. Медсестра говорит вам подождать пять еще минут:
Ваше пальто имеет четыре пуговицы с правой стороны и три пуговицы с левой стороны:
Решение задач
Теперь, когда вы знаете, как писать задачи на сложение, давайте решим некоторые из них. Когда вы только начинаете, вам может быть проще использовать , считая , для решения проблем.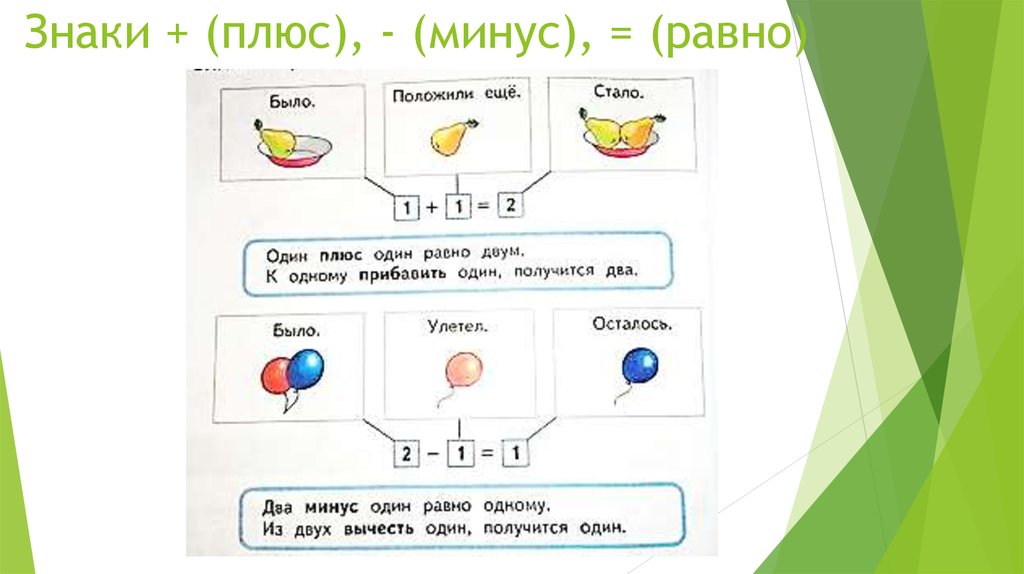
Попробуй!
Например, можете ли вы использовать счет, чтобы написать и решить эту задачу?
С этой проблемой вы могли подсчитывать объекты, которые вы добавляли. В реальной жизни некоторые люди любят считать на пальцах. Другие люди используют небольшие предметы, такие как пуговицы или монеты. Другие могут делать небольшие пометки на листе бумаги. Когда вы учитесь складывать, можно считать! Чем больше вы будете практиковаться, тем легче будет прибавлять, не считая.
Способы счета
Давайте рассмотрим два способа решения задач на сложение со счетом. Сначала мы посчитаем с объектов .
Чтобы считать с помощью объектов, используйте объекты, чтобы показать каждое число в выражении. Давайте попробуем это с этим выражением, 2 + 3.
Первое число равно 2, поэтому нам понадобится 2 объекта.
Первое число равно 2, поэтому нам понадобится 2 объекта.
Первое число равно 2, поэтому нам понадобится 2 объекта.

Следующее число 3. Мы возьмем еще 3 предмета.
Следующее число 3. Мы возьмем еще 3 предмета.
Следующее число 3. Мы возьмем еще 3 предмета.
Теперь мы можем закончить наше уравнение. Все, что нам нужно сделать, это сосчитать !
Теперь мы можем закончить наше уравнение. Все, что нам нужно сделать, это сосчитать !
Теперь мы можем закончить наше уравнение. Все, что нам нужно сделать, это счет !
Теперь мы можем закончить наше уравнение. Все, что нам нужно сделать, это сосчитать !
Теперь мы можем закончить наше уравнение. Все, что нам нужно сделать, это сосчитать !
Всего объектов пять, поэтому наш ответ 5
В завершение напишем 5 справа от знака равенства.
Еще один способ решить задачи на сложение — использовать числовую строку .
Счет с помощью числовой строки занимает всего несколько шагов.
Чтобы использовать числовую линию, вы считаете, перемещая вправо одно число за раз.
Чтобы использовать числовую линию, вы считаете, перемещая вправо одно число за раз.
Чтобы использовать числовую линию, вы считаете, перемещая вправо одно число за раз.
Давайте потренируемся складывать с помощью числовой строки. Мы попробуем эту задачу, 5 + 2.
Нам нужно начать считать с первое число в нашем выражении.
Здесь это число равно 5.
Итак, мы начинаем считать с отметки 5 на числовой прямой.
Далее мы будем считать от второго числа в нашем выражении.
Двигаемся направо 2 раза.
Двигаемся направо 2 раза.
Двигаемся направо 2 раза.
Мы приземлились на 7.
 Это означает, что 5 + 2 равно 7.
Это означает, что 5 + 2 равно 7.Напишем 7 справа от знака равенства. Наше уравнение готово!
Практика!
Потренируйтесь добавлять эти задачи. Имеется 5 наборов задач, по 3 задач в каждом наборе.
Установите 1
6 + 1 =
2 + 0 =
5 + 3 =
Установите 2
4 + 5 =
3 + 1 =
2 + 2 =
Набор 3
1 + 8 =
0 + 3 =
7 + 6 =
SET 4
4 + 8 =
9 + 1 =
7 + 5 =
Установите 5
5 + 5 =
3 + 2 =
6 + 8 = 5 = 5 =
3 + 2 =
6 + 8 = 8 =
ПродолжатьВернуться к плейлисту: сложение и вычитание
Next:Сложение двух- и трехзначных чисел
/ru/дополнение-вычитание/добавление-двух-и-трехзначных-чисел/содержание/
Нарушения обучаемости по математике и СДВГ: как связаны симптомы
На математических конференциях я часто единственный, кто говорит о нарушениях обучаемости. И на конференциях по неспособности к обучению, когда я выступаю с докладом « При чем здесь математика? Неспособность к обучению математике, дислексия и СДВГ», Я часто единственный, кто говорит о математике. Практически отсутствует информация о связях и взаимодействиях между СДВГ, языковыми расстройствами и трудностями в обучении математике, а также о последствиях для лечения. Тем не менее данные говорят нам, что это критическая потребность.
И на конференциях по неспособности к обучению, когда я выступаю с докладом « При чем здесь математика? Неспособность к обучению математике, дислексия и СДВГ», Я часто единственный, кто говорит о математике. Практически отсутствует информация о связях и взаимодействиях между СДВГ, языковыми расстройствами и трудностями в обучении математике, а также о последствиях для лечения. Тем не менее данные говорят нам, что это критическая потребность.
Примерно 35 % населения испытывают те или иные трудности с математикой, а 6,4 % страдают дискалькулией или нарушением способности к обучению математике (MLD). Дети с семейной историей математических трудностей в 10 раз чаще, чем население в целом, имеют проблемы с математикой сами. Это делает MLD таким же распространенным явлением, как дислексия или синдром дефицита внимания и гиперактивности (СДВГ или ADD), но при этом его часто затмевают в классах, IEP и клиниках.
Что такое нарушение способности к обучению математике?
MLD не имеет биологических или качественных маркеров. Его нельзя диагностировать с помощью анализа крови или сканирования мозга. Исследователи до сих пор обсуждают области дефицита и уровень серьезности, которые составляют фактическую неспособность к математике. Это побудило Мишель Маццокко назвать MLD «неясным термином, не имеющим четких границ. 1
Его нельзя диагностировать с помощью анализа крови или сканирования мозга. Исследователи до сих пор обсуждают области дефицита и уровень серьезности, которые составляют фактическую неспособность к математике. Это побудило Мишель Маццокко назвать MLD «неясным термином, не имеющим четких границ. 1
Как и дислексия, MLD — это общий термин, используемый, когда у человека больше проблем с изучением математики, чем можно было бы предсказать по другим факторам. С технической точки зрения, DSM-5 определяет MLD как особое расстройство обучения с нарушением математических способностей, при котором учащийся демонстрирует дефицит в одной или нескольких из следующих областей: чувство числа, запоминание арифметических фактов, точное беглое вычисление и/или точная математика. рассуждения.
[Пройдите этот тест: Симптомы дискалькулии у детей]
Чтобы понять МЛД и их связь с СДВГ и дислексией, полезно рассмотреть два типа когнитивных процессов, связанных с выполнением математических операций. Исследователи разбивают эти процессы на общих доменных процессов и специфичных доменных процессов .
Исследователи разбивают эти процессы на общих доменных процессов и специфичных доменных процессов .
Общие процессы домена относятся к основным процессам мозга, таким как рабочая память, скорость обработки, исполнительные функции и обработка речи, которые лежат в основе многих задач. Это процессы, ответственные за большую часть совпадений с другими нарушениями обучаемости.
Специфичные для предметной области процессы решают математические задачи, используя аппаратную проводку мозга, часто называемую «числовым модулем», расположенную в теменной доле. Эти процессы особенно влияют на математику и несут ответственность за трудности в обучении математике. И, конечно же, у каждого человека будет свой профиль МЛД и сопутствующего СДВГ и других ЛД.
| Общие процессы предметной области | доменные процессы |
| основные процессы | Жесткая проводка для математики |
| лежат в основе многих задач и исполнительных функций | «числовой модуль» |
| ~ совпадает с СДВГ и другими LD | ~ МЛД |
Проблемы с обработкой данных и математические трудности
Оказывается, люди и другие животные, от приматов до птиц и даже пчел, запрограммированы эволюцией на выполнение некоторых математических операций. Числовой модуль в мозгу отвечает за обнаружение, сравнение и управление «численным параметром». Именно здесь мозг субитирует или автоматически распознает небольшое количество без подсчета; сравнивает суммы; и суммы заказов от наименьшего к наибольшему.
Числовой модуль в мозгу отвечает за обнаружение, сравнение и управление «численным параметром». Именно здесь мозг субитирует или автоматически распознает небольшое количество без подсчета; сравнивает суммы; и суммы заказов от наименьшего к наибольшему.
[Пройдите этот тест: есть ли у моего ребенка проблемы с обучением]
Дети, которые борются с этими основными задачами, подвергаются большому риску развития MLD в школе. Их борьба с математикой будет более серьезной и более фундаментальной, чем борьба, основанная только на СДВГ или дислексии, влияя на чувство числа ребенка в его самом основном. Если взрослые смогут распознать и оценить эти трудности на раннем этапе — еще до школы — они смогут начать лечение рано и интенсивно, чтобы опередить MLD и оптимизировать вероятность успеха.
Общие проблемы обработки предметной области и математические трудности
Нарушения рабочей памяти и математика
Рабочая память подобна рабочему столу мозга. Здесь мы храним информацию для немедленного использования. Когда веб-сайт отправляет вам код авторизации, и вы держите его в голове достаточно долго, чтобы перенести из текстового сообщения в онлайн-поле, вы держите его в рабочей памяти.
Здесь мы храним информацию для немедленного использования. Когда веб-сайт отправляет вам код авторизации, и вы держите его в голове достаточно долго, чтобы перенести из текстового сообщения в онлайн-поле, вы держите его в рабочей памяти.
Ограниченная рабочая память в основном вызывает две проблемы с математикой: запоминание математических фактов и способность следовать процедурам. Например, чтобы выучить математические факты, и вопрос (2+3), и ответ (5) должны быть одновременно активны в фонологическом буфере мозга. Таким образом, нейронная связь между ними может быть сформирована и укреплена. Если ответ вытесняет вопрос из-за ограниченной оперативной памяти, то соединение не устанавливается.
Учащиеся с проблемами оперативной памяти нуждаются в четкой инструкции по запоминанию математических фактов. Чем больше нервных путей есть у мозга для доступа к информации, тем эффективнее и точнее он это делает. Тем не менее, механическое запоминание должно сопровождаться манипуляциями и моделями, если они непосредственно и явно связаны с фактами.
Решение задачи вроде 2305 ÷ 0,3 требует как минимум 17 шагов, каждый из которых опирается на оперативную память. Если учащемуся приходится останавливаться, чтобы визуализировать, сколько раз 3 входит в число 23 с остатком, он часто возвращается к задаче совершенно потерянным. Они могут прекрасно понимать концепцию деления и даже деления с десятичной дробью, но их слабая рабочая память приводит к нарушению процедуры.
Этим учащимся нужны приспособления, такие как таблица умножения, мнемоника, контрольные списки и примеры задач. Одно предостережение: учащиеся должны быть четко обучены тому, как использовать свои приспособления.
Нарушения скорости обработки и математика
Низкая скорость обработки, которая влияет на скорость затухания в фонологическом цикле, еще больше затрудняет перемещение фактов из рабочей памяти в долговременную. Даже если учащийся с нарушением скорости обработки информации плохо знает свою таблицу умножения, когда вы спросите его, сколько будет 3 умножить на 7, вы почти увидите, как его шестеренки медленно вращаются, чтобы вывести ответ.
Хотя математические способности не имеют ничего общего со скоростью, многие учителя используют скорость как показатель мастерства. Из-за этого дети чувствуют себя неудачниками. Исследования показали, что тесты на время могут вызвать серьезную математическую тревогу даже у нейротипичных детей. А математическая тревожность может привести к неспособности к обучению математике.
Нарушения исполнительных функций и математика
Нарушения исполнительных функций вызывают ряд проблем у учащихся, изучающих математику. Плохое торможение нерелевантных ассоциаций загромождает и без того ограниченную рабочую память. Представьте студента, думающего 2 + 3 равно… белке! Когда они возвращают свое внимание к проблеме, большая ее часть исчезает, и им приходится начинать все сначала. если они пытаются , а не , чтобы думать об обеде, что также требует значительных вычислительных мощностей.
Сложное переключение между заданиями означает, что учащийся может полностью точно заполнить лист смешанных упражнений на сложение/вычитание, если бы только это были все задания на сложение. Слабый подробный анализ может означать, что учащийся отлично понимает целые числа, а затем полностью пропускает каждый знак минус в тесте. Этим учащимся могут существенно помочь следующие приспособления:
Слабый подробный анализ может означать, что учащийся отлично понимает целые числа, а затем полностью пропускает каждый знак минус в тесте. Этим учащимся могут существенно помочь следующие приспособления:
- Смешанный обзор скаффолдов: вместо того, чтобы переходить со страниц, содержащих только один тип задач, к полностью смешанному обзору с различными перемешанными проблемами, начните со страницы с половинным добавлением (вверху) и полувычитание (внизу). Перейдите на страницу, где задачи переключаются через каждую вторую строку. Как только студент освоит это, вытащите эту традиционную страницу смешанного обзора.
- Подробная информация о цветовом коде: точнее, пусть учащийся придумает и использует цветовой код. Например, на странице, просматривающей порядок операций, они могут использовать синий маркер, чтобы выделить все показатели степени, а затем желтый, чтобы выделить все отрицательные знаки. Во-первых, вы позволяете им заниматься детальным анализом отдельно от остальной обработки, которая им необходима.
 Вы тренируете мозг находить важные детали. Кроме того, они получают страницу с цветовой кодировкой, на заполнение которой учителю не потребовалось несколько часов.
Вы тренируете мозг находить важные детали. Кроме того, они получают страницу с цветовой кодировкой, на заполнение которой учителю не потребовалось несколько часов.
Нарушения обработки речи и математика
Математика требует создания надежных связей внутри и между мирами реальных величин, математическим языком и письменными символами. Сложность языковой обработки затрудняет установление и поддержание этих связей. Эти учащиеся будут медленнее и менее точны в извлечении фактов из основанной на семантике долговременной памяти. Эти дети нуждаются в том, чтобы математические понятия, процедуры и факты были явно, последовательно и неоднократно связаны между собой. Им также нужно гораздо больше практики, чтобы стать автоматическими.
Математика — это отдельный язык, сложный, с несколькими способами выражения одной и той же концепции. Мы знаем, что люди с языковыми LD часто борются с несколькими значениями. Подумайте о простом выражении 15 ÷ 3. Пятнадцать разделить на три, верно? Но что если мы спросим: «Сколько раз три составляют пятнадцать?» или «Сколько групп по три человека в пятнадцати?» или «Трижды сколько будет пятнадцать?» Учащийся с проблемами обработки речи может знать, как разделить 15 на 3, но не может связать это с другими фразами. Как будто им нужно выучить три отдельных понятия. И даже не заводите меня на то, что минус, простите, вычитание может означать отнять или сравнить. Этим детям нужно подробное обучение языку математики, в том числе им нужно объяснить, что некоторые слова означают одно за пределами математики и другое внутри нее. (Операция, кто-нибудь?)
Как будто им нужно выучить три отдельных понятия. И даже не заводите меня на то, что минус, простите, вычитание может означать отнять или сравнить. Этим детям нужно подробное обучение языку математики, в том числе им нужно объяснить, что некоторые слова означают одно за пределами математики и другое внутри нее. (Операция, кто-нибудь?)
Наконец, разговор с самим собой или вербальное посредничество — это стратегия, которую многие из нас используют для укрепления слабых навыков, памяти или понимания, необходимых для достижения чего-то. Мы говорим наш путь через это. Ученик, который изо всех сил пытается найти или произнести слова, будет иметь проблемы с этой внутренней поддержкой.
Сопутствующие заболевания СДВГ
СДВГ и математика
Почти треть детей с СДВГ также имеют проблемы с обучением математике, а 25% детей с MLD имеют СДВГ. Мы знаем, что СДВГ характеризуется, прежде всего, нарушениями в общей области исполнительного функционирования. Недостаток рабочей памяти и скорости обработки также является тревожным сигналом.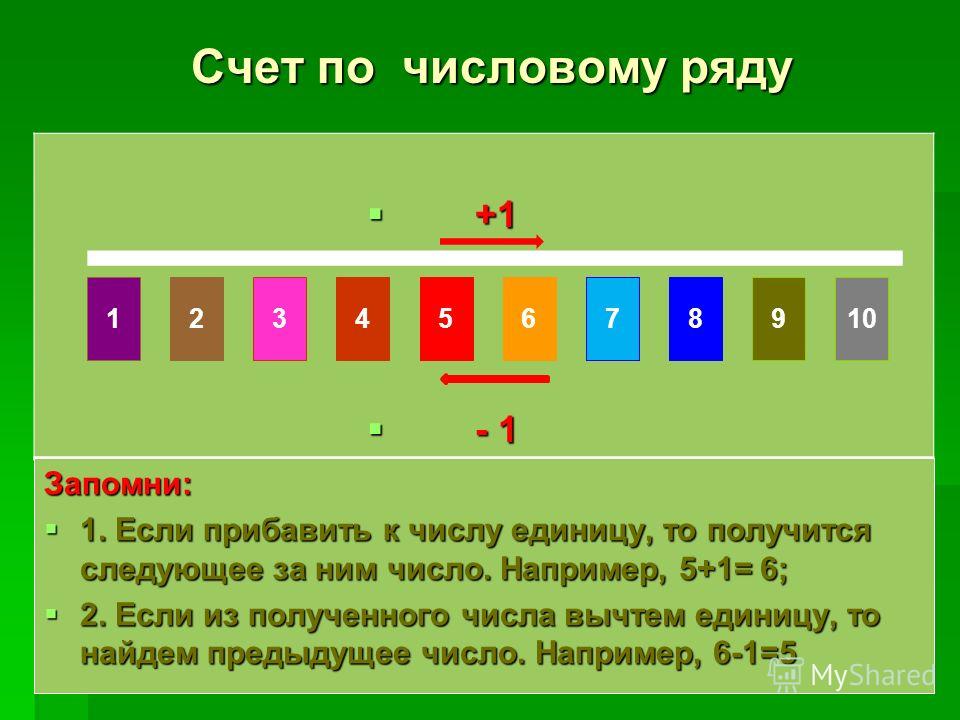 Без сопутствующей дислексии или чистого MLD эти учащиеся, как правило, испытывают затруднения в первую очередь с запоминанием и повторением математических фактов и точным выполнением процедур, а не с концептуальным пониманием самой математики.
Без сопутствующей дислексии или чистого MLD эти учащиеся, как правило, испытывают затруднения в первую очередь с запоминанием и повторением математических фактов и точным выполнением процедур, а не с концептуальным пониманием самой математики.
В дополнение к связанным с СДВГ проблемам с рабочей памятью, скоростью обработки информации и исполнительными функциями, учащиеся с синдромом дефицита внимания сталкиваются с некоторыми уникальными проблемами.
Поскольку мозг с СДВГ очень быстро привыкает к раздражителям, ему может быть трудно удерживать внимание на повторяющихся задачах, например, на математических фактах. Фактически, дети с СДВГ иногда получают 90 380 менее точное 90 381, чем лучше они запоминают факты. Почему? Поначалу запоминание является сложной задачей и держит их мозг в напряжении. Чем ближе к механическому, тем скучнее становится и тем больше неаккуратных ошибок появляется в картине.
Мозг с СДВГ также имеет низкую устойчивость к фрустрации. Придерживаться сложного контента и работать над ошибками для этих детей буквально хуже, чем для их сверстников без СДВГ.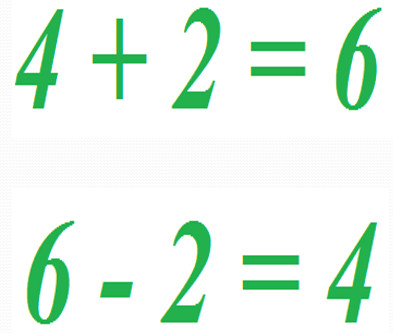 Хуже того, у людей с СДВГ, вероятно, будет то, что исследователи называют «синдромом дефицита вознаграждения». Дофамин — нейротрансмиттер вознаграждения. Всплеск этого заставляет нас чувствовать себя хорошо, когда мы что-то делаем. В мозгу с СДВГ меньше дофамина и слабее дофаминовые рецепторы. Это означает, что решение этой сложной задачи или этой скучной страницы домашнего задания не приносит такого же удовольствия, как другим учащимся.
Хуже того, у людей с СДВГ, вероятно, будет то, что исследователи называют «синдромом дефицита вознаграждения». Дофамин — нейротрансмиттер вознаграждения. Всплеск этого заставляет нас чувствовать себя хорошо, когда мы что-то делаем. В мозгу с СДВГ меньше дофамина и слабее дофаминовые рецепторы. Это означает, что решение этой сложной задачи или этой скучной страницы домашнего задания не приносит такого же удовольствия, как другим учащимся.
Более того, как только люди без СДВГ привыкают к награде, простое ожидание ее дает нам дозу дофамина. Таким образом, просто садясь за эту страницу домашнего задания, мы немного подстегиваемся, когда думаем о награде за выполненную работу. Не так для ребенка с СДВГ. Вдобавок ко всему, люди с СДВГ часто чувствительны к отвержению — ошибки и трудности влияют на их самооценку больше, чем на других. Несколько стратегий, помогающих мозгу с СДВГ, включают:
- Игры, желательно с публичным признанием — побед, а не поражений — (в скобках удивительно, как редко я выигрываю игры, в которые играю со своими учениками!), также желательно на компьютере, который яркий, блестящий и новый даже на уровне пикселей 9.
 0016
0016 - Подробные инструкции по самоконтролю, постановке целей и составлению графиков прогресса
- Любая стимуляция для бодрствования префронтальной коры, например, игрушки-непоседа, музыка, прыгучие мячи и жевательная резинка
- Стимулирующие препараты
Дислексия и математика
Приблизительно от 70% до 80% детей с дислексией также имеют проблемы с обучением математике. Это означает, что учителя, работающие с детьми с дислексией, почти наверняка работают с детьми, у которых проблемы с обучением математике. С другой стороны, от 50% до 60% детей с MLD также имеют дислексию. Дети с MLD и коморбидной дислексией испытывают более серьезные трудности с обучением математике, чем дети только с MLD.
Помните, что дислексия — это не только неспособность к обучению, связанная с речью, но и часто связанная со слабой рабочей памятью и низкой скоростью обработки информации. Это также иногда сочетается с проблемами рецептивной или выразительной речи, влияющими как на устную, так и на письменную речь.
 Это означает, что 5 + 2 равно 7.
Это означает, что 5 + 2 равно 7. Вы тренируете мозг находить важные детали. Кроме того, они получают страницу с цветовой кодировкой, на заполнение которой учителю не потребовалось несколько часов.
Вы тренируете мозг находить важные детали. Кроме того, они получают страницу с цветовой кодировкой, на заполнение которой учителю не потребовалось несколько часов.