Числа от 11 до 20. Сложение и вычитание чисел в пределах 20. Математика, 1 класс: уроки, тесты, задания.

• Предметы
• Математика
• 1 класс

1. Нумерация. Сколько? От 11 до 20

2. Примеры от 11 до 20

3. Сравнения чисел от 11 до 20

4. Задачи на сравнение

5. Текстовые задачи (от 11 до 20)

6. Задачи на смекалку (от 11 до 20)

7. Решение составных задач

8. Уравнение

9. Нумерация двузначных чисел

10. Сложение и вычитание двузначных чисел

11. Таблица сложения в пределах 20

Отправить отзыв

213 задач и примеров по математике для 3 класса (Анна Ефимова)

222 ₽

+ до 33 баллов

Бонусная программа

Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.

Купить

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

Осталось мало

В наличии в 97 магазинах. Смотреть на карте

2

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

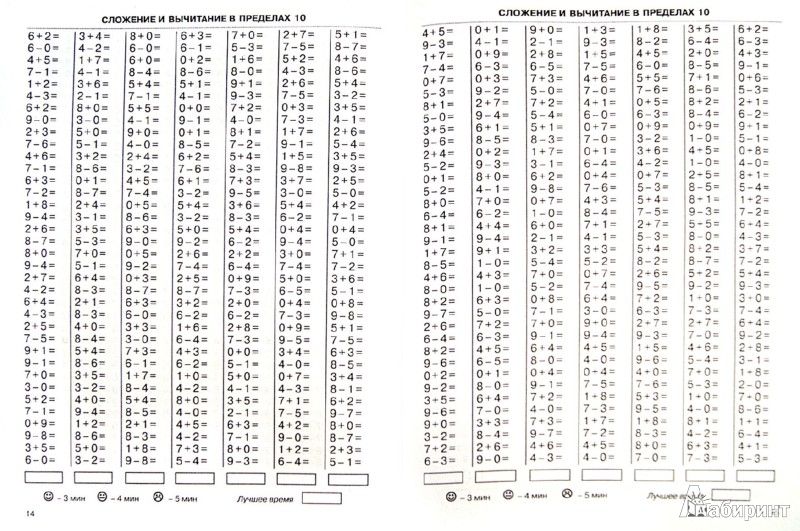
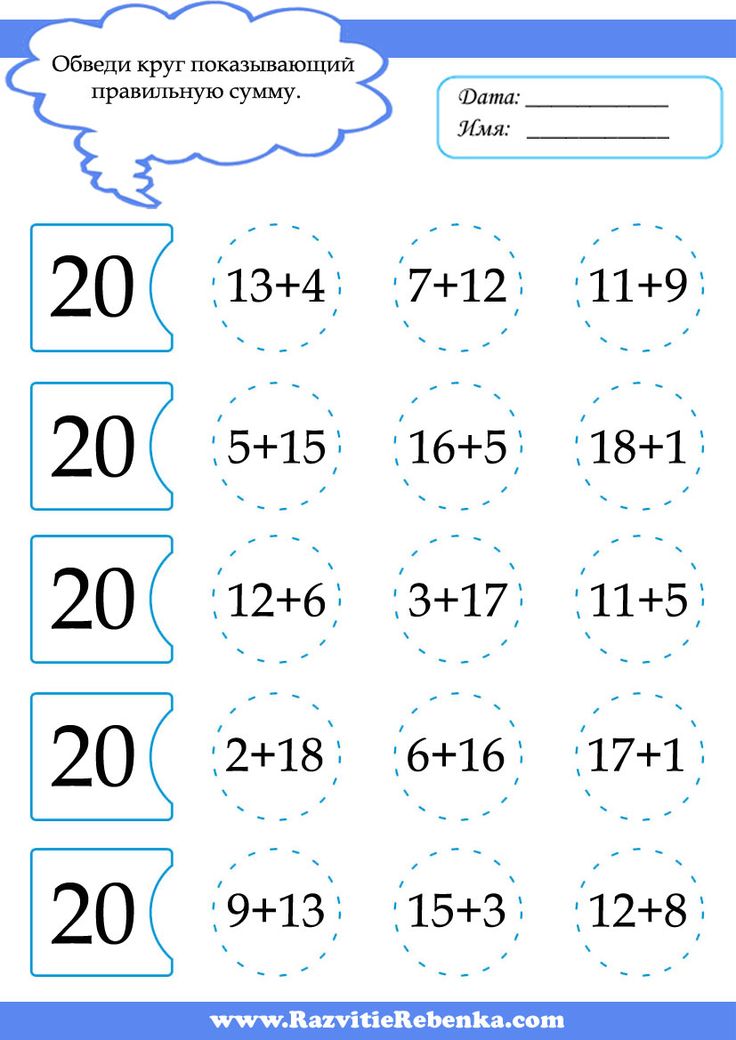
В начальной школе на уроках математики основное внимание уделяется развитию вычислительных навыков, тех, которыми человек пользуется в течение всей своей жизни. .Наша книга дает разнообразный практический материал для тренировки вычислительных навыков, формирования умений решать задачи, упражнения и примеры различных типов, развития логического мышления, сообразительности, усидчивости, интереса к математике.

Описание

Характеристики

В начальной школе на уроках математики основное внимание уделяется развитию вычислительных навыков, тех, которыми человек пользуется в течение всей своей жизни.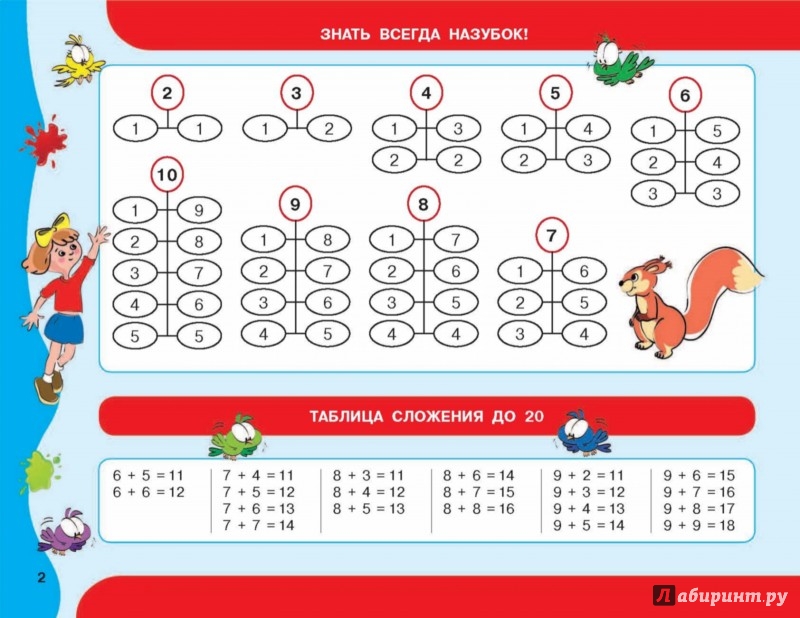 .Наша книга дает разнообразный практический материал для тренировки вычислительных навыков, формирования умений решать задачи, упражнения и примеры различных типов, развития логического мышления, сообразительности, усидчивости, интереса к математике.

Литера

На товар пока нет отзывов

Поделитесь своим мнением раньше всех

Как получить бонусы за отзыв о товаре

1

Сделайте заказ в интернет-магазине

2

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

3

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Книга «213 задач и примеров по математике для 3 класса» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Анна Ефимова «213 задач и примеров по математике для 3 класса» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

Богатые задачи — Часть 1 — Математика для всех

Подробные задачи — Часть 1

Марвин Коэн и Карен Ротшильд богатые проблемы. Разнообразные задачи позволяют ВСЕМ учащимся, с различными сильными сторонами и проблемами в развитии нервной системы, участвовать в математических рассуждениях и стать гибкими и творчески мыслящими математическими идеями. В этом выпуске «Математика для всех» мы рассмотрим что такое богатые проблемы, почему они важны, и где найти готовые к использованию. В более позднем выпуске «Математика для всех» мы обсудим, как создавать собственные сложные задачи, адаптированные к вашему учебному плану.

Что такое расширенные задачи?

В «Математике для всех» мы считаем, что все сложные задачи обеспечивают:

• возможности вовлечь решателя задач в обдумывание математических идей различными нестандартными способами.
• соответствующий уровень продуктивной борьбы.
• возможность для учащихся поделиться своим мнением о математических идеях.

Расширенные задачи улучшают как навыки рассуждения решателя задач, так и глубину его математических знаний. Богатые задачи богаты тем, что не поддаются применению известного алгоритма, а требуют нестандартного использования знаний, умений и изобретательности учащегося. Обычно они предлагают несколько путей входа и методов представления. Это дает учащимся разнообразные способности и дает возможность создавать стратегии решений, которые используют их сильные стороны.

Расширенные задачи обычно имеют одну или несколько следующих характеристик:

• Несколько правильных ответов. Например, «Найдите четыре числа, сумма которых равна 20».
• Один ответ, но множество путей к решению. Например: «На скотном дворе 10 животных, несколько кур, несколько свиней. Всего 24 ноги. Сколько среди животных кур и сколько свиней?»
• Уровень сложности, для решения которого может потребоваться целый урок или более.
• Возможность искать закономерности и устанавливать связи с предыдущими задачами, стратегиями других учащихся и другими областями математики. Например, см. задачу о лестнице ниже.
• «Низкий пол и высокий потолок», означающий как то, что все ваши ученики смогут каким-то образом заниматься математикой задачи, так и то, что задача имеет достаточную сложность, чтобы бросить вызов всем вашим ученикам. NRICH резюмирует этот подход как «каждый может начать, и каждый может застрять» (2013). Например, задача может состоять из множества вопросов, относящихся к следующей последовательности, например: Сколько квадратов на следующей лестнице? Сколько на 20-й лестнице? По какому правилу находят количество квадратов любой лестницы?

• Ожидание, что учащийся сможет изложить свои идеи и защитить свой подход.
• Возможность для учащихся выбирать из ряда инструментов и стратегий для решения проблемы на основе их собственных сильных сторон в развитии нервной системы.
• Возможность изучить новую математику (математический остаток) в процессе работы над задачей.
• Возможность отработать рутинные навыки для решения сложной проблемы.
• Возможность для учителя углубить свое понимание своих учеников как учащихся и построить новые уроки на основе того, что знают учащиеся, их уровня развития, а также их сильных и слабых сторон в развитии нервной системы.

Почему богатые задачи?

Всем взрослым необходимы математические знания для решения задач в повседневной жизни. Большинство взрослых используют калькуляторы и компьютеры для выполнения рутинных вычислений, выходящих за рамки того, что они могут сделать в уме. Однако они должны достаточно понимать математику, чтобы знать, что вводить в машины и как оценивать то, что выходит. Наше личное финансовое положение сильно зависит от нашего понимания схем ценообразования на вещи, которые мы покупаем, ипотечных кредитов, которые мы держим, и сборов, которые мы платим. Как граждане, понимание математики может помочь нам оценивать политику правительства, понимать политические опросы и принимать решения. Строительство и проектирование наших домов, а также масштабирование рецептов для толпы также требуют математики. Особенно сейчас математическое понимание имеет решающее значение для понимания политики, связанной с пандемией. Решения о закрытии, лечении и вакцинах основаны на математике. По всем этим причинам важно, чтобы учащиеся развивали свои способности рассуждать о математике. Исследования показали, что опыт решения сложных задач улучшает математическое мышление детей (Hattie, Fisher, & Frey, 2017).

Где найти сложные задачи

В Интернете доступно несколько типов сложных задач, готовых к использованию или адаптации. Сайты, указанные ниже, являются одними из многих мест, где можно найти сложные задачи:

• Который не принадлежит — эти задачи состоят из квадратов, разделенных на 4 квадранта с числами, фигурами или графиками. В каждой задаче есть по крайней мере один способ, которым каждый из квадрантов «не принадлежит». Таким образом, можно утверждать, что любой квадрант отличается от других.
• Задачи «Открытая середина» — это задачи с одним ответом, но с множеством способов получить ответ. Они организованы как по темам, так и по классам.
• NRICH Maths — это многогранный сайт Кембриджского университета в Великобритании. В нем есть как статьи, так и готовые задачи. На сайте представлены задачи для 1–5 классов (листайте до раздела «Сборники») и задачи для детей младшего возраста. Мы также рекомендуем вам более полно изучить NRICH. На сайте много познавательных статей и обсуждений.
• Расширенные задачи из Вирджинии — это задачи, опубликованные Департаментом образования Вирджинии. Они поставляются с полными планами уроков, а также примерами ожидаемых ответов учащихся.
• Расширенные задания из Джорджии. Этот сайт содержит полную систему заданий, разработанных для соответствия всем стандартам для всех классов. Они включают в себя задачи 3-Act, задачи YouCubed и многие другие задачи с открытым концом или подходом с открытой серединой.

Задачи можно использовать «как есть» или адаптировать к конкретным сильным сторонам развития нервной системы и проблемам ваших учеников. Тщательно адаптированные, они могут вовлечь ВСЕХ ваших учеников в размышления о математических идеях различными способами, тем самым не только улучшая их навыки, но и их способности мыслить гибко и глубоко.

Ссылки

Хэтти Дж., Фишер Д. и Фрей Н. (2017). Видимое обучение математике, классы K-12: что лучше всего помогает оптимизировать обучение учащихся. Таузенд-Оукс, Калифорния: Математика Корвина.

Команда NRICH. (2013). Низкий порог, высокий потолок – введение. Кембриджский университет, Соединенное Королевство: NRICH Maths.https://nrich.maths.org/10345

«Математика для всех» — это программа профессионального развития, которая объединяет учителей общего и специального образования для повышения их квалификации в
планирование и адаптация уроков математики для обеспечения того, чтобы все учащиеся добивались высококачественных результатов обучения по математике.