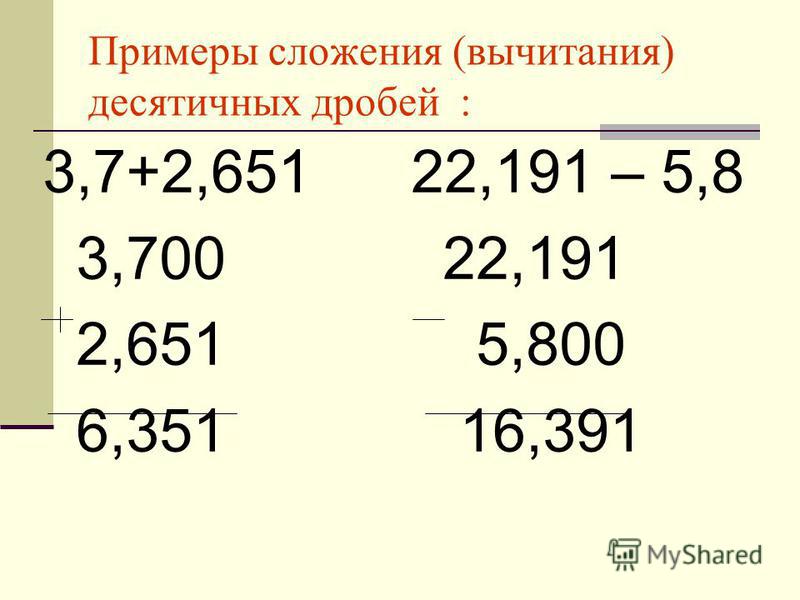
как с разными знаками, основные правила, примеры для 5 класса
Вычитание десятичных дробей в математике
Определение 1Десятичная дробь — это вид дроби, является методом записи действительных чисел в таком виде:
±dm…d1d0,d-1d-2…,
± — знак дроби: + или -;
, — десятичная запятая, отделяет целую часть от дробной части числа;
dk— десятичные цифры.
Последовательность чисел, которые стоят до запятой, является конечной. Последовательность чисел после запятой конечна или бесконечна.
Пример 1Число 123,45 является конечной десятичной дробью.
Число π можно записать, как бесконечную десятичную дробь: 3,1415926535897…
Десятичная дробь ±dm…d1d0,d-1d-2… имеет значение в виде действительного числа:
±dm·10m+…+d1·101+d0·100+d-1·10-1+d-2·10-2+…,
Такое действительное число равно сумме конечного или бесконечного числа слагаемых.
Представлять действительные числа, как десятичные дроби, — значит, обобщать записи целых чисел в десятичной системе счисления. Когда целое число записывают в виде десятичной дроби, после запятой не будет других цифр, кроме нулей:
Когда целое число записывают в виде десятичной дроби, после запятой не будет других цифр, кроме нулей:
±dm…d1d0,
что соответствует записи данного числа в десятичной системе счисления.
Правило 1Сложение и вычитание десятичных дробей выполняется путем записи их друг под другом, чтобы запятая была под запятой. Далее действия аналогичны операциям с обычными числами. В ответ нужно перенести запятую.
Как вычитать десятичные дроби в столбик
В процессе вычитания десятичных дробей, как и сложения, необходимо руководствоваться правилами, согласно которым вычитают в столбик натуральные числа. Последовательность действий:
- Уравнение числа знаков, расположенных после запятой, дописыванием необходимого количества нулей.
- Запись десятичных дробей в столбик, то есть друг под другом — запятая под запятой.
- Вычитание десятичных дробей без учета запятых, исходя из правил, по которым вычитают в столбик натуральные числа.
- Запись в ответе запятой под запятыми.

Источник: math-prosto.ru
Альтернативный способ
Существует другой способ вычитания десятичных дробей. При этом не требуется записывать их в столбик, а действия следует выполнять, опираясь на следующие правила:
- Вычитание десятичных дробей нужно проводить справа налево, то есть началом будет самая правая цифра после запятой.
- Вычитание выполняют по цифрам разрядов. Целые вычитают из целых, десятые вычитают из десятых, сотые вычитают из сотых и так далее.
- Если требуется большую цифру отнять от меньшей, то у соседней цифры слева нужно занять десяток.
Разобрать этот способ можно на примере:
15,21 – 8,31 =
Проводим вычитание, двигаясь с правой стороны в левую. Самой правой цифрой в обеих дробях — сотые. 1 — в первом числе, 1 — во втором. Найдем их разность:
1 – 1 = 0
В результате получен 0, который следует записать на месте сотых в разности:
15,21 – 8,31 = … 0
Далее следует из десятых вычесть десятые. 2 — в первом числе, 3 — во втором числе. Заметим, что из 2 (меньшего) нельзя отнять 3 (большее), поэтому нужно занять десяток у соседа с левой стороны для 2. В данном случае, это 5. Получается, что 3 вычитается из 12:
2 — в первом числе, 3 — во втором числе. Заметим, что из 2 (меньшего) нельзя отнять 3 (большее), поэтому нужно занять десяток у соседа с левой стороны для 2. В данном случае, это 5. Получается, что 3 вычитается из 12:
12 – 3 = 9
В десятые нового числа можно записать 9. Важно помнить о необходимости вычитания единицы из 5, так как был занят десяток из 5.
15,21 – 8,31 = … 90
Переходим к вычитанию целых частей. 14 — в первом числе, 8 — во втором числе.
14 – 8 = 6
15,21 – 8,31 = 6,90
Правило 2Десятые допускается вычитать лишь из десятых, сотые из сотых, тысячные из тысячных и так далее. Когда одна из десятичных дробей не имеет цифру необходимого разряда, ее можно заменить нулем.
Пример 3Рассмотрим вычитание десятичных дробей:
6,9 – 2,52 =
Второе число в крайнем правом положении имеет 2 (сотые), а в первом числе сотые отсутствуют. В этом случае необходимо к первому числу с правой стороны от 9 дописать ноль и выполнить вычитание по стандартному алгоритму.
6,9 = 6,90
6,90 – 2,52 = 4,38
Вычитание десятичных дробей с разными знаками
Вычитать обычные дроби, имеющие неодинаковые знаки, следует по правилам:
- Разность дробей представляет собой дробь.
- В процессе вычитания дробей, разность нужно заменить сложением уменьшаемого и числа, которое противоположно вычитаемому.
6,90 — (-2,52) = 6,90 + 2,52 = 9,42
Как вычесть десятичную дробь из смешанного числа или обыкновенной дроби и наоборот
Правило 3Когда нужно вычислить разность десятичной дроби и целого натурального числа, в конце последнего необходимо дописать запятую, а после нее проставить нули в количестве, равном количеству знаков после запятой в десятичной дроби. Затем нужно выполнить вычитание.
Правило 4Если необходимо найти разность десятичной дроби и простой дроби, то следует рассмотреть 2 варианта и выбрать наиболее подходящий:
- Простую дробь перевести в десятичную. Затем нужно выполнить вычитание.
- Перевести десятичную дробь в обыкновенную.
 В результате действие сводится к вычитанию простых дробей.
В результате действие сводится к вычитанию простых дробей.
В качестве примеров можно рассмотреть вычитание десятичных дробей:
Источник: microexcel.ru
Примеры вычитания числа, которое является целым и натуральным, из десятичной дроби, а также обратный случай:
Источник: microexcel.ru
Правило 5Вычитание десятичной дроби из смешанной, или наоборот, выполняют путем приведения дроби к единому виду дробей.
Данное правило распространяется на все виды дробей при их вычитании и сложении. Рассмотреть действие можно на примере:
125–0,3
Важно заметить, что десятичная дробь в любом случае можно перевести в обычную дробь. С другой стороны, обычную дробь не всегда получается перевести в десятичную, к примеру, 13.
В первую очередь требуется проверка возможности перевода знаменателя смешанной дроби в число, кратное 10, 100 и так далее. Другими словами, необходимо какое-либо из перечисленных чисел разделить на знаменатель. В этом случае при умножении на знаменатель 5 числа 2 получается 10.
Далее следует отделить единицу, то есть целое, умножить дробь на 2. Умножение предусмотрено для числителя и знаменателя. Так как множитель одинаковый, то значение дроби не меняется:
2×25×2=410=0,4
После возврата единицы получим:
1 + 0,4 = 1,4
Выполним вычитание:
1,4 – 0,3 = 1,1
Правило 6Вычитание смешанной дроби из десятичной выполняют путем перевода десятичной дроби в смешанную.
Рассмотрим действие на примере:
2,5-125
Отделим целые части от дробных:
2+510
1+25
Далее следует определить минимальный единый знаменатель. Это число 10. Умножим вторую дробь на 2:
2×25×2=410
Анализируя дроби, которые необходимо отнять 510 и 410, можно заключить, что первая дробь превышает вторую. В этом случае не потребуется занимать, а можно сразу перейти к вычитанию целых частей:
2 – 1 = 1
Далее нужно вычесть дробные части:
510-410=110
Сложим целую и дробную часть, чтобы получить ответ:
1+110=1110
Примеры решения задач для 5 класса
Первая задачаТребуется вычислить:
7,353 – 3,1
Решение
В данном случае количество цифр после запятой разное. Поэтому к 3,1 после единицы нужно дописать пару нулей: 3,100. Далее нужно записать выражение в столбик и выполнить вычисления:
Поэтому к 3,1 после единицы нужно дописать пару нулей: 3,100. Далее нужно записать выражение в столбик и выполнить вычисления:
Источник: spacemath.xyz
Ответ: 4,253
Вторая задачаНужно найти разность:
3,46 – 2,39
Решение
Запишем выражение в столбик:
Источник: spacemath.xyz
Начать следует с вычитания самостоятельных сотых частей: 6-9. При этом необходимо занять единицу у соседнего разряда:
16 – 9 = 7
Полученный ответ нужно записать на место сотой части:
Источник: spacemath.xyz
Далее можно приступить к вычитанию десятых частей. Следует помнить, что ранее была занята единица. Таким образом, в десятых вместо 4 осталась цифра 3. Выполним вычисления в десятых:
3 – 3 = 0
Полученный результат нужно записать в десятые:
Источник: spacemath.xyz
Затем можно вычесть целые части:
3 – 2 = 1
Единицу, которая получилась в результате, следует записать в целой части ответа:
Источник: spacemath. xyz
xyz
Целую часть нужно отделить от дробной:
Источник: spacemath.xyz
Ответ: 1,07
Третья задачаТребуется решить выражение:
3 – 1,2
Решение
Выражение необходимо записать в столбик:
Источник: spacemath.xyz
Следует сравнять количество цифр после запятой путем постановки запятой после 3 и записи одного нуля:
Источник: spacemath.xyz
Далее можно приступить к вычитанию десятых частей: 0 – 2. При этом необходимо занять единицу у соседнего разряда:
Источник: spacemath.xyz
Затем требуется вычесть целые части с учетом того, что была занята единица, и отделить с помощью запятой дробную часть:
Источник: spacemath.xyz
Ответ: 1,8
Четвертая задачаОпределить разность:
37,505 – 17
Решение:
Требуется отделить целую часть от дробной и вычесть из нее указанное число:
37,505 – 17 = 20,505
Ответ: 20,505
| You are here: Home → Статьи → Обучение дробям Как известно многим учителям и родителям, изучение различных операций с дробями может быть трудным для многих детей. И простой причиной, по которой изучение этих операций оказывается трудным для многих студентов, является как их обычно учат . Просто посмотрите на количество правил , чтобы узнать о дробях!
Если учащиеся просто попытаются запомнить эти правила, не зная, откуда они взялись, они, вероятно, будут кажутся бессмысленными джунглями . Они, вероятно, не будут связаны ни с чем, касающимся операции, но вместо этого будут работать как «волшебство»: вы умножаете, делите и делаете разные вещи с числителями и знаменателями, чтобы получить ответ. После этого ученики могут слепо следовать правилам, подбрасывая числа туда и сюда, вычисляя то и это — и получая ответы, не имея ни малейшего представления, разумны они или нет. Кроме того, эти правила довольно легко забыть или неправильно запомнить, особенно через 5-10 лет. Решение: манипулятивные и визуальные модели Вместо того, чтобы просто представить правило, лучше использовать визуальные модели или манипуляции во время изучения арифметики дробей. Типичные учебники ДЕЙСТВИТЕЛЬНО показывают наглядные модели для дробей, и они ДЕЙСТВИТЕЛЬНО показывают один или два примера того, как определенное правило связано с изображением. Но этого недостаточно! Нам нужно, чтобы дети решили множество задач, используя либо визуальные модели, либо дробные манипуляции . Другой способ состоит в том, чтобы попросить их НАРИСОВАТЬ дробные изображения для решения задач. Таким образом, учащиеся сформируют ментальную визуальную модель и смогут продумать картинки. Например, в этом видео показан визуальный метод эквивалентных дробей: дальнейшее разделение частей на определенное количество новых частей: Если вы продумаете картинки , то легко увидите необходимость умножения или деления и числителя, и знаменателя на одно и то же число. Еще один пример — тема сложения разных дробей (см. видео). Учитель может показать, как нужно разделить части в дробях, чтобы все они были одинаковыми, а затем вы можете добавить. Сначала (скажем, в 4-м классе) не нужно обсуждать «наименьший общий знаменатель». Вы можете просто использовать картинки или манипуляторы. Затем дети будут складывать разные дроби, используя манипуляторы или рисуя картинки. Через некоторое время некоторые ученики могут обнаружить правило об общем знаменателе, или на какие части нужно разделить дроби. В любом случае, они наверняка лучше запомнят правило, когда смогут сами проверить его на многочисленных наглядных примерах. Я не говорю, что правила не нужны — потому что они есть. Вы не сможете справиться с алгеброй, не зная правил работы с дробями. Но при широком использовании визуальных моделей на начальных этапах правила обретут больше смысла, и если через 10 лет учащийся забудет правила, он все равно сможет «вычислять» с картинками в уме, а не рассматривать их. дроби как то, что он просто «не умеет». Вам нужна помощь с дробями?Посмотрите эти бесплатные уроки фракций!
Меню уроков математики |
Открытые учебники | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.

 В результате действие сводится к вычитанию простых дробей.
В результате действие сводится к вычитанию простых дробей. Трудно не понятие дроби, а различные операции: сложение, вычитание, умножение, деление, сравнение, упрощение, и т. д. дробей
Трудно не понятие дроби, а различные операции: сложение, вычитание, умножение, деление, сравнение, упрощение, и т. д. дробей Преобразовать смешанное число в дробь
Преобразовать смешанное число в дробь 
 Таким образом, дроби становятся для студента чем-то конкретным, а не просто числом поверх другого без смысла. Учащийся сможет оценить ответ перед расчетом, оценить обоснованность итогового ответа и проделать многие простейшие операции в уме, не применяя заведомо какое-либо «правило».
Таким образом, дроби становятся для студента чем-то конкретным, а не просто числом поверх другого без смысла. Учащийся сможет оценить ответ перед расчетом, оценить обоснованность итогового ответа и проделать многие простейшие операции в уме, не применяя заведомо какое-либо «правило».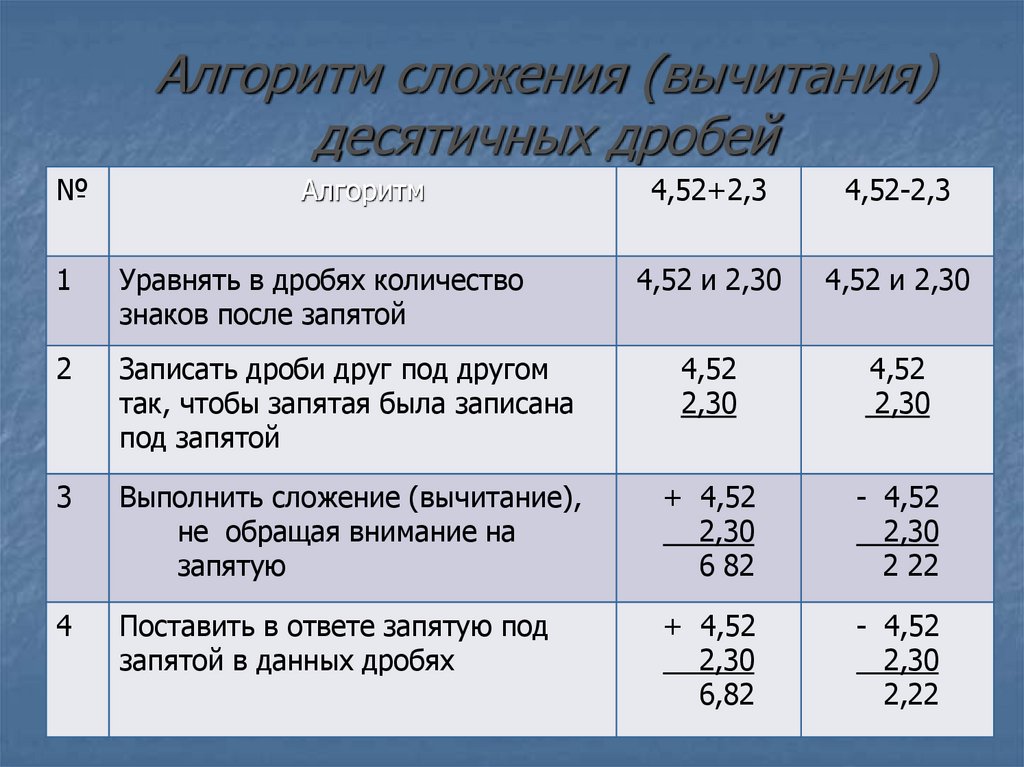 Но прежде чем озвучить это правило, лучше, чтобы дети получили много «практического» опыта с изображениями дробей,
Но прежде чем озвучить это правило, лучше, чтобы дети получили много «практического» опыта с изображениями дробей,