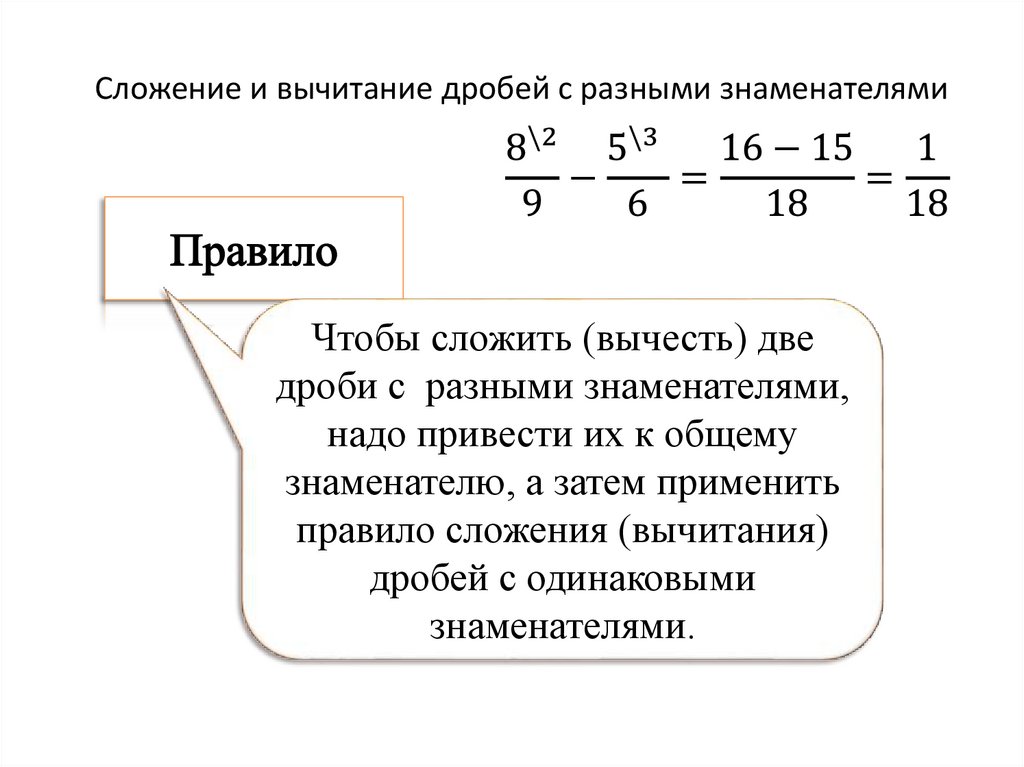
Вычитание дробей с разными знаменателями – примеры, правила (5 класс, математика)

4.2

Средняя оценка: 4.2

Всего получено оценок: 254.

4.2

Средняя оценка: 4.2

Всего получено оценок: 254.

Вычитание дробей само по себе достаточно сложная задача, а уж вычитание дробей с разными знаменателями и вовсе порой ставит учеников 5 класса в ступор. Поэтому стоит разобраться в этой теме подробнее раз и навсегда.

Вычитание дробей

Вычитание дробей возможно только при одинаковых знаменателях.

Если вычитаемое больше уменьшаемого, то результатом станет отрицательное число.

При вычитании дробей мы создаем новую дробь, в числителе которой будет разность числителей изначальных дробей, а знаменатель останется прежним.

Следующим преобразованием будет вычисление разности в числителе.

Вычитание дробей с разными знаменателями

Если у дробей разные знаменатели, то необходимо первым делом привести дроби к общему знаменателю. Для этого нужно воспользоваться правилом дробей.

Основное свойство дробей заключается в том, что при умножении числителя и знаменателя дроби на одно и то же число, значение дроби не изменится. Это обусловлено тем, что по факту дробь является не законченной операцией деления, а умножение делителя и делимого на одно и то же число не изменит частное.

Как найти общий знаменатель?

Общей знаменатель это НОК или наименьшее общее кратное. Наименьшее общее кратное двух и более чисел, это число, которое делится на каждое из них.

Для нахождения наименьшего общего кратного ряда простых чисел, нужно просто перемножить их между собой.

$$НОК=3*5*7=105$$

Но что будет, если в ряде будет три сложных числа?

18,15,25 – найдем для этого ряда НОК.

Для этого, каждое из чисел нужно разложить на простые множители.

$$18=2*3*3$$

$$15=3*5$$

$$25=5*5$$

Для того, чтобы найти НОК нужно перемножить простые множители чисел, которые еще не встречались.

Начнем с числа 2. Двойка встречалась только в простых множителях числа 18, вычеркнем ее.

$$НОК=2*…$$

Следующее число 3. Вычеркиваем одну тройку из разложения числа 18 и из разложения числа 15.

$$НОК=2*3…$$

У нас осталась еще одна тройка в разложении числа 18.

$$НОК=2*3*3…$$

Теперь посмотрим, какое число осталось в разложении 15. Это 5:

$$НОК=2*3*3*5…$$

Вычеркиваем одну 5 из разложения числа 15 и одну из разложения числа 25. Осталось одно число, множители которого не зачеркнуты: это 25, где осталась одна 5. Добавим ее в НОК и получим окончательное значение:

$$НОК=2*3*3*5*5=450$$

Так нужно действовать с любым рядом чисел, для которых необходимо найти НОК.

Пример

Теперь рассмотрим пример вычитания дробей с разным знаменателем. Найдем следующую разность:

$${37\over{81}}-{91\over{180}}$$

• Первым шагом нам нужно найти будущий общий знаменатель, который будет являться НОК(81,180)

Разложим на простые множители число 81

81=3*3*3*3

Разложим на простые множители число 180

180=2*2*3*3*5

Значит, для того, чтобы получить НОК нам необходимо домножить 81 на 5*2*2 или домножить 180 на 3*3. Второй вариант немного проще, поэтому используем его:

180*3*3=180*9=1620

Для того, чтобы сложное число умножить на 9 необязательно умножать. Можно упростить вычисления следующим образом: умножить число на 10 и вычесть это же число. То есть: 180*9=180*10-180=1800-180=1620

• Теперь приведем каждую из дробей к общему знаменателю:

$${37\over{81}}={{37*20}\over{81*20}}={{740}\over{1620}}$$

$${91\over{180}}={{91*9}\over{180*9}}={{809}\over{1620}}$$

• Вычтем получившиеся значения:

$${{740}\over{1620}}-{{809}\over{1620}}={{740-809}\over{1620}}=-{{69}\over{1620}}$$ – получилось отрицательно число, но в этом нет ничего страшного. Просто изначально уменьшаемое было меньше вычитаемого

Что мы узнали?

Мы узнали, как правильно вычитать дроби с разными знаменателями, поговорили о том, как находить НОК и решили небольшой пример.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Милана Черникова

  7/10

• Никита Свирский

  10/10

Оценка статьи

4.2

Средняя оценка: 4.2

Всего получено оценок: 254.

---

А какая ваша оценка?

6 класс. Математика. Сложение и вычитание дробей с разными знаменателями. Сравнение дробей — Сложение и вычитание дробей с разными знаменателями. Сравнение дробей

Комментарии преподавателя

Вспом­ним, что мы уже знаем об обык­но­вен­ных дро­бях.

1. Любая дробь пред­став­ля­ет ко­ли­че­ство – часть от ка­ко­го-то числа. Эту часть мы умеем вы­чис­лять. На­при­мер,  от 100 – это .

2. Одну и ту же часть можно вы­ра­зить эк­ви­ва­лент­ны­ми дро­бя­ми (см. рис. 1). Эк­ви­ва­лент­ные дроби имеют раз­ную за­пись, од­на­ко вы­ра­жа­ют одно и то же ко­ли­че­ство, равны друг другу.

Рис. 1. При­мер эк­ви­ва­лент­ных дро­бей

3. При сло­же­нии/вы­чи­та­нии дро­бей с оди­на­ко­вы­ми зна­ме­на­те­ля­ми скла­ды­ва­ем/вы­чи­та­ем чис­ли­те­ли.

4. При срав­не­нии двух дро­бей с оди­на­ко­вы­ми зна­ме­на­те­ля­ми боль­шая та, у ко­то­рой чис­ли­тель боль­ше (см. рис. 2).

Рис. 2. При­мер срав­не­ния дро­бей с оди­на­ко­вым зна­ме­на­те­лем

Те­перь пе­рей­дем к во­про­су: что де­лать, если у дро­бей будут раз­ные зна­ме­на­те­ли. На­при­мер, как нам сло­жить  и  (см. рис. 3)?

Рис. 3. Ил­лю­стра­ция к при­ме­ру

Если мы за­ме­ним одну из дро­бей на эк­ви­ва­лент­ную, то их сумма, оче­вид­но, не из­ме­нит­ся.

Для дроби  су­ще­ству­ет бес­ко­неч­ное мно­же­ство дро­бей, ко­то­рые ей эк­ви­ва­лент­ны. Да­вай­те будем до­мно­жать чис­ли­тель и зна­ме­на­тель этой дроби на 2, 3, 4 и т.д. Тем самым мы по­лу­чим це­поч­ку эк­ви­ва­лент­ных дро­бей.

Ана­ло­гич­но по­сту­пим и со вто­рой дро­бью:

Мы можем за­ме­нить дробь эк­ви­ва­лент­ной. Нам нужно найти такие две дроби, у ко­то­рых зна­ме­на­тель оди­на­ко­вый, тогда мы смо­жем вы­пол­нить сло­же­ние. Оди­на­ко­вый зна­ме­на­тель у дро­бей  и , за­ме­ним ис­ход­ные дроби на них.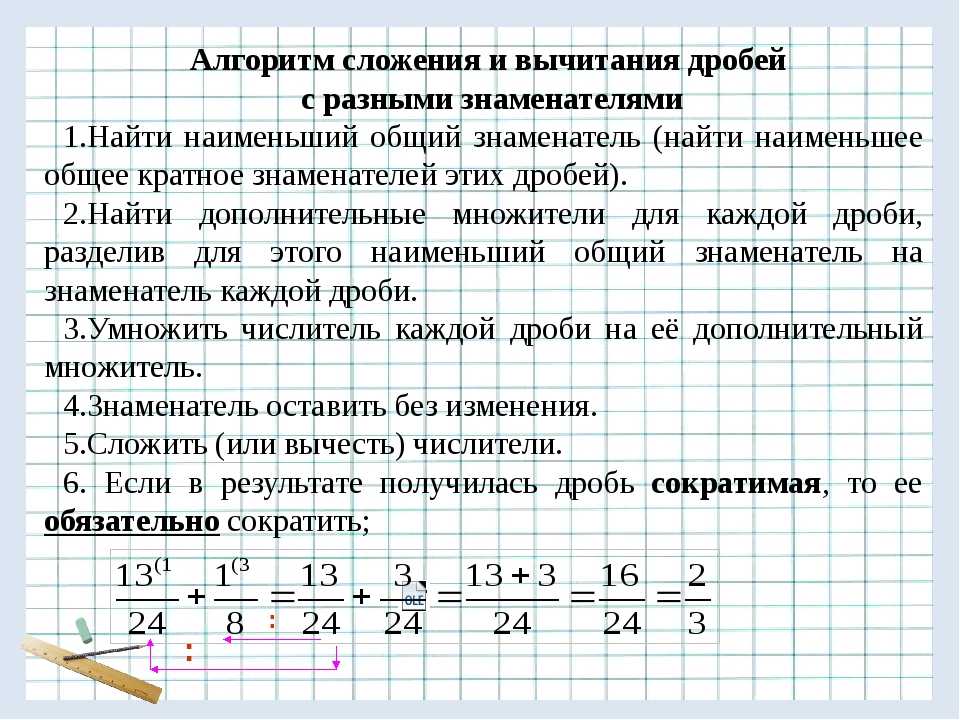

Рас­смот­рим еще несколь­ко при­ме­ров.

Необ­хо­ди­мо сло­жить дроби.

1) 

Ре­ше­ние

1) Неслож­но за­ме­тить, что дробь  легко пре­вра­ща­ет­ся в эк­ви­ва­лент­ную дробь со зна­ме­на­те­лем 4. Для этого нам нужно до­мно­жить ее чис­ли­тель и зна­ме­на­тель на 2.

Опре­де­ли­те раз­ность.

1)                                                2)                                                3) 

Ре­ше­ние

1) Неслож­но уви­деть, что мы вто­рую дробь может пре­вра­тить в дробь со зна­ме­на­те­лем 8, для этого умно­жим ее чис­ли­тель и зна­ме­на­тель на 2.

2) Обе дроби мы можем за­ме­нить эк­ви­ва­лент­ны­ми дро­бя­ми со зна­ме­на­те­лем 6. Чис­ли­тель и зна­ме­на­тель пер­вой дроби до­мно­жим на 3, а вто­рой – на 2.

3) Общим зна­ме­на­те­лем для этих дро­бей яв­ля­ет­ся число 30. По об­раз­цу ре­ша­ем по­след­ний при­мер.

Таким об­ра­зом, для сло­же­ния/вы­чи­та­ния двух дро­бей с раз­ны­ми зна­ме­на­те­ля­ми дроби необ­хо­ди­мо све­сти к об­ще­му зна­ме­на­те­лю.

Срав­ни­те дроби в при­ме­рах. Вы­пол­ни­те дей­ствия.

1)                                            2) 

Ре­ше­ние

1) Общий зна­ме­на­тель сла­га­е­мых дол­жен по­лу­чать­ся из чисел 15 и 18 умно­же­ни­ем на ка­кие-то числа. На­при­мер, зна­ме­на­тель 270 по­лу­ча­ет­ся при умно­же­нии 15 и 18 друг на друга, а зна­чит, может вы­сту­пать в ка­че­стве об­ще­го зна­ме­на­те­ля для ис­ход­ных дро­бей. Те­перь необ­хо­ди­мо умно­жить пер­вое сла­га­е­мое на 18, а вто­рое – на 15. По­лу­чен­ные дроби после умно­же­ния можно срав­нить:

Сле­до­ва­тель­но, пер­вое сла­га­е­мое мень­ше вто­ро­го: .

Опре­де­лим сумму дро­бей: .

2) По­доб­ным об­ра­зом ре­ша­ем вто­рой при­мер. Вна­ча­ле при­во­дим дроби к об­ще­му зна­ме­на­те­лю. Срав­ни­ва­ем по­лу­чив­ши­е­ся зна­че­ния.

Ло­гич­но, что умень­ша­е­мое боль­ше вы­чи­та­е­мо­го. В этом мы убе­ди­лись при све­де­нии дро­бей к оди­на­ко­во­му зна­ме­на­те­лю: .

Вы­пол­ним вы­чи­та­ние до конца: .

источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/slozhenie-i-vychitanie-drobej-s-raznymi-znamenatelyami/slozhenie-i-vychitanie-drobey-s-raznymi-znamenatelyami-sravnenie-drobey

источник видео — http://www.youtube.com/watch?v=7pdDvmttTlM

источник видео — http://www.youtube.com/watch?v=bCtDS1tTmSk

источник видео — http://www.youtube.com/watch?v=vpzGhncogSE

источник видео — http://www.youtube.com/watch?v=Xh9qs-6aw6A

источник презентации — http://ppt4web.ru/matematika/sravnenie-slozhenie-i-vychitanie-drobejj-s-raznymi-znamenateljami0.html

источник теста — http://testedu.ru/test/matematika/5-klass/slozhenie-i-vyichitanie-obyiknovennyix-drobej.html

Сложение и вычитание дробей с разными знаменателями

Результаты обучения

• Сложение и вычитание дробей с разными знаменателями
• Сложение и вычитание дробей с разными знаменателями, которые содержат переменные
• Определять и использовать дробные операции

После того, как мы преобразовали две дроби в эквивалентные формы с общими знаменателями, мы можем складывать или вычитать их, добавляя или вычитая числители.

Сложение или вычитание дробей с разными знаменателями

1. Найдите ЖК-дисплей.
2. Преобразуйте каждую дробь в эквивалентную форму с ЖК-дисплеем в качестве знаменателя.
3. Сложение или вычитание дробей.
4. Запишите результат в упрощенной форме.

Пример

Добавить: [latex]\Large\frac{1}{2}+\Large\frac{1}{3}[/latex]

Решение:

	[латекс]\Большой\фракция{1}{2}+\Большой\фракция{1}{3}[/латекс]
Найдите ЖК-дисплей [латекс]2[/латекс], [латекс]3[/латекс].
Преобразование в эквивалентные дроби с помощью ЖК-дисплея [латекс]6[/латекс].	[латекс]\Large\frac{1\cdot\color{red}{3}}{2\cdot\color{red}{3}} +\Large\frac{1\cdot\color{red}{2 }}{3\cdot\color{red}{2}}[/latex]
Упростите числители и знаменатели.	[латекс]\Большой\фракция{3}{6}+\Большой\фракция{2}{6}[/латекс]
Доп.	[латекс]\большой\фрак{5}{6}[/латекс]

Помните, всегда проверяйте, можно ли упростить ответ. Поскольку [латекс]5[/латекс] и [латекс]6[/латекс] не имеют общих множителей, дробь [латекс]\большой\фрак{5}{6}[/латекс] нельзя сократить.

Попробуйте

Посмотрите следующее видео, чтобы увидеть больше примеров и пояснений о том, как сложить две дроби с разными знаменателями.

Попробуйте

Пример

Добавить: [latex]\Large\frac{7}{12}+\Large\frac{5}{18}[/latex]

Показать решение

Попробуйте

Вы также можете сложить более двух дробей, если сначала найдете для них общий знаменатель. Пример суммы трех дробей показан ниже. В этом примере вы будете использовать метод простой факторизации, чтобы найти LCM.

Подумай об этом

Добавить [латекс]\Большой\фрак{3}{4}+\Большой\фрак{1}{6}+\Большой\фрак{5}{8}[/латекс]. Упростите ответ и запишите в виде смешанного числа.

Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы сложили вместе три дроби с разными знаменателями.

Показать раствор

Вычитание дробей

Когда вы вычитаете дроби, вы должны думать о том, есть ли у них общий знаменатель, как и при сложении дробей. Ниже приведены примеры вычитания дробей, знаменатели которых не совпадают.

Пример

Вычесть: [латекс]\Большой\фрак{7}{15}-\Большой\фрак{19}{24}[/латекс]

Показать решение

Попробуйте

В следующем видео приведены еще два примера вычитания двух дробей с разными знаменателями.

Пример

Добавить: [latex]-\Large\frac{11}{30}+\Large\frac{23}{42}[/latex]

Показать решение

Попробуйте

Пример

Вычесть: [латекс]\Большой\фракция{1}{2}-\влево(-\Большой\фракция{1}{4}\право)[/латекс]

Показать решение

Сложение и вычитание дробей, содержащих переменные

В следующем примере одна из дробей имеет в числителе переменную. Выполняем те же действия, что и в случае, когда оба числителя являются числами.

Пример

Добавить: [latex]\Large\frac{3}{5}+\Large\frac{x}{8}[/latex]

Показать решение

Попробуйте

Посмотрите следующее видео, чтобы увидеть больше примеров сложения и вычитания дробей с разными знаменателями, которые содержат переменные.

Поддержите!

У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.

Улучшить эту страницуПодробнее

Обучение сложению и вычитанию дробей с разными знаменателями

Поделись с друзьями!

11 акции

• Поделиться
• Твит

Этот революционный метод значительно облегчит детям изучение сложения и вычитания дробей с разными знаменателями.

Сложение и вычитание дробей с разными знаменателями

Если вы когда-нибудь пытались научить сложению и вычитанию дробей с разными знаменателями, вы, вероятно, хотели биться головой о стену. Это очень сложная концепция для понимания детьми. Он не только включает в себя несколько шагов, но также требует, чтобы дети понимали, почему они не могут сразу складывать числа.

Почему трудно объяснить. Хорошей новостью является то, что есть метод, который заставит эту концепцию щелкнуть.

Понимание эквивалентных дробей

Прежде чем вы начнете обучать сложению и вычитанию дробей с разными знаменателями, ваши ученики должны понять, как составлять эквивалентные дроби. Вы захотите использовать манипуляции, чтобы показать, что дроби могут быть эквивалентны: 2/4 совпадает с 1/2.

Ваши учащиеся должны иметь твердые навыки составления эквивалентной дроби. (Вам нужно умножить или разделить числитель и знаменатель на одно и то же число. ) 1/2 становится 2/4, когда вы умножаете числитель на 9.0169 и знаменатель на 2. Одна равнозначная дробь не больше и не меньше другой; они равны.

Как обучать сложению и вычитанию дробей с разными знаменателями

При обучении сложению и вычитанию дробей с разными знаменателями начинайте с демонстрации. Вы можете нарисовать фрукты или использовать настоящие фрукты (2 яблока и 1 апельсин). Скажите: «Представьте, что я продавец яблок. В конце дня продажи яблок мне нужно подсчитать, сколько яблок осталось в моих корзинах. Я нахожу одно яблоко в урне слева от себя, а другое яблоко — в урне справа». (Покажите яблоки или нарисуйте их на доске.) «Сколько у меня яблок?» (2) «Точно. 1 яблоко плюс 1 яблоко равно 2 яблокам».

«На следующий день я смотрю в свои закрома, чтобы посмотреть, сколько яблок у меня осталось. Я смотрю в мусорное ведро слева и вижу 1 яблоко. Я смотрю в мусорное ведро справа от себя и, что удивительно, вижу апельсин!» (Покажите фрукты или нарисуйте их на доске. ) «Сколько яблок у меня осталось? Это все, что меня волнует, потому что я продавец яблок». (1) «У меня есть только одно яблоко. Несмотря на то, что у меня есть апельсин, я не могу добавить яблоки и апельсины и получить больше яблок. Это просто не работает».

Сортировка дробей по именам

Напишите на доске четыре дроби: ¼, ⅚, ⅙ и ¾. Скажите учащимся, что эти дроби подобны апельсинам и яблокам. Как вы можете сказать, какие из них какие? Вы смотрите на номер кнопки, на знаменатель. Это название фракции. На доске два названия дробей (два знаменателя): 4-я и 6-я.

Нельзя складывать две дроби с разными именами. Чтобы добавить их, они должны иметь одинаковое имя, точно так же, как вы можете добавлять яблоки только к яблокам, чтобы получить больше яблок. Чтобы добавить дроби с разными именами, вам нужно изменить название одной или нескольких дробей, чтобы они совпадали.

Пример задачи на сложение дробей с разными знаменателями

Проиллюстрируйте эту концепцию, написав эту задачу: ½ + ¼ = __.