Консультация для преподавателей 5 класса (январь)
Тема консультации: «ДРОБИ»Дидактическая основаДидактической основой непрерывного курса математики «Учусь учиться» является дидактическая система деятельностного метода обучения «Школа 2000…». Ее главной особенностью является то, что знания не даются учащимся в готовом виде, а организуется их самостоятельное открытие детьми. Такой подход обеспечивает высокий уровень математической подготовки, развивает мышление учащихся, их способности, повышает интерес к изучению математики, обеспечивают личностные и метапредметные результаты образования, соответствующие ФГОС.
Содержание консультацииВ соответствии с планированием учебного материала по курсу математики «Учусь учиться» для 5 класса в январе продолжается работа с третьей главой «Дроби». Изучаются § 1. «Понятие дроби» (П. 3.1.2 «Основное свойство дроби. Преобразование дробей»; П.3.1.3 «Сравнение дробей») и § 2. «Арифметика дробей» (П.3.2.1 «Сложение и вычитание дробей»), содержание которых продолжает развитие числовой содержательно-методической линии курса.
3.1.2 «Основное свойство дроби. Преобразование дробей»; П.3.1.3 «Сравнение дробей») и § 2. «Арифметика дробей» (П.3.2.1 «Сложение и вычитание дробей»), содержание которых продолжает развитие числовой содержательно-методической линии курса.
Вместе с тем, в процессе изучения этих пунктов параллельно развиваются и все остальные линии курса. Такой подход является общим для данного курса: на каждом этапе его изучения, параллельно с ведущей линией, по которой идет расширение понятийной базы, закрепляются и отрабатываются знания и умения по всем остальным разделам курса.
Основные содержательные цели:- вывести основное свойство дроби, сформировать умение сокращать дроби, приводить дроби к новому знаменателю и числителю;
- сформировать умение сравнивать дроби с помощью приведения дробей к одинаковому числителю, знаменателю, промежуточного числа, дополнения дроби до 1, «перекрёстного» правила;
- сформировать умение складывать и вычитать дроби (общий случай).

В соответствии с принципом минимакса дидактической системы деятельностного метода «Школа 2000…» организовать работу по учебнику 5 класса возможно в условиях различных учебных планов образовательных учреждений. Поэтому тематическое планирование по изучению данного курса разработано для 5 ч и для 6 ч в неделю. При 6 ч в неделю добавочные часы идут на выполнение дополнительных заданий и уроки рефлексии, позволяющие учащимся лучше усвоить изучаемый материал.
Тематическое планирование разработано в двух вариантах: для учителей, закончивших ознакомительные курсы по программе «Школа 2000…» и работающих на базовом (содержательном) уровне реализации дидактической системы «Школа 2000…», и для учителей, закончивших углубленные курсы по программе «Школа 2000…» и работающих на технологическом уровне реализации дидактической системы «Школа 2000…».
Мы предлагаем Вам скачать тематическое планирование на III четверть (5 ч в неделю).
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Методические рекомендации к организации учебного процессаГлава 3. «Дроби»
§ 1. Натуральные числа и дроби. П.2 Основное свойство дроби. Преобразование дробей
1) В результате изучения пункта 3.1.1 учащиеся повторили известные им из курса начальной школы сведения о дробях. Среди них были зафиксированы правила, которые будут уточняться для общего случая в ходе изучения третьей главы: правила сравнения дробей с одинаковыми числителями, знаменателями, правило сложения и вычитания дробей с одинаковыми знаменателями. В связи с этим учащиеся знакомятся с основным свойством дроби в пункте 3.1.2 «Основное свойство дроби. Преобразование дробей».
2) Для открытия основного свойства дроби можно использовать дополнительные свойства умножения и деления (делимое и делитель можно умножать и делить на одно и то же натуральное число) и знание, что результат деления можно записать в виде дроби, а также умение изображать дроби на числовом луче.
3) Учащиеся учатся применять основное свойство дроби для преобразования дробей – сокращение дроби и приведения дроби к новому числителю (знаменателю). После знакомства учащихся с таким преобразованием дроби, как сокращение дроби, вводится понятие несократимой дроби.
4) Для сокращения дробей предлагается использовать три способа: сокращать дробь на НОД числителя и знаменателя, сокращать дробь последовательно на общие делители (с использованием признаков делимости) или представлять числитель и знаменатель в виде произведения.
5) При выполнении системы заданий №№ 66, 67 (б), 86 – 88 идет последовательная работа по построению алгоритма приведения дробей к наименьшему общему знаменателю (при этом сначала формируется представление о новом знаменателе, как о числе кратном старому знаменателю, затем вводится понятие дополнительных множителей, после чего, при выполнении № 87, вводится понятие общего знаменателя двух дробей и формируется понятие общего знаменателя как общего кратного знаменателей). И только после такой подготовительной работы ставится проблема приведения дробей к наименьшему общему знаменателю. При выполнении №№ 88 – 89 формируется умение применять полученный алгоритм.
И только после такой подготовительной работы ставится проблема приведения дробей к наименьшему общему знаменателю. При выполнении №№ 88 – 89 формируется умение применять полученный алгоритм.
6) Аналогичная работа может быть проведена для построения алгоритма приведения дробей к новому числителю.
7) В третьей главе пятиклассникам предлагаются задания, содержащие алгебраические дроби. Так, при отработке умения преобразовывать дроби учащимся могут быть предложены задания сократить алгебраическую дробь, числитель которой имеет вид многочлена (№№ 83 (1, 2, 3), 92). При выполнении заданий такого уровня учителю следует реализовывать принцип минимакса: работать на уроке, ориентируясь на сильных учеников на высоком уровне сложности, оценивая при этом только успех, а контролировать усвоение материала каждым учащимся на уровне минимума, определенного в стандарте.
§ 1. Натуральные числа и дроби. П.3 Сравнение дробей
8) В третьем пункте «Сравнение дробей» учащиеся строят разные способы сравнения дробей: приведение дробей к наименьшему общему знаменателю и к наименьшему общему числителю (№№ 135 – 142).
9) Для отработки приема сравнения с промежуточным числом (1/2) выполняется № 145. При этом учитель может использовать такие модели, как числовой луч или отрезок. После сравнения данных чисел с половиной на моделях учитель может задать вопросы о сравнении пар дробей, одна из которых больше половины, а другая – меньше. Учащимися делается вывод об использовании промежуточного числа для сравнения дробей. Например, можно записать, что 41/80 > 245/504, потому что первая дробь больше половины, а вторая – меньше.
10) Для знакомства учащихся с приемом сравнения правильных дробей путем определения, какая из них «ближе к единице», а значит, и больше (№ 143), можно поступить следующим образом: учащимся предлагается проанализировать данные дроби.
11) Также учащиеся узнают общее правило сравнения дробей – «перекрёстное» правило (a/b < c/d <=> ad < bc) – и учатся его применять ( № 148). Из этого общего правила сравнения дробей следует условие равенства дробей a/b = c/d <=> ad = bc, с которым нужно познакомить учащихся. Необходимо заострить внимание учащихся на этом утверждении, так как данное условие позволит им решать уравнения нового вида, а в дальнейшем будет использоваться в 6 классе при изучении тем «Отношение» и «Пропорция». Условие равенства дробей применяется при выполнении № 151.
Условие равенства дробей применяется при выполнении № 151.
12) После изучения правил сравнения обыкновенных дробей учащиеся получают возможность построить правила сравнения любых смешанных чисел. Для формирования умения применять правила сравнения смешанных чисел учащимся предлагается выполнить № 147 (7, 8).
13) Таким образом, пятиклассники могут выполнить сравнение дробей следующими способами: приведение дробей к наименьшему общему знаменателю, наименьшему общему числителю, пользуясь свойством «любая неправильная дробь больше правильной», сравнение с промежуточным числом (с 1/2), метод «ближе к 1» и универсальный способ – общее правило сравнения дробей. Использование различных способов для сравнения дробей реализует принцип вариативности ДСДМ, который предполагает формирование у учащихся способностей к систематическому перебору вариантов и адекватному принятию решений в ситуациях выбора (
14) Способы сравнения дробей используются учащимися для решения задач (№ 153, № 154).
15) При обсуждении № 155 появляется возможность формировать не только предметные, но и личностные результаты обучения, которые соответствуют новым целям образования. В заданиях учебника математики курса «Учусь учиться» заложены представления о дружбе, доброте, чести, трудолюбии и других ценностных качествах человека, которые опосредованно оказывают эмоциональное воздействие на детей и способствуют выработке морально-этических норм и правил. При выполнении данного задания у учителя появляется возможность выслушать мнения учащихся и подвести их к собственным выводам о самооценке человека.
§ 2. Арифметика дробей. П.1 Сложение и вычитание дробей
16) В начальной школе учащиеся научились складывать и вычитать дроби с одинаковыми знаменателями. В пункте «Сложение и вычитание дробей» они учатся находить значение суммы и разности любых дробей.
17) Перед выполнением пробного задания можно предложить учащимся проанализировать данную сумму 2/21 + 6/35. Пятиклассники фиксируют, что слагаемыми являются дроби с разными знаменателями. При выполнении задания ученики фиксируют затруднение: «не можем найти сумму» или «не можем обосновать своё решение». Причиной затруднения является отсутствие правила сложения дробей с разными знаменателями. В результате работы учащиеся строят алгоритм сложения и вычитания любых дробей:
Пятиклассники фиксируют, что слагаемыми являются дроби с разными знаменателями. При выполнении задания ученики фиксируют затруднение: «не можем найти сумму» или «не можем обосновать своё решение». Причиной затруднения является отсутствие правила сложения дробей с разными знаменателями. В результате работы учащиеся строят алгоритм сложения и вычитания любых дробей:
18) На последующих уроках учащиеся применяют алгоритм сложения и вычитания обыкновенных дробей для решения уравнений, нахождения значения буквенных выражений при заданном значении букв, решения задач.
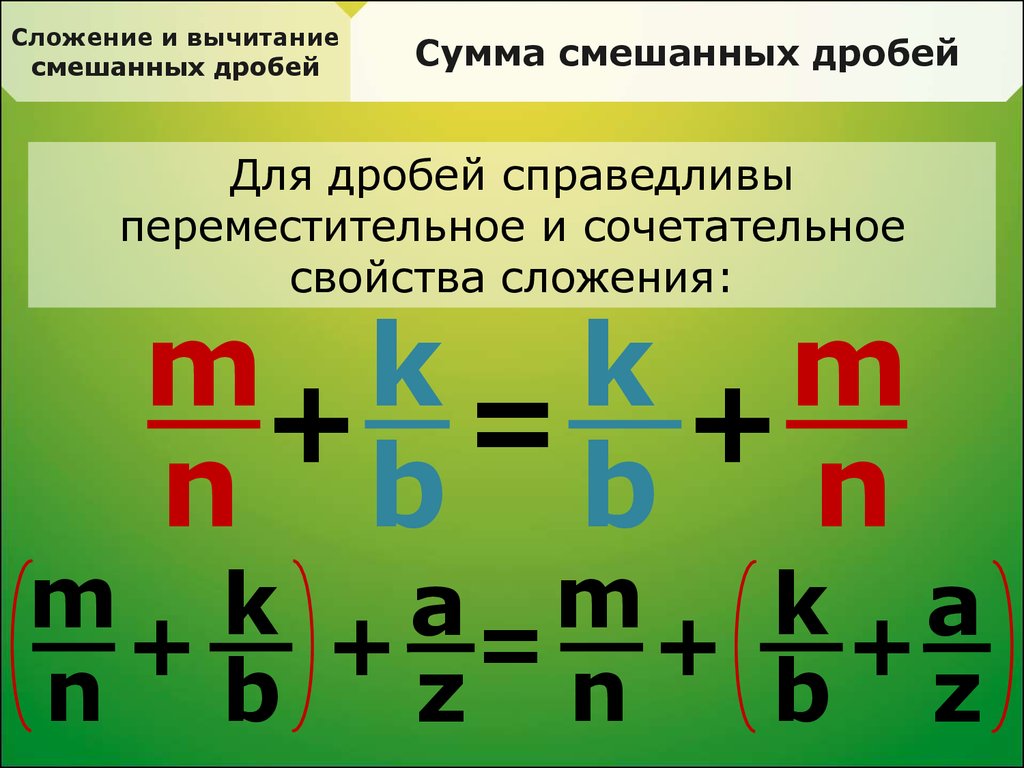
19) Для обыкновенных дробей фиксируются и применяются переместительное и сочетательное свойства сложения и правила вычитания суммы из числа и числа из суммы. (№№ 201 – 202).
Эталоны20) В результате изучения данных тем у учащихся появляются следующие эталоны: основное свойство дроби, алгоритм приведения дробей к наименьшему общему знаменателю (числителю), несколько способов сокращения дробей, понятие несократимой дроби, правила сравнения дробей, алгоритмы сложения и вычитания дробей (общий случай). Данные эталоны приведены в учебном пособии Л.Г. Петерсон, Л.А. Грушевской «Построй свою математику», которое предусматривает специальную работу с ними.
Данные эталоны приведены в учебном пособии Л.Г. Петерсон, Л.А. Грушевской «Построй свою математику», которое предусматривает специальную работу с ними.
Приведем пример эталона из указанного пособия:
Методические рекомендации по планированию уроковПри организации учебного процесса необходимо учитывать, что выполнение всех заданий из учебника не является обязательным. Принципы минимакса и вариативности обеспечивают возможность обучения по курсу математики программы «Школа 2000…» детей разного уровня подготовки, в том числе и высокого. Поэтому уровень и количество заданий, включенных в учебник, определялись в соответствии с зоной ближайшего развития более подготовленных учащихся. Предполагается, что учитель выбирает для работы те задания, которые соответствуют уровню подготовки детей и задачам конкретного урока.
Мы предлагаем Вам скачать методические рекомендации по планированию уроков.
С примерами организации уроков по изучению темы «Дроби» Вы можете познакомиться в серии дисков со сценариями уроков в технологии деятельностного метода к учебнику математики для 5 − 6 классов основной школы авторов Г. В. Дорофеева, Л.Г. Петерсон по программе «Учусь учиться».
В. Дорофеева, Л.Г. Петерсон по программе «Учусь учиться».
Предлагаем Вашему вниманию вариант сценария урока по рассматриваемым темам, в котором описан возможный способ организации самостоятельной познавательной деятельности учащихся на основе технологии деятельностного метода обучения «Школа 2000…».
Урок 80Тип урока: ОНЗ
Тема: «Сокращение дробей»
Автор: Л.А. Грушевская
Основные цели:
1) cформировать понятия сократимой и несократимой дроби, умение сокращать дроби на основе использования основного свойства дроби;
2) повторить и закрепить понятия делителя и кратного, признаки делимости, свойства делимости произведения, чтение и нахождение значений буквенных выражений, тренировать умение строить математические модели текстовых задач.
Мы предлагаем Вам cкачать сценарий урока
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как. ..»)
..»)
Уважаемые коллеги! В соответствии с Вашими просьбами предлагаем Вам скачать решение задач на смекалку, которые входят в данные параграфы.
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Если у Вас возникли какие-либо вопросы, напишите нам, заполнив форму обратной связи.
Мы свяжемся с Вами.
Версия для печати
технологическая карта по теме «Сложение и вычитание дробей с одинаковыми знаменателями» | План-конспект урока по математике (5 класс):
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
по теме: «Сложение и вычитание дробей с одинаковым знаменателем»
Учитель: Иваненко Ольга Викторовна, учитель математики МБОУ «Ложкинская основная общеобразовательная школа»
Предмет: математика.
Класс: 5.
Вид урока: проблемно-диалогический.
Тип урока: открытие новых знаний.
Цели:
Предметные: открытие способа сложения и вычитания дробей с одинаковым знаменателем.
Личностные: формирование ответственного отношения к обучению, готовность к саморазвитию и самообразованию на основе мотивации к обучению и познанию.
Метапредметные: формирование умения делать обобщение, устанавливать аналогии, умение строить математические модели, развивать коммуникативные компетенции учащихся.
Планируемые результаты:
Предметные: учащиеся самостоятельно выведут алгоритм сложения и вычитания дробей с одинаковым знаменателем и научатся применять его при решении заданий.
Метапредметные: умение обрабатывать информацию, умение работать в коллективе, слушать собеседника и вести диалог, аргументировать свою точку зрения, умение контролировать и оценивать процесс и результат своей деятельности, выстаивать логические цепи рассуждений с использованием знаково-символических действий (схема, таблица)
Оборудование и материалы: компьютер, проектор, экран, шоколадка.
Материалы: учебник «Математика 5» А.Г. Мерзляк, В.Б. Полонский, М. С. Якир, Д. А. Номировский, Е.В. Буцко презентация, раздаточный материал.
А. Номировский, Е.В. Буцко презентация, раздаточный материал.
Этапы урока и его цель | Деятельность учителя | Деятельность ученика | УУД |
1.Организационный момент. Цель: создание благоприятного психологического настроя на работу. | Приветствует ребят: «Здравствуйте ребята! Присаживайтесь». | Включаются в деловой ритм работы. | Личностные: самоопределение |
2. Мотивация. Цель: активизация умственной деятельности и подготовка к сознательному восприятию нового материала. | Мотивационная беседа. В начале 5 класса мы выяснили, что в древности людям приходилось вести счёт плодов, животных и т. | Участвуют в беседе с учителем, отвечают на поставленные вопросы. Обосновывают свои ответы. | Коммуникативные: выражение своих мыслей, аргументация своего мнения |
3. Актуализация знаний. Цель: воспроизведение знаний, умений и жизненного опыта учащихся, необходимых для овладения новыми знаниями. | Ребята давайте с вами вспомним, что мы уже знаем про обыкновенные дроби. Вопросы: 1.Как называется число, стоящее над чертой дроби? Под чертой дроби? 2. Что показывает знаменатель? Числитель? Слайд1. Прочитайте дроби. Назовите правильные дроби. Какие дроби называются правильные. Назовите неправильные дроби. Какие дроби называются правильные. Слайд 2.Как сравнить дроби с одинаковыми знаменателями? Как сравнить дроби с одинаковыми числителями? Какая дробь больше: правильная или неправильная? Молодцы! Хорошо справились с заданием. | Устно решают задачи, повторяют теорию, отвечают на вопросы. | Регулятивные: фиксация индивидуального затруднения Коммуникативные: выражение своих мыслей, аргументация своего мнения Познавательные: осознанное построение речевого высказывания, подведение под понятие. |
4. Введение в тему. Постановка цели и задачи урока. Формулирование проблемы. Цель: создание проблемной ситуации и фиксация новой учебной задачи. | Мотивирует учащихся. Создаёт проблемную ситуацию. Слайд 3. Ребята, у нас с вами есть шоколадка, у которой все дольки равные. Предлагаю каждому мальчику подойти и взять по три дольки шоколадки, а девочкам по две. Какую часть шоколадки взяли мальчики? Какую часть шоколадки взяли девочки? Какая часть шоколадки осталась? Какие действия нужно выполнить, чтобы ответить на все эти вопросы? На какой вопрос мы можем ответить? Какое действие мы уже умеем выполнять? Чему бы вы хотели научиться на уроке? Слайд 4. Запишите число и тему урока. | Подходят, берут шоколадку. Отвечают на вопросы, делают выводы. Формулируют тему урока, записывают её в тетрадь | Регулятивные: волевая саморегуляция в ситуации затруднения; целеполагание Коммуникативные: выражение своих мыслей, аргументация своего мнения, достижение договоренности и согласовании общего решения; постановка вопросов Познавательные: проблема выбора эффективного способа решения, умение применять знания для практических задач; самостоятельное выделение-формулирование познавательной цели Личностные: осознание ответственности за общее дело |
5. Цель: поиск решения учебной задачи и открытие способа сложения и вычитания дробей с одинаковым знаменателем. | Предлагает учащимся задания, после выполнения, которых они сами сформулируют алгоритм сложения и вычитания дробей с одинаковыми знаменателями. Слайд 5. А теперь вернёмся к нашей задаче. Выполним необходимые действия и ответим на поставленные вопросы в задаче. | Работают в парах и коллективно. Отвечают на вопросы. | Регулятивные: волевая саморегуляция в ситуации затруднения; целеполагание Коммуникативные: выражение своих мыслей, аргументация своего мнения, достижение договоренности и согласовании общего решения; постановка вопросов Познавательные: проблема выбора эффективного способа решения, умение применять знания для практических задач; самостоятельное выделение-формулирование познавательной цели Личностные: осознание ответственности за общее дело |
6. Цели: организация совместной деятельности, направленной на формулировку нового правила. | Организует проверку правильности выполнения задания. Предлагает учащимся самим сформулировать алгоритм сложения и вычитания дробей с одинаковыми знаменателями. Давайте посмотрим, что у вас получилось. Сформулируйте правило сложения дробей с одинаковым знаменателем. Сформулируйте правило вычитания дробей с одинаковым знаменателем. Слайд 6-7.А теперь построим модель сформулированного нами правила. С помощью трёх геометрических фигур ( трёх букв а, в, с) постройте модель правила сложения и вычитания дробей с одинаковым знаменателем. А где можно проверить правильно ли мы сформулировали правила? Учебник стр.187 найдите правила. Мы с вами правильно сформулировали правила? Необходимо выписать правила записанные в буквенном виде | Проверяют правильность выполнения заданий. Формулируют правила. Строят модель изученного правила. Проверяют, правильно, ли сформулировали правила с учебником | Регулятивные: волевая саморегуляция в ситуации затруднения Коммуникативные: выражение своих мыслей, аргументация своего мнения, достижение договоренности и согласовании общего решения; постановка вопросов Познавательные: проблема выбора эффективного способа решения, умение применять знания для практических задач; самостоятельное выделение-формулирование познавательной цели Личностные: осознание ответственности за общее дело |
7. Первичное закрепление. Цель: организация правильного выполнения заданий в записи и проговаривания нового знания в речи. | Слайд 8. А теперь предлагаю закрепить наши знания, рядом заданий. | Проговаривают действия и правильно записывают их в свои тетради. | Познавательные: выполнение действий по алгоритму. Подведение под понятие, рефлексия способов действий Коммуникативные: выражение своих мыслей, |
8. Самостоятельная работа. Цель: организация первичного закрепления нового правила. | Слайд 9.Предлагает поработать с учебником: стр.189 № 743(1,3,5) № 745 № 747 Слайд 10. Дополнительные задания. | Письменно решают номера, проверяют правильность решения. | Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения Познавательные: анализ, подведение под понятие, выполнение действий по алгоритму |
9. Контроль формируемых умений. Цель: выявление качества усвоения знаний. | Какую задачу мы ставили в начале урока. Слайд 11.Самостоятельная работа. Предлагает решить самостоятельную работу, в которой нужно выполнить сложение и вычитание дробей с одинаковыми знаменателями и впоследствии сверить с ответами. | Выполняют самостоятельную работу, сверяются с ответами | Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения Познавательные: анализ, подведение под понятие, выполнение действий по алгоритму |
10. Рефлексия Цель: организация понимания ценности выполняемой деятельности. | Сайд 12. Мотивирует учащихся на подведение итогов урока. Закончите фразу: — На уроке я узнал… — Мне было легко… — Я пока затрудняюсь… | Оценивают свою работу на уроке. | Познавательные: рефлексия способов и условий действия, адекватное понимание причин успеха и неудач, контроль и оценка процесса и результатов деятельности Коммуникативные: умение выражать свои мысли, аргументация |
11. Домашнее задание. Цель: пояснение особенности выполнения домашнего задания. | Слайд 13. Предлагает на выбор домашнее задание: 1) §27, правила №744 №746 №748 По желанию: 2)написать сказку про дроби; 3)составить карточку с заданием для товарища по теме «Обыкновенные дроби» | Записывают домашнее задание. |
Вычитание дробей с разными знаменателями
Звук:
Мы не можем вычесть два знаменателя, если у них нет ничего общего.
- Итак, как вычитать дроби с разными знаменателями, например 9 ⁄ 28 — 13 ⁄ 56 ?
Дроби говорят нам, сколько частей в целом.
Когда у дробей разные знаменатели , целое делится на разное количество частей. Поэтому детали будут разного размера.
Когда части не одного размера, мы не можем вычесть две дроби.
Например, посмотрите на разницу между 1 / 2 и 1 / 5 :
В первой модели целое разделено на 2 равные части. В другой модели целое разделено на 5 равных частей. Совершенно очевидно, что эти части не имеют одинакового размера из-за этих знаменателей.
Вот почему нельзя вычитать дроби с разными знаменателями — у них должен быть общий знаменатель.
Чтобы вычесть дроби с разными знаменателями, мы можем выполнить три простых шага:
Шаг первый
Найдите общий знаменатель. Умножьте числители на тот же коэффициент, который вы использовали для нахождения общего знаменателя.
Шаг второй
Вычтите числители. Оставьте знаменатель прежним.
Шаг третий
При необходимости упростите дробь.
Найдите минутку, чтобы применить эти шаги на практике. Посмотрите на пример ниже:
- Что такое 1 / 2 — 1 / 5 ?
Шаг первый
Найдите общий знаменатель.
Чтобы найти общий знаменатель, нам нужно найти наименьшее общее кратное двух знаменателей. Наименьшее общее кратное между 2 и 5 равно 10.
И 2, и 5 можно умножить на другие числа, чтобы получить 10. Кроме того, оба числа могут достигать 10 путем пропуска счета.
- Как изменить дроби так, чтобы обе дроби имели знаменатель 10?
Мы умножим верхнюю и нижнюю часть каждой дроби на коэффициент, необходимый для получения знаменателя 10.
Например, чтобы изменить знаменатель с ½ на 10, нам нужно будет умножить верхнюю и нижнюю часть на 5:
| 1 | х | 5 | = | 5 | |
| 2 | х | 5 | = | 10 |
- Для 1 / 5 на что нужно умножить знаменатель 5, чтобы получить 10?
2! Умножьте верхнюю и нижнюю часть на 2.
| 1 | х | 2 | = | 2 | |
| 5 | х | 2 | = | 10 |
Теперь обе дроби имеют общий знаменатель. Вы готовы к следующему шагу.
Шаг второй
Вычтите числители. Оставьте знаменатели одинаковыми.
Посмотрите теперь на модель дроби. Теперь, когда ½ и 1 / 5 имеют одинаковый знаменатель, легко вычесть:
Шаг третий
При необходимости упростите дробь.
3 / 10 в самой простой форме. Числитель и знаменатель не могут делиться на общий множитель. Нам не нужно упрощать дробь.
Итак, 1 / 2 — 1 / 5 = 3 / 10
Вы также использовали модели для визуализации задач на вычитание.
Теперь используйте свои новые стратегии для решения практических задач и действий в Понял? раздел .
Обзор дробей: сложение и вычитание дробей
Сокращение дробейСмешанные и неправильные дробиУмножение и деление полиномиальных дробей
Purplemath
Чтобы складывать дроби, у вас должны быть «общие» (общие) знаменатели. Как гласит пословица, к яблокам можно добавлять только яблоки, а не к апельсинам яблоки. В контексте сложения дробей нельзя комбинировать, скажем, 1/4 и 2/5. Поскольку они представляют собой дроби разных типов (одна из них — четвертая, а другая — пятая), они представляют собой «яблоки и апельсины». Чтобы сложить их, вам сначала нужно преобразовать в знаменатель для всех яблок; в этом случае вы должны преобразовать в двадцатые, получив 5/20 и 8/20 в качестве дробей для всех яблок.
Хотите верьте, хотите нет, но многие развитые в других отношениях древние цивилизации (например, древние египтяне) так и не поняли концепции общего знаменателя. Так что не расстраивайтесь, если у вас возникли проблемы с вычислениями!
Содержание продолжается ниже
MathHelp.com
Сложение и вычитание отличных от дробей
Основная идея приведения к общему знаменателю заключается в умножении дробей на полезные формы 1. Что это значит? Взгляните:
Прежде чем я смогу сложить эти дроби, я должен найти их общий знаменатель. Наименьший (наименьший) общий знаменатель — это просто наименьшее общее кратное (НОК) двух знаменателей, 4 и 5. Простые факторизации и НОК знаменателей 4 и 5 таковы:
4:2*2 5: 5 ---:----------- НОК: 2*2*5 = 20
Другими словами, мне нужно преобразовать четвертые и пятые в двадцатые. Я сделаю это путем умножения на полезную форму 1. В случае первой дроби, 1 / 4 , 4 должно стать 20, поэтому мне нужно умножить 4 на 5. Чтобы сохранить дробь, равная ее первоначальному значению, мне придется также умножить верхнюю часть на 5. Другими словами, я умножу дробь на 5 /9.0012 5 , что является просто полезной формой числа 1:
Чтобы сохранить дробь, равная ее первоначальному значению, мне придется также умножить верхнюю часть на 5. Другими словами, я умножу дробь на 5 /9.0012 5 , что является просто полезной формой числа 1:
Поскольку я умножил на (полезную форму) 1, я не изменил фактическое значение дроби. Все, что я изменил, это то, как указано значение.
В случае второй дроби, 2 / 5 , 5 должно стать 20, поэтому я должен умножить 5 на 4. Чтобы дробь оставалась равной одному и тому же значению, я также должен умножьте вершину на 4 тоже. Другими словами, я умножу на 4 / 4 , что является просто полезной формой 1:
Четвертые и пятые теперь обе двадцатые; Я, наконец, в ситуации, когда все яблоки. Только теперь я могу складывать дроби. Чтобы сложить эти «яблоки», я добавляю числители:
Числитель 13 — простой, и он не является множителем 20, так что я не могу сделать никакого сокращения.
Мой упрощенный окончательный ответ:
13 / 20 .
Кстати, ваш калькулятор может сделать все это за вас; проверьте свое руководство. Но убедитесь, что вы хотя бы понимаете основную идею, потому что этот процесс понадобится вам позже в алгебре, когда вы доберетесь до дробей с многочленами, называемых «рациональными выражениями».
Сначала я найду НОК двух знаменателей:
15:3*5 5: 5 ---:--------- НОК: 3*5 = 15
Поскольку 5 является коэффициентом 15, то НОК равно 15; в частности, одна из фракций уже находится в форме LCM. Приведу другую дробь к этому общему знаменателю, прибавлю и, если возможно, упрощу:
Общих множителей нет, поэтому ничего не упрощается.
Мой окончательный ответ:
8 / 15 .
Сначала я найду НОК двух знаменателей:
8: 2*2*2 6: 2 *3 -------------- НОК: 2*2*2*3 = 24
Обратите внимание, что 8 и 6 имеют множитель 2. Смысл красивого и аккуратного выстраивания факторов в столбцы, как я сделал выше, состоит в том, чтобы помочь избежать чрезмерного дублирования факторов при нахождении НОК. Будьте осторожны: в LCM только три двойки, а не четыре.
Смысл красивого и аккуратного выстраивания факторов в столбцы, как я сделал выше, состоит в том, чтобы помочь избежать чрезмерного дублирования факторов при нахождении НОК. Будьте осторожны: в LCM только три двойки, а не четыре.
Чтобы преобразовать первую дробь в знаменатель 24, я умножу верхнее и нижнее число на 3. Чтобы преобразовать знаменатель второй дроби, я умножу верхнее и нижнее число на 4.
В инструкциях не говорится, что ответ следует представлять в виде смешанных чисел, поэтому я оставлю его в виде неправильной дроби. Между числителем и знаменателем нет общих множителей, поэтому я не могу дальше упрощать.
7 / 8 + 1 / 6 = 25 / 24
Сначала я найду НОК трех знаменателей:
7:7 52: 2*2*13 4: 2*2 ---------------- НОК: 2*2*7*13 = 364
Теперь я приведу три дроби к общему знаменателю, сложим, а потом посмотрю, смогу ли я упростить.
Поскольку 4 является общим делителем 1072 и 364, я смог сократить это и упростить, чтобы получить окончательный ответ:
5 / 7 + 25 / 52 + 7 / 4 = 268 / 91
Сначала, я найду LCM из двух геномов:
.
25:5*5 35:5*7 ------------- НОК: 5*5*7 = 175
Чтобы преобразовать в НОК, я умножу первую дробь, верхнюю и нижнюю, на 7, а вторую дробь, верхнюю и нижнюю, на 5.
Числитель, 106 , делит как 2×53, а 53 — простое число, так что я ничего не могу отменить; дробь не может быть дополнительно упрощена.
Тогда мой окончательный ответ:
106 / 175 .
Вы можете использовать виджет Mathway ниже, чтобы потренироваться в сложении и вычитании дробей. Попробуйте введенное упражнение или введите свое собственное упражнение.

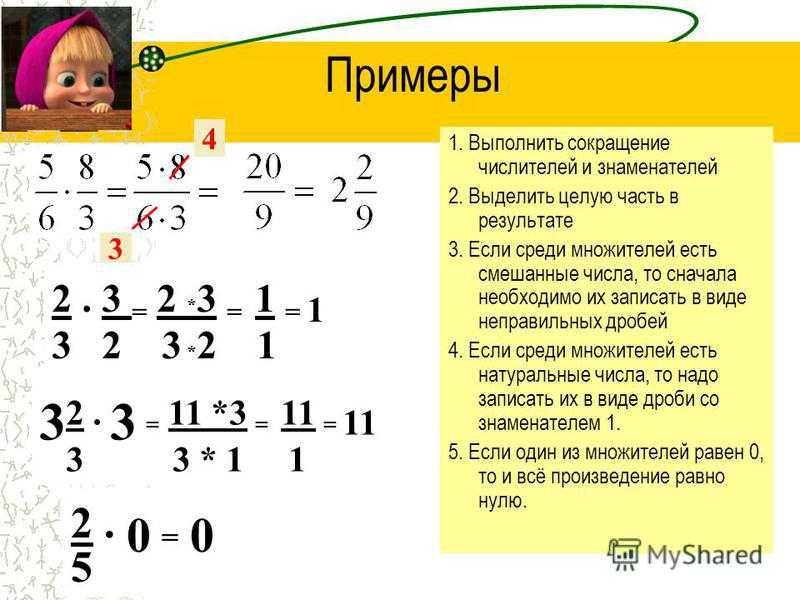 д. Какими числами они пользовались? А дальше людям пришлось делить целое на равные части. Какие числа появились тогда? Вы уже несколько уроков подряд работаете с дробными числами, а конкретно с обыкновенными дробями.
д. Какими числами они пользовались? А дальше людям пришлось делить целое на равные части. Какие числа появились тогда? Вы уже несколько уроков подряд работаете с дробными числами, а конкретно с обыкновенными дробями.

 Открытие нового знания.
Открытие нового знания. Воспроизведение нового знания.
Воспроизведение нового знания.

 Как вы считаете, достигли мы результата? Давайте проверим.
Как вы считаете, достигли мы результата? Давайте проверим.