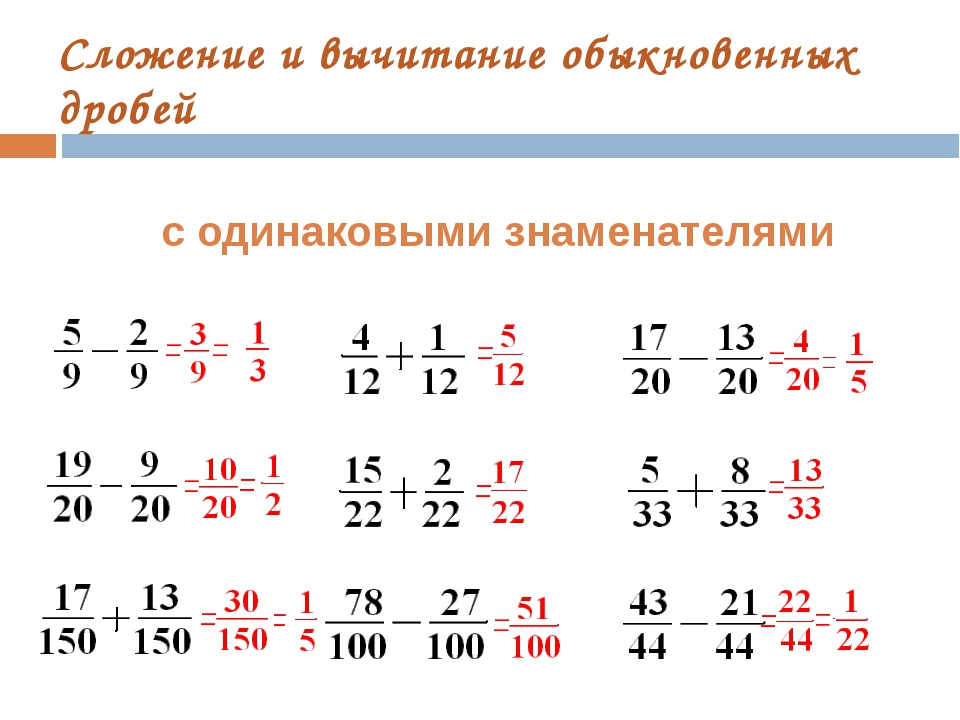
Примеры на вычитание дробей с одинаковыми знаменателями. Сложение и вычитание дробей
Действия с дробями. В этой статье разберём примеры, всё подробно с пояснениями. Рассматривать будем обыкновенные дроби. В дальнейшем разберём и десятичные. Рекомендую посмотреть весь и изучать последовательно.
1. Сумма дробей, разность дробей.
Правило: при сложении дробей с равными знаменателями, в результате получаем дробь – знаменатель которой остаётся тот же, а числитель её будет равен сумме числителей дробей.
Правило: при вычислении разности дробей с одинаковыми знаменателями получаем дробь – знаменатель остаётся тот же, а из числителя первой дроби вычитается числитель второй.
Формальная запись суммы и разности дробей с равными знаменателями:
Примеры (1):
Понятно, что когда даны обыкновенные дроби, то всё просто, а если смешанные? Ничего сложного…
Вариант 1 – можно перевести их в обыкновенные и далее вычислять.
Вариант 2
Примеры (2):
Ещё:
А если будет дана разность двух смешанных дробей и числитель первой дроби будет меньше числителя второй? Тоже можно действовать двумя способами.
Примеры (3):
*Перевели в обыкновенные дроби, вычислили разность, перевели полученную неправильную дробь в смешанную.
*Разбили на целые и дробные части, получили тройку, далее представили 3 как сумму 2 и 1, при чём единицу представили как 11/11, далее нашли разность 11/11 и 7/11 и вычислили результат. Смысл изложенных преобразований заключается в том, чтобы взять (выделить) единицу и представить её в виде дроби с нужным нам знаменателем, далее от этой дроби мы уже можем вычесть другую.
Ещё пример:
Вывод: имеется универсальный подход – для того, чтобы вычислить сумму (разность) смешанных дробей с равными знаменателями их всегда можно перевести в неправильные, далее выполнить необходимое действие.
После этого если в результате получаем неправильную дробь переводим её в смешанную.
Выше мы рассмотрели примеры с дробями, у которых равные знаменатели. А если знаменатели будут отличаться? В этом случае дроби приводятся к одному знаменателю и выполняется указанное действие. Для изменения (преобразования) дроби используется основное свойство дроби.
Рассмотрим простые примеры:
В данных примерах мы сразу видим каким образом можно преобразовать одну из дробей, чтобы получить равные знаменатели.
Если обозначить способы приведения дробей к одному знаменателю, то этот назовём СПОСОБ ПЕРВЫЙ .
То есть, сразу при «оценке» дроби нужно прикинуть сработает ли такой подход – проверяем делится ли больший знаменатель на меньший. И если делится, то выполняем преобразование — домножаем числитель и знаменатель так чтобы у обеих дробей знаменатели стали равными.
Теперь посмотрите на эти примеры:
К ним указанный подход не применим. Существуют ещё способы приведения дробей к общему знаменателю, рассмотрим их.
Существуют ещё способы приведения дробей к общему знаменателю, рассмотрим их.
Способ ВТОРОЙ .
Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой:
*Фактически мы приводим дроби к виду, когда знаменатели становятся равными. Далее используем правило сложения робей с равными знаменателями.
Пример:
*Данный способ можно назвать универсальным, и он работает всегда. Единственный минус в том, что после вычислений может получится дробь которую необходимо будет ещё сократить.
Рассмотрим пример:
Видно что числитель и знаменатель делится на 5:
Способ ТРЕТИЙ.
Необходимо найти наименьшее общее кратное (НОК) знаменателей. Это и будет общий знаменатель. Что это за число такое? Это наименьшее натуральное число, которое делится на каждое из чисел.
Посмотрите, вот два числа: 3 и 4, есть множество чисел, которые делятся на них – это 12, 24, 36, … Наименьшее из них 12. Или 6 и 15, на них делятся 30, 60, 90 …. Наименьшее 30. Вопрос – а как определить это самое наименьшее общее кратное?
Или 6 и 15, на них делятся 30, 60, 90 …. Наименьшее 30. Вопрос – а как определить это самое наименьшее общее кратное?
Имеется чёткий алгоритм, но часто это можно сделать и сразу без вычислений. Например, по указанным выше примерам (3 и 4, 6 и 15) никакого алгоритма не надо, мы взяли большие числа (4 и 15) увеличили их в два раза и увидели, что они делятся на второе число, но пары чисел могут быть и другими, например 51 и 119.
Алгоритм. Для того, чтобы определить наименьшее общее кратное нескольких чисел, необходимо:
— разложить каждое из чисел на ПРОСТЫЕ множители
— выписать разложение БОЛЬШЕГО из них
— умножить его на НЕДОСТАЮЩИЕ множители других чисел
Рассмотрим примеры:
50 и 60 => 50 = 2∙5∙5 60 = 2∙2∙3∙5
в разложении большего числа не хватает одной пятёрки
=> НОК(50,60) = 2∙2∙3∙5∙5 = 300
48 и 72 => 48 = 2∙2∙2∙2∙3 72 = 2∙2∙2∙3∙3
в разложении большего числа не хватает двойки и тройки
=> НОК(48,72) = 2∙2∙2∙2∙3∙3 = 144
* Наименьшее общее кратное двух простых чисел равно их произведению
Вопрос! А чем полезно нахождение наименьшего общего кратного, ведь можно пользоваться вторым способом и полученную дробь просто сократить? Да, можно, но это не всегда удобно. Посмотрите, какой получится знаменатель для чисел 48 и 72, если их просто перемножить 48∙72 = 3456. Согласитесь, что приятнее работать с меньшими числами.
Посмотрите, какой получится знаменатель для чисел 48 и 72, если их просто перемножить 48∙72 = 3456. Согласитесь, что приятнее работать с меньшими числами.
Рассмотрим примеры:
*51 = 3∙17 119 = 7∙17
в разложении большего числа не хватает тройки
=> НОК(51,119) = 3∙7∙17
А теперь применим первый способ:
*Посмотрите какая разница в вычислениях, в первом случае их минимум, а во втором нужно потрудиться отдельно на листочке, да ещё и дробь которую получили сократить необходимо. Нахождение НОК упрощает работу значительно.
Ещё примеры:
*Во втором примере и так видно, что наименьшее число, которое делится на 40 и 60 равно 120.
ИТОГ! ОБЩИЙ АЛГОРИТМ ВЫЧИСЛЕНИЙ!
— приводим дроби к обыкновенным, если есть целая часть.
— приводим дроби к общему знаменателю (сначала смотрим делится ли один знаменатель на другой, если делится то умножаем числитель и знаменатель этой другой дроби; если не делится действуем посредством других указанных выше способов).
— получив дроби с равными знаменателями, выполняем действия (сложение, вычитание).
— если необходимо, то результат сокращаем.
— если необходимо, то выделяем целую часть.
2. Произведение дробей.
Правило простое. При умножении дробей умножаются их числители и знаменатели:
Примеры:
Задача. На базу привезли 13 тонн овощей. Картофель составляет ¾ от всех завезённых овощей. Сколько килограмм картофеля завезли на базу?
С произведением закончим.
*Ранее обещал вам привести формальное объяснение основного свойства дроби через произведение, пожалуйста:
3. Деление дробей.
Деление дробей сводится к их умножению. Здесь важно запомнить, что дробь являющаяся делителем (та, на которую делят) переворачивается и действие меняется на умножение:
Данное действие может быть записано в виде так называемой четырёхэтажной дроби, ведь само деление «:» тоже можно записать как дробь:
Примеры:
На этом всё! Успеха вам!
С уважением, Александр Крутицких.
Действия с дробями.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Итак, что из себя представляют дроби, виды дробей, преобразования — мы вспомнили. Займёмся главным вопросом.
Что можно делать с дробями? Да всё то, что и с обычными числами. Складывать, вычитать, умножать, делить.
Все эти действия с десятичными дробями ничем не отличаются от действий с целыми числами. Собственно, этим они и хороши, десятичные. Единственно, запятую правильно поставить надо.
Смешанные числа , как я уже говорил, малопригодны для большинства действий. Их всё равно надо переводить в обыкновенные дроби.
А вот действия с обыкновенными дробями похитрее будут. И гораздо важнее! Напомню:
 Именно по этой причине мы очень подробно разберём здесь всю эту арифметику.
Именно по этой причине мы очень подробно разберём здесь всю эту арифметику.Сложение и вычитание дробей.
Сложить (отнять) дроби с одинаковыми знаменателями каждый сможет (очень надеюсь!). Ну уж совсем забывчивым напомню: при сложении (вычитании) знаменатель не меняется. Числители складываются (вычитаются) и дают числитель результата. Типа:
Короче, в общем виде:
А если знаменатели разные? Тогда, используя основное свойство дроби (вот оно и опять пригодилось!), делаем знаменатели одинаковыми! Например:
Здесь нам из дроби 2/5 пришлось сделать дробь 4/10. Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь
! Только 2/5 нам неудобно, а 4/10 очень даже ничего.Кстати, в этом суть решений любых заданий по математике. Когда мы из неудобного выражения делаем то же самое, но уже удобное для решения .
Ещё пример:
Ситуация аналогичная. Здесь мы из 16 делаем 48. Простым умножением на 3. Это всё понятно. Но вот нам попалось что-нибудь типа:
Простым умножением на 3. Это всё понятно. Но вот нам попалось что-нибудь типа:
Как быть?! Из семёрки девятку трудно сделать! Но мы умные, мы правила знаем! Преобразуем каждую дробь так, чтобы знаменатели стали одинаковыми. Это называется «приведём к общему знаменателю»:
Во как! Откуда же я узнал про 63? Очень просто! 63 это число, которое нацело делится на 7 и 9 одновременно. Такое число всегда можно получить перемножением знаменателей. Если мы какое-то число умножили на 7, к примеру, то результат уж точно на 7 делиться будет!
Если надо сложить (вычесть) несколько дробей, нет нужды делать это попарно, по шагам. Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например:
И какой же общий знаменатель будет? Можно, конечно, перемножить 2, 4, 8, и 16. Получим 1024. Кошмар. Проще прикинуть, что число 16 отлично делится и на 2, и на 4, и на 8. Следовательно, из этих чисел легко получить 16. Это число и будет общим знаменателем. 1/2 превратим в 8/16, 3/4 в 12/16, ну и так далее.
1/2 превратим в 8/16, 3/4 в 12/16, ну и так далее.
Кстати, если за общий знаменатель взять 1024, тоже всё получится, в конце всё посокращается. Только до этого конца не все доберутся, из-за вычислений…
Дорешайте уж пример самостоятельно. Не логарифм какой… Должно получиться 29/16.
Итак, со сложением (вычитанием) дробей ясно, надеюсь? Конечно, проще работать в сокращённом варианте, с дополнительными множителями. Но это удовольствие доступно тем, кто честно трудился в младших классах… И ничего не забыл.
А сейчас мы поделаем те же самые действия, но не с дробями, а с дробными выражениями . Здесь обнаружатся новые грабли, да…
Итак, нам надо сложить два дробных выражения:
Надо сделать знаменатели одинаковыми. Причём только с помощью умножения ! Уж так основное свойство дроби велит. Поэтому я не могу в первой дроби в знаменателе к иксу прибавить единицу. (а вот бы хорошо было!). А вот если перемножить знаменатели, глядишь, всё и срастётся! Так и записываем, черту дроби, сверху пустое место оставим, потом допишем, а снизу пишем произведение знаменателей, чтобы не забыть:
И, конечно, ничего в правой части не перемножаем, скобки не открываем! А теперь, глядя на общий знаменатель правой части, соображаем: чтобы в первой дроби получился знаменатель х(х+1), надо числитель и знаменатель этой дроби умножить на (х+1). А во второй дроби — на х. Получится вот что:
А во второй дроби — на х. Получится вот что:
Обратите внимание! Здесь появились скобки! Это и есть те грабли, на которые многие наступают. Не скобки, конечно, а их отсутствие. Скобки появляются потому, что мы умножаем весь числитель и весь знаменатель! А не их отдельные кусочки…
В числителе правой части записываем сумму числителей, всё как в числовых дробях, затем раскрываем скобки в числителе правой части, т.е. перемножаем всё и приводим подобные. Раскрывать скобки в знаменателях, перемножать что-то не нужно! Вообще, в знаменателях (любых) всегда приятнее произведение! Получим:
Вот и получили ответ. Процесс кажется долгим и трудным, но это от практики зависит. Порешаете примеры, привыкните, всё станет просто. Те, кто освоил дроби в положенное время, все эти операции одной левой делают, на автомате!
И ещё одно замечание. Многие лихо расправляются с дробями, но зависают на примерах с целыми числами. Типа: 2 + 1/2 + 3/4= ? Куда пристегнуть двойку? Никуда не надо пристёгивать, надо из двойки дробь сделать. Это не просто, а очень просто! 2=2/1. Вот так. Любое целое число можно записать в виде дроби. В числителе — само число, в знаменателе — единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами — то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.
Это не просто, а очень просто! 2=2/1. Вот так. Любое целое число можно записать в виде дроби. В числителе — само число, в знаменателе — единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами — то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.
Ну, по сложению — вычитанию дробей знания освежили. Преобразования дробей из одного вида в другой — повторили. Можно и провериться. Порешаем немного?)
Вычислить:
Ответы (в беспорядке):
71/20; 3/5; 17/12; -5/4; 11/6
Умножение/деление дробей — в следующем уроке. Там же и задания на все действия с дробями.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:
,
,
Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей — правильной из целого числа (натурального числа) :
- Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
- Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
- Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.

Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей .
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.
- найти НОК для всех знаменателей;
- поставить для всех дробей дополнительные множители;
- умножить все числители на дополнительный множитель;
- полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
- произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Например:
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Например:
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример:
Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Найдите числитель и знаменатель. Дробь включает два числа: число, которое расположено над чертой, называется числителем, а число, которое находится под чертой – знаменателем. Знаменатель обозначает общее количество частей, на которые разбито некоторое целое, а числитель – это рассматриваемое количество таких частей.
- Например, в дроби ½ числителем является 1, а знаменателем 2.
Определите знаменатель. Если две и более дроби имеют общий знаменатель, у таких дробей под чертой находится одно и то же число, то есть в этом случае некоторое целое разбито на одинаковое количество частей. Складывать дроби с общим знаменателем очень просто, так как знаменатель суммарной дроби будет таким же, как у складываемых дробей. Например:
Например:
- У дробей 3/5 и 2/5 общий знаменатель 5.
- У дробей 3/8, 5/8, 17/8 общий знаменатель 8.
Определите числители. Чтобы сложить дроби с общим знаменателем, сложите их числители, а результат запишите над знаменателем складываемых дробей.
- У дробей 3/5 и 2/5 числители 3 и 2.
- У дробей 3/8, 5/8, 17/8 числители 3, 5, 17.
Сложите числители. В задаче 3/5 + 2/5 сложите числители 3 + 2 = 5. В задаче 3/8 + 5/8 + 17/8 сложите числители 3 + 5 + 17 = 25.
Запишите суммарную дробь. Помните, что при сложении дробей с общим знаменателем он остается без изменений – складываются только числители.
- 3/5 + 2/5 = 5/5
- 3/8 + 5/8 + 17/8 = 25/8
Если нужно, преобразуйте дробь. Иногда дробь можно записать в виде целого числа, а не обыкновенной или десятичной дроби. Например, дробь 5/5 легко преобразуется в 1, так как любая дробь, у которой числитель равен знаменателю, есть 1. Представьте пирог, разрезанный на три части. Если вы съедите все три части, то вы съедите целый (один) пирог.
Представьте пирог, разрезанный на три части. Если вы съедите все три части, то вы съедите целый (один) пирог.
- Любую обыкновенную дробь можно преобразовать в десятичную; для этого разделите числитель на знаменатель. Например, дробь 5/8 можно записать так: 5 ÷ 8 = 0,625.
Если возможно, упростите дробь. Упрощенная дробь – эта дробь, числитель и знаменатель которой не имеют общих делителей.
- Например, рассмотрим дробь 3/6. Здесь и у числителя, и у знаменателя есть общий делитель, равный 3, то есть числитель и знаменатель нацело делятся на 3. Поэтому дробь 3/6 можно записать так: 3 ÷ 3/6 ÷ 3 = ½.
Если нужно, преобразуйте неправильную дробь в смешанную дробь (смешанное число). У неправильной дроби числитель больше знаменателя, например, 25/8 (у правильной дроби числитель меньше знаменателя). Неправильную дробь можно преобразовать в смешанную дробь, которая состоит из целой части (то есть целого числа) и дробной части (то есть правильной дроби). Чтобы преобразовать неправильную дробь, например, 25/8, в смешанное число, выполните следующие действия:
Чтобы преобразовать неправильную дробь, например, 25/8, в смешанное число, выполните следующие действия:
- Разделите числитель неправильной дроби на ее знаменатель; запишите неполное частное (целый ответ). В нашем примере: 25 ÷ 8 = 3 плюс некоторый остаток. В данном случае целый ответ – это целая часть смешанного числа.
- Найдите остаток. В нашем примере: 8 х 3 = 24; полученный результат вычтите из исходного числителя: 25 — 24 = 1, то есть остаток равен 1. В данном случае остаток – это числитель дробной части смешанного числа.
- Запишите смешанную дробь. Знаменатель не меняется (то есть равен знаменателю неправильной дроби), поэтому 25/8 = 3 1/8.
Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:
,
,
Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей — правильной из целого числа (натурального числа) :
- Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
- Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
- Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.
Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей .
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.

- найти НОК для всех знаменателей;
- поставить для всех дробей дополнительные множители;
- умножить все числители на дополнительный множитель;
- полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
- произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Например:
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Например:
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример:
Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Сложение и вычитание алгебраических дробей с разными знаменателями (более сложные случаи) 8 класс онлайн-подготовка на
Введение
Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Арифметические операции над алгебраическими дробями
Урок: Сложение и вычитание алгебраических дробей с разными знаменателями (более сложные случаи)
1. Повторение сложения/вычитания обыкновенных дробей с разными знаменателями
На уроке мы продолжим тему предыдущего урока и будем рассматривать задачу сложения и вычитания алгебраических дробей с разными знаменателями, т.е. упрощение выражений вида: , где . В основном, задача сводится к нахождению наименьшего общего знаменателя дробей, а это делается, как мы уже знаем, по аналогии с обыкновенными дробями. Рассмотрим примеры.
Пример 1. Выполнить действие .
Решение. Для нахождения наименьшего общего знаменателя дробей воспользуемся основной теоремой арифметики и разложим знаменатели на простые множители.
и . Следовательно, и .
Вспомним, что наименьший общий знаменатель должен содержать множители всех знаменателей, причем так, чтобы множителей было минимально возможное количество. В нашем случае необходимы множители . Следовательно, общий знаменатель , а дополнительные множители: к первой дроби , ко второй дроби .
В нашем случае необходимы множители . Следовательно, общий знаменатель , а дополнительные множители: к первой дроби , ко второй дроби .
.
Как видно из решения, удобно даже не перемножать простые множители в знаменателе до получения числителя общей дроби, чтобы потом было легче сокращать дробь.
Ответ..
2. Примеры на сложение/вычитание двух алгебраических дробей с разными знаменателями с использованием разложения знаменателей на множители
Теперь рассмотрим аналогичные операции с алгебраическими дробями. Не сложно догадаться, что самой трудоемкой частью сложения или вычитания дробей с разными знаменателями является нахождение наименьшего общего знаменателя. Если в случае обыкновенных дробей можно было пользоваться разложением чисел на множители, то в алгебраических дробях на множители необходимо будет раскладывать многочлены. Для этого существует несколько известных нам методов: вынесение общего множителя, применение формул сокращенного умножения и метода группировки слагаемых. Рассмотрим более подробно их применение для решения сложных задач на сложение и вычитание алгебраических дробей с разными знаменателями.
Рассмотрим более подробно их применение для решения сложных задач на сложение и вычитание алгебраических дробей с разными знаменателями.
Пример 2. Выполнить действия .
Решение. Для нахождения наименьшего общего знаменателя и дополнительных множителей разложим знаменатели на множители. Первый знаменатель уже представляет собой простое выражение, а второй раскладывается по формуле разности квадратов:
. Как видно по ходу решения, в качестве наименьшего общего знаменателя выбран знаменатель второй дроби, который делится и на первый знаменатель и сам на себя. Дополнительный множитель в таком случае пригодился только для первой дроби. Во втором переходе можно обратить внимание на внесение минуса перед дробью в один из множителей знаменателя для того, чтобы сделать знаменатели дробей максимально похожими друга на друга; такой прием нам уже знаком из темы «сложение алгебраических дробей с одинаковыми знаменателями (более сложные случаи)» (урок №5).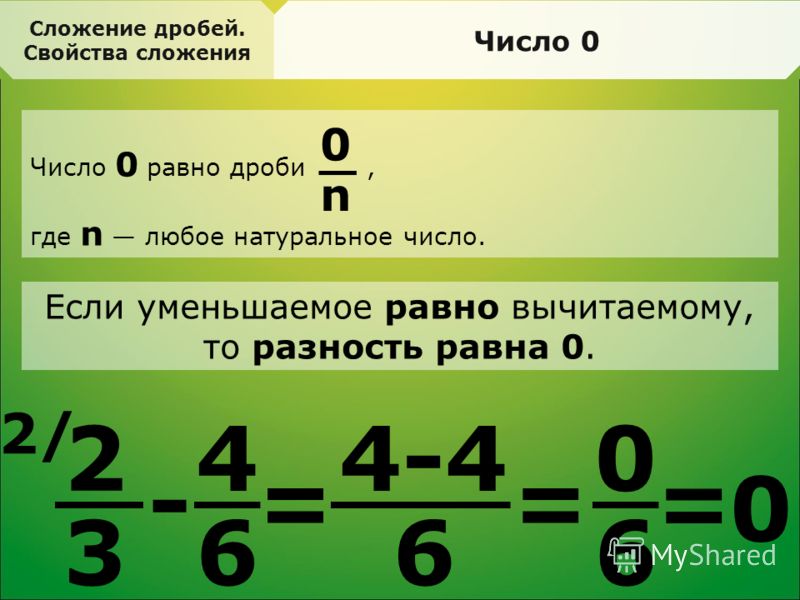
Ответ..
Пример 3. Выполнить действия .
Решение. Поступим аналогично с предыдущим примером и разложим по ходу решения знаменатель второй дроби на множители по формуле разности квадратов, перед этим внесем минус перед дробью в знаменатель для того, чтобы он получил более удобный вид:
.
Ответ..
3. Примеры на сложение/вычитание трех алгебраических дробей с разными знаменателями с использованием разложения знаменателей на множители
Рассмотрим теперь более сложные примеры на сложение/вычитание трех дробей.
Пример 4. Выполнить действия .
Решение. Как и ранее, разложим на множители каждый знаменатель, найдем наименьший общий знаменатель и дополнительные множители.
.
Как и ранее, для приведения выражения к удобному виду, вынесем минус из знаменателя второй дроби. Поскольку в выражении присутствует три дроби, чтобы не запутаться, выпишем наименьший общий знаменатель отдельно, составив его из множителей, входящих во все знаменатели: . Исходя из него, укажем и дополнительные множители для каждой из дробей, как те множители, которых не хватает знаменателю, чтобы стать общим.
Исходя из него, укажем и дополнительные множители для каждой из дробей, как те множители, которых не хватает знаменателю, чтобы стать общим.
.
Последний переход (раскрывание скобок) не принципиален, и можно было указать в ответ выражение, записанное предпоследним.
Ответ..
Пример 5. Выполнить действия .
Решение. Поступаем уже известным для нас образом: раскрываем знаменатели на множители, при необходимости меняем знаки в знаменателях дробей, находим наименьший общий знаменатель и дополнительные множители.
.
Наименьший общий знаменатель: .
.
Можно заметить, что выражение в числителе представимо в виде по формуле квадрата суммы, аналогично выражение .
В конце проведено сокращение на , значит необходимо обязательно записать область недопустимых значений переменной, связанную с этим сокращением: и являются недопустимыми значениями переменных. Во всех остальных случаях выражение равно .
Ответ. .
.
На следующем уроке мы подробно остановимся на технике разложения на множители знаменателей дробей для их последующего сложения и вычитания. Эта техника чрезвычайно важна, т.к. мы видим, что она активно используется во всех рассмотренных ранее операциях с дробями.
Список рекомендованной литературы
1. Башмаков М.И. Алгебра 8 класс. М.: Просвещение. 2004 г.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. М.: Просвещение. 2010 г.
3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет
1. ЕГЭ оп математике (Источник).
2. Так то ЕНТ. Методическая копилка (Источник).
3. Презентации для школьников (Источник).
Рекомендованное домашнее задание
1. № 55, 56, 63, 66, 68. Дорофеев Г.В. , Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. М.: Просвещение. 2010 г.
, Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. М.: Просвещение. 2010 г.
2. Выполнить действия .
3. Выполнить действия .
4. Доказать тождество: .
Сложение дробей, вычитание дробей
Сложение обыкновенных дробей
Сложение дробей с одинаковыми знаменателями
Пример 1
Рассмотрим пример:
Пусть на тарелке лежало $\frac{3}{8}$ доли яблока, к ним положили еще $\frac{2}{8}$ доли того же яблока. Это можно записать следующим образом: $\frac{3}{8}+\frac{2}{8}$. В результате на тарелке оказалось $3+2=5$ восьмых долей яблока, то есть $\frac{5}{8}$ долей. То есть результатом сложения обыкновенных дробей $\frac{3}{8}$ и $\frac{2}{8}$ является обыкновенная дробь $\frac{5}{8}$.
Пример дает возможность сделать вывод, что в результате сложения дробей с одинаковыми знаменателями получается дробь с числителем, равным сумме числителей складываемых дробей, и знаменателем, равным знаменателю исходных дробей.
Таким образом, можно сформулировать правило сложения дробей с одинаковыми знаменателями:
при сложении дробей с одинаковыми знаменателями числители складываются, а знаменатель остается прежним:
Пример 2
Сложить обыкновенные дроби $\frac{7}{18}$ и $\frac{4}{18}$.
Решение.
Т.к. знаменатели у складываемых дробей равны, в результате сложения знаменатель дроби будет $18$, а числитель будет равен сумме числителей складываемых дробей, то есть $7+4=11$. Таким образом, сложение дробей $\frac{7}{18}$ и $\frac{4}{18}$ дает дробь $\frac{11}{18}$.
Краткое решение: $\frac{7}{18}+\frac{4}{18}=\frac{11}{18}$.
Ответ: $\frac{11}{18}$.
После выполнения действий над дробями нужно проверить результат и, при необходимости, преобразовать его следующим образом:
- В результате сложения дробей получили сократимую дробь — необходимо выполнить сокращение дроби.
- В результате получили неправильную дробь — необходимо выделить целую часть.
Пример 3
Вычислить сумму обыкновенных дробей $\frac{3}{10}$ и $\frac{2}{10}$.
Решение.
Применим правило сложения дробей с одинаковыми знаменателями:
\[\frac{3}{10}+\frac{2}{10}=\frac{3+2}{10}=\frac{5}{10}\]
Получили сократимую дробь, т. к. числитель и знаменатель делятся на $5$ (по признаку делимости на $5$). Сократим полученную дробь:
к. числитель и знаменатель делятся на $5$ (по признаку делимости на $5$). Сократим полученную дробь:
\[\frac{5}{10}=\frac{1\cdot 5}{2\cdot 5}=\frac{1}{5}\]
Итак, в результате сложения дробей $\frac{3}{10}$ и $\frac{2}{10}$ получили $\frac{1}{5}$.
Краткое решение: $\frac{3}{10}+\frac{2}{10}=\frac{3+2}{10}=\frac{5}{10}=\frac{1}{5}$.
Ответ: $\frac{1}{5}$.
Пример 4
Выполнить сложение обыкновенных дробей $\frac{52}{69}$ и $\frac{77}{69}$.
Решение.
Выполним сложение дробей с одинаковыми знаменателями:
\[\frac{52}{69}+\frac{77}{69}=\frac{52+77}{69}=\frac{129}{69}\]
Проверим дробь на сократимость. Т.к. и числитель, и знаменатель соответствуют признаку делимости на $3$, полученная дробь может быть сокращена на число $3$. Получим:
\[\frac{129}{69}=\frac{129:3}{69:3}=\frac{43}{23}\]
Полученная дробь является неправильной. Выделим целую часть из неправильной дроби $\frac{43}{23}$, получим $1\frac{20}{23}$.
Выделим целую часть из неправильной дроби $\frac{43}{23}$, получим $1\frac{20}{23}$.
Краткое решение:
\[\frac{52}{69}+\frac{77}{69}=\frac{52+77}{69}=\frac{129}{69}=\frac{43}{23}=1\frac{20}{23}\]
Ответ: $1\frac{20}{23}$.
Сложение дробей с разными знаменателями
Сложение дробей с разными знаменателями сводится к сложению дробей с одинаковыми знаменателями, для чего их приводят к общему знаменателю.
Правило сложения дробей с разными знаменателями:
Складываемые дроби привести к общему знаменателю (чаще всего, к наименьшему общему знаменателю).
Выполнить сложение полученных дробей с одинаковыми знаменателями.
Пример 5
Сложить обыкновенные дроби $\frac{6}{7}$ и $\frac{4}{21}$.
Решение.
Складываемые дроби имеют разные знаменатели, поэтому приведем дроби к наименьшему общему знаменателю.
Наименьшее общее кратное НОК чисел $7$ и $21$ равно $21$: $НОК\left(7,\ \ 21\right)=21$.
Найдем соответствующие дополнительные множители: $21:7=3.$ Получим
\[\frac{6}{7}=\frac{6\cdot 3}{7\cdot 3}=\frac{18}{21}\]
Сложим дроби:
\[\frac{18}{21}+\frac{4}{21}=\frac{18+4}{21}=\frac{22}{21}\]
В результате получили неправильную дробь, из которой выделим целую часть:
\[\frac{22}{21}=1\frac{1}{21}\]
Краткое решение:
\[\frac{6}{7}+\frac{4}{21}=\frac{18+4}{21}=\frac{22}{21}=1\frac{1}{21}\]
Ответ: $1\frac{1}{21}$.
Вычитание обыкновенных дробей
Действие вычитания дробей является обратным сложению.
Вычитание дробей с одинаковыми знаменателями
Рассмотрим пример:
Пусть на тарелке лежало $\frac{6}{8}$ долей яблока. $\frac{3}{8}$ доли съели. Это можно записать как $\frac{6}{8}-\frac{3}{8}$. В результате на тарелке осталось $6-3=3$ восьмых доли яблока, т. е. $\frac{6}{8}-\frac{3}{8}=\frac{3}{8}$.
е. $\frac{6}{8}-\frac{3}{8}=\frac{3}{8}$.
Таким образом, можно сформулировать правило вычитания дробей с одинаковыми знаменателями:
при вычитании дробей с одинаковыми знаменателями числители вычитаются, а знаменатель остается прежним:
Пример 6
Выполнитm вычитание обыкновенных дробей $\frac{13}{18}$ и $\frac{5}{18}$ .
Решение.
У вычитаемых дробей знаменатели одинаковые. Числитель уменьшаемой дроби равен $13$, а числитель вычитаемой дроби равен $5$. Разность числителей равна $13-5=8$. Пользуясь правилом вычитания дробей с одинаковыми знаменателями, запишем:
\[\frac{13}{18}-\frac{5}{18}=\frac{13-5}{18}=\frac{8}{18}\]
В результате вычитания получилась сокращаемая дробь (по признаку деления на $2$. Сократим получившуюся дробь на $2$:
\[\frac{8}{18}=\frac{8:2}{18:2}=\frac{4}{9}\]
Краткое решение:
\[\frac{13}{18}-\frac{5}{18}=\frac{13-5}{18}=\frac{8}{18}=\frac{4}{9}\]
Ответ: $\frac{4}{9}$
Вычитание дробей с разными знаменателями
При вычитании дробей с разными знаменателями их сводят к вычитанию дробей с одинаковыми знаменателями, для чего дроби приводят к общему знаменателю.
Правило вычитания дробей с разными знаменателями:
Привести дроби к общему знаменателю (чаще всего к наименьшему общему знаменателю).
Вычесть полученные дроби с одинаковыми знаменателями.
Пример 7
Вычесть из обыкновенной дроби $\frac{4}{9}$ обыкновенную дробь $\frac{5}{12}$.
Решение.
У вычитаемых дробей знаменатели разные, поэтому воспользуемся правилом вычитания дробей с разными знаменателями:
Приведем дроби к наименьшему общему знаменателю: $НОК\left(9,12\right)=36$.
Дополнительный множитель для дроби $\frac{4}{9}$ будет число $36:9=4$, а дополнительный множитель дроби $\frac{5}{12}$ будет число $36:12=3$. Получим:
\[\frac{4}{9}-\frac{5}{12}=\frac{4\cdot 4}{9\cdot 4}-\frac{5\cdot 3}{12\cdot 3}=\frac{16}{36}-\frac{15}{36}\]Вычитаем дроби с одинаковыми знаменателями:
\[\frac{16}{36}-\frac{15}{36}=\frac{16-15}{36}=\frac{1}{36}\]
Краткое решение:
\[\frac{4}{9}-\frac{5}{12}=\frac{16}{36}-\frac{15}{36}=\frac{16-15}{36}=\frac{1}{36}\]
Вычитание дробей с разными знаменателями.
 Сложение и вычитание обыкновенных дробей
Сложение и вычитание обыкновенных дробейОдной из важнейших наук, применение которой можно увидеть в таких дисциплинах, как химия, физика и даже биология, является математика. Изучение этой науки позволяет развить некоторые умственные качества, улучшить абстрактное мышление и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» — сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.
Как вычесть дроби, знаменатели которых одинаковые
Дроби – это те же числа, с которыми можно производить различные действия. Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:
- Для того чтобы из одной дроби вычесть вторую, необходимо из числителя уменьшаемой дроби вычесть числитель вычитаемой дроби.
 Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m – b/m = (k-b)/m.
Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m – b/m = (k-b)/m.
Примеры вычитания дробей, знаменатели которых одинаковы
Рассмотрим, как это выглядит на примере:
7/19 — 3/19 = (7 — 3)/19 = 4/19.
От числителя уменьшаемой дроби «7» отнимаем числитель вычитаемой дроби «3», получаем «4». Это число мы записываем в числитель ответа, а в знаменатель ставим то же число, что было в знаменателях первой и второй дроби – «19».
На картинке ниже приведено еще несколько подобных примеров.
Рассмотрим более сложный пример, где произведено вычитание дробей с одинаковыми знаменателями:
29/47 — 3/47 — 8/47 — 2/47 — 7/47 = (29 — 3 — 8 — 2 — 7)/47 = 9/47.
От числителя уменьшаемой дроби «29» отниманием по очереди числители всех последующих дробей – «3», «8», «2», «7». В итоге получаем результат «9», который записываем в числитель ответа, а в знаменатель записываем то число, которое находится в знаменателях всех этих дробей, — «47».
Сложение дробей, имеющих одинаковый знаменатель
Сложение и вычитание обыкновенных дробей осуществляется по одному и тому же принципу.
- Для того чтобы сложить дроби, знаменатели которых одинаковы, необходимо числители сложить. Полученное число — числитель суммы, а знаменатель останется тот же: k/m + b/m = (k + b)/m.
Рассмотрим, как это выглядит на примере:
1/4 + 2/4 = 3/4.
К числителю первой слагаемой дроби — «1» — добавляем числитель второй слагаемой дроби — «2». Результат — «3» — записываем в числитель суммы, а знаменатель оставляем тот же, что присутствовал в дробях, — «4».
Дроби с различными знаменателями и их вычитание
Действие с дробями, которые имеют одинаковый знаменатель, мы уже рассмотрели. Как видим, зная простые правила, решить подобные примеры достаточно легко. Но что делать, если необходимо произвести действие с дробями, которые имеют различные знаменатели? Многие учащиеся средних школ приходят в затруднение перед такими примерами. Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.
Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.
О том, как это сделать, мы поговорим подробнее.
Свойство дроби
Для того чтобы несколько дробей привести к одинаковому знаменателю, нужно использовать в решении главное свойство дроби: после деления или умножения числителя и знаменателя на одинаковое число получится дробь, равная данной.
Так, например, дробь 2/3 может иметь такие знаменатели, как «6», «9», «12» и т. д., то есть она может иметь вид любого числа, которое кратно «3». После того как числитель и знаменатель мы умножим на «2», получится дробь 4/6. После того как числитель и знаменатель исходной дроби мы умножим на «3», получим 6/9, а если аналогичное действие произвести с цифрой «4», получим 8/12. Одним равенством это можно записать так:
2/3 = 4/6 = 6/9 = 8/12…
Как привести несколько дробей к одному и тому же знаменателю
Рассмотрим, как привести несколько дробей к одному и тому же знаменателю. Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.
Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.
Знаменатель дроби 1/2 и дроби 2/3 на множители разложить нельзя. Знаменатель 7/9 имеет два множителя 7/9 = 7/(3 х 3), знаменатель дроби 5/6 = 5/(2 х 3). Теперь необходимо определить, какие же множители будут наименьшими для всех этих четырех дробей. Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе. Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.
Рассмотрим первую дробь — 1/2. В ее знаменателе имеется «2», но нет ни одной цифры «3», а должно быть две. Для этого мы знаменатель умножаем на две тройки, но, согласно свойству дроби, мы и числитель должны умножить на две тройки:
1/2 = (1 х 3 х 3)/(2 х 3 х 3) = 9/18.
Аналогично производим действия с оставшимися дробями.
- 2/3 – в знаменателе не хватает одной тройки и одной двойки:
2/3 = (2 х 3 х 2)/(3 х 3 х 2) = 12/18. - 7/9 или 7/(3 х 3) – в знаменателе не хватает двойки:
7/9 = (7 х 2)/(9 х 2) = 14/18. - 5/6 или 5/(2 х 3) – в знаменателе не хватает тройки:
5/6 = (5 х 3)/(6 х 3) = 15/18.
Все вместе это выглядит так:
Как вычесть и сложить дроби, имеющие различные знаменатели
Как уже говорилось выше, для того чтобы произвести сложение или вычитание дробей, имеющих различные знаменатели, их необходимо привести к одному знаменателю, а дальше воспользоваться правилами вычитания дробей, имеющих одинаковый знаменатель, о котором уже рассказывалось.
Рассмотрим это на примере: 4/18 – 3/15.
Находим кратное чисел 18 и 15:
- Число 18 состоит из 3 х 2 х 3.
- Число 15 состоит из 5 х 3.
- Общее кратное будет состоять из следующих множителей 5 х 3 х 3 х 2 = 90.
После того как знаменатель будет найден, необходимо вычислить множитель, который будет отличным для каждой дроби, то есть то число, на которое необходимо будет умножить не только знаменатель, но и числитель. Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.
Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.
- 90 поделить на 15. Полученное число «6» будет множителем для 3/15.
- 90 поделить на 18. Полученное число «5» будет множителем для 4/18.
Следующий этап нашего решения – приведение каждой дроби к знаменателю «90».
Как это делается, мы уже говорили. Рассмотрим, как это записывается в примере:
(4 х 5)/(18 х 5) – (3 х 6)/(15 х 6) = 20/90 – 18/90 = 2/90 = 1/45.
Если дроби с маленькими числами, то можно общий знаменатель определить, как в примере, приведенном на картинке ниже.
Аналогично производится и сложение дробей, имеющих различные знаменатели.
Вычитание дробей и их сложение мы уже детально разобрали. Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:
- Все дроби, имеющие целую часть, перевести в неправильные. Говоря простыми словами, убрать целую часть.
 Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, – числитель неправильной дроби. Знаменатель же остается неизменным.
Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, – числитель неправильной дроби. Знаменатель же остается неизменным. - Если дроби имеют различные знаменатели, следует привести их к одинаковому.
- Произвести сложение или вычитание с одинаковыми знаменателями.
- При получении неправильной дроби выделить целую часть.
Есть и иной способ, при помощи которого можно осуществить сложение и вычитание дробей с целыми частями. Для этого производятся отдельно действия с целыми частями, и отдельно действия с дробями, а результаты записываются вместе.
Приведенный пример состоит из дробей, которые имеют одинаковый знаменатель. В том случае, когда знаменатели различны, их необходимо привести к одинаковому, а далее выполнить действия, как показано на примере.
Вычитание дробей из целого числа
Еще одной из разновидностей действий с дробями является тот случай, когда дробь необходимо отнять от натурального числа. На первый взгляд подобный пример кажется трудно решаемым. Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:
На первый взгляд подобный пример кажется трудно решаемым. Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:
7 — 4/9 = (7 х 9)/9 — 4/9 = 53/9 — 4/9 = 49/9.
Приведенное в этой статье вычитание дробей (6 класс) является основой для решения более сложных примеров, которые рассматриваются в последующих классах. Знания этой темы используются впоследствии для решения функций, производных и так далее. Поэтому очень важно разобраться и понять действия с дробями, рассматриваемые выше.
Как отнять дроби с одинаковыми знаменателями. Сложение и вычитание дробей
В данном уроке будет рассмотрено сложение и вычитание алгебраических дробей с одинаковыми знаменателями. Мы уже знаем, как складывать и вычитать обыкновенные дроби с одинаковыми знаменателями. Оказывается, что алгебраические дроби подчиняются тем же самым правилам. Умение работать с дробями с одинаковыми знаменателями является одним из краеугольных камней в изучении правил работы с алгебраическими дробями. В частности, понимание данной темы позволит легко освоить более сложную тему — сложение и вычитание дробей с разными знаменателями. В рамках урока мы изучим правила сложения и вычитания алгебраических дробей с одинаковыми знаменателями, а также разберём целый ряд типовых примеров
Умение работать с дробями с одинаковыми знаменателями является одним из краеугольных камней в изучении правил работы с алгебраическими дробями. В частности, понимание данной темы позволит легко освоить более сложную тему — сложение и вычитание дробей с разными знаменателями. В рамках урока мы изучим правила сложения и вычитания алгебраических дробей с одинаковыми знаменателями, а также разберём целый ряд типовых примеров
Правило сложения и вычитания алгебраических дробей с одинаковыми знаменателями
Сфор-му-ли-ру-ем пра-ви-ло сло-же-ния (вы-чи-та-ния) ал-геб-ра-и-че-ских дро-бей с оди-на-ко-вы-ми зна-ме-на-те-ля-ми (оно сов-па-да-ет с ана-ло-гич-ным пра-ви-лом для обык-но-вен-ных дро-бей): То есть для сло-же-ния или вы-чи-та-ния ал-геб-ра-и-че-ских дро-бей с оди-на-ко-вы-ми зна-ме-на-те-ля-ми необ-хо-ди-мо со-ста-вить со-от-вет-ству-ю-щую ал-геб-ра-и-че-скую сумму чис-ли-те-лей, а зна-ме-на-тель оста-вить без из-ме-не-ний.
Это пра-ви-ло мы раз-бе-рём и на при-ме-ре обык-но-вен-ных дро-бей, и на при-ме-ре ал-геб-ра-и-че-ских дро-бей.
Примеры применения правила для обыкновенных дробей
При-мер 1. Сло-жить дроби: .
Ре-ше-ние
Сло-жим чис-ли-те-ли дро-бей, а зна-ме-на-тель оста-вим таким же. После этого раз-ло-жим чис-ли-тель и зна-ме-на-тель на про-стые мно-жи-те-ли и со-кра-тим. По-лу-чим: .
При-ме-ча-ние: стан-дарт-ная ошиб-ка, ко-то-рую до-пус-ка-ют при ре-ше-нии по-доб-но-го рода при-ме-ров, за-клю-ча-ет-ся в сле-ду-ю-щем спо-со-бе ре-ше-ния: . Это гру-бей-шая ошиб-ка, по-сколь-ку зна-ме-на-тель оста-ёт-ся таким же, каким был в ис-ход-ных дро-бях.
При-мер 2. Сло-жить дроби: .
Ре-ше-ние
Дан-ная за-да-ча ничем не от-ли-ча-ет-ся от преды-ду-щей: .
Примеры применения правила для алгебраических дробей
От обык-но-вен-ных дро-бей пе-рей-дём к ал-геб-ра-и-че-ским.
При-мер 3. Сло-жить дроби: .
Ре-ше-ние:как уже го-во-ри-лось выше, сло-же-ние ал-геб-ра-и-че-ских дро-бей ничем не от-ли-ча-ет-ся от сло-же-ния обык-но-вен-ных дро-бей. По-это-му метод ре-ше-ния такой же: .
При-мер 4. Вы-честь дроби: .
Ре-ше-ние
Вы-чи-та-ние ал-геб-ра-и-че-ских дро-бей от-ли-ча-ет-ся от сло-же-ния толь-ко тем, что в чис-ли-тель за-пи-сы-ва-ет-ся раз-ность чис-ли-те-лей ис-ход-ных дро-бей. По-это-му .
При-мер 5. Вы-честь дроби: .
Ре-ше-ние: .
При-мер 6. Упро-стить: .
Ре-ше-ние: .
Примеры применения правила с последующим сокращением
В дроби, ко-то-рая по-лу-ча-ет-ся в ре-зуль-та-те сло-же-ния или вы-чи-та-ния, воз-мож-ны со-кра-ще-ния. Кроме того, не стоит за-бы-вать об ОДЗ ал-геб-ра-и-че-ских дро-бей.
При-мер 7. Упро-стить: .
Ре-ше-ние: .
При этом . Во-об-ще, если ОДЗ ис-ход-ных дро-бей сов-па-да-ет с ОДЗ ито-го-вой, то его можно не ука-зы-вать (ведь дробь, по-лу-чен-ная в от-ве-те, также не будет су-ще-ство-вать при со-от-вет-ству-ю-щих зна-че-ни-ях пе-ре-мен-ных). А вот если ОДЗ ис-ход-ных дро-бей и от-ве-та не сов-па-да-ет, то ОДЗ ука-зы-вать необ-хо-ди-мо.
При-мер 8. Упро-стить: .
Ре-ше-ние: . При этом y (ОДЗ ис-ход-ных дро-бей не сов-па-да-ет с ОДЗ ре-зуль-та-та).
При этом y (ОДЗ ис-ход-ных дро-бей не сов-па-да-ет с ОДЗ ре-зуль-та-та).
Сложение и вычитание обыкновенных дробей с разными знаменателями
Чтобы скла-ды-вать и вы-чи-тать ал-геб-ра-и-че-ские дроби с раз-ны-ми зна-ме-на-те-ля-ми, про-ве-дём ана-ло-гию с обык-но-вен-ны-ми дро-бя-ми и пе-ре-не-сём её на ал-геб-ра-и-че-ские дроби.
Рас-смот-рим про-стей-ший при-мер для обык-но-вен-ных дро-бей.
При-мер 1. Сло-жить дроби: .
Ре-ше-ние:
Вспом-ним пра-ви-ло сло-же-ния дро-бей. Для на-ча-ла дроби необ-хо-ди-мо при-ве-сти к об-ще-му зна-ме-на-те-лю. В роли об-ще-го зна-ме-на-те-ля для обык-но-вен-ных дро-бей вы-сту-па-ет наи-мень-шее общее крат-ное (НОК) ис-ход-ных зна-ме-на-те-лей.
Опре-де-ле-ние
Наи-мень-шее на-ту-раль-ное число, ко-то-рое де-лит-ся од-но-вре-мен-но на числа и .
Для на-хож-де-ния НОК необ-хо-ди-мо раз-ло-жить зна-ме-на-те-ли на про-стые мно-жи-те-ли, а затем вы-брать все про-стые мно-жи-те-ли, ко-то-рые вхо-дят в раз-ло-же-ние обоих зна-ме-на-те-лей.
; . Тогда в НОК чисел долж-ны вхо-дить две двой-ки и две трой-ки: .
После на-хож-де-ния об-ще-го зна-ме-на-те-ля, необ-хо-ди-мо для каж-дой из дро-бей найти до-пол-ни-тель-ный мно-жи-тель (фак-ти-че-ски, по-де-лить общий зна-ме-на-тель на зна-ме-на-тель со-от-вет-ству-ю-щей дроби).
Затем каж-дая дробь умно-жа-ет-ся на по-лу-чен-ный до-пол-ни-тель-ный мно-жи-тель. По-лу-ча-ют-ся дроби с оди-на-ко-вы-ми зна-ме-на-те-ля-ми, скла-ды-вать и вы-чи-тать ко-то-рые мы на-учи-лись на про-шлых уро-ках.
По-лу-ча-ем: .
Ответ: .
Рас-смот-рим те-перь сло-же-ние ал-геб-ра-и-че-ских дро-бей с раз-ны-ми зна-ме-на-те-ля-ми. Сна-ча-ла рас-смот-рим дроби, зна-ме-на-те-ли ко-то-рых яв-ля-ют-ся чис-ла-ми.
Сложение и вычитание алгебраических дробей с разными знаменателями
При-мер 2. Сло-жить дроби: .
Ре-ше-ние:
Ал-го-ритм ре-ше-ния аб-со-лют-но ана-ло-ги-чен преды-ду-ще-му при-ме-ру. Легко по-до-брать общий зна-ме-на-тель дан-ных дро-бей: и до-пол-ни-тель-ные мно-жи-те-ли для каж-дой из них.
.
Ответ: .
Итак, сфор-му-ли-ру-ем ал-го-ритм сло-же-ния и вы-чи-та-ния ал-геб-ра-и-че-ских дро-бей с раз-ны-ми зна-ме-на-те-ля-ми :
1. Найти наи-мень-ший общий зна-ме-на-тель дро-бей.
2. Найти до-пол-ни-тель-ные мно-жи-те-ли для каж-дой из дро-бей (по-де-лив общий зна-ме-на-тель на зна-ме-на-тель дан-ной дроби).
3. До-мно-жить чис-ли-те-ли на со-от-вет-ству-ю-щие до-пол-ни-тель-ные мно-жи-те-ли.
4. Сло-жить или вы-честь дроби, поль-зу-ясь пра-ви-ла-ми сло-же-ния и вы-чи-та-ния дро-бей с оди-на-ко-вы-ми зна-ме-на-те-ля-ми.
Рас-смот-рим те-перь при-мер с дро-бя-ми, в зна-ме-на-те-ле ко-то-рых при-сут-ству-ют бук-вен-ные вы-ра-же-ния.
Одной из важнейших наук, применение которой можно увидеть в таких дисциплинах, как химия, физика и даже биология, является математика. Изучение этой науки позволяет развить некоторые умственные качества, улучшить и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» — сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.
У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.
Как вычесть дроби, знаменатели которых одинаковые
Дроби — это те же числа, с которыми можно производить различные действия. Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:
- Для того чтобы из одной дроби вычесть вторую, необходимо из числителя уменьшаемой дроби вычесть числитель вычитаемой дроби. Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m — b/m = (k-b)/m.
Примеры вычитания дробей, знаменатели которых одинаковы
7/19 — 3/19 = (7 — 3)/19 = 4/19.
От числителя уменьшаемой дроби «7» отнимаем числитель вычитаемой дроби «3», получаем «4». Это число мы записываем в числитель ответа, а в знаменатель ставим то же число, что было в знаменателях первой и второй дроби — «19».
Это число мы записываем в числитель ответа, а в знаменатель ставим то же число, что было в знаменателях первой и второй дроби — «19».
На картинке ниже приведено еще несколько подобных примеров.
Рассмотрим более сложный пример, где произведено вычитание дробей с одинаковыми знаменателями:
29/47 — 3/47 — 8/47 — 2/47 — 7/47 = (29 — 3 — 8 — 2 — 7)/47 = 9/47.
От числителя уменьшаемой дроби «29» отниманием по очереди числители всех последующих дробей — «3», «8», «2», «7». В итоге получаем результат «9», который записываем в числитель ответа, а в знаменатель записываем то число, которое находится в знаменателях всех этих дробей, — «47».
Сложение дробей, имеющих одинаковый знаменатель
Сложение и вычитание обыкновенных дробей осуществляется по одному и тому же принципу.
- Для того чтобы сложить дроби, знаменатели которых одинаковы, необходимо числители сложить. Полученное число — числитель суммы, а знаменатель останется тот же: k/m + b/m = (k + b)/m.

Рассмотрим, как это выглядит на примере:
1/4 + 2/4 = 3/4.
К числителю первой слагаемой дроби — «1» — добавляем числитель второй слагаемой дроби — «2». Результат — «3» — записываем в числитель суммы, а знаменатель оставляем тот же, что присутствовал в дробях, — «4».
Дроби с различными знаменателями и их вычитание
Действие с дробями, которые имеют одинаковый знаменатель, мы уже рассмотрели. Как видим, зная простые правила, решить подобные примеры достаточно легко. Но что делать, если необходимо произвести действие с дробями, которые имеют различные знаменатели? Многие учащиеся средних школ приходят в затруднение перед такими примерами. Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.
- 2/3 — в знаменателе не хватает одной тройки и одной двойки:
2/3 = (2 х 3 х 2)/(3 х 3 х 2) = 12/18.
- 7/9 или 7/(3 х 3) — в знаменателе не хватает двойки:
7/9 = (7 х 2)/(9 х 2) = 14/18. - 5/6 или 5/(2 х 3) — в знаменателе не хватает тройки:
5/6 = (5 х 3)/(6 х 3) = 15/18. - Число 18 состоит из 3 х 2 х 3.
- Число 15 состоит из 5 х 3.
- Общее кратное будет состоять из следующих множителей 5 х 3 х 3 х 2 = 90.
- 90 поделить на 15. Полученное число «6» будет множителем для 3/15.
- 90 поделить на 18. Полученное число «5» будет множителем для 4/18.
- Все дроби, имеющие целую часть, перевести в неправильные.
 Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, — числитель неправильной дроби. Знаменатель же остается неизменным.
Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, — числитель неправильной дроби. Знаменатель же остается неизменным. - Если дроби имеют различные знаменатели, следует привести их к одинаковому.
- Произвести сложение или вычитание с одинаковыми знаменателями.
- При получении неправильной дроби выделить целую часть.
Чтобы произвести вычитание дробей с разными знаменателями, необходимо их привести к одинаковому наименьшему знаменателю.
О том, как это сделать, мы поговорим подробнее.
Свойство дроби
Для того чтобы несколько дробей привести к одинаковому знаменателю, нужно использовать в решении главное свойство дроби: после деления или умножения числителя и знаменателя на одинаковое число получится дробь, равная данной.
Так, например, дробь 2/3 может иметь такие знаменатели, как «6», «9», «12» и т. д., то есть она может иметь вид любого числа, которое кратно «3». После того как числитель и знаменатель мы умножим на «2», получится дробь 4/6. После того как числитель и знаменатель исходной дроби мы умножим на «3», получим 6/9, а если аналогичное действие произвести с цифрой «4», получим 8/12. Одним равенством это можно записать так:
2/3 = 4/6 = 6/9 = 8/12…
Как привести несколько дробей к одному и тому же знаменателю
Рассмотрим, как привести несколько дробей к одному и тому же знаменателю. Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.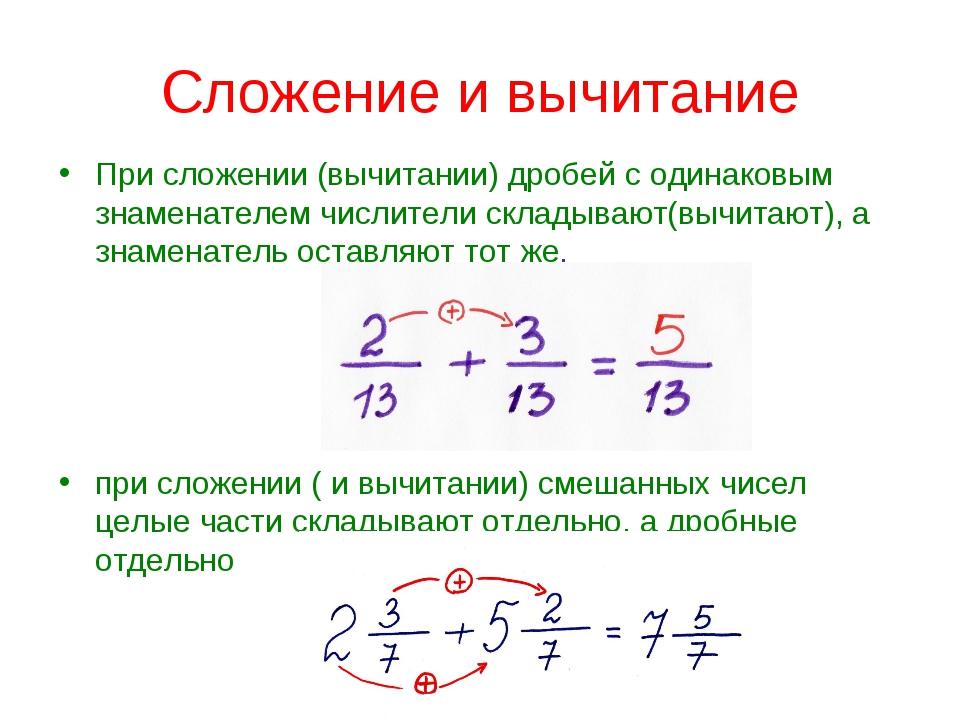
Знаменатель дроби 1/2 и дроби 2/3 на множители разложить нельзя. Знаменатель 7/9 имеет два множителя 7/9 = 7/(3 х 3), знаменатель дроби 5/6 = 5/(2 х 3). Теперь необходимо определить, какие же множители будут наименьшими для всех этих четырех дробей. Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе. Учитывая вышесказанное, определяем, что знаменатель состоит из трех множителей: 3, 2, 3 и равен 3 х 2 х 3 = 18.
Рассмотрим первую дробь — 1/2. В ее знаменателе имеется «2», но нет ни одной цифры «3», а должно быть две. Для этого мы знаменатель умножаем на две тройки, но, согласно свойству дроби, мы и числитель должны умножить на две тройки:
1/2 = (1 х 3 х 3)/(2 х 3 х 3) = 9/18.
Аналогично производим действия с оставшимися дробями.
Все вместе это выглядит так:
Как вычесть и сложить дроби, имеющие различные знаменатели
Как уже говорилось выше, для того чтобы произвести сложение или вычитание дробей, имеющих различные знаменатели, их необходимо привести к одному знаменателю, а дальше воспользоваться правилами вычитания дробей, имеющих одинаковый знаменатель, о котором уже рассказывалось.
Рассмотрим это на примере: 4/18 — 3/15.
Находим кратное чисел 18 и 15:
После того как знаменатель будет найден, необходимо вычислить множитель, который будет отличным для каждой дроби, то есть то число, на которое необходимо будет умножить не только знаменатель, но и числитель. Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.
Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.
Следующий этап нашего решения — приведение каждой дроби к знаменателю «90».
Как это делается, мы уже говорили. Рассмотрим, как это записывается в примере:
(4 х 5)/(18 х 5) — (3 х 6)/(15 х 6) = 20/90 — 18/90 = 2/90 = 1/45.
Если дроби с маленькими числами, то можно общий знаменатель определить, как в примере, приведенном на картинке ниже.
Аналогично производится и имеющих различные знаменатели.
Вычитание и имеющих целые части
Вычитание дробей и их сложение мы уже детально разобрали. Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:
Есть и иной способ, при помощи которого можно осуществить сложение и вычитание дробей с целыми частями. Для этого производятся отдельно действия с целыми частями, и отдельно действия с дробями, а результаты записываются вместе.
Приведенный пример состоит из дробей, которые имеют одинаковый знаменатель. В том случае, когда знаменатели различны, их необходимо привести к одинаковому, а далее выполнить действия, как показано на примере.
Вычитание дробей из целого числа
Еще одной из разновидностей действий с дробями является тот случай, когда дробь необходимо отнять от На первый взгляд подобный пример кажется трудно решаемым. Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:
Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:
7 — 4/9 = (7 х 9)/9 — 4/9 = 53/9 — 4/9 = 49/9.
Приведенное в этой статье вычитание дробей (6 класс) является основой для решения более сложных примеров, которые рассматриваются в последующих классах. Знания этой темы используются впоследствии для решения функций, производных и так далее. Поэтому очень важно разобраться и понять действия с дробями, рассматриваемые выше.
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с разными знаменателями
Понятие о НОК
Приведение дробей к одному знаменателю
Как сложить целое число и дробь
1 Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:
Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,
Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:
2 Сложение и вычитание дробей с разными знаменателями
Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи. Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
3 Наименьшее общее кратное (НОК)
Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:
Для того, чтобы найти НОК нескольких чисел, нужно:
- Разложить эти числа на простые множители
- Взять самое большое разложение, и записать эти числа в виде произведения
- Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
- Перемножить все числа в произведении, это и будет НОК.

Например, найдем НОК чисел 28 и 21:
4Приведение дробей к одному знаменателю
Вернемся к сложению дробей с разными знаменателями.
Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители . Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:
Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.
5Как сложить целое число и дробь
Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например.
Ваш ребенок принес домашнее задание из школы, и вы не знаете как его решить? Тогда этот мини урок для вас!
Как складывать десятичные дроби
Десятичные дроби удобнее складывать в столбик. Чтобы выполнить сложение десятичных дробей, надо придерживаться одного простого правила:
- Разряд должен находиться под разрядом, запятая под запятой.
Как вы видите на примере, целые единицы находятся друг под другом, разряд десятых и сотых находится друг под другом. Теперь складываем числа, не обращая внимания на запятую. Что же делать с запятой? Запятая переносится на то место, где стояла в разряде целых.
Сложение дробей с равными знаменателями
Чтобы выполнить сложение с общим знаменателем, надо сохранить знаменатель без изменения, найти сумму числителей и получим дробь, которая будет являться общей суммой.
Сложение дробей с разными знаменателями методом нахождения общего кратного
Первое, на что надо обратить внимание – это на знаменатели. Знаменатели разные, не делятся ли одно на другое, являются ли простыми числами. Для начала надо привести к одному общему знаменателю, для этого существует несколько способов:
Знаменатели разные, не делятся ли одно на другое, являются ли простыми числами. Для начала надо привести к одному общему знаменателю, для этого существует несколько способов:
- 1/3 + 3/4 = 13/12, для решения этого примера нам надо найти наименьшее общее кратное число (НОК), которое будет делиться на 2 знаменателя. Для обозначения наименьшего кратного чисел a и b – НОК (а;b). В данном примере НОК (3;4)=12. Проверяем: 12:3=4; 12:4=3.
- Перемножаем множители и выполняем сложение полученных чисел, получаем 13/12 – неправильную дробь.
- Для того чтобы перевести неправильную дробь в правильную, разделим числитель на знаменатель, получим целое число 1, остаток 1 – числитель и 12 – знаменатель.
Сложение дробей методом умножения крест на крест
Для складывания дробей с разными знаменателями существует еще один способ по формуле “крест на крест”. Это гарантированный способ уровнять знаменатели, для этого вам надо числители перемножить со знаменателем одной дроби и обратно. Если вы только на начальном этапе изучения дробей, то этот способ самый простой и точный, как получить верный результат при сложении дробей с разными знаменателями.
Если вы только на начальном этапе изучения дробей, то этот способ самый простой и точный, как получить верный результат при сложении дробей с разными знаменателями.
На данном уроке будет рассмотрено сложение и вычитание алгебраических дробей с разными знаменателями. Мы уже знаем, как складывать и вычитать обыкновенные дроби с разными знаменателями. Для этого дроби необходимо привести к общему знаменателю. Оказывается, что алгебраические дроби подчиняются тем же самым правилам. При этом мы уже умеем приводить алгебраические дроби к общему знаменателю. Сложение и вычитание дробей с разными знаменателями — одна из наиболее важных и сложных тем в курсе 8 класса. При этом данная тема будет встречаться во многих темах курса алгебры, которые вы будете изучать в дальнейшем. В рамках урока мы изучим правила сложения и вычитания алгебраических дробей с разными знаменателями, а также разберём целый ряд типовых примеров.
Рассмотрим простейший пример для обыкновенных дробей.
Пример 1. Сложить дроби: .
Сложить дроби: .
Решение:
Вспомним правило сложения дробей. Для начала дроби необходимо привести к общему знаменателю. В роли общего знаменателя для обыкновенных дробей выступает наименьшее общее кратное (НОК) исходных знаменателей.
Определение
Наименьшее натуральное число, которое делится одновременно на числа и .
Для нахождения НОК необходимо разложить знаменатели на простые множители, а затем выбрать все простые множители, которые входят в разложение обоих знаменателей.
; . Тогда в НОК чисел должны входить две двойки и две тройки: .
После нахождения общего знаменателя, необходимо для каждой из дробей найти дополнительный множитель (фактически, поделить общий знаменатель на знаменатель соответствующей дроби).
Затем каждая дробь умножается на полученный дополнительный множитель. Получаются дроби с одинаковыми знаменателями, складывать и вычитать которые мы научились на прошлых уроках.
Получаем: .
Ответ: .
Рассмотрим теперь сложение алгебраических дробей с разными знаменателями. Сначала рассмотрим дроби, знаменатели которых являются числами.
Пример 2. Сложить дроби: .
Решение:
Алгоритм решения абсолютно аналогичен предыдущему примеру. Легко подобрать общий знаменатель данных дробей: и дополнительные множители для каждой из них.
.
Ответ: .
Итак, сформулируем алгоритм сложения и вычитания алгебраических дробей с разными знаменателями :
1. Найти наименьший общий знаменатель дробей.
2. Найти дополнительные множители для каждой из дробей (поделив общий знаменатель на знаменатель данной дроби).
3. Домножить числители на соответствующие дополнительные множители.
4. Сложить или вычесть дроби, пользуясь правилами сложения и вычитания дробей с одинаковыми знаменателями.
Рассмотрим теперь пример с дробями, в знаменателе которых присутствуют буквенные выражения.
Пример 3. Сложить дроби: .
Решение:
Поскольку буквенные выражения в обоих знаменателях одинаковы, то следует найти общий знаменатель для чисел . Итоговый общий знаменатель будет иметь вид: . Таким образом, решение данного примера имеет вид:.
Ответ: .
Пример 4. Вычесть дроби: .
Решение:
Если «схитрить» при подборе общего знаменателя не удаётся (нельзя разложить на множители или воспользоваться формулами сокращённого умножения), то в качестве общего знаменателя приходится брать произведение знаменателей обеих дробей.
Ответ: .
Вообще, при решении подобных примеров, наиболее сложным заданием является нахождение общего знаменателя.
Рассмотрим более сложный пример.
Пример 5. Упростить: .
Решение:
При нахождении общего знаменателя необходимо прежде всего попытаться разложить знаменатели исходных дробей на множители (чтобы упростить общий знаменатель).
В данном конкретном случае:
Тогда легко определить общий знаменатель: .
Определяем дополнительные множители и решаем данный пример:
Ответ: .
Теперь закрепим правила сложения и вычитания дробей с разными знаменателями.
Пример 6. Упростить: .
Решение:
Ответ: .
Пример 7. Упростить: .
Решение:
.
Ответ: .
Рассмотрим теперь пример, в котором складываются не две, а три дроби (ведь правила сложения и вычитания для большего количества дробей остаются такими же).
Пример 8. Упростить: .
Как вычитать обыкновенные дроби: с одинаковыми, разными знаменателями
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Вычитание обыкновенных дробей
В данной публикации мы рассмотрим, каким образом можно найти разность обыкновенных (простых) дробей с разными или одинаковыми знаменателями, и как выполняется вычитание смешанных дробей. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Вычитание дробей
- С одинаковыми знаменателями
- С разными знаменателями
- Разность смешанных дробей
- Примеры задач
Вычитание дробей
С одинаковыми знаменателями
При вычитании дробей с одинаковыми знаменателями, из числителя первой дроби отнимается числитель второй дроби. Знаменатель при этом остается тем же.
a/c
–
b/c
=
a-b/c
Примечание: Следует проверить новую дробь, полученную путем вычитания. Возможно, ее можно сократить.
С разными знаменателями
Чтобы вычесть одну дробь из другой, знаменатель которой отличаются от первой, нам нужно:
1. Привести данные дроби к наименьшему общему знаменателю.
2. Затем выполнить вычитание – как для дробей с одинаковыми знаменателями.
Разность смешанных дробей
Чтобы найти разность смешанных дробей, сперва отдельно вычитаем их целые части, затем – отдельно дробные. Полученные результаты складываем.
Полученные результаты складываем.
X
a/b
– Y
c/d
= (X – Y) + (
a/b
–
c/d
)
Примечание: Если дробные части имеют разные знаменатели, сперва их приводим к наименьшему общему знаменателю, затем – вычитаем.
Примеры задач
Задание 1
Найдите разность дробей
8/14
и
3/14
.
Решение
У данных дробей один и тот же знаменатель, следовательно:
8/14
–
3/14
=
8-3/14
=
5/14
Задание 2
Найдите разность дробей
6/7
и
9/20
.
Решение
Сперва приводим дроби к наименьшему общему знаменателю.
Наименьшее общее кратное обоих знаменателей равняется 140. Значит, дополнительный множитель для первой дроби – 20, для второй – 7.
6/7
=
6⋅20/7⋅20
=
120/140
9/20
=
9⋅7/20⋅7
=
63/120
Теперь у нас дроби с одинаковыми знаменателями, и мы можем вычесть из первой вторую:
120/140
–
63/140
=
120-63/140
=
57/140
Задание 3
Отнимите из дроби 3
5/7
дробь 2
3/7
.
Решение
Так как дробные части имеют одинаковые знаменатели, мы сразу можем выполнить вычитание:
3
5/7
– 2
3/7
= 3 – 2 + (
5/7
–
3/7
) = 1 +
5-3/7
= 1
2/7
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Вычитание дробей – Примеры
Вычитание дробей – это арифметическая операция, которая должна выполняться для нахождения разницы между двумя дробями. Чтобы вычесть две одинаковые дроби, мы должны вычесть их числители и записать разницу над общим знаменателем, а чтобы вычесть две разные дроби, мы должны сначала преобразовать их в подобные дроби, взяв НОК знаменателей. Мы также можем вычесть целое число и дробь, записав целое число в дробной форме, например, 3 = 3/1. Давайте узнаем больше о вычитании дробей подробно в этой статье.
Чтобы вычесть две одинаковые дроби, мы должны вычесть их числители и записать разницу над общим знаменателем, а чтобы вычесть две разные дроби, мы должны сначала преобразовать их в подобные дроби, взяв НОК знаменателей. Мы также можем вычесть целое число и дробь, записав целое число в дробной форме, например, 3 = 3/1. Давайте узнаем больше о вычитании дробей подробно в этой статье.
| 1. | Как вычитать дроби? |
| 2. | Вычитание дробей с одинаковыми знаменателями |
| 3. | Вычитание дробей с разными знаменателями |
| 4. | Вычитание дробей из целых чисел |
| 5. | Часто задаваемые вопросы о вычитании дробей |
Как вычитать дроби?
Дроби считаются частью целого. Группа дробей может быть классифицирована как подобные дроби и разные дроби на основе значения знаменателя. Подобные дроби – это те, у которых одинаковые знаменатели. Например, 3/4 и 5/4. В то время как непохожими являются дроби, имеющие разные знаменатели, например, 2/3 и 4/7. Мы можем найти разницу между двумя одинаковыми дробями, в отличие от дробей и дробей и целых чисел. Шаги для вычитания дробей перечислены ниже:
Подобные дроби – это те, у которых одинаковые знаменатели. Например, 3/4 и 5/4. В то время как непохожими являются дроби, имеющие разные знаменатели, например, 2/3 и 4/7. Мы можем найти разницу между двумя одинаковыми дробями, в отличие от дробей и дробей и целых чисел. Шаги для вычитания дробей перечислены ниже:
- Шаг 1: Определите, имеют ли данные дроби одинаковые знаменатели или разные знаменатели.
- Шаг 2: В случае одинаковых дробей вычтите числители и запишите их разность над общим знаменателем. Например, 5/7 — 2/7 = (5 — 2)/7 = 3/7. С другой стороны, для разных дробей найдите НОК знаменателей.
- Шаг 3: Умножьте числитель и знаменатель каждой дроби на целое число, чтобы получить НОК в знаменателе. Это делается для преобразования неодинаковых дробей в подобные дроби.
- Шаг 4: Вычтите их числители и запишите разницу над общим знаменателем.
Вот как мы вычитаем две дроби.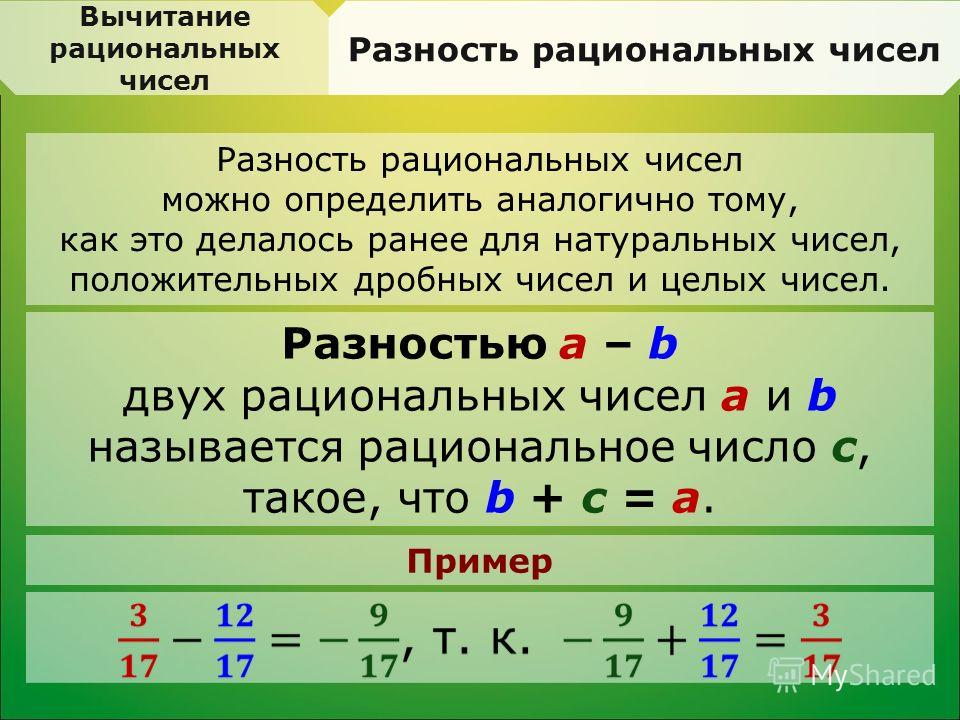 Есть два случая, которые возникают при изучении вычитания дробей: вычитание подобных дробей и непохожих дробей. Давайте узнаем о каждом подробно.
Есть два случая, которые возникают при изучении вычитания дробей: вычитание подобных дробей и непохожих дробей. Давайте узнаем о каждом подробно.
Вычитание дробей с одинаковыми знаменателями
Дроби с одинаковыми знаменателями легко вычитаются путем вычитания их числителей. Шаги для вычитания дробей с одинаковыми знаменателями приведены ниже:
- Вычесть числители.
- Запишите общий знаменатель как знаменатель результирующей дроби.
- Теперь полученный ответ можно при необходимости привести к низшей форме.
Вычтем дроби 4/5 и 2/5, используя прямоугольную модель. Мы представляем 4/5 в этой модели, заштриховывая 4 из 5 частей. Далее мы заштрихуем 2 части из заштрихованных частей модели, чтобы представить удаление 2/5.
Теперь у нас осталось 2 части в заштрихованных частях модели. Таким образом, вычитание дробей дается как (4/5 — 2/5) = 2/5.
Вычитание дробей с разными знаменателями
Две дроби с разными или непохожими знаменателями можно вычесть, выполнив шаги, описанные ниже:
- Сначала возьмите НОК знаменателей.

- Преобразуем данные дроби в подобные дроби со знаменателем в виде НОК.
- Теперь вычтите числители и запишите их разницу над общим знаменателем.
- При необходимости упростите.
Давайте разберемся, как вычитать разные дроби, используя модель площади: (2/5 — 1/3). Это указывает на то, что мы должны удалить (1/3) часть rd из 2/5. Мы можем представить это, как показано ниже.
Поскольку наша модель разделена на 15 частей, это наш знаменатель. Это НОК знаменателей данных дробей. Первый прямоугольник показывает часть, представленную 2/5 (в строках) и 1/3 (в столбцах) в данной модели. Теперь переместите часть 1/3 на 2/5, чтобы мы могли вычесть 1/3 из 2/5. Мы видим, что осталась только 1 часть, которая не заштрихована. Таким образом, ответ дается как 2/5 — 1/3 = 1/15. Численно это можно выразить как
2/5 — 1/3
⇒ (2 × 3)/(5 × 3) — (1 × 5)/(3 × 5) [Поскольку НОК 5 и 3 равен 15]
⇒ 6 /15 — 5/15
⇒ 1/15
Следовательно, 2/5 — 1/3 = 1/15.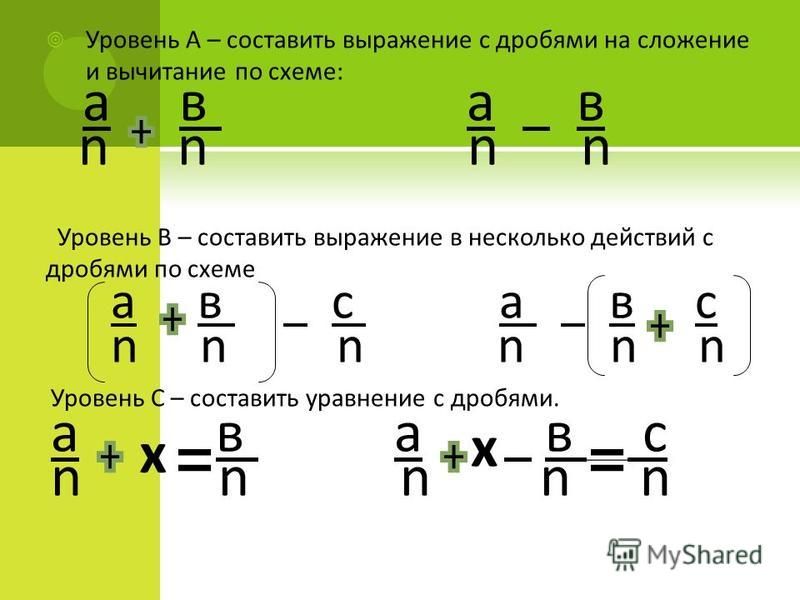
Воспользуйтесь нашим бесплатным онлайн-калькулятором дробей для вычитания, чтобы проверить свои ответы.
Вычитание дробей из целых чисел
Подобно вычитанию двух дробей, мы также можем вычесть дробь из целого числа и наоборот. Каждое целое число можно записать в дробной форме, написав 1 в качестве знаменателя, например, мы можем записать 7 как 7/1. Итак, для вычитания дроби и целого числа мы сначала заставляем их писать в дробной форме, затем мы можем легко найти разницу, применяя те же правила, что и вычитание двух непохожих дробей. Чтобы вычесть дробь из целого числа, рассмотрим следующий пример: 2 — 1/4.
- Преобразуем целое число в дробную форму: 2 = 2/1.
- Теперь вычтите их как разные дроби.
Итак, чтобы вычесть 2/1 — 1/4, НОК 1 и 4 равно 4. Умножьте числитель и знаменатель 2/1 на 4, чтобы получить 4 в знаменателе.
2/1 — 1/4 = (2 × 4)/(1 × 4) — 1/4
= 8/4 — 1/4
= 7/4
= \(1\frac { 3}{4}\)
Следовательно, 2 — 1/4 = 7/4. Вот как мы вычитаем дроби с целыми числами.
Вот как мы вычитаем дроби с целыми числами.
Советы и рекомендации:
Шагов вычитания дробей с разными знаменателями:
а) Преобразуйте данные дроби в подобные дроби, взяв НОК знаменателей.
б) Найдите эквивалентные дроби данных дробей, знаменатель которых равен НОК.
в) Вычесть числители и оставить тот же знаменатель.- Для разных дробей никогда не вычитайте числители и знаменатели напрямую.
(3/5 — 2/3) ≠ (1/2) - При вычитании разных дробей не нужно находить НОК знаменателей. Подойдет любое общее кратное. Таким образом, простое умножение двух знаменателей дает нам общее кратное. Это может привести к большим выглядящим числам, но его можно уменьшить до самой низкой формы.
► Похожие темы
Ознакомьтесь с этими интересными статьями, посвященными вычитанию дробей в математике.
- Умножение дробей
- Деление дробей
- Добавление дробей
Часто задаваемые вопросы о вычитании дробей
Что такое сложение и вычитание дробей?
Сложение и вычитание дробей — это две арифметические операции, выполняемые для сложения или вычитания дробей. Правила сложения и вычитания дробей одинаковы. Подобные дроби можно складывать/вычитать, добавляя/вычитая их числители и сохраняя общий знаменатель, в то время как разные дроби можно складывать/вычитать, сначала преобразовывая их в подобные дроби.
Правила сложения и вычитания дробей одинаковы. Подобные дроби можно складывать/вычитать, добавляя/вычитая их числители и сохраняя общий знаменатель, в то время как разные дроби можно складывать/вычитать, сначала преобразовывая их в подобные дроби.
Как вычитать дроби?
Мы можем вычитать одинаковые и разные дроби, используя следующие шаги:
- Для одинаковых дробей вычесть числители и сохранить тот же знаменатель.
- Для вычитания разных дробей возьмите НОК знаменателей, преобразуйте дроби в одинаковые дроби и вычтите их.
- При необходимости уменьшите до наименьшего значения.
Что такое правило вычитания дробей?
Основное правило вычитания дробей состоит в том, чтобы сначала убедиться, что они имеют общий знаменатель. Если у них разные знаменатели, то мы сначала преобразуем их в одинаковые дроби.
Как вычитать дроби из целых чисел?
Мы можем использовать приведенные ниже шаги, чтобы вычесть дроби из целых чисел:
- Мы запишем целое число как дробь, написав 1 в знаменателе.

- Сделав это, мы получим две разные дроби.
- Теперь вычтем обе разные дроби и получим ответ.
- При необходимости полученное значение можно уменьшить до наименьшего значения.
Рассмотрим пример:
2 — 1/5 = 2/1 — 1/5
(2/1 × 5/5) — (1/5) = 10/5 — 1/5 = 9/5
= \(1\frac{4}{5}\)
Как вычитать дроби с разными знаменателями?
Выполните следующие действия, чтобы вычесть дроби с разными знаменателями:
- Найдите НОК знаменателей.
- Умножьте числитель и знаменатель каждой дроби на целое число, чтобы получить LCM в знаменателе.
- Вычтите их как дроби.
- При необходимости сократите окончательный ответ.
Как решить вычитание дробей?
Мы можем упростить вычитание дробей следующими способами:
- В случае одинаковых дробей дроби можно вычитать, вычитая их числители, и вывод можно легко упростить.
- У разнородных дробей сначала обобщаются знаменатели и только потом вычитаются дроби.
 После вычитания вывод можно легко упростить.
После вычитания вывод можно легко упростить.
Давайте посмотрим на пример.
2/4 — 2/5 = (2/4 × 5/5) — (2/5 × 4/4)
= 10/20 — 8/20
= 2/20
= 1/10
Как вычитать неправильные дроби?
Неправильные дроби вычитаются так же, как и правильные дроби:
- Для одинаковых дробей вычесть числители и оставить тот же знаменатель.
- Для вычитания разных дробей возьмите НОК знаменателей, преобразуйте дроби в эквивалентные дроби и вычтите их как одинаковые дроби.
Если после вычитания полученный ответ представляет собой неправильную дробь, мы преобразуем дробь в смешанное число, чтобы записать ее в простейшей форме.
Вычитание дробей — GCSE Math
Введение
Что такое вычитание дробей?
Что такое вычитание дробей?
Как вычитать дроби
Лист вычитания дробей
Распространенные заблуждения
Похожие уроки
Вопросы по практике вычитания дробей
Вычитание дробей Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое вычитание дробей?
Что такое вычитание дробей?
Как вычитать дроби
Лист вычитания дробей
Распространенные заблуждения
Похожие уроки
Вопросы по практике вычитания дробей
Вычитание дробей Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о вычитании дробей в том числе о том, как вычитать дроби с одинаковым знаменателем и с разными знаменателями (разными знаменателями), и как вычитать смешанные числа.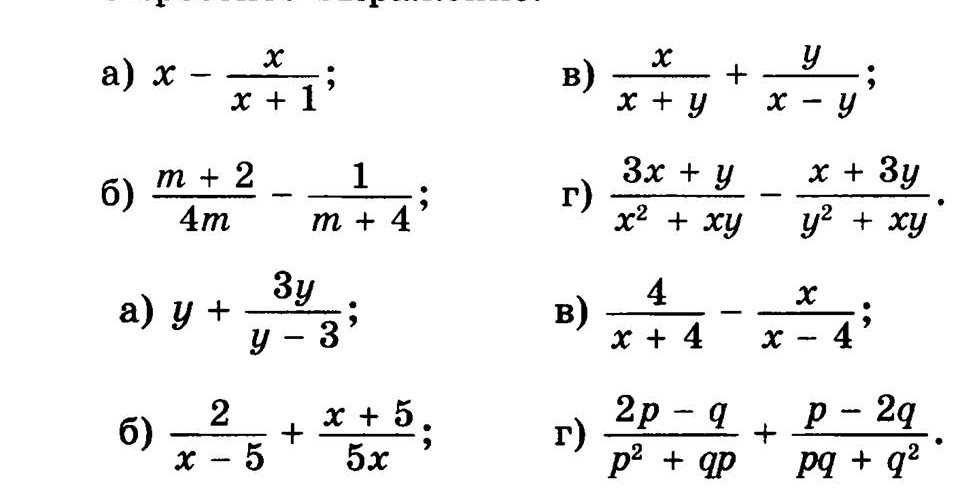
Существуют также рабочие листы для вычитания дробей, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое вычитание дробей?
Вычитание дробей — это когда мы отнимаем одну дробь от другой или находим разницу между дробями.
Чтобы вычитать дроби, они должны иметь одинаковый знаменатель (одинаковые нижние числа).
Затем мы можем вычесть дроби, вычитая числители (верхние числа) и сохраняя знаменатель прежним.
Метод вычитания дробей можно изменить для сложения дробей.
Что такое вычитание дробей?
Как вычитать дроби
Чтобы вычитать дроби:
- Посмотрите на знаменатели (нижние числа), чтобы увидеть, есть ли у них общий знаменатель.
- Вычесть числители (верхние числа).
- Запишите свой ответ в виде дроби, убедившись, что это самая простая форма.

Рабочий лист по вычитанию дробей
Получите бесплатный рабочий лист по вычитанию дробей, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксРабочий лист по вычитанию дробей
Получите бесплатный рабочий лист по вычитанию дробей, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Примеры вычитания дробей
Пример 1: вычитание дробей с общим знаменателем
Разработать
\[\frac{3}{5}-\frac{1}{5}\]
- Посмотрите на знаменатели (нижние числа), чтобы увидеть, есть ли у них общий знаменатель.
5 — знаменатель обеих дробей, поэтому 5 — общий знаменатель.
2 Вычесть числители (верхние числа).
\[\frac{3}{5}-\frac{1}{5}=\frac{3-1}{5}=\frac{2}{5}\]
3 Напишите свой ответьте в виде дроби, убедившись, что это самая простая форма.
Окончательный ответ:
\[\frac{2}{5}\]
2 и 5 не имеют общего делителя, поэтому дробь не может быть упрощена. Эта дробь имеет простейшую форму.
Пример 2: вычитание дробей с общим знаменателем
Расчет
\[\frac{5}{8}-\frac{3}{8}\]
Посмотрите на знаменатели (нижние числа), чтобы посмотреть, есть ли у них общий знаменатель.
8 — знаменатель обеих дробей, поэтому 8 — общий знаменатель.
Вычесть числители (верхние числа).
\[\frac{5}{8}-\frac{3}{8}=\frac{5-3}{8}=\frac{2}{8}\]
Напишите свой ответ как дробь, следя за тем, чтобы она была в простейшей форме.
Ответ:
\[\frac{2}{8}\]
Эта дробь не является простейшей формой, так как ее можно сократить. И 2, и 8 кратны 2. Таким образом, 2 является общим делителем и может быть сокращен:
\[\frac{2}{8}=\frac{2\times1}{2\times4}=\frac{1 {4}\]
Окончательный ответ:
\[\frac{1}{4}\]
Пример 3: вычитание дробей с разными знаменателями
Вычисление
\[\frac{3}{4}-\frac {2}{5}\]
Посмотрите на знаменатели (нижние числа), чтобы увидеть, есть ли у них общий знаменатель.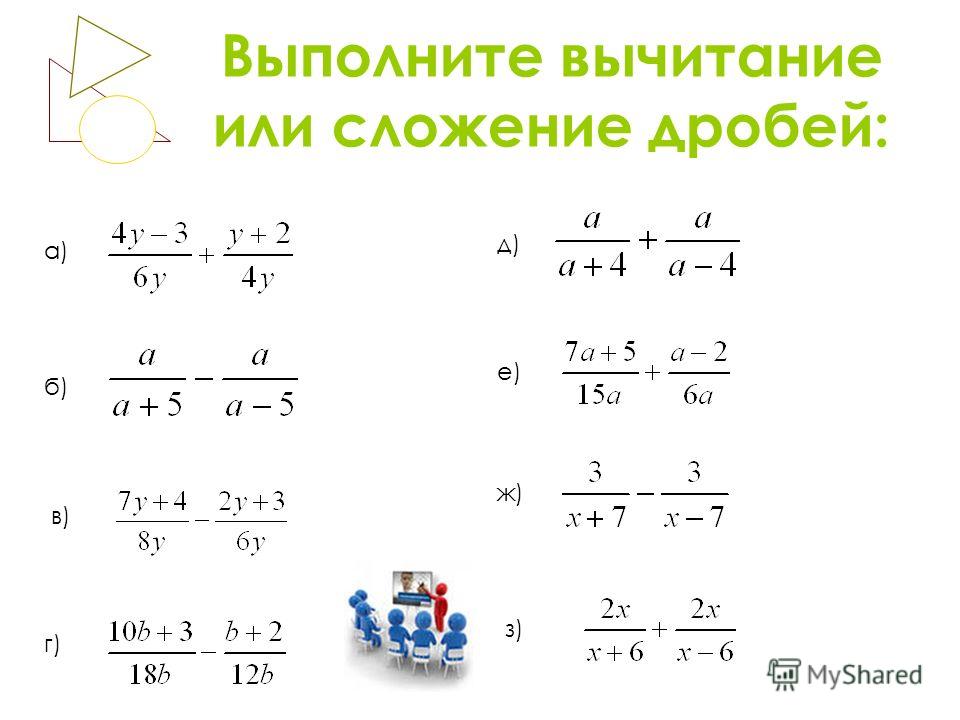
4 — знаменатель первой дроби, а 5 — знаменатель второй дроби. Эти дроби не имеют общего знаменателя.
Чтобы можно было вычитать дроби, у них должен быть общий знаменатель.
4 и 5 имеют наименьшее общее кратное 20 , поэтому мы изменим обе дроби так, чтобы они имели общий знаменатель 20:
\[\frac{3}{4}\times\frac{5} {5}=\frac{3\times5}{4\times5}=\frac{15}{20}\]
\[\frac{2}{5}\times\frac{4}{4}= \frac{2\times4}{5\times4}=\frac{8}{20}\]
Мы преобразовали дроби так, чтобы они имели общий знаменатель и теперь их можно вычитать:
\[\frac{ 3}{4}-\frac{2}{5}=\frac{15}{20}-\frac{8}{20}\]
Вычесть числители (верхние числа).
\[\frac{15}{20}-\frac{8}{20}=\frac{15-8}{20}=\frac{7}{20}\]
Напишите ответ как дробь, следя за тем, чтобы она была в простейшей форме.
Окончательный ответ:
\[\frac{7}{20}\]
7 и 20 не имеют общего делителя, поэтому дробь не может быть упрощена. Эта дробь имеет простейшую форму.
Эта дробь имеет простейшую форму.
В качестве альтернативы этот вопрос можно было бы решить, используя десятичные дроби:
\[\frac{3}{4}-\frac{2}{5}=0,75-0,4=0,35=\frac{35}{100}=\frac{7}{20}\]
Пример 4: вычитание дробей с разными знаменателями
Вычисление
\[\frac{5}{6}-\frac{1}{2}\]
Посмотрите на знаменатели (нижние числа), чтобы увидеть, имеют ли они общий знаменатель.
6 — знаменатель первой дроби, а 2 — знаменатель второй дроби. Эти дроби не имеют общего знаменателя.
Чтобы можно было вычитать дроби, у них должен быть общий знаменатель.
6 и 2 имеют наименьшее общее кратное 6 , поэтому мы убедимся, что обе дроби имеют общий знаменатель 6, изменив вторую дробь:
\[\frac{1}{2}\times\ frac{3}{3}=\frac{1\times3}{2\times3}=\frac{3}{6}\]
Таким образом, мы преобразовали дроби, чтобы они имели общий знаменатель и теперь могут быть вычтено:
\[\frac{5}{6}-\frac{1}{2}=\frac{5}{6}-\frac{3}{6}\]
Вычесть числители (верхние числа).
\[\frac{5}{6}-\frac{3}{6}=\frac{5-3}{6}=\frac{2}{6}\]
Напишите ответ как дробь, следя за тем, чтобы она была в простейшей форме.
Ответ:
\[\frac{2}{6}\]
Эта дробь не имеет простейшей формы, так как ее можно упростить, поскольку и 2, и 6 кратны 2.
Итак, 2 равно общий множитель и может быть сокращен:
\[\frac{2}{6}=\frac{2\times1}{2\times3}=\frac{1}{3}\]
Окончательный ответ:
\[\frac{1}{3}\]
В качестве альтернативы, вы могли бы выбрать 12 в качестве общего знаменателя и сократить на общий множитель 4 для упрощения:
\[\ frac{5}{6}-\frac{1}{2}=\frac{10}{12}-\frac{6}{12}=\frac{10-6}{12}=\frac{4 }{12}=\frac{4\times1}{4\times3}=\frac{1}{3}\]
Пример 5: вычитание смешанных чисел
Вычисление
\[2\frac{1} {2}-1\frac{1}{3}\]
Посмотрите на знаменатели (нижние числа), чтобы увидеть, есть ли у них общий знаменатель.
Поскольку это смешанные числа, рекомендуется записывать их в виде неправильных дробей (где числитель больше знаменателя):
\[2\frac{1}{2}=\frac{4}{ 2}+\frac{1}{2}=\frac{4+1}{2}=\frac{5}{2}\]
\[1\frac{1}{3}=\frac{ 3}{3}+\frac{1}{3}=\frac{3+1}{3}=\frac{4}{3}\]
Итак, вопрос:
\[2\frac {1}{2}-1\frac{1}{3}=\frac{5}{2}-\frac{4}{3}\]
2 – знаменатель первой дроби, 3 – знаменатель второй дроби. Эти дроби не имеют общего знаменателя.
Эти дроби не имеют общего знаменателя.
Чтобы можно было вычитать дроби, у них должен быть общий знаменатель.
2 и 3 имеют наименьшее общее кратное 6 , поэтому мы изменим обе дроби так, чтобы они имели общий знаменатель 6:
\[\frac{5}{2}=\frac{5}{ 2}\times\frac{3}{3}=\frac{5\times3}{2\times3}=\frac{15}{6}\]
\[\frac{4}{3}=\ frac{4}{3}\times\frac{2}{2}=\frac{4\times2}{3\times2}=\frac{8}{6}\]
Мы преобразовали дроби так, что они имеют общий знаменатель и теперь их можно вычесть:
\[\frac{5}{2}-\frac{4}{3}=\frac{15}{6}-\frac{8}{6}\]
Вычесть числители (верхние числа ).
\[\frac{15}{6}-\frac{8}{6}=\frac{15-8}{6}=\frac{7}{6}\]
Напишите свой ответ как дробь, следя за тем, чтобы она была в простейшей форме.
Ответ:
\[\frac{7}{6}\]
7 и 6 не имеют общего делителя для сокращения, но эта дробь является неправильной дробью .
Обычно предполагается, что неправильные дроби записываются в виде смешанных чисел:
\[\frac{7}{6}=\frac{6+1}{6}=\frac{6}{6}+\frac{1}{6}=1+\frac{1}{ 6}=1\frac{1}{6}\]
Окончательный ответ:
\[1\frac{1}{6}\]
В качестве альтернативы вы можете вычесть целые числа, а затем вычесть дроби. .
\begin{align} 2\frac{1}{2}-1\frac{1}{3}=&(2+\frac{1}{2})-(1+\frac{1}{3})\\ =&(2-1)+(\frac{1}{2}-\frac{1}{3})\\ =&(2-1)+(\frac{3}{6}-\frac{2}{6})\\ =&1+\фракция{1}{6}\\ =&1\фракция{1}{6} \end{align}
Пример 6: вычитание смешанных чисел
Вычислите
\[3\frac{1}{2}-1\frac{3}{5}\]
Посмотрите на знаменатели (нижние числа), чтобы увидеть, есть ли у них общий знаменатель.
Поскольку это смешанные числа, рекомендуется записывать их в виде неправильных дробей (где числитель больше знаменателя):
\[3\frac{1}{2}=\frac{6}{ 2}+\frac{1}{2}=\frac{6+1}{2}=\frac{7}{2}\]
\[1\frac{3}{5}=\frac{ 5}{5}+\frac{3}{5}=\frac{5+3}{5}=\frac{8}{5}\]
Итак, вопрос:
\[3\frac{1}{2}-1\frac{3}{5}=\frac{7}{2}-\frac{8}{5}\]
2 знаменатель первая дробь, а 5 — знаменатель второй дроби. Эти дроби не имеют общего знаменателя.
Эти дроби не имеют общего знаменателя.
Чтобы можно было вычитать дроби, у них должен быть общий знаменатель.
2 и 5 имеют наименьшее общее кратное 10 , поэтому мы изменим обе дроби так, чтобы они имели общий знаменатель 10:
\[\frac{7}{2}=\frac{7}{ 2}\times\frac{5}{5}=\frac{7\times5}{2\times5}=\frac{35}{10}\]
\[\frac{8}{5}=\frac{8}{5}\times\frac{2}{2}=\frac{8\times2}{5\times2}=\frac{16} {10}\]
Мы преобразовали дроби, чтобы они имели общий знаменатель и теперь их можно вычитать:
\[\frac{7}{2}-\frac{8}{5}=\frac{ 35}{10}-\frac{16}{10}\]
Вычесть числители (верхние числа).
\[\frac{35}{10}-\frac{16}{10}=\frac{35-16}{10}=\frac{19}{10}\]
Напишите ответ как дробь, следя за тем, чтобы она была в простейшей форме.
Ответ:
\[\frac{19}{10}\]
19 и 10 не имеют общего множителя для сокращения, но это неправильная дробь.
Обычно предполагается, что неправильные дроби записываются как смешанные числа.
\[\frac{19}{10}=\frac{10+9}{10}=\frac{10}{10}+\frac{9}{10}=1+\frac{9}{ 10}=1\frac{9}{10}\]
Окончательный ответ:
\[1\frac{9}{10}\]
Кроме того, вы можете вычесть целые числа, а затем вычесть дроби:
\begin{выравнивание} 3\frac{1}{2}-1\frac{3}{5}=&(3+\frac{1}{2})-(1+\frac{3}{5})\\ =&(3-1)+(\frac{1}{2}-\frac{3}{5})\\ =&(3-1)+(\frac{5}{10}-\frac{6}{10})\\ =&(2)+(-\frac{1}{10})\\ =&1\фракция{9}{10} \end{align}
Распространенные заблуждения
- Вычитание числителей
При вычитании дробей с общими знаменателями вычитаются только числители.
напр.
\[\frac{5}{7}-\frac{2}{7}=\frac{5-2}{7}=\frac{3}{7}\]
- Перепутав сложение и вычитание
Иногда мы можем так увлечься поиском общего знаменателя у дробей, что забываем, что это вычитание.
Например,
\[\frac{3}{5}-\frac{1}{4}=\frac{12}{20}-\frac{5}{20}=\frac{12+5} {20}=\frac{17}{20}\]
Это было бы неправильно , так как вопрос превратился в дополнительный вопрос.
- Не забудьте использовать правильный порядок операций
Если в одном и том же математическом предложении есть сложение и вычитание, выполняйте операции слева направо по мере их чтения.
\[\frac{6}{8}-\frac{1}{8}+\frac{2}{8}=\frac{6-1+2}{8}=\frac{7}{ 8}\]
Правильный порядок: 6 – 1, а затем + 2.
Вычитание дробей является частью нашей серии уроков, направленных на повторение дробей. Возможно, вам будет полезно начать с урока по основным дробям, чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства ниже для получения дополнительной информации по отдельным темам. Другие уроки в этой серии включают в себя:
- Фракции
- Эквивалентные фракции
- Добавление фракций
- Умножение фракций
- Разделительные фракции
- Неправильные фракции и смешанные номера
- . {5}
\frac{1}{5}
\frac{1}{0}
\frac{2}{5}
\frac{2}{5}-\frac{1}{ 5}=\frac{2-1}{5}=\frac{1}{5}
\frac{2}{5}
\frac{2}{0}
\frac{2}{8}
\frac{1}{4}
\frac{3}{8} -\frac{1}{8}=\frac{3-1}{8}=\frac{2}{8}=\frac{1}{4}
\frac{3}{10}
\frac{3}{3}
\frac{9}{10}
\frac{1}{5}
\frac{4}{5}-\frac{1}{2}=\frac {8}{10}-\frac{5}{10}=\frac{8-5}{10}=\frac{3}{10}
\frac{1}{8}
\frac{ 4}{4}
\frac{3}{8}
\frac{3}{12}
\frac{5}{8}-\frac{1}{4}=\frac{5} {8}-\frac{2}{8}=\frac{5-2}{8}=\frac{3}{8}
4\frac{1}{12}
2\frac{5}{12}
1\frac{5}{12}
1\frac{7}{12}
2\frac{ 3}{4}-1\фракция{1}{3} =\frac{11}{4}-\frac{4}{3} =\frac{33}{12}-\frac{16}{12} =\фракция{33-16}{12} =\фракция{17}{12} =1\frac{5}{12}
1\frac{1}{2}
3\frac{13}{15}
1\frac{8}{15}
\frac{8} {15}
2\frac{1}{5}-1\frac{2}{3} =\frac{11}{5}-\frac{5}{3} =\frac{33}{15}-\frac{25}{15} =\фракция{33-25}{15} =\фракция{8}{15}
Вычитание дробей Вопросы GCSE
1.
 Тренировка
Тренировка\frac{4}{5}-\frac{1}{3}
(2 балла)
Показать ответ
\frac{4}{5}-\frac{1}{3}=\frac{12}{15}-\frac{5}{15}
За использование правильного общего знаменателя хотя бы с одной правильной дробью
(1)
=\фракция{7}{12}
За правильный окончательный ответ
(1)
2. Разработать
2\разрыв{5}{8}-1\разрыв{1}{3}
(2 балла)
Показать ответ
2\frac{5}{8}-1\frac{1}{3}=\frac{21}{8}-\frac{4}{3 }=\frac{63}{24}-\frac{32}{24}
За использование правильного общего знаменателя хотя бы с одной правильной дробью
(1)
\frac{63}{24}-\frac{32}{24}=\frac{31}{24}=1\frac{7}{24}
За правильный окончательный ответ
(1)
3.
 Какая из этих двух дробей ближе к 1?
Какая из этих двух дробей ближе к 1?
Вы должны показать всю свою работу.\frac{7}{4} \frac{4}{7}
(3 балла)
Показать ответ
\frac{7}{4}=\frac{49}{28}
и
\frac{4}{7}=\frac{ 16}{28}Для записи дробей с общим знаменателем
(1)
\frac{49{28}-\frac{28}{28}=\frac{21}{28}
и
\frac{28}{28}-\frac{16}{28}=\frac{12}{28 }Для нахождения разности дробей до 1
(1)
\frac{12}{28} это наименьшая разность, 904{12} {28} является наименьшей разностью, 904{12}{28} } ближе к 1.
Для правильного ответа с работами
(1)
Учебный контрольный список
Теперь вы научились:
- Вычитание дробей с одинаковым знаменателем
- Вычитание дробей с разными знаменателями
- Вычитание смешанных чисел
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning.
 Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.Узнайте больше о нашей программе повторения GCSE по математике.
Вычитание дробей – методы и примеры
Как и при сложении дробей, при вычитании дробей с общими знаменателями просто вычитаются числители и остается знаменатель.
Аналогичным образом, в случае дробей с разными знаменателями, сначала следует получить наименьшее общее кратное (НОК), а затем преобразовать дроби в эквивалентные дроби с НОК в качестве знаменателя. Но эти условия применимы только в том случае, если дроби не являются смешанными числами.
Пример 1
а. Решите: 2/5 – 1/4
Решение
Во-первых, сделайте знаменатели одинаковыми.Умножить числитель и знаменатель 2/5 и 1/4 на 4 и 5 соответственно. б. Вычтите 3/8 из 7/8
Решение
7/8 – 3/8
= (7 – 3)/8= 1/2
c.
 Вычтите 5/6 из 11/6
Вычтите 5/6 из 11/6
Решение
11/6 – 5/6
= (11 – 5)/6
= 6/6
= 1/1
= 1d. Вычтите 7/9 из 11/9
Решение
11/9 – 7/9
= (11 – 7)/9
= 4/9e. Вычтите 4/6 из 16/6
Решение
16/6 – 4/6
= (16 – 4)/6= 2/1
= 2
f. 1 – 2/3
Решение
- Начнем с предположения, что целое число равно числу больше единицы, т. е. 1 равно 1/1
Следовательно, наше уравнение будет выглядеть так:
1/1-2/3
- Затем мы продолжаем получать L.C.M. из двух знаменателей, которые будут равны 3, так как L.C.M. числа, и единица становится этим числом.
- Затем мы делим этот L.C.M. на первый знаменатель, который равен 1, чтобы получить ответ 3, затем умножьте 1 на первый числитель, который равен 1, чтобы получить =3
- Затем мы делим L.C.M. на второй знаменатель, который равен 3, чтобы получить ответ 1, затем умножьте 1 на второй числитель, который равен 2, чтобы получить =2
- Затем мы вычитаем два результата над L.
 C.M.
C.M.
=1/1-2/3
= (3-2)/3
=1/3
Как вычитать смешанные числа?
Смешанные дроби можно вычитать так же, как и правильные дроби. Правила вычитания смешанных дробей такие же, как и при работе с правильными дробями. Существует два метода вычитания смешанных дробей.
Метод 1:
Следующие шаги выполняются при вычитании смешанных дробей:
- Сначала преобразуйте все смешанные дроби в неправильные дроби.
- Проверить, имеют ли неправильные дроби общий знаменатель, если нет, найти общий знаменатель дробей
- Попробовать составить эквивалентную дробь
- Вычесть числитель, оставив знаменатель одинаковым.
- Если после вычитания получается неправильная дробь, преобразовать ее обратно в смешанную дробь или уменьшить, если это правильная дробь
Пример 2
6 1// 3 — 3 1 / 12
= (6 × 3) + 1/3 + (3 × 12) + 1/12
.
 = 19/3 – 37/12
= 19/3 – 37/12= 19 × 4/3 × 4 – 37 × 1/12 × 1, (НЦМ 3 и 12 = 12)
= 76/12 – 37/12
= 76 – 37/12
= 39/12
= 13/4
= 3 ¼
Метод 2
В этом методе смешанные дроби разбивают на целые и части.
- Вычитание целых частей дробей.
- Проверить, совпадают ли знаменатели дроби, и если нет, найти общий знаменатель.
- При необходимости составить эквивалентную дробь
- Вычесть числители части дроби, сохранив знаменатель одинаковым.
- Сложите разности целого числа и дробной части.
Пример 3:
6 1 / 3 – 3 1 / 12
= (6 – 3) + (1/3 – 1/12)
= 3 + (1/3 – 1/12)
= 3 + (1 × 4/3 × 4 – 1 × 1/12 × 1) (НОК 12 и 3 = 12)
= 3 + 4/12 – 1/12
= 3 + (4 – 1)/12
= 3 + 3/12
= 3 + ¼
= 3 ¼
Как вычитать дроби с разными знаменателями?
Вычитание дробей с разными знаменателями очень похоже на сложение дробей.
 При вычитании дробей с разными знаменателями важно вычислить общий знаменатель для всех дробей. Затем вычтите числители, сохраняя знаменатель постоянным.
При вычитании дробей с разными знаменателями важно вычислить общий знаменатель для всех дробей. Затем вычтите числители, сохраняя знаменатель постоянным.- Найдите общий знаменатель дробей, найдя наименьшее общее кратное знаменателей.
- Перепишите дроби с новым общим знаменателем.
- Вычесть числитель, сохранив знаменатель постоянным.
Пример 4:
5/6 – 3/4
Решение :- Найдите НОК чисел 6 и 4, перечислив их множители, как показано ниже: 9015 4 20, 24, 28, 32, ….
6, 12, 18, 24, 30, 36, 42, 48,.… - В этом случае наименьшее общее кратное 4 и 6 равно 12.
- Умножьте каждую дробь на НОК как:
5/6 = 5/6 x 2/2 = 10/12 и 3/4 = 3/4 х 3/3 = 9/12.
- Теперь вычтите числители, сохраняя знаменатели постоянными.
10/12 – 9/12 = 1/12
Отсюда 5/6 – 3/4 = 1/12
- Список кратных 5 и 3.
5, 10, 15, 20, 25, 30,….

3, 6, 9, 12, 15, 18, 21,.…Из кратных НОК 3 и 5 равно 15.
- Умножить на НОК,
4/5 = 4/5 X 3/3 = 12/15 и 1/3 = 1/3 x 5/5 = 5/15
- Вычесть числители,
12/15 – 5/15 = 7/15
Таким образом,
4/5 – 1/3 = 7/15
Дроби: сложение и вычитание дробей
Урок 3: сложение и вычитание дробей
/en/fractions/comparing-and-reduction-fractions/content/
Сложение и вычитание дробей
На предыдущих уроках вы узнали, что дробь является частью целого. Дроби показывают, сколько у вас есть чего-то, например, 1/2 бака бензина или 1/3 стакана воды.
В реальной жизни вам может понадобиться складывать или вычитать дроби. Например, вы когда-нибудь проходили 1/2 мили на работу, а затем шли еще 1/2 мили обратно? Или слить 1/4 литра бензина из бензобака, в котором было 3/4 литра? Вы, наверное, не думали об этом в то время, но это примеры сложение и вычитание дробей.

Просмотрите слайд-шоу, чтобы узнать, как решать задачи на сложение и вычитание с дробями.
Представим, что в рецепте торта сказано добавить в тесто 3/5 стакана масла.
Вам также понадобится 1/5 стакана масла, чтобы смазать сковороду. Чтобы узнать, сколько всего масла вам понадобится, вы можете сложить вместе этих дробей.
Когда вы складываете дроби, вы просто добавляете верхние числа или числителя .
Это потому, что нижних чисел или знаменателей показывают, сколько частей будет составлять целое.
Мы не хотим менять количество частей, составляющих целую чашку (5). Мы просто хотим выяснить, сколько частей нам нужно всего.
Итак, нам нужно только сложить числители наших дробей.
Мы можем сложить дроби так, чтобы числители выстроились. Это облегчит их добавление.

И это все, что нам нужно сделать, чтобы настроить пример сложения с дробями. Теперь наши фракции готовы к добавлению.
Мы сделаем то же самое, чтобы настроить пример вычитания. Допустим, у вас было 3/4 бака бензина, когда вы приступили к работе.
Если вы используете 1/4 бака, чтобы добраться до дома, сколько у вас останется? Мы можем вычесть этих дробей, чтобы узнать.
Точно так же, как при добавлении, мы будем сложите наши дроби, чтобы числители были выровнены.
Это потому, что мы хотим вычесть 1 часть из 3 частей.
Теперь, когда наш пример настроен, мы готовы к вычитанию!
Попробуйте!
Попробуйте решить эти задачи на сложение и вычитание с дробями. Не пытайтесь их решить!
Утром вы пробегаете 4/10 мили. Позже вы бежите 3/10 мили.
У вас было 7/8 пачки сливочного масла, и вы использовали 2/8 пачки во время приготовления обеда.

Ваш бензобак заполнен на 2/5, и вы заправляете еще 2/5 бака.
Решение задач на сложение с дробями
Теперь, когда мы знаем, как писать задачи на сложение с дробями, давайте попрактикуемся в решении некоторых из них. Если вы можете складывать целые числа, вы готовы складывать дроби.
Щелкните слайд-шоу, чтобы узнать, как складывать дроби.
Давайте продолжим наш предыдущий пример и добавим следующие части: 3/5 стакана масла и 1/5 стакана масла.
Помните, что когда мы складываем дроби, мы не складываем знаменатели.
Это потому, что мы находим, сколько всего частей нам нужно. Числители показывают, какие части нам нужны, поэтому мы добавим 3 и 1.
3 плюс 1 равно 4. Убедитесь, что 4 выровнены с числами, которые вы только что добавили.
Знаменатели останутся прежними, поэтому мы напишем 5 внизу нашей новой дроби.
3/5 плюс 1/5 равно 4/5.
 Итак, вам понадобится 4/5 стакана масла всего , чтобы сделать свой торт.
Итак, вам понадобится 4/5 стакана масла всего , чтобы сделать свой торт.Возьмем другой пример: 7/10 плюс 2/10.
Как и прежде, мы будем добавлять только числители. В этом примере числители 7 и 2.
7 плюс 2 равно 9, поэтому мы напишем это справа от числителей.
Как и в нашем предыдущем примере, знаменатель остается прежним.
Итак, 7/10 плюс 2/10 равно 9/10.
Попробуйте!
Попробуйте решить некоторые из приведенных ниже задач на сложение.
Решение задач на вычитание с дробями
Вычитание дробей очень похоже на обычное вычитание. Если вы можете вычитать целые числа, вы можете вычитать и дроби!
Просмотрите слайд-шоу, чтобы узнать, как вычитать дроби.
Давайте воспользуемся нашим предыдущим примером и вычтем 1/4 бака бензина из 3/4 бака.
Как и в дополнение, мы не собираемся менять знаменатели.

Мы не хотим менять количество деталей, составляющих целый бак бензина. Мы просто хотим знать, сколько деталей у нас останется.
Начнем с вычитания числителей. 3 минус 1 равно 2, поэтому мы напишем 2 справа от числителя.
Как и при сложении, знаменатель нашего ответа будет таким же, как и другие знаменатели.
Итак, 3/4 минус 1/4 равно 2/4. Когда вы вернетесь домой, у вас останется 2/4 бака бензина.
Попробуем решить другую задачу: 5/6 минус 3/6.
Начнем с вычитания числителей.
5 минус 3 равно 2. Итак, мы поставим 2 справа от числителя.
Как обычно, знаменатель остается прежним.
Итак, 5/6 минус 3/6 равно 2/6.
Попробуйте!
Попробуйте решить некоторые из приведенных ниже задач на вычитание.
После сложения или вычитания дробей у вас иногда может получиться дробь, которую можно преобразовать в более простую дробь.
 Как вы узнали из раздела «Сравнение и сокращение дробей», всегда лучше сократить дробь до ее простейшей формы , когда это возможно. Например, 1/4 плюс 1/4 равно 2/4. Поскольку 2 и 4 можно разделить на 2, мы можем уменьшить 2/4 до 1/2.
Как вы узнали из раздела «Сравнение и сокращение дробей», всегда лучше сократить дробь до ее простейшей формы , когда это возможно. Например, 1/4 плюс 1/4 равно 2/4. Поскольку 2 и 4 можно разделить на 2, мы можем уменьшить 2/4 до 1/2.Сложение дробей с разными знаменателями
На прошлой странице мы научились складывать дроби с одинаковым знаменателем, например 1/4 и 3/4. Но что, если вам нужно сложить дроби с различными знаменателями? Например, в нашем рецепте торта можно сказать, что нужно медленно смешать 1/4 стакана молока, а затем добавить еще 1/3 стакана.
В разделе «Сравнение и сокращение дробей» мы сравнили дроби с другим нижним числом или знаменателем. Нам пришлось изменить дроби, чтобы их знаменатели были одинаковыми. Для этого мы нашли наименьший общий знаменатель или LCD .
Мы можем складывать или вычитать дроби, только если у них одинаковые знаменатели.
 Поэтому нам нужно найти наименьший общий знаменатель, прежде чем складывать или вычитать эти дроби. Когда дроби имеют одинаковый знаменатель, мы можем складывать или вычитать, как обычно.
Поэтому нам нужно найти наименьший общий знаменатель, прежде чем складывать или вычитать эти дроби. Когда дроби имеют одинаковый знаменатель, мы можем складывать или вычитать, как обычно.Просмотрите слайд-шоу, чтобы узнать, как складывать дроби с разными знаменателями.
Добавим 1/4 и 1/3.
Прежде чем мы сможем сложить эти дроби, нам нужно изменить их, чтобы они имели одинаковые знаменатель .
Для этого нам нужно найти LCD , или наименьший общий знаменатель чисел 4 и 3. и 4, так что 12 это наш LCD .
Поскольку 12 — это LCD, это будет новый знаменатель наших дробей.
Теперь изменим числители дробей так же, как мы изменили знаменатели.
Во-первых, давайте посмотрим на дробь слева: 1/4.
Чтобы преобразовать 4 в 12, мы умножаем его на 3.
Поскольку знаменатель умножался на 3, мы также умножаем числитель на 3.

2 1 умножить на 90 5
1/4 равно 3/12.
Теперь посмотрим на дробь справа: 1/3. Мы также изменили его знаменатель на 12.
Наш старый знаменатель был 3. Мы умножили его на 4, чтобы получить 12.
Мы также умножим числитель на 4. 1 умножить на 4 равно 4.
Итак, 1/3 равно 4/12.
Теперь, когда наши дроби имеют одинаковый знаменатель, мы можем сложить их, как обычно.
3 плюс 4 равно 7. Как обычно, знаменатель остается прежним. Таким образом, 3/12 плюс 4/12 равно 7/12.
Попробуйте!
Попробуйте решить приведенные ниже задачи на сложение.
Вычитание дробей с разными знаменателями
Мы только что видели, что дроби можно складывать, только если у них один и тот же знаменатель. То же самое верно, когда мы вычитаем дроби. Прежде чем мы сможем вычитать, нам нужно изменить наши дроби, чтобы у них был один и тот же знаменатель.

Просмотрите слайд-шоу, чтобы узнать, как вычитать дроби с разными знаменателями.
Попробуем вычесть 1/3 из 3/5.
Во-первых, мы изменим знаменатели обеих дробей, чтобы они были одинаковыми, найдя наименьший общий знаменатель .
Похоже, 15 — это наименьшее число, которое можно разделить без остатка на 3 и 5, поэтому 15 — это наш ЖК-дисплей.
Теперь изменим нашу первую дробь. Чтобы изменить знаменатель на 15, мы умножим знаменатель и числитель на 3.
5 умножить на 3 равно 15. Итак, наша дробь теперь равна 9/15.
Теперь изменим вторую дробь. Чтобы изменить знаменатель на 15, мы умножим оба числа на 5, чтобы получить 5/15.
Теперь, когда наши дроби имеют одинаковый знаменатель, мы можем вычитать, как обычно.
9 минус 5 равно 4. Как всегда, знаменатель остается прежним. Итак, 9/15 минус 5/15 равно 4/15.
Попробуйте!
Попробуйте решить приведенные ниже задачи на вычитание.

Сложение и вычитание смешанных чисел
На последних нескольких страницах вы практиковались в сложении и вычитании различных дробей. Но для некоторых проблем потребуется один дополнительный шаг. Например, можете ли вы сложить приведенные ниже дроби?
В разделе «Введение в дроби» вы узнали о смешанных числах . Смешанное число имеет как дробь , так и целое число . Например, 2 1/2, или два с половиной . Другой способ написать это будет 5/2, или пять половин . Эти два числа выглядят по-разному, но на самом деле они одинаковы.
5/2 — это неправильная дробь . Это просто означает, что верхнее число на больше, чем нижнее число на . Несмотря на то, что неправильные дроби выглядят странно, их можно складывать и вычитать так же, как обычные дроби. Смешанные числа складывать непросто, поэтому сначала вам придется преобразовать их в неправильные дроби.

Сложим эти два смешанных числа: 2 3/5 и 1 3/5.
Нам нужно преобразовать эти смешанные числа в неправильные дроби. Начнем с 2 3/5.
Как вы узнали из Урока 2, мы умножим целое число 2 на нижнее число 5.
2 умножить на 5 равно 10.
Теперь добавим 10 к числителю. , 3.
10 + 3 равно 13.
Точно так же, как если вы сложите дроби, знаменатель останется прежним. Наша неправильная дробь 13/5.
Теперь нам нужно преобразовать наше второе смешанное число: 1 3/5.
Сначала умножим целое число на знаменатель. 1 x 5 = 5.
Далее мы добавим 5 к числителям. 5 + 3 = 8.
Как и в прошлый раз, знаменатель остался прежним. Итак, мы изменили 1 3/5 на 8/5.
Теперь, когда мы изменили наши смешанные числа на неправильные дроби, мы можем складывать, как обычно.

13 плюс 8 равно 21. Как обычно, знаменатель останется прежним. Итак, 13/5 + 8/5 = 21/5.
Поскольку мы начали со смешанного числа, давайте преобразуем эту неправильную дробь обратно в смешанное число.
Как вы узнали из предыдущего урока, разделите верхнее число на нижнее число. 21 разделить на 5 равно 4 с остатком 1,
Ответ 4 станет нашим целым числом.
И остаток , 1 станет числителем дроби.
Итак, 2 3/5 + 1 3/5 = 4 1/5.
Предыдущий: Сравнение и сокращение дробей
Next:Умножение и деление дробей
/en/fractions/multipliing-and-dividing-fractions/content/
Сложение и вычитание дробей с помощью программы «Пошаговое решение математических задач»
С самого начала изучения математики вы много раз сталкивались с дробями.
 Они встречаются в формулах и во многих повседневных практических задачах. Однако арифметические дроби состоят строго из чисел. Теперь мы изучим действия над дробями, компоненты которых являются алгебраическими выражениями.
Они встречаются в формулах и во многих повседневных практических задачах. Однако арифметические дроби состоят строго из чисел. Теперь мы изучим действия над дробями, компоненты которых являются алгебраическими выражениями.РЕШЕНИЕ УРАВНЕНИЙ, ВКЛЮЧАЮЩИХ ЗНАКОВЫЕ ЧИСЛА
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Разложите числитель и знаменатель дроби на множители.
- Упростите алгебраические дроби.
Алгебраическая дробь — это указанное отношение двух алгебраических выражений.
При изучении арифметики вам сказали, что дробные ответы всегда следует оставлять в сокращенной или упрощенной форме. Для дроби, до которой вы «уменьшили», разделив числитель и знаменатель на 4. Дробь нельзя уменьшить, потому что никакое число (кроме 1) не будет делить и числитель, и знаменатель. Упрощая дроби таким образом, вы использовали следующее определение.
Дробь в представляет собой упрощенную (или сокращенную) форму , если числитель и знаменатель не содержат общего множителя (кроме 1).

Дробь, представленная в упрощенной форме, поскольку числитель 2 и знаменатель 3 не имеют общего делителя, кроме единицы. Для получения упрощенной формы дроби применяется следующее правило.
Чтобы упростить дробь , полностью разложите числитель и знаменатель, а затем разделите числитель и знаменатель на все общие множители.
Дробь , однако, не является упрощенной формой, так как числитель и знаменатель имеют общий делитель 2. Затем разделите на общие делители, получив
8 9 делимого множителя. само по себе равно 1. Теперь разделите на общий множитель (x + 2) как в числителе, так и в знаменателе, чтобы получить
Мы можем делить только общие множители, но не общие термины. 
В таком выражении, как у некоторых учащихся, возникает соблазн разделить тройки. Обратите внимание, что это неправильное , поскольку они являются терминами , а не факторами. Обратите внимание, что даже если мы смогли разложить на множители числитель и знаменатель, мы все равно не можем разделить, поскольку у них нет общих множителей. Данная дробь уже в упрощенном виде.
Тот факт, что для данной дроби может потребоваться любой из изученных вами методов факторинга, еще раз подчеркивает важность владения факторингом.
Решение Здесь вы можете использовать «пробы и ошибки» для числителя и «группировку» для знаменателя.
Здесь (x + 2) — общий множитель, поэтому можно разделить и числитель, и знаменатель. Обратите внимание, что числитель 2x + 5 можно записать как (2x 4- 5) * 1.  Таким образом, при делении множителя (2x + 5) остается множитель 1.
Таким образом, при делении множителя (2x + 5) остается множитель 1.Решение Этот тип проблемы требует особого внимания, так как это частая причина ошибки. На первый взгляд множители могут быть ошибочно приняты за общие, или дробь может быть ошибочно принята за уже упрощенную. Обратите внимание, что факторы нельзя разделить, поскольку знаки не позволяют им быть идентичными. Если, однако, минус 1 факторизуется от одного из множителей, то есть подобные множители, и деление может быть выполнено.
Любые множители в виде a — b и b — a являются отрицательными друг для друга, таким образом, 2x — 3 и 3 — 2x являются отрицательными друг для друга. Все это эквивалентные формы одного и того же выражения. Предпочтительной формой будет та, в которой используется наименьшее количество письменных знаков. 
Всегда проверяйте свой ответ, чтобы убедиться, что он эквивалентен форме, указанной в разделе ответов.УМНОЖЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Числители и знаменатели всех умножаемых дробей.
- Определить и разделить на все общие множители.
- Запишите произведение в простейшей форме.
Алгебраическая дробь — это указанное отношение двух алгебраических выражений.
— это определение произведения двух дробей. На словах это означает «умножить числитель на числитель и знаменатель на знаменатель». Вы использовали это правило много раз в арифметике, когда умножали дроби.
Однако помните, что все дробные ответы должны быть в упрощенной форме. Мы могли бы следовать приведенному выше определению, а затем упростить ответ, как в предыдущем разделе. Но с алгебраическими дробями это может привести к очень сложным выражениям. Следующее правило позволяет нам упрощать по мере умножения, поэтому ответ будет в упрощенной форме.

При умножении алгебраических дробей полностью разложите все числители и знаменатели, затем перед умножением разделите на все множители, общие для числителя и знаменателя.
Произведение остальных множителей числителя будет числителем ответа, а произведение остальных множителей знаменателя будет знаменателем ответа.
Опять же, помните, что общие факторы должны быть совершенно одинаковыми. Мы будем использовать точку * для обозначения умножения, поскольку использование X можно спутать с переменной x. Обратите внимание, что (x + 2) и (2 + x) одинаковы, но (x — 4) и (4 — x) являются отрицательными значениями друг друга.
Опять же, есть много возможных форм для окончательных ответов. Приведенная здесь форма предпочтительнее, поскольку она содержит наименьшее количество знаков.
Приведенная здесь форма предпочтительнее, поскольку она содержит наименьшее количество знаков.В этой проблеме много факторов. Будь осторожен! ДЕЛЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Замените задачу на деление связанной с ней задачей на умножение.
- Разделить алгебраические дроби.
Деление дробей определяется с помощью умножения.
Чтобы разделить, умножить на величину, обратную делителю.
Чтобы разделить одно алгебраическое выражение на другое , инвертируйте делитель и измените операцию на умножение.
Делитель следует за знаком. Не инвертируйте неправильную дробь. Если знаменатель не указан, считается, что он равен 1. 
После того, как задача на деление заменена на задачу на умножение, она выполняется так же, как и в предыдущем разделе.
Опять же, обратите внимание, что инвертируется только дробь после знака. ПОИСК НАИМЕНЬШЕГО ОБЩЕГО ЗНАМЕНАТЕЛЯ
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Полностью разложить знаменатель дроби на множители.
- Найдите наименьший общий знаменатель двух или более дробей.
Правило сложения и вычитания дробей требует, чтобы объединяемые дроби имели одинаковый знаменатель. В качестве подготовки к выполнению этих операций мы теперь исследуем метод нахождения наименьшего общего знаменателя для любой группы дробей.
общий знаменатель лот двух или более дробей представляет собой выражение, содержащее все множители знаменателя каждой дроби. А наименьший общий знаменатель содержит минимальное количество делителей, чтобы быть общим знаменателем.

Наименьший общий знаменатель набора дробей иногда называют наименьшим общим кратным знаменателей. Ментальная арифметика позволит вам найти наименьший общий знаменатель для небольших чисел. Если попросить прибавить , то легко получить наименьший общий знаменатель 12. Если спросить, как мы получили 12, мы просто знаем, что 12 — это наименьшее число, которое делится и на 4, и на 6. Однако необходим более сложный метод. если числа больше или если дроби являются алгебраическими дробями.
Пример 1 Найдите наименьший общий знаменатель для
Решение Если бы у нас не было общего метода, эта задача потребовала бы значительного количества предположений или возможностей проверки.
Мы могли бы получить общий знаменатель этих дробей, найдя произведение
12 х 14 х 15 х 18 = 45 360.
Хотя это число является общим знаменателем, оно не является наименьшим общим знаменателем.Рассмотрим определение. Из него мы знаем, что общий знаменатель этих чисел должен содержать все множители каждого из них. Другими словами, мы ищем наименьшее число, которое делится на 12, 14, 15 и 18.
Сначала полностью разложите каждое число.Искомое число должно содержать (2)(2)(3), чтобы оно делилось на 12. Оно должно содержать (2)(7), чтобы делиться на 14, и так далее. Действуйте следующим образом:
Запишите множители первого числа, 12.
(2)(2)(3)
Теперь посмотрите на множители следующего числа, 14, и убедитесь, что нам нужно (2)(7). Но так как у нас уже есть 2, нам нужен только множитель (7). Это дает
(2)(2)(3)(7).
Теперь это число делится и на 12, и на 14. Делители следующего числа, 15, равны (3) и (5). Поскольку у нас уже есть 3, нам нужен только множитель 5, что дает
(2)(2)(3)(7)(5).
Теперь это число делится на 12, 14 и 15. Делители следующего числа, 18, равны (2)(3)(3). У нас уже есть 2 и одна 3. Следовательно, нам нужно еще 3.
Делители следующего числа, 18, равны (2)(3)(3). У нас уже есть 2 и одна 3. Следовательно, нам нужно еще 3.
(2)(2)(3)(7)(5)(3) = 1,260
Это число, 1,260, является общим знаменателем 12, 14 , 15 и 18, потому что он содержит все множители каждого и, следовательно, делится на каждый. Это наименьший общий знаменатель, поскольку он содержит только те множители, которые необходимы для того, чтобы он делился на 12, 14, 15 и 18.Обратите внимание, что 1260 значительно меньше, чем число, полученное простым нахождением произведения всех знаменателей. Из предыдущего обсуждения вытекает правило получения наименьшего общего знаменателя для любого количества дробей, будь то числа или алгебраические выражения.
Чтобы найти наименьший общий знаменатель для двух или более дробей:
1. Полностью разложить каждый знаменатель на множители.
2. Запишите знаменатель первой дроби в разложенном виде как предлагаемый общий знаменатель.
3. Путем проверки определить, какие факторы второго знаменателя еще не входят в предлагаемый общий знаменатель, и включить их.
4. Повторите третий шаг для каждой фракции.После освоения эта пошаговая процедура значительно упростит вашу работу. Обратите внимание, что при нахождении наименьшего общего знаменателя мы не обращаем внимания на числитель.
Это всего лишь знаменатель первой дроби.При проверке второго знаменателя нам нужен дополнительный множитель (x — 2). Наименьший общий знаменатель равен (3x — 4)(2x + l)(x — 2).
Опять же, числители не влияют на то, каким будет наименьший общий знаменатель.
Иногда наименьший общий знаменатель обозначается аббревиатурой LCD.Обратите внимание, что x 2 является множителем в знаменателе первой дроби, но не во второй дроби. 
Здесь у нас три знаменателя. Решение
Первый знаменатель: 3(x + 2)
Второй знаменатель: 2(2)(3)
Третий знаменатель: 2(x + 3)(x + 2)
Предлагаемый общий знаменатель: 3( x + 2)
Изучив второй знаменатель, мы видим, что нам нужно включить множители (2) и (2). Теперь у нас есть 2(2)(3)(x + 2). Изучив третий знаменатель, мы видим, что нам нужен множитель (x + 3). Наименьший общий знаменатель равен 2(2)(3)(x + 2)(x + 3) или 12(x + 2)(x + 3).ЭКВИВАЛЕНТНЫЕ Дроби
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Понять фундаментальный принцип дробей.
- Заменить дробь эквивалентной дробью.
При дальнейшей подготовке к сложению и вычитанию дробей мы должны иметь возможность заменить заданную дробь дробью с новым знаменателем, не изменяя значение исходной дроби.
называется фундаментальным принципом дробей .

Когда мы анализируем это утверждение, мы видим две эквивалентные дроби и отмечаем, что числитель и знаменатель были умножены на одно и то же ненулевое число, a.
Чтобы заменить дробь эквивалентной дробью , умножьте числитель и знаменатель на одно и то же ненулевое выражение.
Почему выражение должно быть ненулевым? Этот процесс можно рассматривать как процесс, обратный сокращению дробей. Решение Поскольку новый знаменатель находится в факторизованной форме, при проверке мы видим, что первоначальный знаменатель (2x + 3) был умножен на множитель (x — 4). Следовательно, исходный числитель (x + 1) также необходимо умножить на множитель (x — 4), что даст
Обратите внимание, что в окончательной форме дроби мы умножили множители в числителе, но оставили знаменатель в факторизованной форме.  Это предпочтительный способ написания ответа.
Это предпочтительный способ написания ответа.Решение Поскольку исходный знаменатель (x — 3) был умножен на (2) и (x + 1), исходный числитель (2x + 1) также необходимо умножить на (2) и ( х + 1).
Опять же, обратите внимание на форму ответа. СЛОЖЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Сложите дроби с одинаковыми знаменателями.
- Найдите наименьший общий знаменатель двух или более дробей.
- Применить правило сложения дробей.
Теперь мы готовы складывать алгебраические дроби, используя методы, описанные в двух предыдущих разделах. Следует вспомнить следующее правило из арифметики.
Сумма двух или более дробей, имеющих одинаковый знаменатель, равна сумме числителей над их общим знаменателем.
Обратите внимание, что это правило допускает только сумму дробей с одинаковым знаменателем.
 Другими словами, две или более дроби могут быть сложены только в том случае, если они имеют общий знаменатель. Правило сложения любых двух или более дробей потребует навыков, полученных в последних двух разделах, в дополнение к знанию комбинирования одинаковых терминов.
Другими словами, две или более дроби могут быть сложены только в том случае, если они имеют общий знаменатель. Правило сложения любых двух или более дробей потребует навыков, полученных в последних двух разделах, в дополнение к знанию комбинирования одинаковых терминов.Чтобы сложить две или более дроби, выполните следующие действия:
Шаг 1 Найдите наименьший общий знаменатель (НОД) для всех дробей, используя метод, описанный в разделе 9-4.
Шаг 2 Замените каждую дробь эквивалентной дробью с наименьшим общим знаменателем (раздел 9-5).
Шаг 3 Найдите сумму числителей и поместите эту сумму на наименьший общий знаменатель.
Шаг 4 Упростите (или уменьшите) дробь, полученную на шаге 3.Эти четыре шага следует использовать при сложении дробей. Не забудьте умножить числитель и знаменатель на одно и то же выражение. 
Этот ответ в сокращенной форме.
Опять же, не забудьте умножить числитель на то же выражение, на которое вы умножили знаменатель. Всякий раз, когда знаменатели не имеют общих множителей, LCD является произведением знаменателей. Здесь нужно изменить форму только первой дроби. Сумма равна
Обратите внимание, что числитель 3x — 15 можно разложить как 3(x — 5), а множитель (x — 5) соответствует множителю в знаменателе. Мы можем использовать меньше письменных шагов, если заметим, что «общий знаменатель» означает, что все дроби имеют один и тот же знаменатель, а если у всех один и тот же знаменатель, то знаменатель необходимо написать только один раз.
 Чтобы проиллюстрировать это, мы переработаем предыдущий пример.
Чтобы проиллюстрировать это, мы переработаем предыдущий пример.Этот ярлык подходит, если вы не забываете умножать числители на необходимые коэффициенты. Опять же, знаменатели не имеют общих множителей, поэтому LCD является произведением всех трех знаменателей. ВЫЧИТАНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Вычитание дробей с одинаковыми знаменателями.
- Применить правило вычитания дробей с разными знаменателями.
Вычитание определяется в терминах сложения, поэтому метод вычитания алгебраических дробей будет таким же, как сложение алгебраических дробей, описанный в предыдущем разделе. Вы скоро поймете, почему мы представили их отдельно.
Разность любых двух дробей, имеющих один и тот же знаменатель, равна разнице их числителей над их общим знаменателем.

Обратите внимание, что это правило совпадает с правилом сложения двух дробей с одинаковым знаменателем.
Таким образом, шаги для вычитания дробей такие же, как и для сложения дробей.
Чтобы вычесть дроби:
Шаг 1 Найдите наименьший общий знаменатель двух дробей.
Шаг 2 Замените каждую дробь эквивалентной дробью с наименьшим общим знаменателем.
Шаг 3 Найдите разность числителей и поместите этот результат над наименьшим общим знаменателем.
Шаг 4 Упростите (или уменьшите) дробь, полученную на шаге 3.Возникает очевидный вопрос: «Если эти две операции одинаковы, зачем изучать их по отдельности?» Ответ заключается в том, что вычитание порождает очень распространенную ошибку, которой ученик должен быть готов избежать.
Обратите внимание, что мы вычитаем весь числитель второй дроби. Поэтому будет хорошей практикой заключать весь числитель в круглые скобки со знаком вычитания перед ним. 
Упомянутая ошибка часто возникает из-за того, что знак минус влияет на весь числитель второй дроби, а НЕ только на первый член.
Это произойдет, если вы не используете круглые скобки. Стрелка указывает на ошибку, наиболее часто допускаемую при вычитании дробей. Лучший способ избежать этого — всегда использовать круглые скобки
, и вы вряд ли не сможете правильно изменить знак.
Обратите внимание, что мы заключили в скобки числитель второй дроби.
Обратите внимание, что сначала мы умножили (x — 4) (2x — 1), а затем умножили (2×2 — 9x + 4) на -l. Одновременно умножать и менять знаки — значит вызывать ошибку.СЛОЖНЫЕ Дроби
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Распознавание сложной дроби.

- Упростите сложную дробь.
Дроби определяются как указанное частное двух выражений. В этом разделе мы представим метод упрощения дробей, в которых числитель, знаменатель или оба они сами состоят из дробей. Такие дроби называются сложными фракциями .
Таким образом, если числитель и знаменатель сложной дроби составлены из простых дробей, ее можно упростить, разделив числитель на знаменатель.
Как правило, более эффективный метод упрощения сложной дроби включает использование фундаментального принципа дробей. Умножаем и числитель, и знаменатель на общий знаменатель всех отдельных дробей сложной дроби.
Напомним, что фундаментальный принцип дробей гласит Мы будем использовать фундаментальный принцип, чтобы еще раз упростить
LCD 3 и 4 равно 12. Таким образом,
Отдельные дроби: Этот ответ можно записать в виде смешанного числа Убедитесь, что каждый термин равен множителю и знаменателю. 
Нужен ЖКИ отдельных дробей, y не дробь. УРАВНЕНИЯ С АЛГЕБРАИЧЕСКИМИ ДРОБЯМИ
ЗАДАЧИ
По завершении этого раздела вы должны уметь:
- Применить метод решения дробных уравнений.
- Определите, когда дробное уравнение не имеет решения.
В главе 2 мы столкнулись с уравнениями, в которых есть дроби. Однако все эти дроби имели числовые знаменатели. Теперь обсудим уравнения, в знаменателях которых есть дроби с переменными.
Метод решения этих уравнений будет таким же, как и в главе 2, но есть некоторые дополнительные предостережения, к которым вы должны быть готовы.
Вы можете вернуться к некоторым примерам в главе 3, чтобы освежить свою память. Чтобы освежить вашу память, здесь повторяются шаги решения таких уравнений.

Во-первых: Исключите дроби, умножив каждый член уравнения на наименьший общий знаменатель всех дробей в уравнении.
Второй: упростите, объединив одинаковые члены с каждой стороны уравнения.
Третье: Сложите или вычтите необходимые количества, чтобы получить неизвестное количество с одной стороны и числа арифметики с другой.
Четвертый: Разделить на коэффициент неизвестной величины.
Пятое: проверьте свой ответ.Основное отличие решения уравнений с арифметическими дробями от уравнений с алгебраическими дробями заключается в проверке. Процесс проверки будет заключаться не только в том, чтобы найти возможную ошибку, но и в том, чтобы определить, есть ли у уравнения ответ.
Последняя возможность возникает потому, что алгебраические дроби умножаются на неизвестную величину. Эта неизвестная величина может быть на самом деле равна нулю, что сделает всю работу недействительной.
Помните, мы можем умножать каждую часть уравнения только на ненулевую величину. 
Это означает, что ни (x — 1), ни (x + 1) не могут быть равны нулю.
Если x = 1, то множитель (x — 1) равен нулю и у нас проблемы!Поскольку деление на ноль невозможно, мы должны заключить, что x = 1 не является решением. А так как мы не ошиблись в вычислениях, то должны заключить, что это уравнение не имеет решения.
Правильный ответ: «нет решения».Проверка необходима в алгебраических уравнениях. В противном случае вы могли бы проделать большую работу — не ошибитесь — и все равно упустить проблемы.
Другими словами, x = 1 не является решением, поскольку дает утверждение, не имеющее смысла.Помните, что проверка является чрезвычайно важным шагом, поскольку она определит, есть решение или нет. 
Обратите внимание, что в этих примерах, когда у нас есть x 2 членов, они сокращаются, и мы остаемся с линейным уравнением. Если бы они не сокращались, в уравнении было бы x 2 члена. Уравнение этого типа (квадратное) будет рассмотрено в главе 11. Таким образом, x = -5 является решением.
Следовательно, 11 — это сумма, на которую был увеличен числитель.
РЕЗЮМЕ
Ключевые слова
- Алгебраическая дробь — это указанное отношение двух алгебраических выражений.
- Дробь представляет собой упрощенную форму числа , если числитель и знаменатель не имеют общего делителя, отличного от 1.
- Общий знаменатель для двух или более дробей — это выражение, содержащее все множители знаменателей каждой дроби.
- наименьший общий знаменатель содержит минимальное количество множителей, чтобы быть общим знаменателем.

- Фундаментальный принцип дробей равен
- Сложные дроби — это дроби, в которых числитель или знаменатель (или оба) содержат дробь.
Процедуры
- Чтобы упростить или сократить дроби до наименьшего члена, разложите числитель и знаменатель и разделите на все подобные множители.
- Чтобы умножить дроби, умножьте все числители и знаменатели и разделите на все одинаковые множители перед умножением.
- Чтобы разделить на дробь, переверните делитель, а затем умножьте.
- Чтобы найти наименьший общий знаменатель (НОД), сначала факторизуйте все знаменатели, а затем найдите знаменатель, который содержит все множители каждого знаменателя, но не содержит ненужных множителей.
- Чтобы преобразовать дробь в эквивалентную дробь, умножьте числитель и знаменатель на одно и то же ненулевое выражение.
- Чтобы сложить дроби, выполните следующие действия:
- Найдите наименьший общий знаменатель.

- Измените каждую дробь на эквивалентную дробь, в знаменателе которой будет ЖК-дисплей.
- Добавьте числители и поместите над ЖК-дисплеем.
- Упростите или сократите ответ.
- Найдите наименьший общий знаменатель.
- Чтобы вычесть дроби, действуйте как сложение, но объединяйте числители путем вычитания.
- Сложные дроби можно упростить, умножив числитель и знаменатель сложной дроби на ЖКД всех дробей в выражении.
- Чтобы решить уравнения, содержащие дроби, сначала удалите все дроби, умножив все уравнение на ЖК-дисплей участвующих дробей. Полученное уравнение затем решается, и решение должно быть проверено в исходном уравнении.
Сложение и вычитание неправильных дробей
ВведениеМы узнали, что дробь — это число, представляющее часть целого. Целое может быть одним или группой объектов. Давайте теперь узнаем о сложении и вычитании одинаковых дробей. Но перед этим мы должны вспомнить, что мы понимаем под подобными дробями.
Простейшая дробь Дроби, имеющие одинаковые знаменатели, называются подобными дробями. Например, дроби $\frac{4}{9}, \frac{13}{9}, \frac{1}{9} и \frac{5}{9}$ похожи на дроби, имеющие общий знаменатель 9.
Дроби, имеющие одинаковые знаменатели, называются подобными дробями. Например, дроби $\frac{4}{9}, \frac{13}{9}, \frac{1}{9} и \frac{5}{9}$ похожи на дроби, имеющие общий знаменатель 9.Также важно помнить, что Говорят, что дробь имеет стандартную форму, если знаменатель положительный, а числители не имеют общего делителя, отличного от 1.
Чтобы представить данную дробь в стандартной форме, необходимо выполнить следующие шаги – Шаг 1 – Проверить, является ли заданное число дробью.
Шаг 2 – Посмотрите, положительный знаменатель дроби или нет. Если оно отрицательное, умножьте или разделите числитель и знаменатель на -1, чтобы знаменатель стал положительным.
Шаг 3 – Найдите наибольший общий делитель (НОД) абсолютных значений числителя и знаменателя.
Шаг 4 – Разделите числитель и знаменатель данной дроби на НОД (HCF), полученный в шаге III.
 Полученная дробь является стандартной формой данной дроби.
Полученная дробь является стандартной формой данной дроби.Это было важно понять, потому что после сложения или вычитания дробей нам нужно будет сводить их в простейшем виде.
Теперь давайте научимся складывать две или более неправильные дроби. Но перед этим напомним, что мы понимаем под неправильными дробями
Неправильные дробиДроби, у которых числитель больше или равен знаменателю, называются неправильными дробями. Например, рассмотрим дроби $\frac{5}{2} и \frac{7}{3}$. В обеих этих дробях числители больше соответствующих знаменателей. Следовательно, это неправильные дроби. Даже дробь $\frac{3}{3}$ является неправильной дробью, так как в этом случае числитель равен знаменателю. Итак, мы можем сказать, что условием того, что дробь является неправильной, является то, что ее 9Числитель 0003 должен быть больше или равен его знаменателю . Давайте теперь разберемся, как складывать или вычитать неправильные дроби.
Сложение неправильных дробей
Сложение неправильных дробей производится на основе эквивалентности их знаменателей, т.е. имеют ли они одинаковые разные знаменатели. Обсудим оба случая.
Неправильные дроби с одинаковыми знаменателямиНапомним, что дроби с одинаковыми знаменателями называются одинаковыми дробями. Следовательно, если знаменатели неправильных дробей одинаковы, то дроби будут называться одинаковыми. Таким образом, чтобы сложить две неправильные дроби, проделываем следующие шаги:
- Получите числители двух данных дробей и их общий знаменатель
- Сложите числители, полученные на первом шаге.
- Запишите дробь, числитель которой равен сумме, полученной на втором шаге, а знаменатель — общий знаменатель данных дробей.
Давайте разберемся на примере.
Пример
Предположим, мы хотим сложить дроби $\frac{8}{5} и \frac{13}{5}$
Решение
Здесь мы видим, что обе дроби имеют один и тот же знаменатель, т.
 е. 5.
е. 5.Таким образом, мы идем по указанным выше шагам.
Проверяем числители обеих дробей. Это 8 и 13.
Затем складываем эти числители и получаем 8 + 13 = 21.
Теперь запишем сумму этих дробей в виде $\frac{21}{5}$
Следовательно, $\frac{8}{5} + \frac{13}{5} = \frac{21}{5}$
В приведенном выше примере мы видели, как сложить две неправильные дроби, имеющие одинаковый знаменатель. А если их знаменатели разные?
Неправильные дроби с разными знаменателямиНеправильными дробями называются разные знаменатели. . Например, $\frac{9}{7} и \frac{11}{8}$ не являются дробями, так как обе дроби имеют разные знаменатели. Но они являются несобственными функциями, так как их числитель больше соответствующего знаменателя.
Давайте посмотрим, как сложить эти неправильные дроби. Мы будем использовать следующие шаги, чтобы найти сумму неправильных дробей с разными знаменателями.

- Получить дроби и их знаменатели. Знаменатели дробей должны быть такими, чтобы они не совпадали.
- Найдите наименьшее общее кратное (НОК) знаменателей. Другими словами, сделайте знаменатели одинаковыми, найдя наименьшее общее кратное (НОК) их знаменателей. Этот шаг точно такой же, как нахождение наименьшего общего знаменателя (LCD).
- Преобразуйте каждую функцию в эквивалентную дробь, имеющую тот же знаменатель, равный МНК, полученному на предыдущем шаге. Это означает, что вам нужно переписать каждую дробь в эквивалентную ей дробь со знаменателем, равным наименьшему общему кратному, который вы нашли на предыдущем шаге.
- Так как дроби теперь подобны дробям, сложите их, как мы это делаем для подобных дробей, т.е. сложите их числители.
- При необходимости приведите дробь к простейшей форме.
Давайте разберем приведенные выше шаги на примере.

Пример
Добавить $\frac{7}{3} и \frac{8}{7}$
Решение
Нам даны дроби, $\frac{7}{3} и \frac{8}{7}$. Мы ясно видим, что знаменатели этих дробей различны, следовательно, они не похожи на дроби. Поэтому мы будем действовать в соответствии с шагами, определенными выше, чтобы получить их сумму.
Сначала найдем НВМ 3 и 7.
НВМ 3 и 7 = 21
Итак, преобразуем данные дроби в равнозначные дроби со знаменателем 21.
Получим,
$\ frac{7}{3} = \frac{7 x 7}{3 x 7} = \frac{49}{21}$
Аналогично,
$\frac{8}{7} = \frac{8 x 3}{7 x 3} = \frac{24}{21}$
Теперь у нас есть две дроби, $\frac{49}{21} и \frac{24}{21}$, которые имеют общий знаменатель 21 и, таким образом, похожи на дроби. Итак, мы сложим их числители, чтобы получить
$\frac{49}{21} + \frac{24}{21} = \frac{73}{21}$
Следовательно,
$\frac{7}{3} + \frac{8 }{7} = \frac{73}{21}$
Вычитание неправильных дробейВычитание неправильных дробей аналогично сложению неправильных дробей, где расчеты основаны на эквивалентности их знаменателей, т.
Неправильные дроби с одинаковыми знаменателями е. имеют ли они одинаковые разные знаменатели. Обсудим оба случая.
е. имеют ли они одинаковые разные знаменатели. Обсудим оба случая.Напомним, что дроби с одинаковым знаменателем называются одинаковыми дробями. Следовательно, если знаменатели неправильных дробей одинаковы, то дроби будут называться одинаковыми. Поэтому, чтобы сложить две неправильные дроби, проделываем следующие шаги:
- Получите числители двух данных дробей и их общий знаменатель
- Найдите разность числителей, полученных на первом шаге. Важно проверить, какой числитель является вычитаемым, а какой — уменьшаемым, поскольку мы знаем, что в случае вычитания a — b не всегда может быть равно b — a.
- Запишите дробь, числитель которой равен разности суммы, полученной на втором шаге, а знаменатель — общий знаменатель данных дробей.
Давайте разберемся на примере.
Пример
Предположим, мы хотим найти разницу между дробями $\frac{9}{4} и \frac{5}{4}$
Решение
Здесь мы видим, что обе дроби имеют один и тот же знаменатель, т.
 е. 4.
е. 4.Следовательно, идем по определенным выше шагам.
Проверяем числители обеих дробей. Это 9 и 5.
Затем из 9 вычтем 5, получим 9 – 5 = 4
Теперь запишем разность этих дробей в виде $\frac{4}{3}$
Отсюда , $\frac{9}{4} – \frac{5}{4} = \frac{4}{3}$
Теперь разберемся, как найти разницу между неправильными дробями, имеющими разные знаменатели.
Неправильные дроби с разными знаменателямиЕще раз напомним, что дроби с одинаковым знаменателем называются одинаковыми дробями. Следовательно, если знаменатели неправильных дробей одинаковы, то дроби будут называться одинаковыми. Таким образом, чтобы сложить две неправильные дроби, проделываем следующие шаги:
- Получить дроби и их знаменатели. Знаменатели дробей должны быть такими, чтобы они не совпадали.
- Найдите наименьшее общее кратное (НОК) знаменателей. Другими словами, сделайте знаменатели одинаковыми, найдя наименьшее общее кратное (НОК) их знаменателей.
 Этот шаг точно такой же, как нахождение наименьшего общего знаменателя (LCD).
Этот шаг точно такой же, как нахождение наименьшего общего знаменателя (LCD).
- Преобразуйте каждую функцию в эквивалентную дробь, имеющую тот же знаменатель, равный МНК, полученному на предыдущем шаге. Это означает, что вам нужно переписать каждую дробь в эквивалентную ей дробь со знаменателем, равным наименьшему общему кратному, который вы нашли на предыдущем шаге.
- Поскольку дроби теперь подобны дробям, вычтите их, как мы делаем для подобных дробей, т.е. вычтите их числители.
- При необходимости приведите дробь к простейшей форме.
Давайте разберем приведенные выше шаги на примере.
Пример
Решить $\frac{33}{4} – \frac{17}{6}$
Решение
Нам даны дроби, $\frac{33}{4} и \frac{17}{6}$
Мы ясно видим, что знаменатели этих дробей различны, следовательно, они не похожи на дроби. Поэтому мы будем действовать в соответствии с шагами, определенными выше, чтобы получить их разницу.

Сначала найдем НВМ 4 и 6
НВМ 4 и 6 = 12
Итак, преобразуем данные дроби в равнозначные дроби со знаменателем 12.
Получим,
$\frac{ 33}{4} = \frac{33 x 3}{4 x 3} = \frac{99}{12}$
Аналогично,
$\frac{17}{6} = \frac{17 x 2}{6 x 2} = \frac{34}{12}$
Теперь две дроби, $\frac{99 {12} и \frac{34}{12}$, которые имеют общий знаменатель 12 и, таким образом, подобны дробям. Итак, мы вычтем их числители, чтобы получить
$\frac{99}{12} – \frac{34}{12} = \frac{99- 34}{12} = \frac{65}{12} $
Следовательно, $\frac{33}{4} – \frac{17}{6} = \frac{65}{12}$
Графическое представление сложения и вычитания неправильных дробейКак изобразить сложение и вычитание графически. Для этого рассмотрим две дроби, $\frac{5}{4} и \frac{6}{4}$
Нарисуем картинку, чтобы понять, как дроби выглядят в наглядном виде. Поскольку в знаменателе этих дробей у нас 4, это означает, что каждое целое было разделено на четыре равные части.

Следовательно, $\frac{5}{4}$ можно представить в виде –
Аналогично, $\frac{6}{4}$ можно представить в виде –
Если мы суммируем эти заштрихованные части выше, мы получим 5 + 6 = 11 заштрихованных частей.
Следовательно, сумма $\frac{5}{4} и \frac{6}{4}$ будет равна $\frac{11}{4}$
Если бы мы нашли разницу между $ \frac{5}{4} и \frac{6}{4}$, то для нахождения значения $\frac{6}{4} – \frac{5}{4}$ мы должны вычесть заштрихованные частей двух дробей, чтобы получить, 6 – 5 = 1
Следовательно, $\frac{6}{4} – \frac{5}{4} = \frac{1}{4}$
Решенные примерыПример 1 Эми купила $\frac{5}{2}$ кг сахара, а Патрисия купила $\frac{7}{2}$ кг сахара. Найдите общее количество сахара, купленного ими обоими.
Решение Нам известно, что Эми купила $\frac{5}{2}$ кг сахара, а Патриция купила $\frac{7}{2}$ кг сахара. Требуется найти общее количество сахара, купленного ими обоими.

Чтобы найти ответ на поставленную выше задачу, давайте сначала разберемся с данными нам значениями дробей.
Сахар, купленный Эми = $\frac{5}{2}$ кг
Сахар, купленный Патрисией = $\frac{7}{2}$ кг
Хорошо видно, что обе дробные значения имеют одинаковые знаменатель, то есть 2. Поэтому первое, что нужно заметить, это то, что они подобны дробям.
Теперь, чтобы найти стоимость всего купленного ими сахара, нам нужно сложить две дроби. Мы продолжим складывать эти дроби, добавляя числители, как мы узнали выше.
Итак, общее количество сахара, купленного ими обоими = Сахар, купленный Эми + Сахар, купленный Патрисией
Теперь, сложив их числители, мы имеем 5 + 7 = 12
Следовательно, 5 / 2 + 7 / 2 = 12 / 2 = 6 кг
Следовательно, Эми и Патрисия вместе купили 6 кг сахара.
Пример 2 Роза съела 15/7 пицц и 17/14 отдала своей матери. Сколько пицц было у Розы изначально?
Решение Нам известно, что Роза съела 15/7 пицц и отдала 17/14 пицц своей матери.
 Требуется найти, сколько пицц было у Розы изначально.
Требуется найти, сколько пицц было у Розы изначально.Сначала суммируем данные нам дроби.
Доля пиццы, съеденной Розой = $\frac{15}{7}$
Доля пиццы, съеденной матерью Розы = $\frac{17}{14}$
Пиццы, которые изначально были доступны у Розы, будут дается сложением этих двух дробей. Итак, нам нужно найти $\frac{15}{7} + \frac{17}{14}$
Обратите внимание, что обе дроби имеют разные знаменатели; следовательно, нам сначала придется взять НОК знаменателей, чтобы сделать их эквивалентными дробями.
L.C.M 7 и 14 = 14
Теперь мы преобразуем данные дроби в эквивалентные дроби со знаменателем 14.
Обратите внимание, что у дроби $\frac{17}{14}$ знаменатель уже равен 8, поэтому нам не нужно преобразовывать его дальше.
$\frac{15}{7} = \frac{15 x 2}{7 x 2} = \frac{30}{14}$
Теперь
$\frac{15}{7} + \frac{17}{14} = \frac{30}{14} + \frac{17}{14} = \frac{47}{14}$
Следовательно, общее количество пицц, которые изначально были доступны у Розы = $\frac{47}{14}$
Пример 3 У Эмили 11/3 акра земли.
 Она дает 5/4 акра земли своей подруге. Сколько акров земли сейчас у Эмили?
Она дает 5/4 акра земли своей подруге. Сколько акров земли сейчас у Эмили?Решение Нам известно, что у Эмили есть 11/3 акра земли. Она дает 5/4 акра земли своей подруге. Нам нужно узнать, сколько земли осталось у Эмили сейчас. Чтобы вычислить это, сначала мы суммируем данные нам дроби.
Земля, доступная вместе с Эмили = $\frac{11}{3}$ акров
Земля, которую Эмили дает своей подруге = $\frac{5}{4}$ акров
Земля, оставшаяся у Эмили, может быть найдена путем нахождения разницы между этими двумя дробями, т.е. путем нахождения значения $\frac{11 }{3} – \frac{5}{4}$
Обратите внимание, что обе дроби имеют разные знаменатели; следовательно, нам сначала придется взять НОК знаменателей, чтобы сделать их эквивалентными дробями.
НОК 3 и 4 равно 12
Следовательно,
$\frac{11}{3} = \frac{11 x 4}{3 x 4} = \frac{44}{12}$ и
$\frac{5}{4} = \frac{5 x 3}{4 x 3} = \frac{15}{12}$
Теперь
$\frac{11}{3} – \frac{5}{4} = \frac{44}{12} – \frac{15}{12} = \frac{44 – 15}{12} = \frac{29}{12}$
Следовательно, у Эмили осталось $\frac{29}{12}$ акра земли.
Ключевые факты и резюме
- Дробь — это число, представляющее часть целого. Целое может быть одним или группой объектов.
- Говорят, что дробь имеет стандартную форму, если знаменатель положительный и числители не имеют общего делителя, отличного от 1.
- Чтобы привести дробь к простейшей форме Найдите наибольший общий делитель (НОД) абсолютных значений числителя и знаменателя. Разделите числитель и знаменатель данной дроби на НОД (HCF), полученный на шаге III. Полученная дробь является стандартной формой данной дроби.
- Число, которое вычитается, называется вычитаемым, а число, из которого вычитается вычитаемое, называется уменьшаемым. Результат этого вычитания называется разностью.
- Дроби, у которых числитель больше или равен знаменателю, называются неправильными дробями.
- Дроби с одинаковым знаменателем называются одинаковыми дробями, а дроби с разными знаменателями называются разными дробями.



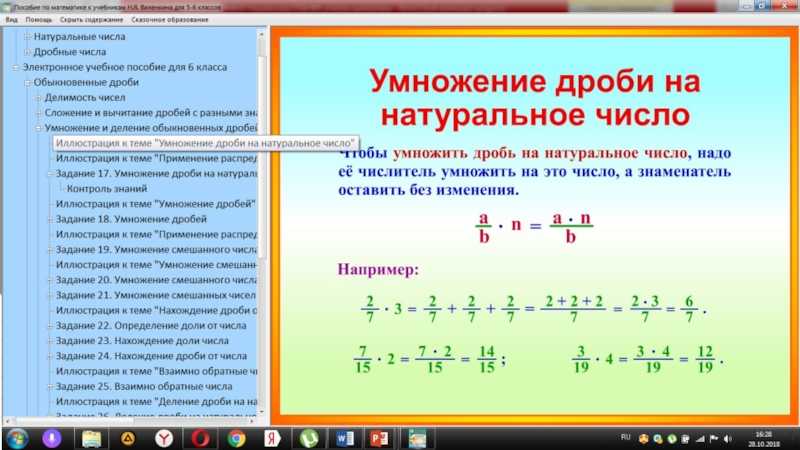
 Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m – b/m = (k-b)/m.
Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m – b/m = (k-b)/m. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, – числитель неправильной дроби. Знаменатель же остается неизменным.
Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, – числитель неправильной дроби. Знаменатель же остается неизменным.

 Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, — числитель неправильной дроби. Знаменатель же остается неизменным.
Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, — числитель неправильной дроби. Знаменатель же остается неизменным.


 После вычитания вывод можно легко упростить.
После вычитания вывод можно легко упростить.
 Тренировка
Тренировка Какая из этих двух дробей ближе к 1?
Какая из этих двух дробей ближе к 1?  Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики. Вычтите 5/6 из 11/6
Вычтите 5/6 из 11/6 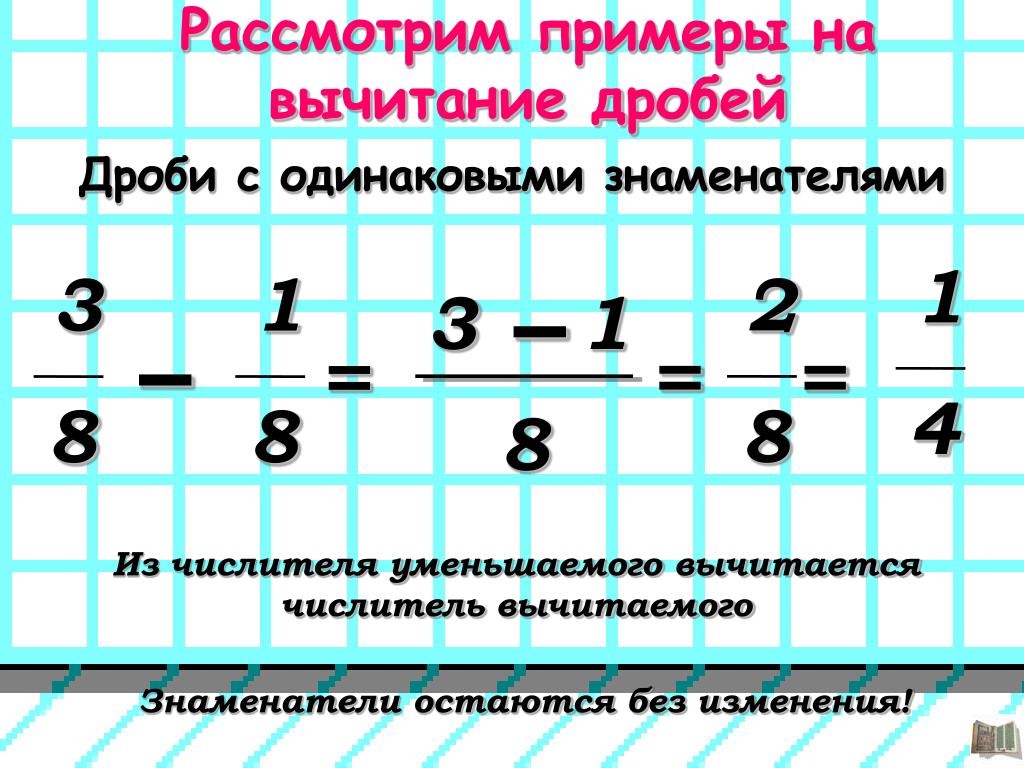 C.M.
C.M. = 19/3 – 37/12
= 19/3 – 37/12 При вычитании дробей с разными знаменателями важно вычислить общий знаменатель для всех дробей. Затем вычтите числители, сохраняя знаменатель постоянным.
При вычитании дробей с разными знаменателями важно вычислить общий знаменатель для всех дробей. Затем вычтите числители, сохраняя знаменатель постоянным.



 Итак, вам понадобится 4/5 стакана масла всего , чтобы сделать свой торт.
Итак, вам понадобится 4/5 стакана масла всего , чтобы сделать свой торт.
 Как вы узнали из раздела «Сравнение и сокращение дробей», всегда лучше сократить дробь до ее простейшей формы , когда это возможно. Например, 1/4 плюс 1/4 равно 2/4. Поскольку 2 и 4 можно разделить на 2, мы можем уменьшить 2/4 до 1/2.
Как вы узнали из раздела «Сравнение и сокращение дробей», всегда лучше сократить дробь до ее простейшей формы , когда это возможно. Например, 1/4 плюс 1/4 равно 2/4. Поскольку 2 и 4 можно разделить на 2, мы можем уменьшить 2/4 до 1/2. Поэтому нам нужно найти наименьший общий знаменатель, прежде чем складывать или вычитать эти дроби. Когда дроби имеют одинаковый знаменатель, мы можем складывать или вычитать, как обычно.
Поэтому нам нужно найти наименьший общий знаменатель, прежде чем складывать или вычитать эти дроби. Когда дроби имеют одинаковый знаменатель, мы можем складывать или вычитать, как обычно.




 Они встречаются в формулах и во многих повседневных практических задачах. Однако арифметические дроби состоят строго из чисел. Теперь мы изучим действия над дробями, компоненты которых являются алгебраическими выражениями.
Они встречаются в формулах и во многих повседневных практических задачах. Однако арифметические дроби состоят строго из чисел. Теперь мы изучим действия над дробями, компоненты которых являются алгебраическими выражениями.

 Таким образом, при делении множителя (2x + 5) остается множитель 1.
Таким образом, при делении множителя (2x + 5) остается множитель 1.

 Приведенная здесь форма предпочтительнее, поскольку она содержит наименьшее количество знаков.
Приведенная здесь форма предпочтительнее, поскольку она содержит наименьшее количество знаков.


 Делители следующего числа, 18, равны (2)(3)(3). У нас уже есть 2 и одна 3. Следовательно, нам нужно еще 3.
Делители следующего числа, 18, равны (2)(3)(3). У нас уже есть 2 и одна 3. Следовательно, нам нужно еще 3. 


 Это предпочтительный способ написания ответа.
Это предпочтительный способ написания ответа. Другими словами, две или более дроби могут быть сложены только в том случае, если они имеют общий знаменатель. Правило сложения любых двух или более дробей потребует навыков, полученных в последних двух разделах, в дополнение к знанию комбинирования одинаковых терминов.
Другими словами, две или более дроби могут быть сложены только в том случае, если они имеют общий знаменатель. Правило сложения любых двух или более дробей потребует навыков, полученных в последних двух разделах, в дополнение к знанию комбинирования одинаковых терминов.
 Чтобы проиллюстрировать это, мы переработаем предыдущий пример.
Чтобы проиллюстрировать это, мы переработаем предыдущий пример.






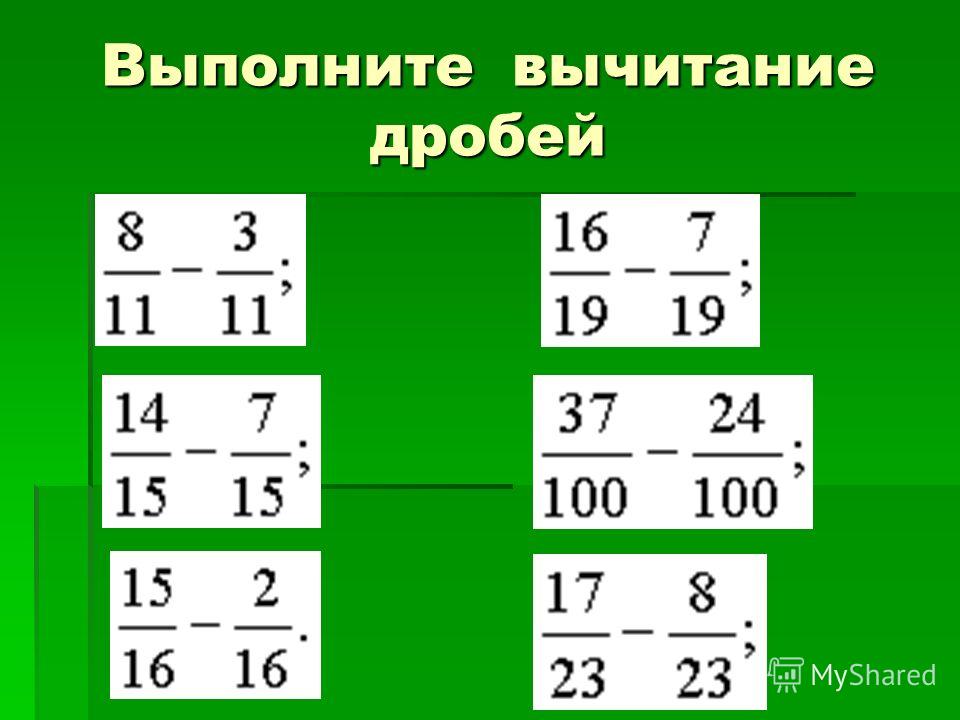

 Дроби, имеющие одинаковые знаменатели, называются подобными дробями. Например, дроби $\frac{4}{9}, \frac{13}{9}, \frac{1}{9} и \frac{5}{9}$ похожи на дроби, имеющие общий знаменатель 9.
Дроби, имеющие одинаковые знаменатели, называются подобными дробями. Например, дроби $\frac{4}{9}, \frac{13}{9}, \frac{1}{9} и \frac{5}{9}$ похожи на дроби, имеющие общий знаменатель 9. Полученная дробь является стандартной формой данной дроби.
Полученная дробь является стандартной формой данной дроби.
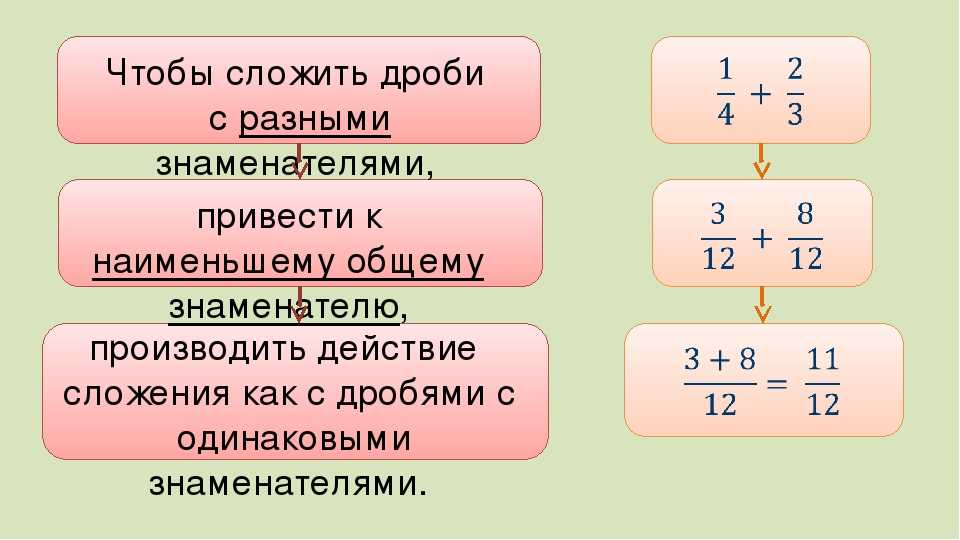 е. 5.
е. 5.
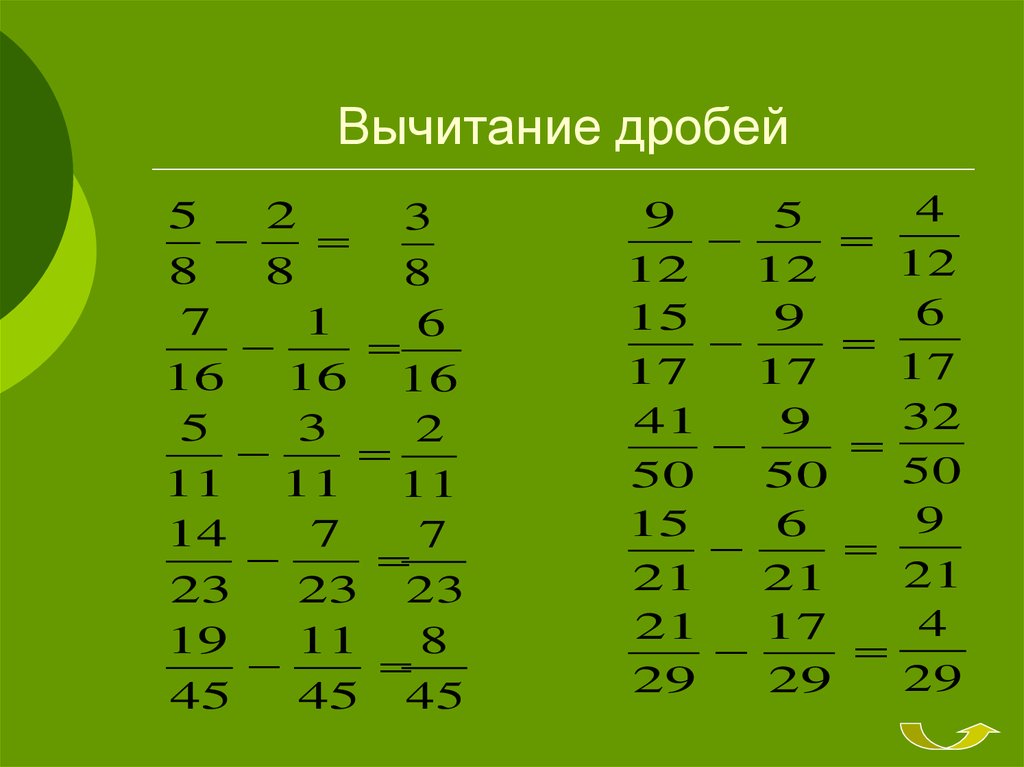
 е. имеют ли они одинаковые разные знаменатели. Обсудим оба случая.
е. имеют ли они одинаковые разные знаменатели. Обсудим оба случая. е. 4.
е. 4. Этот шаг точно такой же, как нахождение наименьшего общего знаменателя (LCD).
Этот шаг точно такой же, как нахождение наименьшего общего знаменателя (LCD).


 Требуется найти, сколько пицц было у Розы изначально.
Требуется найти, сколько пицц было у Розы изначально. Она дает 5/4 акра земли своей подруге. Сколько акров земли сейчас у Эмили?
Она дает 5/4 акра земли своей подруге. Сколько акров земли сейчас у Эмили?