5 класс. Математика. Обыкновенные дроби — Сложение и вычитание обыкновенных дробей
Комментарии преподавателяДля начала давайте вспомним, что такое смешанные числа. Смешанное число – число, записанное в таком виде, что у него есть целая часть и дробная часть. Например, . Здесь 3 – целая часть, – дробная.
Задача 1
Предположим, нам дали такую задачу. Вася пробежал первый из двух кругов дистанции за 1 минуту 40 секунд, а второй круг – за 1 минуту 20 секунд. За какое время Вася пробежал всю дистанцию и насколько быстрее он пробежал второй круг, чем первый?
Решение
Несложно видеть, что мы можем сложить минуты с минутами, секунды – с секундами. Получится 2 мин + 60 секунд, т. е. 3 мин. Но, с другой стороны, 40 секунд – это минуты, а 20 секунд – . И тогда, по аналогии, чтобы сложить эти смешанные числа, мы можем не переводить их в неправильные дроби, а сразу сложить целые минуты друг с другом, и отдельно – дробные. Это дает 2 минуты и , то есть еще одну целую минуту. Итого 3 минуты.
Это дает 2 минуты и , то есть еще одну целую минуту. Итого 3 минуты.
Можно было все это проделать и так. Заметим, что смешанное число есть сумма своих целой и дробной частей. А дальше воспользуемся переместительным свойством:
А что с вычитанием? То же самое. Из чисто практических соображений первый круг по минутам одинаков со вторым, а по секундам – на 20 дольше (или на треть минуты). Можно и так:
Думаю, вы уже поняли алгоритм? Из целого вычитаем (к целому прибавляем) целое, из дробного – дробное. Рассмотрим еще несколько примеров.
Примеры на сложение
Закрепим эти выкладки правилом. Чтобы сложить два смешанных числа, необходимо:
- сложить их целые части;
- сложить их дробные части;
- если нужно, перевести сумму дробных частей в смешанное число;
- сложить полученные числа.
Перейдем к вычитанию. Рассмотрим несколько примеров, после чего сформулируем общий алгоритм.
Рассмотрим несколько примеров, после чего сформулируем общий алгоритм.
Найти ошибки в примерах на сложение
Рассмотрим внимательно первый пример: смешанное число заменили дробью , а число – , но данные дроби не равны. Если мы решим переводить дроби в неправильные, то получим следующее:
Теперь перейдем ко второму примеру, в нем действия выполняются согласно рассмотренному нами алгоритму. Как видим, все действия выполнены правильно, однако принято записывать смешанные числа так, чтобы их дробная часть являлась правильной дробью. Поэтому представим дробь в виде смешанного числа, а потом уже выполним сложение.
Примеры на вычитание
Если пойти по плану, то надо из вычесть . Этого мы сделать не можем. Тогда поступим так, как мы делаем при вычитании натуральных чисел: займем у старшего разряда. Только роль старшего разряда здесь будет играть целая часть. Ведь единица – это , так что можно вместо записать . А дальше – по плану:
Только роль старшего разряда здесь будет играть целая часть. Ведь единица – это , так что можно вместо записать . А дальше – по плану:
А что делать, если пришлось вычитать из натурального числа смешанное? То же самое:
.
Закрепим эти выкладки правилом. Чтобы вычесть одно смешанное число из другого, вы должны:
- сравнить дробные части уменьшаемого и вычитаемого;
- если дробная часть уменьшаемого больше, то вычесть из целой части целую часть, из дробной части дробную часть, а результаты сложить;
- если же больше дробная часть вычитаемого, то одну единицу от целой части уменьшаемого мы переводим в дробь, чтобы дробь стала неправильной, а затем вычитаем из целой части целую, а из дробной – дробную, и результаты складываем.
Найти ошибки в примерах на вычитание
Рассмотрим первый пример. Согласно алгоритму, мы должны сначала 12 представить в виде смешанного числа, а затем уже выполнять вычитание:
Согласно алгоритму, мы должны сначала 12 представить в виде смешанного числа, а затем уже выполнять вычитание:
Рассмотрим второй пример. Здесь ошибка при вычитании дробных частей: нам необходимо из дробной части уменьшаемого вычесть дробную часть вычитаемого, а не наоборот. Чтобы это выполнить, нам придется занять 1 единицу и представить ее в виде дроби.
Заключение
На этом уроке мы познакомились со смешанными числами, научились складывать их и вычитать, сформулировали алгоритмы для сложения и вычитания. Узнали, что для сложения и вычитания смешанных чисел вовсе не обязательно переводить их в неправильные дроби, а достаточно просто сложить либо вычесть целые части и сложить либо вычесть дробные части, после чего записать окончательный ответ.
В каждом из случаев у нас была одна тонкость. Для сложения мы понимали, что иногда получается сумма дробных частей в виде неправильной дроби, поэтому при необходимости полученную неправильную дробь нужно приводить к правильной, то есть выделять целую часть. А при вычитании появлялась такая тонкость, что не всегда из дробной части уменьшаемого можно вычесть дробную часть вычитаемого, поэтому нам необходимо было «занимать» единицу у целой части и переводить ее в дробную, чтобы получить неправильную дробь, из которой уже можно было вычесть дробную часть.
А при вычитании появлялась такая тонкость, что не всегда из дробной части уменьшаемого можно вычесть дробную часть вычитаемого, поэтому нам необходимо было «занимать» единицу у целой части и переводить ее в дробную, чтобы получить неправильную дробь, из которой уже можно было вычесть дробную часть.
Источник видео: https://www.youtube.com/watch?v=Q4UViwjnGVQ
Источник конспекта: http://interneturok.ru/ru/school/matematika/5-klass/drobnye-chisla/slozhenie-i-vychitanie-smeshannyh-chisel?seconds=0&chapter_id=842#videoplayer
Источник теста: Тесты по математике 5 класс к учебнику Зубаревой И.И., Мордкович А.Г. — Рудницкая В.Н. 2013г.
Операции с дробями — Инструмент решения задач Tiger Algebra Solver
Введи уравнение или задачу
Подключенная камера не распознана!
Дробь — это часть целого, которую обычно записывают как числитель (представляющий меньшую часть) над знаменателем (представляющим целое). Чтобы выразить дробь как одно число (частное), числитель делится на знаменатель. Существует три вида дробей:
Чтобы выразить дробь как одно число (частное), числитель делится на знаменатель. Существует три вида дробей:
- Правильная дробь: дробь, в которой числитель меньше знаменателя. является правильной дробью.
- Неправильная дробь: дробь, в которой числитель больше знаменателя. является неправильной дробью.
- Смешанная дробь: целое число плюс правильная дробь. является смешанной дробью.
Важно отметить, что неправильные и смешанные дроби могут выражать одни и те же значения. Например,
. При выполнении операций с дробями лучше сначала преобразовать целые числа и/или смешанные дроби в неправильные дроби:
- Чтобы преобразовать целое число в неправильную дробь, следует просто поместить целое число над . Так, становится .
- Чтобы преобразовать смешанную дробь в неправильную, необходимо умножить знаменатель (число внизу) на целое число (число впереди или слева от дроби), сложить результат с числителем (число вверху) и записать сумму над исходным знаменателем как новый числитель.
 Например, чтобы преобразовать в неправильную дробь, необходимо умножить знаменатель на целое число , что в результате дает . Затем следует сложить это число с числителем , что равно . Последнее число в конце помещают над исходным знаменателем , что дает .
Например, чтобы преобразовать в неправильную дробь, необходимо умножить знаменатель на целое число , что в результате дает . Затем следует сложить это число с числителем , что равно . Последнее число в конце помещают над исходным знаменателем , что дает .
Сложение и вычитание дробей
Общее правило сложения дробей выглядит следующим образом:
Общее правило вычитания дробей выглядит следующим образом:
Для сложения и вычитания дробей необходимо выполнить 4 шага:
- Сначала следует по возможности упростить дроби, сократив их. Разделить числитель (число вверху) и знаменатель (число внизу) на их наибольший общий делитель (НОД). НОД множества чисел представляет собой наибольшее число, которое может делиться на все числа множества без остатка. Например, — наибольшее число, на которое можно разделить и , поэтому мы можем разделить числитель и знаменатель на , чтобы сократить дробь до .
 Еще один пример — дробь , которую можно сократить до .
Еще один пример — дробь , которую можно сократить до . - Найти общий знаменатель дробей. Существует два способа найти общий знаменатель:
1. Умножить верхнюю и нижнюю часть каждой дроби на знаменатель другой дроби. Например,
2. Найти наименьший общий знаменатель. Для этого найдем наименьшее общее кратное (НОК) знаменателей и используем его как общий знаменатель. Существует два способа найти НОК: перечисление кратные чисел (скоро будет доступно!) и разложение на простые множители. - Сложить или вычесть числители. Сейчас дроби должны иметь одинаковый знаменатель, то есть можно просто сложить или вычесть числители, записав результат над найденным ранее знаменателем. Так, становится .
- Упростить полученную дробь, сократив по возможности согласно инструкции в шаге 1. Если результат был , то мы сократили бы его до .
Умножение дробей
Общее правило умножения дробей выглядит следующим образом:
Для умножения дробей следует выполнить 4 шага:
- Сначала следует по возможности упростить дроби, сократив их.
 Разделить числитель (число вверху) и знаменатель (число внизу) на их наибольший общий делитель (НОД). НОД множества чисел представляет собой наибольшее число, которое может делиться на все числа множества без остатка. Например, — наибольшее число, на которое можно разделить и , поэтому мы можем разделить числитель и знаменатель на , чтобы сократить дробь до . Еще один пример — дробь , которую можно сократить до .
Разделить числитель (число вверху) и знаменатель (число внизу) на их наибольший общий делитель (НОД). НОД множества чисел представляет собой наибольшее число, которое может делиться на все числа множества без остатка. Например, — наибольшее число, на которое можно разделить и , поэтому мы можем разделить числитель и знаменатель на , чтобы сократить дробь до . Еще один пример — дробь , которую можно сократить до . - Умножить числители (числа вверху). Так, становится
- Умножить знаменатели (числа внизу). Так, становится .
- Упростить полученную дробь, сократив по возможности согласно инструкции в шаге 1. Если результат был , то мы сократили бы его до .
Деление дробей
Операция деления дробей очень похожа на их умножение, но включает дополнительный шаг: мы меняем местами числитель и знаменатель делителя, то есть числа, на которое будем делить другую дробь, чтобы найти обратную ему величину. Далее мы просто перемножаем дроби. Общее правило деления дробей выглядит следующим образом:
Общее правило деления дробей выглядит следующим образом:
Для деления дробей следует выполнить 5 шагов:
- Сначала следует по возможности упростить дроби, сократив их. Разделить числитель (число вверху) и знаменатель (число внизу) на их наибольший общий делитель (НОД). НОД множества чисел представляет собой наибольшее число, которое может делиться на все числа множества без остатка. Например, — наибольшее число, на которое можно разделить и , поэтому мы можем разделить числитель и знаменатель на , чтобы сократить дробь до . Еще один пример — дробь , которую можно сократить до .
- Перевернуть дробь, на которую мы делим (делитель), чтобы ее числитель оказался внизу, а знаменатель — вверху. Так, становится .
- Умножить числители (числа вверху). Так, становится
- Умножить знаменатели (числа внизу). Так, становится .
- Упростить полученную дробь, сократив по возможности согласно инструкции в шаге 1.
 Если результат был , то мы сократили бы его до .
Если результат был , то мы сократили бы его до .
Определения, советы и рекомендации с примерами
В математике дробь — это числовое значение, представляющее части целого. Дробь состоит из двух частей, а именно числителя и знаменателя. Верхняя часть дроби называется числителем, а нижняя часть дроби – знаменателем. Например, \(\frac{7}{9}\) – это дробь. Здесь \(7\) — числитель, а \(9\) — знаменатель. Вычитание дробей — это арифметическая операция, выполняемая для нахождения разницы между двумя дробями.
В этой статье по математике мы изучим концепцию вычитания дробей, этапы вычитания дробей, вычитание дробей с одинаковыми и разными знаменателями и т. д., советы и рекомендации по вычитанию дробей, а также решим задачи, основанные на вычитании дробей.
Вычитание дробей
Вычитание дробей означает процесс вычитания двух дробных значений. Мы знаем, как вычитать целые числа. Например, вычитание \(2\) из \(7\) дает \(5\). (т.е. \(7 – 2 = 5\)). Точно так же можно производить вычитание дробей. Вычитание дробей включает:
(т.е. \(7 – 2 = 5\)). Точно так же можно производить вычитание дробей. Вычитание дробей включает:
- Вычитание дробей с одинаковыми знаменателями.
- Вычитание дробей с разными знаменателями.
- Вычитание дробей с целыми числами.
- Вычитание смешанных дробей.
Шаги к вычитанию дробей?
Группа дробей может быть классифицирована как сходные дроби и непохожие дроби на основе значения знаменателя. Подобные дроби – это те, у которых одинаковые знаменатели. В то время как неодинаковые дроби — это те, которые имеют разные знаменатели. Шаги для вычитания дробей перечислены ниже:
Шаг 1: Проверить, имеют ли данные дроби одинаковые знаменатели или разные знаменатели.
Шаг 2: В случае одинаковых дробей вычтите числители и запишите их разность над общим знаменателем. С другой стороны, для разных дробей найдите НОК знаменателей.
Шаг 3: Умножьте числитель и знаменатель каждой дроби на целое число, чтобы получить НОК в знаменателе. Это делается для преобразования неодинаковых дробей в подобные дроби.
Это делается для преобразования неодинаковых дробей в подобные дроби.
Шаг 4: Вычтите их числители и запишите разницу над общим знаменателем.
Теперь давайте подробно обсудим все эти дроби вычитания с примерами.
Чтобы узнать о различных типах фракций, нажмите здесь.
Вычитание дробей с одинаковыми знаменателями
При вычитании дробей с одинаковыми знаменателями нам просто нужно вычесть числители дробей. Шаги для вычитания дробей с одинаковыми знаменателями приведены ниже:
Шаг 1: Вычтите числители.
Шаг 2: Запишите общий знаменатель как знаменатель полученной дроби.
Шаг 3: Теперь полученный ответ можно при необходимости привести к низшей форме.
Например, , вычтите дроби \(\frac{4}{5}\) и \(\frac{2}{5}\), используя прямоугольную модель.
Решение: Сначала представим \(\frac{4}{5}\) в этой модели, заштриховав \(4\) из \(5\) частей. Теперь заштрихуйте \(2\) части заштрихованных частей модели, чтобы обозначить удаление \(\frac{2}{5}\).
Теперь заштрихуйте \(2\) части заштрихованных частей модели, чтобы обозначить удаление \(\frac{2}{5}\).
Теперь в заштрихованных частях модели осталось \(2\) деталей. Таким образом, вычитание дробей задается как
\(\frac{4}{5}-\frac{2}{5}=\frac{2}{5}\)
Следовательно, вычитание \( \frac{4}{5}-\frac{2}{5}\) равно \(\frac{2}{5}\).
Чтобы узнать о сложении дробей, нажмите здесь.
Вычитание дробей с разными знаменателями
Чтобы вычесть разные дроби, мы сначала преобразуем их в одинаковые дроби. Шаги для вычитания дробей с разными знаменателями приведены ниже:
Шаг 1: Сначала возьмите НОК знаменателей
Шаг 2: Теперь преобразуйте данные дроби в подобные дроби со знаменателем в качестве НОК.
Шаг 3: Вычтите числители и запишите их разницу над общим знаменателем.
Шаг 4: При необходимости упростите.
Давайте разберемся, как вычитать разные дроби на примере.
Например, , вычтите дроби \(\frac{2}{5} – \frac{1}{3}\), используя модель площади. 9{rd}\) часть из \(\frac{2}{5}\). См. рисунок ниже
Поскольку модель разделена на \(15\) частей, это знаменатель. Это НОК знаменателей данных дробей. Первый прямоугольник показывает часть, представленную \(\frac{2}{5}\) (в строках) и \(\frac{1}{3}\) (в столбцах) в данной модели. Теперь сместите часть \(\frac{1}{3}\) на \(\frac{2}{5}\), чтобы мы могли вычесть \(\frac{1}{3}\) из \ (\ гидроразрыва {2} {5} \). Теперь мы видим, что осталась только \(1\) часть, которая не заштрихована. Таким образом, ответ дается как \(\frac{2}{5}-\frac{1}{3}=\frac{1}{15}\).
Численно это выражается как
\(\frac{2}{5}-\frac{1}{3}\)
\(\Rightarrow\) \(\frac{(2\times 3 )}{(5\times 3)}-\frac{(1\times 5)}{(3\times 5)}\) …[ Поскольку LCM \(5\) и \(3\) равен \ (15\)]
\(\Стрелка вправо\) \(\frac{6}{15}-\frac{5}{15}\)
\(\Стрелка вправо\) \(\frac{1}{ 15}\)
Таким образом, вычитание \(\frac{2}{5} – \frac{1}{3}\) равно \(\frac{1}{15}\).
Вычитание дробей с целыми числами
Каждое целое число можно представить в виде дроби, написав \(1\) в качестве знаменателя, например, мы можем записать \(7\) как \(\frac{7}{ 1}\). Вычитание дробей из целых чисел не так сложно, как кажется. Существует два основных способа вычитания дробей из целых чисел.
Метод 1:
Шаги для вычитания дробей из целых чисел приведены ниже:
Шаг 1: Преобразование целого числа в дробь. Для этого присвойте целому числу знаменатель \(1\).
Шаг 2: Преобразование в дроби с одинаковыми знаменателями.
Шаг 3: Вычтите числители.
Шаг 4: Преобразование в смешанное число (необязательно).
Например, , вычтите \(\frac{4}{5}\) из \(8\).
Решение: \(8-\frac{4}{5}\)
\(=\frac{8}{1}-\frac{4}{5}\)
\(=\ frac{8\times 5}{1\times 5}-\frac{4}{5}\)
\(=\frac{40}{5}-\frac{4}{5}\)
\(=\frac{36}{5}\)
\(=7\frac{1}{5}\)
Таким образом, вычитание \(\frac{4}{5}\) из \ (8\) равно \(7\frac{1}{5}\).
Метод 2:
Шаги для вычитания дробей из целых чисел приведены ниже:
Шаг 1: Преобразование неправильных дробей в смешанные числа. Пропустите этот шаг, если ваша дробь не является неправильной (у неправильной дроби число сверху больше, чем снизу).
Шаг 2: Разделите целое число на \(1\) и другое целое число. Например, перепишите \(5\) как \(4 + 1\) или \(22\) как \(21 + 1\).
Шаг 3: Преобразуйте \(1\) в дробь.
Шаг 4: Умножьте, чтобы получить дроби как знаменатели.
Шаг 5: Объедините две фракции.
Например, , вычтите \(\frac{4}{3}\) из \(11\).
Решение: \(11-\frac{4}{3}\)
\(=11-1\frac{1}{3}\)
\(=10-\frac{1}{3}\)
\(=9+1-\frac{1}{) 3}\)
\(=9+\frac{1}{1}-\frac{1}{3}\)
\(=9+\frac{3}{3}-\frac{1 }{3}\)
\(=9+\frac{3-1}{2}\)
\(=9+\frac{2}{3}\)
\(=9\frac {2}{3}\)
Таким образом, вычитание \(\frac{4}{3}\) из \(11\) равно \(9\frac{2}{3}\).
Вычитание смешанных дробей
Здесь мы научимся решать вычитание смешанных дробей или вычитание смешанных чисел. Существует два метода вычитания смешанных дробей.
Метод 1:
Шаги для вычитания дробей со смешанными дробями приведены ниже:
Шаг 1: Вычтите целые числа.
Шаг 2: Чтобы вычесть дроби, мы преобразуем их в подобные дроби.
Шаг 3: Сложите разности целых чисел и подобных им дробей.
Например, , вычтите \(6\frac{1}{3}\) из \(3\frac{1}{12}\), используя метод 1.
Решение: \(6\frac {1}{3}-3\frac{1}{12}\)
\(=(6-3)+\left(\frac{1}{3}-\frac{1}{12}\right)\)
\(=3+\left(\frac{1) }{3}-\frac{1}{12}\right)\)
\(=3+\left(\frac{1\times 4}{3\times 4}-\frac{1\times 1 }{12\times 1}\right)\), [НОК из \(12\) и \(3\) равно \(12\)]
\(=3+\left(\frac{4}{ 12}-\frac{1}{12}\right)\)
\(=3+\left(\frac{4-1}{12}\right)\)
\(=3+\frac {3}{12}\)
\(=3+\frac{1}{4}\)
\(=3\frac{1}{4}\)
Таким образом, вычитание \( 6\frac{1}{3}\) из \(3\frac{1}{12}\) равно \(3\frac{1}{4}\).
Метод 2:
Шаги для вычитания дробей со смешанными дробями приведены ниже:
Шаг 1: Преобразуйте смешанные числа в неправильные дроби.
Шаг 2: Приведите дроби к общему знаменателю.
Шаг 3: Вычтем и представим дробь в простейшей форме.
Например, , вычтите \(6\frac{1}{3}\) из \(3\frac{1}{12}\), используя метод 2.
Решение: \(6\frac{1}{3}-3\frac{1}{12}\)
\(=\frac{(6\times 3)+1}{3}+\frac {(3\times 12)+1}{12}\)
\(=\frac{19}{3}-\frac{37}{12}\)
\(=\frac{19\times) 4}{3\times 4}-\frac{37\times 1}{12\times 1}\), [НОК из \(12\) и \(3\) равно \(12\)]
\ (=\frac{76}{12}-\frac{37}{12}\)
\(=\frac{76-37}{12}\)
\(=\frac{39}{12) }\)
\(=\frac{13}{4}\)
\(=3\frac{1}{4}\)
Таким образом, вычитание \(6\frac{1}{ 3}\) из \(3\frac{1}{12}\) равно \(3\frac{1}{4}\).
Советы и приемы решения вопросов
Несколько важных советов и приемов решения вопроса о вычитании дробей перечислены ниже:
- Для одинаковых дробей вычтите непосредственно числители.

- Для разных дробей никогда не вычитайте числители и знаменатели напрямую.
- При вычитании разных дробей не нужно находить НОК знаменателей. Подойдет любое общее кратное. Таким образом, простое умножение двух знаменателей дает нам общее кратное. Это может привести к большим выглядящим числам, но его можно уменьшить до самой низкой формы.
Вычитание дробей Пример решения
1. Найдите разницу между \(\frac{6}{7}\) и \(\frac{3}{7}\).
Решение: Здесь данные дроби подобны дробям. Для вычитания дробей с одинаковым знаменателем вычтите числитель и сохраните общий знаменатель.
\(\frac{6}{7}-\frac{3}{7}=\frac{(6-3)}{7}=\frac{3}{7}\)
Таким образом, разница между \(\frac{6}{7}\) и \(\frac{3}{7}\) равна \(\frac{3}{7}\).
2. Вычесть \(\frac{2}{5}\) из \(\frac{4}{3}\).
Решение: Для вычитания разных дробей сначала найдите НОК знаменателей и преобразуйте \(\frac{2}{5}\) и \(\frac{4}{3}\) в эквивалентные дроби тот же знаменатель, а затем вычесть.
НОК\((3, 5) = 15\)
\(\frac{4}{3}-\frac{2}{5}\)
\(=\frac{4\times 5} {3\times 5}-\frac{2\times 3}{5\times 3}\)
\(=\frac{20}{15}-\frac{6}{15}\)
\(=\frac{14}{15}\)
Таким образом, вычитание \(\frac{2}{5}\) из \(\frac{4}{3}\) равно \(\ гидроразрыв{14}{15}\).
3. Вычесть \(\frac{1}{3}\) из \(5\).
Решение: Для вычитания дробей с целыми числами запишите заданное целое число (\(5\)) в дробной форме как \(\frac{5}{1}\). Отсюда следует, что
\(5-\frac{1}{3}\)
\(=\frac{5}{1}-\frac{1}{3}\)
\(=\frac {5\times 3}{1\times 3}-\frac{1}{3}\)
\(=\frac{15}{3}-\frac{1}{3}\)
\(=\frac{15-1}{3}\)
\(=\frac{14} {3}\)
\(=4\frac{2}{3}\)
Таким образом, вычитание \(\frac{1}{3}\) из \(5\) равно \(= 4\разрыв{2}{3}\).
4. Вычесть \(1\frac{5}{12}\) из \(3\frac{3}{8}\).
Решение: Сначала преобразуйте смешанную дробь в неправильную дробь.
\(1\frac{5}{12}=\frac{(1\times 12)+5}{12}=\frac{17}{12}\)
\(3\frac{3} {8}=\frac{(3\times 8)+3}{8}=\frac{27}{8}\)
Теперь \(\frac{27}{8}-\frac{17}{12}\)
\(=\frac{27\times 3}{8\times 3}-\frac{17\ умножить на 2}{12\умножить на 2}\), [НОК из \(8\) и \(12\) равно \(24\)]
\(=\frac{81}{24}-\frac{ 34}{24}\)
\(=\frac{81-34}{24}\)
\(=\frac{47}{24}\)
\(=1\frac{23} {24}\)
Таким образом, вычитание \(1\frac{5}{12}\) из \(3\frac{3}{8}\) равно \(1\frac{23}{24 }\).
Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о вычитании дробей
В.1 Как вычитать дроби с разными знаменателями?
Ответ 1 Шаги для вычитания дробей с разными знаменателями приведены ниже:
- Сначала возьмите НОК знаменателей
- Теперь преобразуйте данные дроби в подобные дроби со знаменателем как НОК .

- Вычтите числители и запишите их разницу над общим знаменателем.
Q.2 Какие шаги необходимо выполнить при вычитании дробей?
Ответ 2 Шаги для вычитания дробей перечислены ниже:
В.3 Как поэтапно вычитать смешанные дроби?
Ответ 3 Шаги для вычитания дробей со смешанными дробями приведены ниже:

Q.4 Как вычитать дроби из целых чисел?
Ответ 4 Шаги для вычитания дробей из целых чисел приведены ниже:
В.5 Как вычитать неправильные дроби?
Ответ 5 Шаги для вычитания неправильных дробей приведены ниже:
В.6 Каково правило вычитания дробей?
Ответ 6
Основное правило вычитания дробей состоит в том, чтобы сначала убедиться, что они имеют общий знаменатель. Если у них разные знаменатели, то сначала преобразуйте их в одинаковые дроби. Скачать публикацию в формате PDF
Если у них разные знаменатели, то сначала преобразуйте их в одинаковые дроби. Скачать публикацию в формате PDF| Декартова плоскость: определение, части и график с решенными примерами |
| Преимущества и недостатки пластика0512 |
| Узнайте о связи между вязкостью и плотностью |
| Оксид цинка: узнайте его формулу, степень окисления, свойства, получение и применение Ядро: Математические ресурсы для 4-го класса 7 диагностических тестов 189 практических тестов Вопрос дня Карточки Learn by Concept ← Предыдущий 1 2 Далее → Common Core: Справка по математике для 4-го класса » Числа и операции: Дроби » Построить дроби из единичных дробей » Сложение и вычитание смешанных чисел с одинаковыми знаменателями: CCSS.Math.Content.4.NF.B.3c » Вычитание смешанных чисел
Возможные ответы: Правильный ответ: Объяснение: Когда мы вычитаем смешанные числа, мы вычитаем целые числа на целые числа и дроби на дроби. Помните, когда мы вычитаем дроби, у нас должны быть общие знаменатели, и мы вычитаем только числители. Сообщить об ошибке. Объяснение: Когда мы вычитаем смешанные числа, мы вычитаем целые числа на целые числа и дроби на дроби. Помните, что при вычитании дробей у нас должны быть общие знаменатели, и мы вычитаем только числители. Сообщить об ошибке. Объяснение: Когда мы вычитаем смешанные числа, мы вычитаем целые числа на целые числа и дроби на дроби. Помните, когда мы вычитаем дроби, у нас должны быть общие знаменатели, и мы вычитаем только числители. Сообщить об ошибке. Объяснение: Когда мы вычитаем смешанные числа, мы вычитаем целые числа на целые числа и дроби на дроби. Помните, когда мы вычитаем дроби, у нас должны быть общие знаменатели, и мы вычитаем только числители. Сообщить об ошибке Возможные ответы: Правильный ответ: Объяснение: Когда мы вычитаем смешанные числа, мы вычитаем целые числа на целые числа и дроби на дроби. Помните, когда мы вычитаем дроби, у нас должны быть общие знаменатели, и мы вычитаем только числители. Сообщить об ошибке
Правильный ответ: Объяснение: Когда мы вычитаем смешанные числа, мы вычитаем целые числа на целые числа и дроби на дроби. Помните, когда мы вычитаем дроби, у нас должны быть общие знаменатели, и мы вычитаем только числители. Сообщить об ошибке
Возможные ответы: Правильный ответ: Объяснение: Когда мы вычитаем смешанные числа, мы вычитаем целые числа на целые числа и дроби на дроби. Помните, когда мы вычитаем дроби, у нас должны быть общие знаменатели, и мы вычитаем только числители. Сообщить об ошибке Решите следующее: Возможные ответы: Правильный ответ: Объяснение: Когда мы вычитаем смешанные числа, мы вычитаем целые числа на целые числа и дроби на дроби. Помните, когда мы вычитаем дроби, у нас должны быть общие знаменатели, и мы вычитаем только числители. Сообщить об ошибке
Возможные ответы: Правильный ответ: Объяснение: Когда мы вычитаем смешанные числа, мы вычитаем целые числа на целые числа и дроби на дроби. |
 Например, чтобы преобразовать в неправильную дробь, необходимо умножить знаменатель на целое число , что в результате дает . Затем следует сложить это число с числителем , что равно . Последнее число в конце помещают над исходным знаменателем , что дает .
Например, чтобы преобразовать в неправильную дробь, необходимо умножить знаменатель на целое число , что в результате дает . Затем следует сложить это число с числителем , что равно . Последнее число в конце помещают над исходным знаменателем , что дает . Еще один пример — дробь , которую можно сократить до .
Еще один пример — дробь , которую можно сократить до . Разделить числитель (число вверху) и знаменатель (число внизу) на их наибольший общий делитель (НОД). НОД множества чисел представляет собой наибольшее число, которое может делиться на все числа множества без остатка. Например, — наибольшее число, на которое можно разделить и , поэтому мы можем разделить числитель и знаменатель на , чтобы сократить дробь до . Еще один пример — дробь , которую можно сократить до .
Разделить числитель (число вверху) и знаменатель (число внизу) на их наибольший общий делитель (НОД). НОД множества чисел представляет собой наибольшее число, которое может делиться на все числа множества без остатка. Например, — наибольшее число, на которое можно разделить и , поэтому мы можем разделить числитель и знаменатель на , чтобы сократить дробь до . Еще один пример — дробь , которую можно сократить до .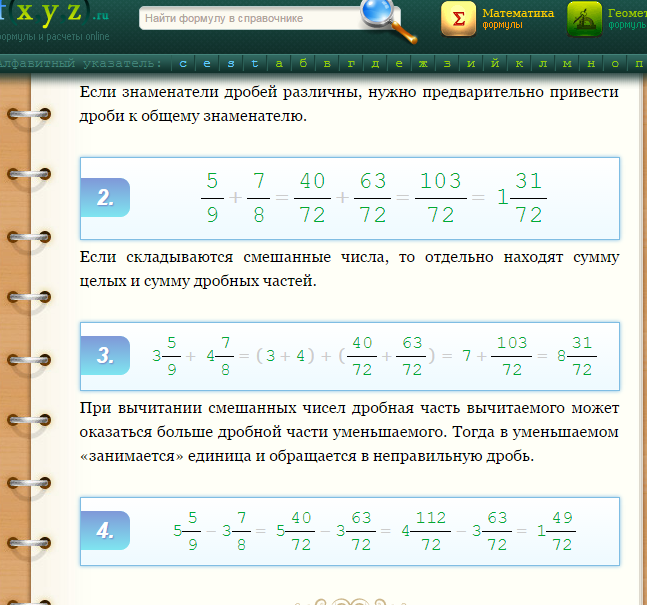 Если результат был , то мы сократили бы его до .
Если результат был , то мы сократили бы его до .




