Как решить выражение по действиям. Порядок выполнения действий

Числовые и буквенные выражения могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, так как существует строгий порядок выполнения математических действий

Сначала умножение и деление, затем сложение и вычитание

Порядок выполения действий в выражениях без скобок:

— действия выполняются по порядку слева направо,

— причем сначала выполняется умножение и деление, а затем – сложение и вычитание .

1. Рассмотрим пример: выполните действия 17−3+6

Исходное выражение не содержит умножения и деления и не содержит скобок. Поэтому нам следует выполнить все действия по порядку слева направо , то есть, сначала мы от 17 отнимаем 3, получаем 14, после чего к полученной разности 14 прибавляем 6, получаем 20.

Кратко решение можно записать так: 17 − 3 + 6 = 14 + 6 = 20

2.

Вычислите значение выражения 17 − 5 · 6: 3 − 2 + 4: 2

Сначала определим, в каком порядке следует выполнять действия в выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление .

4: 2 теперь 4 делим на 2, получаем 2.

Подставляем в исходное выражение вместо 5 · 6: 3 найденное значение 10, а вместо 4: 2 — значение 2, получаем следующее выражение 17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2+ 2 .

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7.

Действия первой и второй ступени

Для удобства принятия решения о последовательности выполнения действий их разделили на две ступени:

первая ступень — сложение и вычитание,

вторая ступень — умножение и деление.

Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание)

Порядок выполнения арифметических действий в выражениях со скобками

Правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Рассмотрим пример: 99: (45 – 39 + 5) – 25: 5

Порядок вычисления такой. Сначала выполним действия в скобках:

45 – 39 = 6 ; 6 + 5 = 11 ,

затем действия второй ступени

Правила порядка выполнения действий в сложных выражениях изучаются во 2 классе, но практически некоторые из них дети используют еще в 1 классе.

Сначала рассматривается правило о порядке выполнения действий в выражениях без скобок, когда над числами производят либо только сложение и вычитание, либо только умножение и деление. Необходимость введения выражений, содержащих два и более арифметических действий одной ступени, возникает при знакомстве учеников с вычислительными приемами сложения и вычитания в пределах 10, а именно:

Аналогично: 6 — 1 — 1, 6 — 2 — 1, 6 — 2 — 2.

Так как для нахождения значений этих выражений школьники обращаются к предметным действиям, которые выполняются в определенном порядке, то они легко усваивают тот факт, что арифметические действия (сложение и вычитание), которые имеют место в выражениях, выполняются последовательно слева направо.

С числовыми выражениями, содержащими действия сложения и вычитания, а также скобки, учащиеся впервые встречаются в теме «Сложение и вычитание в пределах 10». Когда дети встречаются с такими выражениями в 1 классе, например: 7 — 2 + 4, 9 — 3 — 1 , 4 +3 — 2; во 2 классе, например: 70 — 36 +10, 80 — 10 — 15, 32+18 — 17; 4*10:5, 60:10*3, 36:9*3, учитель показывает, как читают и записывают такие выражения и как находят их значение (например, 4*10:5 читают: 4 умножить на 10 и полученный результат разделить на 5). К моменту изучения во 2 классе темы «Порядок действий» учащиеся умеют находить значения выражений этого вида. Цель работы на данном этапе — опираясь практические умения учащихся, обратить их внимание на порядок выполнения действий в таких выражениях и сформулировать соответствующее правило. Учащиеся самостоятельно решают подобранные учителем примеры и объясняют, в каком порядке выполняли; действия в каждом примере. Затем формулируют сами или читают по учебнику вывод: если в выражении без скобок указаны только действия сложения и вычитания (или только действия умножения и деления), то их выполняют в том порядке, в каком они записаны (т.

е. слева направо).

Несмотря на то, что в выражениях вида а+в+с, а+(в+с) и (а+в)+с наличие скобок не влияет на порядок выполнения действий в силу сочетательного закона сложения, на этом этапе учащихся целесообразнее сориентировать на то, что сначала выполняется действие в скобках. Это связано с тем, что для выражений вида а — (в+с) и а — (в — с) такое обобщение неприемлемо и учащимся на начальном этапе довольно трудно будет сориентироваться в назначении скобок для различных числовых выражений. Использование скобок в числовых выражениях, содержащих действия сложения и вычитания, в дальнейшем получает свое развитие, которое связано с изучением таких правил, как прибавление суммы к числу, числа к сумме, вычитание суммы из числа и числа из суммы. Но при первом знакомстве со скобками важно нацелить учащихся на то, что сначала выполняется действие в скобках.

Учитель обращает внимание детей на то, как важно соблюдать это правило при вычислениях, иначе можно получить неверное равенство.

Например, учащиеся объясняют, каким образом, получены значения выражений: 70 — 36 +10=24, 60:10 — 3 =2, почему они неверны, какие значения в действительности имеют эти выражения. Аналогично изучают порядок действий в выражениях со скобками вида: 65 — (26 — 14), 50:(30 — 20), 90:(2 * 5). С такими выражениями учащиеся также знакомы и умеют их читать, записывать и вычислять их значение. Объяснив порядок выполнения действий в нескольких таких выражениях, дети формулируют вывод: в выражениях со скобками первым выполняется действие над числами, записанными в скобках. Рассматривая эти выражения нетрудно показать, что действия в них выполняются не в том порядке, в каком записаны; чтобы показать другой порядок их выполнения, и использованы скобки.

Следующим вводится правило порядка выполнения действий в выражениях без скобок, когда в них содержатся действия первой и второй ступени. Поскольку правила порядка действий приняты по договоренности, учитель сообщает их детям или же учащиеся знакомятся с ними по учебнику.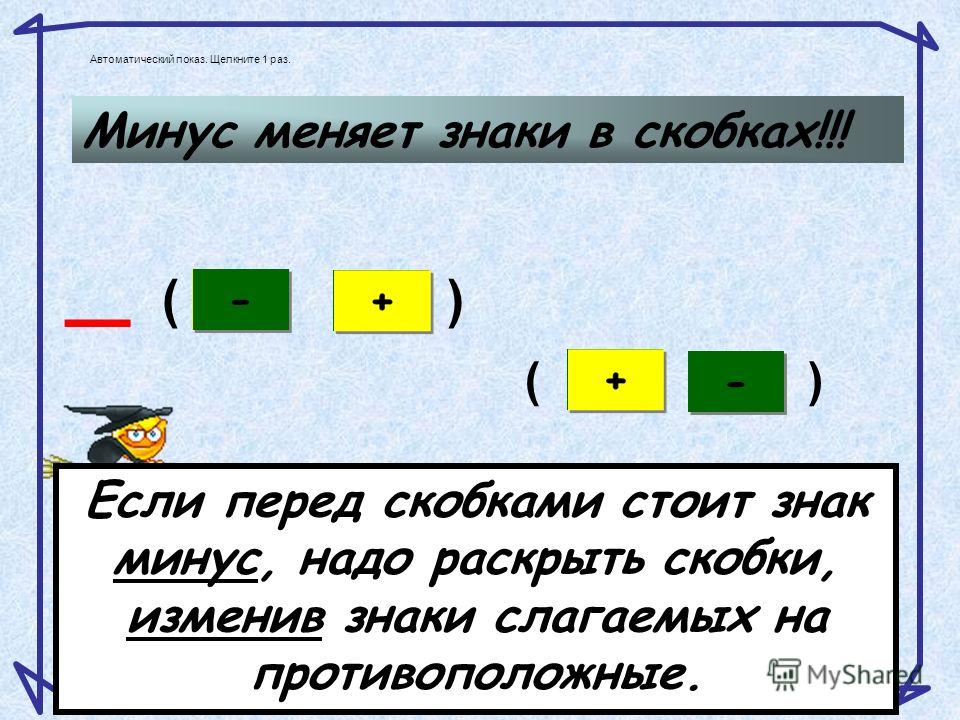

Чтобы учащиеся усвоили введенные правила, наряду с тренировочными упражнениями включают решение примеров с пояснением порядка выполнения их действий. Эффективны также упражнения в объяснении ошибок на порядок выполнения действий. Например, из заданных пар примеров предлагается выписать только те, где вычисления выполнены по правилам порядка действий:

После объяснения ошибок можно дать задание: используя скобки, изменить порядок действий так, чтобы выражение имело заданное значение. Например, чтобы первое из приведенных выражений имело значение, равное 10, надо записать его так: (20+30):5=10.

Особенно полезны упражнения на вычисление значения выражения, когда ученику приходится применять все изученные правила. Например, на доске или в тетрадях записывается выражение 36:6+3*2. Учащиеся вычисляют его значение. Затем по заданию учителя дети изменяют с помощью скобок порядок действий в выражении:

• 36:6+3-2
• 36:(6+3-2)
• 36:(6+3)-2
• (36:6+3)-2

Интересным, но более трудным является обратное упражнение: расставить скобки так, чтобы выражение имело заданное значение:

• 72-24:6+2=66
• 72-24:6+2=6
• 72-24:6+2=10
• 72-24:6+2=69

Также интересными являются упражнения следующего вида:

• 1. Расставьте скобки так, чтобы равенства были верными:
• 25-17:4=2 3*6-4=6
• 24:8-2=4
• 2. Поставьте вместо звездочек знаки «+» или «-» так, чтобы получились верные равенства:
• 38*3*7=34
• 38*3*7=28
• 38*3*7=42
• 38*3*7=48
• 3. Поставьте вместо звездочек знаки арифметических действий так, чтобы равенства были верными:
• 12*6*2=4
• 12*6*2=70
• 12*6*2=24
• 12*6*2=9
• 12*6*2=0

Выполняя такие упражнения, учащиеся убеждаются в том, что значение выражения может измениться, если изменяется порядок действий.

Для усвоения правил порядка действий необходимо в 3 и 4 классах включать все более усложняющиеся выражения, при вычислении значений которых ученик применял бы каждый раз не одно, а два или три правила порядка выполнения действий, например:

• 90*8- (240+170)+190,
• 469148-148*9+(30 100 — 26909).

При этом числа следует подбирать так, чтобы они допускали выполнение действий в любом порядке, что создает условия для сознательного применения изученных правил.

Альфа обозначает действительное число. Знак равенства в приведенных выражениях свидетельствует о том, что если к бесконечности прибавить число или бесконечность, ничего не изменится, в результате получится такая же бесконечность. Если в качестве примера взять бесконечное множество натуральных чисел, то рассмотренные примеры можно представить в таком виде:

Для наглядного доказательства своей правоты математики придумали много разных методов . Лично я смотрю на все эти методы, как на пляски шаманов с бубнами. По существу, все они сводятся к тому, что либо часть номеров не занята и в них заселяются новые гости, либо к тому, что часть посетителей вышвыривают в коридор, чтобы освободить место для гостей (очень даже по-человечески). Свой взгляд на подобные решения я изложил в форме фантастического рассказа о Блондинке. На чем основываются мои рассуждения? Переселение бесконечного количества посетителей требует бесконечно много времени. После того, как мы освободили первую комнату для гостя, один из посетителей всегда будет идти по коридору из своего номера в соседний до скончания века.

Конечно, фактор времени можно тупо игнорировать, но это уже будет из разряда «дуракам закон не писан». Всё зависит от того, чем мы занимаемся: подгоняем реальность под математические теории или наоборот.

Что же такое «бесконечная гостиница»? Бесконечная гостиница — это гостиница, в которой всегда есть любое количество свободных мест, независимо от того, сколько номеров занято. Если все номера в бесконечном коридоре «для посетителей» заняты, есть другой бесконечный коридор с номерами «для гостей». Таких коридоров будет бесконечное множество. При этом у «бесконечной гостиницы» бесконечное количество этажей в бесконечном количестве корпусов на бесконечном количестве планет в бесконечном количестве вселенных, созданных бесконечным количеством Богов. Математики же не способны отстраниться от банальных бытовых проблем: Бог-Аллах-Будда — всегда только один, гостиница — она одна, коридор — только один. Вот математики и пытаются подтасовывать порядковые номера гостиничных номеров, убеждая нас в том, что можно «впихнуть невпихуемое».

Логику своих рассуждений я вам продемонстрирую на примере бесконечного множества натуральных чисел. Для начала нужно ответить на очень простой вопрос: сколько множеств натуральных чисел существует — одно или много? Правильного ответа на это вопрос не существует, поскольку числа придумали мы сами, в Природе чисел не существует. Да, Природа отлично умеет считать, но для этого она использует другие математические инструменты, не привычные для нас. Как Природа считает, я вам расскажу в другой раз. Поскольку числа придумали мы, то мы сами будем решать, сколько множеств натуральных чисел существует. Рассмотрим оба варианта, как и подобает настоящим ученым.

Вариант первый. «Пусть нам дано» одно-единственное множество натуральных чисел, которое безмятежно лежит на полочке. Берем с полочки это множество. Всё, других натуральных чисел на полочке не осталось и взять их негде. Мы не можем к этому множеству прибавить единицу, поскольку она у нас уже есть. А если очень хочется? Без проблем. Мы можем взять единицу из уже взятого нами множества и вернуть её на полочку. После этого мы можем взять с полочки единицу и прибавить её к тому, что у нас осталось. В результате мы снова получим бесконечное множество натуральных чисел. Записать все наши манипуляции можно так:

Я записал действия в алгебраической системе обозначений и в системе обозначений, принятой в теории множеств, с детальным перечислением элементов множества. Нижний индекс указывает на то, что множество натуральных чисел у нас одно и единственное. Получается, что множество натуральных чисел останется неизменным только в том случае, если из него вычесть единицу и прибавить эту же единицу.

Вариант второй. У нас на полочке лежит много разных бесконечных множеств натуральных чисел. Подчеркиваю — РАЗНЫХ, не смотря на то, что они практически не отличимы. Берем одно из этих множеств. Потом из другого множества натуральных чисел берем единицу и прибавляем к уже взятому нами множеству. Мы можем даже сложить два множества натуральных чисел. Вот что у нас получится:

Нижние индексы «один» и «два» указывают на то, что эти элементы принадлежали разным множествам. Да, если к бесконечному множеству прибавить единицу, в результате получится тоже бесконечное множество, но оно не будет таким же, как первоначальное множество. Если к одному бесконечному множеству прибавить другое бесконечное множество, в результате получится новое бесконечное множество, состоящее из элементов первых двух множеств.

Множество натуральных чисел используется для счета так же, как линейка для измерений. Теперь представьте, что к линейке вы добавили один сантиметр. Это уже будет другая линейка, не равная первоначальной.

Вы можете принимать или не принимать мои рассуждения — это ваше личное дело. Но если когда-то вы столкнетесь с математическими проблемами, задумайтесь, не идете ли вы по тропе ложных рассуждений, протоптанной поколениями математиков. Ведь занятия математикой, прежде всего, формируют у нас устойчивый стереотип мышления, а уже потом добавляют нам умственных способностей (или наоборот, лишают нас свободомыслия).

воскресенье, 4 августа 2019 г.

Дописывал постскриптум к статье о и увидел в Википедии этот замечательный текст:

Читаем: «… богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приемов, лишенных общей системы и доказательной базы.»

Вау! Какие мы умные и как хорошо можем видеть недостатки других. А слабо нам посмотреть на современную математику в таком же разрезе? Слегка перефразируя приведенный текст, лично у меня получилось следующее:

Богатая теоретическая основа современной математики не имеет целостного характера и сводится к набору разрозненных разделов, лишенных общей системы и доказательной базы.

За подтверждением своих слов я далеко ходить не буду — имеет язык и условные обозначения, отличные от языка и условных обозначений многих других разделов математики. Одни и те же названия в разных разделах математики могут иметь разный смысл. Наиболее очевидным ляпам современной математики я хочу посвятить целый цикл публикаций. До скорой встречи.

суббота, 3 августа 2019 г.

Как разделить множество на подмножества? Для этого необходимо ввести новую единицу измерения, присутствующую у части элементов выбранного множества. Рассмотрим пример.

Пусть у нас есть множество А , состоящее из четырех человек. Сформировано это множество по признаку «люди» Обозначим элементы этого множества через букву а , нижний индекс с цифрой будет указывать на порядковый номер каждого человека в этом множестве. Введем новую единицу измерения «половой признак» и обозначим её буквой b . Поскольку половые признаки присущи всем людям, умножаем каждый элемент множества А на половой признак b . Обратите внимание, что теперь наше множество «люди» превратилось в множество «люди с половыми признаками». После этого мы можем разделить половые признаки на мужские bm и женские bw половые признаки. Вот теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, безразлично какой — мужской или женский. Если он присутствует у человека, тогда умножаем его на единицу, если такого признака нет — умножаем его на ноль. А дальше применяем обычную школьную математику. Смотрите, что получилось.

После умножения, сокращений и перегруппировок, мы получили два подмножества: подмножество мужчин Bm и подмножество женщин Bw . Приблизительно так же рассуждают математики, когда применяют теорию множеств на практике. Но в детали они нас не посвящают, а выдают готовый результат — «множество людей состоит из подмножества мужчин и подмножества женщин». Естественно, у вас может возникнуть вопрос, насколько правильно применена математика в изложенных выше преобразованиях? Смею вас заверить, по сути преобразований сделано всё правильно, достаточно знать математическое обоснование арифметики, булевой алгебры и других разделов математики. Что это такое? Как-нибудь в другой раз я вам об этом расскажу.

Что касается надмножеств, то объединить два множества в одно надмножество можно, подобрав единицу измерения, присутствующую у элементов этих двух множеств.

Как видите, единицы измерения и обычная математика превращают теорию множеств в пережиток прошлого. Признаком того, что с теорией множеств не всё в порядке, является то, что для теории множеств математики придумали собственный язык и собственные обозначения. Математики поступили так, как когда-то поступали шаманы. Только шаманы знают, как «правильно» применять их «знания». Этим «знаниям» они обучают нас.

В заключение, я хочу показать вам, как математики манипулируют с .

понедельник, 7 января 2019 г.

В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как она звучит:

Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.

Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.

С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.

Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».

Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:

За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.

Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.

Другая интересная апория Зенона повествует о летящей стреле:

Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.

В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.

среда, 4 июля 2018 г.

Я вам уже рассказывал, что , при помощи которой шаманы пытаются сортировать » » реальности. Как же они это делают? Как фактически происходит формирование множества?

Давайте внимательно разберемся с определением множества: «совокупность различных элементов, мыслимая как единое целое». А теперь почувствуйте разницу между двумя фразами: «мыслимое как единое целое» и «мыслимое как целое». Первая фраза — это конечный результат, множество. Вторая фраза — это предварительная подготовка к формированию множества. На этом этапе реальность разбивается на отдельные элементы («целое») из которых потом будет сформировано множество («единое целое»). При этом фактор, позволяющий объединить «целое» в «единое целое», внимательно отслеживается, иначе у шаманов ничего не получится. Ведь шаманы заранее знают, какое именно множество они хотят нам продемонстрировать.

Покажу процесс на примере. Отбираем «красное твердое в пупырышку» — это наше «целое». При этом мы видим, что эти штучки есть с бантиком, а есть без бантика. После этого мы отбираем часть «целого» и формируем множество «с бантиком». Вот так шаманы добывают себе корм, привязывая свою теорию множеств к реальности.

А теперь сделаем маленькую пакость. Возьмем «твердое в пупырышку с бантиком» и объединим эти «целые» по цветовому признаку, отобрав красные элементы. Мы получили множество «красное». Теперь вопрос на засыпку: полученные множества «с бантиком» и «красное» — это одно и то же множество или два разных множества? Ответ знают только шаманы. Точнее, сами они ничего не знают, но как скажут, так и будет.

Этот простой пример показывает, что теория множеств совершенно бесполезна, когда речь заходит о реальности. В чем секрет? Мы сформировали множество «красное твердое в пупырышку с бантиком». Формирование происходило по четырем разным единицам измерения: цвет (красное), прочность (твердое), шероховатость (в пупырышку), украшения (с бантиком). Только совокупность единиц измерения позволяет адекватно описывать реальные объекты на языке математики . Вот как это выглядит.

Буква «а» с разными индексами обозначает разные единицы измерения. В скобках выделены единицы измерения, по которым выделяется «целое» на предварительном этапе. За скобки вынесена единица измерения, по которой формируется множество. Последняя строчка показывает окончательный результат — элемент множества. Как видите, если применять единицы измерения для формирования множества, тогда результат не зависит от порядка наших действий. А это уже математика, а не пляски шаманов с бубнами. Шаманы могут «интуитивно» придти к такому же результату, аргументируя его «очевидностью», ведь единицы измерения не входят в их «научный» арсенал.

При помощи единиц измерения очень легко разбить одно или объединить несколько множеств в одно надмножество. Давайте более внимательно рассмотрим алгебру этого процесса.

суббота, 30 июня 2018 г.

Если математики не могут свести понятие к другим понятиям, значит они ничего не понимают в математике. Отвечаю на : чем элементы одного множества отличаются от элементов другого множества? Ответ очень простой: числами и единицами измерения.

Это сегодня всё, что мы не возьмем, принадлежит какому-либо множеству (как нас уверяют математики). Кстати, вы в зеркале видели у себя на лбу список тех множеств, к которым принадлежите именно вы? И я такого списка не видел. Скажу больше — ни одна вещь в реальности не имеет бирочки со списком множеств, к которым эта вещь принадлежит. Множества — это всё выдумки шаманов. Как они это делают? Давайте заглянем немного в глубь истории и посмотрим, как выглядели элементы множества до того, как математики-шаманы растащили их по своим множествам.

Давним-давно, когда о математике ещё никто и не слышал, а кольца были только у деревьев и у Сатурна, огромные стада диких элементов множеств бродили по физическим полям (ведь математических полей шаманы ещё не придумали). Выглядели они приблизительно так.

Да, не удивляйтесь, с точки зрения математики все элементы множеств больше всего похожи на морских ежей — из одной точки, как иголки, во все стороны торчат единицы измерений. Для тех, кто , напоминаю, что любую единицу измерения геометрически можно представить как отрезок произвольной длины, а число — как точку. Геометрически любую величину можно представить как пучок отрезков, торчащих в разные стороны из одной точки. Эта точка — точка ноль. Рисовать это произведение геометрического искусства я не буду (нет вдохновения), но вы легко это можете представить.

Какие же единицы измерения образуют элемент множества? Всякие, описывающие данный элемент с разных точек зрения. Это и древние единицы измерения, которыми пользовались наши предки и о которых все давно забыли. Это и современные единицы измерения, которыми мы пользуемся сейчас. Это и неизвестные нам единицы измерения, которые придумают наши потомки и которыми будут пользоваться они для описания реальности.

С геометрией мы разобрались — предлагаемая модель элементов множества имеет четкое геометрическое представление. А как с физикой? Единицы измерения — это и есть прямая связь математики с физикой. Если шаманы не признают единицы измерения как полноправный элемент математических теорий — это их проблемы. Настоящую науку математику без единиц измерения лично я уже не представляю. Вот почему в самом начале рассказа о теории множеств я говорил о ней как о каменном веке.

Но перейдем к самому интересному — к алгебре элементов множеств. Алгебраически любой элемент множества представляет из себя произведение (результат умножения) разных величин.Выглядит это так.

Я умышленно не применял условные обозначения, принятые в теории множеств, поскольку мы рассматриваем элемент множества в естественной среде обитания до возникновения теории множеств. Каждая пара буковок в скобках обозначает отдельную величину, состоящую из числа, обозначенного буквой «n » и единицы измерения, обозначенной буквой «a «. Индексы возле буковок указывают на то, что числа и единицы измерения — разные. Один элемент множества может состоять из бесконечного числа величин (на сколько у нас и наших потомков хватит фантазии). Каждая скобка геометрически изображается отдельным отрезком. В примере с морским ежом одна скобка — это одна иголка.

Как шаманы формируют множества из разных элементов? Фактически, по единицам измерения или по числам. Ничего не понимая в математике, они берут разных морских ежей и внимательно их рассматривают в поисках той единственной иголки, по которой они формируют множество. Если такая иголка есть, значит этот элемент принадлежит множеству, если такой иголки нет — это элемент не из этого множества. Нам же шаманы рассказывают басни о мыслительных процессах и едином целом.

Как вы уже догадались, один и тот же элемент может принадлежать к самым разным множествам. Дальше я вам покажу, как формируются множества, подмножества и прочая шаманская галиматья. Как видите, «во множестве не может быть двух идентичных элементов», но если идентичные элементы во множестве есть, такое множество называется «мультимножество». Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.

Когда-то инженеры, построившие мост, во время испытаний моста находились в лодке под мостом. Если мост обрушивался, бездарный инженер погибал под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.

Как бы математики не прятались за фразой «чур, я в домике», точнее «математика изучает абстрактные понятия», есть одна пуповина, которая неразрывно связывает их с реальностью. Этой пуповиной являются деньги. Применим математическую теорию множеств к самим математикам.

Мы очень хорошо учили математику и сейчас сидим в кассе, выдаем зарплату. Вот приходит к нам математик за своими деньгами. Отсчитываем ему всю сумму и раскладываем у себя на столе на разные стопки, в которые складываем купюры одного достоинства. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.

В первую очередь, сработает логика депутатов: «к другим это применять можно, ко мне — низьзя!». Дальше начнутся уверения нас в том, что на купюрах одинакового достоинства имеются разные номера купюр, а значит их нельзя считать одинаковыми элементами. Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…

А теперь у меня самый интересный вопрос: где проходит та грань, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой грани не существует — всё решают шаманы, наука здесь и близко не валялась.

Вот смотрите. Мы отбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинакова — значит у нас получилось мультимножество. Но если рассматривать названия этих же стадионов — у нас получается множество, ведь названия разные. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.

Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая её к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких «мыслимое как не единое целое» или «не мыслимое как единое целое».

Начальная школа подходит к концу, скоро ребёнок шагнёт в углубленный мир математики. Но уже в этот период школьник сталкивается с трудностями науки. Выполняя простое задание, ребёнок путается, теряется, что в результате приводит к отрицательной отметке за выполненную работу. Чтобы избежать подобных неприятностей, нужно при решении примеров, уметь ориентироваться в порядке, по которому нужно решать пример. Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.

Перед выполнением задания попросите своё чадо пронумеровать действия, которые он собирается выполнить. Если возникли затруднения – помогите.

Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:

Если в задании необходимо выполнить ряд действий, нужно сначала выполнить деление или умножение, затем . Все действия выполняются по ходу письма. В противном случае, результат решения будет не верным.

Если в примере требуется выполнить , выполняем по порядку, слева направо.

27-5+15=37 (при решении примера руководствуемся правилом. Сначала выполняем вычитание, затем – сложение).

Научите ребёнка всегда планировать и нумеровать выполняемые действия.

Ответы на каждое решённое действие записываются над примером. Так ребёнку гораздо легче будет ориентироваться в действиях.

Рассмотрим ещё один вариант, где необходимо распределить действия по порядку:

Как видим, при решении соблюдено правило, сначала ищем произведение, после — разность.

Это простые примеры, при решении которых, необходима внимательность. Многие дети впадают в ступор при виде задания, в котором присутствует не только умножение и деление, но и скобки. У школьника, не знающего порядок выполнения действий, возникают вопросы, которые мешают выполнить задание.

Как говорилось в правиле, сначала найдём произведение или частное, а потом всё остальное. Но тут же есть скобки! Как поступить в этом случае?

Решение примеров со скобками

Разберём конкретный пример:

• При выполнении данного задания, сначала найдём значение выражения, заключённого в скобки.
• Начать следует с умножения, далее – сложение.
• После того, как выражение в скобках решено, приступаем к действиям вне их.
• По правилам порядка действий, следующим шагом будет умножение.
• Завершающим этапом станет .

Как видим на наглядном примере, все действия пронумерованы. Для закрепления темы предложите ребёнку решить самостоятельно несколько примеров:

Порядок, по которому следует вычислять значение выражения уже расставлен. Ребёнку останется только выполнить непосредственно решение.

Усложним задачу. Пусть ребёнок найдёт значение выражений самостоятельно.

7*3-5*4+(20-19) 14+2*3-(13-9)
17+2*5+(28-2) 5*3+15-(2-1*2)
24-3*2-(56-4*3) 14+12-3*(21-7)

Приучите ребёнка решать все задания в черновом варианте. В таком случае, у школьника будет возможность исправить не верное решение или помарки. В рабочей тетради исправления не допустимы. Выполняя самостоятельно задания, дети видят свои ошибки.

Родители, в свою очередь, должны обратить внимание на ошибки, помочь ребёнку разобраться и исправить их. Не стоит нагружать мозг школьника большими объёмами заданий. Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.

Делайте перерыв. Ребёнок должен отвлекаться и отдыхать от занятий. Главное помнить, что не все обладают математическим складом ума. Может из вашего ребёнка вырастет знаменитый философ.

И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .

В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.

Навигация по странице.

Сначала умножение и деление, затем сложение и вычитание

В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :

• действия выполняются по порядку слева направо,
• причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.

Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.

Пример.

Выполните действия 7−3+6 .

Решение.

Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .

Кратко решение можно записать так: 7−3+6=4+6=10 .

Ответ:

7−3+6=10 .

Пример.

Укажите порядок выполнения действий в выражении 6:2·8:3 .

Решение.

Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.

Ответ:

Сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.

Пример.

Вычислите значение выражения 17−5·6:3−2+4:2 .

Решение.

Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .

Ответ:

17−5·6:3−2+4:2=7 .

На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .

Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.

Действия первой и второй ступени

В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.

Определение.

Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .

В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).

Порядок выполнения арифметических действий в выражениях со скобками

Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Пример.

Выполните указанные действия 5+(7−2·3)·(6−4):2 .

Решение.

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .

Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .

Ответ:

5+(7−2·3)·(6−4):2=6 .

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Пример.

Выполните действия в выражении 4+(3+1+4·(2+3)) .

Решение.

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .

Ответ:

4+(3+1+4·(2+3))=28 .

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .

Порядок выполнения действий первой и второй ступени по фгос Перспективная начальная школа

Прежде чем приступить к изучению новой темы, я предлагаю провести математический диктант. Откройте тетради, запишите число, месяц, классная работа.

На 3 слайде выражения, на которые вам необходимо в тетради записать только ответы.

1. Какое число надо умножить на 7, чтобы получить 42? (6)

2. Запишите число, которое меньше 24 на 6. (18)

3. Из какого числа надо вычесть 18, чтобы получить 3? (21)

4. Запишите значение произведения 9 и 3. (27)

5. Увеличьте 7 в 6 раз. (42)

6. Найдите сумму чисел 25 и 33. (58)

7. Какое число больше 28 на 4? (32 )

8.Чему равна разность чисел 25 и 8? (17).

— А сейчас обменяйтесь тетрадями, проверти ответы которые вы видите на 4 слайде. Оцените работу соседа:

Правильные ответы:

7-8 ответов – 5 баллов

5-6 ответа – 4 балла

4 ответа – 3 балла

— На парте у каждого лежит лист самооценки. В первой колонке, где написано «Математический диктант», выставите себе тот балл, который вам поставил сосед по парте.

Молодцы все справились. А теперь игра «Сортировщик». Обратите на 5 слайде даны примеры, вам нужно их разделить на два столбика. Что мы будем сортировать?.

Игра «Сортировщик»

3+8-5= 6 4*3:6= 2 5+7*2=19
2+2+2+2= 8 18:3:3=2

19-9-10=0

7-4=3

Выбери выражения, состоящие только из сложения и вычитания ( в 1столбик)

Только из умножения и деления (во 2 столбик) Сложение и вычитание – действия первой ступени
Умножение и деление – действие 2 ступени.

Знаем как решать такие примеры.(Да) В каком порядке выполняли вычисления( по порядку слева направо) 6 слайд

Оцените свою работу в игре «Сортировщик». Если все примеры разделили на 3 столбика без ошибок ставите себе 5 баллов, если есть одна ошибка 4 балла, 2 ошибки – 3 балла

Сложение

Вычитание

Умножение

Деление

Действия
первой ступени

Действия
второй ступени

Назовите выражение, в котором есть действия первой и второй ступени

Найдите значение выражения.(запишите ответы в тетрадь)

Выполняют задания математического диктанта.

Меняются тетрадями и производят взаимопроверку.

Выставляют баллы в лист самооценки.

Делят выражения на 2 столбика

1 столбик – сложение, вычитание

2 столбик – умножение, деление

Оценивают свою работу игры «Сортировщик» в листах самооценки

Конспект урока ««Порядок выполнения действий в выражениях без скобок и со скобками».»

Тема урока: «Порядок выполнения действий в выражениях без скобок и со скобками».

Цель урока: создать условия для закрепления умений применять знания о порядке выполнения действий в выражениях без скобок и со скобками в различных ситуациях, умений решать задачи выражением.

Задачи урока.

Образовательные:

— закрепить знания учащихся о правилах выполнения действий  в  выражениях без скобок и со скобками; формировать у них умение пользоваться этими  правилами при вычислении конкретных выражений; совершенствовать  вычислительные навыки; повторить табличные случаи умножения и деления;

Развивающие:

— развивать вычислительные навыки, логическое мышление, внимание, память, познавательные способности учащихся,

коммуникативные навыки;

Воспитательные: 

— воспитывать толерантное  отношение друг к другу, взаимное сотрудничество,

культуру поведения на уроке, аккуратность, самостоятельность,  воспитывать интерес к занятиям  математикой.

Формируемые УУД:

Регулятивные УУД:

работать по предложенному плану, инструкции;

выдвигать свои гипотезы на основе учебного материала;

 осуществлять самоконтроль.

Познавательные УУД:

знать правила порядка выполнения действий:

уметь разъяснить их содержание;

понимать правило порядка выполнения действий;

находить значения выражений согласно правилам порядка выполнения;

действий, используя для этого текстовые задачи;

 записывать решение задачи выражением;

 применять правила порядка выполнения действий;

уметь применять полученные знания при выполнении контрольной работы.

Коммуникативные УУД:

слушать и понимать речь других;

 выражать свои мысли с достаточной полнотой и точностью;

 допускать возможность различных точек зрения, стремиться понимать позицию собеседника;

работать в команде разного наполнения (паре, малой группе, целым классом), участвовать в обсуждениях, работая в паре;

Личностные УУД:

устанавливать связь между  целью деятельности и её результатом;

определять общие для всех правила поведения;

  уметь осознанно и внимательно читать задания;

выражать способность к самооценке на основе критерия успешности учебной деятельности.

Планируемый результат:

Предметные:

Знать правила порядка выполнения действий.

Уметь разъяснить их содержание.

Уметь решать задачи с помощью выражений.

Личностные:
Уметь проводить самооценку на основе критерия успешности учебной деятельности.

Метапредметные:

Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану;  оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки;  планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение(Регулятивные УУД).

Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им  (Коммуникативные УУД).

Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД).

Ход урока

1. Организационный  момент. 

Чтоб урок наш стал светлее,

Мы поделимся добром.

Вы ладони протяните,

В них любовь свою вложите,

Ей с друзьями поделитесь

И друг другу улыбнитесь.

— Займите свои рабочие места.

Открыли тетради, записали число и классная работа.

2. Актуализация знаний.

— На уроке нам с вами предстоит подробно рассмотреть порядок выполнения арифметических действий в выражениях без скобок и со скобками.

Устный счёт.

Игра «Найди правильный ответ».

( У каждого ученика лист с числами)

55	56	57	58	59	60	61
62	63	64	65	66	67	68
69	70	71	72	73	74	75
76	77	78	79	80	81	82
83	84	85	86	87	88	89
90	91	92	93	94	95	96
97	98	99	100	101	102	103

— Я читаю задания, а вы, выполнив в уме действия, должны полученный результат, т. е. ответ, зачеркнуть крестиком.

1. Я задумала число, из него вычла 80, получила 18. Какое число я задумала? (98)

2. Я задумала число, к нему прибавила 12, получила 70. Какое число я задумала? (58)

3. Первое слагаемое 90, второе слагаемое 12. Найдите сумму. (102)

— Соедините полученные результаты.

— Какую геометрическую фигуру вы получили? ( Треугольник)

— Расскажите, что вы знаете о данной геометрической фигуре. (Имеет 3 стороны, 3 вершины, 3 угла)

— Продолжаем работать по карточке.

1. Найдите разность чисел 100 и 22. (78)

2. Уменьшаемое 99, вычитаемое 19. Найдите разность. (80).

3. Возьмите число 25 4 раза. (100)

— Начертите внутри треугольника еще 1 треугольник, соединяя полученные результаты.

— Сколько треугольников получилось? (5)

3. Работа над темой урока. Наблюдение за изменением значения выражения от порядка выполнения арифметических действий

В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.

А в математике обязательно ли выполнять арифметические действия в определенном порядке?

Давайте проверим

Сравним выражения: 
8-3+4 и 8-3+4

Видим, что оба выражения совершенно одинаковы.

Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий

В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.

Запишем.

8-3+4=5+4=9

Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.

8-3+4=8-7=1

Видим, что значения выражений получаются разные.

Сделаем вывод: порядок выполнения арифметических действий менять нельзя.

Порядок выполнения арифметических действий в выражениях без скобок

Узнаем правило выполнения арифметических действий в выражениях без скобок.

Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.

Потренируемся.

Рассмотрим выражение

38-10+6

В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени.

Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий

Рассмотрим второе выражение

24:3*2

В этом выражении имеются только действия умножения и деления – это действия второй ступени.

Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий

В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Рассмотрим выражение.

18:2-2*3+12:3

Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.

    1   4  2  5    3

18:2-2*3+12:3

Вычислим значение выражения.

    1   4  2  5    3

18:2-2*3+12:3=9-6+4=3+4=7

Порядок выполнения арифметических действий в выражениях со скобками

В каком порядке выполняются арифметические действия, если в выражении имеются скобки?

Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.

Рассмотрим выражение.

30 + 6 * (13 — 9)

Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.

     3   2      1

30 + 6 * (13 — 9)

Вычислим значение выражения.

3    2   1

30+6*(13-9)=30+6*4=30+24=54

Правило выполнения арифметических действий в выражениях без скобок и со скобками

Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?

Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:

1. действия, записанные в скобках;

2. умножение и деление;

3. сложение и вычитание.

Схема поможет запомнить это несложное правило (рис. 4).

Рис. 4. Порядок действий

4. Закрепление Выполнение тренировочных заданий на изученное правило

Потренируемся.

Рассмотрим выражения, установим порядок действий и выполним вычисления.

43 — (20 — 7) +15

32 + 9 * (19 — 16)

2 * 9 — 18:3

Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.

2*9-18:3=18-6=12

Узнаем, правильно ли определен порядок действий в следующих выражениях.

     4    3    1   2

37 + 9 — 6 : 2 * 3 =

    3       1     2

18 : (11 — 5) + 47=

   1  3       2

7 * 3 — (16 + 4)=

Рассуждаем так.

     3     4   1   2

37 + 9 — 6 : 2 * 3 =

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

     3 4  1  2

37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37

Продолжаем рассуждать.

    3    1    2

18:(11-5)+47=

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

    2    1    3

18:(11-5)+47=18:6+47=3+47=50

Рассуждаем далее.

  1  3     2

7*3-(16+4)=

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

 

   2  3   1

7*3-(16+4)=7*3-20=21-20=1

Выполним задание.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

5. Подведение итогов.

— Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками. В ходе выполнения заданий определяли, зависит ли значение выражений от порядка выполнения арифметических действий, узнали, отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренировались в применении изученного правила, искали и исправляли ошибки, допущенные при определении порядка действий.

Числовые выражения

Числовые выражения.

Числовое выражение – это любая запись из чисел, знаков арифметических действий и скобок. Числовое выражение может состоять и просто из одного числа. Напомним, что основными арифметическими действиями являются «сложение», «вычитание», «умножение» и «деление». Этим действиям соответствуют знаки «+», «-», «∙», «:».

Конечно же, чтобы у нас получилось числовое выражение, запись из чисел и арифметических знаков должна быть осмысленной. Так, например, такую запись 5 : + ∙  нельзя назвать числовым выражением, так как это случайный набор символов, не имеющий смысла. Напротив, 5 + 8 ∙ 9 — уже настоящее числовое выражение.

Значение числового выражения.

Сразу скажем, что если мы выполним действия указанные в числовом выражении, то в результате мы получим число. Это число называется значением числового выражения.

Попробуем вычислить, что у нас получится в результате выполнения действий нашего примера. Согласно порядку выполнения арифметических действий, сначала выполним операцию умножения. Умножим 8 на 9. Получим 72. Теперь сложим 72 и 5. Получим 77.
Итак, 77 – значение числового выражения 5 + 8 ∙ 9.

Числовое равенство.

Можно это записать таким образом: 5 + 8 ∙ 9 = 77. Здесь мы впервые использовали знак «=» («Равно»). Такая запись, при которой два числовых выражения разделены знаком «=», называется числовым равенством. При этом, если значения левой и правой части равенства совпадают, то равенство называют верным. 5 + 8 ∙ 9 = 77 – верное равенство.
Если же мы напишем 5 + 8 ∙ 9 = 100, то это уже будет неверное равенство, так как значения левой и правой части данного равенства уже не совпадают.

Следует отметить, что в числовом выражении мы также можем использовать скобки. Скобки влияют на порядок выполнения действий. Так, например, видоизменим наш пример, добавив скобки: (5 + 8) ∙ 9. Теперь сначала нужно сложить 5 и 8. Получим 13. А затем умножить 13 на 9. Получим 117. Таким образом, (5 + 8) ∙ 9 = 117.
117 – значение числового выражения (5 + 8 ) ∙ 9.

Как прочитать числовое выражение?

Чтобы правильно прочитать выражение, нужно определить какое именно действие выполняется последним для вычисления значения данного числового выражения. Так, если последнее действие вычитание, то выражение называют «разностью». Соответственно, если последнее действие сумма — «суммой», деление – «частным», умножение – «произведением», возведение в степень – «степенью».

Например, числовое выражение (1+5)(10-3) читается так: «произведение суммы чисел 1 и 5 на разность чисел 10 и 3».

Примеры числовых выражений.

Приведем пример более сложного числового выражения:

\[\left( \frac{1}{4}+3,75 \right):\frac{1,25+3,47+4,75-1,47}{4\centerdot 0,5}\]

В данном числовом выражении используются простые числа, обыкновенные и десятичные дроби. Также используются знаки сложения, вычитания, умножения и деления. Черта дроби также заменяет знак деления. При кажущейся сложности, найти значение данного числового выражения довольно просто. Главное уметь выполнять операции с дробями, а также внимательно и аккуратно делать вычисления, соблюдая порядок выполнения действий.

В скобках у нас выражение $\frac{1}{4}+3,75$. Преобразуем десятичную дробь 3,75 в обыкновенную.

$3,75=3\frac{75}{100}=3\frac{3}{4}$

Итак, $\frac{1}{4}+3,75=\frac{1}{4}+3\frac{3}{4}=4$

Далее, в числителе дроби \[\frac{1,25+3,47+4,75-1,47}{4\centerdot 0,5}\] у нас выражение 1,25+3,47+4,75-1,47. Для упрощения данного выражения применим переместительный закон сложения, который гласит: «От перемены мест слагаемых сумма не изменяется». То есть, 1,25+3,47+4,75-1,47=1,25+4,75+3,47-1,47=6+2=8.

В знаменателе дроби выражение $4\centerdot 0,5=4\centerdot \frac{1}{2}=4:2=2$

Получаем $\left( \frac{1}{4}+3,75 \right):\frac{1,25+3,47+4,75-1,47}{4\centerdot 0,5}=4:\frac{8}{2}=4:4=1$

Когда числовые выражения не имеют смысла?

Рассмотрим еще один пример. В знаменателе дроби $\frac{5+5}{3\centerdot 3-9}$ значением выражения $3\centerdot 3-9$ является 0. А, как мы знаем, деление на нуль невозможно. Следовательно, у дроби $\frac{5+5}{3\centerdot 3-9}$ нет значения. Про числовые выражения, у которых нет значения, говорят, что они «не имеют смысла».

Если мы в числовом выражении помимо чисел будем использовать буквы, то у нас получится уже алгебраическое выражение.

Дата публикации: 30.08.2014 10:58 UTC

Теги: числовые выражения :: 7 класс

---

Смотрите также учебники, книги и учебные материалы:

Следующие учебники и книги:

Предыдущие статьи:

• Уроки математики, Пособие для учителей, 2 класс, Дорофеев Г.В., Миракова Т.Н., 2009
• Математика, 6 класс, Методические рекомендации, Суворова С.Б., Кузнецова Л.В., Минаева С.С., Рослова Л.О., 2013
• Математика, 6 класс, Методические рекомендации, Потапов М.К., Шевкин А.В., 2013
• Математика, 5 класс, Методические рекомендации, Суворова С.Б., Кузнецова Л.В., Минаева С.С., Рослова Л.О., 2013

---

абстрактной алгебры — Порядок операций — почему они в том порядке, в котором они находятся?

При просмотре сообщений о математике на r / askscience, я натолкнулся на тот же вопрос!

---

u / KyleG подтверждает этот комментарий:

Это произвольно, потому что вся письменная математика является произвольной символической обозначение изобретено людьми. Есть много языков программирования и другие типы систем обозначений, которые не соответствуют PEMDAS. Для Например, обратная польская нотация (которую предпочитали ранние компьютерные ученых) пишется «операнд-операнд-оператор».»Так, например, 3 4 + 7 / оценивается как 1, потому что слева направо 3 4 + оценивается как 3 + 4 = 7. Тогда у вас есть 7 /, поэтому 7, полученное из 3 4 +, вы делите на 7.

http://en.wikipedia.org/wiki/Reverse_polish_notation

Как бы то ни было, экспоненты и скобки относительно недавние дополнения к математической нотации, поэтому имеет смысл, что наши произвольно определенная система письма адаптировалась к новым символам с помощью говоря «все работает точно так же, как и раньше, но прежде чем что мы должны делать что-то новое и убирать его с дороги.«

---

Тем не менее, u / paolog отваживается на причину для PEDMAS:

По сути, мы используем PEDMAS, потому что мы нашли его полезным в арифметике и алгебре (хотя есть области математики, где это не обязательно так). Нет ничего, что могло бы помешать нам использовать, скажем, ~~ SAMDEP ~~ PSAMDE, если бы мы захотели, но, если бы мы это сделали, все стало бы очень запутанно. 2 + 5b + 1 $

, и мы знаем, что это означает, что нам нужно вычислить $ a \ times a \ times 4 $ и $ 5 \ times b $, сложить их вместе и добавить 1.2 + 5b + 1 $

  = 4 х (3 х 3) + b + b + b + b + b + 1

  = 3 х 3 + 3 х 3 + 3 х 3 + 3 х 3 + b + b + b + b + b + 1

  = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + b + b + b + b + b + 1
  

Теперь у нас есть только одна операция, поэтому мы можем выполнять сложение в любом порядке, но вы можете видеть, что если мы вернемся к исходному выражению, каждый раз, когда мы собираем слагаемые для умножения, мы получаем один продукт, который необходимо добавил еще один результат. Таким образом, мы складываем вместе продукты, то есть умножение должно предшествовать сложению.Возведение в степень объединяет множимые, готовые к умножению на другие члены, поэтому возведение в степень необходимо выполнить до умножения.

Если мы рассматриваем только целые числа, деление можно рассматривать как просто повторное вычитание, а вычитание — это просто сложение отрицательных членов, следовательно, деление происходит на том же уровне, что и умножение, и вычитание на том же уровне, что и сложение.

Круглые скобки дают нам возможность переопределить существующий порядок, поэтому P должен стоять перед всем остальным, чтобы мы могли легче решать задачи со словами, например, следующие: «Сколько унций овощей в трех пакетах овощной смеси, каждый из которых содержит четыре унции моркови и шести унций гороха? » (Ответ: $ 3 \ times (4 + 6) $ oz = 3 x 10 oz = 30 oz.) Без скобок нам пришлось бы написать $ 3 \ times 4 + 3 \ times 6 $, существенно расширив скобки. Представьте, что круглые скобки содержат какое-то гораздо более сложное выражение — нам нужно было бы написать его полностью несколько раз, если бы круглые скобки были недоступны.

TL; DR: для целых чисел возведение в степень — это повторное умножение и собирает множимые, готовые для умножения или сложения с другими членами, в то время как умножение — это повторное сложение и собирает слагаемые для сложения других членов.2 $ и 3 по x. Затем вы складываете все вместе.

На самом деле это не что иное, как правило набора, вроде «всегда ставьте точку перед кавычкой». В какой-то момент это был самый удобный способ делать что-то, а в какой-то момент его формализовали.

Простая математическая задача разделила Интернет | Статья

.

Математика: это огонь на этой неделе

Математика может быть интересной, но может быть и сложной.

Сложение, вычитание, умножение и деление — числа иногда действительно поражают воображение.

И действительно, это верно для любого возраста, и на этой неделе в Интернете появилось множество мнений об ответе на эту математическую задачу:

Пользователь Twitter с именем @pjmdoll опубликовал уравнение 8 ÷ 2 (2 + 2) =?

Ответ… не сразу понятно, учитывая разнообразие ответов.

Многие в Твиттере были абсолютно уверены, что ответ один.

И многие были уверены, что ответ — 16.

Другие были уверены, что и то, и другое.

Но в целом многим напомнили, почему они не любят математику.

Но каков истинный ответ, особенно если два разных калькулятора дают два разных результата?

На самом деле все сводится к вашему подходу к математике, когда вам требуется выполнить порядок операций.

В Канаде преподают BEDMAS, что означает, что сначала обрабатывается все, что указано в скобках, затем следуют экспоненты, деление или умножение (слева направо) и, наконец, сложение или вычитание (опять же, слева направо).

Это означало бы, что вы должны сначала добавить в скобки (2 + 2), чтобы получить результат четыре.

Остается 8 ÷ 2 (4) =?

Работая слева направо, вы должны сначала позаботиться о делении, поскольку 2 (4) — это операция умножения, а не какая-то случайная работа со скобками.

Разделив восемь на два, вы получите четыре, а это значит, что ваше уравнение теперь будет выглядеть так: 4 (4) =?

Теперь все, что вам нужно сделать, это умножить два числа, получив в итоге 16.

Так почему люди получают результат? Что ж, похоже, это как-то связано с порядком операций, называемым PEMDAS.

Этот метод просит людей сначала сделать круглые скобки (скобки), затем показатели, умножение или деление, а затем сложение или вычитание.

Но здесь все идет немного в сторону: PEMDAS по-прежнему требует от вас деления / умножения и сложения / вычитания слева направо.

Так что результат должен быть таким же: 16.

Но если вы сначала умножите, как это делают некоторые, ответ будет единым.

Math — это хитрый!

What’s Fire This Week — это ваш еженедельный дайджест того, о чем все говорят.

Порядок операций | NZ Maths

Назначение

Цель этого раздела — развить понимание учащимися того, как ведут себя числовые операции, осознать необходимость правил, которые будут направлять нас в том порядке, в котором мы выполняем эти операции, а также интерпретировать и применять эти правила в решения проблемных ситуаций.

Конкретные результаты обучения

• Признайте, что порядок операций имеет значение в практических жизненных ситуациях.
• Поймите и объясните взаимосвязь между сложением и вычитанием, а также между умножением и делением.
• Распознавайте неоднозначность выражений и уравнений, которые включают более одной операции.
• Распознавайте порядок операций в задачах с голосовыми числами.
• Поймите и объясните правила порядка операций, включая объяснение аббревиатуры BEDMAS.
• Применяйте порядок операций для решения проблем.

Описание математики

Когда учащиеся научатся понимать и правильно использовать общие символы для отношений (=, ≠, <,>) и для числовых операций (+ — x ÷), они могут выражать простые математические идеи и проблемные ситуации, используя эти символы, и могут и интерпретировать (и решать) знакомые математические уравнения и выражения. Однако когда они сталкиваются с проблемами, связанными с более чем одной операцией, они могут быть озадачены неоднозначностью некоторых выражений и уравнений.Это может привести к разным толкованиям и результатам. Например, 4 + 2 x 5 = ☐. Это равно 30 или 14?

В устной и письменной речи мы принимаем как должное очень важную пунктуацию, которую мы используем. Спорное утверждение: «Женщина без мужчины — ничто», например, имеет совсем другое значение, когда знаки препинания вставляются так: «Женщина: без нее мужчина — ничто». То же самое и с простой математической задачей, такой как, «Четыре плюс два, умноженные на пять, равно чему?» Или «Четыре плюс два, умноженные на пять, равно чему?»

При отсутствии этой пунктуации были установлены правила, в которых скобки (скобки) и установленный порядок выполнения числовых операций устраняют любую двусмысленность.Хотя научные калькуляторы дают правильные ответы на многоступенчатые уравнения, учащиеся должны понимать необходимость согласованного порядка, знать правильные условные обозначения и уметь применять их для решения задач.

Действия, предлагаемые в этой серии уроков, могут лечь в основу самостоятельных практических заданий.

Ссылки на числовую систему
Мультипликатив
Расширенный мультипликативный

Необходимые ресурсные материалы

• Диаграммная бумага
• Ручки цветные (фломастеры)
• Калькуляторы
• Научные калькуляторы
• Один и два копировщика

Деятельность

Сессия 1

SLO:

• Признайте, что порядок операций имеет значение в практических жизненных ситуациях.
• Поймите и объясните взаимосвязь между сложением и вычитанием, а также между умножением и делением.
• Изучите гипотезы и доказательства.
• Распознавайте неоднозначность выражений и уравнений, которые включают более одной операции.
• Распознавайте порядок операций в задачах с голосовыми числами.

Деятельность 1

1. Распечатайте на карточке наборы утверждений о действиях в Copymaster 1.
   Начните с раздачи по одному каждому ученику в классе.Попросите учащихся всей группой прочитать свои утверждения вслух и внимательно выслушать утверждения друг друга. Затем студенты формируют группы связанных утверждений и согласовывают логический порядок своих утверждений действий.
   Попросите группы представить свои действия для всего класса. Например:
   1. Встаньте с постели. 2. Примите душ. 3. Одевайся. 4. Выйти из дома. 5. Приехать в школу.
2. Пусть некоторые группы затем прочтут их вне очереди , чтобы подчеркнуть факт, что это абсурд, и что существует разумный порядок их действий и что одни действия должны быть выполнены раньше других .

Деятельность 2

1. Попросите учащегося записать в таблице класса числовые операции (используйте этот термин). Попросите учащихся объяснить каждый из символов операций: + — x ÷ .
2. Попросите учащихся попарно обсудить связь между операциями сложения и вычитания, а также между умножением и делением.
   Выделите обратную связь в каждой паре операций.Попросите учащихся объяснить это уравнениями и примерами слов, например:
   30 + 4 = 34 и 34 — 4 = 30
   ‘Пип держит в бумажнике тридцать долларов банкнотами и четыре доллара монетами. Итого тридцать четыре доллара. Она платит четыре доллара за кофе, и у нее остается тридцать долларов ».
   Вычитание отменено сложение. Это обратная операция.
   16 x 4 = 64 и 64 ÷ 4 = 16
   Четыре друга заработали по шестнадцать долларов каждый. Всего работодатель выплатил шестьдесят четыре доллара. Каждый получил свою долю в шестнадцать долларов, так что получилось шестьдесят четыре, разделенные на четыре.
   Деление невыполненного умножения. Это обратная операция.

Деятельность 3

1. См. Задачу упорядочивания действий в действии 1, шаг 1 (выше). Порядок был важен.
   Поза: « В математике порядок, в котором мы выполняем числовые операции, не меняет результат / результат».
   Попросите учащихся обсудить это и указать свое согласие / несогласие и причины своей позиции .
   Запишите и обсудите свои идеи. Основываясь на этом:
2. Напишите это уравнение в таблице классов.
   12 + 4 x 5 — 4 = ☐
   Попросите пары учащихся решить уравнение и объяснить свое решение (я).
   Попросите трех студентов прочитать уравнение вслух тремя разными способами .
   Напишите это, используя слова, подчеркивая различные знаки препинания .
   Двенадцать плюс четыре, умноженное на пять минус четыре, равно семидесяти шести.
   Двенадцать, плюс четыре, умноженные на пять, минус четыре, равно двадцати восьми.
   Двенадцать плюс четыре, умноженное на пять минус четыре, равно шестнадцати.
3. Предложите учащимся поработать в парах, чтобы записать каждую из этих трех интерпретаций в виде уравнений, придумав свою собственную «математическую пунктуацию» . Попросите их поделиться ими и записать их в таблице класса, чтобы другие могли их увидеть. Примите и изучите все предложения.
4. Согласитесь, что скобки полезны, и запишите их. Объясните, что скобки также известны как скобки , скобки .
   (12 + 4) x 5-4 = 76
   12 + (4 x 5) — 4 = 28
   (12 + 4) x (5-4) = 16
5. Предложите учащимся обсудить и предложить возможные практических сценариев для каждого представления проблемы.Например:
   (12 + 4) x 5-4 = 76
   Льюис зарабатывает двенадцать долларов в час за упаковку коробок, но получает бонус в четыре доллара каждый час, если он превышает общее количество коробок, установленное как часовое целевое значение. Он работает пять часов, получая бонус каждый час. Как только он потратит четыре доллара на кофе, у него останется семьдесят шесть долларов.

Деятельность 4

1. Раздайте учащимся бумагу для диаграмм и цветные ручки.
   Попросите пары учащихся вместе написать на диаграммах по крайней мере три своих собственных многоступенчатых уравнений, каждое из которых состоит из слов с пунктуацией и символов .
   Попросите их написать сценарии из реальной жизни хотя бы для одной «версии» каждой из их проблем.
2. Попросите учеников поделиться ими.
   NB. Графики будут добавлены в Сессию 2, когда будет представлена ​​BEDMAS.

Деятельность 5

Завершите занятие, рассмотрев гипотезу, сформулированную в Задании 3, Шаге 1 (выше).
«Порядок, в котором мы выполняем числовые операции, не влияет на результат».
Не согласен с утверждением. Согласитесь, , что порядок, в котором выполняются операции с числами , влияет на результат и что использование скобок помогает нам понять порядок операций.

Сессия 2

SLO:

• Поймите и объясните правила порядка операций, включая объяснение аббревиатуры BEDMAS.
• Применяйте порядок операций для решения проблем.

Деятельность 1

1. Просмотрите порядок действий, предпринятых в начале занятия 1, и выводы из этого занятия.
2. Объясните студентам, что математики согласовали порядок операций или математических действий. Напишите BEDMAS, объяснив, что это аббревиатура от согласованного соглашения.
   Спросите: «Что такое аббревиатура ?»
   Кто может предложить еще одну хорошо известную аббревиатуру?
   Что такое соглашение ?
   Что может означать BEDMAS ?
   Попросите учащихся обсудить каждый из этих вопросов, а затем записать свои идеи рядом с акронимами в таблице класса.(E для экспонент может быть неизвестен).
   B: скобки. E: показатели, D: деление, M: умножение, A: сложение, S: вычитание.
   Объясните, что порядок операций иногда известен как , приоритет операций . Это правило, которое мы используем, чтобы уточнить, какую операцию мы выполняем в первую очередь. (до предшествовать означает прийти (или уйти) раньше или первым.)
   Если не совсем понятно, объясните возведение в степень , демонстрируя, что оно повторяется умножение : т.е. 4 ² = 4 x 4 = 16 , или 10 ³ = 10 x 10 x 10 = 1000

Деятельность 2

1. Раздать Copymaster 2.Объясните, что ученики должны исследовать, как работает BEDMAS, применяя его к уравнениям. Напомните им, что может быть полезно сначала прочитать вслух каждую задачу, чтобы понять уравнение, «услышав» его.
   Попросите учащихся решить задачи в парах. Они должны записать, какую операцию они выполняют в первую очередь, и словами объяснить почему. Им также следует обсудить и записать любые вопросы, которые у них возникают.
2. Попросите учащихся поделиться своими решениями каждого уравнения, объясняя порядок операций, которые они применяли в каждом примере. Сделайте следующие учебных пунктов , как они это делают:
   • Деление и умножение выполняются в том порядке, в котором они появляются, слева направо.
   • Сложение и вычитание выполняются в том порядке, в котором они появляются, слева направо.
   • Обратите внимание на примеры 3, 4, 5, 6, 13 и 15, на эффект использования обратных операций.
   • При решении того, что указано в скобках, применяется порядок операций.

Деятельность 3

1. Соберитесь классом.Попросите учащихся прочитать вслух несколько уравнений, разделяя их запятыми (паузами) там, где выражения находятся в скобках, например:
   9. (25-5) ÷ 5 = ☐
   Двадцать пять минус пять, разделенные на пять, — это равно четырем.
   и расставив показания запятыми (паузами), чтобы распознать порядок операций, например:
   13. 25 + 5 x 5 ÷ 5 ² = ☐
   Двадцать пять плюс, пять раз пять, разделенное на пять в квадрате равно двадцати шести.
2. Сделайте вывод, что порядок, в котором мы выполняем числовые операции, безусловно, действительно меняет результат / результат .

Деятельность 4

Попросите пары учащихся добавить к таблицам, начатым на занятии 1. Объяснить порядок операций своими словами , показать значение аббревиатуры BEDMAS и выделить «эффект пунктуации» скобок.

Сессия 3

SLO:

• Применяйте порядок действий для решения проблем.

Деятельность 1

1. Поза: Принятие соглашения BEDMAS означает, что мы все согласны с величиной неизвестной суммы в уравнении.
   Попросите учащихся обсудить это в парах, а затем поделится с классом, объяснив, почему они согласны или не согласны с утверждением.
2. В ходе обсуждения уточните, что является неизвестным в уравнении, например (25 — 5) ÷ 5 = ☐. Также поясните, что иногда неизвестный (сумма) отображается с буквенным символом , например ‘n’ .

Деятельность 2

1. Раздайте каждому ученику бумагу и карандаши.
   Задайте эту проблему. «Я думаю о числе. Мы назовем этот номер «н». Я добавляю к нему шесть. Я удваиваю это. Это равно двадцати восьми ».
   Спросите: Можете ли вы записать эту задачу в виде уравнения? [Уравнение: (n + 5) x 2 = 28]
2. Попросите некоторых студентов записать свое уравнение в таблице класса. Обсудите идеи студентов, подчеркнув важность использования скобок для обозначения порядка действий.Основное внимание уделяется тому, чтобы правильно записал уравнение в этот момент, не находя значение n.
   Задайте еще две задачи, например:
   «Я думаю о числе. Я вычитаю из него 10. Я делю это на девять. Это равно десяти ». [Уравнение: (n — 10) ÷ 9 = 10]
   «Я думаю о числе. Я вычитаю два. Я возьму в квадрат и получаю двадцать пять ». [Уравнение: (n — 2) ² = 25]
   и попросите учащихся записать каждое уравнение, поделиться и обсудить то, что они написали .
3. Теперь посмотрим на каждое из уравнений по очереди.
   (n + 5) x 2 = 28
   (n — 10) ÷ 9 = 10
   (n — 2) ² = 25
   Спросите студентов, как они могли бы вычислить, какое число вы думали в каждом примере (n).
   Выделите замечания, сделанные в Занятии 1, Задание 2, о том, что существует обратная связь между сложением и вычитанием, а также между умножением и делением. Обратная операция «отменяет» другую операцию.
   Просмотрите первый пример в обратном направлении, применив обратную операцию: 28 ÷ 2 = 14, 14 — 5 = 9 и проверьте, что n = 9, заменив его на n в исходном уравнении.(9 + 5) х 2 = 28
4. Попросите учащихся парами обсудить два других примера и поделиться своими решениями.

Деятельность 3

1. Сделайте 2 небольших листа бумаги и карандаши для каждого ученика. Попросите каждого ученика написать пять собственных вопросов: «О каком числе я думаю?» проблемы. Им следует написать слова каждой проблемы на одном листе бумаги, а на втором листе — свои собственные решения проблем, с числом, которое они думают, вместо «н».
2. Предложите учащимся обменяться проблемами с партнером. Попросите учащихся записать свои решения проблем своего партнера отдельно от страницы проблемы. Затем эти проблемы можно обменять с другой парой студентов и обсудить.

Деятельность 4

Предложите учащимся сравнить способ, которым простые калькуляторы и научные калькуляторы дают различных результатов для их задач.
Им следует ввести решения своих уравнений, но опустить сумму.Например, для исходной задачи (n + 5) x 2 = 28 введите вместо этого: 9 + 5 x 2 = ☐
Научные калькуляторы запрограммированы так, чтобы следовать соглашениям, а простые классные калькуляторы — нет.
Попросите учащихся исследовать свои проблемы и обсудить результаты обоих видов калькуляторов.

Деятельность 5

1. Завершите занятие, предложив учащимся записать одну из своих задач со словами «Я думаю о числе» с уравнением в нижней части плаката к занятиям 1 и 2.Покажите плакаты и подумайте об обучении.
2. Поразмышляйте над символами, выражениями и уравнениями, которые мы используем, чтобы выразить математические задачи и помочь нам обдумать их. Подчеркните, насколько важно , как правильно читать и понимать используемые символы и выражения.

Домашняя ссылка

Уважаемые родители и Ванау,

На этой неделе по алгебре студенты изучали числовые операции и порядок, в котором мы выполняем их в многошаговых задачах.BEDMAS — это соглашение, которое мы используем для решения такой задачи, как 3 + 4 x 5 = ☐. Результат 23 или 35?

Попросите ребенка объяснить вам решение, а затем вместе составить несколько задач-головоломок: «О каком числе я думаю?» Ваш ребенок хотел бы показать вам, как создавать эти проблемы.

Приятных обсуждений.

Спасибо.

Приоритет | Математика | RSC Education

Опытному математику не составит труда взглянуть на такое выражение, как:

3 + 4 x 2 — 1

и присвоив ему значение 10.Это получается путем умножения 4 и 2, добавления 3 и вычитания 1. Однако менее опытные могут разумно прибавить 3 к 4, чтобы получить 7, и умножить это на 1 (полученное из 2 — 1), чтобы получить 7.

Чтобы получить правильное значение, необходимо знать правила приоритета, которые определяют порядок, в котором мы применяем операторы, с помощью которых числа объединяются в выражении.

BIDMAS

Такие правила часто запоминаются с помощью мнемонических BIDMAS, которые обозначают B rackets, I ndices, D ivision, M ultiplication, A ddition и S ubtraction.Применяя это к приведенному выше выражению, мы сначала выполняем умножение, чтобы получить:

3 + 8–1

, затем добавляем:

11–1

и, наконец, вычитание, чтобы получить окончательное значение 10. Обратите внимание, что для изменения этого порядка можно использовать скобки. Если бы они были включены в исходное выражение:

(3 + 4) х (2–1)

Сначала мы выполняем операции в скобках, чтобы получить:

7 х 1

, который, как мы видели выше, имеет значение 7.

Более сложный пример

Более сложное выражение покажет, как правила также относятся к индексам и делению. Рассмотрим

Сначала мы оценим количество в скобках. Поскольку это состоит из нескольких шагов, мы также должны применить правила к выражению в скобках. В этом примере есть еще одна сложность, заключающаяся в том, что дробная величина также содержит то, что мы можем рассматривать как подразумеваемые скобки. Часто бывает полезно явно включать такие подразумеваемые скобки, чтобы это можно было записать как:

Итак, нам нужно вычислить числитель и знаменатель дроби отдельно.

Посмотрев сначала на числитель, мы идентифицируем любые индексы и видим, что:

2 ³ = 8

Теперь мы можем выполнить вычитание:

24–8 = 16

Знаменатель состоит из простого суммирования:

3 + 1 = 4

Возвращаясь к полному исходному выражению, мы теперь имеем:

Оценка скобки дает:

, поэтому общее выражение сокращается до:

2 х 4 = 8

Преподавание

Высокий и Разали ¹ предположили, что менее способные ученики видят символы в выражении как процесс, который должен выполняться в письменном порядке, в то время как более способные ученики могут разбивать символы вместе в соответствии с заданными соглашениями.Они также отмечают, что первый подход — это способ, которым вычисления выполняются на некоторых калькуляторах.

Рэдклифф обозначил ряд недоразумений, которые могут возникнуть при применении правила, изложенного выше.

1. После определения скобок правило необходимо применить к операторам в каждой скобке. Упрощение внутри скобки — это не то же самое, что ее исключение.
2. Дроби часто означают, что члены числителя и знаменателя должны быть сгруппированы вместе, как в приведенном выше примере.Я склонен думать об этом как о подразумеваемых скобках, которые часто бывает полезно показать явно.
3. Несмотря на использование мнемоники BIDMAS, умножение и деление имеют одинаковый приоритет, как и сложение и вычитание. Это может обеспечить эффективность вычислений, когда правило не нужно применять на шести (или более) отдельных этапах.

Примеры

Следующие три примера иллюстрируют правильное применение операторов, которые встречаются в математических выражениях в химии.

1. Расчет относительной атомной массы хлора

²

Это выражение основано на атомных массах и относительном содержании отдельных изотопов хлора.

Применение правил старшинства показывает, что сначала нам нужно выполнить умножение, чтобы получить:

Что оценивается как 35,45 с использованием правил цитирования соответствующего количества значащих цифр и обработки 100 как точного целого числа.

2. Мольная доля растворенного вещества в растворе

³ может быть выражена как

, где w — масса растворенного вещества, m — молекулярная масса растворенного вещества, W — масса растворителя и M — молекулярная масса растворителя.

Рассмотрим раствор хлорида натрия, образованный растворением 10,0 г растворенного вещества в 100 г воды. Подстановка величин в уравнение дает:

Я бы посоветовал полезным первым этапом включить подразумеваемые скобки, чтобы он читался так:

Это побуждает нас сначала оценить скобки, и обе могут оцениваться параллельно.Наши правила предписывают нам выполнять деления перед сложением, поэтому у нас есть:

Теперь оценка скобки знаменателя дает:

0,1709 моль г ^-1 + 5,5556 моль г ^-1 = 5,7265 моль г ^-1

Итак, общее выражение:

, а мольная доля оценивается как 0,0298.

3. Для реакции

PCl _{5 (г)} = PCl _{3 (г)} + Cl _{2 (г)}

константа равновесия K _p может быть определена ⁴ как:

, где a — степень диссоциации, а P — полное давление в системе.Если мы хотим оценить K _p , когда P = 4,38 x 10 ⁵ Па и a = 0,250, снова может быть полезно начать с включения подразумеваемых скобок, чтобы дать:

Как и раньше, по эффективности мы можем оценивать каждую скобку параллельно. Наши правила приоритета предписывают нам сначала оценить индексы.

Теперь мы можем выполнить умножение в верхней скобке и вычитание в нижней скобке, чтобы получить:

Теперь мы можем выполнить последнее умножение и деление, чтобы получить:

Kp = 29200 Па

История деятельности

Это было исследовано Петерсоном, который, однако, отмечает, что получить какие-либо окончательные ответы не удалось.Возрастающий характер правил подчеркивается тем, что в этой области все еще ведутся разработки, например, при обсуждении того, должно ли неявное умножение (например, 2a) иметь приоритет над явным умножением (2 xx) или делением (2 / x). .

Пол Йейтс — ведущий специалист по физическим наукам в Академии высшего образования и автор книги «Химические расчеты».

Эта математическая задача стала вирусной, потому что PEMDAS сбивает людей с толку

by TeachThought Staff

Кажется, каждые несколько недель передают математическую задачу, которая вызывает спор и становится вирусной, потому что никто не может прийти к единому мнению.И это почти всегда связано с PEMDAS.

Почему PEMDAS так сбивает с толку? Это связано с математикой как языком. Википедия объясняет PEMDAS:

«В математике и компьютерном программировании порядок операций , (или приоритет оператора , ) — это набор правил, отражающих соглашения о том, какие процедуры выполнять в первую очередь, чтобы вычислить данное математическое выражение.

Например, в математике и большинстве компьютерных языков умножение имеет более высокий приоритет, чем сложение, и так было с момента появления современных алгебраических обозначений.Таким образом, выражение 2 + 3 × 4 интерпретируется как имеющее значение 2 + (3 × 4) = 14, а не (2 + 3) × 4 = 20. С введением экспонент в XVI и XVII веках они имели приоритет как над сложением, так и над умножением и могли быть помещены только как верхний индекс справа от их основания. Таким образом, 3 + 5 ² = 28 и 3 × 5 ² = 75.

Эти соглашения существуют для устранения двусмысленности обозначений, позволяя при этом быть как можно более краткими. Там, где желательно переопределить соглашения о приоритете или даже просто подчеркнуть их, можно использовать круглые скобки (), чтобы указать альтернативный порядок операций (или просто усилить порядок операций по умолчанию).Например, (2 + 3) × 4 = 20 заставляет сложение предшествовать умножению, а (3 + 5) ² = 64 заставляет сложение предшествовать возведению в степень. Если в математическом выражении требуется несколько пар круглых скобок (например, в случае вложенных круглых скобок), скобки можно заменить скобками или фигурными скобками, чтобы избежать путаницы, как в [2 × (3 + 4)] — 5 = 9 . »

Эта математическая задача стала вирусной, потому что PEMDAS сбивает людей с толку

Так в чем проблема? Например, твиттер, природа дезинформации и разногласий, а также тип контента, которым с большей вероятностью будут делиться.Вот последний распространенный пример.

Социальные сети были созданы для обмена мнениями и несогласия, так что вот и мы. Как мы уже упоминали, они часто становятся вирусными, и в 2019 году доктор философии по математике Университета Кентукки. Джаред Антробус объяснил, почему все делают все неправильно, в книге «Провал PEMDAS».

В своем посте он объясняет, что проблема не может быть решена, как указано, потому что она неоднозначна.

«Проблема с этой проблемой в том, что деление не ассоциативно .Если бы нас попросили оценить 12 ÷ 6 ÷ 3, у нас возникла бы очень похожая проблема. Какой знак деления делать в первую очередь? Независимо от того, что нам сказал учитель начальной школы, мы не можем предположить, что автор задачи намеревался работать слева направо. Фактически, разные калькуляторы дадут разные ответы, в зависимости от того, как они запрограммированы!

Как мы работаем с неассоциативными операциями?

Единственная причина, по которой мы можем отказаться от написания круглых скобок с длинными строками сложения и умножения, — это их ассоциативность.Для деления мы должны указать , какую операцию выполнить в первую очередь. Мы должны написать (12 ÷ 6) ÷ 3 или 12 ÷ (6 ÷ 3), чтобы читатель точно знал, что мы имеем в виду.

Выражение 12 ÷ 6 ÷ 3 неоднозначно. Это могло означать две разные вещи. Единственный способ узнать, что задумал автор, — это попросить разъяснений. То же самое и с 6 ÷ 2 × 3 ».

Из-за неоднозначности ответы на вопросы невозможны!

Неоднозначные утверждения относятся не только к математике.Не меньшее беспокойство вызывает и следующий вопрос:

Если женщина играет в шахматы со своей сестрой, и она гроссмейстер, может ли она выиграть?

И снова намерения автора неясны. К какой женщине относится каждое слово «она»? Единственный способ узнать это — попросить разъяснений ».

Заключение

Мы просто подумали, что учителя математики могут найти здесь хороший перерыв от почти непрерывного цикла плохих новостей, который был в 2020 году.