Математики обнаружили идеальный способ перемножения чисел / Хабр

Разбивая крупные числа на мелкие, исследователи превысили фундаментальное математическое ограничение скорости

Четыре тысячи лет назад жители Вавилонии изобрели умножение. А в марте этого года математики усовершенствовали его.

18 марта 2019 два исследователя описали самый быстрый из известных методов перемножения двух очень больших чисел. Работа отмечает кульминацию давнишнего поиска наиболее эффективной процедуры выполнения одной из базовых операций математики.

«Все думают, что метод умножения, который они учили в школе, наилучший, но на самом деле в этой области идут активные исследования», — говорит Йорис ван дер Хувен, математик из Французского национального центра научных исследований, один из соавторов работы.

Сложность множества вычислительных задач, от подсчёта новых цифр числа π до обнаружения крупных простых чисел сводится к скорости перемножения. Ван дер Хувен описывает их результат как назначение своего рода математического ограничения скорости решения множества других задач.

«В физике есть важные константы типа скорости света, позволяющие вам описывать всякие явления, — сказал ван дер Хувен. – Если вы хотите знать, насколько быстро компьютеры могут решать определённые математические задачи, тогда перемножение целых чисел возникает в виде некоего базового строительного блока, по отношению к которому можно выразить такую скорость».

Почти все учатся перемножать числа одинаково. Записываем числа в столбик, перемножаем верхнее число на каждую цифру нижнего (с учётом разрядов) и складываем результат. При перемножении двух двузначных чисел приходится проделать четыре более мелких перемножения для получения итогового результата.

Школьный метод «переноса» требует выполнения n² шагов, где n – количество цифр в каждом из перемножаемых чисел. Вычисления с трёхзначными числами требуют девяти перемножений, а со стозначными – 10 000.

Метод переноса нормально работает с числами, состоящими из нескольких цифр, однако начинает буксовать при перемножении чисел, состоящих из миллионов или миллиардов цифр (чем и занимаются компьютеры при точном подсчёте π или при всемирном поиске больших простых чисел). Чтобы перемножить два числа с миллиардом цифр, нужно будет произвести миллиард в квадрате, или 10¹⁸, умножений, – на это у современного компьютера уйдёт порядка 30 лет.

Несколько тысячелетий считалось, что быстрее перемножать числа нельзя. Затем в 1960 году 23-летний советский и российский математик Анатолий Алексеевич Карацуба посетил семинар, который вёл Андрей Николаевич Колмогоров, советский математик, один из крупнейших математиков XX века. Колмогоров заявил, что не существует обобщённого способа умножения, требующего меньше, чем n² операций. Карацуба решил, что такой способ есть – и после недели поисков он его обнаружил.

Анатолий Алексеевич Карацуба

Умножение Карацубы заключается в разбиении цифр числа и повторной их комбинации новым способом, который позволяет вместо большого количества умножений провести меньшее количество сложений и вычитаний. Метод экономит время, поскольку на сложения уходит всего 2n шагов вместо n².

Традиционный метод умножения 25х63 требует четыре умножения на однозначное число и несколько сложений

Умножение Карацубы 25х63 требует трёх умножений на однозначное число и несколько сложений и вычитаний.
a) разбиваем числа
b) перемножаем десятки
c) перемножаем единицы
d) складываем цифры
e) перемножаем эти суммы
f) считаем e – b – c
g) собираем итоговую сумму из b, c и f

При росте количества знаков в числах метод Карацубы можно использовать рекурсивно.

Традиционный метод умножения 2531х1467 требует 16 умножений на однозначное число.

Умножение Карацубы 2531х1467 требует 9 умножений.

«Сложение в школе проходят на год раньше, потому что это гораздо проще, оно выполняется за линейное время, со скоростью чтения цифр слева направо», — сказал Мартин Фюрер, математик из Пенсильванского государственного университета, создавший в 2007 быстрейший на то время алгоритм умножения.

Имея дело с крупными числами, умножение Карацубы можно повторять рекурсивно, разбивая изначальные числа почти на столько частей, сколько в них знаков. И с каждым разбиением вы меняете умножение, требующее выполнения многих шагов, на сложение и вычитание, требующие куда как меньше шагов.

«Несколько умножений можно превратить в сложения, учитывая, что с этим компьютеры будут справляться быстрее», — сказал Дэвид Харви, математик из Университета Нового Южного Уэльса и соавтор новой работы.

Метод Карацубы сделал возможным умножать числа с использованием лишь n^1,58 умножений на однозначное число. Затем в 1971 году Арнольд Шёнхаге и Фолькер Штрассен опубликовали метод, позволяющий умножать большие числа за n × log n × log(log n) небольших умножений. Для умножения двух чисел из миллиарда знаков каждое метод Карацубы потребует 165 трлн шагов.

Йорис ван дер Хувен, математик из Французского национального центра научных исследований

Метод Шёнхаге-Штрассена используется компьютерами для умножения больших чисел, и привёл к двум другим важным последствиям. Во-первых, он ввёл в использование технику из области обработки сигналов под названием быстрое преобразование Фурье. С тех пор эта техника была основой всех быстрых алгоритмов умножения.

Во-вторых, в той же работе Шёнхаге и Штрассен предположили возможность существования ещё более быстрого алгоритма – метода, требующего всего n × log n умножений на один знак – и что такой алгоритм будет наибыстрейшим из возможных. Это предположение было основано на ощущении, что у такой фундаментальной операции, как умножение, ограничение операций должно записываться как-то более элегантно, чем n × log n × log(log n).

«Большинство в общем-то сошлось на том, что умножение – это такая важная базовая операция, что с чисто эстетической точки зрения ей требуется красивое ограничение по сложности, — сказал Фюрер. – По опыту мы знаем, что математика базовых вещей в итоге всегда оказывается элегантной».

Нескладное ограничение Шёнхаге и Штрассена, n × log n × log(log n), держалось 36 лет. В 2007 году Фюрер побил этот рекорд, и всё завертелось. За последнее десятилетие математики находили всё более быстрые алгоритмы умножения, каждый из которых постепенно подползал к отметке в n × log n, не совсем достигая её. Затем в марте этого года Харви и ван дер Хувен достигли её.

Их метод является улучшением большой работы, проделанной до них. Он разбивает числа на знаки, использует улучшенную версию быстрого преобразования Фурье и пользуется другими прорывами, сделанными за последние 40 лет. «Мы используем быстрое преобразование Фурье гораздо более грубо, используем его несколько раз, а не один, и заменяем ещё больше умножений сложением и вычитанием», — сказал ван дер Хувен.

Алгоритм Харви и ван дер Хувена доказывает, что умножение можно провести за n × log n шагов. Однако он не доказывает отсутствия более быстрого метода. Гораздо сложнее будет установить, что их подход максимально быстрый. В конце февраля команда специалистов по информатике из Орхусского университета опубликовала работу, где утверждает, что если одна из недоказанных теорем окажется верной, то этот метод и вправду будет скорейшим из способов умножения.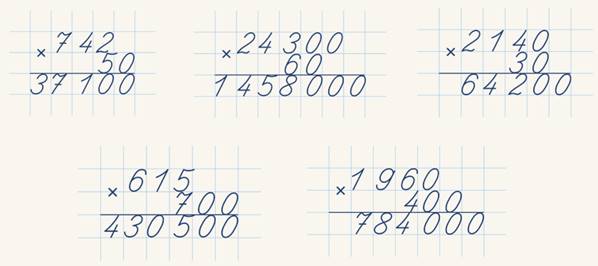

И хотя в теории этот новый алгоритм весьма важен, на практике он мало что поменяет, поскольку лишь немного выигрывает у уже используемых алгоритмов. «Всё, на что мы можем надеяться, это на трёхкратное ускорение, — сказал ван дер Хувен. – Ничего запредельного».

Кроме того, поменялись схемы компьютерного оборудования. Двадцать лет назад компьютеры выполняли сложение гораздо быстрее умножения. Разрыв в скоростях умножения и сложения с тех пор серьёзно уменьшился, в результате чего на некоторых чипах умножение может даже обгонять сложение. Используя определённые виды оборудования, «можно ускорить сложение, заставляя компьютер умножать числа, и это какое-то безумие», — сказал Харви.

Оборудование меняется со временем, но лучшие алгоритмы своего класса вечны. Вне зависимости от того, как компьютеры будут выглядеть в будущем, алгоритм Харви и ван дер Хувена всё ещё будет самым эффективным способом умножать числа.

Математика для блондинок: Умножение столбиком

В порядке оказания «скорой решательной помощи», сейчас мы рассмотрим одним глазом умножение столбиком. Не весь процесс целиком, а маленькие технические детали. Наши умные калькуляторы очень легко справляются с умножением разных чисел, но они не выдают распечатку умножения столбиком этих же чисел. Очень жаль. Рецепт приготовления чисел не в микроволновке (на калькуляторе), а на костре (ручками на бумажке в столбик) иногда вызывает затруднения.

Сейчас мы приготовим два блюда из чисел и умножения тем древним способом, которым пользовались наши предки в те далекие времена, когда электричества ещё не было (ведь все калькуляторы работают от электричества). Умножим столбиком две пары чисел:

0,15 * 20

120 * 60

Числа очень простые, но вот все эти нолики и запятые, как сырые дрова, мешают разгореться костру наших знаний. Для победы силы разума над древними суевериями, прежде всего, числа нужно расположить фотогенично. Не для того, чтобы сделать красивую фотку на память, а для того, чтобы нам было проще считать. Для этого хвосты из нулей в конце чисел нужно просто игнорировать. Они есть, но мы их не видим. Очки мы надели такие — противонулевые. Когда мы подобным образом разделали наши числа, можно приступать к приготовлению блюда — располагаем одно число под другим, выравнивая столбик по правому краю чисел. Нолики у наших чисел остаются (вы же не станете отрывать хвост у своего любимого домашнего животного, даже ради умножения его столбиком). Если нолики не хотят выстраиваться ровно, не обращайте на них внимания.

В результате нам нужно умножить в столбик числа 15 на 2 и 12 на 6 (я думаю, любой уважающий себя математик с этой задачей справится). После умножения столбиком мы получим числа 30 и 72. Всё! Наше блюдо готово! Но, прежде чем подавать его на стол учителя, результат необходимо украсить нулями или запятыми. Другими словами, нужно навести порядок в нулях и запятых. Не пугайтесь! Это гораздо проще, чем наводить порядок на кухне.

Снимаем наши противонулевые очки и занимаемся нулями. Если числа при умножении в столбик мы складываем, то хвостики из нулей складывать нельзя. Их нужно просто перенести в низ и приписать к полученному результату. В первом примере у нас остался один нолик от числа 20, во втором примере у нас аж два нолика — один от числа 120, второй от числа 60. Если вам попадутся числа, у которых в конце по мешочку ноликов, то высыпайте в результат сперва один мешочек, потом второй. Смотрим, что получилось у нас:

15 * 2 = 30 плюс нолик = 300

12 * 6 = 72 плюс два нолика = 7200

Теперь берем бинокль и начинаем выискивать запятые. Во втором примере ничего похожего на запятую не наблюдается. Значит, со вторым примером мы покончили — блюдо учителю на стол! А вот в первом примере нам удалось обнаружить эту маленькую пакость. И что теперь делать? Ведь всё было так красиво… Придется эту бяку, словно пучок петрушки, воткнуть в наш результат. Иначе учитель обидится. Остается решить, куда именно втыкать. Правило очень простое — сколько знаков после запятой было до умножения, столько же знаков после запятой отделяется после умножения.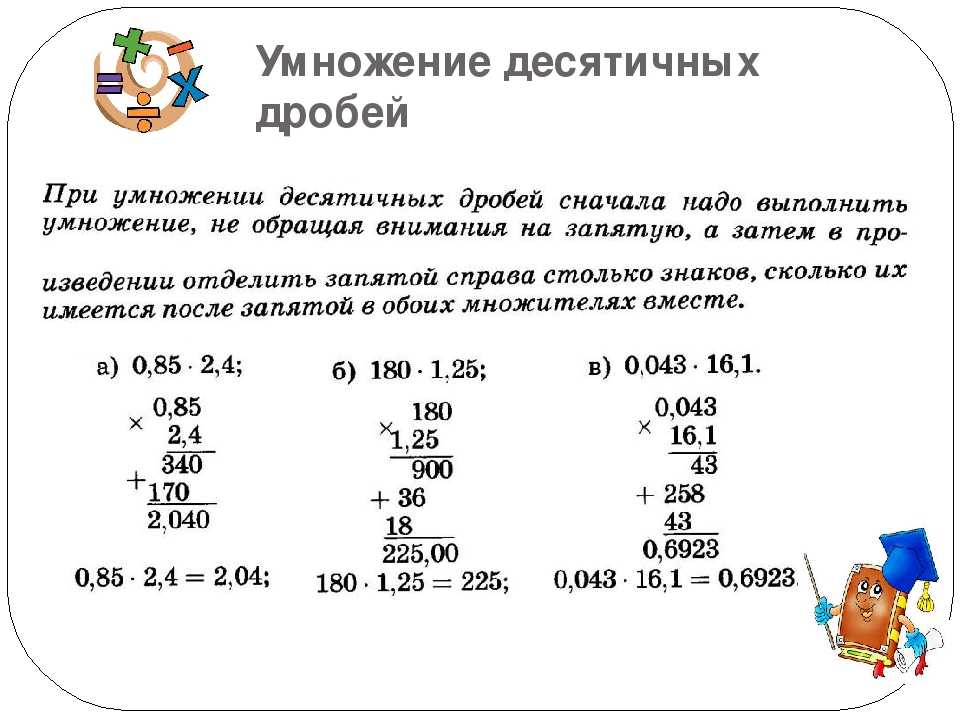 Если запятые прокрались в оба числа, тогда блюдо подается с двойным гарниром — отделяется столько знаков, сколько их было в двух числах, вместе взятых. А у нас мы имеем:

0,15 — это два знака после запятой

300 минус два знака после запятой = 3,00 = 3

Всё! Задание выполнено. Можете брать в руки калькулятор и проверять. Я же, для проверки, займусь любимым делом математиков — по жонглирую числами. Следите внимательно за каждым моим движением:)

0,15 * 20 = (15 : 100) * 20 = 20 * 15 : 100 = 2 * 10 * 15 : 100 = 2 * 15 * 10 : 100 = 30 * 10 : 100 = 3 * 10 * 10 : 100 = 3 * 100 : 100 = 3 * 1 = 3

120 * 60 = 12 * 10 * 60 = 12 * 10 * 6 * 10 = 12 * 6 * 10 * 10 = (10 + 2) * 6 * 10 * 10 = (10 * 6 + 2 * 6) * 10 * 10 = (60 + 2 * 6) * 10 * 10 = (60 + 12) * 10 * 10 = (60 + 12) * 100 = 72 * 100 = 7200

Что не говорите, а математическое жонглирование — прикольная штука. Как видите, даже без калькулятора и умножения столбиком, можно довольно просто получить результат (жаль, не всегда так получается).

Умножение матриц | Формула, правила, умножение и факты

Матрица определяется как прямоугольный массив чисел, символов или выражений, расположенных в строках и столбцах (множественное число: матрицы). Если в массиве n строк и m столбцов, то это матрица размера n×m. Размеры матрицы обозначаются числами n и m. Числа в матрице обозначаются как их элементов .

Обозначение матриц

Мы обычно обозначаем матрицы заглавными буквами, например A, B, C и т. д.

A≔ Матрица обозначается заглавной буквой.
a≔ Элемент матрицы обозначается строчной буквой.

Прямоугольные скобки обычно используются для записи матриц. Горизонтальные и вертикальные линии элементов в матрице называются соответственно строками и столбцами.

Размерность матрицы

Количество строк и столбцов, содержащихся в матрице, определяет ее размер. Матрица с m строками и n столбцами называется матрицей размера m × n или матрицей размера m на n, где m и n называются размерами матрицы. При описании матрицы вы указываете количество строк по количеству столбцов. Иногда это называют порядком матрицы. Например, матрица

A=[12       34]

называется матрицей размера один на четыре, поскольку она имеет одну строку и четыре столбца. Мы также можем сказать, что порядок A равен 1 × 4. Матрица

B = [123  456]

является матрицей 3 × 2, поскольку она имеет три строки и два столбца. Он имеет порядок 3×2.

Совет: Помните, что сначала указывается количество строк, а затем количество столбцов.

Рассмотрите аббревиатуру «RC» для «Row then Column», чтобы запомнить это.

Жак Филипп Мари Бине, французский математик, впервые описал матричное умножение в 1812 году, чтобы показать состав линейных карт, представленных матрицами. В результате умножение матриц является фундаментальным инструментом линейной алгебры с различными приложениями во многих областях математики, включая прикладную математику, статистику, физику, экономику и инженерию. Вычисление матричного произведения является фундаментальным процессом во всех вычислительных приложениях линейной алгебры.

Существует только два метода умножения матриц. Первый метод включает умножение матрицы на скаляр. Это называется скалярным умножением. Второй способ заключается в умножении одной матрицы на другую. Это называется умножением матриц.

Скалярное умножение

Поскольку выражение A+A представляет собой сумму двух матриц с одинаковыми размерами, матрицу A можно сложить с самой собой. В итоге мы удваиваем каждую запись в A, когда вычисляем A+A. В результате мы можем интерпретировать выражение 2A как предписывающее нам умножить каждый элемент в A на  2. 

Обычно, чтобы умножить матрицу на число, умножьте это число на каждый элемент матрицы. Например,

Отдельные числа обычно называют скалярами при обсуждении матриц. В результате мы называем операцию умножения матрицы на число скалярным умножением.

Скалярное произведение

Чтобы умножить одну матрицу на другую, мы должны сначала понять, что такое скалярное произведение. Скалярное произведение — это метод нахождения произведения двух векторов, также известный как умножение векторов. Предположим, что следующие два вектора:

u=[123] , v=[456]

Чтобы умножить эти два вектора, просто перемножьте соответствующие элементы и сложите полученные произведения.

u∙v=(1)(4)+(2)(5)+(3)(6)
=4+10+18
=32

В результате перемножения векторов получаем единственное значение . Обратите внимание, однако, что два вектора имеют одинаковое количество записей. Что, если один из векторов содержит меньше элементов, чем другой?

 Например, пусть

u=[214] , v=[310     2]

Когда соответствующие записи были перемножены и сложены вместе, решение будет:

u∙v= [214] [310     2]
=2(3)+1(1)+0(4)+?(2)

Здесь возникла проблема. Первые три записи скалярного произведения имеют соответствующие записи для умножения, а четвертая — нет. Это означает, что скалярное произведение этих двух векторов не может быть вычислено.

В результате скалярное произведение двух векторов с разным количеством элементов не может быть найдено. Они оба должны содержать одинаковое количество записей.

Когда мы хотим перемножить матрицы, мы должны сначала убедиться, что операция возможна, что не всегда так. Кроме того, в отличие от числовой арифметики и алгебры, даже если произведение существует, порядок умножения может повлиять на результат.

Изучение скалярного произведения необходимо при умножении матриц. При умножении одной матрицы на другую строки и столбцы должны рассматриваться как векторы.

Пример 1. Найти AB, если A=[1234] и B=[5678]

А∙В= [1234] ^. [5678]

Сосредоточьтесь на следующих строках и столбцах

, где r ₁ — первая строка, r ₂ ​ — вторая строка, c ₁ , c _{2 90are первая и ​вторые столбцы. Рассматривайте каждую строку и столбец как вектор.}

Обратите внимание, что умножение матрицы 2×2 на другую матрицу 2×2 дает матрицу 2×2. Таким образом, в полученной матрице должно быть четыре элемента.

Убедитесь, что первая запись находится в первой строке и первом столбце. Итак, чтобы получить значение первой записи, просто возьмите скалярное произведение r ₁ и с ₁ . Таким образом, первая запись будет

Теперь обратите внимание, что расположение второй записи находится в первой строке и втором столбце. Итак, чтобы получить значение второй записи, просто возьмите скалярное произведение r ₁ и c ₂ . Таким образом, вторая запись будет

. Ту же стратегию можно использовать для получения значения двух последних записей.

Пример 2. Найти AB, если A=[14   25 36] и B=[111  111 111 111]

A∙B= [14  25 36] x [111 111 111 111]

Используйте скалярные произведения для вычисления каждой записи.

Следовательно, две матрицы можно перемножить, если количество столбцов первой матрицы равно количеству строк второй матрицы. Умножение дает другую матрицу с тем же количеством строк, что и у первой, и тем же количеством столбцов, что и у второй. Если это не так, умножение не может быть выполнено.

В символах пусть A будет матрицей m×p, а пусть B будет матрицей q×n. Тогда произведение A×B=AB будет матрицей размера m×n при условии, что p=q. Если p≠q, умножение матриц не определено. Например, матрицу 2×5 нельзя умножить на матрицу 3×4, потому что 5≠3, тогда как матрицу 2×5 можно умножить на 5×3, и в результате получится матрица 2×3.

Умножение матриц имеет некоторые общие свойства с обычным умножением. Умножение матриц, с другой стороны, не определено, если число столбцов в первом сомножителе отличается от числа строк во втором сомножителе, и оно некоммутативно, даже если произведение остается определенным после того, как порядок сомножителей измененный.

Некоммутативность 

Некоммутативность умножения матриц является одним из наиболее существенных различий между умножением действительных чисел и умножением матриц. Следовательно, порядок умножения двух матриц имеет значение при умножении матриц.

Операция является коммутативной, если для двух элементов A и B, таких, что произведение AB

определено, тогда также определено BA, AB=BA

Например,

A=[0100] и B=[0010 ]

затем,

AB= [0100] x [0010] = [1000]

но

BA= [0010] x [0010] = [1000]

Обратите внимание, что продукты не совпадают с AB ≠БА. Следовательно, умножение матриц не является коммутативным.

Коммутативность имеет место в одном особом случае. Это при умножении диагональных матриц одинаковой размерности.

Помимо этого важного отличия, свойства умножения матриц в основном аналогичны свойствам умножения действительных чисел.

Дистрибутивность

Умножение матриц является дистрибутивным по отношению к сложению матриц. То есть, если A, B, C, D являются матрицами соответствующих размеров m×n,n×p, n×p и p×q, то дистрибутивность слева

AB+C=AB+AC

и другое имеет правильное распределение

B+CD=BD+CD

Пример 1: 

Обратите внимание, что AB+C=AB+AC. Теперь найдите B+CA и  BA+CA

. Обратите внимание, что B+CA=BA+CA. Также примечательно, что AB + CB + CA и что AB + AC ≠ BA + CA, что напоминает нам о некоммутативности матричного умножения.

Ассоциативность

Это свойство указывает, что группировка, окружающая умножение матриц, может быть изменена.

Если A, B, C являются матрицами m×n, n×p и p×q соответственно, то (AB)C=A(BC)

Например, вы можете умножить матрицу A на матрицу B, а затем умножить результат на матрицу C, или вы можете умножить матрицу B на матрицу C, а затем умножить результат на матрицу A.

Применяя это свойство, помните о порядке перемножения матриц, поскольку умножение матриц не является коммутативным.

Пример 1: 

Мы можем найти (AB)C следующим образом:

Мы можем найти A(BC) следующим образом:

Обратите внимание, что ABC= A(BC).

Свойство мультипликативной идентичности

Матрица n×n , обозначенная In, представляет собой матрицу с n строками и n столбцами. Все записи по диагонали от верхнего левого угла до нижнего правого – это единицы, а все остальные – нули.

Например:

Свойство мультипликативной идентичности утверждает, что произведение любой матрицы размера n × n A и I n всегда равно A, независимо от порядка выполнения умножения. Другими словами, A∙I=I∙A=A

Роль, которую единичная матрица размера n×n играет в умножении матриц, аналогична роли, которую играет число 1 в действительной системе счисления. Если a — действительное число, то мы знаем, что a∙1=a и 1∙a=a

Мультипликативное свойство нуля

Нулевая матрица — это матрица, в которой все элементы равны 0. Например, 3× 3 нулевая матрица O _3×3 =[0 0 0 0 0 0 0 0 0]

Нулевая матрица обозначается буквой O, и при необходимости можно добавить нижний индекс для указания размеров матрицы.

Мультипликативное свойство нуля гласит, что произведение любой матрицы размера n × n и нулевой матрицы размера n × n является нулевой матрицей размера n × n. Другими словами, А∙О=О∙А=О.

Роль, которую нулевая матрица n×n играет в умножении матриц, подобна роли, которую играет число 0 в действительной системе счисления. Если a — действительное число, то мы знаем, что a∙0=0 и 0∙a=0

Свойство измерения

Свойство измерения — это свойство, уникальное для матриц. Это свойство состоит из двух частей:

1. Если количество столбцов в первой матрице равно количеству строк во второй матрице, определяется произведение двух матриц.

2. Если произведение определено, результирующая матрица будет иметь то же количество строк, что и первая матрица, и то же количество столбцов, что и вторая матрица.

Например, если A — матрица 3×2, а B — матрица 2×4, свойство размерности говорит нам, что произведение AB определено и AB будет матрицей 3×4.

 (1,2,3).(4,5,6)
= (1x4)+(2x5)+(3x6)
= 4+10+18
= 32