справочник 4-6 — WQERTFGH — Действия в столбик Сложение «в столбик» Запишем числа столбиком (одно
Действия в столбик
Сложение «в столбик»
Запишем числа столбиком (одно под другим, выравнивая по правому краю, сверху более длинное число — так удобней). пр:
Складываем по одной цифре справа налево, результат записываем под чертой. пр:
Если получится число > 10, записываем только последнюю цифру результата, а первую цифру ставим пока над соседней цифрой слева (для сложения на следующем шаге). пр:
(1 будем потом прибавлять к 7)
Умножение «в столбик» Запишем числа столбиком (одно под другим, выравнивая по правому краю, сверху более длинное число — так удобней). пр:
Сначала умножаем верхнее число на последнюю цифру нижнего числа. Результат записываем под чертой. пр: умножаем число сверху по одной цифре справа налево: 7 · 6 = 42 (под черту идет только последняя цифра результата 2, а цифру десятков 4 ставим пока над соседней цифрой слева) 2 · 6 = 12 (не забудем, что над 2 стоит 4, это значит, что к результату умножения надо прибавить 4) 12 + 4 = 16 (6 записываем под чертой, 1 записываем над 4) 4 · 6 = 24 (и добавляем 1) 24 + 1 = 25
Переходим к умножению на следующую цифру
второго числа. Результат умножения на
следующую цифру записывается со сдвигом.
пр:
умножаем 427 на 3 (по тем же
правилам)
Результат умножения на
следующую цифру записывается со сдвигом.
пр:
умножаем 427 на 3 (по тем же
правилам)
После того, как верхнее число будет умножено на все цифры нижнего, подводим черту и складываем полученные результаты по правилам сложения в столбик.
Если во втором числе есть нули, то получится «нулевая строчка» — ее можно не писать, но тогда нужно будет сделать сдвиг на две клетки. При умножении чисел, оканчивающихся нулями, нужно сначала «отделить» нули — записать и умножить числа без последних нулей, потом все нули добавить к результату. пр:
Вычитание «в столбик»
Запишем числа столбиком (одно под другим, выравнивая по правому краю, сверху уменьшаемое, снизу вычитаемое). пр:
Выполняем вычитание по одной цифре справа налево, результат записываем под чертой. пр:
Если сверху окажется меньшая цифра, то нужно «занять десяток» из соседней цифры слева (над соседней цифрой ставим точку). пр:
займем десяток из соседнего разряда (из 6 потом нужно будет отнять 1)
займем десяток из соседнего разряда
займем десяток из соседнего разряда
займем десяток из соседнего разряда
Деление «в столбик» Запишем делимое и делитель «в столбик». Результат (частное) будем записывать в «уголке»
под делителем.
пр:
Результат (частное) будем записывать в «уголке»
под делителем.
пр:
Чтобы избежать ошибок (связанных с пропуском нулей в результате), можно заранее поставить на место результата столько точек, сколько цифр в делимом. А при выполнении деления следить за тем, чтобы для каждой из цифр делимого была записана какая-то цифра в результат. пр: в делимом «5121200» семь цифр, поставим в результат семь точек Будем делить не все делимое сразу, а «по частям». Для объяснения этих действий используется понятие «неполное частное» — это та часть делимого, с которой в данный момент работают. Сначала берем первую цифру делимого — принимаем ее за «неполное частное». Далее действуем по алгоритму:
1)Делим «неполное частное» на делитель,
результат запишем на место первой свободной
точки. Если «неполное частное» меньше
делителя, то в результат запишем 0 и перейдем
сразу к шагу 2)
«Обратно» умножаем делитель на полученную
цифру результата, произведение записываем
ниже делимого (для вычитания), вычитаем и
получаем остаток. Остаток должен быть
меньше делителя! Принимаем остаток за
«неполное частное».
2)Берем следующую цифру делимого и
добавляем ее к «неполному частному».
Переходим снова к шагу 1)
пр: берем первую цифру (5) — принимаем за
«неполное частное»
Остаток должен быть
меньше делителя! Принимаем остаток за
«неполное частное».
2)Берем следующую цифру делимого и
добавляем ее к «неполному частному».
Переходим снова к шагу 1)
пр: берем первую цифру (5) — принимаем за
«неполное частное»
- делим «неполное частное» (5) на делитель (8)
записываем в результат полученную цифру (0) 2) берем следующую цифру (1), добавляем к «неполному частному» (51)
- делим «неполное частное» (51) на делитель (8) (можно по таблице умножения на 8 найти ближайшее к 51 произведение) 6 · 8 = 48 записываем в результат полученную цифру (6) а ее произведение на делитель (48) под
вычитаем, получаем остаток (3), который теперь принимаем за «неполное частное» 2) «сносим» из делимого следующую цифру (2) и припишем ее к «неполному частному» (32)
- делим «неполное частное» (32) на делитель (8)
записываем в результат полученную цифру (4) 2) «сносим» следующую цифру (1)
- делим «неполное частное» (1) на делитель (8)
записываем в результат полученную цифру (0) 2) «сносим» следующую цифру (2)
- делим «неполное частное» (12) на делитель (8)
записываем в результат полученную цифру (1) 2) «сносим» следующую цифру (0)
- делим «неполное частное» (40) на делитель (8)
записываем в результат полученную цифру (5) 2) «сносим» следующую цифру (0)
- делим «неполное частное» (0) на делитель (8)
записываем в результат полученную цифру (0)
Математика — 4 класс
Таблица умножения Арифметические действия
сложение a — слагаемое b — слагаемое c — сумма
вычитание a — уменьшаемое b — вычитаемое c — разность
умножение a — множитель b — множитель c — произведение
деление a — делимое b — делитель c — частное
Простые уравнения Уравнение — это равенство, содержащее неизвестную величину (ее значение надо найти) пр :
Длина 1 км = 1000 м 1 м = 100 см 1 дм = 10 см 1 см = 10 мм
Периметр для прямоугольника
Площадь для прямоугольника
Запись натуральных чисел _ _ _ _ _ _ _ _ _ _ _ _ млрд млн тыс едн (по три цифры в каждом классе)
пр: 2 000 040 300 (два миллиарда сорок тысяч триста) Римская система записи чисел I = 1 V = 5 X = 10 L = 50 С = 100 D = 500 M 1000 =
пр:
= 1974
= 4444
= 70000
Масса
1 т = 1000 кг 1 кг = 1000 г
Время
1 год 365/366 сут 1 сут 24 ч 1 ч = 60 мин 1 мин = 60 с високосные года (+29)
Примеры действий в столбик
Скорость
(S — путь, v — скорость, t — время)
Математика — 5 класс
Законы арифметики
переместительный
сочетательный
распределительный
пр: раскрытие скобок пр: вынесение общего множителя за скобки вычитание суммы и разности
Длина 1 км = 1000 м 1 м = 100 см = 1000 мм 1 дм = 10 см = 100 мм 1 см = 10 мм Периметр (длина по границе фигуры) для прямоугольника
Площадь (мера плоской фигуры)
(ар, сотка) (гектар) для прямоугольника
Объем (мера пространства)
(литр)
для прямоугольного параллелепипеда
Скорость
(S — путь, v — скорость, t — время)
Движение двух объектов в разных направлениях:
_в одном направлении: (если )
- скорость сближения или удаления_ Движение по воде
_- скорость течения
- скорость по течению
- скорость против течения
- собственная скорость (лодки)_
Порядок действий слева направо 1. скобки 2. степень 3. умножение, деление
4. сложение, вычитание
скобки 2. степень 3. умножение, деление
4. сложение, вычитание
обозначение единиц измерения (приставки СИ) да дека д деци г гекто с санти к кило м милли М мега мк микро Г гига н нано Т тера п пико
умножение
степень «a в степени n»
«a в квадрате» «a в кубе» пр:
углы
полный развернутый прямой острый тупой Таблица простых чисел простое число — делится только на 1 и само себя (1 «не считается» простым числом)
входят в разложения этих чисел (без повторения): 168 = 2 · 2 · 2 · 3 · 7 180 = 2 · 2 · 3 · 3 · 5
НОК(168; 180) = 2 · 2 · 2 · 3 · 3 · 5 · 7 = 2520 «объединение»
взаимно простые числа — не имеют общих делителей (кроме 1) для них
наименьшие дополнительные множители — взаимно простые числа (тогда общий знаменатель — это НОК знаменателей)
Умножение и деление дробей
просто умножаем числители и знаменатели
деление «переводим»
в умножение на перевернутую (обратную) дробь перед умножением можно (и нужно) сократить: пр: пр:
Смешанные дроби запись числа в виде целой и дробной части
на координатной оси:
перевод смешанной дроби в простую: к числителю прибавить целую часть, умноженную на знаменатель пр: перевод простой дроби в смешанную: выполнить деление с остатком, остаток записать в числитель пр: сложение:
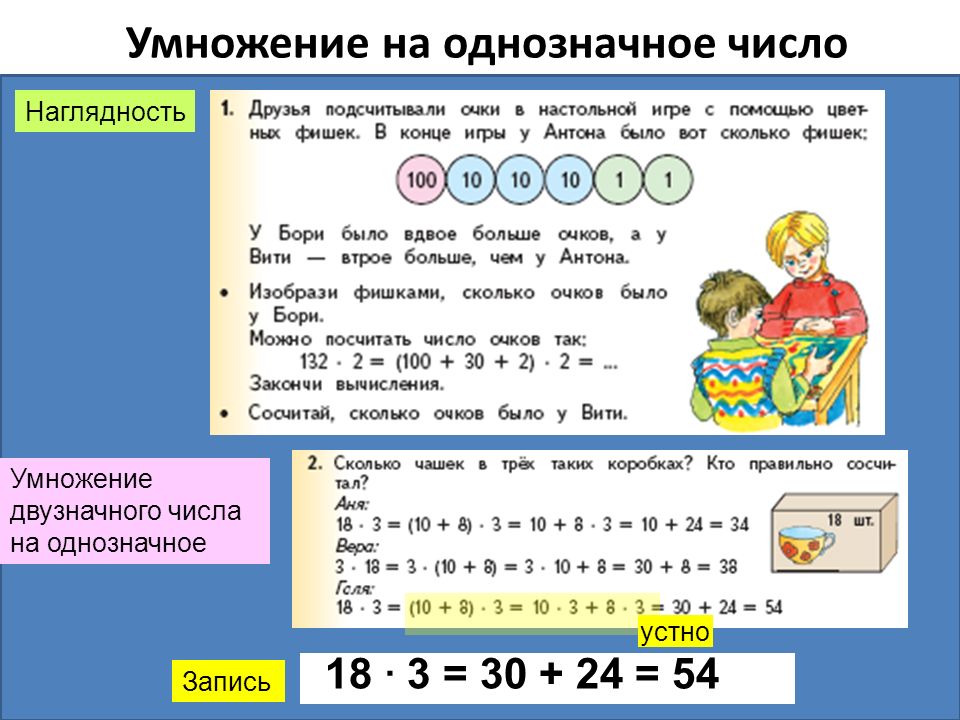 ..
если получится неправильная дробь, выделить из нее целую
часть
пр: … вычитание: отдельно вычитать целые и дробные части
пр: …
если вычитаемая дробь больше, то из целой части
«занять 1»
пр: … умножение и деление: перевести смешанные дроби в простые
пр:
или представить смешанную дробь в виде суммы
пр:
..
если получится неправильная дробь, выделить из нее целую
часть
пр: … вычитание: отдельно вычитать целые и дробные части
пр: …
если вычитаемая дробь больше, то из целой части
«занять 1»
пр: … умножение и деление: перевести смешанные дроби в простые
пр:
или представить смешанную дробь в виде суммы
пр:целые числа можно записать в виде дроби со знаменателем 1:
пр:
пр: пр:
пр:
полезно запомнить, что
Задачи на части Чтобы найти часть от числа , нужно умножить это число на соответствующую дробь. где p — часть (дробь), A — некоторая величина, Q — часть этой величины пр: найти от 12
пр: найти число, которого равно 12
пр: какую часть от числа 100 составляет число 15?
дополнительные дроби — в сумме дают 1 пр: пр: кот съел сосиски, сколько осталось?
Задачи на совместную работу работа = производительность время производительность ~ «скорость работника» пр: труба заполняет 2 бассейна на 5 мин
Если в задаче не уточняется, какая работа выполняется, то работа принимается за 1 пр: работник выполняет какую-то работу на 5 мин
При совместной работе производительности складываются (общая производительность) Если один работник выполняет работу за время , другой —
за время , а вместе они выполнят эту работу за время ,
то (общая производительность)
Математика — 6 класс
Отрицательные числа
пр: отрицательное число «-5» противоположно положительному числу «+5»
противоположные числа расположены по разные стороны от 0, но имеют одинаковую «абсолютную величину» — модуль
противоположные числа «по модулю» равны
если к одному числу относятся два знака:
«-» и «-» дают «+» «-» и «+» дают «-»
пр:
аналогично при умножении и делении чисел с разными знаками
пр:
действия с отрицательными числами:
- упростить запись (если несколько знаков относятся к одному числу)
- определить знак результата
- найти его «абсолютную величину»
пр:
пр:
пр:
пр:
сравнение: больше то число, которое находится на оси правее пр:
запись действий с отрицательными числами: пр: расставляем порядок действий
остались знаки «-», не занятые под действия, они относятся к отрицательным числам; при выполнении действий, сначала записываем знак результата, потом вычисляем его абсолютную величину (действие записывается «в строчку», а ниже столбик с положительными числами) 1)
Десятичные дроби обыкновенная дробь − запись числа в виде (p,q — натуральные числа) десятичная дробь − запись числа в десятичной системе с дробной частью после запятой
пр:
примеры действий с десятичными дробями: запятая под запятой
количество цифр после запятой складывается
сдвигаем запятые, чтобы получить целый делитель; при переходе через запятую в делимом -ставим запятую в результат; дописываем нужное количество нулей после запятой
сдвинуть запятую на n позиций вправо сдвинуть запятую на n позиций влево пр: перевод обыкновенной дроби в десятичную: привести знаменатель дроби к круглому числу пр: или разделить числитель на знаменатель «столбиком», получится конечная или бесконечная периодическая десятичная дробь пр: «ноль целых сорок пять в периоде»
перевод десятичной дроби в обыкновенную: знаменатель определяется количеством цифр после запятой пр: способ для периодических дробей: пр: пусть , тогда чтобы перенести запятую в конец периода, нужно , а чтобы перенести запятую в начало периода, нужно ; вычтем из первого второе
Буквенные выражения
Знак умножения «» перед буквой или перед скобкой обычно не пишут пр:
упрощение выражений:
пр :
пр:
составление выражений и уравнений : «запись на математическом языке» пр: x на 10 больше, чем y x на 10 меньше, чем y x в 10 раз больше, чем y x в 10 раз меньше, чем y x равно от y x равно удвоенному значению y
схема решения уравнений:
«избавляемся» от дробей (умножаем уравнение на общий знаменатель) пр:
раскрываем скобки пр: слагаемые, содержащие «неизвестную», переносим налево, все остальное — направо пр: «приводим подобные слагаемые» пр: делим уравнение на «коэффициент при неизвестной» пр: можно сделать проверку — подставить найденный корень в уравнение и проверить, получилось ли верное равенство пр: Уравнение может не иметь корней или иметь бесконечно много корней: пр:
уравнение не имеет корней, т. е. не может быть
верным равенством «ни при каком x»
пр:
е. не может быть
верным равенством «ни при каком x»
пр:
уравнение имеет бесконечно много корней, т.е. «верно при любом x»
Уравнения
Уравнение — это равенство, содержащее неизвестную величину, значение которой нужно найти. Корень уравнения — это значение «неизвестной», при котором из уравнения получается верное равенство. Решить уравнение — значит, найти все его корни (или убедиться, что корней нет).
простые уравнения: пр:
свойства уравнений:
- левую и правую части уравнения можно увеличить или уменьшить на одно число
пр: (отнимем 3 слева и справа)
т.е. «слагаемое» можно перенести из одной части уравнения в другую, изменив знак на противоположный
- левую и правую части уравнения можно умножить или разделить на одно число
пр: (разделим на 3 слева и справа)
чтобы решить уравнение, нужно привести его к виду:
Проценты 1% какой-либо величины – это одна сотая
часть этой величины, т. е. задачи на проценты
е. задачи на проценты
- это задачи на части
1% от A = p% от A 100% от A
проценты принято записывать в виде десятичных дробей пр: 1% от 120 25% от 120 50% от 120 100% от 120 210% от 120 0,5% от 120 5% от 12% от 120
увеличить на p% — взять уменьшить на p% — взять пр: увеличить число 120 на 4%
100+4=104%
уменьшить число 120 на 4%
100-4=96%
пр: Товар стоил 300 р, потом цена повысилась на 10%, потом понизилась на 10%. Сколько теперь стоит товар? увеличить на 10% умножить на 1, уменьшить на 10% умножить на 0, (р)
Задачи на проценты
найти процент от числа найти число по его проценту найти процентное соотношение
пр: найти 14% от числа 150 пр: найти число, 14% которого равны 21
пр: сколько процентов от 150 составляет число 21?
1 способ — по формуле где p — процент (дробь), A — целая величина, Q — часть этой величины
2 способ — найти сначала 1%
(1%) (14%)
(1%)
3 способ — составить пропорцию
(%)
Деление в столбик
Деление многозначных или многоразрядных чисел удобно производить письменно в столбик.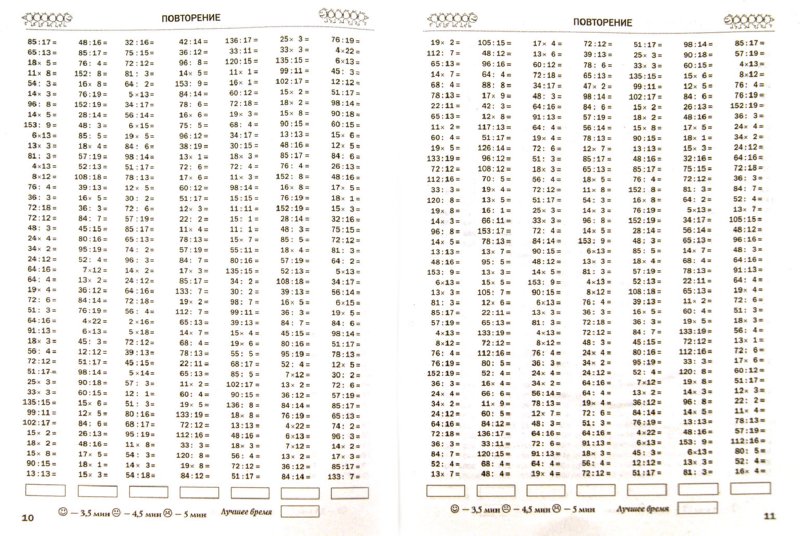 Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.
Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.
Итак, поделим 354 на 2 . Для начала разместим эти числа как показано на рисунке:
Делимое размещаем слева, делитель справа, а частное будем записывать под делителем.
Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое, для этого берем первый слева разряд, в нашем случае 3 и сравниваем с делителем.
3 больше 2 , значит 3 и есть неполное делимое. Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:
Для того чтобы 3 разделить на 2 вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3.
2 × 1 = 2 (2 < 3)
2 × 2 = 4 (4 > 3)
2 меньше 3 , а 4 больше, значит, берем первый пример и множитель 1 .
Записываем 1 в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым:
Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем:
Далее находим второе неполное делимое, для этого значение следующего разряда делимого опускаем к разности:
Полученное значение сравниваем с делителем. 15 больше 2 , значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15 :
2 × 7 = 14 (14 < 15)
2 × 8 = 16 (16 > 15)
Искомый множитель 7 , записываем его в частное на место второй точки (в десятки). Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
Продолжаем деление, для чего находим третье неполное делимое. Спускаем следующий разряд делимого:
Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления:
2 × 7 = 14
Результат деления третьего неполного делимого на делитель пишем в частное, находим разность:
Разность мы получили равную нулю, значит деление произведено правильно.
Усложним задачу и приведем другой пример:
1020 ÷ 5
Запишем наш пример в столбик и определим первое неполное частное:
Разряд тысяч делимого составляет 1 , сравниваем с делителем:
1 < 5
Добавляем в неполное делимое разряд сотен и сравниваем:
10 > 5 – мы нашли неполное делимое.
Делим 10 на 5 , получаем 2 , записываем результат в частное. Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.
Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.
10 – 10 = 0
0 мы не пишем, опускаем следующий разряд делимого – разряд десятков:
Сравниваем второе неполное делимое с делителем.
2 < 5
Нам следует добавить в неполное делимое ещё один разряд, для этого в частное, на разряд десятков ставим 0 :
20 ÷ 5 = 4
Записываем ответ в разряд единиц частного и проверяем: записываем произведение под второе неполное делимое и вычисляем разность. Получаем 0 , значит пример решён правильно.
И ещё 2 правила деления в столбик:
1. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить, например:
Сколько нулей в младшем разряде делимого мы убираем, столько же нулей убираем в младших разрядах делителя.
2. Если в делимом после деления остались нули, то их следует перенести в частное:
Итак, сформулируем последовательность действий при делении в столбик.
- Размещаем делимое слева, делитель справа. Помним, что делимое мы делим, поразрядно выделяя неполные делимые и деля их последовательно на делитель. Разряды в неполное делимое выделяются слева направо от старших к младшим.
- Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить.
- Определяем первый неполный делитель:
а) выделяем в неполный делитель старший разряд делимого;
б) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (в), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
в) добавляем в неполное делимое следующий разряд и переходим к пункту (б).
- Определяем сколько разрядов будет в частном, и ставим столько точек на месте частного (под делителем) сколько будет в нем разрядов. Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого.

- Делим неполное делимое на делитель, для этого находим число, при умножении которого на делитель получилось бы число либо равное неполному делимому, либо меньше его.
- Найденное число записываем на место очередного разряда частного (точки), а результат умножения его на делитель записываем под неполным делимым и находим их разность.
- Если найденная разность меньше или равна неполному делимому значит, мы правильно поделили неполное делимое на делитель.
- Если в делимом остались еще разряды, то продолжаем деление, иначе переходим к пункту 10.
- Опускаем к разности следующий разряд делимого и получаем очередное неполное делимое:
а) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (б), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
б) добавляем к неполному делимому следующий разряд делимого, при этом в частное на место следующего разряда (точки) пишем 0;
в) переходим к пункту (а).
10. Если мы выполняли деление без остатка и последняя найденная разность равна 0 , то мы правильно выполнили деление.
Мы говорили о делении многоразрядного числа на одноразрядное. В случае, когда разрядность делителя больше, деление выполняется аналогично:
Пакет «Деление, умножение, сложение, вычитание, дроби и округление» в App Store
В этом комплекте 10 математических приложений iDevBooks. Сэкономьте 62 % по сравнению с покупкой приложений по отдельности.
Long Division
Приложение Long Division было представлено Apple в разделах «Новое и интересное», «Математика — числа и операции» и «Математические приложения для средней школы». Обзор образовательного приложения (iear.org): «Это фантастическое приложение!!»
Раздел частных частных
Традиционный метод длинного деления может быть труден для понимания из-за его абстрактности. В методе частичных частных учащийся может сделать ряд оценок, а затем сложить оценочные частные вместе.
Длинное умножение
В арифметике длинное умножение является стандартной процедурой, подходящей для умножения чисел. Этот метод разбивает задачу на умножение на ряд более простых шагов.
Это универсальное приложение является частью набора математических приложений idevbooks. Отзыв от Wired.com: «Набор отличных математических приложений для iPhone для детей старшего возраста».
Умножение частичных произведений
Метод умножения частичных произведений состоит из двух шагов. В примере 39 x 24 каждое разрядное значение сначала умножается отдельно. Частичные произведения складываются, и 36 + 120 + 180 + 600 дает ответ 936.
Р. Зени, Начальная школа Сэнди Хилл: «Эти математические приложения позволяют учащимся практиковать и закреплять определенные вычислительные стратегии, которым обучают в классе, с максимально возможной или как можно меньше строительных лесов по мере необходимости.Они также обеспечивают индивидуальную обратную связь с каждым учеником, с немедленностью, которая не всегда возможна при карандашной и бумажной практике. Возможность регулировать уровень сложности в соответствии со своими потребностями также очень мотивирует учеников. Я так рада, что наткнулась на этот замечательный образовательный инструмент!»
Возможность регулировать уровень сложности в соответствии со своими потребностями также очень мотивирует учеников. Я так рада, что наткнулась на этот замечательный образовательный инструмент!»
Дополнение к столбцу
Тим Пелтон, доцент кафедры математического образования Университета Виктории: «Поскольку недопустимы неправильные вводы, приложение обеспечивает пассивную форму положительного подкрепления, и ваш ребенок, скорее всего, улучшит как уверенность, так и компетентность в отношении процедура.»
Сложение частичных сумм
Метод сложения частичных сумм представляет собой двухэтапный процесс. В примере 764 + 340 каждое разрядное значение сначала добавляется отдельно слева направо. Результат сложения 1000 + 100 + 4 дает ответ 1104.
Wired.com: «Все приложения Эсы Хелттулы отлично подходят для изучения и практики математики, и в них нет мини-игр, поощрений или надоедливой музыки».
Вычитание столбцов
Тим Пелтон, доцент кафедры математического образования Университета Виктории: «Поскольку недопустимы неправильные вводы, приложение обеспечивает пассивную форму положительного подкрепления, и ваш ребенок, скорее всего, улучшит как уверенность, так и компетентность в отношении процедура.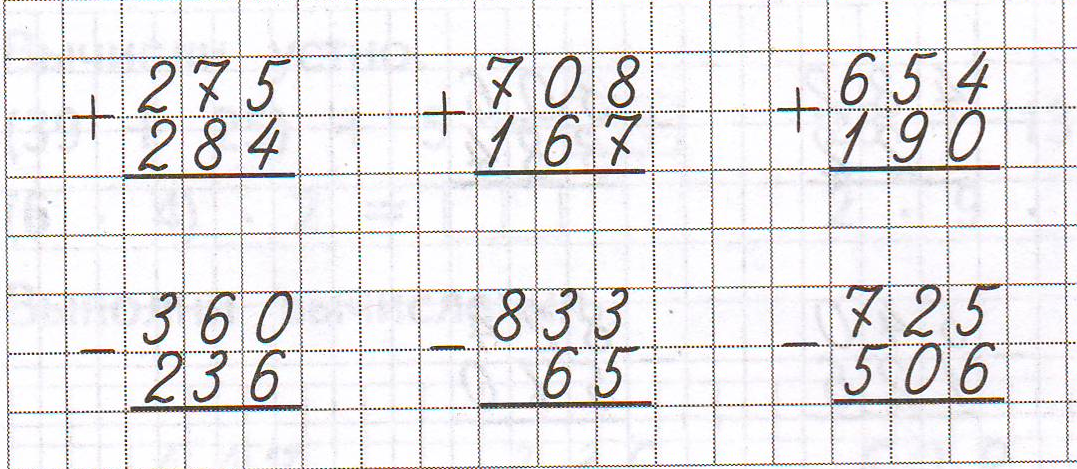 »
»
Математика дробей
Приложение «Математика дробей» можно использовать для обучения и изучения дробей путем пошагового решения задач на сложение, вычитание, деление и умножение дробей. Wired.com: «Довольно полезное приложение для обучения вычислению многих дробей».
Приложение Fraction Math может обрабатывать положительные и отрицательные дроби, неправильные дроби, целые числа и смешанные числа. Пользователь также может уменьшить полученные дроби.
Пользователь может вводить собственные дроби, смешанные и целые числа. Приложение также имеет иллюстрированный глоссарий наиболее распространенных терминов.
Округление десятичных дробей
Это математическое приложение можно использовать для обучения и изучения округления десятичных дробей. Вы можете ставить свои собственные задачи или решать случайные задачи. Десятичные числа можно округлить до ближайшего целого числа, десятых, сотых или тысячных долей. Их также можно округлить до 0, 1, 2 или 3 знаков после запятой.
Округление целых чисел
Это математическое приложение можно использовать для обучения и изучения округления целых чисел. Вы можете ставить свои собственные задачи или решать случайные задачи. Округляемые числа могут содержать до 8 цифр.
Конфиденциальность
В приложениях нет рекламы или встроенных покупок, и они не передают никаких данных во время работы приложения. Приложения также не содержат ссылок на другие приложения или Интернет.
Видео
Десятки видео этих и других приложений можно найти на idevbooks.com.
Сложение, вычитание, умножение и деление матриц
Используйте этот онлайн-калькулятор для выполнения операций с матрицами (суммирование, вычитание, умножение и деление).
Как сложить две матрицы?
Обе матрицы должны иметь одинаковую размерность, то есть одинаковое количество строк и одинаковое количество столбцов.
Сложить две матрицы просто: просто добавьте соответствующие элементы и поместите сумму в ту же соответствующую позицию.
Пример:
A и B две матрицы размерности 2 x 2
`A = [[1,5], [6, -4]]`
`B = [[0, -12], [3,7]]`
Тогда мы можем просуммировать,
`A + B = [[1+0,5-12], [6+3, -4+7]] = [[1, -7 ], [9,3]]`
Как вычесть две матрицы?
Точно так же две матрицы должны иметь одинаковую размерность, то есть одинаковое количество строк и одинаковое количество столбцов.
Чтобы их вычесть, просто вычтите элементы, находящиеся в одной и той же позиции, и поместите результат в ту же соответствующую позицию.
Пример:
A и B две матрицы размерности 3 x 2
`A = [[2,6], [7, -2], [5,11]]`
`B = [[ 1, -10], [4,7], [-9,13]]`
затем,
`A — B = [[2-1,6- (-10)], [7-4, -2-7], [5- (-9) ,11-13]] = [[1, 16], [3, -9], [14, -2]]`
Как перемножить две матрицы?
Для заданных двух матриц A и B умножение двух матриц A.B возможно только в том случае, если число столбцов матрицы A равно числу строк матрицы B. Таким образом, можно умножить матрицу 2 x 3 на матрицу 3 x 4. но не матрицей 2 x 2. Мы можем обобщить следующим образом:
Таким образом, можно умножить матрицу 2 x 3 на матрицу 3 x 4. но не матрицей 2 x 2. Мы можем обобщить следующим образом:
Произведение матриц A.B определяется только для матриц со следующими размерностями:
Размер A m x n
Размер B n x p
Произведение двух матриц P = A.B является матрицей размера m x p.
Обратите внимание: порядок A и B в произведении имеет значение, это A.B, а не B.A, который не определен, если p отличается от m (умножение матриц некоммутативно).
Как рассчитать произведение матриц?
Предположим, что A — матрица 2 x 3, а B — матрица 3 x 2. В соответствии с приведенными выше определениями (m=2, n=3 и p=2) умножение возможно, и произведение матриц P = A.B имеет размерность 2 x 2
`A = [[1,5,2], [3,4,7]]`
`B = [[0, -1], [8,6], [-2,10]]`
`P = A*B = [[\цвет {красный} {1},\цвет {красный} {5},\цвет {красный} {2}], [3,4,7]] * [[ \color {красный} {0}, -1], [\color {красный} {8}, 6], [\color {красный} {-2} ,10]] = [[\color {красный} {c_11 }, c_12], [c_21, c_22]]`
— Для расчета коэффициента `c_11` мы «умножаем» 1-ю строку на 1-й столбец. Итак, мы имеем
Итак, мы имеем
`c_11 = [1,5,2] * [[0], [8], [-2]] = 1*0 +5*8 +2* (-2) = 36`
— Для расчета коэффициента `c_12` мы «умножаем» 1-ю строку на 2-й столбец. Итак, у нас
`c_12 = [1,5,2] * [[-1], [6], [10]] = 1* (-1) +5*6 +2* (10) = 49`
— Для расчета коэффициента `c_21` мы «умножаем» 2-ю строку на 1-й столбец. Итак, мы имеем
`c_21 = [3,4,7] * [[0], [8], [-2]] = 3*0 +4*8 +7* (-2) = 18`
— Для расчета коэффициента `c_22` мы «умножаем» 2-ю строку на 2-й столбец. Итак, мы имеем
`c_22 = [3,4,7] * [[-1], [6], [10]] = 3* (-1) +4*6 +7* (10) = 91 `
Записываем окончательный результат,
`P = A*B = [[36,49], [18,91]]`
Мы обобщаем этот метод следующим образом:
Предположим, что A и B — две матрицы соответствующих размерностей m x n и n x p, тогда произведение P = A.B является матрицей размерности m x p. Обозначим через `c_ (ij)` элемент матрицы P, находящийся в первой строке и j-м столбце.
Коэффициент `c_ (ij)`вычисляется путем «умножения» строки i матрицы A на столбец j матрицы B.
