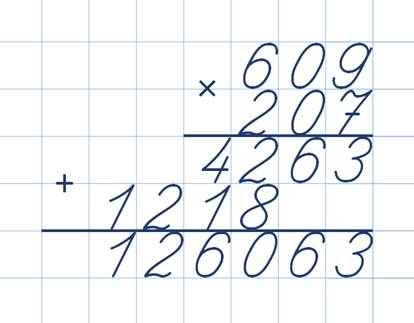Умножение чисел,запись которых оканчивается нулями.
Открытый урок математики в 4 «Г» классе 9 декабря 2014 г.
Предметная область: математика, УМК « Школа России»
Тип урока: урок «открытия» новых знаний.
Учебник с. 79
Задачи урока: способствовать развитию умений выполнять умножение многозначного числа, оканчивающегося нулями, на однозначное в столбик, решать задачи изученных видов, выполнять деление с остатком и проверкой, преобразование величин, соблюдать порядок выполнения действий в числовых выражениях.
Учебные цели, направленные на достижение личностных результатов обучения:
— принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения.
Учебные цели, направленные на достижение метапредметных результатов обучения:
— овладение способностью принимать и сохранять цели и задачи учебной деятельности, поиска средств её осуществления;
— освоение способов решения проблем творческого и поискового характера;
— готовность слушать собеседника и вести диалог; готовность признавать возможность существования различных точек зрения и права каждого иметь свою; излагать своё мнение и аргументировать свою точку зрения и оценку событий.
Учебные цели, направленные на достижение предметных результатов обучения:
— Формирование умения выполнять устно и письменно арифметические действия с числами и числовыми выражениями; решать текстовые задачи; выполнять и строить алгоритмы и стратегии; представлять, анализировать и интерпретировать данные.
Оборудование урока: ПК, проектор, презентация к уроку, раздаточный материал ( фишки разного цвета, алгоритм умножения на карточках, карточки с примерами, лесенки успеха, смайлики.). Учебник: М.И.Моро « Математика» 4 класс, часть1, рабочие тетради, лестница успеха, смайлики.
Содержание взаимодействия педагога и учащихся
№ п/п | Этапы урока | Деятельность учителя | Деятельность учащихся | Формируемые УУД (называть виды с расшифровкой) |
1. | Орг момент /2 мин/ Цель: Мотивация учащихся к учебной деятельности на личностно-значимом уровне | Создаю условия для возникновения внутренней потребности включения в деятельность. Необычный день у нас, и гостями полон класс. Что гостям сказать нам надо? — Видеть вас мы очень рады! Прозвенел звонок – начинается урок. Чтоб урок прошёл прекрасно, Хорошо, отлично, классно Говорю вам пожеланье: Пожелание удачи, пожелание добра. Пожелание терпенья и, конечно же, уменья. В этом классе все друзья? Да! Я, ты, он, она, — вместе дружная семья? Да! Посмотри-ка на себя, На соседа справа, на соседа слева. В этом классе все друзья? Да! Я, ты, он, она – вместе дружная семья! Повернитесь друг к другу, пожелайте удачи, добра… улыбнитесь. — Ребята, а что нужно человеку, чтобы быть успешным, жизнерадостным, здоровым? — Улыбаясь друг другу, какие эмоции вы получили? Займите свои рабочие места. — Одна хорошая минута сделала одно хорошее дело. Десять минут сделали 10 хороших дел. А сколько хороших дел можно сделать за урок? Итак, ребята, я желаю вам сегодня на уроке сделать много хороших дел, получить положительные эмоции от своих результатов, от результата урока. И начать я хочу с высказывания: « Математика – гимнастика ума». Как вы его понимаете? Давайте подумаем, что же мы должны будем сделать сегодня, чтобы гимнастика принесла нам пользу? Нам предстоит много думать, решать, повторять. Да, да! Мы будем как спортсмены на тренировке, ведь нам предстоит много работы, чтобы повторить пройденный материал и научиться новому. Спортсмены тренируют свои мышцы, а мы будем тренировать свой мозг .Не будем терять времени. | Стоят в круге. Включаются в учебную деятельность. Поддерживают диалог. Хором дополняют реплику учителя. Диалог в круге. — Положительные эмоции, внимание других, доброе отношение окружающих, хорошие знания и т. Садятся за парты. Объясняют смысл высказывания. | Коммуникативные УУД: планируют учебное сотрудничество с учителем и со сверстниками Личностные УУД: Понимают и принимают значение знаний для человека; проявляют интерес к изучаемому предмету, понимают его важность |
2 3. | Устный счёт. минутка чистописания | Для начала небольшая разминка. — А задание называется : «Реши пример». Тот кто первым решит этот пример, тот окажется победителем в беге. 7 200 : (2 + 7) + (140 – 90)= 850 48+530+70+52 = 700 12 м 65 см + 9 м 37 см =22 м 02 см — А теперь задание усложняется. И беговые упражнения переходят в беговую эстафету. Главная задача этого задания выполнить все правильно и как можно быстрее. Работа в парах. Решаем пример, передаем на следующую парту, какой ряд быстрее решит примеры, тот победитель. 420 : 6 + 70:10*100 = 1400 70*5-200:3-50= 0 180*5:10+60*2=300 — Молодцы! Бегать вы умеете. Написание, каких цифр мы сегодня повторим, вы скажите, выполнив задания устного счёта. Откройте тетради, запишите сегодняшнее число : 9 декабря. Классная работа. В сумерках над рекой кружило несколько летучих мышей. Когда рыбий косяк подошел близко к поверхности воды, прилетело еще 9 мышей. Теперь уже 15 мышей ожидало, когда рыбы выставят над водой плавник или голову, чтобы схватить их. Сколько летучих мышей прилетело? (9) – Кто из вас знает, кто такой энтомолог? (Энтомолог – это специалист по разделу зоологии, изучающий насекомых.) 2.У ученого энтомолога в коллекции было несколько Южноамериканских бабочек. Из экспедиции он привез еще 15 изумительных экспонатов, и в его коллекции стало 19 бабочек. Сколько бабочек из Южной Америки было у ученого до экспедиции?(4) 3. В террариуме было 14 рогатых игуан, из тропических лесов привезли в 2 раза меньше зеленых игуан. 4. У орнитолога было 20 фотографий черного журавля и 19 фотографий уток-мандаринок. На сколько больше было фотографий с черным журавлем, чем с утками-мандаринками?(на 1) – Догадайтесь, чем занимается орнитолог? (Орнитолог-это специалист, который изучает птиц и их распространение.) -Какое число получили? Получили число: 9 471. | Познавательные УУД: – проводят анализ, синтез; извлекают необходимую информацию из текстов; владеют базовыми предметными понятиями, способами выполнения заданий творческого и поискового характера. Личностные УУД: . осознают свои возможности в учении; способны адекватно рассуждать о причинах своего успеха или неуспеха в учении, связывая успехи с усилиями, трудолюбием, проявляют познавательный интерес к изучению предмета. Коммуникативные УУД: умеют слушать друг друга, строить понятные для партнёра по коммуникации речевые высказывания, задают вопросы с целью получения необходимой для решения проблемы информации; могут работать в коллективе, уважают мнения других участников образовательного процесса |
2. | Актуализация знаний . /5 мин./ Цель: Готовность мышления и осознания потребности к построению нового способа действий. | Веду подводящий диалог. ( Активизирую у учащихся мыслительные операции, внимание, память) — Посмотрите внимательно на экран. Перед вами числовые выражения. -Какую закономерность вы установили, исследуя первое выражение.? -Предлагаю, прежде чем вы назовёте произведение, объяснить приём умножения. 1)6·9= 54 2) 26·3 3) 139·0 4) 264·10 5) 92· 100 6) 500·5 ( По мере поступления ответов на экране появляются результаты рассуждения) | Участвуют в диалоге. — Можно выявить закономерность. 1) табличное умножение 2) внетабличное умножение ( разбиваем на разрядные слагаемые) 3) умножение на нуль 4) увеличение числа в 10 раз, приём умножения на 10 5) приём умножения на 100 6) затрудняются | Познавательные УУД: — Общеучебные; — Логические; Коммуникативные УУД: — умение вступать в диалог и участвовать в коллективном обсуждении проблемы; |
3. | Постановка учебной задачи. Создание проблемной ситуации. /5 мин/ Цель: Выявление места и причины затруднения, постановка цели урока. | 1. Веду побуждающий диалог. — Почему вы затруднились назвать произведение в 6 снежинке? Побуждаю к осознанию темы и цели урока. — Как вы думаете, какова же тема нашего урока? — Я предлагаю вам два варианта решения данной проблемы. 2. Стимулирую к деятельности. Предлагаю два варианта: — Первый : Сама покажу вам приём умножения. Второй – на основе ранее полученных знаний попробуете решить сами. — Какой вариант выберете вы и почему | Участвуют в диалоге. — Не можем, так как с этим приёмом умножения ещё не знакомы (умножение числа, оканчивающегося нулями) Формулируют тему урока. -Умножение чисел, запись которых оканчивается нулями. Дети предпочитают « открывать» новое знание сами. | Познавательные УУД: — постановка и формулирование проблемы — поиск и выделение необходимой информации Регулятивные УУД: — целеполагание; Коммуникативные: — умение выражать свои мысли; |
4 | . « Открытие» детьми нового знания. /9 мин./ Цель: Построение детьми нового способа действий и формирование способности к его выполнению. | 1. Организую деятельность. — Великий Сократ говорил о том, что научиться играть на флейте можно только, играя самому. -Так и вы можете научиться умножать такие числа, думая только своей головой и пытаясь решить самостоятельно. — У кого есть предположения, как можно его вычислить? — Хорошо, если вычислим на калькуляторе, получим готовый ответ, мы пополним копилку наших знаний? Как будем выполнять? — Вы предложили устно выполнить вычисления. Как именно? Может кто-то из вас сможет объяснить, как можно умножить 500 на 5? 18000* 3 =18 тыс. * 3 = 54 тыс.= 54 000 — Какой способ мы можем ещё использовать? — Умеем мы это правильно делать? — Дайте более точную формулировку темы нашего урока. — Какую учебную задачу вы поставите перед собой? 2.Предлагаю записать пример столбиком самостоятельно и решить его. А сейчас научимся записывать столбиком.
380 .9 8400 .7 69000 . 4 380 8400 69000 9 7 4 3420 58800 276000
— Сейчас объясним приём умножения на доске. 3. Вызываю к доске ученика, верно решившего пример. 8400 * 7 — У кого другая запись? 4. Организую работу в парах по составлению алгоритма умножения. — Чтобы правильно решать такие примеры, нужно знать алгоритм решения. — Что такое алгоритм? — Сейчас мы его составим. У вас на партах карточки, на которых напечатаны действия алгоритма. Работая и обсуждая в парах, вы разложите карточки в нужном порядке. Вывожу алгоритм на экран. | Выдвигают гипотезы: — устно — на калькуляторе — столбиком. -Нет. -устно. Объясняют приём умножения. Умножаем числа без нулей, а потом их приписываем. — Не всегда. — Решение столбиком. Дети формулируют тему и учебную задачу урока. — Письменное умножение чисел, запись которых оканчивается нулями. — Мы должны научиться письменно умножать многозначные числа /в столбик Пытаются решить пример самостоятельно. Под первой цифрой справа отличной от нуля. Объясняют приём умножения. — Выполняем умножение, не глядя на нули, а затем к результату приписываем столько нулей, сколько содержится в множителе. — Пошаговое выполнение действий. Располагают карточки в нужном порядке. Одна пара зачитывает. 1.Второй множитель подписываю под первой цифрой справа, чтобы нули остались в стороне. 2.Умножаю многозначное число на число, не обращая внимания на нули. 3.К полученному результату приписываю столько нулей, сколько их на конце первого множителя. 4.Читаю ответ. | Познавательные УУД: — построение логической цепи рассуждений; — самостоятельное создание способов решения проблем поискового характера; Коммуникативные УУД: — инициативное сотрудничество в поиске и сборе информации со сверстниками и учителем; |
5. | Первичное закрепление с проговарива- нием. /5 мин./ Цель: Зафиксировать способ письменного умножения на числа, оканчивающиеся нулями. | Два ученика работают у доски, остальные в тетради. — Решить примеры самостоятельно. Прогнозируют результат и выполняют задание. Взаимопроверка по готовым ответам с доски. — Ответы детей / Мой прогноз совпал с результатом, был уверен и правильно выполнил. — Мой прогноз не совпал с результатом, я был уверен, что справлюсь, но допустил ошибку./ | КоммуникативныеУУД: Умение выражать свои мысли; Регулятивные УУД: Овладение алгоритмом умножения; | |
1.Организую работу по закреплению нового знания. Фронтальная работа с проговариванием вслух. — Закрепим полученные знания, выполнив письменное умножение с объяснением на доске. К доске вызываю сначала « сильного» ученика, затем «слабого». — Понятен ли вам этот вычислительный приём? — Как проверить, что вы его усвоили? Даюинструктаж по выполнению задания. — У каждого из вас имеется карточка. На ней записаны примеры. 390*3 = 1 170 6800*6 = 40 800 20080*7 = 140 560 7 320*5=36 600 Предлагаю спрогнозировать предполагаемый результат: в верхнем углу карточки вы видите круг. Закрасьте его зелёным цветом, если вы уверены в своих силах. Жёлтым цветом – если сомневаетесь. Красным цветом – если вам нужна помощь. Кому нужна помощь, обращайтесь к алгоритму. Критерий оценки – правильность счёта, безошибочность. А теперь приступим. — Передайте карточку соседу. Вывожу ответы к заданию на экран. — Если нет ошибок, закрасьте нижний треугольник зелёным цветом, если есть ошибки – жёлтым. — Верните карточку владельцу. — Совпал ли ваш прогноз с результатом | ||||
6. | Взаимоконтроль с проверкой по эталону. /3 мин./ Цель: -Тренировать способность к самоконтролю и самооценке. — Проверить способность к умножению многозначных чисел на числа, оканчивающиеся нулями. | Регулятивные УУД: Прогнозирование; Самоконтроль; Коррекция; Коммуникативные УУД: Учебное сотрудничество; | ||
физминутка | Каждый день по утрам Делаем зарядку Вот мы руки развели, (Руки в стороны.) Словно удивились. И друг другу до земли В пояс поклонились! (Наклоны вперед.) Наклонились, выпрямились, Наклонились, выпрямились. Ниже, дети, не ленитесь, Поклонитесь, улыбнитесь. Всем друзьям — физкультпривет! Всем друзьям Физкультпривет, (Прогнуться назад, потянуться. Сделал паузу, иль нет? (Поморгать глазами, несильно потереть глаза.) Быстроногому гонцу (Бег на носках, сидя.) И отважному борцу, (Наклоны вправо-влево, руки согнуты — в стороны.) И гимнасту, (Руки вниз, спину выпрямить, подбородок поднять.) И пловцу — (Движения руками «брасс».) Всем друзьям Физкультпривет! | Выполняют физкультминутку | КоммуникативныеУУД: Проявляют готовность слушать Личностные УУД: Имеют установку на здоровый образ жизни |
8. | Включение нового в систему знаний и повторения. /7 мин./ Цель: — закрепить умение решать текстовые задачи; — применение нового способа действия; — создание ситуации успеха. Физминутка для глаз Работа над величинами. | Организую работу над задачей. Прочитайте задачу. с. 79 № 351 — как составим краткую запись? Что изготовляли на фабрике? (обувь) О каких видах обуви идет речь в задаче? (мужской, женской, детской) Что обозначает 8900 число? (Количество мужской обуви) Что обозначает 40000 число в задаче? (Сколько пар обуви изготовили всего.) А что сказано о женской обуви? (Ее изготовили в два раза больше) (записываю краткую запись на доске) Вся ли краткая запись выполнена верно? (Нет главного вопроса.) Каков главный вопрос задачи? (Сколько пар детской обуви изготовили?) Сможете ли вы сразу ответить на главный вопрос задачи? (Нет.) Почему? (Не знаем, сколько пар женской обуви изготовили.) Какие слова вам помогут выбрать действие? (в, раза.) На какие действия они указывают? ( Умножение или деление.) Какое слово вам поможет? (Больше) Каким действием будем находить женскую обувь? (Умножением.) Что сказано о детской обуви? (Остальная. Как ищем остаток? (Вычитанием.) Что надо найти в задаче? (Детскую обувь.) – План решения наметили, а вы подумайте и решите задачу. Рисуй глазами треугольник. Теперь его переверни Вершиной вниз. И вновь глазами ты по периметру веди. Рисуй восьмерку вертикально. Ты головою не крути, А лишь глазами осторожно ты вдоль по линиям води. И на бочок ее клади. Теперь следи горизонтально, И в центре ты остановись. Зажмурься крепко, не ленись. Глаза открываем мы наконец. Зарядка окончилась. Ты молодец! №352 Свёклы – 80 м. по 3 т. Сахар – 1 часть — ? т. 6 С. 79 № 355 3ч 45 мин =180+45=225 мин 6ч 40 мин = 360+40=400 мин 5 мин 05 сек = 5*60 = 300+05=305 с 10 мин = 600 с 6 ц = 600 кг 15 т =150 кг 7 000 г =7 кг | Используя опорные слова. Дети отвечают на вопросы по содержанию задачи. М 40 000 п. ужская – 8 900 п.Женская — ? в 2 раза.> Детская — ? 1 ученик записывает решение задачи на доске. Х8900 +17 800 — 40 000 2 8 900 26 700 17800(п.) 26 700(п.) 13 300(п.) Женской женской и детской обуви мужской обуви Ответ: 13 300 пар детской обуви. Один ученик работает у доски, остальные в тетрадях. 3 * 80 = 240 (т) –свёклы 240 : 6 = 40 (т) Ответ 40 тонн сахара изготовили. Выполняют самостоятельно. Проверка | Познавательные УУД: — анализ с целью выделения главных признаков; — умение осознанно строить речевое высказывание в устной форме; — выделение и поиск необходимой информации; Коммуникативные УУД: — умение достаточно полно и чётко выражать мысли; -интегрирование в группы и продуктивное взаимодействие. Регулятивные УУД: — планирование; — контроль; — коррекция; — самооценка. |
9. | Рефлексия учебной деятельности. / 3 мин./ Цель: — Оценить результаты собственной деятельности; Д/ задание — Осознание метода построения границ применения нового знания. | Благодарю ребят за работу. Урок сегодня был удачный, Не прошёл для вас он зря. Вы все очень постаралась. Вам понравилось, друзья? — Вспомните девиз нашего урока. «Математика – гимнастика ума» — Огромное трудолюбие и ваша тяга к знаниям помогла нам сделать на уроке открытие. Эта удача приблизила ещё на один шаг каждого из вас к успеху. — Какая тема нашего урока? — Какую учебную задачу мы ставили перед собой? — Чему новому научились? — Достигли мы успеха? На память о нашем уроке, чтобы вы ничего не забыли: домашнее задание. Давайте поспешим, друзья. Записать задания. А дома… Приложить прошу Максимум старания. Провожу инструктаж домашнего задания. С.79 № 350 4 столбик, № 354 – обязательные для всех № 356 – предлагаю тем, кто не боится трудностей. Оцениваю работы учащихся Оцените себя, отметив свои успехи на своих индивидуальных лестницах, и на нашей лестнице успеха ( если вы считаете, что хорошо усвоили эту тему раскрашиваете и прикрепляете фигурку на верхней ступеньке. Если вам ещё нужно время, чтобы выучить алгоритм, но ошибок вы не допустили- на вторую ступеньку. Если вам нужно ещё время , чтобы выучить алгоритм ,хорошенько потренироваться на третью ступеньку. Если вам ещё нужно послушать объяснение, так как вы не понимаете, как действовать – на четвёртую ступеньку. — Молодцы! Вы хорошо потрудились, и получили за это свои результаты. А чтобы достичь высот в математике, необходимо как альпинистам взбираться на гору знаний, медленно шаг за шагом не торопясь, дружно. Подошёл к концу урок, Прозвенит сейчас звонок, Вам девчонки и мальчишки – Всем спасибо за урок. | проговаривают девиз урока. Дети вспоминают поставленную цель и учебную задачу урока. — Умножение чисел, запись которых оканчивается нулями. — Научиться письменно умножать числа, оканчивающиеся нулями. — Научиться письменно умножать числа, оканчивающиеся нулями. -Достигли. Записывают задание в дневники. Раскрашивают « смайлики» и крепят на доску. Высказывают своё мнение. | Регулятивные: — оценивают собственную деятельность на уроке Познавательные: — умение ориентироваться в своей системе знаний Коммуникативные УУД: —аргументировать свои высказывания; Личностные УУД: проявляют познавательный интерес к предмету Регулятивные: Принимают и сохраняют учебную задачу, осуществляют поиск средств для её выполнения. |
Прогнозируемый результат:
Предметные:
В конце урока ученики
1.Знают алгоритм письменного умножения чисел, запись которых оканчивается нулями.
2.Умеют письменно умножать числа, запись которых оканчивается нулями.
Метапредметные
1.Умеют ставить учебную задачу и самостоятельно формулировать выводы.
2.Умеют слушать собеседника, излагать своё мнение и аргументировать свою точку зрения.
Личностные:
1.Умеют сотрудничать с учителем и сверстниками
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/156663-urok-matematiki-4-klass-po-temeumnozhenie-ch
Этап урока (задача каждого этапа) | Деятельность учителя | Деятельность обучающегося | Предполагаемый результат |
1. Задача этапа: создать у школьников направленность на учебную работу | Здравствуйте, ребята. Меня зовут Евгения Дмитриевна, и сегодня я проведу у вас урок. Давайте улыбнёмся друг другу и с хорошим настроением начнём наш урок. | Приветствуют учителя, улыбаются друг другу. | Л: положительная мотивация и познавательный интерес к изучаемому. П: уметь слушать и слышать. |
2. Актуализация знаний Задача этапа: актуализировать опорные знания и изученные способы действий; подготовить учащихся к изучению материала, необходимого для «открытия нового знания» | Начать предлагаю с небольшой разминки. На доске представлены выражения, которые необходимо решить устно. 20·8:40 72:3·2 60:10·8 40:5·6 84:42·4 96:4·3 А теперь давайте вспомним, о чем говорили на прошлом уроке. Верно! На прошлом уроке вы научились умножать на числа, оканчивающиеся нулями. Давайте повторим алгоритм записи и умножения. Сейчас предлагаю вам решить вот такой математический ребус Отлично! | Выполняют устный счёт Называю предыдущую тему Вспоминают алгоритм Решают ребус | Л: положительная мотивация и познавательный интерес к изучаемому. К: уметь строить монологические высказывания; уметь вступать в учебный диалог с учителем, участвовать в общей беседе; уметь слушать; уметь высказывать и обосновывать свою точку зрения; П: активно использовать операции анализа, синтеза, сравнения, классификации; уметь следовать алгоритму при выполнении заданий; уметь устанавливать причинно-следственные связи, делать обобщения, выводы. |
3. Задача этапа: Подвести учащихся к самостоятельной постановке и принятию учебных задач; определить и сформулировать проблему; разработать план учебных действий по достижению цели урока. | Обратите внимание на слайд. Что мы видим? Чем эти примеры отличаются друг от друга? Умеете ли вы решать такие примеры? Как вы думаете, чему будет посвящён сегодняшний урок? Вы правы. Тема нашего урока «Письменное умножение двух чисел, оканчивающихся нулями». Какие задачи мы можем поставить перед собой? Отлично! Тогда, давайте начнём. | Отвечают на вопросы учителя Нет Формулируют тему и задачи урока | Р: осознавать цели и задачи изучения темы. П: уметь устанавливать причинно-следственные связи, делать обобщения, выводы активно использовать операции анализа, синтеза, сравнения, классификации. К: уметь строить монологические высказывания; уметь высказывать и обосновывать свою точку зрения. |
4. Открытие нового знания Задача этапа: организовать ситуацию решения учебной задачи, систематизировать полученную информацию. | Давайте, попробуем найти произведение следующих двух чисел: 80 ∙ 40 Как мы можно представить число 80? А как можно представить число 40? 80 ∙ 40=8 дес. ∙(4∙10)=320 дес.=3 200 Рассмотрим еще один пример и попробуем найти произведение чисел: 600 ∙ 90 Как мы можем представить число 600? А число 90? 600 ∙ 90=6 сот. Но так считать не очень удобно, поэтому давайте попробуем записать эти примеры столбиком. Как вы думаете, сколько нолей мы поставим в произведении? Почему? Давайте проверим. А поможет нам в этом алгоритм умножения двух чисел, оканчивающихся нулями. Алгоритм умножения: 1.Перемножить числа, не обращая внимания на нули в конце 2.В полученном произведении приписать справа столько нулей сколько их на конце обоих множителей вместе Обратите внимание, что это не алгоритм записи выражения в столбик. Алгоритм записи будет полностью совпадать с тем, который вы изучали ране и повторяли сегодня. Откройте тетради и запишите число, классная работа. А теперь откройте учебник на стр. 15. Обратимся к заданию № 54. Первый столбик решает первый ряд, второй достанется второму, а третий третьему. Проверим, что у вас получилось. Физминутка Прочитайте задачу под номером 56. Что нам известно? Как двигались теплоходы? Что нам известно о первом теплоходе? Что известно о втором теплоходе? Так как теплоходы вышли одновременно навстречу друг другу, время до встречи у них будет разное или одинаковое? Давайте занесём известные нам данные в таблицу. Что нам неизвестно? Какой вопрос мы можем задать к этой задаче? Какое действие нужно выполнить, чтобы найти расстояние? Решите задачу. | Как 8 дес. Как произведение чисел (4∙10) Как 6 сот. Как произведение чисел (9 ∙ 10) 1 ученик у доски решает пример, с комментированием правила записи данных примеров, остальные работают в тетрадях. Анализируют алгоритм Записывают число, вид работы Работают с учебником. Выполняют задание учителя по вариантам (кто может, выполняет самостоятельно, остальные фронтально, у доски) Выполняют физминутку Читают задачу Анализируют задачу, отвечают на вопросы учителя Навстречу друг другу Составляют таблицу Какое расстояние прошёл теплоход №2? Время умножить на скорость Решают задачу самостоятельно, если могут (остальные работают у доски, фронтально) | Р: осознавать цели и задачи изучения темы; осознавать способы и приёмы действий при решении языковых задач; осуществлять само- и взаимопроверку, находить и исправлять собственные ошибки. К: уметь строить монологические высказывания; уметь вступать в учебный диалог с учителем, участвовать в общей беседе; уметь слушать; уметь высказывать и обосновывать свою точку зрения. П: активно использовать операции анализа, синтеза, сравнения, классификации; уметь следовать алгоритму при выполнении заданий; уметь устанавливать причинно-следственные связи, делать обобщения, выводы. |
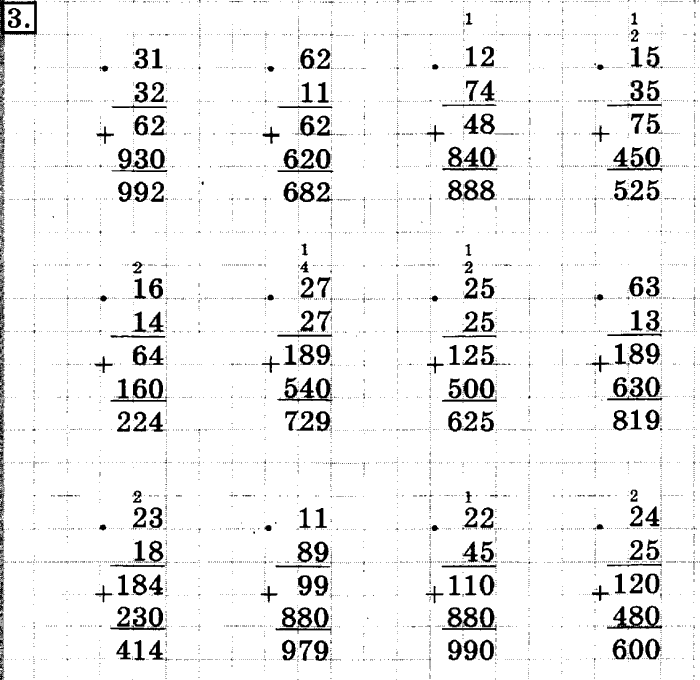
5. Первичное закрепление Задача этапа: создать условия для отработки навыка записи и умножения двух чисел, оканчивающихся нулями | Теперь обратимся к задаче под номером 12 на странице 21. Прочитайте её. Что нам известно о мальчиках? Что нам известно о первом мальчике? Что нужно узнать в задаче? Давайте решим задачу устно все вместе. А сейчас снова поработаем самостоятельно. Примеры под цифрой 1 решают первый и третий ряд, а под цифрой 2 – второй. | Читают задачу Отвечают на вопросы учителя Устно решают задачу Выполняют самостоятельную работу | : осознавать цели и задачи изучения темы; осознавать способы и приёмы действий при решении языковых задач; осуществлять само- и взаимопроверку, находить и исправлять собственные ошибки. К: уметь строить монологические высказывания; уметь вступать в учебный диалог с учителем; уметь высказывать и обосновывать свою точку зрения; уметь работать в группе; учитывать мнение других. П: активно использовать операции анализа, синтеза, сравнения, классификации; уметь следовать алгоритму при выполнении заданий; уметь устанавливать причинно-следственные связи, делать обобщения, выводы. |
6. Итог урока. Рефлексия Задача этапа: установить соответствие между поставленной целью и результатом урока; организовать рефлексию и самооценку учащихся; проанализировать и оценить успешность достижения цели. | Что нового вы узнали на сегодняшнем уроке? Все ли задачи, поставленные в начале урока, мы смогли выполнить? Вам понравился урок? Оцените свою деятельность на уроке, если вы считаете, что отлично поработали сегодня, то встаньте со своего места, если думаете, что поработали хорошо, но были недочёты, то привстаньте, а если вам было непонятно, вы допустили много ошибок, оставайтесь сидеть на своих местах. | Отвечают на вопросы учителя Анализируют урок, свою деятельность на уроке | Л: развивать способность к самооценке своих действий, поступков. Р: осознавать цели и задачи изучения темы; уметь адекватно оценивать свои достижения, осознавать возникающие трудности, искать их причины и пути преодоления. К: уметь строить монологические высказывания. П: уметь устанавливать причинно-следственные связи, делать обобщения, выводы. |
7. Домашнее задание Задача этапа: сообщить объем и содержание домашнего задания с фиксацией в дневнике; проверить понимание выполнения домашнего задания. | Стр.21 , №13, №18 | Слушают учителя, записывают домашнее задание. Задают уточняющие вопросы по его содержанию. | Р: осознавать цели и задачи изучения темы; осознавать способы и приёмы действий при решении языковых задач. |
Когда вы умножаете на 10, просто добавляете ноль? Ужасы!?! – МЭРИЛИН БЕРНС МАТЕМАТИКА
Мы спрашиваем, слушаем, учимся – это одна из моих первых записей в блоге. (Я разместил его 5 января 2015 года.) В пост включены интервью нескольких студентов, отвечающих на вопрос: Сколько стоит 12,6 x 10?
Один из видеоклипов показывает, как Маллика Скотт берет интервью у Наташи, которая объясняет, как она выбрала неверный ответ 12.60. Наташа объясняет: «К любому числу, умноженному на 10, в конце можно добавить ноль».
Несмотря на то, что я вел блог более трех лет назад, Уэстли Янг недавно опубликовал комментарий, который частично касается стратегии «добавить ноль»: которые меня давно волнуют. Одна из проблем заключается в том, что я беспокоюсь о том, что учащиеся начальных классов замечают закономерность умножения целых чисел на 10, а затем ошибочно применяют эту закономерность к десятичным дробям, как это сделала Наташа.
Одна из проблем заключается в том, что я беспокоюсь о том, что учащиеся начальных классов замечают закономерность умножения целых чисел на 10, а затем ошибочно применяют эту закономерность к десятичным дробям, как это сделала Наташа.
Моя вторая проблема связана с моей борьбой с тем, что делать с моей проблемой.
В начальной математике учащиеся ищут закономерности. Это может быть хорошо. Они изучают алгоритмы. Это тоже может быть хорошо. Их язык часто неточен. Это не так хорошо, но они находятся в процессе обучения, а обучение беспорядочно. Преподавание тоже грязное.
Много мыслей проносится в моей голове, пока я размышляю над видеоклипом Наташи и комментарием Уэстли. Что я должен делать как учитель? Как я могу помочь Наташе и таким же ученикам передумать?
Моя первая мысль
Что, если бы я сказал Наташе что-то вроде этого:
Если бы Наташа ответила «да», я бы хотел услышать, почему она считает это правдой. (Я думаю, что важно попросить учащихся объяснить свои рассуждения, даже если они верны. Может быть, даже особенно, когда они верны.) Затем я мог бы сказать что-то вроде: «Интересно, как я мог бы умножить число на 10 и накрутить получил ответ, который совпадает с числом до умножения». Может ли это помочь? К чему это могло привести?
(Я думаю, что важно попросить учащихся объяснить свои рассуждения, даже если они верны. Может быть, даже особенно, когда они верны.) Затем я мог бы сказать что-то вроде: «Интересно, как я мог бы умножить число на 10 и накрутить получил ответ, который совпадает с числом до умножения». Может ли это помочь? К чему это могло привести?
Моя вторая мысль
Что, если я скажу что-то подобное Наташе:
Да, тогда я провалюсь в семантическую дыру, которая больше стимулирует закатывание глаз у студентов, чем глубокое математическое мышление. Наташа не прибавляла ноль в том смысле, что выполняла операцию сложения; вместо этого она писала/прибавляла/добавляла (или как бы вы это описали) ноль к числу. Для 8 x 10 она делала так и получала 80. Для 12,6 она делала так и получала 12,60.
Моя третья мысль
Что, если бы я сказал Наташе что-то вроде этого:
Это идея, которую я хотел бы, чтобы студенты поняли, как указал Уэстли в своем комментарии. В классе, возможно, я бы написал это на доске, чтобы студенты сначала поговорили с партнером, а затем попросили бы студентов поделиться своими идеями с классом о том, почему то, что я сказал, математически верно. Я думаю, они бы согласились.
В классе, возможно, я бы написал это на доске, чтобы студенты сначала поговорили с партнером, а затем попросили бы студентов поделиться своими идеями с классом о том, почему то, что я сказал, математически верно. Я думаю, они бы согласились.
Предположим, студенты согласны со всеми этими утверждениями. Поможет ли это им думать об умножении на 10 по-другому? Я не уверен. По моему опыту преподавания, обучение с помощью рассказов часто неэффективно. Мои утверждения могут быть ясны для меня, но такие заявления слишком часто являются математическим вздором для студентов.
Когда я прочитал это, я сказал себе: «Да!»
Роль контекстов
Хорошо, еще одна мысль. Марк Чабб (который пишет в Твиттере как @MarkChubb3) написал блог под названием Важность контекстов и визуальных эффектов . В разделе об использовании контекстов он написал:
Когда я прочитал это, я сказал себе: «Да!»
И тут мне вспомнился другой клип из того же интервью Маллики и Наташи. Через несколько вопросов после того, как Наташа решила 12,6 х 10, Маллика попросила ее решить задачу со словами: Одна ручка стоит 1,39 доллара. Сколько стоят десять ручек?
Через несколько вопросов после того, как Наташа решила 12,6 х 10, Маллика попросила ее решить задачу со словами: Одна ручка стоит 1,39 доллара. Сколько стоят десять ручек?
Здесь Наташа снова сталкивается с умножением на 10. Она повторяет то, что она сказала при умножении 12,6 x 10: «Каждый раз, когда вы умножаете число на 10, вы просто добавляете ноль в конце». Но здесь, в контексте покупки ручек, она получает правильный ответ: 13,90 долларов. Размышляя о том, что написал Марк, контекст задачи побуждал Наташу дать разумный ответ, а не то, что она сделала с задачей о голых числах. Взглянем.
Где сейчас мои мысли?
Я все еще думаю. Как писал Марк, при умножении десятичных чисел на 10, если мы закрепим опыт учащихся в контексте, у них будет больше шансов применить рассуждения, чтобы понять смысл, а не применять шаблон, который они выучили для целого числа. (Возможно, было бы интересно поговорить со студентами о том, почему «прибавка к нулю» работает с целыми числами, а не с десятичными. Но это позже.)
(Возможно, было бы интересно поговорить со студентами о том, почему «прибавка к нулю» работает с целыми числами, а не с десятичными. Но это позже.)
Также в ответ на комментарий Уэстли о важности того, что происходит на самом деле математически, когда мы умножаем целые числа на 10, я думаю, что мне нужно признать, что учащиеся узнают закономерность, но продолжать помогать им понимать закономерность математически. Слишком многие ученики видят в схеме умножения на 10 чистую удачу, особенно если им не так легко умножать на другие числа.
Я знаю, что не рассмотрел другую часть комментария Уэстли о том, что ученики «передвигают десятичную точку» как стратегию умножения десятичных чисел на 10. Я также слышал это объяснение и согласен с тем, что десятичная дробь на самом деле не перемещается. . Может другой блог?
Я все еще думаю. Я приветствую ваши мысли.
A Постскриптум
Я понимаю, что один пример мало что доказывает. Вот видеоклипы двух других студентов, Дженнифер и Серджио, которые отвечают на те же два вопроса, что и Наташа. Для 12,6 x 10 Серхио попросил пропустить его, заявив, что не может понять ответ без бумаги и карандаша, а Дженнифер дала неверный ответ 120,6. Для контекстуальной задачи о покупке 10 ручек по 1,39 доллара.каждый, Серджио и Дженнифер, оба получают правильный ответ, каждый рассуждая по-своему.
Для 12,6 x 10 Серхио попросил пропустить его, заявив, что не может понять ответ без бумаги и карандаша, а Дженнифер дала неверный ответ 120,6. Для контекстуальной задачи о покупке 10 ручек по 1,39 доллара.каждый, Серджио и Дженнифер, оба получают правильный ответ, каждый рассуждая по-своему.
Умножение чисел с использованием разрядного значения (определение, типы и примеры)
Содержание
- Что такое разрядное значение?
- Использование разрядного числа при умножении
- Использование разрядного значения для умножения на 10, 100 или 1000
- Правила умножения на 10, 100 или 1000
- Факты об умножении
- Решенные примеры
- Часто задаваемые вопросы
Что такое разрядное значение?
Разрядное значение — это значение позиции каждой цифры в числе.
Рассмотрим, например, число 242.
Разрядное значение цифры 2 на месте единиц равно 2 × 1 = 2 или 2 единицы.
Разрядное значение цифры 4 в разряде десятков равно 4 × 10 = 40 или 4 десятка.
Аналогично, разрядное значение цифры 2 в сотых долях равно 2 × 100 = 200 или 2 сотых.
Использование разрядного значения при умножении
При умножении двух чисел учитывается разрядное значение каждой цифры в числах и выполняется индивидуальное умножение.
Позже результаты отдельных умножений складываются, чтобы получить окончательный результат.
Давайте воспользуемся разрядным значением для вычисления 15 × 5. Мы нарисуем диаграмму разрядного значения для выполнения умножения.
\(\Стрелка вправо\)( 5 × 5) + (5 × 10)
= 25 + 50
= 75
Это можно представить в виде столбца: цифра на единицу в первом числе.
(5 × 5) = 25 (Умножьте 5 и 5)
(ii) Цифра, стоящая на месте единиц во втором числе, умножается на цифру на месте десятков в первом числе.
5 × 10 = 50 (Умножьте 5 на 10)
10 × 10
(iii) Затем результаты обоих шагов складываются для получения окончательного результата.
25 + 50 = 75 (Добавить)
Аналогичные шаги будут предприняты для умножения чисел, имеющих цифры в разряде сотен или тысяч.
Использование разрядного числа для умножения на 10, 100 или 1000
Это простое применение умножения с разрядным значением, в котором мы упрощаем умножение, выражая числа, которые нужно умножить, через десятки, сотни или тысячи и позже выполните стандартное умножение.
Рассмотрим следующее умножение:
7 × 10 (здесь 10 можно записать как 1 десяток)
= 7 × 1 десяток
= 7 десятков
= 70
200Рассмотрим другой пример: 09 (здесь 200 можно записать как 2 сотни)
9 × 2 сотни
= 18 сотен
= 1800
Правила умножения на 10, 100 или 1000
при умножении любых ненулевых чисел на 10, 100 или 1000.
- При умножении любого ненулевого числа на 10 просто добавьте ноль в конце этого числа.
Например:
5 × 10 = 50 - При умножении любого ненулевого числа на 100 просто добавьте два нуля в конце этого числа.
 Например:
Например:
5 × 100 = 500 - При умножении любого ненулевого числа числа на 1000, просто добавьте три нуля в конце этого числа.
Например:
2 × 1000 = 2000
Факты об умножении
- Если число умножается на 0, результатом будет 0.
10 × 0 = 0
0 × 0 = 0
112 × 0 = 0
- Если ненулевое число1 , 100 или 1000 соответственно, произведением будет само число с 1, 2 или 3 нулями соответственно на конце.
- При умножении умножаемое число называется множимым, а число, на которое оно умножается, называется множителем.
Результат умножения называется произведением.
10 × 7 = 70
10 → Множимое
7 → Множитель
70 → Произведение
- Если число умножается на 1, произведением будет само число.
Решенные примеры
Пример 1:
Найдите произведение для каждого из следующих умножений.
(i) 7 × 3 ________
(ii) 7 × 30 _________
(iii) 7 × 300 _________
(iv) 7 × 3000 __________
Решение:
(i) 7 × 3 = 21
(II) 7 × 3 TENS
=. 21 TENS
= 210
(III) 7 × 3 Сотни
= 21 Сотни
= 2100
(IV) 7 × 3 тысячи
= 21 тысячи
= 21000999
= 21 тысячи
= 21000999
= 21 тысячи
= 21000999
= 21 тысячи
= 21000
9= 21 тысячи
= 21000
9= 21 тысячи
= 2100099
9000 21. Пример 2:Найдите недостающий множитель.
(i) ______ × 100 = 600
(ii) 5 × ______ = 50
(iii) 9 × 20 = ______
Решение:
(i) Мы знаем, что
(
(i) Множимое) × (Множитель) = Произведение
Поскольку множимое умножается на 100, получается произведение 600, это означает, что множимое равно 6.
(ii) Мы знаем, что ) = Продукт
5 × _____= 50
Используя правило умножения числа на 10, мы видим, что множитель равен 10.
(iii) 9 × 20
= 180
Пример 3:
У продавца есть две разновидности блестящих ручек. 10 упаковок одного сорта по 5 ручек в каждой и 20 упаковок второго сорта по 7 ручек в каждой. Итак, сколько всего блестящих ручек у продавца?
Решение:
Первый сорт → 10 × 5 = 50 (умножение)
Второе сорт → 20 × 7 = 140 (умноженная)
50 + 140
= 190 [Добавить]
. Всего у лавочника 190 блестящих ручек.
Пример 4:
У Лиама есть 2 коробки по 20 карамельных конфет в каждой. У него также есть 5 коробок по 30 шоколадных конфет в каждой.
Сколько всего конфет у Лиама?
Решение:
У Лиама есть 2 коробки по 20 карамельных конфет в каждой.
Общее количество карамельных конфет,
= 2 × 20
= 40 [Умножить]
Всего у Лиама 40 карамельных конфет.
У Лиама также есть 5 коробок по 30 кофейных конфет в каждой.
Общее количество шоколадных конфет,
= 5 × 30
= 150 [Умножить]
Всего у него 150 шоколадных конфет.
Итак, общее количество конфет у Лиама
= 40 + 150
= 190 [Добавить]
Следовательно, всего у Лиама 190 конфет.
Часто задаваемые вопросы
Какое свойство можно использовать для определения произведения числа на 0?
Согласно нулевому свойству умножения, если число умножить на ноль, произведение будет 0,
Что означает разрядное значение цифры в числе?
В математике каждая цифра в числе имеет определенное разрядное значение. Его можно определить как значение цифры в числе на основе ее позиции в числе.
 д.
д.
 Сколько привезли зеленых игуан? (7)
Сколько привезли зеленых игуан? (7)


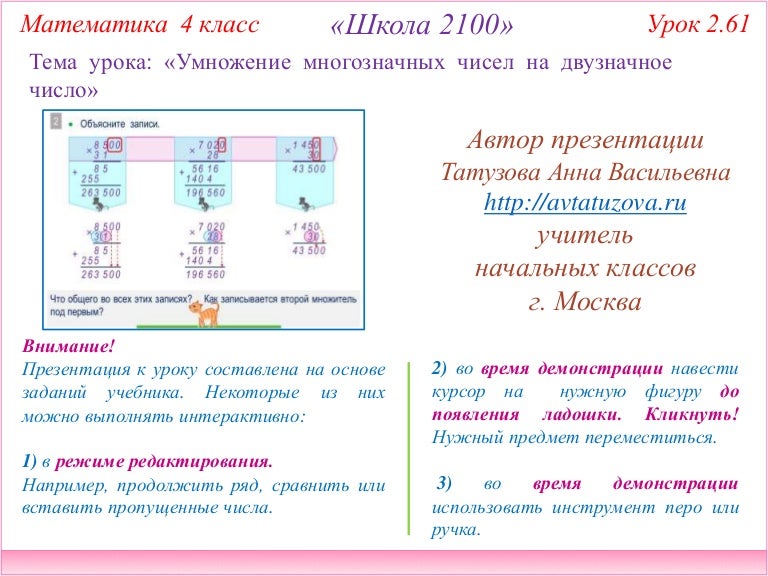 · 5 = 25 сот. = 2500
· 5 = 25 сот. = 2500 Только в конце решения сносим столько нулей, сколько их в множителе.
Только в конце решения сносим столько нулей, сколько их в множителе.

 ( с.79 №50 – 1 строчка 1,2,3 столбик)
( с.79 №50 – 1 строчка 1,2,3 столбик)
 )
)
 )
)


 И тогда, у вас будут высокие результаты. И подводя итог, я хочу сказать спасибо всем за хорошую плодотворную работу на уроке, за поддержку одноклассников и взаимопонимание на всем уроке.
И тогда, у вас будут высокие результаты. И подводя итог, я хочу сказать спасибо всем за хорошую плодотворную работу на уроке, за поддержку одноклассников и взаимопонимание на всем уроке.

 Организационно-мотивационный
Организационно-мотивационный
 Определение темы. Постановка целей и задач урока
Определение темы. Постановка целей и задач урока
 ∙(9 ∙ 10)=540 сот.=54 000
∙(9 ∙ 10)=540 сот.=54 000