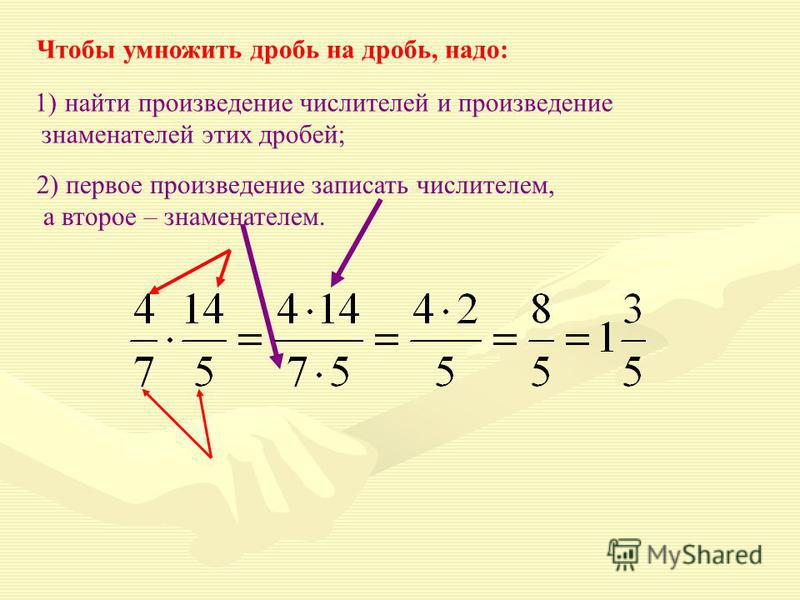
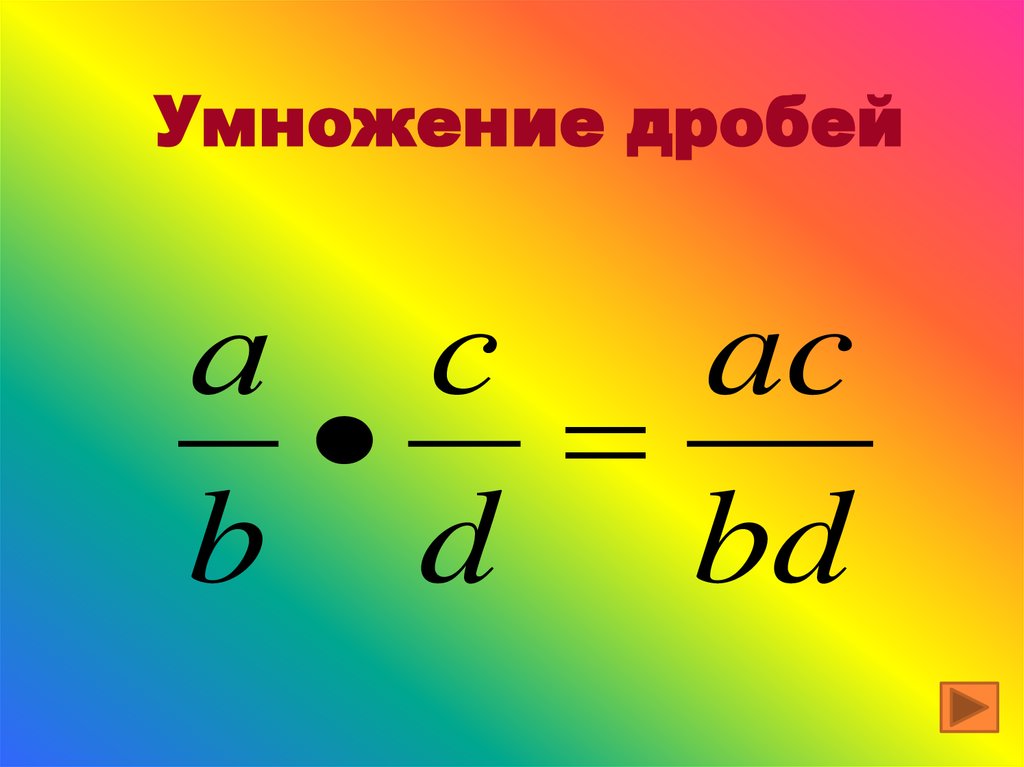Умножение дробей
Зачем уметь работать с дробями?
Дроби используются в различных областях жизни, в том числе:
- Математика: вычисление дробных величин, операции с дробями и т.д.
- Кулинария: расчет ингредиентов для приготовления блюд.
- Финансы: вычисление процентов, деление денежных сумм на части и т.д.
- Строительство: расчет объема материалов и работ.
- Производственные процессы: расчет долей ресурсов и материалов.
- Образование: вычисление средних оценок, расчет долей в статистике.
- Медицина: расчет доз лекарств и необходимого количества компонентов.
- Геодезия: расчет длины линий и площади.
- Дизайн: расчет пропорций и размеров.
- Технологии: расчет долей энергии, памяти, дискового пространства и т.

И это далеко не полный список – дроби можно встретить и во многих других сферах. И в каждой из этих областей дроби используются для точного вычисления величин и удобного представления частей целого.
Кроме того, решение математических задач – прекрасный инструмент для тренировки математических навыков и отличная гимнастика для мозга. Вот лишь несколько причин, почему полезно время от времени умножать дроби и решать другие примеры:
- Это развивает логику: математические задачи требуют применения логических умений, учат связывать факты и делать выводы.
- Это улучшает память: математика требует запоминать формулы и методы решения задач, что способствует улучшению памяти.
- Это способствует креативному мышлению: некоторые математические задачи требуют применения нестандартных подходов и инициативности.
- Это улучшает мышление: математическая активность тренирует мозг на устойчивость к сложным концептам и улучшает способность к анализу и синтезу.

В целом, решение математических задач может улучшать ментальные способности и способствовать развитию мозга. Поэтому знать, как умножать дроби, и уметь это делать полезно любому человеку, а школьникам, студентам и специалистам, чья деятельность связана с математикой, особенно.
Что такое дроби и какие бывают дроби?
Дробью называют число, состоящее из одной или более равных частей единицы. Если говорить проще, то дробь обозначает часть чего-либо. К примеру, может быть один пирог, а может быть одна часть и еще несколько, например, один целый пирог и три кусочка.
Существуют дроби обыкновенные и десятичные:
Обыкновенные дроби – это дроби, состоящие из числителя, расположенного верху (делимое), и знаменателя, расположенного внизу (делитель).
Они могут быть разделены либо горизонтальной, либо косой чертой, обозначающей деление. Знаменателем отражается то, на сколько частей можно разделить целое, а числитель показывает, сколько частей имеется. Например: 1/2, 3/4, 7/10. Также следует знать, что обыкновенные дроби могут быть правильными и неправильными. В правильных дробях знаменатель больше числителя (6/8, 9/15), а в неправильных дробях легко выделить целую часть и дробную (14/5, 32/7). Число, которое получается, принято называть смешанной дробью.
Например: 1/2, 3/4, 7/10. Также следует знать, что обыкновенные дроби могут быть правильными и неправильными. В правильных дробях знаменатель больше числителя (6/8, 9/15), а в неправильных дробях легко выделить целую часть и дробную (14/5, 32/7). Число, которое получается, принято называть смешанной дробью.
Десятичные дроби – это дроби, в знаменателе которых расположена степень числа «10». Записываются такие дроби несколько иначе – через запятую, и имеют вид 0,7 или 0, 63 и т.п.
А еще советуем запомнить, что есть дроби:
- Числовые, т.е. состоящие из чисел. Например: 6/8, 0,3 и т.п.
- Алгебраические, т.е. состоящие из переменных. Например: (a + b)(a – b). Причем здесь значение дроби будет зависеть от значений переменных.
С этими дробями и приходится работать в школе или вузе, а некоторым еще и по роду деятельности.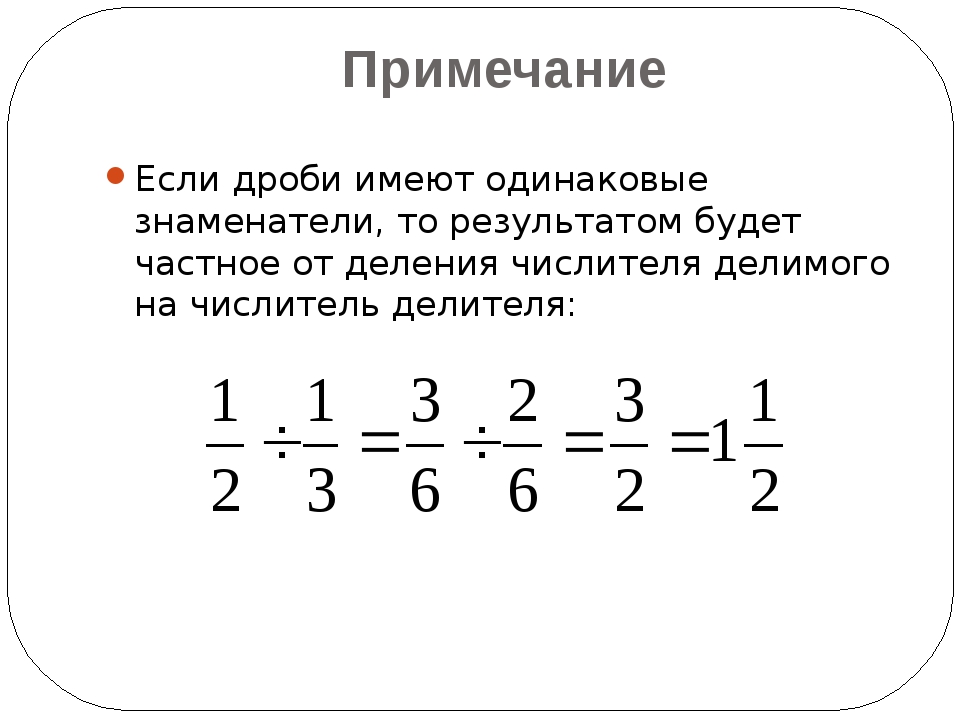 Кстати, стоит заметить, что некоторые люди, как мы и сказали, производят математические операции с дробями ради развлечения, для тренировки своих математических способностей и/или поддержания в тонусе мозга.
Кстати, стоит заметить, что некоторые люди, как мы и сказали, производят математические операции с дробями ради развлечения, для тренировки своих математических способностей и/или поддержания в тонусе мозга.
Основные правила дробей
Прежде чем осваивать методы умножения дробей, необходимо усвоить несколько правил, которые могут пригодиться в самых разных ситуациях и заметно облегчить процесс решения задач. Эти правила таковы:
- Перед сложением или вычитанием дробей необходимо привести их к общему знаменателю.
- Умножение дробей производится путем умножения числителей и знаменателей.
- Деление дробей производится путем перемножения первой дроби на обратную второй дроби.
- После выполнения операций над дробями их можно сократить, деля числитель и знаменатель на их наибольший общий делитель (НОД). НОД нескольких чисел – это наибольшее натуральное число, на которое эти числа делятся без остатка.

В дополнение к этому:
- Если делитель дроби равен нулю, у дроби не будет значения.
- Дробь всегда будет равна нулю, если ее числитель равен нулю, а знаменатель не равен.
- Две дроби a/bи c/dбудут равными, если ad = bc.
- При умножении или делении числителя и знаменателя на одно и то же натуральное число значение дроби останется прежним.
Это основные правила работы с дробями, которые следует знать и применять при решении математических задач с использованием дробей.
Как умножать дроби?
Здесь необходимо разобрать три основных случая: когда требуется умножить дробь на дробь, когда требуется перемножить смешанные дроби и когда требуется умножить дробь на натуральное число.
Умножение дроби на дробь
Умножить дробь на дробь очень просто. Для этого нужно числитель одной дроби умножить на числитель другой, и точно так же поступить со знаменателями. В процессе также стоит подумать, можно ли дробь сократить.
В процессе также стоит подумать, можно ли дробь сократить.
Пример:
Говоря проще, числитель будет равен произведению числителей обеих дробей, а знаменатель будет равен произведению знаменателей
Это правило применимо ко всем дробям как с одинаковыми, так и с разными знаменателями. Когда дробь большая (к примеру, 26/37), можно попробовать сократить ее сразу, чтобы производить вычисления было проще.
В случае, когда в примере есть смешанное число, сначала нужно преобразовать его в неправильную дробь, а затем умножить предлагаемым способом, а итоговый результат вновь преобразовать в смешанное число.
Умножение десятичных дробей
Чтобы умножить десятичные дроби, нужно следовать алгоритму:
- Записать дроби столбиком и умножить, как на натуральные числа (запятые пока в расчет не берем).
- Посмотреть, сколько знаков после запятой имелось в дробях, и сложить их количество.

- Справа налево отсчитать после умножения столько цифр, сколько знаков после запятой получилось на предыдущем этапе.
- Поставить запятую перед нужным количеством цифр.
Пример:
При умножении на 0,1, на 0,01, на 0, 001 и т.п. нужно переставить запятую влево на количество знаков, имеющееся после запятой в множителе. Например: 0,15 х 0,1 = 0,015 или 0,3 х 0,001 = 0,0003.
Умножение дробей на натуральные числа
При умножении дробей на натуральные числа мы снова можем столкнуться с умножением как обычных, так и десятичных дробей.
Умножение на натуральные числа обыкновенных дробей
При умножении обыкновенной дроби на натуральное число необходимо умножить лишь числитель, а знаменатель не менять. Если в результате получается неправильная дробь, нужно выделить из нее целую часть, чтобы прийти к смешанному числу.
Пример:
При умножении смешанного числа достаточно перевести его в неправильную дробь, а далее умножить по такой же схеме:
Но есть и еще один вариант. Вы можете разделить знаменатель на имеющееся натуральное число, оставив числитель без изменений. Такой способ лучше всего использовать при делении знаменателя на натуральное число без остатка.
Вы можете разделить знаменатель на имеющееся натуральное число, оставив числитель без изменений. Такой способ лучше всего использовать при делении знаменателя на натуральное число без остатка.
Пример:
Можете попробовать решить парочку примеров двумя разными способами, и вы увидите, что ответ останется неизменным.
Умножение на натуральные числа десятичных дробей
При умножении десятичной дроби на натуральное число можно применить тот же способ, что и для умножения дроби на дробь. Сначала умножьте числа столбиком, а затем отсчитайте количество цифр, имеющееся после запятой в десятичной дроби. В этом месте должна стоять запятая.
Пример:
Когда требуется умножить десятичную дробь на 10, на 100, на 1000 и т.п., нужно просто переместить запятую вправо на количество знаков равное количеству нулей после единицы. К примеру: 0,025 х 10 = 0,25 или 0,025 х 100 = 2,5.
Как вы заметили, умножать дроби очень просто, несмотря на то что изначально примеры с дробями могут пугать и вводить в ступор. Немного попрактиковавшись, вы научитесь решать массу математических задач и выполнять вычисления, требующие дробных ответов, в различных областях, таких как финансы, наука, инженерия и, конечно же, математика.
Вопросы и ответы
А ещё предлагаем обратить внимание на ответы на некоторые часто задаваемые вопросы по умножению дробей.
Какие дроби называются правильными?
Правильными дробями называются дроби, у которых числитель меньше знаменателя.
Какие дроби называются неправильными?
Неправильными дробями называются дроби, у которых числитель больше или равен знаменателю.
Что обозначает числитель?
org/Answer»>Числителем называется число, которое обозначает часть, которую вы хотите выделить из общего числа в дроби.Что обозначает знаменатель?
Знаменателем называется число в дроби, которое обозначает, на сколько частей разделено общее число. Знаменатель дроби делится на числитель для получения дробного числа.
Какие дроби называются многоэтажными?
Составная (или многоэтажная) дробь – это дробь, где в числителе или знаменателе, или в обоих элементах содержится одна или несколько дробей. Упрощение составной дроби может быть легким или сложным в зависимости от количества дробей в числителе и знаменателе, а также от наличия в них переменных и их типов.
Как умножить обыкновенную дробь: на число, другую дробь
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel. ru Математика Алгебра Умножение обыкновенных дробей
ru Математика Алгебра Умножение обыкновенных дробей
В данной публикации мы рассмотрим, каким образом можно обыкновенную (простую) дробь умножить на число или другую дробь, и как найти произведение смешанных дробей. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Умножение дроби
- На число
- На другую дробь
- Произведение смешанных дробей
- Примеры задач
Умножение дроби
На число
Умножение обыкновенной дроби на число n равно сумме, слагаемыми которой является данная дробь n-ое количество раз.
Другими словами, числитель дроби умножается на данное число n, а знаменатель остается тем же.
Примечание: дробь, полученную в результате умножения, следует проверить на предмет того, можно ли ее сократить.
На другую дробь
В результате умножения одной дроби на другую получается новая дробь, числитель которой равняется произведению числителей исходных дробей, а знаменатель – произведению знаменателей.
a/b
⋅
c/d
=
a⋅b/c⋅d
Произведение смешанных дробей
Чтобы умножить смешанные дроби, необходимо их сперва представить в виде неправильных дробей, и только после этого выполнить умножение.
X
a/b
⋅ Y
c/d
=
X ⋅ b + a/b
⋅
Y ⋅ d + c/d
Примеры задач
Задание 1
Умножьте дробь
3/15
на число 5.
Решение
3/15
⋅ 5 =
3⋅5/15
=
15/15
=1
Задание 2
Найдите произведение дробей
9/17
и
4/7
.
Решение
9/17
⋅
4/7
=
9⋅4/17⋅7
=
36/119
Задание 3
Найдите произведение дробей 3
3/8
и 7
1/9
.
Решение
Т.к. мы имеем дело со смешанными дробями, сперва представим их в виде неправильных, затем выполним умножение.
3
3/8
⋅ 7
1/9
=
3⋅8+3/8
⋅
7⋅9+1/9
=
27/8
⋅
64/9
=
27⋅64/8⋅9
=
1728/72
=24
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Умножение дробей с помощью стержней Кюизенера
Умножение — операция, значение которой многие учащиеся не понимают. Когда он сочетается с дробными значениями, проблема понимания операции умножения с дробными значениями требует серьезного изучения с множеством различных возможностей. Использование стержней Кюизенера может быть одним из них. Они могут обеспечить конкретные пропорциональные представления для числовых значений и операций. В этой статье рассматривается умножение с дробными значениями.
Когда он сочетается с дробными значениями, проблема понимания операции умножения с дробными значениями требует серьезного изучения с множеством различных возможностей. Использование стержней Кюизенера может быть одним из них. Они могут обеспечить конкретные пропорциональные представления для числовых значений и операций. В этой статье рассматривается умножение с дробными значениями.
Обзор
- Знакомство с Жезлами
- Представление дробей с помощью стержней Кюизенера
- Дробные представления
- Введение в умножение дробей
- Дробные числа меньше, чем одно целое число
- Дробные числа, умноженные на дробные числа
- Смешанный раз смешанный
Знакомство со стержнями Кюизенера
Всего стержней десять, и их длина варьируется от 1 до 10 см.
Каждая длина определяется уникальным цветом:
Белый, красный, светло-зеленый, пурпурный, желтый, темно-зеленый, черный, коричневый, синий и оранжевый
Заглавные буквы используются для обозначения различных стержней. Обратите внимание, что шаблон использует начальную букву до тех пор, пока не появятся три буквы «В», поэтому используются конечные буквы, а затем возвращаются к начальной букве для оранжевого цвета.
Обратите внимание, что шаблон использует начальную букву до тех пор, пока не появятся три буквы «В», поэтому используются конечные буквы, а затем возвращаются к начальной букве для оранжевого цвета.
Представление дробей с помощью стержней Кюизенера
Для представления дробей или операций с дробями с помощью стержней Кюизенера необходимо выбрать стержень или комбинацию стержней для одного целого или единичного значения.
Ниже приведены некоторые из бесконечных возможностей, которые можно использовать целиком или по отдельности.
Задания, в которых используются конкретные модели, позволяют учащимся научиться создавать мысленные представления на основе визуальных аспектов конкретных моделей. Эти мысленные представления необходимы для понимания дробей и их операций.
Некоторые примеры дробных представлений
Пример с более короткими обозначениями.
Как бы вы завершили эти пять?
Ответы :
- W = 1/2
- Г = 1/3
- Р = 2
- R = 2/3 и D = 2
Образцы больше единицы
Когда учащиеся освоят дроби меньше единицы, им следует давать задачи с целыми числами и дробями больше единицы, смешанными числами.
Как бы вы их завершили?
Ответы :
- 2
- 3
- 4 1/2
Введение в умножение дробей
Умножение дробей можно разделить на четыре группы. Давайте кратко рассмотрим каждый тип, чтобы увидеть отношения между факторами и продуктами.
Позже мы рассмотрим каждый тип более подробно и некоторые учебные аспекты.
Первое: умножение дроби на дробь .
Когда дробь, меньшая единицы, умножается на другую дробь, меньшую единицы, результатом является произведение, меньшее любого из множителей.
Например , представьте себе такую задачу:
У человека есть половинка шоколадного батончика и он делится ею с другом. Сколько получает каждый человек?
1/2 1/2 батончика = 1/4 батончика.
Три способа установки со стержнями Кюизенера:
При умножении целых чисел произведение всегда больше любого из множителей.
Произведение меньше любого множителя. Это может быть проблемой для студентов, которые считают, что произведение умножения всегда больше, чем множители.
Это может быть проблемой для студентов, которые считают, что произведение умножения всегда больше, чем множители.
Второй тип: умножение целого числа на дробь
Второй тип — целое число, умноженное на дробь.
Например, после того, как дети закончили есть пиццу, осталось только три коробки с пиццей, и в каждой было около 1/4 пиццы. Сколько пиццы осталось?
3 коробки х 1/4 пиццы = 3/4 пиццы фракция. Стоимость этого продукта находится между двумя факторами, если только один из факторов не равен единице; тогда он равен другому множителю. Задачи этого типа по-прежнему не соответствуют ложному предположению, что умножение производит больше произведений, чем множители.
Мама говорит, что я могу посмотреть половину фильма, потом заняться домашними делами, а когда работа будет сделана, я смогу посмотреть остальное. Фильм идет два с половиной часа. Когда я должен заняться домашними делами, если я начну смотреть фильм сейчас?
1/2 от 2 1/2 часов = 1 1/4 часа
Четвертый: умножение смешанного числа на смешанное число
чем любой фактор. Например,
Например,
Хуан берет напрокат два фильма по два с половиной часа каждый. Он посмотрел полтора, прежде чем уйти на тренировку. Сколько часов фильмов он отсмотрел (просмотрел)?
1 1/2 от 2 1/2 =
Краткое изложение четырех способов умножения дробей
Четыре сравнения, рассмотренные выше:
- Дробь, умноженная на дробь: 1/2 * 1/2,
- Целое число, умноженное на дробь: 2 * 1/2 или дробь, умноженная на целое число 1/2 * 2,
- Дробь, умноженная на дробь: 1/2 * 1 1/2 или смешанное число, умноженное на дробь: 1 1/2 * 1/2, и
- Смешанное число, умноженное на смешанное число 1 1/2 * 1 1/2.
Частично они выводятся из физического вида цифр для каждого фактора.
Однако существует также связь между значениями продукта и факторами. Продукты не только наименьшие, когда факторы наименьшие, но и величины этих продуктов меньше, чем сами факторы. Это интересно и полезно знать.
Например:
Коэффициенты меньше единицы:
- 1/2 от 1/2 = 1/4
- 1/2 * 2/3 = 1/3
- 1/2 х 1/5 = 1/10
- 1/2 * 1/4 = 1/8
Один множитель меньше единицы, а другой больше единицы:
- 1/2 от 2 = 1
- 1 /2 х 3 = 1 1/2
- 1/2 * 1 1/2 = 3/4
Оба множителя больше единицы:
- 1 1/2 * 1 1/2 = 2 1/4
- 1 1/2 x 2 1/2 = 3 3/4
- 1 1/2 от 2 = 3
Один фактор равен одному:
- 1/2 от 1 = 1/2
- 1 * 2 1/2 = 2 1/2
- 2 1/4 х 1 = 2 1/4
Учебные рекомендации
При обучении умножению дробей большинство преподавателей начинают с умножения дробей меньше единицы и целых чисел. Обычно находят дробные части целых чисел, которые приводят к хорошим продуктам (1/2 x 4 = 2, хорошо, 1/2 от 5 не очень).
Обычно находят дробные части целых чисел, которые приводят к хорошим продуктам (1/2 x 4 = 2, хорошо, 1/2 от 5 не очень).
Затем перейдите к целым числам, умноженным на дроби: 4 * 1/2 = 2.
Затем обе дроби меньше одной 1/2 от 1/2 = 1/4. Как только учащиеся узнают, как решать такие типы задач, слишком многие учителя считают, что учащиеся могут обобщить процедуру, которая работает для умножения дробей всех типов. Эта практика, отсутствие понимания умножения дробей оставляет большинство людей в неведении о понимании умножения дробных чисел и различных отношениях факторов и продуктов.
Палочки Кюизенера помогают учащимся создавать и обобщать мысленные представления, расширяя их понимание дробей до операции умножения на дроби и возникающих взаимосвязей.
Постановка и решение задач на дробные числа, меньшие одного умножения на целые числа
Начнем с 1/3 от 3.
Первое, что нужно сделать, это решить, что использовать для представления единицы. Если белый выбран как один, то светло-зеленый будет иметь значение три, потому что три белых составляют светло-зеленый, следовательно, одна треть светло-зеленого стержня может быть представлена белым, а мы уже знаем, что белый — это один, поэтому 1 /3 из 3 = 1,
Если белый выбран как один, то светло-зеленый будет иметь значение три, потому что три белых составляют светло-зеленый, следовательно, одна треть светло-зеленого стержня может быть представлена белым, а мы уже знаем, что белый — это один, поэтому 1 /3 из 3 = 1,
Давайте посмотрим на другое произведение, которое больше единицы, 1/3 от 6 = 2.
Опять же, первое, что нужно сделать, это решить, что использовать для представления одного. Если мы выберем белый как один, то светло-зеленый будет иметь значение шесть. Три красных составляют зеленый, поэтому одна треть светло-зеленого — это красный, поскольку белый — это один, тогда красных будет два.
Давайте попробуем решить задачу с продуктом меньше единицы, 1/3 от 1.
У Чи есть упаковка мясного фарша весом один фунт, и она хочет приготовить три гамбургера.
Если белый представляет один, это означает, что у нас не будет стержней меньше белого цвета, которые можно было бы использовать для представления трех гамбургеров. Чтобы решить эту проблему, выберите стержень большего размера, чтобы использовать его для упаковки мяса весом в один фунт, чтобы были стержни меньшего размера для представления гамбургеров.
Чтобы решить эту проблему, выберите стержень большего размера, чтобы использовать его для упаковки мяса весом в один фунт, чтобы были стержни меньшего размера для представления гамбургеров.
Учащиеся, которые раньше использовали стержни, узнают, что если они считают светло-зеленый = 1, то белый цвет можно использовать для представления гамбургеров, потому что 3 белых стержня = 1 зеленому стержню. Следовательно, светло-зеленый в этом представлении равен единице, а белый меньше единицы, или 1/3.
Учащимся необходимо несколько раз попрактиковаться в задачах на умножение дробных значений меньше единицы и целых чисел с помощью стержней, а также с другими манипуляциями и представлениями.
Самая большая трудность для учащихся – умение связать дробные числа.
значения и целые значения на один и тот же стержень и плавно переходя от задачи к задаче. это развитие
веха, которую учащиеся изо всех сил пытаются получить для понимания дробей,
разрядное значение, кратные числа и другие математические понятия.
Постановка и решение задач на целые числа, умноженные на дробные числа меньше единицы
Предыдущие примеры включали дробную часть, умноженную на целое число меньше одного раза со значением единицы и больше: 1/3 X 3 = 1, 1/3 X 6 = 2 и 1/3 X 1 = 1/3
Однако примеры целых чисел, умноженных на дробные числа меньше единицы: 3 X 1/3 = 1, 6 X 1/3 = 2 и 1 X 1 /3 = 1/3 не были включены.
В то время как учащиеся, которые понимают свойства умножения, могут использовать свойство перестановочности и рационализировать три раза, когда одна треть равна одной трети от трех (3 * 1/3 = 1/3 * 3) и аналогично для других. Есть разница в том, как эти проблемы возникают в мире и представляются.
Способность понимать, представлять и решать задачи с дробными значениями и операцией умножения требует большего, чем знание 3 * 1/3 = 1/3 * 3 по свойству коммутативности.
Итак, давайте рассмотрим пример с целым числом и дробью со значением меньше единицы.
У Кейт три видео. Каждая длится треть часа (20 минут). Если она будет смотреть их всех подряд, сколько это займет времени?
Каждая длится треть часа (20 минут). Если она будет смотреть их всех подряд, сколько это займет времени?
Для этой задачи треть часа нужно представить три раза. Если светло-зеленый представляет один час, то белый может представлять одну треть часа.
Для решения задачи требуется три белых, по одному на каждое третьечасовое видео. Три трети часа или 1 час.
Больше дробных чисел меньше, чем одно целое число
Вы можете подумать, что примеры были подогнаны под размеры стержней, и задаетесь вопросом, что происходит, когда подгонка не так хороша.
Давайте посмотрим, как настроить такую задачу, как одна треть из пяти.
- Что составляет треть пяти пальцев? (брутто?)
- Если у меня есть пять мешков с почвой, и я хочу положить по одной трети в каждый из трех горшков, сколько мешков пойдет в каждый?
Поскольку светло-зеленый — это первая известная нам удочка, которая может быть сопоставлена с тремя другими удочками (тремя белыми), мы можем использовать ее как одну. Если представить светло-зеленый цвет как один, то пять светло-зеленых палочек представляют пять. Пять светло-зеленых палочек или сочетание оранжевого и желтого также представляют собой пять светло-зеленых. В любом случае желтый стержень будет на 1/3 из пяти светло-зеленым или комбинацией оранжевого и желтого.
Если представить светло-зеленый цвет как один, то пять светло-зеленых палочек представляют пять. Пять светло-зеленых палочек или сочетание оранжевого и желтого также представляют собой пять светло-зеленых. В любом случае желтый стержень будет на 1/3 из пяти светло-зеленым или комбинацией оранжевого и желтого.
Еще …
Вы, наверное, заметили, что все примеры имеют только одну дробную часть или числитель один. Также возможно представлять дробные числа меньше единицы, с несколькими дробными частями (числитель больше единицы), умноженными на целое число.
Пример 1
У Майка было десять десятицентовиков, и он отдал три пятых Хозе. Сколько получил Хоза?
Три пятых десяти. Нужно представлять группу из десяти десятицентовиков. Если белый представляет собой одну центовую монету, то оранжевый представляет десять. Одна пятая — это красный цвет, поэтому три пятых — это три красных, один красный равен двум десятицентовым монетам, а три — шести десятицентовым монетам.
Пример 2
Группа из одиннадцати детей шла в кино, когда один из них заметил, что потерял деньги, чтобы попасть на представление. Остальные десять решили, что если каждый даст три пятых доллара этому одиннадцатому человеку, этого будет достаточно для того, чтобы купить билет в кино. Сколько дали этому человеку? (10 х 3/5).
Давайте попробуем два способа: 3/5 х 10 и 10 х 3/5:
Если мы позволим белым представлять один доллар, то оранжевый будет десять долларов. Одна пятая часть оранжевого — красный, поэтому три пятых — это три красных. Стоимость в долларах была установлена как белая, равная одному доллару. Следовательно, оранжевый цвет равен десяти долларам, красный — двум долларам, а три красных — шести долларам.
Второй способ представления этого числа состоит в том, чтобы изобразить три пятых доллара светло-зеленым цветом, взять десять из них и найти значение для всех десяти.
Пример 3
Папа всегда пытается заставить людей думать, поэтому он говорит такие вещи, как на столе три пакета, вам нужно взять две трети из них (2/3 X 3). Сколько мне нужно было взять?
Сколько мне нужно было взять?
Давайте попробуем это же двумя способами: 2/3 X 3 и 3 X 2/3:
Первые две трети из трех:
Второй три раза по две трети или три группы по две трети:
Для 3 x 2/3.
Зеленый был выбран для обозначения одного из них.
Если зеленый = 1, то красный = 2/3
Следовательно, три красных стержня представляют собой три группы по две трети.
Резюме
Учащимся труднее работать с дробными частями больше единицы/части (1/2, 1/3, 1/4, 1/5…). Им требуется время, чтобы обобщить свое понимание от одной трети до двух третей и других кратных дробных частей для других дробей.
Учащимся нужно дать время, чтобы соединить свое прежнее понимание сложения и умножения целых и дробных чисел. Когда они это сделают, они поймут, что две трети можно представить себе как две трети, умноженные на одну треть, или одну треть, добавленную дважды.
Чтобы получить представление о дробных значениях, когда множитель имеет числитель больше единицы, мы должны знать, что он кратен единице дробной части. Например, три пятых кратны одной пятой. Следовательно, три пятых имеют множители 3 и 1/5.
Например, три пятых кратны одной пятой. Следовательно, три пятых имеют множители 3 и 1/5.
Предыдущий опыт работы с множителями, пропуском счета, умножением в виде строк и столбцов, площадью, прямоугольниками, квадратами и повторным сложением необходим для понимания дробей и умножения.
Дробные числа меньше единицы, умноженные на дробное число меньше единицы
Правильная дробь умножается на правильную дробь, но я не люблю называть дроби правильными и неправильными. Это дроби, и иногда одна полезнее другой, но эта полезность может определяться только использованием, а не формой, в которой находится число.
Вы наверняка поняли, что знание того, что представлять как единицу, является ключом к получению точного решения. Любая реальная или мировая проблема требует, чтобы для каждой проблемы было выбрано единичное значение, представляющее значение единицы. Это действительно помогает отметить это как часть представления, чтобы все знали присвоенные значения.
Давайте посмотрим несколько примеров того, как дробные числа меньше единицы умножаются на дробное число меньше единицы.
Пример 1:
Папа, брат и я косили соседский двор. Мы с братом скосили половину переднего двора, что, по словам отца, составляло две пятых всего двора. Какую часть всего двора я косил? 1/2 фасада, что составляет 2/5 всего двора.
Сначала решите, что использовать как единицу, чтобы можно было представить две пятых.
Затем спросите, что такое половина двух пятых, и изобразите ее.
Затем определите значение Белого, если Желтый — единица. Учащимся, возможно, потребуется напомнить, чтобы они спросили, какую часть целого (одного стержня или единицы) представляет верхний стержень. В этом случае белый — это и 1/2 от 2/5, и 1/5 от желтого или один. Это проблема многих маленьких детей. Объекты, имеющие одинаковые одновременные значения.
Вам может быть интересно, как учащиеся выбирают удочку для единицы (одной). Для задачи, которую мы только что решили, мы знали, что хотим сделать две пятых, поэтому имеет смысл выбрать стержень, который можно использовать для представления пятых. Есть только два стержня, из которых можно выбрать: Желтый и Оранжевый. Если вы раньше не использовали удилища Кюизенера, вам придется подумать об этом. Те, кто испытал их в течение нескольких часов, думая о том, какие стержни можно использовать для создания поездов, чтобы соответствовать другим стержням, будут знать, какие цветные стержни можно использовать, чтобы равномерно соответствовать другим. Может быть даже полезно предложить учащимся составить список или таблицу этих отношений.
Есть только два стержня, из которых можно выбрать: Желтый и Оранжевый. Если вы раньше не использовали удилища Кюизенера, вам придется подумать об этом. Те, кто испытал их в течение нескольких часов, думая о том, какие стержни можно использовать для создания поездов, чтобы соответствовать другим стержням, будут знать, какие цветные стержни можно использовать, чтобы равномерно соответствовать другим. Может быть даже полезно предложить учащимся составить список или таблицу этих отношений.
Итак, для этой задачи мы использовали желтый цвет, но давайте посмотрим, как он был бы представлен, если бы он был оранжевым.
Во-первых, мы решили использовать Оранжевый как единицу, чтобы две пятых были представлены красным.
Затем спросите, что такое половина двух пятых, и изобразите ее красным цветом.
Затем определите значение 1/2 от 2/5. Так как Оранжевый — один, то Красный — 1/5 его. Опять же, многим учащимся нужно будет напомнить, чтобы они спросили, какая часть
целого (одного стержня или единицы) представляет верхний стержень.
При выборе чего-либо для представления единицы или единицы, думать о том, какие стержни соответствуют другим стержням, не работает, тогда это простое правило всегда будет работать:
Сначала попробуйте использовать знаменатель второго множителя. Если это не сработает, умножьте знаменатели и определите, какой стержень или комбинация стержней потребуется, чтобы получить длину (см) такого количества белых.
Например, если проблема была 2/3 X 4/5. Желтый был бы первым выбором, но 2/3 желтого цвета не могут быть представлены целыми стержнями. Таким образом, 3 * 5 = 15, и вместо одного можно использовать три желтых или оранжевый и желтый. Две трети могут быть представлены двумя желтыми).
Не говорите об этом ученикам. Скажите им, чтобы они подумали о размере частей, которые они хотят использовать. Если не поможет, то подскажите что поможет. Поиск единичного стержня может быть интересным и сложным, но если учащимся предложить умножать знаменатели, некоторые будут продолжать делать это, даже когда это нежелательно. Например, 1/5 х 5/9. Если знаменатели перемножить (45), то четыре оранжевых стержня и один желтый стержень будут представлять один. Эта комбинация будет работать, но использование blueE обеспечивает лучшее представление, чтобы облегчить концептуальное понимание, что облегчит решение задач учащимися и беглость математики. Изучение правил без концептуализации — это процедурное знание без знания того, когда и как его использовать.
Например, 1/5 х 5/9. Если знаменатели перемножить (45), то четыре оранжевых стержня и один желтый стержень будут представлять один. Эта комбинация будет работать, но использование blueE обеспечивает лучшее представление, чтобы облегчить концептуальное понимание, что облегчит решение задач учащимися и беглость математики. Изучение правил без концептуализации — это процедурное знание без знания того, когда и как его использовать.
Другой пример
Этот пример представляет собой наиболее сложный тип задачи на правильную дробь, умноженную на другую правильную дробь. Их следует избегать до тех пор, пока ученики не освоят остальные.
Мать дала Мэри пакет конфет и велела разделить его с братом и сестрой. Когда ее брат увидел ее с конфетами, он спросил, можно ли ему немного. Мэри сказала ему, что он может, но она должна разделить его между ними тремя. Итак, она и ее брат разделили его на три равные группы. Ее брат взял свою долю и оставил Мэри с двумя третями в мешке. Когда ее сестра обнаружила конфеты, она подошла к Мэри и попросила свою долю. Мэри снова сказала, что ей сказали разделить его на три части и поделиться. Итак, они разделили его на три равные группы, ее сестра ушла со своей, а Мэри положила две трети в мешок. Сколько конфет из первоначального мешка в итоге досталось Мэри?
Мэри снова сказала, что ей сказали разделить его на три части и поделиться. Итак, они разделили его на три равные группы, ее сестра ушла со своей, а Мэри положила две трети в мешок. Сколько конфет из первоначального мешка в итоге досталось Мэри?
Проблема :
Конфеты, оставшиеся после того, как ее брату и сестре дали долю, составляют 2/3 конфет, оставшихся после того, как она дала долю ее брату и оставила Мэри 2/3 первоначального мешка.
Сначала подумайте, что вы хотите оштрафовать две трети мешка, в котором две трети того, что было в исходном мешке (2/3 мешка из 2/3 мешка).
Затем решите Пусть bluE = один и найдите две трети синего цвета. Два светло-зеленых.
Затем найдите две трети светло-зеленого (2/3 от 2/3).
Это можно представить двумя способами.
- светло-зеленый представляет 2/3 синего, а красный представляет 2/3 двух светло-зеленых, которые считаются одним темно-зеленым
- светло-зеленый представляет 2/3 синего, а белый представляет 2/3 светло-зеленого
Сложность понимания умножения дробей связана с распознаванием частей и целых чисел, а также того, как они соотносятся и изменяются в зависимости от их значений и операции умножения.
Примером такой двойственности значений является ситуация, когда две светло-зеленые палочки используются как две части (2/3), а также вместе как единое целое (2/3), чтобы определить, что составляет две трети.
Чтобы понять эти взаимосвязи, учащимся требуется много времени, чтобы испытать, интерпретировать, построить понимание и связать это понимание. Один из способов выделить время для достаточного опыта состоит в том, чтобы либо отложить обучение умножению дробей процедурно, либо полностью прекратить обучение этому процедурно и позволить ученику изобретать свои собственные алгоритмические процедуры.
Чтобы понять, почему произведения дробей так разнообразны. Использование конкретных представлений помогает учащимся понять, почему, и начинает предлагать различные подходы к размышлению о проблемах.
Смешанная дробь, умноженная на смешанную дробь
Задачи со смешанными дробями, умноженными на смешанную дробь, могут быть решены путем умножения четырех множителей и сложения произведений. Хотя эта идея важна для понимания умножения, она не так очевидна, когда для решения подобных задач используется стандартный алгоритм.
Хотя эта идея важна для понимания умножения, она не так очевидна, когда для решения подобных задач используется стандартный алгоритм.
Давайте посмотрим, как можно объединить предыдущие идеи для умножения смешанных дробей:
Пример 1 1/2 X 2 1/2:
Сначала определите коэффициенты, которые необходимо умножить.
Затем решите, как его изобразить.
После того, как решено, как будет представлена единица, можно решить задачу путем умножения четырех пар чисел: 1 x 2, 1 x 1/2, 1/2 x 2 и 1/2 x 1/. 2. Как показано выше.
Однако, когда человек поймет, как работает умножение дробей, он сможет найти всевозможные короткие пути. Например: в задаче 1 1/2 умножить на 2 1/2 ее можно решить мысленно, подумав:
1 х 2 1/2 = 2 1/2 и 1/2 х 2 1/2 = 1 1/4.
Затем объедините 2 1/2 + 1 1/4, чтобы получить 3 3/4
Другой пример: 12 1/4 X 12 1/4
12 х 12 = 144
12 х 1/4 = 3
1/4 х 12 = 3
1/4 х 1/4 = 1/16
144 + 3 + 3 + 1/16 = 150 1/16
Я считаю, что это проще, чем использование традиционного алгоритма, когда нужно умножить 49 x 49 и разделить этот продукт, 1401, на 16, и, что более важно, это приходит с пониманием.
Учащиеся, имеющие достаточный конкретный опыт, поймут все методы и будут иметь уверенность и способность выбирать стратегию, основанную на точных мысленных образах. Алгоритм не помогает учащимся концептуально понять умножение дробей. Поэтому, хотя это может быть быстрее, нужно понимать, почему пары чисел должны быть умножены и что это означает для каждого типа.
Резюме
Некоторые ученики всегда хотят запомнить правило, потому что они отказались от мысли, что они могут понять математику, или они не видят никаких преимуществ в решении задач, кроме как с помощью правил. Они обнаруживают, что все, что им обычно нужно сделать, это взять правило и использовать его, когда им представляют проблемы, уже поставленные на рабочих листах, но жизнь не представляет проблемы таким образом.
Предлагая задачи в реальных ситуациях и предлагая учащимся понять их мир, большинство учащихся будут тратить время и усилия, чтобы научиться использовать математику, чтобы понимать и объяснять мир.
Представление сложных задач и достаточно тщательно подобранных задач, таких как:
2/3 X 4/4
Учащиеся, использующие правило, в итоге получают больше работы, тогда как те, кто уделяет время изучению задачи, думают
4/ 4 = 1
И переходим к ответу.
Другие проблемы, такие как:
1/2 X 22/36
1/3 X 9 3/8
2/3 X 27
9 1/3 X 9 1/3
Enco призвать студентов к понимать умножение дробей.
Использование жезлов — это только начало.
Заметки доктора Роберта Суитленда
Умножение дробей — Math28
Contenido
Что такое умножение дробей?Умножение дробей — одна из основных операций, позволяющая получить третью дробь, которая будет произведением предыдущих, что известно как «Произведение» или «Результат умножения».
Узнать больше о: » Умножение » →
Символ или знак умножения дробей Умножение дробей представлено символом креста или «х», оно также может быть представлено с помощью средней точки, символ умножения известен как «на».
Узнать больше о: » Операции с дробями » →
Как мы умножаем дроби?
Для получения числового значения в виде дробей существует только одна процедура умножения дробей либо с разными знаменателями, либо с одинаковыми знаменателями.
При умножении дробей числители дробей умножаются, а знаменатели расходятся.
2 / 2
х
1 / 2
=
2 / 4
2/2
1/2
2/4
В следующем примере дроби 1/3 и 2/6 перемножаются, определяются числители обеих дробей, соответствующие 1 и 2, перемножаются и результат помещается в числитель. Теперь определите знаменатели обеих дробей, соответствующие 3 и 6, умножьте и поместите результат в знаменатель.
1 / 3
х
2 / 6
=
1 х 2 / 3 х 6
=
Результат 2/18 можно упростить, потому что и числитель, и знаменатель можно уменьшить вдвое. Таким образом, половина от 2 равна 1, а половина от 18 равна 9.
Таким образом, половина от 2 равна 1, а половина от 18 равна 9.
=
1 / 9
Примечание : Дроби 2/18 и 1/9 эквивалентны, поскольку они представляют одну и ту же сумму.
Пример:
2 / 3
х
4 / 3
=
2 х 4 /
=
8 / 9
5 / 2
х
6 / 2
=
5 х 6 /
=
30 /
5 / 6
х
4 / 3
=
5 х 4 /
=
20 /
8 / 3
х
2 / 4
=
8 х 2 /
=
16 /
Из предыдущих примеров можно упростить 30/4 = 15/2, 20/18 = 10/9 и 16/12 = 4/3.
Упражнение:
А)
5 / 3
х
3 / 3
= ?
Б)
9 / 2
х
5 / 2
= ?
С)
6 / 5
х
4 / 3
= ?
Д)
6 / 8
х
2 / 2
= ?
Умножение трех или более дробей
Процедура похожа на две дроби, умножение выполняется в строке, числитель на числитель и знаменатель на знаменатель.
4 / 2
х
5 / 3
х
3 / 2
=
4 х 5 х 3 / 2 х 3 х 2
=
60 / 12
=
10 /
= 5
Пример:
3 / 2
х
4 / 2
х
8 /
=
3 х 4 х 8 /
=
96 /
3 / 4
х
5 / 4
х
10 /
=
3 х 5 х 10 /
=
150 /
2 / 3
х
4 / 2
х
4 /
=
2 х 4 х 4 /
=
32 /
5 / 4
х
4 / 8
х
3 /
=
5 х 4 х 3 /
=
60 /
Из предыдущих примеров можно упростить 96/8 = 12, 32/36 = 8/9 и 60/64 = 15/18.
Упражнение:
А)
4 / 3
х
7 / 2
х
3 / 2
= ?
Б)
4 / 2
х
5 / 2
х
3 / 4
= ?
С)
3 / 2
х
7 / 2
х
3 / 2
= ?
Д)
6 / 6
х
7 / 6
х
2 / 6
= ?
Умножение смешанных дробей
При умножении смешанных дробей необходимо, чтобы вся часть выражалась в виде дроби, имеющей тот же знаменатель, что и в сопровождающей ее дробной части.