Умножение | Математика

Умножить одно целое число на другое значит повторить одно число столько раз, сколько в другом содержится единиц. Повторить число значит взять его слагаемым несколько раз и определить сумму.

Определение умножения

Умножение целых чисел есть такое действие, в котором нужно взять одно число слагаемым столько раз, сколько в другом содержится единиц, и найти сумму этих слагаемых.

Умножить 7 на 3 значит взять число 7 слагаемым три раза и найти сумму. Искомая сумма есть 21.

Умножение есть сложение равных слагаемых.

Данные в умножении называются множимым и множителем, а искомое — произведением.

В предложенном примере данными будут множимое 7, множитель 3, а искомым произведением 21.

Множимое. Множимое есть то число, которое умножается или повторяется слагаемым. Множимое выражает величину равных слагаемых.

Множитель. Множитель показывает, сколько раз множимое повторяется слагаемым. Множитель показывает число равных слагаемых.

Произведение. Произведение есть число, которое получается от умножения. Оно есть сумма равных слагаемых.

Множимое и множитель вместе называются производителями.

При умножении целых чисел одно число увеличивается во столько раз, сколько в другом содержится единиц.

Знак умножения. Действие умножения обозначают знаком × (косвенным крестом) или . (точкой). Знак умножения ставится между множимым и множителем.

Повторить число 7 три раза слагаемым и найти сумму значит 7 умножить на 3. Вместо того, чтобы писать

7 + 7 + 7

пишут при помощи знака умножения короче:

7 × 3 или 7 · 3

Умножение есть сокращенное сложение равных слагаемых.

Знак (×) был введен Отредом (1631 г.), а знак . Христианом Вольфом (1752 г.).

Связь между данными и искомым числом выражается в умножении

письменно:

7 × 3 = 21 или 7 · 3 = 21

словесно:

семь, умноженное на три, составляет 21.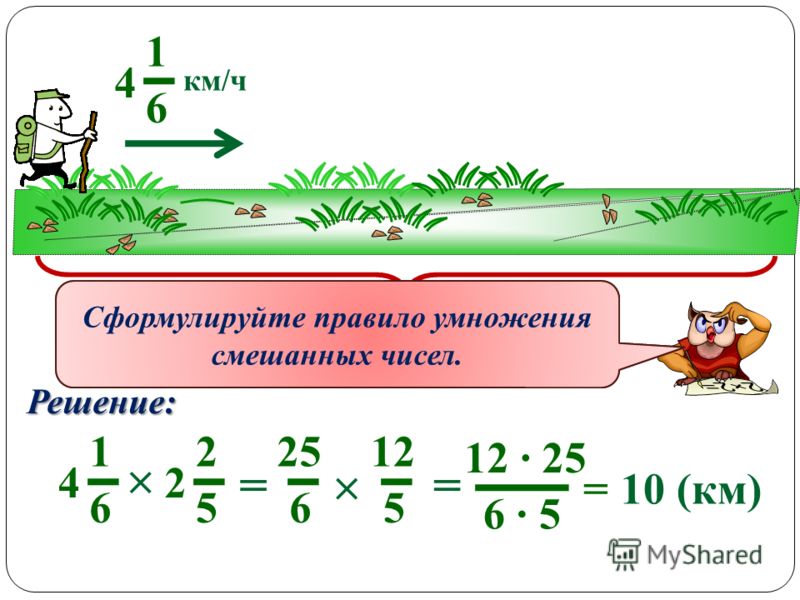

Чтобы составить произведение 21, нужно 7 повторить три раза

21 = 7 + 7 + 7

Чтобы составить множитель 3, нужно единицу повторить три раза

3 = 1 + 1 + 1

Отсюда имеем другое определение умножения: Умножение есть такое действие, в котором произведение точно так же составляется из множимого, как множитель составлен из единицы.

Основное свойство произведения

Произведение не изменяется от перемены порядка производителей.

Доказательство. Умножить 7 на 3 значит 7 повторить три раза. Заменив 7 суммою 7 единиц и вложив их в вертикальном порядке, имеем:

Таким образом, при умножении двух чисел мы можем считать множителем любой из двух производителей. На этом основании производители называются сомножителями или просто множителями.

Самый общий прием умножения состоит в сложении равных слагаемых; но, если производители велики, этот прием приводит к длинным вычислениям, поэтому самое вычисление располагают иначе.

Умножение однозначных чисел. Таблица Пифагора

Чтобы умножить два однозначных числа, нужно повторить одно число слагаемым столько раз, сколько в другом содержится единиц, и найти их сумму. Так как умножение целых чисел приводится к умножению однозначных чисел, то составляют таблицу произведений всех однозначных чисел попарно. Такая таблица всех произведений однозначных чисел попарно называется таблицей умножения.

Таблица Пифагора. Изобретение ее приписывают греческому философу Пифагору, по имени которого ее называют таблицей Пифагора. (Пифагор родился около 569 года до н. э.).

Чтобы составить эту таблицу, нужно написать первые 9 чисел в горизонтальный ряд:

1, 2, 3, 4, 5, 6, 7, 8, 9.

Затем под этой строкой надо подписать ряд чисел, выражающих произведение этих чисел на 2. Этот ряд чисел получится, когда в первой строке сложим каждое число само с собою. От второй строки чисел последовательно переходим к 3, 4 и т. д. Каждая последующая строка получается из предыдущей через прибавление к ней чисел первой строки.

Продолжая так поступать до 9 строки, мы получим таблицу Пифагора в следующем виде

Чтобы по этой таблице найти произведение двух однозначных чисел, нужно отыскать одного производителя в первой горизонтальной строке, а другого в первом вертикальном столбце; тогда искомое произведение будет на пересечении соответствующих столбца и строки. Таким образом, произведение 6 × 7 = 42 находится на пересечении 6-й строки и 7-го столбца. Произведение нуля на число и числа на нуль всегда дает нуль.

Так как произведение числа на 1 дает само число и перемена порядка множителей не изменяет произведения, то все различные произведения двух однозначных чисел, на которые следует обратить внимание, заключаются в следующей таблице:

Произведения однозначных чисел, не содержащиеся в этой таблице, получаются по данным, если только изменить в них порядок множителе; таким образом, 9 × 4 = 4 × 9 = 36.

Умножение многозначного числа на однозначное

Умножение числа 8094 на 3 обозначают тем, что подписывают множитель под множимым, ставят слева знак умножения и проводят черту с тем, чтобы отделить произведение.

Умножить многозначное число 8094 на 3 значит найти сумму трех равных слагаемых

следовательно, для умножения нужно все порядки многозначного числа повторить три раза, то есть умножить на 3 единицы, десятки, сотни, и т. п. Сложение начинают с единицы, следовательно, и умножение нужно начинать с единицы, а затем переходят от правой руки к левой к единицам высшего порядка.

При этом ход вычислений выражают словесно:

1. Начинаем умножение с единиц: 3 × 4 составляют 12, подписываем под единицами 2, а единицу (1 десяток) прикладываем к произведению следующего порядка на множитель (или запоминаем ее в уме).

2. Умножаем десятки: 3 × 9 составляет 27, да 1 в уме составят 28; подписываем под десятками 8 и 2 в уме.

3. Умножаем сотни: Нуль, умноженный на 3, дает нуль, да 2 в уме составит 2, подписываем под сотнями 2.

4. Умножаем тысячи: 3 × 8 = 24, подписываем вполне 24, ибо не имеем следующих порядков.

Это действие выразится письменно:

Из предыдущего примера выводим следующее правило. Чтобы умножить многозначное число на однозначное, нужно:

1. Подписать множитель под единицами множимого, поставить слева знак умножения и провести черту.

2. Умножение начинать с простых единиц, затем, переходя от правой руки к левой, последовательно умножают десятки, сотни, тысячи и т. д.

3. Если при умножении произведение выражается однозначным числом, то его подписывают под умножаемой цифрой множимого.

4. Если же произведение выражается двухзначным числом, то цифру единиц подписывают под тем же столбцом, а цифру десятков прибавляют к произведению следующего порядка на множитель.

5. Умножение продолжается до тех пор, пока не получат полного произведения.

Умножение чисел на 10, 100, 1000 …

Умножить числа на 10 значит простые единицы превратить в десятки, десятки в сотни и т. д., то есть повысить порядок всех цифр на единицу. Этого достигают, прибавляя справа один нуль. Умножить на 100 значит повысить все порядки множимого двумя единицами, то есть превратить единицы в сотни, десятки в тысячи и т. д.

Этого достигают, приписывая к числу два нуля.

Отсюда заключаем:

Для умножения целого числа на 10, 100, 1000 и вообще на 1 с нулями нужно приписать справа столько нулей, сколько их находится во множителе.

Умножение числа 6035 на 1000 выразится письменно:

Когда множитель есть число, оканчивающееся нулями, подписывают под множимым только значащие цифры, а нули множителя приписывают справа.

Умножение на число с нулями в конце

Чтобы умножить 2039 на 300 нужно взять число 2029 слагаемым 300 раз. Взять 300 слагаемых все-равно, что взять три раза по 100 слагаемых или 100 раз по три слагаемых. Для этого умножаем число на 3, а потом на 100, или умножаем сначала на 3, а потом приписываем справа два нуля.

Ход вычисления выразится письменно:

Правило. Чтобы умножить одно число на другое, изображаемое цифрой с нулями, нужно сначала помножить множимое на число, выражаемое значащей цифрой, и затем приписать столько нулей, сколько их находится в множителе.

Умножение многозначного числа на многозначное

Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.

Три произведения

называются частными произведениями.

Полное произведение 3029 × 429 равно сумме трех частных:

3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.

Найдем величины этих трех частных произведений.

1. Умножая 3029 на 9, находим:

    3029
   ×   9 
   27261 первое частное произведение

2. Умножая 3029 на 20, находим:

    3029
   ×   20 
    60580 второе частное произведение

3. Умножая 3026 на 400, находим:

    3029
   ×   400 
   1211600 третье частно произведение

Сложив эти частные произведения, получим произведение 3029 × 429:

Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.

Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:

В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры.

Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.

Отыскивая произведение 3247 на 209, имеем:

Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.

Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.

Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,

1. нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.

2. Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.

3. Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.

4. Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.

Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.

Пример. Найти произведение 342 на 2700.

Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.

Пример. Вычисляя произведение 2700 на 35000, умножаем 27 на 35

Приписывая к 945 пять нулей, получаем искомое произведение:

2700 × 35000 = 94500000.

Число цифр произведения. Число цифр произведения 3728 × 496 можно определить следующим образом. Это произведение более 3728 × 100 и меньше 3728 × 1000. Число цифр первого произведения 6 равно числу цифр в множимом 3728 и во множителе 496 без единицы. Число цифр второго произведения 7 равно числу цифр во множимом и во множителе. Данное произведение 3728 × 496 не может иметь цифр менее 6 (числа цифр произведения 3728 × 100, и более 7 (числа цифр произведения 3728 × 1000).

Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы.

В нашем произведении может содержаться или 7 или 6 цифр.

Степени

Между различными произведениями заслуживают особого внимания такие, в которых производители равны. Так, например:

2 × 2 = 4,    3 × 3 = 9.

Квадраты. Произведение двух равных множителей называется квадратом числа.

В наших примерах 4 есть квадрат 2, 9 есть квадрат 3.

Кубы. Произведение трех равных множителей называется кубом числа.

Так, в примерах 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, число 8 есть куб 2, 27 есть куб 3.

Вообще произведение нескольких равных множителей называется степенью числа. Степени получают свои названия от числа равных множителей.

Произведения двух равных множителей или квадраты называются вторыми степенями.

Произведения трех равных множителей или кубы называются третьими степенями, и т. д.

Умножение целых чисел, правила, примеры, как умножать не целые числа, произведение двух чисел

В этом материале мы покажем, как правильно выполнять умножение целых чисел. Начнем, как всегда, с основных понятий и обозначений и выясним, какой смысл вкладывается в умножение двух целых чисел. Затем сформулируем правила, по которым перемножают целые положительные и целые отрицательные числа, а также числа, имеющие разные знаки. Как всегда, нашу мысль будем пояснять наглядными примерами решений задач. Далее рассмотрим те случаи, когда один из множителей нулевой или равен единице, посмотрим, как можно проверить верность результата, полученного после умножения, а в конце объясним, как правильно перемножать 3, 4 и большее количество целых чисел.

Основные определения при умножении целых чисел

При умножении целых чисел используются те же термины и знаки, о которых мы говорили ранее в статье об умножении натуральных чисел. У нас есть два множителя, которые являются целыми числами, результат, называемый произведением, и знак умножения в виде точки, звездочки или знака «x» (в целях единообразия в дальнейшем будем использовать точку).

Если обозначить множители и произведение буквами a, b и c, то действие умножения можем записать в виде равенства a·b=c. Само числовое выражение a·b тоже называется произведением. Произведение двух целых чисел также является целым числом.

В чем состоит смысл умножения целых чисел?

До этого мы уже объясняли смысл умножения на примере натуральных чисел. Произведение натуральных чисел a и b представляет собой сумму b слагаемых, каждое из которых равно a.

Целые положительные числа – это натуральные числа, поэтому смысл действия умножения для них точно такой же. В буквенном виде его также можно представить как

(значения a и b – целые положительные числа).

В принципе, этот смысл распространяется на все произведения, где одно слагаемое целое и положительное. Второе при этом также должно быть целым, однако оно может быть отрицательным или даже равным нулю. Так, схема умножения числа -3 на 5 будет выглядеть как (−3)·5=(−3)+(−3)+(−3)+(−3)+(−3).

Если вторым множителем является единица, то результат умножения – это сумма одного слагаемого, которое равно другому множителю. Это можно записать как a·1=a. Результат умножения целого числа на единицу есть само это число.

А как быть в случае, если одно из множителей нулевое? Получается, что в ответе будет сумма из 0 слагаемых. Очевидно, что это будет 0. Запишем, что a·0=0 для любого целого a. Умножение целого числа на ноль дает в результате ноль.

В случае с отрицательными числами общий смысл действия умножения сформулировать достаточно сложно. Примем это действие как данность и подчеркнем, что правила умножения в таком случае должны сохранять справедливыми свойства умножения для целых положительных чисел. В частности, такое числовое выражение должно обладать переместительным и сочетательным свойствами.

Основные правила, применяемые при умножении целых чисел

Можно выполнить умножение исходя из того, что оно по сути представляет собой сложение одинаковых слагаемых. Но, как мы уже отмечали, это долгий и трудный процесс, если таких слагаемых у нас много. А если одним из множителей является отрицательное число, то воспользоваться этим способом мы не можем. Поэтому нам надо вывести особые правила для умножения целых чисел. Сформулируем и запишем их.

Как умножать одно целое положительное число на другое

Целые положительные числа относятся к натуральным, поэтому правила умножения натуральных чисел распространяются и на них. В итоге мы, разумеется, получим целый положительный результат, т.е. натуральное число. Разберем конкретные примеры.

Пример 1

Подсчитайте, сколько будет 9 умножить на 7.

Решение

Обратимся к таблице умножения и возьмем из нее готовый результат.

Получим: 9·7=63.

Ответ: 63.

Пример 2

Сколько будет 127 умножить на 5?

Решение

Представим первый из множителей как сумму разрядных слагаемых, т.е. 100+20+7.

Теперь последовательно умножим слагаемые на данное число: 127·5=(100+20+7)·5=100·5+20·5+7·5.

Заканчиваем вычисление: 100·5+20·5+7·5=500+100+35=600+35=635.

Ответ: 635.

Чтобы перемножать многозначные числа, удобно пользоваться методом подсчета в столбик.

Пример 3

Условие: умножьте 712 на 92.

Решение: запишем множители в столбик и вычислим результат.

Ответ: 65 504.

Как правильно перемножить целые числа, имеющие разные знаки

Для того чтобы вывести правило для такого случая, приведем пример.

Итак, нам надо вычислить произведение числа -5 на 3. Вспомним смысл умножения и запишем: (−5)·3=(−5)+(−5)+(−5)=−15. Если учесть переместительное свойство, то должно быть верным и (−5)·3=3·(−5). Очевидно, что модуль числа, полученного в результате, соответствует произведению данных множителей. Таким образом, произведение двух чисел с разными знаками есть число отрицательное.

Определение 1

Чтобы умножить одно отрицательное число на одно положительное, надо перемножить между собой модули этих чисел и поставить перед результатом минус.

Разберем несколько примеров, подтверждающих это правило.

Пример 4

Умножьте 7 на -14.

Решение

Запишем отдельно модули исходных множителей. Получим 7 и 14. Подсчитаем, чему будет равно их произведение: 7·14=98. Все, что нам нужно сделать дальше, – это поставить знак минуса перед полученным числом.

Ответ: 7·(−14)=−98.

Пример 5

Подсчитайте, сколько будет (−36)·29.

Решение

Согласно правилу умножения чисел с разными знаками, нам нужно начать с умножения модулей. Считаем: 36·29=1 044. Здесь удобно будет воспользоваться методом умножения в столбик. Нам осталось поставить минус перед результатом и записать готовый ответ.

Ответ: (−36)·29=−1 044.

В последней части параграфа мы попробуем доказать, что равенство a·(−b)=−(a·b) справедливо (a и b здесь – любые целые числа). Правило умножения целых чисел с разными знаками, которое мы записали выше, является частным случаем этого равенства.

Задача сводится к тому, что нам надо доказать, что значениями выражений a·(−b) и a·b будут противоположные числа. Для этого вычислим сумму a·(−b)+a·b. Она будет равна 0. Учитывая распределительное свойство умножения целых чисел относительно сложения,  справедливым будет a·(−b)+a·b=a·((−b)+b). Сумма (−b)+b –это ноль, потому что это сумма противоположных чисел, в итоге получается, что a·((−b)+b)=a·0. Итоговое произведение равно 0, согласно свойству умножения целого числа на 0. Получается, что a·(−b)+a·b=0, значит, a·(−b) и a·b являются противоположными числами. Отсюда вытекает справедливость равенства a·(−b)=−(a·b). Таким же образом можно показать, что (−a)·b=−(a·b).

Как перемножить целые отрицательные числа

Для получения этого правила нам понадобится равенство (−a)·(−b)=a·b. Ниже мы приведем его доказательство.

Перед этим мы писали, почему a·(−b)=−(a·b) и (−a)·b=−(a·b), следовательно, мы можем записать цепочку равенств (−a)·(−b)=−(a·(−b))=−(−(a·b)).

У  нас получилось выражение −(−(a·b)), которое идентично a·b в силу определения противоположных чисел. Таким образом, (−a)·(−b)=a·b.

Теперь мы можем перейти к формулировке правила умножения целых отрицательных чисел.

Определение 2

Чтобы найти произведение целых отрицательных чисел, нам надо вычислить произведение их модулей.

Из правила ясно, что результат умножения двух отрицательных свойств есть число положительное.

Посмотрим, как применить это правило на практике.

Пример 6

Умножьте (−34)·(−2).

Решение

Воспользуемся правилом и просто перемножим между собой модули: -34=34 и -2=2.

Весь ход решения можно записать как (−34)·(−2)=34·2=68.

Ответ: 68.

Пример 7

Умножьте −1 041 на -538.

Решение

Вычисляем модули и перемножаем их столбиком.

 

Ответ: (−1 041)·(−538)=560 058.  

Как умножить целое число на единицу

Мы уже упоминали, что если мы умножим на единицу любое целое число, то результат будет равен этому же числу, то есть a·1=a. Так как числовое выражение с умножением обладает переместительным свойством, то a·1=1·a тоже должно быть верным. Получается, что 1·a=a. Выведем основное правило и запомним его:

Определение 3

Если умножить два целых числа, одно из которых равно 1, то результат будет равен второму числу.

К примеру, 58·1=58, 1·0=0 и 1·(−602)=−602. Как видно, от значения второго множителя результат не зависит: произведение −53 и 1 – это −53, а результат умножения 1 и отрицательного целого числа −989 981 – это  −989 981.

Как умножить целое число на нуль

Умножение любого целого числа на нуль дает нам в итоге нулевой результат, т. е. a·0=0. С учетом переместительного свойства умножения мы получим, что 0·a=0 тоже будет верно. Запомним:

Определение 4

Если умножить два целых числа, одно из которых равно 0, то результат тоже будет равен 0. Умножение нуля на нуль в итоге также дает нуль.

Так, произведение 678 на 0 – это 0; произведение -45 на нуль – тоже нуль; (−90 7789)·0=0.

Обратное утверждение тоже будет верным: если произведение двух чисел равно нулю, то один или оба множителя тоже равны нулю.

Как проверить результат умножения целых чисел

Для проверки точности результата умножения нам потребуется вспомнить действие деления. Нужно разделить итоговый результат на один из множителей. Если в итоге мы получим второй множитель, то мы все посчитали правильно. Если же результат будет отличен от значения другого множителя, значит, расчет ошибочен и его нужно переделать.

Посмотрим на примерах, как правильно проверить результат умножения целых чисел.

Пример 8

После умножения 21 на -5 получилось -115. Проверьте, верен ли результат.

Решение

Для проверки нам надо разделить произведение на любой множитель. Возьмем -5. Делимое и делитель у нас отрицательные, значит, в итоге мы получим частное от деления их модулей: (−115):(−5)=115:5 (посмотрите статью о том, как делить целые отрицательные числа).

В итоге мы получим 23, хотя второй множитель в исходных данных равен 21. Значит, вычисления были ошибочными.

Ответ: результат деления неверен.

Пример 9

Умножьте -17 на -67 и проверьте точность результата.

Решение

Вспоминаем, как правильно умножать целые отрицательные числа. Считаем: (−17)·(−67)=17·67=1 139. Теперь переходим к проверке. Для этого делим столбиком результат на любой множитель, например, на -67.

Согласно правилам деления чисел с разными знаками, сначала мы проводим подсчеты с их модулями:

Теперь перед результатом мы должны поставить минус.

У нас получилось -17, что соответствует первоначальному условию. Значит, мы все сделали правильно.

Ответ: (−17)·(−67)=1 139. 

Как перемножить три целых числа и более

Зная, что числовое выражение с умножением имеет сочетательное свойство, мы можем точно подсчитать произведение 3,4, 5 и большего количества множителей. А благодаря остальным свойствам можно сказать, что результат произведения не будет определяться положением множителей в примере и способом расстановки скобок. Ранее мы уже приводили обоснования этих утверждений в случае с натуральными числами. Для примера с целыми множителями эти правила работают таким же образом.

Посмотрим на конкретный пример.

Пример 10

Найдите произведение 5-ти множителей: 5, −12, 1, −2 и 15.

Решение

Заменим соседние множители их произведением и запишем, что

 5·(−12)·1·(−2)·15=(−60)·1·(−2)·15=(−60)·(−2)·15=120·15=1 800

С расстановкой скобок можно записать так: (((5·(−12))·1)·(−2))·15. Это позволит нам делать вычисления быстрее и проще.

Можно было переставить множители и по-другому: 1·5·(−12)·(−2)·15, в таком случае скобки надо было расставить так: ((1·5)·(−12))·((−2)·15)=(5·(−12))·((−2)·15)=(−60)·(−30)=1 800.

Мы видим, что результат будет одинаков вне зависимости от метода расстановки скобок и последовательности вычислений.

Ответ: 1800. 

Если хоть один из множителей в примере был бы нулевым, то подсчет не имел бы смысла. Мы сразу могли бы сказать, что результат будет равен 0. Это не зависит от значения других множителей, они могли бы быть любыми. Обратное утверждение также будет справедливо: если произведение нескольких множителей равно 0, то один из этих множителей будет нулевым.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Умножение / Справочник по математике для начальной школы

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Умножение

В этом разделе познакомимся с умножением и узнаем, что сложение одинаковых слагаемых можно заменить умножением.

В математике существует знак для умножения — это точка посередине строки между числами, которые нужно перемножить.

Например, 6 + 6 + 6 + 6 = 24 можно записать по-другому: 6 • 4 = 24

---

Смысл действия умножения состоит в том, что при умножении находится сумма одинаковых слагаемых.

Первое число при умножении показывает, какое слагаемое повторяют несколько раз.

Второе число при умножении показывает, сколько раз повторяют это слагаемое.

Результат умножения показывает, какое число получается.

6 • 4 значит, что число 6 повторяют 4 раза: 6 + 6 + 6 + 6 = 24

6 — первый множитель

4 — второй множитель

24 — произведение

---

Числа при умножении

Первый множитель

Второй множитель

Результат умножения, или Произведение

---

Чтение числовых выражений

6 • 4 = 24

Этот пример можно прочитать по-разному.

• 6 умножить на 4 равняется 24.
• 6 увеличить в 4 раза – получится 24.
• Первый множитель – 6, второй множитель – 4, произведение – 24.
• Произведение 6 и 4 равно 24.

---

Умножение на 1

4 • 1 = 4, потому что это значит, что число 4 повторяют только 1 раз.

23 • 1 = 23, потому что это значит, что число 23 повторяют только 1 раз.

---

Умножение на 0

8 • 0 = 0, потому что это значит, что число 8 повторяют 0 раз.

26 • 0 = 0, потому что это значит, что число 26 повторяют 0 раз.

---

Умножение на 10

8 • 10 = 80, потому что число 8 повторяют 10 раз.

15 • 10 = 150, потому что число 15 повторяют 10 раз.

---

Связь деления и умножения

8 • 3 = 24, потому что 8 повторяют 3 раза.

24 : 3 = 8, потому что в 24 по 3 содержится 8 раз.

24 : 8 = 3, потому что в 24 по 8 содержится 3 раза.

---

В несколько раз больше

Решим задачу:

В магазине было 2 лисички, а котят в 4 раза больше. Сколько было котят?

Это значит, что котят было 4 раза по 2.

2 + 2 + 2 + 2 = 4 (к.)

Заменяем сложение умножением и получаем: 

2 • 4 = 8 (к.)

Вывод: Если в задаче есть слова «в … раз больше», то задача решается умножением.

---

Во сколько раз больше? Во сколько раз меньше?

Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?

Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?

8 : 2 = 4 (раза)

Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.

---

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Табличное умножение

Внетабличное умножение

Умножение суммы на число

Умножение на однозначное число в столбик

Умножение на числа, оканчивающиеся нулями

Свойства умножения

Правило встречается в следующих упражнениях:

2 класс

Страница 66. Вариант 1. Тест 2, Моро, Волкова, Проверочные работы

Страница 51, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 76, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 55, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 65, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 52. Урок 20, Петерсон, Учебник, часть 2

Страница 108. Урок 44, Петерсон, Учебник, часть 2

Страница 18. Урок 6, Петерсон, Учебник, часть 3

Страница 46. Урок 16, Петерсон, Учебник, часть 3

Страница 71. Урок 26, Петерсон, Учебник, часть 3

3 класс

Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 37, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 80, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 109, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 24, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 44, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 51, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 99, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 107, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 12, Моро, Волкова, Рабочая тетрадь, часть 2

4 класс

Страница 24, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 10, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 90. Вариант 2. Итоговый тест за курс начальной школы, Моро, Волкова, Проверочные работы

Страница 36, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 51, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 64, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 82, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 93, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 94, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 47, Моро, Волкова, Рабочая тетрадь, часть 2

5 класс

Номер 36, Мерзляк, Полонский, Якир, Учебник

---

Правило умножения для расчета вероятностей

Правило умножения в вероятности позволяет вам вычислить вероятность нескольких событий, происходящих вместе, используя известные вероятности этих событий по отдельности. Есть две формы этого правила, специальные и общие правила умножения.

В этом посте вы узнаете, когда и как использовать как специальные, так и общие правила умножения. Кроме того, я буду использовать и объяснять стандартные обозначения вероятностей повсюду, помогая вам научиться их интерпретировать. Мы рассмотрим несколько примеров задач, чтобы вы могли увидеть их в действии. В конце есть даже проблема с бонусами!

Прежде чем мы перейдем к самим правилам, вам необходимо знать определения независимых и зависимых событий:

• Независимые события : Возникновение одного события не влияет на вероятность другого события. Например, при подбрасывании монеты выпадение «орла» не влияет на вероятность выпадения «орла» при следующем подбрасывании монеты.
• Зависимые события : Возникновение одного события влияет на вероятность другого события. Например, если вы вытягиваете короля из колоды карт и не заменяете его, это снижает вероятность вытягивания другого короля.

Используя правило умножения, вы можете вычислить вероятность того, что события A и B произойдут вместе, если вы знаете вероятность того, что событие A и событие B произойдут по отдельности.

Обозначение совместной вероятности появления событий A и B следующее: P(A ∩ B).

Когда события независимы, вы можете использовать определенное правило умножения. Когда у вас есть зависимые события, вы должны использовать общее правило умножения.

Связанный пост : Основы вероятности

Специфическое правило умножения

Используйте конкретное правило умножения для расчета общей вероятности независимых событий. Чтобы использовать это правило, умножьте вероятности независимых событий. Для независимых событий появление события A не влияет на вероятность события B. Это правило не действует для зависимых событий.

Используя обозначение вероятности, конкретное правило умножения следующее:

P(A ∩ B) = P(A) * P(B)

Или, совместная вероятность появления А и В равна вероятности появления А, умноженной на вероятность появления В.

Примеры специального правила умножения

Например, чтобы вычислить вероятность выпадения орла при двух последовательных подбрасываниях монеты, умножьте вероятность выпадения орла при первом подбрасывании монеты (0,5) на вероятность выпадения орла при второй монете. флип (0,5).

0,5 X 0,5 = 0,25

Совместная вероятность двух последовательных орлов равна 0,25.

Представьте, что вам особенно нравится носить коричневые брюки с синей рубашкой. Однако утром вы сонный и наугад берете штаны и рубашку из шкафа. Брюки находятся на одной стороне шкафа, а рубашки — на другой. Это независимые события, потому что получение пары брюк не влияет на вероятность получения рубашки.

У тебя десять пар штанов и три коричневые. Следовательно, вероятность выпадения коричневой пары (событие TP) равна 0,3.

У вас есть 16 футболок и четыре синие. Следовательно, вероятность получить синюю рубашку (событие BS) равна 0,25.

Это независимые события, потому что выбор пары брюк не влияет на вероятность получения синей рубашки и наоборот.

Используя специальное правило умножения для этих независимых событий:

P(TP ∩ BS)= P(TP) * P(BS)

0,3 X 0,25 = 0,075

Или совместная вероятность случайного выбора пары коричневые штаны и синяя рубашка равняется 0,075, то есть вероятность светло-коричневых брюк, умноженная на вероятность синей рубашки.

Вероятность получения нужной вам комбинации мала! Вы можете выпить кофе, чтобы увеличить свои шансы!

Общее правило умножения

Используйте общее правило умножения для расчета совместных вероятностей независимых или зависимых событий. Когда у вас есть зависимые события, вы должны использовать общее правило умножения, поскольку оно позволяет учитывать, как возникновение события А влияет на вероятность события В.

Используя стандартные обозначения, общее правило умножения выглядит следующим образом:

P(A ∩ B) = P(A) * P(B|A)

Или, совместная вероятность появления А и В равна вероятности появления А, умноженной на условную вероятность появления В при условии, что А произошло .

Неудивительно, что разница между общими и специальными правилами заключается в том, что вы можете использовать общее правило в более широком смысле. Оно работает как для независимых, так и для зависимых событий, тогда как конкретное правило действует только для независимых событий.

Почему можно использовать общую форму как для независимых, так и для зависимых событий? В обозначениях сосредоточьтесь на P(B|A), которая представляет собой условную вероятность того, что событие B произойдет при условии, что произошло событие A.

В контексте независимых событий P(B|A) = P(B), поскольку событие A не влияет на вероятность события B. Это и есть определение независимых событий. Следовательно, это правило становится эквивалентным конкретному мультипликативному правилу для независимых событий.

Однако для зависимых событий P(B|A) ≠ P(B). Это просто еще один способ сказать, что событие А влияет на вероятность события Б (т. е. это зависимые события). Общее правило мультипликативности позволяет учитывать другое событие, как вы увидите в следующих двух примерах!

Связанный пост : Использование таблиц непредвиденных обстоятельств для расчета вероятностей

Примеры общего правила умножения

Классический пример для зависимых событий — вытягивание карт из колоды карт без замены. Когда вы берете карты, это влияет на вероятность следующей карты, которую вы можете взять.

Предположим, вас интересует вероятность выпадения червы в двух последовательных розыгрышах. Изначально в колоде 13 червей из 52 карт (13/52 = 0,25). Если вы рисуете сердце (событие h2), это меняет вероятность того, что выпадет еще одно сердце. Зависимая вероятность вытянуть вторую черву (событие h3) теперь равна 12/51 = 0,235.

В форме записи:

P(h2 ∩ h3) = P(h2) * P(h3|h2)

вторая черва, учитывая, что первая карта была червой.

0,25 * 0,235 = 0,059

Зависимые события: пример светло-коричневых брюк и синих рубашек

Вернемся к примеру со брюками и рубашкой. Представьте, что мы собираемся в короткую поездку и случайным образом выбираем две пары брюк и две пары рубашек, чтобы положить их в наш чемодан. Мы надеемся на две пары коричневых брюк и две синие рубашки.

Начнем с рассмотрения этого как двух наборов зависимых событий, один для брюк, а другой для рубашек.

Начнем с 10 пар штанов, три из которых коричневые. Следовательно, вероятность того, что первая пара брюк будет желто-коричневой (событие T1), равна 0,30. Вероятность того, что вторая пара будет желто-коричневой (T2), составляет 2/9 = 0,22. Отсюда:

P(T1 ∩ T2) = P(T1) * P(T2|T1)

0,30 * 0,22 = 0,066

Совместная вероятность вытянуть две пары светло-коричневых штанов равна 0,066, что равно вероятности первая пара коричневых штанов, умноженная на условную вероятность появления второй пары коричневых штанов при условии, что первая пара была коричневой.

Что касается футболок, мы начнем с четырех синих из 16. Используя тот же подход, мы получаем следующее:

P(B1 ∩ B2) = P(B1) * P(B2|B1)

0,25 * 0,20 = 0,05

У нас есть две совместные вероятности 0,066 для двух тангенсов. штаны и 0,05 за две синие рубашки.

Связанный пост : Использование перестановок для расчета вероятностей и использование комбинаций для расчета вероятностей

Бонус Пример задачи!

Наша конечная цель как случайного упаковщика состоит в том, чтобы иметь в чемодане две коричневые штаны и две синие рубашки. Можете ли вы понять, как рассчитать эту вероятность, учитывая приведенную выше информацию?

Чтобы решить эту проблему, мы определим две коричневые штаны как событие 2TP и две синие рубашки как событие 2BS. Из наших предыдущих расчетов зависимых событий с использованием общего правила умножения мы знаем следующее:

P(2TP) = 0,066

P(2BS) = 0,05

Как рассчитать совместную вероятность P(2TP ∩ 2BS)?

Вспомните пример независимых событий, когда мы нарисовали одну пару брюк и одну рубашку. Выбор брюк не влияет на вероятность получения рубашки и наоборот. Следовательно, мы можем рассматривать события 2TP и 2BS как независимые события, хотя у нас были зависимые события при расчете вероятностей для нескольких штанов и нескольких рубашек. Другими словами, выбор нескольких брюк влияет на вероятность получения следующей пары брюк, но не влияет на рубашки.

Следовательно, мы можем использовать конкретное правило умножения для независимых событий для этой части решения:

P(2TP ∩ 2BS) = P(2TP) * P(2BS)

0,066 * 0,05 = 0,0033

Вероятность вытянуть две пары светло-коричневых брюк и две синие рубашки составляет всего 0,0033 или 0,33%! Это вряд ли произойдет случайно. Если мы действительно хотим эту комбинацию, мы должны рассмотреть неслучайный подход к упаковке!

Вычисление совместных вероятностей с помощью правила умножения очень просто. Определите, являются ли ваши события независимыми или зависимыми, а затем используйте правильную форму правила!

Что такое правило умножения вероятности? (Видео и практика)

TranscriptPractice

Привет, и добро пожаловать в это видео о правиле умножения вероятности!

Чтобы освежить вашу память, вероятность — это мера вероятности того, что данное событие произойдет.

Осознаете вы это или нет, но каждый божий день вы используете вероятность, чтобы делать выбор и принимать решения в своей повседневной жизни. Например, если вы просыпаетесь с 80-процентной вероятностью дождя, вы, скорее всего, возьмете с собой на работу зонтик. Питчер, столкнувшийся с отбивающим со средним показателем 0,347, скорее всего, будет подавать осторожно и стратегически.

«Вероятность дождя 80 %» — это еще один способ сказать, что из 100 дней с такой конкретной погодой в 80, скорее всего, будет дождь. Среднее количество ударов 0,347 указывает на то, что отбивающий в среднем наносит 347 ударов из 1000 ударов летучими мышами.

Это просто вероятности одного события. Чтобы определить вероятность возникновения нескольких событий, нам нужно использовать правило умножения вероятности. Чтобы понять это правило, нам нужно глубже погрузиться в область вероятностей.

Независимые и зависимые события

Во-первых, важно различать независимые и зависимые события.

Два события независимы друг от друга, если появление первого не влияет на второе. Например, монету можно подбросить дважды, но независимо от того, какая сторона выпадет после первого подбрасывания, при втором подбрасывании шанс выпадения орла или решки составляет 50/50.

Напротив, предположим, что вы делаете два выбора из стандартной колоды карт и выбираете туза при первом выборе, не возвращая его обратно в колоду. Вероятность вашего второго выбора изменилась, потому что теперь у вас на одну карту меньше в колоде. Эти два выбора будут зависимыми, поскольку первый из них оказывает влияние и влияет на вероятность второго выбора.

Исходя из этого, давайте копнем глубже и исследуем еще один элемент вероятности — что, если вы хотите определить вероятность двух событий, происходящих в последовательности?

Определение вероятности нескольких событий

Пример 1

В качестве примера предположим, что у вас есть традиционный шестигранный кубик и вы хотите определить вероятность выпадения 2 при первом броске И 3 при втором броске.

Поскольку каждое число появляется на кубике только один раз, мы знаем, что вероятность выпадения 2 равна 1 из 6. Помните, что, поскольку числа на кубике не меняются независимо от того, сколько раз его бросают, выпадение кости будут считаться независимыми событиями. Следовательно, вероятность выпадения 3 при втором броске также равна 1 из 6.

Но как определить вероятность ОБОИХ событий? Чтобы ответить на этот вопрос, воспользуемся правилом умножения вероятности.

Это правило гласит, что если вы хотите найти вероятность того, что произойдут как событие A, так и событие B, вы должны умножить вероятность события A на вероятность события B.

В нашем примере событие A будет вероятностью выпадение 2 при первом броске, то есть \(\frac{1}{6}\). Событие B будет выбрасывать 3 при втором броске, вероятность которого также равна \(\frac{1}{6}\).

Следовательно, чтобы найти вероятность того, что произойдут оба этих события, мы возьмем вероятность события A и умножим ее на вероятность события B.

\(\frac{1}{6} \times \frac {1}{6}\)

 

Умножение числителей даст нам 1, а умножение знаменателей даст нам 36, что даст нам ответ 1 на 36.

\(\frac{1}{ 6} \times \frac{1}{6}= \frac{1}{36}\)

 

Это означает, что, по всей вероятности, человек будет выбрасывать 2, а затем 3 один раз в каждые 36 попытки.

Пример 2

Рассмотрим другой пример.

Допустим, у вас есть стандартная колода карт, и вы хотите определить вероятность того, что сначала выпадет король червей, а затем любая карта червовой масти.

Давайте рассмотрим эту задачу по одному событию за раз.

Первое событие — розыгрыш червового короля. Мы знаем, что в стандартной колоде 52 карты, и в каждой колоде есть только один король червей. Следовательно, вероятность вытянуть короля червей равна \(\frac{1}{52}\).

Теперь давайте рассмотрим второе событие — вытягивание одной из оставшихся карт червовой масти. Помните, что второе событие является зависимым событием. Это означает, что он должен отражать изменения обстоятельств, вызванные первым событием.

Вот что я имею в виду: Обычно в колоде 13 карт каждой масти. Но так как червового короля мы уже вытащили, то в червовой масти осталось всего 12 карт. Если мы запишем нашу вероятность в виде дроби, это даст нам 12 в нашем числителе для 12 оставшихся червей.

И хотя в стандартной колоде обычно 52 карты, поскольку мы уже вытащили одну карту, осталась только 51 карта. Это дает нам 51 в нашем знаменателе и вероятность \(\frac{12}{51}\) для второго события.

Следуя правилу умножения, мы должны умножить \(\frac{1}{52}\) и \(\frac{12}{51}\).

\(\frac{1}{52} \times \frac{12}{51}\)

 

Умножение числителей даст нам 12, а умножение знаменателей, 52 и 51, даст нам 2652, что дает нам вероятность \(\frac{12}{2652}\). Поскольку и числитель, и знаменатель являются четными числами, мы знаем, что их можно упростить, по крайней мере, разделив оба на 2. В этом случае мы действительно можем разделить оба на 12, что даст нам окончательный ответ \(\frac{1} {221}\). Это означает, что вероятность вытянуть короля червей, за которым следует еще одна карта червовой масти, будет один раз на каждые 221 попытку.

Итак, помните, чтобы определить вероятность возникновения нескольких событий, просто умножьте вероятность события A на вероятность события B, по возможности упростив дроби.

Надеюсь, отзыв был полезен! Спасибо за просмотр и удачной учебы!

Таблица умножения и печатные формы

 

Практические вопросы

Вопрос №1:

 
Какой сценарий описывает два независимых события?

Неоплата счета за электроэнергию, а затем отключение электричества.

Незаконная парковка, а затем получение парковочного талона.

Сначала сесть в самолет, а потом найти хорошее место.

Завести собаку, а потом посадить цветник.

Показать Ответ

Ответ:

Зависимые события описывают ситуации, когда первое событие оказывает прямое влияние на второе событие. Например, если вы припарковались неправильно, в результате вы, скорее всего, получите штраф. Первое событие влияет на второе событие. Только один предоставленный сценарий является примером независимых событий. Посадка цветника не зависит от того, есть ли у вас собака. Два события независимы друг от друга.

Скрыть ответ

Вопрос №2:

 
Определите вероятность того, что на обычном игральном кубике выпадет шестерка, а затем пятерка.

\(\frac{1}{6}\)

\(\frac{2}{6}\)

\(\frac{1}{36}\)

\(\frac{2 }{36}\)

Показать ответ

Ответ:

При определении вероятности двух или более событий вероятность первого события можно умножить на второе событие. В этом примере вероятность выпадения шестерки равна \(\frac{1}{6}\), а вероятность выпадения пятерки также равна \(\frac{1}{6}\). Правило умножения вероятности гласит, что \(\frac{1}{6}\times\frac{1}{6}\) будет вероятностью того, что произойдут оба события: \(\frac{1}{6}\times \frac{1}{6}=\frac{1}{36}\)

Скрыть ответ

Вопрос № 3:

 
Определите вероятность того, что выпадет нечетное число, а затем число больше семи.


\(\frac{1}{10}\)

\(\frac{2}{10}\)

\(\frac{1}{9}\)

\(\frac{ 3}{3}\)

Показать ответ

Ответ:

Для решения этой задачи можно использовать правило умножения вероятности. Вероятность выпадения нечетного числа равна \(\frac{5}{10}\), а вероятность выпадения числа больше семи равна \(\frac{2}{10}\). Когда эти две вероятности перемножаются, мы видим, что наш ответ равен \(\frac{10}{100}\), или в простейшей форме \(\frac{1}{10}\).

Скрыть ответ

Вопрос № 4:

 
В классе из 30 учеников 8 учеников занимаются в кружке искусств, 12 учеников в драматическом кружке и 17 учеников в футбольном клубе. Какова вероятность случайного выбора студента, который участвует в драматическом кружке?

\(\frac{2}{5}\)

\(\frac{15}{6}\)

\(\frac{5}{3}\)

\(\frac{12 }{35}\)

Показать Ответ

Ответ:

В драматическом кружке 12 учеников, всего 30 учеников. Это означает, что 12 из 30 студентов находятся в драматическом клубе. Эта дробь представляет вероятность \(\frac{12}{30}\) или, в простейшей форме, \(\frac{2}{5}\).

Скрыть ответ

Вопрос №5:

 
В мешке 20 шариков. 12 шариков красного цвета и 8 шариков зеленого цвета. Шарики не заменяются после того, как они выбраны из мешка. Какова вероятность выбрать сначала красный, а затем зеленый шарик?

\(\frac{24}{95}\)

\(\frac{12}{50}\)

\(\frac{6}{20}\)

\(\frac{8 }{20}\)

Показать ответ

Ответ:

Для решения этой задачи можно использовать правило умножения вероятности. Вероятность выбора красного шарика равна \(\frac{12}{20}\). Этот шарик не помещается в мешок, так что теперь вероятность выбора зеленого шарика равна \(\frac{8}{19}\). Когда эти две вероятности перемножаются, мы получаем \(\frac{96}{380}\), или в простейшей форме \(\frac{24}{95}\).

Скрыть ответ

 

Вернуться к видео о вероятностях

782598

Правило умножения вероятности | Теорема умножения о вероятности

Правило умножения вероятности определяет условие между двумя данными событиями. Для двух событий, A и B, связанных с пространством выборки S, A ∩ B обозначает события, в которых произошли оба события. Это также известно как теорема умножения в вероятности. Вероятности двух заданных событий перемножаются, чтобы получить вероятность того, что эти события произойдут одновременно.

1.	Что такое правило умножения вероятности?
2.	Правило умножения формулы вероятности
3.	Правило умножения вероятностного доказательства
4.	Правило умножения вероятности для n событий
5.	Вероятностное правило умножения Примеры
6.	Часто задаваемые вопросы о правиле умножения вероятности

Что такое правило умножения вероятности?

Правило вероятности умножения гласит, что всякий раз, когда событие является пересечением двух других событий, то есть события A и B должны произойти одновременно. Тогда P(A и B)=P(A)⋅P(B). Множество A ∩ B обозначает одновременное появление событий A и B, то есть множество, в котором произошли оба события A и событие B. Событие A∩B можно записать как AB. Вероятность события AB получается с использованием свойств условной вероятности, которая задается как P (A ∩ B) = P (A) P (B | A).

Правило умножения вероятности для зависимых событий

Если исход одного события влияет на исход другого, то такие события называются зависимыми событиями. Иногда возникновение первого события влияет на вероятность второго события. Из теоремы имеем P(A ∩ B) = P(A) P(B | A), где A и B — независимые события.

Правило умножения вероятности для независимых событий

Если исход одного события не влияет на исход другого, то такие события называются независимыми событиями. Правило умножения вероятности для зависимых событий может быть распространено на независимые события. Имеем P(A ∩ B) = P(A) P(B | A), поэтому, если события A и B независимы, то P(B | A) = P(B), и, таким образом, приведенное выше теорема сводится к P(A ∩ B) = P(A) P(B). Это означает, что вероятность того, что оба события произойдут одновременно, является произведением их соответствующих вероятностей.

Правило умножения формулы вероятности

Правило умножения вероятности гласит, что вероятность того, что события A и B произойдут вместе, равна вероятности того, что B произойдет, умноженной на условную вероятность того, что A произойдет при условии, что B произойдет.

• Правило умножения можно записать как P(A∩B)=P(B)⋅P(A|B).
• Общее правило умножения вероятности можно получить простым способом, просто умножив обе части уравнения условной вероятности на знаменатель.

Правило умножения вероятностного доказательства

Вероятность пересечения двух событий, А и В, получается с использованием свойств условной вероятности.

• Мы знаем, что условная вероятность события A при условии, что произошло B, обозначается P(A|B) и определяется как: P(A|B) = P(A∩B)P(B), где , Р(В)≠0. P(A∩B) = P(B)×P(A|B) …….(1)
• P(B|A) = P(B∩A)P(A), где P(A) ≠ 0. P(B∩A) = P(A)×P(B|A)
• Так как P(A∩B) = P(B∩A), P(A∩B) = P(A)×P(B|A) ……..(2)
• Из (1) и (2) P(A∩B) = P(B)×P(A|B) = P(A)×P(B|A), P(A) ≠ 0,P( Б) ≠ 0. Следовательно, полученный таким образом результат известен как правило умножения вероятности.
• Для независимых событий A и B P(B|A) = P(B). Уравнение (2) можно изменить следующим образом: P(A ∩ B) = P(B) × P(A)

Правило умножения вероятности для n событий

Теперь, чтобы получить правило умножения вероятности для n событий, распространение теоремы умножения вероятности на n событий для n событий A ₁ , A ₂ , … , A _n , имеем P(A ₁ ∩ A ₂ ∩ … ∩ A _n ) = P(A _{) 2 P(A ) | A 1 ) P (A 3 | A 1 ∩ A 2 )… × P (A N | A 1 ∩ A 2 | A 1 ∩ A 2 . .. ∩ 1 ∩ A 2 … ∩ 1 ∩ A 2 .} )

Для n независимых событий теорема умножения сводится к P(A ₁ ∩ A ₂ ∩ … ∩ A _n ) = P(A ₁ ) P(A ₂ ) … P(A _n ).

Связанные темы

Следующие связанные темы помогают лучше понять правило умножения вероятности.

• Вероятность и статистика
• Вероятностные правила
• Взаимоисключающие события
• Независимые события
• Биномиальное распределение
• Формула Байе
• Формула распределения Пуассона

 

Правило вероятностей умножения Примеры

1. Пример 1: Какова вероятность того, что на обычном шестигранном кубике выпадет 5, а затем 2?

   Решение:

   Пространство выборки = {1, 2, 3, 4, 5, 6}

   Всего событий = 6

   Вероятность получения 5 = 1/6

   Вероятность получения 6 = 1 /6

   Применение правила умножения вероятности для независимых событий,

   P(получение 5, а затем 2 ) = (1/6). (1/6) = 1/36.

   Следовательно, вероятность выпадения 5, а затем 2 на обычном шестигранном кубике равна 1/36.

2. Пример 2: Две карты выбираются без замены первой карты из колоды. Найти вероятность выбора короля, а затем выбора ферзя.

   Решение:

   Всего событий = 52

   Поскольку первая карта не заменена, события зависимы.

   Вероятность выбора короля = P(K) = 4/52

   Вероятность получения дамы = P(Q) = 4/51 (одна карта, взятая первой, не была заменена)

   P(король и тогда ферзь) = P(K).P(Q|K)

   =4/52 . 4/51 = 16/2652 = 1/166.

   Таким образом, вероятность выбора короля, а затем ферзя равна 1/166.

перейти к слайдуперейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по правилу умножения вероятности

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о правиле умножения вероятности

Что такое теорема умножения вероятности?

Согласно теореме умножения вероятности, вероятность одновременного возникновения двух событий А и В равна произведению вероятности другого события при условии, что произошло первое из них. Это называется теоремой умножения вероятности.

Почему мы используем правило умножения в вероятности?

Используя правило умножения, мы можем вычислить вероятность того, что события A и B произойдут вместе, при условии, что события A и B происходят по отдельности.

Как найти вероятность 3 событий, используя правило умножения вероятности?

В случае трех событий, A, B и C, правило умножения задается как вероятность пересечения P(A и B и C) = P(A)P(B|A)P(C |А и Б).

Как использовать правило умножения вероятности?

В случае, если одновременно происходят два события, просто умножьте вероятность первого события на второе. Например, если вероятность события А равна 2/7, а вероятность события В равна 5/7, то вероятность того, что оба события произойдут одновременно, вычисляется с использованием правила умножения вероятности, т. е. (2/7) *(5/7) = 10/49.

Правило умножения используется для расчета вероятности какого типа?

Правило умножения вычисляет вероятность одновременного возникновения нескольких событий, используя известные вероятности отдельных событий.