Действия с дробями
Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе, всё что можно делать с обычными числами, можно делать и с дробями.
Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями;
- Сложение дробей с разными знаменателями.
Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
Например, слóжим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка.
Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Сложение дробей с разными знаменателями
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1. Сложим дроби и
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2.
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести).
Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби?
Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6.
Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателями Вычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей.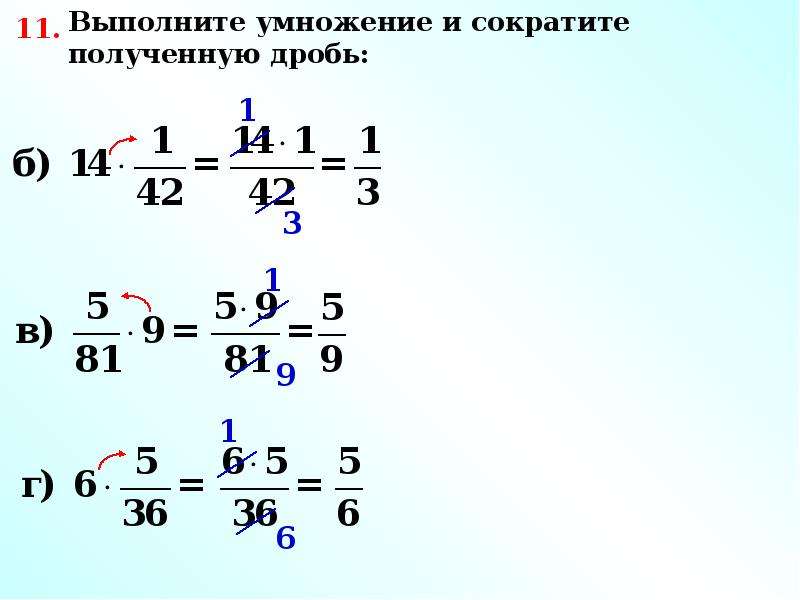
Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка.
Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку.
Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1. Умножить дробь на число 1.
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2. Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби разрешается сокращать, если они имеют общий делитель, бóльший единицы.
Например, выражение можно вычислить двумя способами.
Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
Второй способ. Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4, поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
А вот к примеру выражение можно вычислить только первым способом — умножить число 7 на числитель дроби , а знаменатель оставить без изменений:
Связано это с тем, что число 7 и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробей
Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
Получили ответ .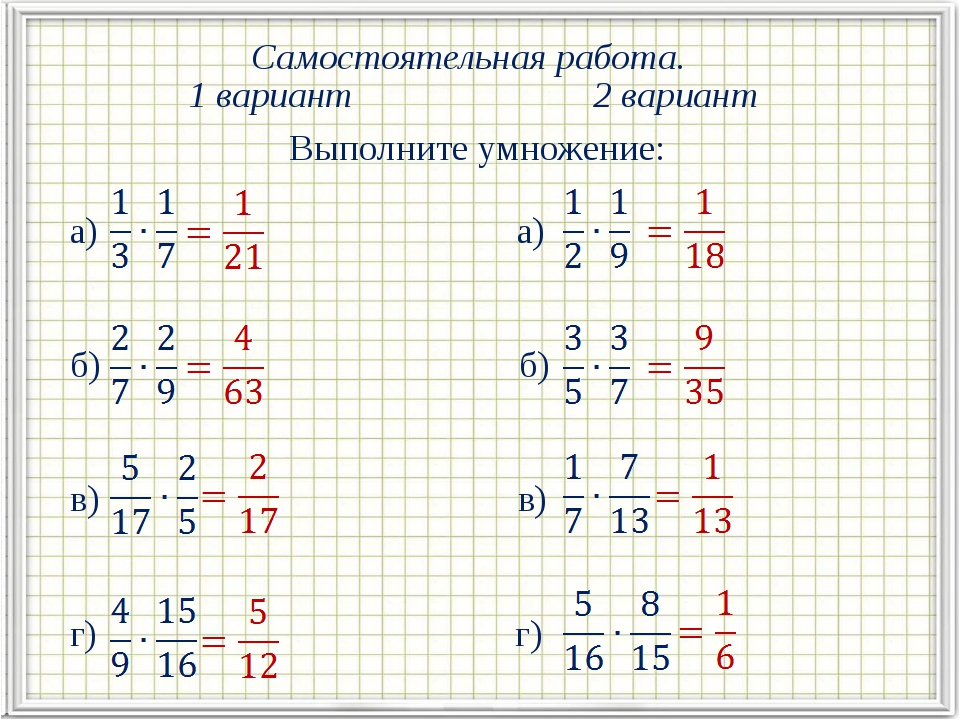
Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дроби
Любое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числа
Сейчас мы познакомимся с очень интересной темой в математике.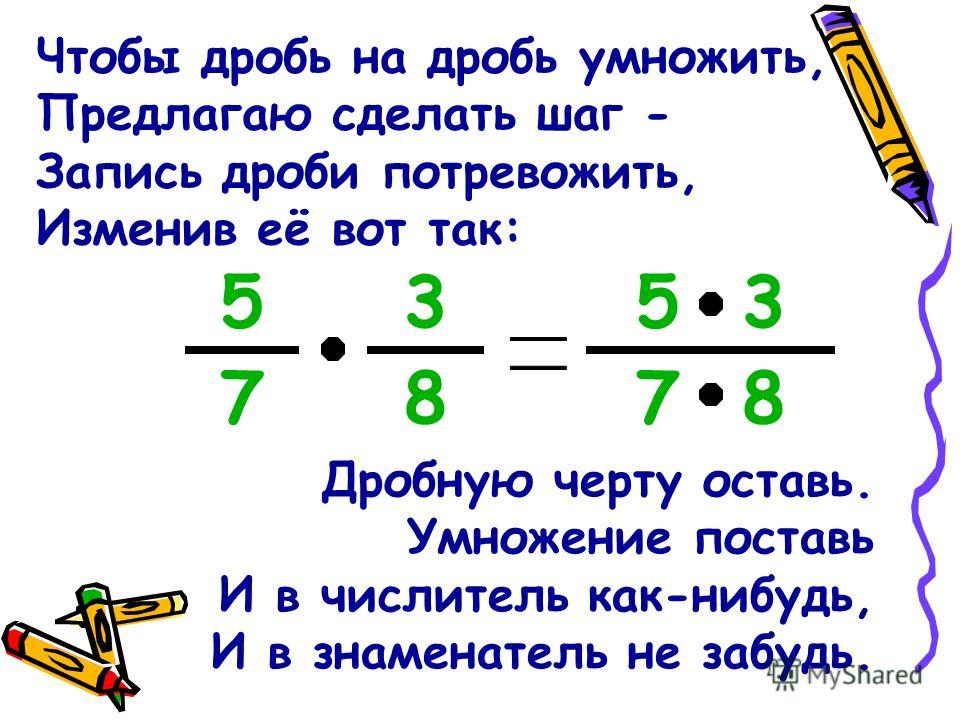
Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Примеры:
- обратным числа 2 является дробь
- обратным числа 3 является дробь
- обратным числа 4 является дробь
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Примеры:
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2.
Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
Получили ответ . Значит при делении половины на две части получается четверть.
Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:
Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:
Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь
В обоих случаях получился один и тот же результат.
Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь
Пример 2. Найти значение выражения
Умножим первую дробь на число, обратное делителю:
Допустим, имеется четверть пиццы и нужно разделить её на двоих:
Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:
Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5
10 : 2 = 5
Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь
Как видно результат не изменился. Мы снова получили ответ 5.
Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.
Пример 3. Найти значение выражения
Умножим первую дробь на число, обратное делителю.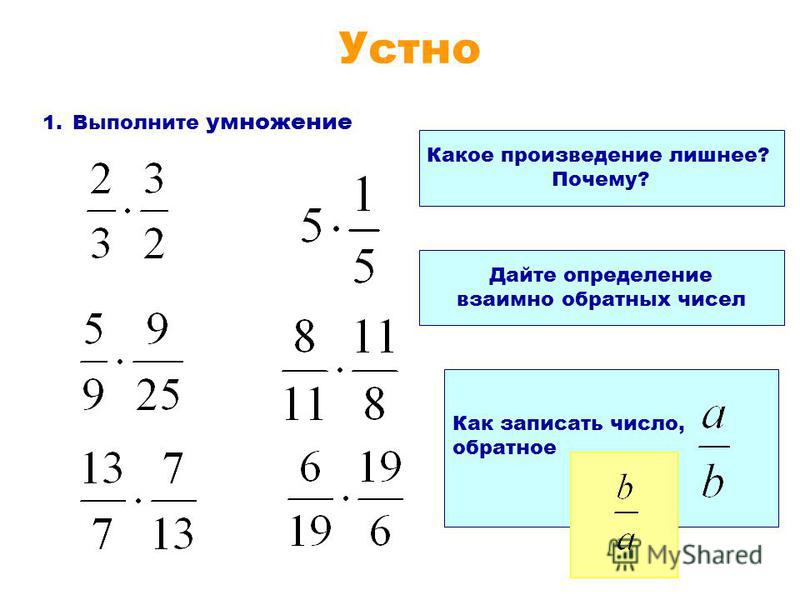
Обратное делителю число это дробь
Допустим, имелось пиццы:
Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков
Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении на 6 получается
Деление числа на дробь
Правило деления числа на дробь такое же, как и правило деления дроби на число.
Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.
Например, разделим число 1 на .
Чтобы разделить число 1 на , нужно это число 1 умножить на дробь, обратную дроби . А обратная дроби это дробь
Выражение можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:
Если зададим вопрос «сколько раз половина содержится в этой пицце», то ответом будет 2. Действительно, половина содержится в одной целой пицце два раза
Пример 2. Найти значение выражение
Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь
Допустим, у нас имеются две целые пиццы:
Если зададим вопрос «сколько раз половина содержится в двух пиццах», то ответом будет 4. Действительно, половина содержится в двух пиццах четыре раза:
Деление дробей
Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.
Например, разделим на
Чтобы разделить на , нужно умножить на дробь, обратную дроби . А обратная дроби это дробь
Допустим, имеется половина пиццы:
Если зададим вопрос «сколько раз четверть пиццы содержится в этой половине», то ответом будет 2. Действительно, четверть пиццы содержится в половине пиццы два раза:
Пример 1.
Найти значение выражения
Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую:
Пример 2. Найти значение выражения
Умножаем первую дробь на дробь обратную второй:
Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой.
Каждая следующая тема будет более сложной, поэтому нужно тренироваться.
Задания для самостоятельного решения:
Задание 1. Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Задание 6. Найдите значение выражения:
Решение:
Задание 7. Найдите значение выражения:
Решение:
Задание 8. Найдите значение выражения:
Решение:
Задание 9. Найдите значение выражения:
Решение:
Задание 10. Найдите значение выражения:
Решение:
Задание 11. Найдите значение выражения:
Решение:
Задание 12. Найдите значение выражения:
Решение:
Задание 13. Найдите значение выражения:
Решение:
Задание 14. Найдите значение выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Как умножить обыкновенную дробь на десятичную дробь
В данной публикации мы рассмотрим, каким образом обыкновенную (простую) дробь можно умножить на десятичную.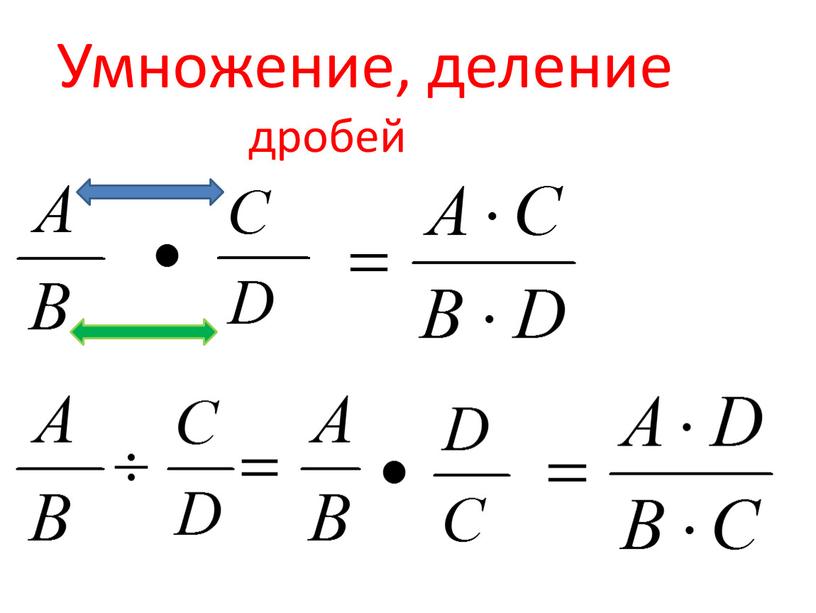
Также разберем примеры для закрепления теоретического материала.
Произведение обыкновенной и десятичной дробей
Чтобы умножить обыкновенную дробь на десятичную (и наоборот, т.к. от перестановки множителей результат не меняется), необходимо одну из дробей представить в виде другой.
Примечания:
1. Бесконечные десятичные дроби сначала требуется округлить, т.е. оставить конечное количество цифр после запятой.
2. Смешанные обыкновенные дроби сперва необходимо превратить в неправильные.
Примеры
Пример 1
Давайте найдем результат произведения дроби3/20
и 2,19.
Решение 1
Переведем обыкновенную дробь в десятичную:
3/20
=
3⋅5/20⋅5
=
15/100
= 0,15
Теперь выполним умножение десятичных дробей:
0,15 ⋅ 2,19 = 0,3285.
Решение 2
Преобразуем десятичную дробь в обыкновенную:
2,19 = 219/100
=
2 ⋅ 100 + 19/100
=
219/100
Остается только найти произведение двух обыкновенных дробей:
219/100
⋅
3/20
=
219 ⋅ 3/100 ⋅ 20
=
657/2000
Пример 2
4/9
.
Решение
Преобразуем заданную смешанную дробь в неправильную:
24/9
=
2 ⋅ 9 + 4/9
=
22/9
Далее у нас есть выбор: либо мы переводим десятичную дробь в обыкновенную, либо наоборот. Выберем первый вариант.
24/100
=
6 ⋅ 100 + 24/100
=
624/100
Теперь разделим одну простую дробь на другую:
624/100
:
22/9
=
624/100
⋅
9/22
=
624 ⋅ 9/100 ⋅ 22
=
5616/2200
= 2
1216/2200
= 2
152/275
≈ 2,5528
Умножение обыкновенных и десятичных дробей
Умножение обыкновенных и десятичных дробей сводится к умножению либо обыкновенных дробей, либо десятичных дробей.
Чтобы умножить обыкновенную дробь на десятичную, надо обе дроби привести к одному виду.
Любую десятичную дробь можно перевести в обыкновенную (как слышим, так и пишем).
Например,
Если возможно, полученную дробь следует сократить.
Например,
Обыкновенную дробь перевести в десятичную (речь идёт о несократимой дроби) можно только в том случае, когда её знаменатель равен 2, 5 или числу, которое можно разложить на множители, состоящие только из двоек и пятёрок.
Например,
40=2∙2∙2∙5.
Разложение числа состоит только из двоек и пятёрок, значит, любое число можно разделить на 40. Делим 7 на 40 и получает представление обыкновенной дроби в виде десятичной.
Перейдём к примерам умножения обыкновенных и десятичных дробей.
Примеры.
1-й способ
Так как знаменатель обыкновенной дроби равен 5, эту дробь можно перевести в десятичную и выполнить умножение десятичных дробей:
2-й способ
Переведём десятичную дробь в обыкновенную, сократим полученную дробь и выполним умножение обыкновенных дробей:
то есть при любом способе получаем одинаковый ответ, отличается только форма записи.
Знаменатель обыкновенной дроби равен 14. 14=2∙7. Такую дробь перевести в десятичную перевести не получится. Значит, десятичную дробь представим в виде обыкновенной:
Здесь ответ может быть записан как в виде обыкновенной, так и в виде десятичной дроби.
Дробь со знаменателем 11 не можем представить в виде десятичной. Поэтому переводим десятичную дробь в обыкновенную:
1-й способ
Раскладываем знаменатель на простые множители: 4=2∙2.
Переводим обыкновенную дробь в десятичную:
2-й способ:
Сведём умножение десятичной и обыкновенной дробей к умножению обыкновенных дробей:
Я рекомендую при возможности выбора стараться работать как с обыкновенными, так и с десятичными дробями.
Важно освоить навыки счёта на уроках математики в 5-6 классах, а старших классах вам предстоит решать другие задачи.
Вычисления с обыкновенными и десятичными дробями
Калькулятор осуществляет умножение, разность, сумму и деление двух простых или десятичных дробей. Результат сокращяется.
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.
lt/public_html/trupmena-1-ru.php on line 93Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 93
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 110
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Warning: A non-numeric value encountered in /home/skraidan/domains/kontroliniai.lt/public_html/trupmena-1-ru.php on line 112
Как рассчитать проценты, процент от числа
Квадратное уравнение — Калькулятор
Другие полезные темы:
| Делимся | знаниями |
Если думаешь, что Это интересно для друга, напиши
Умножение дробей и смешанных чисел. Деление дробей и смешанных чисел. Примерно 6-класс (11-12 лет)
Умножение дробей и смешанных чисел.
Деление дробей и смешанных чисел. Примерно 6-класс (11-12 лет)
Главное замечание по теме от проекта dpva.ru: Дети часто путают действия с правильыми дробями (это такие дроби, где числитель меньше знаменателя) и со смешанными числами (состоящими из целой и дробной части).
Умножение правильных дробей и смешанных чисел на натуральное число: Чтобы умножить правильную дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения. Для того, чтобы умножить смешанное число на натуральное число, можно смешанное число предстваить в виде неправильной дроби, а затем ее числитель умножить на это число, а знаменатель оставить без изменения, после чего выделить целую часть.
Умножение дробей : Чтобы умножить дробь на дробь, надо 1) найти произведение числителей и произведение знаменателей этих дробей. 2) первое произведение записать числителем, второе — знаменателем.
Умножение смешанных чисел: Для того, чтобы выплнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Деление правильных дробей и смешанных чисел на натуральное число: Чтобы разделить правильную дробь на натуральное число, надо ее знаменатель умножить на это число, а числитель оставить без изменения. Для того, чтобы разделить смешанное число на натуральное число, можно смешанное число предстваить в виде неправильной дроби, а затем ее знаменатель умножить на это число, а числитель оставить без изменения, после чего выделить целую часть.
Памятка: Взаимно обратные числа это числа, произведение которых равно 1. Например: дроби 71/17 и 17/71 взаимно обратны. Делимое — то, что делят. Делитель — то, на что делят.
Деление дробей: Для того, чтобы разделить одну дробь на другую, надо делимое умножить на число обратное делителю.
Деление смешанных чисел: Для того, чтобы выполнить деление смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом деления дробей.
Умножение и деление десятичных дробей
С десятичными дробями намного проще производить разные действия, чем с обычными, но здесь также есть свои недостатки. Например, необходимо очень тщательно следить за положением десятичной запятой.
Например, рассмотрим пример умножения: 0,2х0,2.
Вы можете попробовать решить этот пример по аналогии со сложением: 2+2=4, также 2×2=4, тогда, поскольку 0,2+0,2=0,4. Возможно, и 0,2х0,2=0,4? Нет, этого не может быть, и я сейчас докажу вам это.
Перейдем обратно к обыкновенным дробям, с которыми мы научились так хорошо обращаться: $0,2=\frac{2}{10}$. Теперь перемножим дроби по старой методике: $\frac{2}{10} \times \frac{2}{10}=\frac{4}{100}$ (числитель умножаем на числитель, знаменатель на знаменатель). А в десятичных дробях — это 0,04. Следовательно, 0,2 х 0,2 отнюдь не равно 0,4. 0,2х0,2=0,04. Мы можем решить еще несколько примеров на умножение десятичных дробей, заменяя их на эквиваленты в обычных дробях. Например: 0,82х0,21=0,1772, а 0,82х2,1=1,772. (Это можно проверить следующим образом: $\frac{82}{100} \times \frac{21}{100}=\frac{1772}{10000}$, а $\frac{82}{100} \times \frac{21}{10}=\frac{1772}{1000}$.)
Теперь мы можем сформулировать общее правило:
При умножении десятичных дробей количество цифр справа от десятичной запятой в ответе равно общему количеству цифр справа от десятичной запятой в перемножаемых числах.
Так, при умножении 0,2х0,2 общее количество цифр справа от десятичной запятой в перемножаемых числах равно 2, и это означает, что 0,2х0,2=0,04 (ноль справа от десятичной запятой также является значащей цифрой).
Естественно, что если один из сомножителей является целым числом, то он не влияет на положение десятичной запятой.
Положение десятичной запятой в произведении будет таким же, как и в том сомножителе, который является десятичной дробью.
То есть 0,2х2=0,4; 1,5х5=7,5; а 1,1х154=169,4.
Эти результаты соответствуют правилу умножения, и в любом случае количество цифр справа от десятичной запятой в ответе равно общему количеству цифр справа от десятичной запятой в перемножаемых числах.
Определить положение запятой в случае деления десятичных дробей можно по аналогичной методике, действуя в обратном порядке. Но обычно при делении процедуру стараются упростить и приводят делитель или знаменатель (если деление проводят с помощью обычных дробей) к виду целого числа, не содержащего значащих чисел справа после запятой.
Предположим, нам надо 1,82 разделить на 0,2. Это выражение можно записать как $\frac{1,82}{0,2}$. Не изменяя величины дроби, умножаем числитель и знаменатель на 10. Тогда 1,82х10 (в соответствии с правилом определения положения десятичного знака) равно 18,20, или 18,2, поскольку ноль, стоящий справа после последней значащей цифры, не изменяет величины числа и, следовательно, его можно опустить. Точно так же 0,2х10=2,0, или просто 2 (поскольку 2 плюс ноль десятых равно 2).
Следовательно, дробь можно записать как $\frac{18,2}{2}$ – и теперь знаменатель является целым числом, следовательно, при делении положение десятичного знака после запятой не меняется, так же как и в случае деления. Раз в числителе одна значащая цифра справа после запятой, то и результат должен иметь одну значащую цифру справа после запятой, то есть — $\frac{18,2}{2}=9,1$.
Освоив деление десятичных дробей, мы сможем переводить обычные дроби в десятичные. Предположим, нам нужно найти десятичный эквивалент для $\frac{1}{40}$. Мы можем представить эту дробь в виде $\frac{1,000}{40}$, а затем произвести деление. Поскольку мы делим на целое число, то положение десятичной запятой не меняется. Проведем деление:
Таким образом, мы показали, что десятичный эквивалент $\frac{1}{40}$ равен 0,025.
Это можно проверить, переведя 0,025 в обычную дробь: $0,025=\frac{2}{100}+\frac{5}{1000}$, или $\frac{20}{1000}+\frac{5}{1000}$, или $\frac{25}{1000}$, или если произвести деление, то получим $\frac{1}{40}$.
Ну, а если вы все-таки допустили ошибку при исчислении находясь заграницей, то что бы не выглядеть глупо в глазах иностранцев, обязательно надо исправится и извинится. Для тех, которые, как и я, не знаю, как извиниться по-английски, рекомендую почитать статью на сайте e-english.ru. Это значительно улучшит ваши познания и даст возможность не делать ошибок, хотя бы в этом.
Материалы по теме:
Поделиться с друзьями:
Загрузка…Умножение и деление дробей. Тест — тренажер 6 класс — Kid-mama
Умножение и деление обыкновенных дробей
Лимит времени: 0
0 из 20 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Информация
Выполните умножение или деление и введите ответ.
Сократите дробь, если это возможно. Неправильную дробь переведите в смешанное число, иначе будет засчитана ошибка.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- С ответом
- С отметкой о просмотре
Если вы не знаете, как умножать и делить обыкновенные дроби, читайте статью:
Тест можно использовать как тренажер, проходя его несколько раз.
Каждый раз задания выпадают разные.
Умножение дроби на целое число
Чтобы умножить дробь на целое число, помните, что умножение — это повторное сложение.
Пример 1:
Умножить 1 7 ⋅ 3 .
Запишите умножение в виде сложения. Добавлять 1 7 три раза.
1 7 ⋅ 3 знак равно 1 7 + 1 7 + 1 7
Теперь нам просто нужно добавить дроби с одинаковыми знаменателями.Знаменатели оставьте неизменными, а числители сложите.
знак равно ( 1 + 1 + 1 ) 7 знак равно 3 7
Пример 2:
Умножить 5 ⋅ 3 16 .
5 ⋅ 3 16 знак равно 3 16 + 3 16 + 3 16 + 3 16 + 3 16 знак равно 5 ⋅ 3 16 знак равно 15 16
Другой способ подумать об этом — переписать целое число в виде дроби со знаменателем 1 .
5 ⋅ 3 16 знак равно 5 1 ⋅ 3 16
Затем умножьте
числители
а также
знаменатели
, согласно обычным правилам для
умножение дробей
.
знак равно 5 ⋅ 3 1 ⋅ 16 знак равно 15 16
В некоторых случаях ваш ответ может быть больше, чем 1 , поэтому вы захотите переписать его как смешанное число .Возможно, вам также придется уменьшить фракцию чтобы получить его в простейшем виде.
Пример 3:
Умножить 1 4 ⋅ 10 .
1 4 ⋅ 10 знак равно 10 4
И числитель, и знаменатель имеют общий множитель: 2 . Разделите оба на 2 .
знак равно 5 2
Перепишите эту неправильную дробь как смешанное число.
знак равно 2 1 2
Рабочий лист умножения дробей с общими знаменателями
Ричард Вильялонundefined undefined / Getty Images
Обновлено 21 февраля 2019 г.
Рабочий лист № 1 (Ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 1
Каждый рабочий лист содержит множество дробей с общим (одинаковым) знаменателем.При умножении дробей просто умножьте числитель (верхнее число), затем умножьте знаменатель (нижнее число) и при необходимости уменьшите до наименьшего члена.
- Пример 1: 1/4 x 3/4 = 3/16 (1 x 3 вверху и 3 x 4 внизу) в этом примере дробь не может быть уменьшена дальше.
- Пример 2: 1/3 x 2/3 = 2/9 Это не может быть уменьшено дальше.
- Пример 3: 1/6 x 2/6 = 2/36 В этом случае дробь может быть дополнительно уменьшена.
Оба числа можно разделить на 2, что дает нам 1/18, что является сокращенным ответом.
Оба числа можно разделить на 2, что дает нам 1/18, что является сокращенным ответом.Подобные рабочие листы содержат упражнения для учащихся, чтобы улучшить их понимание.
Рабочий лист № 2 (ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 2
Умножение неправильных дробей, Рабочий лист № 3 (ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 3
Рабочий лист № 4 (ответы на 2-й странице PDF)
Д.РасселРаспечатать PDF: Рабочий лист № 4
Рабочий лист № 5 (Ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 5
Рабочий лист № 6 (ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 6
Рабочий лист № 7 (ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 7
Рабочий лист № 8 (ответы на 2-й странице PDF)
Д.РасселРаспечатать PDF-файл: Рабочий лист № 8
Рабочий лист № 9 (ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 9
Рабочий лист № 10 (Ответы на 2-й странице PDF)
Д. РасселРаспечатать PDF-файл: Рабочий лист № 10
Умножение и деление дробей, Урок 2
Mathscene — Умножение и деление дробей, Урок 2| 2006 Rasmus ehf | Фракции и | Печать |
Урок 2.
Умножение дробей и целых номера:
| Изменить целое число в фракция | |
Тогда
умножить. |
Только числитель умножается на целое числа.
Умножение дроби на дробь: (общий знаменатель не обязателен)
| Первый умножить числители | ||
| Тогда умножаем знаменатели | ||
2 2 = 1 | 2 1 = 2 | Вы можно упростить, прежде чем умножить, и мы можем отменить обычное коэффициент 2 |
| 2 4 = 8 | ||
Замена смешанных чисел на неправильные дроби:
Пример: Умножьте целое число (2) на знаменатель (3) и прибавляем к числителю (1)
| Вы так это 2 3 + 1 = 7 | |
| В знаменатель остается прежним. |
Смешанные числа заменены на неправильные дроби перед умножением.
| Изменить смешанные числа в неправильные дроби | |
| Look для исключения общих факторов | |
| ср может отбросить множитель 4 из | |
| Тогда упростить, чтобы получить правильный ответ |
Сначала изменяются смешанные числа на неправильные дроби, а затем упрощается.
Иногда переменные (буквы) используются.
Применяются те же правила: первый
уменьшить, а затем упростить.
На дроби
Чтобы разделить дроби, инвертируйте делитель (вторая дробь) и умножаем.
| инвертировать делитель (второй дробь) и умножаем | |
| Тогда упростить, исключив общие множители, умножить и упростить. |
Целые числа необходимо заменить на фракции.
| Изменить целое число в дробь | |
| инвертировать делитель (вторая дробь) и умножаем |
Смешанные числа необходимо заменить на неправильные дроби.
| Изменить смешать число в неправильную дробь | |
| инвертировать делитель (вторая дробь) и умножаем | |
| Затем продажа общие факторы и упростить |
Иногда алгебраические переменные использовал.
| инвертировать делитель (вторая дробь) и умножаем | |
| Тогда исключая общие факторы и упрощая |
Те же правила применяются для номеров и буквы.
Попробовать тест 2 на
Умножение и деление дробей.
Не забудьте использовать свой
Контрольный список.
| Параметр | Описание |
|---|---|
| Неправильное преобразование | Если дробь смешанная, отображаются шаги для преобразования в неправильную дробь. |
| Неправильная фракция | Если дробь смешанная, значения окончательной неправильной дроби. |
| Умножить | Показывает последний шаг умножения. |
| Ответ | Показывает решение. Обратите внимание, это решение не упрощено. |
| Наибольший общий делитель | Используется для упрощения ответа. Наибольшее или наибольшее целое число, которое разделит числитель и знаменатель без получения дроби. |
| Разделить на GCD | Показывает числитель и знаменатель, разделенные на НОД, чтобы уменьшить дробь. |
| Ответ (упрощенный) | Решение в правильном или неправильном формате. |
| Ответ (смешанный) | Если раствор является неправильной дробью, отображается преобразованная смешанная дробь. Смешанная фракция показывает дробь с целой частью в дополнение к оставшейся части фракции. |
Он принимает правильные, неправильные, смешанные дроби и целые числа. Если они существуют, решения и ответы представлены в упрощенном виде,
смешанные и целые форматы.Калькулятор дробей
Ниже приведены несколько калькуляторов дробей, способных выполнять сложение, вычитание, умножение, деление, упрощение и преобразование дробей в десятичные дроби.Поля над сплошной черной линией представляют числитель, а поля ниже — знаменатель.
Калькулятор смешанных чисел
Калькулятор упрощенных дробей
Калькулятор десятичных дробей в дроби
Калькулятор дробей в десятичную
Калькулятор дробей большого числа
Используйте этот калькулятор, если числители или знаменатели являются очень большими целыми числами.
В математике дробь — это число, которое представляет собой часть целого.Он состоит из числителя и знаменателя. В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих указанное целое. Например, в дроби
числитель равен 3, а знаменатель — 8. Более наглядный пример может включать пирог с 8 кусочками. 1 из этих 8 ломтиков будет составлять числитель дроби, а всего 8 ломтиков, составляющих весь пирог, будут знаменателем. Если бы человек съел 3 ломтика, оставшаяся часть пирога была бы такой, как показано на изображении справа.Обратите внимание, что знаменатель дроби не может быть 0, так как это сделает дробь неопределенной. Дроби могут подвергаться множеству различных операций, некоторые из которых упомянуты ниже.Дополнение:
В отличие от сложения и вычитания целых чисел, таких как 2 и 8, для этих операций с дробями требуется общий знаменатель. Один из методов нахождения общего знаменателя заключается в умножении числителей и знаменателей всех участвующих дробей на произведение знаменателей каждой дроби.Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.
Этот процесс можно использовать для любого количества фракций. Просто умножьте числители и знаменатели каждой дроби в задаче на произведение знаменателей всех остальных дробей (не включая соответствующий знаменатель) в задаче.
Альтернативный метод нахождения общего знаменателя состоит в том, чтобы определить наименьшее общее кратное (НОК) для знаменателей, а затем сложить или вычесть числители, как если бы это было целое число. Использование наименьшего общего кратного может быть более эффективным и, скорее всего, приведет к дроби в упрощенной форме.В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное этих трех чисел.
| Кратное 2: 2, 4, 6, 8 10, 12 |
| Кратное 4: 4, 8, 12 |
| Кратное 6: 6, 12 |
Первое общее кратное — 12, так что это наименьшее общее кратное. Чтобы выполнить задачу сложения (или вычитания), умножьте числители и знаменатели каждой дроби в задаче на любое значение, которое сделает знаменатели 12, а затем сложите числители.
вычитание:
Вычитание фракции по сути то же самое, что и сложение дроби. Для выполнения операции требуется общий знаменатель. Обратитесь к разделу добавления, а также к приведенным ниже уравнениям для пояснения.
Умножение:
Умножение дробей довольно просто. В отличие от сложения и вычитания, нет необходимости вычислять общий знаменатель для умножения дробей. Просто числители и знаменатели каждой дроби умножаются, и результат образует новый числитель и знаменатель.По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения.
Отдел:
Процесс деления дробей аналогичен процессу умножения дробей. Чтобы разделить дроби, дробь в числителе умножается на величину, обратную дроби в знаменателе. Число , обратное , равно
. Когда a является дробью, это, по сути, включает в себя замену числителя и знаменателя местами.Следовательно, величина, обратная дроби. Обратитесь к приведенным ниже уравнениям для пояснения.Упрощение:
Часто проще работать с упрощенными дробями. Таким образом, фракционные растворы обычно выражаются в их упрощенных формах.
, например, более громоздко, чем. Предоставленный калькулятор возвращает входные дроби как в неправильной форме дроби, так и в форме смешанных чисел. В обоих случаях дроби представлены в их низшей форме путем деления числителя и знаменателя на их наибольший общий множитель.Преобразование дробей в десятичные дроби:
Преобразование десятичных дробей в дроби выполняется просто. Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 1 , второй — 10 2 , третий — 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь
, что упрощается до, поскольку наибольший общий делитель между числителем и знаменателем равен 2.Точно так же дроби, знаменатели которых являются степенями 10 (или могут быть преобразованы в степени 10), могут быть переведены в десятичную форму, используя те же принципы. Возьмем, к примеру, дробь
. Чтобы преобразовать эту дробь в десятичную, сначала преобразуйте ее в дробь.Зная, что первый десятичный разряд представляет 10 -1 , можно преобразовать в 0,5. Если бы вместо этого была дробь, десятичная дробь была бы 0,05 и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик.Преобразование общей инженерной дроби в десятичную дробь
В машиностроении дроби широко используются для описания размеров таких компонентов, как трубы и болты. Наиболее распространенные дробные и десятичные эквиваленты перечислены ниже.
| 64 th | 32 nd | 16 th | 8 th | 4 th | 2 nd | 905 902 (десятичное) 905(десятичное) | ||||||||||||||||||||||||||||||||||||||||||||||
| 1/64 | 0,015625 | 0,396875 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 2/64 | 1/32 | 03125 | 0,79375 | |||||||||||||||||||||||||||||||||||||||||||||||||
| 3/64 | 0,046875 | 1,1 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 4/64 2/64 | 0,0625 | 1,5875 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 5/64 | 0,078125 | 1,984375 | 9015 9015 9015 9015 9015 9015 90150.09375 | 2.38125 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 7/64 | 0.109375 | 2.778125 | 8/64 | 9015 | 8/64 | 0,125 | 3,175 | |||||||||||||||||||||||||||||||||||||||||||||
| 9/64 | 0,140625 | 3,571855 | 3,571875 | 0.15625 | 3.96875 | |||||||||||||||||||||||||||||||||||||||||||||||
| 11/64 | 0.171875 | 4.365625 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,1875 | 4,7625 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| 13/64 | 0.203125 | 5,159375 | 9015/9015 9015 9015 9015 9015 9015 9015 9015 9015 90150.21875 | 5.55625 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 15/64 | 0,234375 | 5.953125 | 1/4 | 0,25 | 6,35 | |||||||||||||||||||||||||||||||||||||||||||||||
| 17/64 | 0,265625 | 9015 9015 9015 9015 9015 9015 9015 9015 90150.28125 | 7,14375 | |||||||||||||||||||||||||||||||||||||||||||||||||
| 19/64 | 0,296875 | 7,540625 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 20/64 10/64 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20/64 10/64 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20/64 10/64 | 90150,3125 | 7,9375 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 21/64 | 0,328125 | 8,334375 | 9015/9015 9015 9015 9015 9015 9015||||||||||||||||||||||||||||||||||||||||||||||||||
| 0.34375 | 8,73125 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| 23/64 | 0,359375 | 9.128125 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 24/50 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24/50 9015 | 0,375 | 9,525 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 25/64 | 0,3 | 9.9218875 | 9015 9.9218759.921875 | 0.40625 | 10.31875 | |||||||||||||||||||||||||||||||||||||||||||||||
| 27/64 | 0,421875 | 10.715625 | 10.715625 | |||||||||||||||||||||||||||||||||||||||||||||||||
| 1450 9015 9015 9015 9015 7/64 | 0,4375 | 11,1125 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 29/64 | 0,453125 | 9015 9015 9015 9015 9015 9015 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 0.46875 | 11. | |||||||||||||||||||||||||||||||||||||||||||||||||||
| 31/64 | 0,484375 | 12.303125 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 2/4 | 1/2 | 0,5 | 12,7 | |||||||||||||||||||||||||||||||||||||||||||||||||
| 33/64 | 0,515625 | 13166875 | 13166875 | 0.53125 | 13.49375 | |||||||||||||||||||||||||||||||||||||||||||||||
| 35/64 | 0,546875 | 13.8 | 36/64 9015 9015 9015 9015 | 0.5625 | 14.2875 | |||||||||||||||||||||||||||||||||||||||||||||||
| 37/64 | 0.578125 | 14.684375 | 9015 9015 9015 9015 9015 9015 90150.59375 | 15.08125 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 39/64 | 0.609375 | 15.478125 | 0,625 | 15.875 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 41/64 | 0,640625 | 16.2161875 9015 9015 9015 9015 9015 9015 9015 9015 9015 | 9015 50.65625 | 16.66875 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 43/64 | 0,671875 | 17,065625 | 17.065625 | |||||||||||||||||||||||||||||||||||||||||||||||||
| 44/64 9015 9015 | 0,6875 | 17,4625 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 45/64 | 0,703125 | 17.859375 | 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 9015 90150.71875 | 18.25625 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 47/64 | 0,734375 | 18.653125 | 48/64 | 90151250/64 | 3/4 | 0,75 | 19,05 | |||||||||||||||||||||||||||||||||||||||||||||
| 49/64 | 0,765625 | 9015 9015 9015 9015 9015 9015 9015 90150.78125 | 19.84375 | |||||||||||||||||||||||||||||||||||||||||||||||||
| 51/64 | 0,796875 | 20.240625 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 9015/64/64 9015 9015 9015 9016 52/64 9015 | 0,8125 | 20,6375 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 53/64 | 0,828125 | 21,034375 | 9015 545 90159015 545 905 | 0.84375 | 21,43125 | |||||||||||||||||||||||||||||||||||||||||||||||
| 55/64 | 0,859375 | 21,828125 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,875 | 22,225 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| 57/64 | 0,8 | 22.621875 9015 9015 9015 9015 9015 9015 | 0. | 23,01875 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 59/64 | 0,921875 | 23,415625 | 9015 9015 9015 9015 9015 9015 9015 901560/64 9015 9015 9015 9015 | 0,9375 | 23,8125 | |||||||||||||||||||||||||||||||||||||||||||||||
| 61/64 | 0,953125 | 24.2093151 9015 625 9015 625 9015 9015 9015 625 | 0.96875 | 24.60625 | ||||||||||||||||||||||||||||||||||||||||||||||||
| 63/64 | 0,984375 | 25,003125 | 64/64 | 9015 9015 | 64/64 9015 | 4/4 | 2/2 | 1 | 25,4 |
Как рассчитать дроби
Что такое дроби?
Дробное число или дробь используется для представления сегмента целого числа.
Дробь состоит из двух чисел, расположенных одно над другим. Первое число, которое находится над строкой, — это числитель . Второе число, расположенное под чертой, — это знаменатель .
Знаменатель указывает общее количество равных частей, на которые что-либо делится. Числитель показывает, сколько из этих равных частей необходимо учитывать.
Самый простой способ запомнить дроби — обозначить линию, разделяющую каждое число, «из».Таким образом, дробь, записанная как 3/5, просто относится к 3 частям из 5 равных частей.
Как можно представить дроби?
Дроби могут быть представлены тремя способами: как правильные дроби, неправильные дроби и смешанные дроби.
- Правильная дробь — это дробь, в которой числитель меньше знаменателя. Например, ⅔ (две трети) или ⅞ (семь восьмых).
- У неправильной дроби числитель больше знаменателя. Например, 8/5 (восемь пятых) или 13/4 (тринадцать четвертей).
- Смешанное число объединяет целое число и дробь. Например, 5¾ (пять и три четверти) или 12⅖ (двенадцать и две пятых).
Упрощение дробей
Процесс упрощения дробей сводит их к простейшей форме. Например, гораздо проще называть что-то ½, а не 4/8.
Есть два способа упростить дробь.
Первый метод — разделить верхнюю и нижнюю части дроби поровну на целые числа больше 1, пока вы не сможете продолжить.В качестве примера возьмем дробь 24/108:
- Разделите каждое число на 2, чтобы получить 12/54
- Разделите еще раз на 2, чтобы получить 6/27
- Разделите на 3, чтобы получить 2/9
Сложение дробей
Чтобы сложить дроби, вам нужно изменить их так, чтобы знаменатели (нижние числа) были одинаковыми. Затем вы суммируете числители.
Дополнение: Пример 1
Допустим, вы хотите добавить дробь ¼ к ¼.
Знаменатели уже те же, поэтому вы можете перейти ко второму шагу и прибавить 1 к 1.
Вторая половина дроби остается неизменной, поэтому сложение дробей ¼ и ¼ дает 2/4 (или ½).
Дополнение: Пример 2
Допустим, вы хотите сложить дроби ⅓ и ⅙.
Чтобы знаменатели совпали, измените ⅓ на 2/6.
Добавьте 1 к 2, чтобы получить 3, и поместите 6 ниже. Ответ — 3/6. Упростите это до ½.
Вычитание дробей
Вычитание дробей работает аналогично:
- Шаг 1. Убедитесь, что знаменатели совпадают.
- Шаг 2. Вычтите числители
- Шаг 3 — При необходимости упростите дробь
Вычитание: Пример 1
Допустим, вас попросили потренироваться ¾ — ¼
Первый шаг относительно прост, потому что числа совпадают.
Второй шаг включает в себя вычитание первых чисел и затем перенос ответа над тем же знаменателем.
Таким образом, ¾ — be будет обработано как 3-1 = 2
Следовательно, ответ будет 2/4, что составляет ½.
Умножение дробей
Умножение дробей относительно легко; вы просто умножаете верхние числа и нижние числа.
Если, например, вы умножите дроби ½ и ⅓, вы получите. От вас не ждут, что вы найдете общий знаменатель путем умножения.
На дроби
Чтобы разделить дроби, вам нужно перевернуть дробь, которую вы делите, вверх дном. Например, если вы хотите разделить ½ на, вы переписываете уравнение так, чтобы вторая дробь была 3/1. Затем умножьте ½ на 3/1, и у вас останется 3/2.
Может потребоваться дальнейшее уменьшение фракции для получения сложной фракции.
Распространенные ошибки и на что следует обращать внимание
При сложении и вычитании дробей может быть легко запутаться.Студенты часто складывают или вычитают знаменатели или числители двух дробей и обычно не замечают связи между знаменателем. Чтобы еще больше усугубить путаницу, к числителям и знаменателям следует подходить в расчетах как к целым числам, например, когда вам нужно умножить дробь.
Возьмем для примера сложение ¾ и ⅙.
Первое, что нужно сделать, это получить одинаковые знаменатели, поэтому мы умножаем их, чтобы получить 24.
Мы умножили знаменатель 4 на 6, чтобы получить 24, поэтому мы также умножаем числитель на 6, чтобы получить 18/24.
Мы умножили знаменатель 6 на 4, чтобы получить 24, поэтому мы также умножаем числитель на 4, чтобы получить 4/24.
Теперь мы можем просто добавить 18/24 к 4/24, чтобы получить 22/24, что упрощается до 11/12.
Прочие типичных ошибок включают:
- При сложении или вычитании дробей кандидаты могут забыть сначала преобразовать дроби, чтобы у них был общий знаменатель.
- Изменение знаменателя дроби без внесения необходимых изменений в числитель.
- Непонимание вопроса полностью; например, деление вместо вычитания или умножение вместо сложения.
- Знаменатель остается неизменным при ответах на вопросы, касающиеся умножения или сложения.
Понимание взаимосвязи между смешанными числами и неправильными дробями, а также того, как переводить одно в другое, имеет решающее значение при работе с дробями.
Дроби и десятичные дроби: умножение дробей и смешанных чисел Учебное пособие
Умножение дробей и смешанных чисел
Умножение дробей довольно просто по сравнению со сложением и вычитанием.И угадай что? Нам не нужно искать общий знаменатель. Мы, и , должны убедиться, что каждое число является дробной частью: смешанные числа или целые числа недопустимы. Это клуб элитной фракции.
Просто выполните следующие четыре простых шага:
- Преобразуйте все смешанные числа или целые числа в неправильные дроби.
- Умножьте числители.
- Умножьте знаменатели.
- Уменьшите окончательный ответ и при необходимости преобразуйте его обратно в смешанное число.
Пример умножения 1
| Умножьте числители, затем умножьте знаменатели. | |
| Уменьшить дробь. 12 и 72 имеют GCF 12, поэтому разделите верхнюю и нижнюю на 12. | |
| Стрела, вот и наш ответ. |
Пример умножения 2
Сокращение: перекрестное сокращение
Вместо уменьшения дроби в конце задачи мы можем перекрестно сократить перед умножением .Это не обязательно, но это сэкономит несколько шагов.
Перекрестное сокращение означает, что при умножении дробей мы можем уменьшить любой числитель с любым знаменателем . В этом примере 5 и 10 можно разделить на 5, даже если они не принадлежат к одной и той же дроби.
Давайте еще раз посмотрим на пример 1 и посмотрим, как использовать этот метод.