Из истории математических действий | Образовательная социальная сеть

Арифметика, или числительница.

Есть художество честное, независимое, всем удобопонятное, многополвзнейшее и многохвальнейшее. от древнейших же к новейших в разные вре мена явившихся наряднейших арифметиков изобретенное и изложенное.

Л. Ф. Магницкий

Сложение

Еще в древности люди научились считать предметы, называя число их по порядку: 1, 2, 3… Но сущность счета не только в том, чтобы называть по порядку числа, но и в присчиты вании, т. е. в прибавлении единицы к перво начальному числу, затем еще одной единицы,

затем еще одной и т. д. Овладе ние счетом требует умения при бавлять единицу к любому числу и к полученному от этого сложе ния числу снова прибавлять еди ницу и т. д.

Итак, сложение числа с едини цей возникло с появлением счета. В дальнейшем сложение двух чи сел выразилось в присчитывании к данному числу по одному всех единиц второго слагаемого. По наблюдайте, как складывают чи сла малыши. Например, чтобы прибавить к трем два, ребенок на одной руке оставляет незагнуты ми 3 пальца,

а на второй—2 паль ца и сначала считает три пальца (загибая каждый) на одной руке, а затем также присчитывает к ним по одному пальцы другой руки. Когда все пальцы загнуты — сло жение закончено. На следующем этапе обучения ребенок уже не пересчитывает единицы первого слагаемого, а сразу называет его и присчитывает к нему по одному все единицы второго слагаемого.

Сотни лет люди древнего мира выполняли сложение подобным же образом, присчитывая к пер вому данному множеству предме тов по одному предмету, взятому из второго множества, до тех пор, пока все предметы (члены) второ го множества не будут исчерпаны.

Длительное время сложение чисел люди выполняли только устно с помощью каких-либо предметов — пальцев, камешков, ракушек, бобов и пр., а позже на специальных приборах—счетной скамье, абаке, счетах.

Только после того как была изобретена позиционная система счисления и числа стали записы вать цифрами, подобно тому как это делаем мы, индийские мудре цы нашли способ сложения чисел в письменном виде.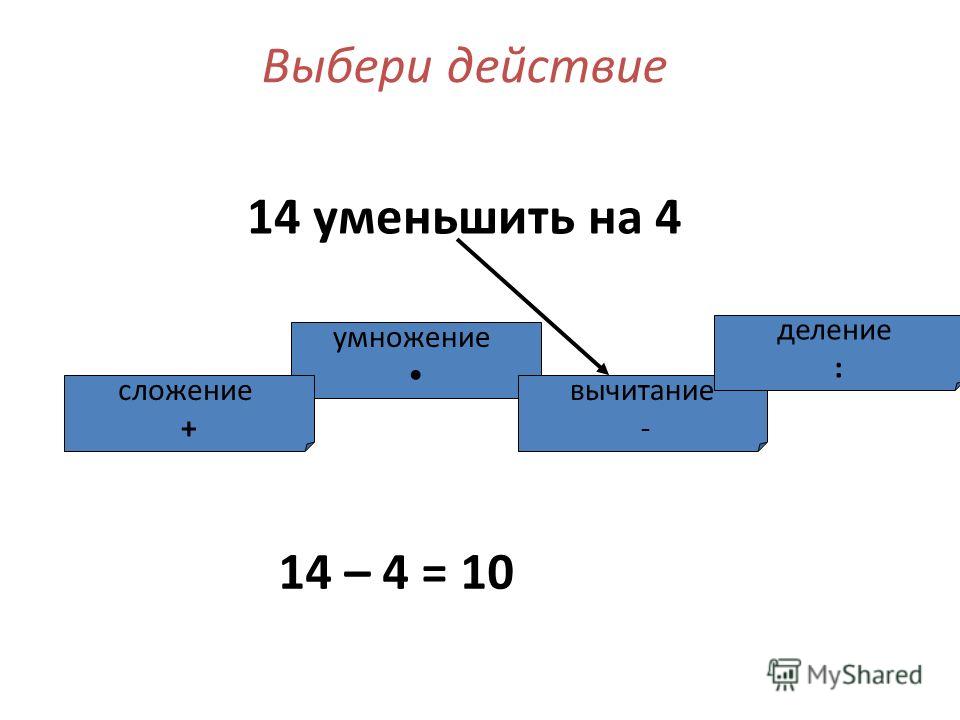 При вычисле ниях они записывали числа па лочкой на песке, насыпанном на специально приготовленную дос ку. Цифры, изображенные на пес ке, легко было стирать, а на их ме сте записывать другие. Вероятно, этим можно объяснить некоторые особенности индийского приема сложения чисел. мудре цы нашли способ сложения чисел в письменном виде. При вычисле ниях они записывали числа па лочкой на песке, насыпанном на специально приготовленную дос ку. Цифры, изображенные на пес ке, легко было стирать, а на их ме сте записывать другие. Вероятно, этим можно объяснить некоторые особенности индийского приема сложения чисел.

В Древней Индии было принято записывать слагаемые в стол бик — одно под другим; сумму же записывали над слагаемыми, сло жение начинали с наивысшего разряда, т. е. слева направо. Если записанная в сумме цифра при сложении последующего низшего разряда изменялась, то ранее за писанную цифру стирали, а на ее место вписывали новую.

Индийский прием сложения по заимствовали математики Сред него и Ближнего Востока, а от них в начале IX в. он перекочевал в Европу.

С XV в. способ письменного сло жения чисел принял современный вид,

л    л   т

                                                           2  +  3

В Древнем Египте знаком сложения служило схематическое изображение шагающих ног человека.

а до этого долгое время сла гаемые записывали одно подле другого без всякого знака между ними. В начале XV в. действие сложения стали обозначать на чальной буквой слова плюс (в ла тинском алфавите — Р), которое означало «сложить». К концу того же века отдельные математики стали обозначать сложение зна ком +, который вскоре получил всеобщее признание. Это быст рое признание нового знака прои зошло, видимо, потому, что его начертание напоминает сложе ние двух палочек.

Однако изобретение особых знаков для обозначения арифме тических действий нельзя полно стью приписывать только евро пейским математикам. Еще древние египтяне обозначали сложе ние особым знаком — рисунком шагающих ног.

Название слагаемое впервые встречается в работах математи ков XIII в. , а понятие «сумма» по лучило современное толкование только в XV в. До этого времени оно имело более широкий смысл — суммой называли результат лю бого из четырех арифметических действий.

Вычитание

В Древней Индии вычитание чи сел выполняли способом отсчитывания от уменьшаемого по од ному, пока не получится вычитаемое. Например, вычитая от девя ти пять, считали: «Девять без од ного — восемь, девять без двух — семь, девять без трех — шесть, девять без четырех — пять, де вять без пяти — четыре. Все еди ницы вычитаемого (пять) исчерпа ны, следовательно, 9-5 = 4».

   Второй способ вычитания (ав стрийский) состоит в прибавле нии к вычитаемому такого числа, которое в сумме с вычитаемым даст уменьшаемое. При таком способе, например, считали: «9 — 5: пять прибавить один — шесть, пять прибавить два — семь, пять прибавить три — во семь, пять прибавить четы ре — девять. Следовательно, 9-5 = 4, так как, прибавив к пя ти четыре, получаем уменьшае мое— девять».

Индийские математики выполняли   вычитание больших чисел способом, похожим на сложение. Они начинали вычитание с наи высших разрядов, причем те циф ры, от которых приходилось «за нимать» единицу, чтобы раздро бить ее в десяток низших разряд ных единиц, они стирали и запи сывали на место стертой новую, на единицу меньшую цифру. Для них это было удобно, так как в Ин дии черновые вычисления выпол няли на доске, посыпанной пес ком.

Индийский способ вычитания переняли арабы. Но они не стира ли цифры, а перечеркивали их и надписывали новую цифру над перечеркнутой. Это было очень неудобно. Тогда арабские мате матики, используя тот же прием вычитания, стали начинать дей ствие с низших разрядов, т. е. раз работали новый способ вычита ния, сходный с современным.

Для обозначения вычитания в III в. до н. э. в Греции использова ли перевернутую греческую букву пси (Ф). Итальянские математики пользовались для обозначения вычитания буквой М (ц), началь ной в слове минус. В XVI в. для обозначения вычитания стали применять знак -. Вероятно, этот знак перешел в математику из торговли. Торговцы, отливая для продажи вино из бочек, черточ кой мелом обозначали число мер проданного из бочки вина. Чтобы отличать знак минус от тире, Л. Ф. Магницкий (XVIII в.) обозна чал вычитание знаком +.

Индийский способ вычитания переняли арабы. Но они не стира ли цифры, а перечеркивали их и надписывали новую цифру над перечеркнутой. Это было очень неудобно. Тогда арабские мате матики, используя тот же прием вычитания, стали начинать дей ствие с низших разрядов, т. е. раз работали новый способ вычита ния, сходный с современным.

Знак равенства (=)   впервые введен английским учителем ма тематики Р. Рикоррдом в XVI в. Он пояснял: «Никакие два предмета не могут в большей степени быть равны между собой, как две па раллельные линии». Но еще в еги петских папирусах встречается знак, который обозначал равен ство двух чисел, хотя этот знак совершенно не похож на знак =.

Названия уменьшаемое и вычи таемое появились в Европе толь ко в XVIII в. А слово разность вве дено на 250 лет раньше.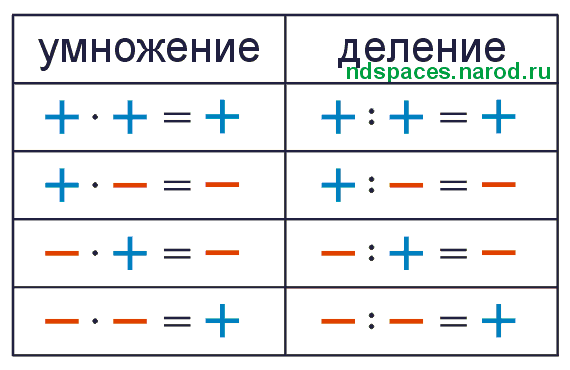

Умножение

Умножение — это особый (част ный) случай сложения несколь ких одинаковых чисел. В далекие времена люди учились умножать уже при счете предметов. Так, считая по порядку числа 17, 18, 19, 20, они должны были пред ставлять 20 не только как 10+10, но и как два десятка, т. е. 2 • 10, 30 — как три десятка, т. е. три раза повторить слагае мым десяток—3- 10 — и т. д.

Умножать люди начали значи тельно позже, чем складывать. Египтяне выполняли умножение посредством повторного сложе ния или последовательного уд воения. Например, чтобы умно жить 27 на 13, они составляли за пись, подобную следующей:

*1—27 (складывая 27 + 27 или удваивая 27 • 2, они получали 2— 54; сложение или удвоение повто ряли):

Ч—108 (и т. д.)

‘8—216 13    351

Из первого столбика вычисли тель выбирал те числа, которые в сумме составляли множитель (13), т. е. 1 + 4 + 8, и отмечал их условными значками (у нас эти чи сла отмечены звездочкой *). За тем удвоенные числа, стоящие против отмеченных звездочкой, складывали и получали произве дение. Этот прием (им пользова лись во многих местах, в том чи сле и в нашей стране) применялся на практике продолжительное время. Ему даже дали название «способ умножения, применя емый русскими крестьянами».

В Вавилоне при умножении чи сел пользовались специальными таблицами умножения — «пред ками» современных.

В Древней Индии применяли способ умножения чисел, тоже довольно близкий к современно му. Индийцы производили умно жение чисел начиная с высших разрядов. При этом они стирали те цифры, которые при последу ющих действиях надо было заме нять, так как к ним прибавляли число, ныне запоминаемое нами при умножении.

Таким образом, математики Ин дии сразу записывали произведе ние, выполняя промежуточные вычисления на песке или в уме.

Индийский прием умножения, напомню, перешел к арабам. Но арабы не стирали цифры, а пере черкивали их и надписывали но вую цифру над перечеркнутой.

В Европу индийский способ ум ножения пришел через арабов. Только в XV в. европейские мате матики отказались от перечерки вания неточных цифр и стали на чинать умножение с низших раз рядов. Европейскими математи ками было разработано около де сятка различных вариантов при ема умножения, например умно жение «решеткой» и др.

В Европе продолжительное время произведение называли сумма умножения. Название мно житель упоминается в работах VI в., а множимое — в XIII в.

В России впервые дал названия всем членам (компонентам) умно жения в начале XVIII в. Л. Ф. Маг ницкий — автор учебника «Ариф метика». В нем он указал:

34 — еличество      (количе ство),

2 ■— множитель,

68 — продукт, или произве дение.

Для обозначения действия ум ножения одни из европейских ма тематиков XVI в. употребляли букву М, которая была начальной в латинском слове, обозначав шем увеличение, умножение, — мультипликация (от этого слова произошло название «мульт фильм»). В XVII в. некоторые из математиков стали обозначать умножение косым крестиком — х, а иные употребляли для это го точку. В XVI—XVII вв. для обо значения   действий   применяли различные символы — едино образия в их употреблении не бы ло. Только в конце XVIII в. боль шинство математиков стали упо треблять в качестве знака умно жения точку, но допускали и упо требление косого креста. Знаки умножения (•, х) и знак равенства (=) стали общепризнанными бла годаря авторитету знаменитого немецкого математика Готфрида Вильгельма Лейбница (1646— 1716).

Деление

Два любых натуральных числа всегда можно сложить, а также умножить. Вычитание из нату рального числа можно выполнить лишь тогда, когда вычитаемое меньше уменьшаемого. Деление же без остатка выполнимо только для некоторых чисел, причем уз нать, делится ли одно число на другое, трудно. Помимо того, есть числа, которые вообще нельзя разделить ни на какое число, кро ме единицы. Делить на нуль нельзя. Эти особенности действия значительно усложнили путь к уяснению приемов деления.

В Древнем Египте деление чи сел выполняли способом удвое ния и медиации, т. е. делением на два с последующим сложением отобранных чисел. Например, чтобы разделить 60 на 12, египет ские математики поступали так: 60:12

1—12*

2 — 24

4 — 48*

8 — 96

(т. е. составляли табличку, в кото рой делитель (12) сначала удваи вали, затем учетверяли и т. д.). Из второго столбика отбирали чи сла, которые в сумме составляли делимое. Строки с этими числа ми — первую и третью (1 — 12 и 4 — 48, так как 12 + 48 = 60) отмеча ли особым значком (здесь они от мечены звездочкой). Отмечен ные числа складывали и получа ли ответ: 1 +4 = 5, так как 12 + 48 = 60. Следовательно, 60 :12 = 5.

А вот более сложный пример: 492:12

1        —12*

2        — 24
4 — 48
8 — 96*
16—192
32 — 384*

Поступаем так же, как в пер вом случае: так как
492 = 384 + 96 + 12,        то

492 : 12 = (32 + 8 + 1). Следова тельно, 492 : 12 = 41.

Математики Индии изобрели способ «деление вверх». Они за писывали делитель под делимым, а все промежуточные вычисле ния — вверху над делимым. При чем те цифры, которые при про межуточных вычислениях подвер гались изменению, индийцы стира ли и на их место писали новые.

Позаимствовав этот способ, арабы в промежуточных вычисле ниях стали цифры перечеркивать и надписывать над ними другие. Такое нововведение значительно усложнило «деление вверх». За пись деления получалась очень громоздкой и для многих непонятной (поэтому мы его здесь не при водим). Даже знающие люди до пускали при таком способе деле ния ошибки. Однако европейские математики восприняли способ деления от арабов и пользова лись им до XVIII в. Вот почему сре ди итальянских поговорок сохра нилась: «Трудная вещь — деле ние», а человек, усвоивший в то время деление, получал звание «доктора абака».

Способ деления, близкий к сов ременному, впервые появился в итальянской рукописи 1460 г. Этот способ отличался от совре менного лишь тем, что остаток при вычитании частичного произ ведения делителя на отдельные разряды частного записывался дважды. Вот, например, как дели ли числа в XV—XVII вв.

6912:27

делимое 6912 256 частное

делитель27 (27-2; 69-54= 15,

сносим 1, будет 151)

151

делитель27 (27-5; 151-135=16

и снесли 2)

162

делитель 27 (27-6=162.

Остатка нет)

Примечание: подчеркнутые циф ры записывали в частное, словесные по яснения и вычисления в скобках приведе ны для ясности; все приведенные вычи сления выполняли в уме.

Потребовалось около трех ве ков, чтобы указанный способ де ления был окончательно усовер шенствован и в современном виде принят всеми математиками мира

Попыток усовершенствовать деление было сделано немало, и поэтому приемов деления суще ствовало около десятка.

На протяжении тысячелетий действие деления не обозначали каким-либо знаком — его просто называли и записывали словом. Индийские математики первыми стали обозначать деление на чальной буквой из названия этого действия. Арабы ввели для обо значения деления черту. Черту для обозначения деления от ара бов перенял в XIII в. итальянский математик Фибоначчи. Он же впервые употребил термин част ное.

Знак двоеточия (:) для обозна чения деления вошел в употреб ление в конце XVII в. До этого у не которых математиков встречался знак -5-, которым они обозначали это действие.

Результат деления в продол жение нескольких столетий назы вали сумма. В России названия делимое., делитель, частное впер вые ввел Л. Ф. Магницкий в нача ле XVIII в. Он в своей книге «Арифметика» привел два спосо ба деления — «деление вверх» и второй способ, близкий к совре менному

Сложение, вычитание, умножение и деление обыкновенных дробей

Тема: Сложение, вычитание, умножение и деление обыкновенных дробей.

(Урок по математике в 6 классе)

Тип урока:урок – повторения и закрепления ЗУН.

Цели урока:

— отрабатывать умения складывать, вычитать, умножать, делить дроби, решения простейших задач жизненной практики, способствовать умению рассуждать и логически мыслить, проверить ЗУН обучающихся по теме «Сложение и вычитание дробей с разными знаменателями», «Умножение и деление обыкновенных дробей»;

— способствовать воспитанию умения работать в парах и группах;

— способствовать развитию умения рассуждать и логически мыслить.

Задачи:

Способствовать овладению навыками критического и креативного мышления для генерации новых идей при решении задач динамично изменяющегося мира.

Оборудование: номера столов и участников, карточки с логическими задачами.

На уроке применяются элементы сингапурской методики обучения.

Ход урока:

Организационный момент.

ХАЙ ФАЙВ (СИГНАЛ ТИШИНЫ).

Учитель: Здравствуйте, садитесь. Сегодня мы проведём урок, применяя сингапурские структуры урока. Сообщение темы, цели, плана урока.

Повторение.

Цель: повторение изученного.

ФИНК-РАЙТ-РАУНД РОБИН (ПОДУМАЙТЕ – ЗАПИШИТЕ – ОБСУДИТЕ)

Учитель: Подумайте, запишите и обсудите в группах ответ на вопрос:

— Какие темы мы изучили в этом полугодии?

Запишите как можно больше тем и математических терминов, которые вы узнали в этом учебном году.

Время по 1 минуте каждому подумать и записать на листочках, обсудить по очереди и выслушать друг друга, записать новые идеи команды.

По команде учителя выслушать 2-3 учеников команды.

(Ответы: Делитель, Кратное, Сокращение дробей, Признаки делимости, НОД, НОК, Простые числа, Сравнение, сложение, вычитание, дробей с разными знаменателями, Сравнение, сложение, вычитание смешанных чисел, Умножение, деление дробей.)

Проверка домашнего задания.

Цель: повторение сложения, вычитания, умножения, деления дробей.

Учитель: Домашним заданием было записать на одной стороне листочка любой пример или вопрос, а на обратной стороне – ответ. КУИЗ – КУИЗ – ТРЕЙД (ОПРОСИ – ОПРОСИ – ОБМЕНЯЙСЯ КАРТОЧКАМИ).

Учитель: Ребята, вы будете проверять и обучать друг друга по пройденному материалу, используя карточки с вопросами и ответами.

Учитель: 1)Ребята, встаньте, задвиньте стулья, возьмите свои карточки, поднимите руку и найдите ближайшую пару.

2)Ученик А у которого день рождения ближе к 19 декабрю спрашивает ученика В (задаёт вопрос из своей карточки).

3)Ученик В отвечает.

4)Ученик А помогает и хвалит (подскажи, научи, переспроси, похвали).

5)Ученики меняются ролями (ученик В спрашивает ученика А).

6)Ученики меняются карточками и благодарят друг друга.

Можно повторить шаги 1-6 несколько раз.

Учитель: контролирует время процесса.

4. Математический диктант. (в тетрадях по вариантам, с последующей взаимопроверкой, чётные номера – 1 вариант, не чётные номера – 2 вариант)

Цель: проверить знания по сложению, вычитанию, умножению, делению дробей.

В-1

+

—

·

В — 2

+

—

·

 

Ответы записаны на обратной стороне доски.

Учитель: — Поменяйтесь тетрадями с партнёром по лицу, оцените работу партнёра.

5. Физминутка.— А теперь ребята встали,

Дружно руки вверх подняли,

В стороны, вперёд, назад,

Наклонились вправо, влево,

Тихо сели вновь за дело.

6. Домашнее задание Составить и записать по 2 примера на сложение вычитание, умножение, деление дробей.

7. Занимательные задачи.

Цель: способствовать развитию логического мышления.

Учитель: Раздаёт карточки с заданиями (или уже они на столе). Учащиеся каждый сам решают задачи. Через определённое время учитель проверяет ответы. ТЭЙК – ОФ – ТАЧ ДАУН ( ВСТАТЬ – СЕСТЬ) для получения информации о классе.

Учитель: Встаньте, пожалуйста, те, у кого ответ в первой задаче ответ = 4 . Спасибо, садитесь.

Встаньте, пожалуйста, те, у кого ответ во второй задаче ответ – одной девочке дали клетку с кроликом. Спасибо, садитесь.

Встаньте, пожалуйста, те, у кого ответ в третьей задаче ответ — всего 3 человека: сын, отец и дед . Спасибо, садитесь.

Встаньте, пожалуйста, те, у кого ответ в четвёртой задаче ответ = 2,3 . Спасибо, садитесь.

Встаньте, пожалуйста, те, у кого ответ в пятой задаче ответ = на 12 равных частей. Спасибо, садитесь.

Задачи:

1.В каждом из четырёх углов комнаты сидит кошка. Напротив каждой из этих кошек сидит кошка. Сколько всего в этой комнате кошек?

2.В клетке находится три кролика. Три девочки попросили дать им по одному кролику. Просьба девочек была удовлетворена, каждой из них дали кролика. И всё же в клетке остался один кролик. Как могло такое случиться?

3.Два отца и два сына разделили между собой три апельсина так, что каждому досталось по одному апельсину. Как такое могло случиться?

4.Какой знак надо поставить между 2 и 3, чтобы число стало больше 2, но меньше 3?

5. Как разрезать торт на части, чтобы его можно было разделить поровну как на трёх, так и на четырёх человек?

8. Рефлексия.

Учитель: Ребята, перед вами новогодняя ёлка и ёлочные украшения. Если вы сегодня получили удовольствие от урока, выберите яркую красную игрушку, если вам не понравился урок – тёмную, если вам было всё равно – зелёную. Нарядите нашу ёлку.

Отменить умножение (сложение) с делением (вычитание)

Отменить умножение (сложение) с делением (вычитание)

Свойства равенства, о которых упоминалось ранее, некоторыми учащихся, реализуется неправильно даже тогда, когда ситуация требует их использование. Например, при решении уравнения как

требуются два шага:

и

Обратите внимание, что в выражении порядок операций диктует, что умножение на 3 предшествует добавлению 7, и «отмены» этих процессов — вычитание 7 и деление на 3 — производилось в обратном порядке. Это не сказать, что мы не могли бы отменить вещи в другом порядке, но студенты, которые делают это, часто делают следующую ошибку. Деление на 3, они часто пренебрегают тем, что все термины с обеих сторон должны быть разделены на 3. Другими словами, после деления на 3 они записывать

Они слишком увлечены идеей, что будут вычитать 7 из обеим сторонам понять, что, разделив сначала на 3, это не 7, а , который нужно вычесть, давая тот же ответь как раньше. Здесь уместно еще одно замечание. Если круглые скобки появляются в уравнении, таком как

то порядок операций выгружается (вычитание внутри скобки стоят перед умножением на 3). При решении для , мы можем, конечно, распределить 3, тем самым исключив круглые скобки и сделать проблему похожей на последнюю обсуждалось. Требуется еще меньше шагов, если просто «отменить» умножение и вычитание в обратном порядке:

а потом

Теперь вернемся к уравнению

и исследуйте более красноречивые ошибки, которые дали названия UMD и UAS в этот раздел. Некоторый учащиеся осознают необходимость за два шага (подобно тем, которые выполнялись, когда это уравнение было рассмотрено выше) изолировать , но мало чувствовать для каких операций это будет достигнуто. За например, понимая, что, как и в правой части уравнение, является «не-» термином, учащийся может написать

недоразумение, что она вычла 7 слева стороны, но делится на 7 на Обратная сторона. Исходное уравнение и новое больше не имеют те же решения в результате. Тот же ученик может затем признать, что ей нужно переместить на другую сторону. Так как 3 умножается на , она должна «отменить» это на деля обе стороны на 3. Но она может (ошибочно) написать

разделив слева, но вычитая справа. Еще раз, решение отличается от того, которое решило исходное уравнение , а именно .

Еще хуже, когда ученик думает, что может решить за один шаг. (то есть позаботьтесь как об умножении на 3, так и о сложении из 7 за одну операцию). Такой студент может написать что-то вроде

Опять же, ответ, который получает этот студент, , это отличается чем правильный.

---

главных ошибок в алгебре, сделанных студентами, изучающими исчисление (полный документ)
Полный список кодов оценок

---

Томас Л. Скофилд 2003-09-04

3.1: Свойства сложения, вычитания, умножения и деления равенства

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

20035

• Келли Брукс
• Общественный колледж Восточных ворот

Свойства сложения, вычитания, умножения и деления равенства позволяют нам складывать, вычитать, умножать или делить одно и то же значение в обеих частях уравнения, это гарантирует, что уравнение остается верным (обратите внимание, мы не можем делить на ноль).

Концепция: Мы знаем, что это истинное утверждение: \(5=5\)

Утверждение останется верным, если мы проделаем одну и ту же операцию с обеих сторон уравнения.

• Добавьте 4 к обеим частям уравнения, чтобы получить: \[\begin{align*} 5+4 &=5+4 \\[4pt] 9 &=9 \end{align*}\]
• Вычтите 10 с обеих сторон исходного уравнения, чтобы получить: \[\begin{align*} 5-10&=5-10 \\ -5&=-5 \end{align*}\]
• Умножьте на 2 обе части исходного уравнения, чтобы получить: \[ \begin{align*} 5\cdot 2&=5\cdot 2 \\ 10&= 10 \end{align*} \]
• Разделите на 15 обе части исходного уравнения, чтобы получить: \[\begin{align*} \frac{5}{15}&= \frac{5}{15}\\ \frac{1}{3} &=\frac{1}{3} \end{align*}\]

Мы используем свойства равенства сложения, вычитания, умножения и деления для решения уравнений для указанной переменной или неизвестной.

Процесс решения основного линейного уравнения с одной переменной

• Изолировать переменную, «отменив» операцию над переменной, то есть применив противоположную операцию к обеим частям уравнения, используя свойства равенства

Пример \(\PageIndex{1}\)

Решить для x: \(x+2=9\)

Решение

Поскольку 2 добавляется к x, чтобы изолировать x, нам нужно «отменить» прибавление 2, противоположностью прибавления 2 является вычитание 2, поэтому, используя свойство равенства вычитания, давайте вычтем 2 из обеих частей уравнения, чтобы получить:

\[x+2-2=9-2 \]

\[x=7\]

Пример \(\PageIndex{2}\)

Решить для x: \(x-7=13\)

Решение

Так как 7 вычитается из х, чтобы изолировать х, нам нужно «отменить» вычитание 7, противоположность вычитанию 7 — это добавление 7, поэтому, используя свойство равенства сложения, давайте добавим 7 к обе части уравнения, чтобы получить:

\[x-7+7=13+7\]

\[x=20\]

Пример \(\PageIndex{3}\)

Решите для x: \(3x=12\)

Решение

Поскольку х умножается на 3, чтобы изолировать х, нам нужно «отменить» умножение на 3, противоположное умножению на 3 деление на 3, поэтому используя свойство равенства деления, давайте разделим на 3 обе части уравнения, чтобы получить:

\[\frac{3x}{3}=\frac{12}{3}\]

\[x=\frac{12}{3}=4\]

Пример \(\PageIndex{4 }\)

Решите для x: \(\frac{x}{8}=2\)

Решение

Поскольку x делится на 8, чтобы изолировать x, нам нужно «отменить» деление на 8. Противоположностью деления на 8 является умножение на 8, поэтому, используя свойство равенства умножения, давайте умножим на 8 обе части уравнения, чтобы получить:

\[\frac{x}{8}\cdot 8=2\cdot 8\]

\[\frac{x}{8}\cdot \frac{8}{1}=2\cdot 8\]

\[x=16\]

Пример \(\PageIndex{5}\)

Решите для x: \(\frac{1}{2}x=5\)

Решение

Мы можем подойти к этой задаче несколькими способами,

Вариант 1: прочитать задачу как x умножается на ½, поэтому мы можем разделить обе части на ½, чтобы изолировать переменную x.

\[\frac{\frac{1}{2}x}{\left(\frac{1}{2}\right)}=\frac{5}{\left(\frac{1}{2) }\справа)}\]

\[x=\frac{5}{\left(\frac{1}{2}\right)}=\frac{5}{1}\cdot \frac{2}{1}=\frac{ 10}{1}=10\]

Вариант 2. Перепишите задачу или представьте, что задача читается как деление x на 2, поскольку ½ \(x\) эквивалентно \(\frac{x {2}\), поэтому мы можем умножить обе части уравнения на 2, чтобы выделить \(x\):

\[\frac{1}{2}x=5\]

\[\frac{ x}{2}=5\]

\[\frac{x}{2}\cdot 2=5\cdot 2\]

\[x=10\]

Аналогично, если у нас есть доля раз переменная, скажем, x, тогда мы можем умножить обе части уравнения на обратную дробь (перевернуть дробь так, чтобы числитель стал знаменателем, а знаменатель стал числителем):

Пример \(\PageIndex{6}\)

Найти x: \(\frac{2}{3}x=7\)

Решение

\[\frac{2}{3} x=7\]

\[\boldsymbol{\frac{3}{2}}\cdot \frac{2}{3}x=\boldsymbol{\frac{3}{2}}\cdot 7\]

\[x=\frac{3}{2}\cdot \frac{7}{1}=\frac{21}{2}\]

Процесс решения линейного уравнения с одной переменной с несколькими операциями

При решении линейного уравнения с несколькими операциями мы меняем порядок операций, потому что мы «отменяем» исходные операции.

Пример:

1. Решите для x: \(2x+5=15\)

Порядок операций состояния для выполнения умножения, затем сложения, поэтому при решении мы изменим этот порядок, чтобы «отменить» сначала сложение, затем мы «отменяем» умножение

\[2x+5=15\нечисло \]

Шаг 1: «Отменить сложение на 5», вычитая 5 с обеих сторон уравнения

\[2x +5-\boldsymbol{5}=15-\boldsymbol{5} \без номера \]

\[2x=10\без номера \]

Шаг 2: «Отмените умножение на 2», разделив на 2 обе части уравнения

\[\frac{2x}{\boldsymbol{2}}=\frac{10}{\boldsymbol{2}} \nonumber \]

\[x=5 \nonumber \]

Мы можем проверить наш ответ, подставив значение x в исходное уравнение и убедившись, что уравнение верно: \(2\left(5\right) +5=10+5=15 \, ✓ \)

2. Найдите x: \(\frac{2}{3}x+\frac{1}{5}=\frac{2}{7 }\)

\[\frac{2}{3}x+\frac{1}{5}=\frac{2}{7}\nonumber \]

Шаг 1. Вычтите \(\frac{1}{5}\) из обеих частей уравнения

\[\frac{2}{3}x+\frac{1}{5}-\boldsymbol{\ frac{1}{5}}=\frac{2}{7}-\boldsymbol{\frac{1}{5}}\nonumber \]

\[\frac{2}{3}x=\frac {2}{7}-\frac{1}{5} \nonumber \]

Шаг 2: Найдите ЖК-дисплей для вычитания дробей с правой стороны:

\[\frac{2}{3}x= \frac{2}{7}\cdot \frac{5}{5}-\frac{1}{5}\cdot \frac{7}{7}\nonumber \]

\[\frac{2} {3}x=\frac{10}{35}-\frac{7}{35} \nonumber \]

\[\frac{2}{3}x=\frac{3}{35}\nonumber \]

Шаг 3. Умножьте обе части уравнения на обратную величину \(\frac{2}{3} \), что будет \(\frac{3}{2}\) :

\[\boldsymbol{\frac{3}{2}}\cdot \frac{2}{3}x=\boldsymbol{\ frac{3}{2}}\cdot \frac{3}{35}\nonumber \]

\[x=\frac{9}{70}\nonumber \]

Процесс решения линейных уравнений со скобками

Когда уравнение содержит круглые скобки, мы можем очистить круглые скобки, используя свойство дистрибутивности.

Распределительное свойство: \(a\left(b+c\right)=ab+ac\)

Примеры

1. Решите для m: \(5\left(m+3\right)-2\left (7-m\right)=12\)

Шаг 1: Примените распределительное свойство, чтобы убрать скобки:

\[5m+5\left(3\right)-2\left(7\right)-2 (-m)=12 \нечисло \]

\[5m+15-14+2m=12 \нечисло \]

Шаг 2: Объедините одинаковые члены

\[5m+2m+15-14+1=12 \nonumber \]

\[7m+1=12 \nonumber \]

Шаг 3: Изолируйте переменную, вычитая 1 с обеих сторон, затем разделив обе стороны на 7

\[7m+1-\boldsymbol{1}=12-\boldsymbol{1}\номер \]

\[7m=11\неномер \]

\[\frac{7m}{\boldsymbol{7 }}=\frac{11}{\boldsymbol{7}}\nonumber \]

\[m=\frac{11}{7}\nonumber \]

2.