Как называется арифметическое действие?

Как называется арифметическое действие?

Нахождение по нескольким данным числам одного нового числа называется арифметическим действием. В арифметике рассматривается шесть действий: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.

Какие бывают арифметические действия?

Основные арифметические действия

• Сложение Сложение – одна из основных операций, позволяющая объединить два слагаемых. …
• Вычитание Вычитание – действие, обратное сложению. …
• Умножение Умножение – арифметическое действие в виде краткой записи суммы одинаковых слагаемых. …
• Деление …
• Возведение в степень …
• Извлечение корня

Что такое знаки арифметических действий?

символические обозначения, при посредстве которых указываются арифметические действия над данными числами. Совокупность нескольких чисел, подлежащая в результате новому действию, заключается в «скобки», например (7—3+8), либо [7—3+8]. …

Какое арифметическое действие выполняется первым?

действия выполняются по порядку слева направо, причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Что первым идет деление или умножение?

Вывод: Если в выражениях только сложение и вычитание или умножение и деление, то действия выполняются по порядку слева направо. Выражения могут содержать сложение и вычитание, и умножение, и деление. В этом случае сначала выполняются деление и умножение по порядку. В математике эти действия считаются сильными.

Как умножать в столбик?

Умножение в столбик

1. Запишем числа столбиком (одно под другим). В верхней строчке — большее число, в нижней — меньшее. …
2. Сначала умножаем целиком верхнее число на последнюю цифру нижнего числа. Результат записывается под чертой под самой правой цифрой. …
3. Умножаем «2» на «6». …
4. Умножаем «4» на «6». …
5. Переходим к умножению числа «427» на «3».

Как складывать и вычитать целые числа?

Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила: Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.

Что такое сложить цифры?

Если кто-либо складывает цифры, то это означает, что этот человек прибавляет одно число к другому, производит операцию математического сложения. св. Сложить несколько трёхзначных чисел.

Как называется одно из чисел при сложении?

Слагаемые — это числа, единицы которых складываются. Например, в записи: 2 + 5, 2 — это первое слагаемое, 5 — второе слагаемое.

Как рассчитать разность?

Разность получается путем вычитания одного числа (вычитаемого) из другого (уменьшаемого). То есть, чтобы определить разность, нужно просто вычесть из большего числа меньшее.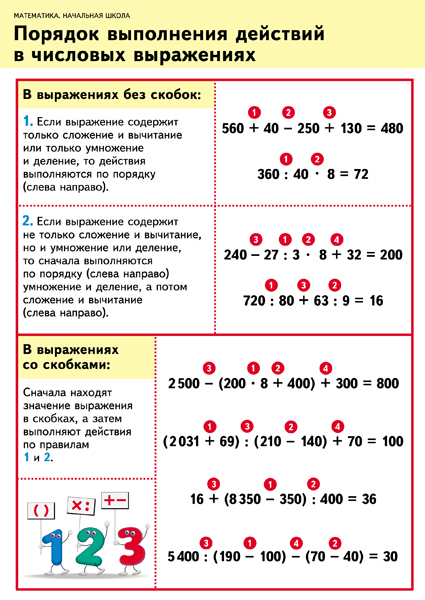 Например, числа 15 и 10.

Как связаны действия сложения и вычитания?

— Связаны ли между собой действия сложения и вычитания? Д. Да, связаны. — Арифметические действия сложения и вычитания дружат между собой, поэтому их называют взаимообратные.

Что такое сумма и разность чисел?

Вычитаемое – число, которое вычитают. Разность – результат вычитания. Слагаемое – число, которое складывают. Сумма – результат сложения.

Как найти сумму и разность?

Как обыкновенные числа. Чтобы найти сумму длин двух отрезков, нужно сложить длины этих отрезков. Чтобы найти разность длин двух отрезков, нужно из длины большего отрезка вычесть длину меньшего отрезка.

Выражения в 2 действия. Порядок выполнения действий, правила, примеры. Вставь пропущенное число — примеры со скобками. Тренажер

На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.

В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.

А в математике обязательно ли выполнять арифметические действия в определенном порядке?

Давайте проверим

Сравним выражения:
8-3+4 и 8-3+4

Видим, что оба выражения совершенно одинаковы.

Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий

В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.

Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.

Видим, что значения выражений получаются разные.

Сделаем вывод: порядок выполнения арифметических действий менять нельзя .

Узнаем правило выполнения арифметических действий в выражениях без скобок.

Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.

Потренируемся.

Рассмотрим выражение

В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .

Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий

Рассмотрим второе выражение

В этом выражении имеются только действия умножения и деления — это действия второй ступени.

Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий

В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Рассмотрим выражение.

Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.

Вычислим значение выражения.

18:2-2*3+12:3=9-6+4=3+4=7

В каком порядке выполняются арифметические действия, если в выражении имеются скобки?

Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.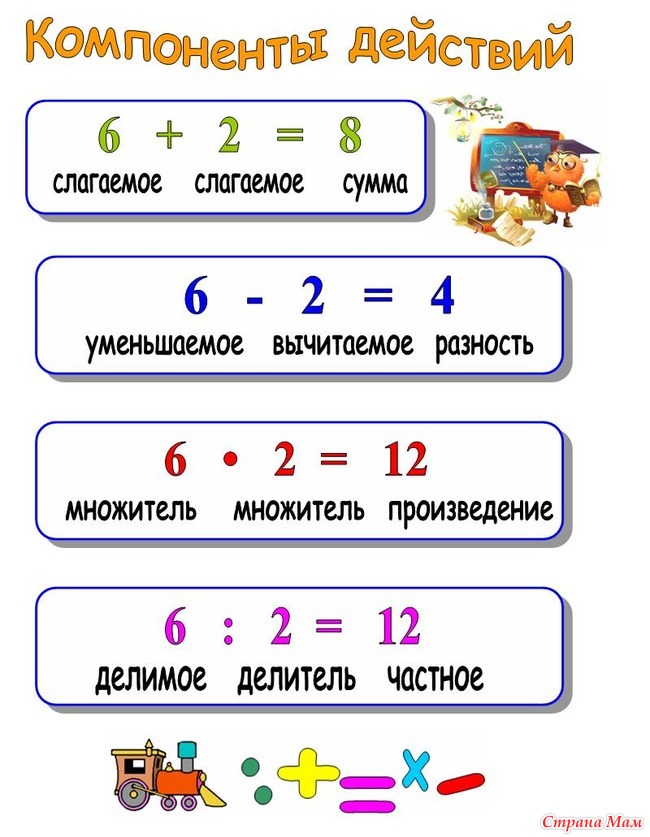

Рассмотрим выражение.

30 + 6 * (13 — 9)

Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.

30 + 6 * (13 — 9)

Вычислим значение выражения.

30+6*(13-9)=30+6*4=30+24=54

Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?

Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:

1. действия, записанные в скобках;

2. умножение и деление;

3. сложение и вычитание.

Схема поможет запомнить это несложное правило (рис. 4).

Рис. 4. Порядок действий

Потренируемся.

Рассмотрим выражения, установим порядок действий и выполним вычисления.

43 — (20 — 7) +15

32 + 9 * (19 — 16)

Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.

2*9-18:3=18-6=12

Узнаем, правильно ли определен порядок действий в следующих выражениях.

37 + 9 — 6: 2 * 3 =

18: (11 — 5) + 47=

7 * 3 — (16 + 4)=

Рассуждаем так.

37 + 9 — 6: 2 * 3 =

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие — деление, второе — умножение. Третье действие должно быть сложение, четвертое — вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37

Продолжаем рассуждать.

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

18:(11-5)+47=18:6+47=3+47=50

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

7*3-(16+4)=7*3-20=21-20=1

Выполним задание.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого — вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.

1. Festival.1september.ru ().
2. Sosnovoborsk-soobchestva.ru ().
3. Openclass.ru ().

Домашнее задание

1. Определи порядок действий в данных выражениях. Найди значение выражений.

2. Определи, в каком выражении такой порядок выполнения действий:

1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.

3. Составь три выражения, в которых такой порядок выполнения действий:

1. умножение; 2. сложение; 3. вычитание

1. сложение; 2. вычитание; 3. сложение

1. умножение; 2. деление; 3. сложение

Найди значение этих выражений.

Сегодня мы поговорим о порядке выполнения математических действий . Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.

Итак, вспомним о том, что сначала вычисляются выражения в скобках

38 – (10 + 6) = 22 ;

1) в скобках: 10 + 6 = 16 ;

2) вычитание: 38 – 16 = 22 .

Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.

10 ÷ 2 × 4 = 20 ;

Порядок выполнения действий :

1) слева направо, сначала деление: 10 ÷ 2 = 5 ;

2) умножение: 5 × 4 = 20 ;

10 + 4 – 3 = 11 , т. е.:

1) 10 + 4 = 14 ;

2) 14 – 3 = 11 .

Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.

18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7

Порядок выполнения действий:

1) 18 ÷ 2 = 9 ;

2) 2 × 3 = 6 ;

3) 12 ÷ 3 = 4 ;

4) 9 – 6 = 3 ; т.е. слева направо – результат первого действия минус результат второго;

5) 3 + 4 = 7 ; т.е. результат четвертого действия плюс результат третьего;

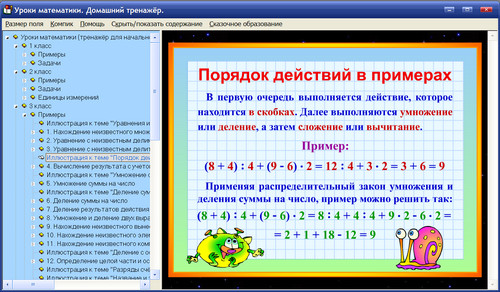
Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.

30 + 6 × (13 – 9) = 54 , т.е.:

1) выражение в скобках: 13 – 9 = 4 ;

2) умножение: 6 × 4 = 24 ;

3) сложение: 30 + 24 = 54 ;

Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются.

После этого приступать к вычислениям в следующем порядке:

1) действия, заключенные в скобках;

2) умножение и деление;

3) сложение и вычитание.

Если вы хотите получать анонсы наших статей подпишитесь на рассылку “ “.

Для правильного вычисления выражений, в которых нужно произвести более одного действия, нужно знать порядок выполнения арифметических действий. Арифметические действия в выражении без скобок условились выполнять в следующем порядке:

1. Если в выражении присутствует возведение в степень, то сначала выполняется это действие в порядке следования, т. е. слева направо.
2. Затем (при наличии в выражении) выполняются действия умножения и деления в порядке их следования.
3. Последними (при наличии в выражении) выполняются действия сложения и вычитания в порядке их следования.

В качестве примера рассмотрим следующее выражение:

Сначала необходимо выполнить возведение в степень (число 4 возвести в квадрат и число 2 в куб):

3 · 16 — 8: 2 + 20

Затем выполняются умножение и деление (3 умножить на 16 и 8 разделить на 2):

И в самом конце, выполняются вычитание и сложение (из 48 вычесть 4 и к результату прибавить 20):

48 — 4 + 20 = 44 + 20 = 64

Действия первой и второй ступени

Арифметические действия делятся на действия первой и второй ступени. Сложение и вычитание называются действиями первой ступени , умножение и деление — действиями второй ступени .

Если выражение содержит действия только одной ступени и в нём нет скобок, то действия выполняются в порядке их следования слева направо.

Пример 1.

15 + 17 — 20 + 8 — 12

Решение. Данное выражение содержит действия только одной ступени — первой (сложение и вычитание). Надо определить порядок действий и выполнить их.

Ответ: 42.

Если выражение содержит действия обеих ступеней, то первыми выполняются действия второй ступени, в порядке их следования (слева направо), а затем действия первой ступени.

Пример. Вычислить значение выражения:

24: 3 + 5 · 2 — 17

Решение. Данное выражение содержит четыре действия: два первой ступени и два второй. Определим порядок их выполнения: согласно правилу первым действием будет деление, вторым — умножение, третьим — сложение, а четвёртым — вычитание.

Теперь приступим к вычислению.

И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .

В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.

Навигация по странице.

Сначала умножение и деление, затем сложение и вычитание

В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :

• действия выполняются по порядку слева направо,
• причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.

Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.

Пример.

Выполните действия 7−3+6 .

Решение.

Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .

Кратко решение можно записать так: 7−3+6=4+6=10 .

Ответ:

7−3+6=10 .

Пример.

Укажите порядок выполнения действий в выражении 6:2·8:3 .

Решение.

Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.

Ответ:

Сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.

Пример.

Вычислите значение выражения 17−5·6:3−2+4:2 .

Решение.

Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .

Ответ:

17−5·6:3−2+4:2=7 .

На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .

Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.

Действия первой и второй ступени

В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.

Определение.

Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .

В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).

Порядок выполнения арифметических действий в выражениях со скобками

Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Пример.

Выполните указанные действия 5+(7−2·3)·(6−4):2 .

Решение.

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .

Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .

Ответ:

5+(7−2·3)·(6−4):2=6 .

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Пример.

Выполните действия в выражении 4+(3+1+4·(2+3)) .

Решение.

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .

Ответ:

4+(3+1+4·(2+3))=28 .

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .

Задание 192.

Выполни задания устно.

• 1) Найти сумму чисел 5 и 2. Вычесть эту сумму из числа 10.
• 2) К числу 8 прибавить разность чисел 9 и 3.

Решение:

• 1) 10 — (5 + 2) = 3
• 2) 8 + (9 — 3) = 14

Задание 193.

В рулоне было 15 м ткани. Первый покупатель приобрёл 5 м ткани, а второй 3 м. Сколько метров ткани осталось в рулоне?
Чтобы узнать, сколько метров ткани осталось в рулоне, продавец поступил так: вычислил, сколько всего метров ткани он продал, а потом полученное число вычел из 15.

15 — (5 + 3) = 7 (м)

Скобки обозначают, что сначала ну ясно найти сумму, а потом выполнить действие вычитания.

Задание 194.

Прочитай и вычисли.
От числа 12 отнять сумму чисел 7 и 2.

К числу 8 прибавить разность чисел 13 и 6.

Решение:

• 1) 12 — (7 + 2) = 3
• 2) 8 + (13 — 6) = 15

Задание 195.

На стоянке было 12 автомобилей. Сначала отъехало 4 автомобиля, а потом — ещё 3. Сколько автомобилей осталось на стоянке?

Решение:

• 1) 12 — (4 + 3) = 5
• Ответ: 5 автомобилей.

Задание 196.

У одной белки 9 орехов и столько же — у другой. Сколько всего орехов у белок?

Решение:

• 1) 9 + 9 = 18
• Ответ: 18 орехов.

Задание 197.

Прочитай и вычисли.

• 1) Из числа 14 вычесть разность чисел 7 и 2.
• 2) К числу 8 прибавить сумму чисел 3 и 6.

Решение:

• 1) 14 — (7 — 2) = 9
• 2) 8 + (3 + 6) = 17

Задание 198.

На стоянке было 13 грузовых автомобилей, а легковых на 8 меньше. Подъехало еще 6 легковых автомобилей. Сколько легковых автомобилей стало на стоянке?

Решение:

• 1) (13 — 8) + 6 = 11
• Ответ: 11 легковых автомобилей.

Задание 199.

Дополни и реши задачу.
В одном классе 7 компьютеров, а в другом на 2 компьютера… .

Решение:

В одном классе 7 компьютеров, а в другом на 2 компьютера меньше. Сколько компьютеров в 2 классах вместе.

• 1) 7 — 2 = 5
• 2) 7 + 5 = 12
• Выражение: (7 — 2) + 7 = 12
• Ответ: 12 компьютеров.

Задание 200.

Реши примеры.

Решение:

Решение:

Задание 202.

Из каждого примера на сложение составь два примера на вычитание.

9 + 7 = 16

14 — 6 = 8

Решение:

Задание 204.

Решение:

• 1) Сложить 9 и 7, равно 16. 9 плюс 7 равно 16. 9 увеличить на 7, равно 16. Сумма девяти и семи равна шестнадцати.
• 2) 14 вычесть 6 равно 8. 14 минус 6 равно 8. 14 уменьшить на 6 равно 8. Разность четырнадцати и шести равна восьми.

Задание 205.

Утром от коровы надоили 9 л молока, | а вечером — на 1 л меньше. | 3 л молока от вечернего удоя оставили, | а остальное продали. Сколько литров молока от вечернего удоя продали?
Прочитай всю задачу. Подумай, о чём в ней рассказывается.
Прочитай задачу по частям, на которые она разделена линиями.
Реши задачу.
План решения

• 1) Сколько литров молока надоили вечером?
• 2) Сколько литров молока от вечернего удоя продали?

Решение:

• 1) 9 — 1 = 8
• 2) 8 — 3 = 5
• Выражение: (9 — 1) — 3 = 5
• Ответ: 5 литров.

Задание 206.

В субботу отец и сын вместе обрезали 4 дерева. В воскресенье отец обрезал 3 дерева и столько же деревьев обрезал сын. Сколько всего деревьев они обрезали за 2 дня?

Решение:

• 1) 3 + 3 = 6
• 2) 4 + 6 = 10
• Выражение: 4 + 3 + 3 = 10
• Ответ: 10 деревьев.

Задание 207.

Реши примеры.

Решение:

14 — 6 — 6 = 2	7 + 5 + 1 = 13	16 — 8 + 1 = 9
14 — (6 — 6) = 14	7 + (5 + 1) = 13	16 — (8 + 1) = 7

Задание 208.

Составь задачу по рисунку и реши её.

Решение:

Под деревом лежало 12 яблок. Один ежик забрал 4 яблока, а другой еще 3. Сколько яблок осталось под деревом?

• 1) 4 + 3 = 7
• 2) 12 — 7 = 5
• Выражение: 12 — (4 + 3) = 5
• Ответ: 5 яблок.

Вы сначала делите или умножаете?

Порядок операций говорит вам сначала выполнить умножение и деление, работая слева направо, прежде чем выполнять сложение и вычитание. Продолжайте выполнять умножение и деление слева направо. Далее складываем и вычитаем слева направо.

Какие 3 правила алгебры?

Существует множество законов, определяющих порядок выполнения операций в арифметике и алгебре. Три наиболее широко обсуждаемых закона — это коммутативный, ассоциативный и распределительный законы. С годами люди обнаружили, что когда мы складываем или умножаем, порядок чисел не влияет на результат.

Каков порядок операций в математике?

Порядок операций — это правило, указывающее правильную последовательность шагов для вычисления математического выражения. Мы можем запомнить порядок, используя PEMDAS: скобки, экспоненты, умножение и деление (слева направо), сложение и вычитание (слева направо).

Каков правильный порядок операций?

Что это означает в Порядке операций \

Как узнать, когда умножать и когда делить, чтобы преобразовать единицы измерения написать три-четыре предложения?

Основное правило: если вам нужно преобразовать большую единицу в меньшую, умножьте . Если вам нужно преобразовать меньшую единицу в большую, разделите . Вы уменьшите число, а, как вы уже знаете, деление — это уменьшение числа.

Когда у вас есть выбор умножения или деления, что вы должны сделать в первую очередь?

При упрощении выражения, такого как 12 ÷ 4 + 5 x 3 — 6, вы должны сначала вычислить 12 ÷ 4, поскольку порядок операций требует, чтобы вы начинали с левой стороны выражения и выполняли умножение или деление (в зависимости от того, что наступит раньше) перед сложением или вычитанием.

Всегда ли сначала идет умножение?

Порядок операций говорит вам сначала выполнить умножение и деление, работая слева направо, прежде чем выполнять сложение и вычитание. Продолжайте выполнять умножение и деление слева направо. Далее складываем и вычитаем слева направо. … Сначала умножьте .

Каковы правила умножения и деления научных обозначений?

Поскольку все числа в экспоненциальном представлении имеют основание 10, мы всегда можем их умножать и делить. Чтобы умножить два числа в экспоненциальном представлении, умножьте их коэффициенты и сложите их степени. Чтобы разделить два числа в экспоненциальном представлении, разделите их коэффициенты и вычтите их степени.

Вы умножаете перед сложением?

Порядок операций говорит вам сначала выполнить умножение и деление слева направо, прежде чем выполнять сложение и вычитание. Продолжайте выполнять умножение и деление слева направо. Далее складываем и вычитаем слева направо.

Что такое математическое правило?

Четыре основных математических правила: сложение, вычитание, умножение и деление.

Какое правило умножения и деления?

Поскольку деление является обратным умножению, правила деления такие же, как и правила умножения. Поэтому при умножении и делении положительных и отрицательных чисел помните следующее: если знаки одинаковые, ответ положительный, если знаки разные, ответ отрицательный.

GEMDAS Порядок операций

GEMDAS — это правило, которое можно использовать для упрощения или вычисления сложных числовых выражений с помощью более чем одной двоичной операции.