Математика — Центр дополнительного образования

01.01.2001

Умножение на 9, 11, 99, 101

Проще всего умножать и делить числа на 10, 100 и т.д. При этом к множимому приписывается столько нулей, сколько их имеется в множителе. Отсюда получаем простое правило для умножения на 9, 11, 99, 101.

Чтобы умножить какое-нибудь число на 9, нужно увеличить его 10 раз и от полученного результата отнять само данное число. Но это правило не стоит применять, когда число записано с помощью единиц и нулей. В этом случае легче произвести умножение на 9 непосредственно.

Чтобы умножить какое-нибудь число на 11, нужно увеличить его в 10 раз и к полученному результату прибавить само это число.

Особенно просто умножение двузначного числа на 101. Нужно мысленно приписать справа к данному числу его само, и прочесть то, что получиться.

При умножении на 99 нужно, очевидно, увеличить данное число в 100 раз, и от полученного числа отнять само данное число.

Умножение на 2, 4

Умножение на 2 начинают со старших разрядов.

Умножение на 4 сводится к двукратному умножению на 2.

Умножение и деление на 5, 25, 50

Умножение на 5 сводится к делению пополам (надо умножить на 10 и результат разделить пополам).

Деление на 5 – это удвоение данного числа и последующее деление на 10.

При умножении на 25 мы умножаем на 100 и результат делим на 4.

При делении на 25 – умножаем на 4 (т. е. два раза на 2) и делим на 100.

При умножении на 50 умножаем на 100 и делим пополам; при делении на 50 сперва удваиваем, потом делим на 100.

Умножение на 3, 6 и 7

При умножении двузначного числа на 3, 6 или 7 сначала умножаем десятки, потом единицы, затем оба результата складываем.

86 x 3

80 x 3=240 6 x 3=18 86 x 3=258

35 x 7

30 x 7=210 5 x 7=35 35 x 7=245

Трёхзначное число умножается на 3 по такому же правилу: сначала умножаются сотни, потом десятки, потом единицы, затем всё складывается. Умножать по такому же правилу на 6 было бы невыгодно. Лучше сначала умножить на три, а затем результат удвоить.

519 x 6

519 x 3

500 x 3 = 1500 10 x 3 = 30 9 x 3 = 27 1557

1557 x 2 = 1500 x 2 + 57 x 2 = 3114

Умножение многозначных чисел на 7 требует особой тренировки.

Проценты

При вычислении процентов от некоторого числа удобно связывать проценты с представлением доли этого числа. Для некоторых процентов приведём таблицу соответствий.

% Доли 50 2 25 4 20 5

30 10 75 1 40 60 80

Умножение двузначных чисел, близких к 100

Покажем на примере:

93 x 98 = (93 — 2)	x 100 +	2 x 7 = 9114
|		|
дополнение до 100 для второго числа		произведение дополнений исходных чисел до 100

Обоснование этого способа дано ниже:

(100 — a) (100 — b) = (100 – а) x 100 – 100 x b + ab =
= 100 ((100 –

a) – b) + ab,

где а и b — дополнения первого и второго сомножителей до 100 соответственно.

Умножение чисел, близких к 1000

Покажем на примере:

987 x 996 = (987 – 4) x 1000 + 4 x 13 = 983052

Обоснование:

(1000 — a) (1000 — b) = (1000 – а) x 1000 – 1000 x b + ab =
= 1000 ((1000 – a) – b) + ab,

где а и b — дополнения первого и второго сомножителей до 1000 соответственно.

Информация к размышлению

Предложите способ для быстрого умножения и деления чисел на 125, для умножения на 2,5, на 0,75, на 1,25.

Корень квадратный в уме

Каким способом можно быстро извлечь корень квадратный из целого числа, имеющего в десятичной записи не более четырех знаков? Предполагается, что корень извлекается из данного числа нацело.

Найдите корни , . Попробуйте найти .

Алгоритм извлечения корня квадратного

Рассмотрим на примере .

Для нахождения произведем следующие действия:

1) десятичную запись числа 273529 разобьем на группы по две цифры, начиная справа;

2) для старшей группы, образующей число 27, подберем такую цифру, чтобы ее квадрат был наибольшим, но не превосходил числа 27; такой цифрой будет 5, ее запишем в качестве первой цифры ответа;

3) из старшей группы цифр вычтем найденный в предыдущем пункте квадрат первой цифры ответа и к полученной разности 27 – 25 = 2 припишем справа следующую группу цифр 35; получим число 235;

4) удвоив записанное в ответе число 5, припишем справа такую цифру, чтобы произведение полученного в результате числа на эту цифру было наибольшим, но не превосходило числа 235; такой цифрой будет 2 (ибо 102 x 2 = 204 < 235, но 103 x 3 = 309 > 235), ее и запишем в качестве второй цифры ответа;

5) из числа 235 вычтем найденное в предыдущем пункте произведение 204 и к остатку 31 снесем следующую группу цифр 29; получим число 3129;

6) удвоив записанное в ответе число 52, припишем справа такую цифру, чтобы произведение полученного в результате числа на эту цифру было наибольшим, но не превосходило числа 3129; такой цифрой будет 3 (ибо 1043 x 3 = 3129), ее и запишем в качестве третьей цифры ответа;

7) разность между снесенным числом 3129 и полученным в предыдущем пункте произведением равна 0, поэтому корень квадратный из числа 273529 извлекается нацело и равен записанному в ответе числу 523.

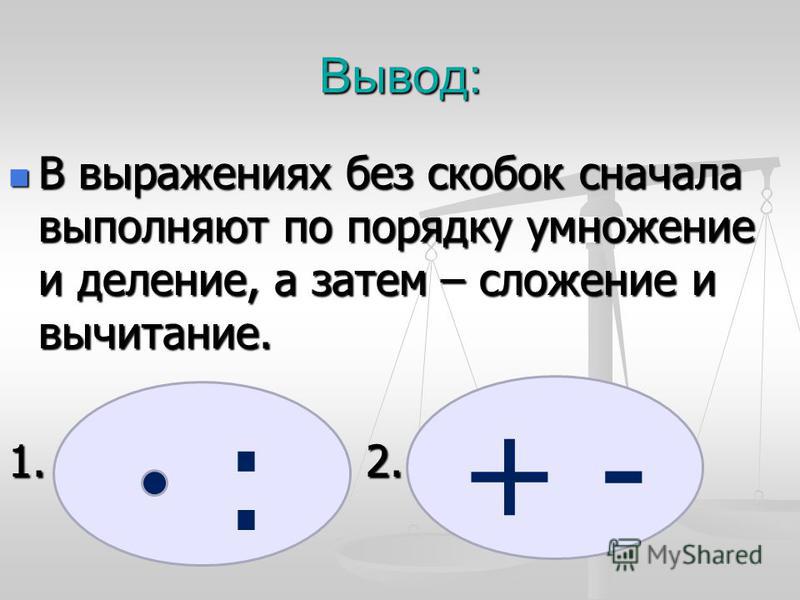
Применение порядка операций

ВведениеСложение и вычитаниеУмножение и делениеПорядок действийПорядок действий с группировкойСводка

В предыдущих классах вы научились складывать, вычитать, умножать и делить. Вы узнали, насколько важна математика и как она используется в повседневной жизни.

Ниже представлены примеры из повседневной математики. Нажмите на прямоугольник ниже, чтобы просмотреть выражение, представляющее повседневный опыт. Появится операция, связанная с термином, и пример.

В этом уроке вы увидите другие примеры того, как эти навыки используются в нашей повседневной жизни, включая ведение банковского реестра. Вы также упростите выражения, используя порядок операций, и узнаете больше о том, почему используется порядок операций.

Несмотря на то, что навыки сложения и вычитания приобретаются в раннем возрасте, они используются на протяжении всей жизни. Давайте посмотрим на банковские регистры, которые клиенты банка используют для отслеживания суммы денег на своем банковском счете.

• Банковский реестр — это таблица, которую банк обычно предоставляет при открытии счета. Он используется для записи всех транзакций и отслеживания текущего баланса счета.

• Транзакция может быть депозитом или снятием средств.
• Депозит — это когда клиент банка вносит больше денег на свой счет, например, внося зарплатный чек.
• Снятие средств — это когда клиент банка снимает деньги со своего счета. Снятие средств может быть в форме чека, снятия наличных в банке или онлайн-оплаты счета.

Ниже приведен пример использования банковского реестра.

Саманта хочет накопить на новый компьютер. У нее есть сбережения \($\)10,00, поэтому она работает няней, чтобы заработать больше денег. Каждый раз, когда Саманта нянчится, она прибавляет свой заработок к своим предыдущим сбережениям.

 

На этой неделе Саманта трижды сидела с детьми. В первый день она получила \($\)25.00. На второй день она получила \($\)36,00, а на третий день она получила \($\)15,50.

Она должна платить своим родителям \($\)1,75 каждый раз, когда они возят ее на работу или обратно, поэтому Саманта вычитает свои транспортные расходы из своего заработка, чтобы получить текущий баланс сэкономленных денег.

Саманта решила внести информацию в банковский реестр. Таким образом, она может иметь точный текущий баланс своих сбережений.

Ниже приведен чековый регистр, который Саманта использует для отслеживания своего текущего баланса. Нажмите на стрелку, чтобы увидеть, как Саманта заполнила чековый регистр.

1. Как математические операции представлены в контрольном регистре?
2. Саманта платит своим родителям в конце месяца, но она использует чековый журнал, чтобы подсчитывать дневную сумму. Как она может определить общую сумму, которую она заплатит своим родителям в конце месяца?

 

В этом разделе вы познакомитесь с числовыми выражениями, включающими показатели степени и факторизацию простых чисел.

Источник: Clipboard/Lined Paper, algotruneman, Open Clipart

Используйте интерактив для просмотра и тренировки показателей степени и простой факторизации. Сопоставьте карточки с эквивалентными выражениями.

Используя информацию из интерактива, ответьте на следующие вопросы:

1. Какие пары чисел простые, а какие составные?
2. Объясните, почему при разложении простых чисел использовались показатели степени.

Практика

    A. Найдите простую факторизацию для каждого числа.
    B. Если возможно, запишите его в экспоненциальной записи.

1. 300
2. 195
3. 693
4. 357

В последних двух разделах вы рассмотрели сложение, вычитание, умножение и деление. В этом разделе вы заметите, что при упрощении выражений существует определенный математический порядок.

Чтобы начать эту часть урока, используйте калькулятор или приложение, чтобы упростить следующее выражение. Сделав это, продолжите урок и посмотрите, как другие ученики упростили выражение.

Мэтт и Джози упростили одно и то же выражение ниже и получили разные результаты. Сравните свое решение с их.

Знание того, как определить правильный ответ
Как видите, можно получить разные ответы, если у нас нет указаний, которым нужно следовать. Направления, используемые для упрощения выражений, называются порядком операций.

В приведенном выше примере в выражении были выполнены четыре операции: вычитание, умножение, сложение и деление. Как узнать, что делать первым? Мэтт начал слева и работал прямо справа. Джози начал размножаться первым. См. правильный порядок операций ниже.

Порядок операций был разработан, чтобы обеспечить последовательные направления для решения математических задач. По сути, начните с группировки, а затем выполните операцию от самой мощной до наименее мощной.

Еще раз посмотрите на работу Мэтта и Джози и ответьте на следующие вопросы.

1. Опишите, как они оба начинали и повлияли ли их первые шаги на их ответ.
2. Объясните, почему важно использовать порядок операций при решении задач.
3. Можно ли упростить выражение и получить тот же результат, не соблюдая порядок операций?

Практика

Упростите каждое приведенное ниже выражение, используя порядок операций.

1. 131 + 26 ÷ 2 − 16 × 6
2. 21 × 3 − 24 ÷ 8 − 8 × 5
3. 25 × 3 ÷ 5 + 15 × 4 ÷ 3 − 5 × 7

В предыдущем разделе вы использовали порядок операций для упрощения основных выражений. Теперь вы познакомитесь с другими способами запомнить порядок операций и попрактикуетесь в упрощении еще нескольких выражений.

 

 

Другим способом запомнить порядок операций является GEMA. Нажмите на каждую букву аббревиатуры, чтобы увидеть, что каждая буква обозначает.

Завершить упрощение выражения.

Практика

Упростите каждое приведенное ниже выражение, используя порядок операций.

1. 7 + ((9 + 3) × 6)
2. (5 ² + (8 ÷ 2 + 2 ² )) − 2 ²
3. (8 + 55 − 3) ÷ 5 + 4 ²

В этом уроке вы рассмотрели сложение и вычитание с десятичными числами путем балансировки контрольного регистра. Вы узнали, как использовать показатели степени и факторизацию простых чисел для представления целых чисел. Вы также применили порядок операций, чтобы упростить числовые выражения. 9b$$, где a — целое число, такое что $$1≤ |a| <10$$ и b тоже целое число.

Умножение: Чтобы умножить числа в экспоненциальном представлении, умножьте десятичные числа. Затем добавьте показатели степени числа 10. Поместите новую степень числа 10 с десятичной дробью в экспоненциальной форме. Если ваше десятичное число больше 10, подсчитайте, сколько раз десятичная дробь перемещается влево, и добавьте это число к показателю степени.

Раздел: Чтобы разделить числа в экспоненциальном представлении, сначала разделите десятичные числа. Затем вычтите показатели вашей степени 10. Поместите новую степень 10 с десятичной дробью в научной форме записи. Если полученное десятичное число меньше 1, переместите десятичную точку вправо и уменьшите показатель степени на количество знаков, на которые переместилась десятичная точка.