Деление в столбик ➗ примеры и правила, как научиться
Деление с остатком
Прежде чем перейти к делению в столбик на двузначные и трехзначные числа, давайте вспомним, что значит «разделить с остатком». Если кратко, это такое деление, в результате которого получается остаток меньше делителя:
Например, делим 19 на 5. Наибольшее число, которое делится на 5 до 19 — это 15. Проверяем: 5 × 3 = 15, 19 − 15 = 4. Ответ: 3 и остаток 4. Записываем так: 19 : 5 = 3 (4).
Еще пример: делим 29 на 6. Также определяем максимальное число, которое делится на 6 до 29. Подходит 24. Ответом будет 4 и остаток 5. А записываем: 29 : 6 = 4 (5).
Как правильно делить в столбик
Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который потом будет срабатывать автоматически.
Деление трехзначного числа на однозначное
Рассмотрим пример деления трехзначного числа на однозначное в столбик — 322 : 7. Для начала определимся с терминами:
Для начала определимся с терминами:
- 322 — делимое или то, что необходимо поделить;
- 7 — делитель или то, на что нужно поделить:
- частное — результат действия.
Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.
Шаг 2. Смотрим на делимое слева направо, находим первое неполное делимое — оно должно быть больше делителя или равно ему.
Для этого рассмотрим первую цифру делимого. Она меньше делимого: 3 < 7 — не подходит. Рассмотрим теперь две первые цифры делимого: 32 ﹥7. Подходит!
Теперь нужно определить, сколько раз наш делитель 7 содержится в числе 32. Выполним деление с остатком. В результате деления 32 на 7 получили неполное частное 4 и остаток 4.
Важно
Результат вычитания должен быть меньше делителя. Если это не так, значит, есть ошибка в расчетах. Нужно увеличить выбранное число и выполнить действие еще раз.
Шаг 3. Запишем следующую цифру делимого справа от остатка 4. Говорят «сносим двойку». Получим следующее делимое — 42.
Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем 6 к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.
Мы закончили решать пример и в результате получили целое число 46.
Деление трехзначного числа на двузначное с примерами
Теперь разберем случаи деления трехзначных чисел на двузначные для 3 класса. Будьте внимательны: мы перешли к самому сложному.
Пример №1.
Разделим трехзначное число 324 на двузначное 81.
Шаг 1. В этом случае 324 будет делимым, его нужно поместить в уголок слева. 81 — это делитель, его вписываем справа.
Шаг 2. Чтобы понять, как делить в столбик на двузначное число, сначала нужно найти то, которое сможем разделить на 81. 3 и 32 не подходят — они меньше делителя. Поэтому придется искать частное к изначальному делимому методом подбора. Умножаем в столбик 81: сначала на 2, потом на 3 и на 4. 81*4=324. Подходит!
3 и 32 не подходят — они меньше делителя. Поэтому придется искать частное к изначальному делимому методом подбора. Умножаем в столбик 81: сначала на 2, потом на 3 и на 4. 81*4=324. Подходит!
Шаг 3. Записываем 4 в столбик под делителем. Это и есть ответ.
Ответ: 324:81=4.
Пример №2.
Продолжим разбираться, как делить столбиком многозначные числа, на следующем примере. В этот раз разделим 368 на 92.
Шаг №1. Здесь трехзначное число 368 будет делимым, а двузначное 92 — делителем. Расставляем их в столбике по своим местам.
Шаг №2. Теперь мы должны понять, какое наибольшее число в составе делимого можно нацело поделить на 92. 3 и 36 не подходят, придется снова подбирать частное. Для этого возьмем десятки и поделим их: 36:9=4. Проверим, подходит ли это число — умножим 92 на 4 столбиком.
Шаг №4. Подошло! Вписываем 4 в окошко для частного в столбике.
Ответ: 368:92=4.
Как делить однозначные и многозначные числа в столбик с остатком
Как мы писали в начале, это такое же деление, только в результате получается неровное число. Теперь разберем те же примеры, только поделим в столбик.
Пример №1
Разделим двузначное число 19 на однозначное 5. В этом случае 19 будет делимым, а 5 — делителем.
Шаг 1. Рисуем уголок. Делимое 19 ставим слева, а делитель 5 — справа.
Шаг 2. Подбираем наибольшее число до 19, которое нацело делится на 5. Это 15. Проверяем, так ли это: 5*3=15. Теперь 3 можно записать в столбик под делителем, а 15 — под делимым.
Шаг 3. Вычитаем число, которое получили делением нацело, из делимого. 19-15=4. Это остаток.
Ответ: 19:5=3
Пример №2.
Разделим двузначное число 29 на однозначное 6. Теперь 29 будет делимым, а 6 — делителем.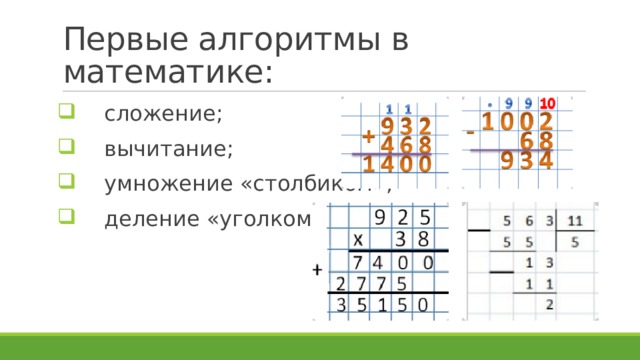
Шаг 1. Располагаем числа в столбике. Как обычно, 29 ставим на место делимого справа, а делитель 6 — слева от уголка.
Шаг 2. Теперь найдем число до 29, которое можно целиком разделить на 6. Проверим, подходит ли 24: 6*4=24. Записываем 24 под делимым 29, а 4 — в свободном отсеке снизу уголка. Это будет целая часть в результате деления.
Шаг 3. Вычитаем из делимого 29 число, которое мы получили в шаге 2. 29-24=5. Это остаток от деления.
Ответ: 29:9=4(5)
Примеры на деление в столбик для 3 класса
Давайте закрепим знания на практике. Ниже мы оставили примеры деления двузначных и трехзначных чисел для 3 класса. Решите их столбиком, а после проверьте полученные цифры — чур, не подглядывать! Обратите внимание: в сложном уровне есть деление многозначных чисел на двузначные, которые мы не разбирали в статье. Это задание со звездочкой.
Легкий уровень | Средний уровень | Сложный уровень |
27:3= 48:4= 56:8= 72:9= 95:5= | 270:15= 504:14= 315:5= 728:8= 855:9= | 1749:11= 1080:45= 3888:72= 5248:64= 4818:66= |
Ответы:
- легкий уровень: 9; 12; 7; 8; 19;
- средний уровень: 18; 36; 63; 91; 95;
- сложный уровень: 159; 24; 54; 82; 73.

Если вам интересно, как еще можно научить ребенка делить двузначные и трехзначные числа, приглашаем на вводный урок в Skysmart! На на онлайн-курсах по математике для детей можно закрепить тему «Деление в столбик» и разобраться в других разделах из школьной программы.
Умножение в столбик — как умножать в столбик в 3 и 4 класс
Основные понятия
Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.
Название числа напрямую зависит от количества знаков.
- Однозначное — состоит из одного знака.
- Двузначное — из двух.
- Трехзначное — из трех и так далее.
Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитывать с конца.
Разряд единиц — то, чем заканчивается любое число. Разряд десятков — то, что находится перед разрядом единиц. Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.
На место отсутствующего разряда всегда можно поставить ноль.
- Например, в числе 429 содержится 0 тысяч, 4 сотни, 2 десятка и 9 единиц.
Умножение — арифметическое действие, в котором участвуют два аргумента — множители. Результат их умножения называется произведением.
Свойства умножения
От перестановки множителей местами произведение не меняется.
- a × b = b × a
Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.
- a × b × c = (a × b) × c = a × (b × c)
Самое главное в процессе вычисления — это знание таблицы умножения. Это сделает подсчет упорядоченным и быстрым.
Важно помнить правило: умножение в столбик с нулями дает в результате ноль:
- а × 0 = 0, где а — любое натуральное число.
Алгоритм умножения в столбик
Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:
Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.
Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения. Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д.
Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.
Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.

После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.
Складываем то, что нашли и получаем ответ.
Умножение на однозначное число
Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика. Для вычисления воспользуемся последовательностью шагов, которую рассмотрели выше.
Возьмем пример 234 × 2:
Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.
Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.
Ответ запишем под чертой:
Производить действия необходимо в следующей последовательности:
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Умножение двух многозначных чисел
Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.
Рассмотрим пример 207 × 8063:
Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:
Последовательно перемножаем значения разрядов. Результатом является неполное произведение.
Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т. д. Результат запишем под чертой.
По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:
Далее складываем два произведения в столбик.
Получившееся семизначное число — результат умножения исходных натуральных чисел.
Ответ: 8 063 × 207 = 1 669 041.
Примеры на умножение в столбик
Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость. Не важно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем.
Умножение и деление чисел в Excel
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Еще…Меньше
Умножение и деление в Excel не представляют никаких сложностей: достаточно создать простую формулу. Не забывайте, что все формулы в Excel начинаются со знака равенства (=), а для их создания можно использовать строку формул.
Умножение чисел
Предположим, требуется определить количество бутылок воды, необходимое для конференции заказчиков (общее число участников × 4 дня × 3 бутылки в день) или сумму возмещения транспортных расходов по командировке (общее расстояние × 0,46). Существует несколько способов умножения чисел.
Умножение чисел в ячейке
Для выполнения этой задачи используйте арифметический оператор * (звездочка).
Например, при вводе в ячейку формулы =5*10 в ячейке будет отображен результат 50.
Умножение столбца чисел на константу
Предположим, необходимо умножить число в каждой из семи ячеек в столбце на число, которое содержится в другой ячейке. В данном примере множитель — число 3, расположенное в ячейке C2.
-
Введите =A2*$B$2 в новом столбце таблицы (в примере выше используется столбец D). Не забудьте ввести символ $ в формуле перед символами B и 2, а затем нажмите ввод.
Примечание: Использование символов $ указывает Excel, что ссылка на ячейку B2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку B2.
 Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения.
Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения. -
Перетащите формулу вниз в другие ячейки столбца.
Примечание: В Excel 2016 для Windows ячейки заполняются автоматически.
Перемножение чисел в разных ячейках с использованием формулы
Функцию PRODUCT можно использовать для умножения чисел, ячеек и диапазонов.
Функция ПРОИЗВЕД может содержать до 255 чисел или ссылок на ячейки в любых сочетаниях. Например, формула =ПРОИЗВЕДЕНИЕ(A2;A4:A15;12;E3:E5;150;G4;h5:J6) перемножает две отдельные ячейки (A2 и G4), два числа (12 и 150) и три диапазона (A4:A15, E3:E5 и h5:J6).
Деление чисел
Предположим, что вы хотите узнать, сколько человеко-часов потребовалось для завершения проекта (общее время проекта ÷ всего людей в проекте) или фактический километр на лилон для вашего последнего меж страны(общее количество километров ÷ лилонов). Деление чисел можно разделить несколькими способами.
Деление чисел в ячейке
Для этого воспользуйтесь арифметическим оператором / (косая черта).
Например, если ввести =10/5 в ячейке, в ячейке отобразится 2.
Важно: Не забудьте ввести в ячейку знак равно(=)перед цифрами и оператором /. в противном случае Excel интерпретирует то, что вы введите, как дату. Например, если ввести 30.07.2010, Excel может отобразить в ячейке 30-июл. Если ввести 36.12.36, Excel сначала преобразует это значение в 01. 12.1936 и отобразит в ячейке значение «1-дек».
12.1936 и отобразит в ячейке значение «1-дек».
Примечание: В Excel нет функции DIVIDE.
Деление чисел с помощью ссылок на ячейки
Вместо того чтобы вводить числа непосредственно в формулу, можно использовать ссылки на ячейки, такие как A2 и A3, для обозначения чисел, на которые нужно разделить или разделить числа.
Пример:
Чтобы этот пример проще было понять, скопируйте его на пустой лист.
Копирование примера
-
Создайте пустую книгу или лист.
org/ListItem»>
-
Нажмите клавиши CTRL+C.
-
Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.
-
Чтобы переключиться между просмотром результатов и просмотром формул, которые возвращают эти результаты, нажмите клавиши CTRL+’ (ударение) или на вкладке «Формулы» нажмите кнопку «Показать формулы».

Выделите пример в разделе справки.
Примечание: Не выделяйте заголовки строк или столбцов.
Выделение примера в справке
|
A |
B |
C |
|
|
1 |
Данные |
Формула |
Описание (результат) |
|
2 |
15000 |
=A2/A3 |
Деление 15000 на 12 (1250). |
|
3 |
12 |
Деление столбца чисел на константу
Предположим, вам нужно разделить каждую ячейку в столбце из семи чисел на число, которое содержится в другой ячейке. В этом примере число, на которые нужно разделить, составляет 3, содержалось в ячейке C2.
|
A |
B |
C |
|
|
1 |
Данные |
Формула |
Константа |
|
2 |
15000 |
=A2/$C$2 |
3 |
|
3 |
12 |
=A3/$C$2 |
|
|
4 |
48 |
=A4/$C$2 |
|
|
5 |
729 |
=A5/$C$2 |
|
|
6 |
1534 |
=A6/$C$2 |
|
|
7 |
288 |
=A7/$C$2 |
|
|
8 |
4306 |
=A8/$C$2 |
В ячейке B2 введите =A2/$C$2. Не забудьте в формуле включить символ $ перед символами C и 2.
Перетащите формулу в ячейке B2 вниз в другие ячейки в столбце B.
Примечание: Символ $ указывает Excel, что ссылка на ячейку C2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Если вы не использовали в формуле символы $ и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3/C3, которая не будет работать, так как в ячейке C3 нет значения.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Умножение столбца чисел на одно и то же число
Умножение на процентное значение
Создание таблицы умножения
Операторы вычислений и порядок операций
😃 Деление — правила, секретные примеры, упражнения, игры
Деление – одна из четырех основных математических операций (сложение, вычитание, умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
- Умножение и деление
- Деление числа на классы
- Деление натуральных чисел
- Примеры на деление
- Игры на развитие счета
- Развитие феноменального устного счета
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение. 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5.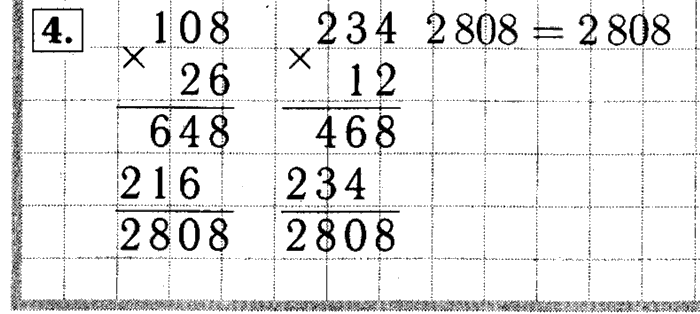 Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение. В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение. В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Записаться на курсПодробнее
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1. Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2. На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3. Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4. Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг. Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг. Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг. Ставим точку под делителем.
5 шаг. После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
Ставимвторую точку:
6 шаг. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг. Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг. Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг*. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3)(4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3)(4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Записаться на курсПодробнее
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Презентация на тему «Деление»
Примеры на деление
Легкий уровень
28:4=
16:8=
27:3=
32:8=
64:8=
54:6=
42:6=
49:7=
40:8=
Средний уровень
225:15=
512:8=
144:9=
312:6=
315:7=
625:25=
392:4=
984:8=
Сложный уровень
5712:68=
1035:23=
1121:59=
2352:49=
1610:35=
6300:75=
875:35=
297000:270=
385000:11=
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег. В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Играть сейчас
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Записаться на курсПодробнее
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Записаться на курсБесплатный урок
Развитие памяти и внимания у ребенка 5-10 лет
Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.
После прохождения курса ребенок сможет:
- В 2-5 раз лучше запоминать тексты, лица, цифры, слова
- Научится запоминать на более длительный срок
- Увеличится скорость воспоминания нужной информации
Записаться на курсПодробнее
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Записаться на курсПодробнее
Как улучшить память и развить внимание
Бесплатное практическое занятие от advance.
Записаться бесплатноПодробнее
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Записаться на курсПодробнее
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Записаться на курсПодробнее
Деление в столбик больших чисел примеры
Содержание
- 1 Правила записи при делении столбиком
- 2 Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
- 3 Деление столбиком многозначных натуральных чисел
- 3.0.0.1 Деление в столбик введение
- 3.0.0.2 Пример Разделить столбиком число 558 на 18.

- 3.0.0.3 Примеры деления чисел столбиком
- 3.0.0.4 Пример Выполните деление 1750 на 25.
- 3.0.0.5 Пример 2415 разделить на 23 столбиком.
- 3.0.0.6 Пример Разделить 5538 на 26.
- 4 Калькулятор деления столбиком
- 4.1 Ввод данных в калькулятор деления столбиком
- 4.2 Дополнительные возможности калькулятора деления столбиком
- 4.3 Инструкция использования калькулятором деления столбиком
Содержание
- Правила записи при делении столбиком
- Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
- Деление столбиком многозначных натуральных чисел
- Калькулятор деления столбиком
- Ввод данных в калькулятор деления столбиком
- Дополнительные возможности калькулятора деления столбиком
- Инструкция использования калькулятором деления столбиком
Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик). Также можно встретить название деление уголком. Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
Также можно встретить название деление уголком. Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Навигация по странице.
Правила записи при делении столбиком
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105 , а делителем – 5 5, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808 на 51 234 ( 614 808 – шестизначное число, 51 234 – пятизначное число, разница в количестве знаков в записях равна 6−5=1 ) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058 и 4 (здесь разница в количестве знаков равна 4−1=3 ). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Пусть нам нужно разделить столбиком 8 на 2 .
Конечно, мы можем выполнить деление при помощи таблицы умножения, и сразу записать ответ 8:2=4 .
Но нас интересует, как выполнить деление этих чисел столбиком.
Сначала записываем делимое 8 и делитель 2 так, как того требует метод:
Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0 , 1 , 2 , 3 , … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком). Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Поехали: 2·0=0 ; 2·1=2 ; 2·2=4 ; 2·3=6 ; 2·4=8 . Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4 . При этом запись примет следующий вид:
Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком. Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.
Читайте также: Бортовой компьютер гамма 115 инструкция
В нашем примере получаем
Теперь перед нами законченная запись деления столбиком числа 8 на 2 . Мы видим, что частное 8:2 равно 4 (и остаток равен 0 ).
Мы видим, что частное 8:2 равно 4 (и остаток равен 0 ).
Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.
Разделим столбиком 7 на 3 .
На начальном этапе запись выглядит так:
Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3 на 0 , 1 , 2 , 3 и т.д. до того момента, пока не получим число равное или большее, чем делимое 7 . Получаем 3·0=0 ; 3·1=3 ; 3·2=6 ; 3·3=9>7 (при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6 (оно получено на предпоследнем шаге), а на место неполного частного записываем число 2 (на него проводилось умножение на предпоследнем шаге).
Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7 и 3 будет завершено.
Таким образом, неполное частное равно 2 , и остаток равен 1 .
Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.
Сейчас мы разберем алгоритм деления столбиком. На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288 на однозначное натуральное число 4 . Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.
Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
Первой слева цифрой в записи делимого 140 288 является цифра 1 . Число 1 меньше, чем делитель 4 , поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14 , с которым нам и предстоит работать дальше. Выделяем это число в записи делимого.
Выделяем это число в записи делимого.
Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.
Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x ). Для этого последовательно умножаем делитель на 0 , 1 , 2 , 3 , … до того момента, пока не получим число x или число больше, чем x . Когда получается число x , то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4 пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге.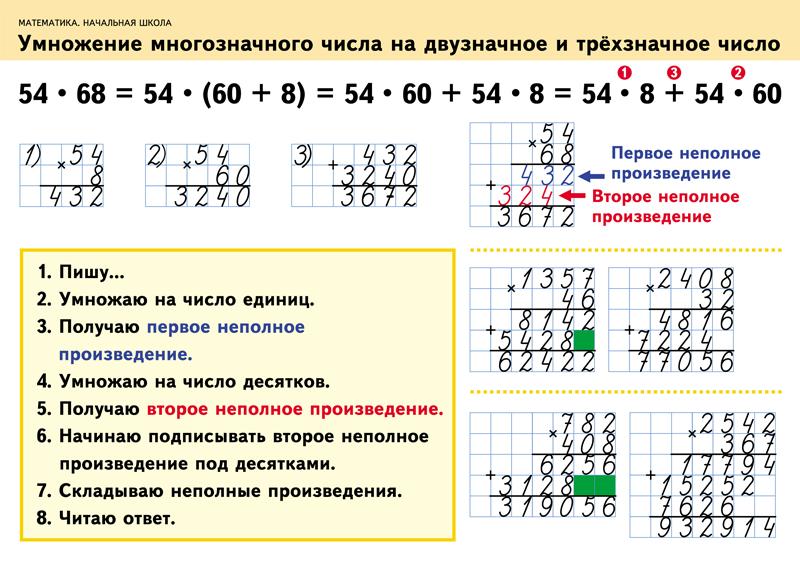 (Аналогичные действия мы проводили в двух примерах, разобранных выше).
(Аналогичные действия мы проводили в двух примерах, разобранных выше).
Умножаем делитель 4 на числа 0 , 1 , 2 , …, пока не получим число, которое равно 14 или больше 14 . Имеем 4·0=0 , 4·1=4 , 4·2=8 , 4·3=12 , 4·4=16>14 . Так как на последнем шаге мы получили число 16 , которое больше, чем 14 , то под выделенным числом записываем число 12 , которое получилось на предпоследнем шаге, а на место частного записываем число 3 , так как в предпоследнем пункте умножение проводилось именно на него.
На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.
Нам нужно вычесть столбиком из числа 14 число 12 (для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2 . Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2 меньше делителя 4 , то можно спокойно переходить к следующему пункту.
Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2 по 4 пункты алгоритма.
Читайте также: Для получения на компьютере звука служит
Под горизонтальной чертой справа от уже имеющейся там цифры 2 записываем цифру 0 , так как именно цифра 0 находится в записи делимого 140 288 в этом столбце. Таким образом, под горизонтальной чертой образуется число 20 .
Таким образом, под горизонтальной чертой образуется число 20 .
Это число 20 мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.
Умножаем делитель 4 на 0 , 1 , 2 , …, пока не получим число 20 или число, которое больше, чем 20 . Имеем 4·0=0 , 4·1=4 , 4·2=8 , 4·3=12 , 4·4=16 , 4·5=20 . Так как мы получили число, равное числу 20 , то записываем его под отмеченным числом, а на месте частного, справа от уже имеющегося там числа 3 записываем число 5 (на него производилось умножение).
Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).
Под горизонтальной линией справа от запомненного места записываем цифру 2 , так как именно она находится в записи делимого 140 288 в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2 .
Таким образом, под горизонтальной чертой мы имеем число 2 .
Число 2 принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4 пунктов алгоритма.
Умножаем делитель на 0 , 1 , 2 и так далее, и сравниваем получающиеся числа с отмеченным числом 2 . Имеем 4·0=0 , 4·1=4>2 . Следовательно, под отмеченным числом записываем число 0 (оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0 (на 0 мы проводили умножение на предпоследнем шаге).
Выполняем вычитание столбиком, получаем число 2 под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4 . Так как 2 , то можно спокойно двигаться дальше.
Под горизонтально чертой справа от числа 2 дописываем цифру 8 (так как она находится в этом столбце в записи делимого 140 288 ). Таким образом, под горизонтальной линией оказывается число 28 .
Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4 пунктов.
Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.
Осталось последний раз провести действия из пунктов 2 , 3 , 4 (предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288 и 4 в столбик:
Обратите внимание, что в самой нижней строчке записано число 0 . Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.
Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288 на однозначное натуральное число 4 , мы видим, что частным является число 35 072 , (а остаток от деления равен нулю, он находится в самой нижней строке).
Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.
Выполните деление в столбик, если делимое равно 7 136 , а делителем является однозначное натуральное число 9 .
На первом шаге алгоритма деления натуральных чисел столбиком мы получим запись вида
После выполнения действий из второго, третьего и четвертого пунктов алгоритма запись деления столбиком примет вид
Повторив цикл, будем иметь
Еще один проход дет нам законченную картину деления столбиком натуральных чисел 7 136 и 9
Таким образом, неполное частное равно 792 , а остаток от деления равен 8 .
7 136:9=792 (ост. 8) .
А этот пример демонстрирует, как должно выглядеть деление в столбик.
Разделите натуральное число 7 042 035 на однозначное натуральное число 7 .
Удобнее всего выполнить деление столбиком.
7 042 035:7=1 006 005 .
Деление столбиком многозначных натуральных чисел
Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел. Это действительно так, так как со 2 по 4 этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
Это действительно так, так как со 2 по 4 этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2 , 3 и 4 пункте алгоритма до получения конечного результата.
Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.
Читайте также: Блок питания дельта схема
Выполним деление столбиком многозначных натуральных чисел 5 562 и 206 .
Так как в записи делителя 206 участвуют 3 знака, то смотрим на первые 3 цифры слева в записи делимого 5 562 . Эти цифры соответствуют числу 556 . Так как 556 больше, чем делитель 206 , то число 556 принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Эти цифры соответствуют числу 556 . Так как 556 больше, чем делитель 206 , то число 556 принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Теперь умножаем делитель 206 на числа 0 , 1 , 2 , 3 , … до того момента, пока не получим число, которое либо равно 556 , либо больше, чем 556 . Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0 , 206·1=206 , 206·2=412 , 206·3=618>556 . Так как мы получили число, которое больше числа 556 , то под выделенным числом записываем число 412 (оно было получено на предпоследнем шаге), а на место частного записываем число 2 (так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:
Выполняем вычитание столбиком. Получаем разность 144 , это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.
Под горизонтальной линией справа от имеющегося там числа записываем цифру 2 , так как она находится в записи делимого 5 562 в этом столбце:
Теперь мы работаем с числом 1 442 , выделяем его, и проходим пункты со второго по четвертый еще раз.
Умножаем делитель 206 на 0 , 1 , 2 , 3 , … до получения числа 1 442 или числа, которое больше, чем 1 442 . Поехали: 206·0=0 , 206·1=206 , 206·2=412 , 206·3=618 , 206·4=824 , 206·5=1 030 , 206·6=1 236 , 206·7=1 442 . Таким образом, под отмеченным числом записываем 1 442 , а на месте частного правее уже имеющегося там числа записываем 7 :
Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:
Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:
Введите числа и калькулятор разделит числа столбиком и отобразит подробное решение.
Деление в столбик
введениеМетод деления столбиком, позволяет упростить деления чисел.
Рассмотрим как делить в столбик на примере нахождения частного двух чисел 6344 ÷ 61.
- 1 Запишем числа которые будем делить следующим образом: . Слева расположено делимое 6344, справа от черты делитель 61, ниже делителя будем записывать частное.
- 2 Найдем первую цифру частного, для этого сравниваем делитель 61 с числом состоящим из первый цифр делимого, пока не сформируем число большее или равное делителю. На первом шаге: 6 3 Добавляем следующую не использованную цифру равную 4 из делимого к 2, получаем 24 4 Добавляем следующую не использованную цифру равную 4 из делимого к 24, получаем 244 > 61, следовательно мы нашли третью цифру частного; записываем в частное 4=244 ÷ 61. Мы использовали все цифры и получили что число 61 делит на цело число 6344 а частное равно 104.
Ниже обозначены основные термины:
Пример Разделить столбиком число 558 на 18.

Примеры деления чисел столбиком
Пример деления многозначных чисел, частное которых содержит цифру ноль.
Пример Выполните деление 1750 на 25.
Рассмотрим подробнее как получили частное 70:
- Вычислим первую цифру частного, для этого найдем наименьшее целое делимое которое разделится на 25. Наименьшее целое делимое равно 175 = 25 × 7.
- Для вычисления первой цифры частного мы использовали 3 цифры делимого( 175 0), в добавок после нахождения первой цифры мы получили остаток равным нулю 175 — 175 = 0, следовательно для вычисления второй цифры частного мы должны использовать цифры числа начиная с 4 (175 0 ). Для вычисления 2 цифры частного остается только цифра 0, следовательно переносим 0 в частное.
Пример 2415 разделить на 23 столбиком.
Рассмотрим на примере как разделить числа столбиком.
Пример Разделить 5538 на 26.
В примере показано деление столбиком чисел 17714 на 34:
Этот онлайн калькулятор поможет вам понять как разделить целые числа и десятичные дроби столбиком. Калькулятор деления столбиком очень просто и быстро вычислит частное и выдаст подробное решение задачи.
Калькулятор деления столбиком очень просто и быстро вычислит частное и выдаст подробное решение задачи.
Калькулятор деления столбиком
Ввод данных в калькулятор деления столбиком
В онлайн калькулятор можно вводить натуральные числа или десятичные дроби.
Дополнительные возможности калькулятора деления столбиком
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Инструкция использования калькулятором деления столбиком
Для вычисления достаточно ввести числа (целые иди десятичные дроби) и нажать кнопку «=».
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Решение по действиям в столбик.
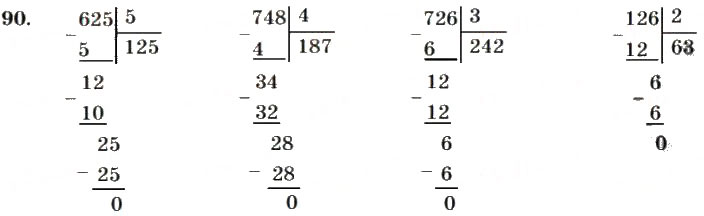 Деление натуральных чисел столбиком, примеры, решения
Деление натуральных чисел столбиком, примеры, решенияНаучить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
- Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
- Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
- Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
- Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
- Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3.
 Записываем 3 в ответ под чертой справа
Записываем 3 в ответ под чертой справа - Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
- Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
- Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6.
 Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4 - Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
- Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30.
 Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6 - Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
- К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).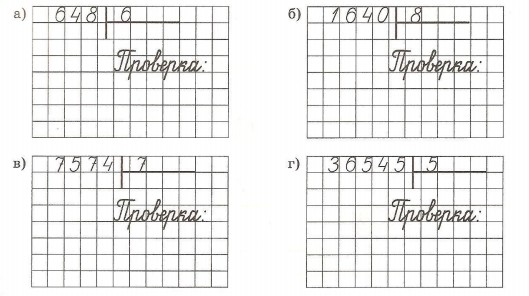
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером.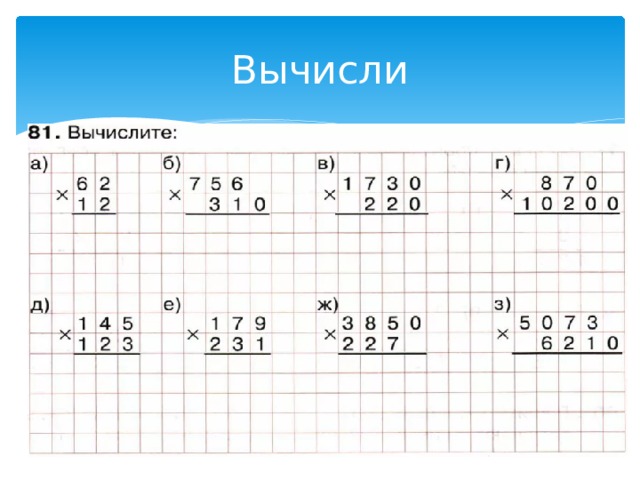 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Деление многозначных или многоразрядных чисел удобно производить письменно в столбик . Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.
Итак, поделим 354 на 2 . Для начала разместим эти числа как показано на рисунке:
Делимое размещаем слева, делитель справа, а частное будем записывать под делителем.
Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое , для этого берем первый слева разряд, в нашем случае 3 и сравниваем с делителем.
3 больше 2 , значит 3 и есть неполное делимое. Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:
Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:
Для того чтобы 3 разделить на 2 вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3.
2 × 1 = 2 (2
2 × 2 = 4 (4 > 3)
2 меньше 3 , а 4 больше, значит, берем первый пример и множитель 1 .
Записываем 1 в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым:
Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем:
Полученное значение сравниваем с делителем. 15 больше 2 , значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15 :
Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15 :
2 × 7 = 14 (14
2 × 8 = 16 (16 > 15)
Искомый множитель 7 , записываем его в частное на место второй точки (в десятки). Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
Продолжаем деление, для чего находим третье неполное делимое . Спускаем следующий разряд делимого:
Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления:
2 × 7 = 14
Результат деления третьего неполного делимого на делитель пишем в частное, находим разность:
Разность мы получили равную нулю, значит деление произведено правильно .
Усложним задачу и приведем другой пример:
1020 ÷ 5
Запишем наш пример в столбик и определим первое неполное частное:
Разряд тысяч делимого составляет 1 , сравниваем с делителем:
1
Добавляем в неполное делимое разряд сотен и сравниваем:
10 > 5 – мы нашли неполное делимое.
Делим 10 на 5 , получаем 2 , записываем результат в частное. Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.
10 – 10 = 0
0 мы не пишем, опускаем следующий разряд делимого – разряд десятков:
Сравниваем второе неполное делимое с делителем.
2
Нам следует добавить в неполное делимое ещё один разряд, для этого в частное, на разряд десятков ставим 0 :
20 ÷ 5 = 4
Записываем ответ в разряд единиц частного и проверяем: записываем произведение под второе неполное делимое и вычисляем разность. Получаем 0 , значит пример решён правильно .
И ещё 2 правила деления в столбик:
1. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить, например:
Сколько нулей в младшем разряде делимого мы убираем, столько же нулей убираем в младших разрядах делителя.
2. Если в делимом после деления остались нули, то их следует перенести в частное:
Итак, сформулируем последовательность действий при делении в столбик.
- Размещаем делимое слева, делитель справа. Помним, что делимое мы делим, поразрядно выделяя неполные делимые и деля их последовательно на делитель. Разряды в неполное делимое выделяются слева направо от старших к младшим.
- Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить.
- Определяем первый неполный делитель:
а) выделяем в неполный делитель старший разряд делимого;
б) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (в) , если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4 ;
в) добавляем в неполное делимое следующий разряд и переходим к пункту (б) .
- Определяем сколько разрядов будет в частном, и ставим столько точек на месте частного (под делителем) сколько будет в нем разрядов.
 Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого.
Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого. - Делим неполное делимое на делитель, для этого находим число, при умножении которого на делитель получилось бы число либо равное неполному делимому, либо меньше его.
- Найденное число записываем на место очередного разряда частного (точки), а результат умножения его на делитель записываем под неполным делимым и находим их разность.
- Если найденная разность меньше или равна неполному делимому значит, мы правильно поделили неполное делимое на делитель.
- Если в делимом остались еще разряды, то продолжаем деление, иначе переходим к пункту 10 .
- Опускаем к разности следующий разряд делимого и получаем очередное неполное делимое:
а) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (б), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
б) добавляем к неполному делимому следующий разряд делимого, при этом в частное на место следующего разряда (точки) пишем 0;
в) переходим к пункту (а).
10. Если мы выполняли деление без остатка и последняя найденная разность равна 0 , то мы правильно выполнили деление .
Мы говорили о делении многоразрядного числа на одноразрядное. В случае, когда разрядность делителя больше, деление выполняется аналогично:
Как вычитать столбиком
Вычитание многозначных чисел обычно выполняют столбиком, записывая числа друг под другом (уменьшаемое сверху, вычитаемое снизу) так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Слева между числами ставится знак действия. Под вычитаемым проводят черту. Вычисление начинают с разряда единиц: из единиц вычитают единицы, затем из десятков — десятки и т. д. Результат вычитания записывают под чертой:
Рассмотрим пример, когда в каком-либо разряде цифра уменьшаемого меньше цифры вычитаемого:
От 2 мы не можем отнять 9, что нам делать в этом случае? В разряде единиц у нас нехватка, но в разряде десятков у уменьшаемого аж 7 десятков, поэтому мы можем один из этих десятков перекинуть в разряд единиц:
В разряде единиц у нас было 2, мы перекинули десяток, стало 12 единиц. Теперь мы легко можем от 12 отнять 9. Записываем под чертой в разряде единиц 3. В разряде десятков у нас было 7 единиц, одну из них мы перекинули в простые единицы, осталось 6 десятков. Записываем под чертой в разряде десятков 6. В результате мы получили число 63:
Теперь мы легко можем от 12 отнять 9. Записываем под чертой в разряде единиц 3. В разряде десятков у нас было 7 единиц, одну из них мы перекинули в простые единицы, осталось 6 десятков. Записываем под чертой в разряде десятков 6. В результате мы получили число 63:
Вычитание столбиком обычно не записывают так подробно, вместо этого, над цифрой разряда, у которого будет занята единица, ставят точку, чтобы не запоминать, у какого разряда надо будет дополнительно вычесть единицу:
При этом говорят так: из 2 вычесть 9 нельзя, занимаем единицу, из 12 вычитаем 9 — получим 3, пишем 3, в разряде десятков у нас было 7 единиц, мы одну перекинули, осталось 6, пишем 6 .
Теперь рассмотрим вычитание столбиком из чисел, содержащих нули:
Начинаем вычитать. От 7 отнимаем 3, пишем 4. От нуля мы не можем отнять 5, поэтому мы вынуждены занять единицу в старшем разряде, но в старшем разряде у нас тоже 0, поэтому и для этого разряда мы вынуждены занять в более старшем разряде. Занимаем единицу из разряда тысяч, получаем 10 сотен:
Одну из единиц разряда сотен мы занимаем в младший разряд, получаем 10 десятков. Из 10 вычитаем 5, пишем 5:
Из 10 вычитаем 5, пишем 5:
В разряде сотен у нас осталось 9 единиц поэтому, от 9 отнимаем 6, пишем 3. В разряде тысяч у нас была единица, но мы её потратили на младшие разряды, поэтому здесь остаётся нуль (его записывать не надо). В результате мы получили число 354:
Такая подробная запись решения была приведена, чтобы было проще понять, как выполняется вычитание столбиком из чисел содержащих нули. Как уже упоминалось, на практике решение обычно записывается так:
А все упомянутые действия выполняются в уме. Чтобы было легче выполнять вычитание, запомните простое правило:
Если при вычитании столбиком над нулём стоит точка, нуль превращается в 9.
Калькулятор вычитания столбиком
Данный калькулятор поможет вам выполнить вычитание чисел столбиком. Просто введите уменьшаемое и вычитаемое и нажмите кнопку Вычислить.
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Как делить и умножать в одной формуле Excel (4 способа)
В большинстве случаев функции Excel включают умножение и деление различных типов данных. Вопрос о том, как делить и умножать в Excel по одной формуле, будет рассмотрен на адекватных примерах.
Скачать практическую рабочую тетрадь
4 способа делить и умножать в одной формуле Excel
1. Использование традиционной формулы деления и умножения
2. Объедините QUOTIENT с функцией PRODUCT в одной формуле Excel.
3. Реализация специальной команды «Вставить»
4. Встраивание макроса VBA для деления и умножения в Excel
Встраивание макроса VBA для деления и умножения в Excel
Вывод
Статьи по Теме
Скачать рабочую тетрадь
Загрузите эту практическую рабочую тетрадь ниже.
4 способа деления и умножения в одной формуле Excel
В этой статье приведенный ниже набор данных предназначен для демонстрационных целей. Для целей умножения на и деления мы помещаем два отдельных числовых столбца. Мы разделим Число 1 на Число 2 , а затем снова умножит частное на Число 1 . И окончательный результат будет представлен в столбце Result . Как нам удалось прийти к такому результату, объясним на адекватных примерах.
1. Использование традиционных формул деления и умножения
Используя традиционную формулу деления и умножения, мы можем легко применить деление и умножение в одной ячейке, используя одну формулу.
Ступени
- Сначала нужно выделить ячейку D5 и ввести следующую формулу:
=(B5/C5)*B5
Здесь знак звездочки ( * ) выполняет операцию умножения, а знак деления (/) выполняет операцию деления.
- И эта операция будет продолжена после PEMDAS Где операции Суммирование , Раздел , Вычитание и Умножение выполняются в порядке скобок сначала, затем экспоненциально после этого Умножение и Деление затем. В формуле в ячейке D5 деление находится внутри круглых скобок, то есть ячейка B5 делится на ячейку C5 , что получится сначала, потом снова будет умножено на ячейку B5 .
- После завершения формулы вы заметите, что значение в ячейке D5 показывает конечный продукт операций.
- Получив результат в ячейке D5 , перетащите значок маркера заполнения в ячейку D10.
- После этого все ячейки в столбце результатов теперь заполнены нужными значениями от деления и умножения данных из одной формулы Excel.

Подробнее: Как умножить одну ячейку на несколько ячеек в Excel (4 способа)
2. Объединить ЧАСТНОЕ с функцией ПРОИЗВЕД в одной формуле Excel
В этом методе мы собираемся использовать функции ЧАСТНОЕ и ПРОИЗВЕДЕНИЕ для деления и умножения значений столбца номер 1 и значений числа 2. Здесь обе эти функции будут иметь почти ту же роль, что и знаки «/» и «*». делать. Внедрение полезных функций, таких как QUOTIENT и PRODUCT , позволяет легко разделить и умножить данные из одной формулы Excel в одной ячейке.
Ступени
- Сначала выберите ячейку D5 и следующую формулу:
= ПРОИЗВЕД(ЧАСТНОЕ(B5, C5),B5)
- После этого вы увидите деление значения в ячейке B5 на ячейку C5 и умножение этого деления на B5 в ячейке D5 .

- После этого перетащите маркер заполнения в углу ячейки D5 и перетащите его к ячейке D10 . Вы заметите, что весь диапазон ячеек D5 : D10 теперь имеет результат вычислений.
Как на самом деле работает формула?
- ЧАСТНОЕ(B5, C5): Эта функция возвращает деление значения в ячейке B5 на ячейку C5.
- ПРОИЗВЕД(ЧАСТНОЕ(B5, C5), B5): Эта функция возвращает значение, возвращенное функцией ЧАСТНОЕ , умноженное на значение в ячейке B5 .
Подробнее: Если ячейка содержит значение, умножьте его с помощью формулы Excel (3 примера)
Аналогичные показания
- Как умножить столбцы в Excel (9 простых и полезных способов)
- Умножение двух столбцов в Excel (5 самых простых способов)
- Как использовать функцию умножения в Excel (с 3 альтернативными методами)
- Умножение столбца на число в Excel (4 простых метода)
- Как умножить столбец в Excel на константу (4 простых способа)
3.
 Выполнение специальной команды «Вставить»
Выполнение специальной команды «Вставить»Специальная команда «Вставить» — это наиболее удобный инструмент для вставки данных для разделения и умножения существующих данных в ячейке. Он напрямую вставляет данные, которые будут либо делить, либо умножать изначально существующие числа.
Ступени
- Сначала выделите диапазон ячеек B5 : B10 и скопируйте их в диапазон ячеек E5:E10.
- Затем выберите значения ячеек в диапазоне ячеек C5 : C10, и щелкните правой кнопкой мыши. В контекстном меню нажмите Копировать.
- Далее выберите уже существующие значения в диапазоне ячеек E5 : E10 , затем щелкните правой кнопкой мыши в контекстном меню и выберите Специальная паста .
- После нажатия на значок Специальная вставка откроется новое окно.
 В этом окне выберите Разделить в группе Операция . После этого нажмите OK.
В этом окне выберите Разделить в группе Операция . После этого нажмите OK.
- После нажатия OK, вы заметите, что все числа теперь вставляются, но в то же время они также разделяют ранее существовавшие значения.
- Затем снова выберите значения в диапазоне ячеек D5 : D10. Щелкните правой кнопкой мыши в контекстном меню и выберите Копировать.
- Далее выделите уже существующие значения в диапазоне ячеек E5 : E10 , затем щелкните правой кнопкой мыши в контекстном меню и выберите Специальная вставка .
- После нажатия на значок Специальная вставка откроется новое окно. В этом окне выберите Умножить в группе Operation . После этого нажмите OK.

- После нажатия OK, вы заметите, что значения, существовавшие до вставки, теперь умножаются на вставленные значения из диапазона ячеек D5 : D10 .
Подробнее: Как умножать в Excel: столбцы, ячейки, строки и числа
4. Внедрение макроса VBA для деления и умножения в Excel
Использование простого макроса VBA позволяет значительно сократить время деления и умножения чисел в одной ячейке.
Ступени
- Сначала перейдите на вкладку Developer , затем щелкните Visual Basic.
- Затем нажмите Вставить > Модуль .
- В окне редактора Module введите следующий код.
Функция Multiply_Division (число1 как целое число, число2 как целое число) Multiply_Division = (число1 / число2) * число1 Завершить функцию
- Далее закройте окно модуля и введите в ячейку D5 следующую формулу:
= Умножить_Деление (B5, C5)
- После ввода формулы вы заметите, что ячейка D5 будет иметь желаемый результат.

- Затем перетащите Значок Fill Handle в углу ячейки и перетащите его вниз к ячейке D10 , чтобы заполнить столбец Result выходными значениями.
Подробнее: Как умножить несколько ячеек в Excel (4 метода)
Заключение
Подводя итог, на вопрос «как делить и умножать в одной формуле Excel» здесь отвечают 4 различными способами, которые состоят из традиционных формул, с ЧАСТНЫМ и 9Функция 0003 PRODUCT продолжалась с использованием инструмента Paste Special и, наконец, заканчивалась использованием VBA Macro . Среди всех методов, используемых здесь, использование формул ЧАСТНОЕ и ПРОИЗВЕД является более простым для понимания и простым. Процесс VBA также требует меньше времени и упрощений, но требует предварительных знаний, связанных с VBA. Другие методы не имеют такого требования.
Другие методы не имеют такого требования.
Для решения этой задачи доступна для загрузки рабочая книга с поддержкой макросов, в которой можно попрактиковаться в этих методах.
Не стесняйтесь задавать любые вопросы или отзывы в разделе комментариев. Любое предложение по улучшению сообщества Exceldemy будет весьма ценным.
Связанные статьи
- Как умножать из разных листов в Excel (5 методов)
- Округление формулы умножения в Excel (5 простых методов)
- Как составить таблицу умножения в Excel (4 метода)
- Умножение строк в Excel (4 самых простых способа)
- Как умножить два столбца, а затем суммировать в Excel
Excel XP: создание сложных формул
Урок 6: создание сложных формул
/en/excelxp/creating-simple-formulas/content/
Введение
К концу этого урока вы должны уметь:
- Создание сложных формул
- Ввод формулы в другую ячейку
- Копирование и вставка формулы в другую ячейку
- Изменение формулы
- Создание абсолютной ссылки
Определение сложных формул
Простые формулы содержат одну математическую операцию. Сложные формулы включают более одной математической операции.
Сложные формулы включают более одной математической операции.
Порядок математических операций важен. Если вы вводите формулу, содержащую несколько операций, таких как сложение, вычитание и деление, Excel XP выполняет эти операции в определенном порядке. Порядок операций:
- Операции, заключенные в скобки
- Экспоненциальные вычисления (в степени)
- Умножение и деление, в зависимости от того, что наступит раньше
- Сложение и вычитание, в зависимости от того, что наступит раньше
Используя этот порядок, посмотрим, как формула 120 /(8-5)*4-2 вычисляется на следующем рисунке:
Рассмотрим другой пример:
2*(6-4) =?
Ответ 8 или 4? Если вы проигнорируете круглые скобки и подсчитаете в порядке появления чисел, 2*6-4, вы получите неправильный ответ, 8. Вы должны следовать порядку операций, чтобы получить правильный ответ.
Чтобы вычислить правильный ответ:
- Вычислите операцию в скобках (6-4), где ответ равен 2.

- Умножьте ответ, полученный на шаге 1, т.е. 2, на число 2*, которое открыло уравнение. Другими словами, умножьте 2*2.
- Ответ: 4.
При использовании формул со ссылками на ячейки результаты меняются каждый раз, когда редактируются числа .
В Excel никогда не занимайтесь математикой в уме и не вводите ответ в ячейку, где вы ожидаете, что формула вычислит ответ.
Определены сложные формулы
Прежде чем двигаться дальше, давайте рассмотрим еще несколько формул, чтобы убедиться, что вы понимаете порядок операций, с помощью которых Excel вычисляет ответ.
| 5*3/2 | Умножьте 5*3 перед выполнением операции деления, потому что знак умножения стоит перед знаком деления. Ответ: 7,5 . |
| 5/3*2 | Разделите 5/3 перед выполнением операции умножения, потому что знак деления стоит перед знаком умножения. Ответ 3.333333 . Ответ 3.333333 . |
| 5/(3*2) | Сначала выполните операцию в скобках (3*2) и разделите 5 на этот результат. Ответ: 0,833333 . |
| 5+3-2 | Добавьте 5+3 перед выполнением операции вычитания, потому что знак сложения стоит перед знаком вычитания. Ответ: 6 . |
| 5-2+3 | Вычтите 5-2 перед выполнением операции сложения, поскольку знак вычитания стоит перед знаком сложения. Ответ 6 . |
| 5-2*3 | Умножьте 2*3 перед выполнением операции вычитания, поскольку знак умножения имеет более высокий порядок, чем знак вычитания. Ответ: -1 . |
| (5-2)*3 | Сначала выполните операцию в скобках (5-2), а затем умножьте на 3. Ответ: 9 . Ответ: 9 . |
Создание сложных формул
Excel XP автоматически следует стандартному порядку операций в сложной формуле. Если вы хотите, чтобы определенная часть формулы вычислялась первой, поместите ее в круглые скобки.
Если бы мы хотели сложить, например, содержимое ячеек B2 и B3, а затем взять этот ответ и умножить его на данные в ячейке A4, нам нужно было бы определить следующую формулу: =(B2+B3)* А4 .
- Введите числа, которые вы хотите рассчитать.
- Щелкните ячейку, в которой вы хотите, чтобы формула отображала результат .
- Введите знак равенства (=), чтобы Excel знал, что формула определяется.
- Введите открывающую скобку или (.
- Щелкните первую ячейку , которую нужно включить в формулу (например, ячейку B2).
- Введите знак добавления (+) , чтобы Excel знал, что необходимо выполнить операцию добавления.

- Щелкните вторую ячейку в формуле. Эталон B3 отображается там, где вы хотите получить результат.
- Завершите операцию B2+B3, добавив закрывающую скобку или ).
- Введите следующий математический оператор или символ умножения (*) , чтобы Excel знал, что необходимо выполнить операцию умножения.
- Щелкните третью ячейку для включения в формулу, ячейка A4.
- Нажмите Введите или нажмите кнопку Ввод в строке формул, чтобы завершить формулу.
Попробуйте изменить одно из значений в формуле и посмотрите, как изменится ответ на формулу.
Excel не всегда будет сообщать вам , если ваша формула содержит ошибку, поэтому вы должны проверить все свои формулы. Чтобы узнать, как это сделать, прочитайте урок «Перепроверьте свои формулы» из нашего учебника по формулам Excel.
Заполнение формулами других ячеек
Иногда вы пишете формулу, которая используется в различных местах рабочего листа. Например, электронная таблица может содержать несколько столбцов чисел. Каждый столбец будет содержать формулу, которая складывает все числа в нем. Вы можете написать формулу несколько раз, по одному разу в каждом столбце, или скопировать и вставить ее в каждый столбец. Метод заполнения формулы позволяет копировать формулу и заполнять ею множество разных ячеек одновременно.
Например, электронная таблица может содержать несколько столбцов чисел. Каждый столбец будет содержать формулу, которая складывает все числа в нем. Вы можете написать формулу несколько раз, по одному разу в каждом столбце, или скопировать и вставить ее в каждый столбец. Метод заполнения формулы позволяет копировать формулу и заполнять ею множество разных ячеек одновременно.
При наведении указателя мыши на маркер заполнения или квадратную рамку в правом нижнем углу ячейки указатель мыши принимает вид черного перекрестия.
Чтобы использовать маркер заполнения для копирования формулы в соседнюю ячейку:
- Щелкните ячейку, содержащую формулу, которую необходимо скопировать.
- Наведите указатель мыши на маркер заполнения.
- Нажмите и удерживайте левую кнопку мыши, затем перетащите содержимое в ячейку, которая получит формулу заполнения.
- Отпустите кнопку мыши.
- Выберите параметр Копировать ячейки в раскрывающемся меню формулы заполнения.

Ссылки на ячейки в формуле автоматически обновляются, когда формула копируется в другие ячейки электронной таблицы.
Вы также можете копировать и вставлять формулы в другие ячейки. Это обсуждается на следующей странице.
Копирование и вставка формул
Процесс копирования и вставки формулы идентичен процессу копирования и вставки текста.
Чтобы скопировать и вставить формулу:
- Выберите ячейку, содержащую формулу, которую вы хотите скопировать.
- Нажмите кнопку Копировать . Марширующие муравьи появляются вокруг скопированных ячеек.
- Выберите ячейку, в которую будет вставлена скопированная формула.
- Нажмите клавишу Enter . Формула копируется в новое место.
Проверка формул
Вы можете пересмотреть любую формулу, которая ранее была написана на листе.
Чтобы изменить формулу с помощью клавиатуры:
- Дважды щелкните ячейку, содержащую формулу, которую вы хотите изменить.

- Теперь курсор может перемещаться влево и вправо между значениями формулы в ячейке B5.
- Внесите необходимые изменения в формулу.
- Нажмите клавишу Enter или нажмите кнопку Enter, чтобы принять новую формулу.
Создание абсолютной ссылки
В предыдущих уроках мы видели, как ссылки на ячейки в формулах автоматически адаптируются к новым местоположениям, когда формула вставляется в другие ячейки.
Иногда при копировании и вставке формулы вы не хотите изменять одну или несколько ссылок на ячейки. Абсолютные ссылки решают эту проблему. Абсолютные ссылки на ячейки в формуле всегда относятся к одной и той же ячейке или диапазону ячеек в формуле. Если формула копируется в другое место, абсолютная ссылка остается прежней.
Абсолютная ссылка обозначается в формуле добавлением знака доллара ($). Он может предшествовать ссылке на столбец, ссылке на строку или и той, и другой. Примеры абсолютной ссылки включают:
| $A$2 | Столбец и строка не изменяются при копировании. |
| 2 австралийских доллара | Строка не изменяется при копировании. |
| $A2 | Столбец не изменяется при копировании. |
Чтобы создать абсолютную ссылку:
- Введите числа, которые вы хотите вычислить (например, 34 567 в ячейке B2 и 1 234 в ячейке B3).
- Создайте простую формулу (=B2+B3).
- Чтобы создать абсолютную ссылку в формуле, вставьте значение $ перед B (ссылка на столбец) и 2 (ссылка на строку) в ссылке на B2, чтобы новая формула читалась как =$B$2+B3 .
- Скопируйте и вставьте формулу в соседнюю ячейку. Формула теперь включает абсолютную ссылку на B2: =$B$2+D3.
Вызов
- Введите следующую информацию:
В ячейке A1 введите 12345 .
В ячейке A2 введите 15865 .
В ячейке B1 введите 9347 .
В ячейке B2 введите 11942 .
В ячейке C1 введите 19348 .
В ячейке C2 введите 17103 . - Создайте следующую простую формулу:
В ячейке A3, напишите формулу , чтобы сложить ячейки A1 и A2.
- Введите формулу в ячейку A3 как в ячейку B3, так и в ячейку C3.
- Создайте следующую сложную формулу:
В ячейку A5, напишите формулу , которая делит ячейку A1 на сумму ячеек A3, B3 и C3.
- В формуле, определенной в ячейке A5, создайте абсолютную ссылку на все ячейки и строки, указанные в следующей части формулы: сумма ячеек A3, B3 и C3.
- Скопируйте формулу и абсолютную ссылку в ячейку A5 и вставьте ее в ячейки B5 и C5.
- Обратите внимание, что формулы в ячейках A5, B5 и C5 отличаются друг от друга.
Предыдущий: Создание простых формул
Далее:Использование функций
/en/excelxp/using-functions/content/
Что такое метод столбца? Определение, сложение, вычитание, деление
Что такое столбцовый метод?
Когда мы располагаем числа, фигуры или объекты друг над другом, мы называем это методом столбца. Другими словами, метод столбцов — это математический способ выполнения вычислений, при котором числа, которые нужно сложить, вычесть или умножить, располагаются друг над другом в столбцах.
Другими словами, метод столбцов — это математический способ выполнения вычислений, при котором числа, которые нужно сложить, вычесть или умножить, располагаются друг над другом в столбцах.
Например:
Мы используем метод столбцов для трех основных операций: сложения, вычитания и умножения.
Столбчатый метод сложения и вычитания
Столбчатый метод сложения и вычитания — это метод, в котором числа «переносятся» и «заимствуются». Она изложена так: вычисления при сложении и вычитании производятся путем «переноса» и «заимствования» чисел из столбца в столбец.
Колоночный метод сложения
Колоночный метод сложения также известен как колоночный метод сложения. Добавление столбца — это формальный метод добавления двух или более чисел.
Например:
Что такое вычитание столбцов?
Вычитание по столбцу — это способ найти разницу между двумя или более числами, расположив их одно над другим.
Столбчатый метод Вычитание:
Почему разрядное значение важно в столбцовом методе?
Метод столбца — самый быстрый способ сложения и вычитания, но разрядное значение играет важную роль в методе столбца.
Давайте посмотрим на пример ниже и используем добавление столбцов.
- Сначала числа выстраиваются одно над другим.
- Во-вторых, добавляем единицы и пишем ответ.
Например: Сложение $9$ и $5$ дает ответ $14$, но мы пишем только те, которые находятся под чертой – в данном случае это цифра $4$.
- Третий шаг — перегруппировать десятки в столбце десятков. В $14$ цифра $1$ является значением десятков.
- Сложите цифры в разряде десятков. В нашем примере $8 + 1 = 9$, но мы добавляем 1 из-под черты. Таким образом, ответ для десятков составляет 9 долларов.$.
- Когда два числа с разными цифрами складываются, мы можем правильно разместить их, используя разрядность. Например: десятичное число $0,1$ и число $28$.
Метод расширенного столбца
Расширенный метод заключается в разбиении каждого числа в вашей сумме на меньшие, более управляемые числа, из которых они состоят. Мы в основном разбиваем числа в развернутом виде.
Например, число $782$ можно разбить на: $700 + 80 + 2$
Расширенный метод сложения суммы осуществляется следующим образом:
Допустим, нам нужно сложить 47$ + 134$
Во-первых, мы расширим 47$ и 134$.
47$ = 40 и 7 и 134 = 100, 30 и 4$
Теперь рассортируем числа по сотням, десяткам и единицам и сложим их по группам.
- Мы будем складывать цифры на единицу.
В этом примере мы складываем 7 долларов + 4 = 11 долларов. Оставляем 1 на разряде единиц и берем еще $1$ на разряде десятков.
- Мы добавим цифры в разряде десятков.
В этом примере мы сложим 30$ + 40 + 10 = 80$
- Мы добавим цифры в разряде сотен.
В этом примере мы складываем 100 долларов США + 0 = 200 долларов США
Теперь мы складываем все наши цифры вместе, мы получаем 100 долларов США + 80 + 1 = 181 доллар США
Другой пример приведен ниже:
Возьмем пример метода расширенного столбца вычитания.
Метод столбца для вычитания без заимствования
Иногда нам не нужно заимствовать цифры из столбца при вычитании.
Например: $76 – 42$
Первый шаг – рассортировать числа по десяткам и единицам:
Десятки $→ 7 и 6$
Единицы $→ 4 и 2$
Мы всегда должны ставить самые большие числа в верхней строке столбцов.
Теперь вы можете вычесть числа в каждом столбце:
Ответ на сумму $76 – 42$ равно $34$.
Колонковый метод сложения без заимствования
Мы используем метод столбца для добавления без заимствования или переноса каких-либо значений между столбцами.
Например: 282$ + 615$
При расширении получаем
Сотни $→ 200$ и 600$
Десятки $→ 80$ и 10$
Единицы$→ 2$ и 5$
5, поместите значения в свои столбцы:
Затем мы сложим все ваши значения в их группах.
Следовательно, ответом на сумму $262 + 615$ будет $897$.
Столбчатый метод умножения
Мы также используем метод столбца для умножения двух чисел, который включает запись одного числа под другим аналогично сложению и вычитанию столбца.
Когда мы умножаем два числа, используя метод умножения столбца, мы используем следующие шаги:
Предположим, мы умножаем $96$ и $36$.
Шаг I: Умножаем множимое $(96)$ на единицу множителя $(6)$, т. е.
Шаг II: Следующим шагом является умножение множимого $(96)$ на разряд десятков множителя $(3)$, т.е.
Шаг III: Следующим шагом является сложение частичных произведений, т.е.
Частичное произведение $1 (576 единиц) +$ Частичное произведение $2 (288 десятков) $
$ 576 × 1 + 288 × 10 $
$ 576 + 2880 = 3456 $
На самом деле это означает:
Теперь мы применим тот же метод для умножения трехзначного числа на двузначное число.
Пример:
Возьмем другой пример. Найдите произведение 145$, умноженное на 12$, используя метод столбца.
Шаг I:
Шаг II:-
Шаг III:
Шаг IV:
Шаг V:
Шаг VI:
.
 1. Найдите ошибку в следующем.
1. Найдите ошибку в следующем. Ответ: Ошибка в том, что столбцы десятков и сотен добавлены неправильно. Переходящие цифры не добавлялись. Правильная сумма будет:
2. Найдите значение «А» в следующем.
Решение: $300 – $A$ = 200$
$Итак, $A$ = 100$
3. Стоимость 1 ожерелья составляет рупий 342 $ . Какова будет стоимость ожерелий стоимостью 23$ ? Если у Шэрон есть рупий 8000 долларов долларов, сколько денег останется после оплаты ожерелий?
Ответ: Стоимость 1 ожерелья $=$ Rs $342$
Стоимость ожерелья $23$ $= 342 ✕ 23 =$ Rs $7866$
Стоимость ожерелья $23$ $= 6000 + 900 + 800 + 120 + 40 + 6 = $ рупий $ 7866 $
Сумма, оставленная $ = 8000 — 7866 $
Сумма, оставленная $ = $ 134 $
Практические задачи
7
8
6
Ни один из этих
Правильный ответ: 8
$ 6 \ Time3 = = = = = = = = = 3 = = = 3 = = = = 3 = = = 3 = = = 3 = = = 3 = = = = = 3 = = = = = 3 = = = = = 3 = = = = 3 =. 18$, так что в одном месте мы получим 8$.
18$, так что в одном месте мы получим 8$.
4
5
3
2
Правильный ответ: 4
$ 4500 — 1352 = 3148 $
. С. TENS Place, мы получаем 4.
4533
4674
4733
4534 40009
9000 2 4674
9000 47339000 2 4534 40009 9000 2 4674
9000 473 39000 2 4534
4674
9000 473 39000 2 4534
4674
9000 4734533
4674
9000 4734533
4674
9000 4000 2 45330005 Правильный ответ: 4733
$2785 + 1948 = 4733$
Часто задаваемые вопросы
В чем разница между столбчатым методом и горизонтальным методом?
Метод столбцов — это метод расположения чисел друг над другом и сложения, вычитания или умножения в столбцах. С другой стороны, горизонтальный метод — это способ расположения чисел в горизонтальной строке, а затем термины располагаются так, чтобы собрать все группы одинаковых терминов.
С другой стороны, горизонтальный метод — это способ расположения чисел в горизонтальной строке, а затем термины располагаются так, чтобы собрать все группы одинаковых терминов.
Как иначе называется метод сложения столбцов?
Другое название столбцового метода сложения — столбцовое сложение или вертикальное сложение.
Что такое разделение методом столбца?
Деление методом столбцов представляет собой простой способ традиционного метода деления в длину. Линии рисуются для того, чтобы разделить цифры делителя. Каждый столбец разрядных значений решается слева направо.
Вычисления с числовыми значениями — Amazon Redshift
В этом контексте вычисление относится к двоичному
математические операции: сложение, вычитание, умножение и деление.
В этом разделе описаны ожидаемые типы возврата для этих операций, а также
как конкретная формула, которая применяется для определения точности и масштаба при
Задействованы типы данных DECIMAL.
Когда во время обработки запроса вычисляются числовые значения, вы можете встречаются случаи, когда вычисление невозможно, а запрос возвращает ошибка числового переполнения. Вы также можете столкнуться со случаями, когда масштаб вычисленные значения варьируются или являются неожиданными. Для некоторых операций можно использовать явное приведение (продвижение типа) или параметры конфигурации Amazon Redshift для работы вокруг этих проблем.
Для получения информации о результатах подобных вычислений с помощью SQL функции, см. Агрегатные функции.
Типы возвращаемых данных для вычислений
Учитывая набор числовых типов данных, поддерживаемых в Amazon Redshift, следующие
Таблица показывает ожидаемые типы возврата для сложения, вычитания,
операции умножения и деления. Первая колонка слева
таблицы представляет первый операнд в вычислении, а верхний
строка представляет второй операнд.
| INT2 | INT4 | INT8 | ДЕСЯТИЧНЫЙ | ПОПЛАВКА4 | ПЛАВАЮЩИЙ 8 | |
| INT2 | INT2 | INT4 | INT8 | ДЕСЯТИЧНОЕ | FLOAT8 | FLOAT8 |
| INT4 | INT4 | INT4 | INT8 | ДЕСЯТИЧНОЕ | FLOAT8 | FLOAT8 |
| INT8 | INT8 | INT8 | INT8 | ДЕСЯТИЧНОЕ | FLOAT8 | FLOAT8 |
| ДЕСЯТИЧНЫЙ | ДЕСЯТИЧНОЕ | ДЕСЯТИЧНОЕ | ДЕСЯТИЧНОЕ | ДЕСЯТИЧНОЕ | FLOAT8 | FLOAT8 |
| ПОПЛАВКА4 | FLOAT8 | FLOAT8 | FLOAT8 | FLOAT8 | ПЛАВ4 | FLOAT8 |
| ПЛАВАЮЩИЙ 8 | FLOAT8 | FLOAT8 | ПЛАВ8 | FLOAT8 | FLOAT8 | FLOAT8 |
Точность и масштаб вычисляемых результатов DECIMAL
В следующей таблице приведены правила вычисления результирующих
точность и масштаб, когда математические операции возвращают результаты DECIMAL. В
эта таблица,
В
эта таблица, p1 и s1 представляют точность и
масштаб первого операнда в вычислении и p2 и s2 представляют точность и масштаб второго операнда.
(Независимо от этих расчетов, максимальная точность результата равна 38, а
максимальная шкала результата 38.)
| Операция | Точность и масштаб результата |
|---|---|
| + или — | Масштаб = макс(с1,с2) Точность = |
| * | Масштаб = с1+с2 Точность = |
| / | Масштаб = макс. Точность = |
Например, столбцы PRICEPAID и COMMISSION в таблице SALES оба столбца DECIMAL(8,2). Если разделить ЦЕНУ на КОМИССИЮ (или наоборот наоборот), формула применяется следующим образом:
Точность = 8-2 + 2 + макс(4,2+8-2+1) = 6 + 2 + 9 = 17 Масштаб = макс.(4,2+8-2+1) = 9 Результат = DECIMAL(17,9)
Следующее вычисление является общим правилом для вычисления результирующего точность и масштаб для операций, выполняемых над значениями DECIMAL с набором такие операторы, как UNION, INTERSECT и EXCEPT, или такие функции, как COALESCE и РАСШИФРОВАТЬ:
Масштаб = max(s1,s2) Точность = мин(макс(p1-s1,p2-s2)+ 9масштаб 1170 ,19)
Например, таблица DEC1 с одним столбцом DECIMAL(7,2) соединяется с
Таблица DEC2 с одним столбцом DECIMAL(15,3) для создания таблицы DEC3. Схема
DEC3 показывает, что столбец становится столбцом NUMERIC(15,3).
Схема
DEC3 показывает, что столбец становится столбцом NUMERIC(15,3).
создать таблицу dec3 как select * from dec1 union select * from dec2;
Результат
выберите "столбец", тип, кодировку, distkey, sortkey из pg_table_def, где имя_таблицы = 'dec3'; колонка | тип | кодирование | ключ | ключ сортировки -------+---------------+-----------+---------+----- ---- с1 | числовое (15,3) | нет | ж | 0
В приведенном выше примере формула применяется следующим образом:
Точность = min(max(7-2,15-3) + max(2,3), 19) = 12 + 3 = 15 Масштаб = макс (2,3) = 3 Результат = ДЕСЯТИЧНОЕ (15,3)
Примечания к операциям деления
Для операций деления условия деления на ноль возвращают ошибки.
Ограничение масштаба 100 применяется после того, как точность и масштаб вычислено. Если рассчитанная шкала результата больше 100, деление результаты масштабируются следующим образом:
Если расчетная точность превышает максимальную точность (38),
точность уменьшается до 38, а масштаб становится результатом: макс(38 + шкала - точность), мин(4, 100))
Переполнение условия
Переполнение проверяется для всех числовых вычислений. ДЕСЯТИЧНЫЕ данные с
точность 19 или меньше хранится как 64-битные целые числа. ДЕСЯТИЧНЫЕ данные с
точность выше 19хранится как 128-битное целое число. Максимум
точность для всех значений DECIMAL равна 38, а максимальный масштаб равен 37.
Ошибки переполнения возникают, когда значение превышает эти пределы, которые применяются к обоим
промежуточные и окончательные наборы результатов:
ДЕСЯТИЧНЫЕ данные с
точность 19 или меньше хранится как 64-битные целые числа. ДЕСЯТИЧНЫЕ данные с
точность выше 19хранится как 128-битное целое число. Максимум
точность для всех значений DECIMAL равна 38, а максимальный масштаб равен 37.
Ошибки переполнения возникают, когда значение превышает эти пределы, которые применяются к обоим
промежуточные и окончательные наборы результатов:
Явное приведение приводит к ошибкам переполнения во время выполнения, когда указано значения данных не соответствуют требуемой точности или масштабу, указанным литая функция. Например, вы не можете привести все значения из Столбец PRICEPAID в таблице SALES (столбец DECIMAL(8,2)) и возврат ДЕСЯТИЧНЫЙ (7,3) результат:
выбрать pricepaid::decimal(7,3) из продаж; ОШИБКА: переполнение числовых данных (точность результата)
Эта ошибка возникает из-за того, что какой-то из больших значения в столбце PRICEPAID не могут быть преобразованы.

Операции умножения дают результаты, в которых масштаб результата является суммой масштабов каждого операнда. Если оба операнда имеют шкалу из 4, например, шкала результата равна 8, оставляя только 10 цифр для левая часть десятичной точки. Поэтому относительно легко столкнуться с условиями переполнения при умножении двух больших чисел что оба имеют значительный масштаб.
Числовые вычисления с типами INTEGER и DECIMAL
Когда один из операндов в вычислении имеет тип данных INTEGER и другой операнд — DECIMAL, операнд INTEGER неявно приводится как ДЕСЯТИЧНЫЙ:
INT2 (SMALLINT) приводится как DECIMAL(5,0)
INT4 (INTEGER) преобразуется в DECIMAL(10,0)
INT8 (BIGINT) приводится как DECIMAL(19,0)
Например, если вы умножаете КОМИССИЯ ПРОДАЖ, столбец DECIMAL(8,2) и
SALES. QTYSOLD, столбец SMALLINT, этот расчет приводится как:
QTYSOLD, столбец SMALLINT, этот расчет приводится как:
DECIMAL(8,2) * DECIMAL(5,0)
Javascript отключен или недоступен в вашем браузере.
Чтобы использовать документацию Amazon Web Services, должен быть включен Javascript. Инструкции см. на страницах справки вашего браузера.
Решено: Математические (деление и умножение) функции…
core.noscript.text
8 ОТВЕТОВ 8
Этикетки
- ААХ
1 - ААХ Добро пожаловать
2 - Академия
21 - АДАПТ
87 - Добавить столбец
1 - Добавить новый столбец
1 - Настройки администратора
1 - Администрация
32 - Adobe
160 - Расширенная аналитика
1 - Появление кода
5 - Псевдоним Менеджер
95 - Альтерикс
1 - Альтерикс 2020.
 1
1 4 - Академия Альтерикс
3 - Альтерикс Аналитика
1 - Центр аналитики Alteryx
2 - Введение в сообщество Alteryx — студент MSA в CSUF
1 - Альтерикс Коннект
1 - Альтерикс Дизайнер
79 - Альтерикс Двигатель
1 - Галерея Альтерикс
1 - Концентратор Альтерикс
1 - альтерикс с открытым исходным кодом
1 - Alteryx Post ответ
1 - Альтерикс Практика
129 - Alteryx SDK API
1 - Команда Альтерикс
1 - Инструменты Альтерикс
1 - АльтериксФорГуд
1 - Амазонка s3
181 - Двигатель AMP
93 - АНАЛИТИЧЕСКИЙ ИННОВАТОР
1 - Аналитическая поддержка приложений
1 - Аналитические приложения
18 - Аналитические приложения ACT
1 - Аналитика
2 - Анализатор
19 - Объявление
4 - API
1187 - Приложение
2 - Добавить поля
1 - Приложения
1372 - Процесс архивации
1 - АРИМА
1 - Присвоение метаданных CSV
1 - Аутентификация
4 - Автоматическое обновление
1 - Кодировка Base64
1 - Основная таблица отчетов
1 - Пакетный макрос
1270 - Новичок
1 - Анализ поведения
234 - Лучшие практики
2520 - BI + аналитика + наука о данных
1 - Книжный червь
2 - Ошибка
625 - Ошибки и проблемы
1 - Расчет рабочих дней
1 - Калгари
86 - КАСС
70 - Человек-кошка
1 - Категория Приложения
1 - Категория Соединители
1 - Категория Документация
1 - Категория Вход Выход
2 - Категория Прогностический
1 - Категория Пространственная
1 - Категория Временной ряд
3 - Преобразование категории
1 - Сертификация
4 - Связанное приложение
248 - Вызов
17 - Диаграмма
1 - Клиенты
5 - Кластеризация
1 - Распространенные варианты использования
3409 - Связь
1 - Сообщество
262 - Объединить
1 - Условный столбец
1 - Условный оператор
1 - СОЕДИНИТЕ И РЕШИТЕ
1 - Соединители
1279 - Содержит
1 - Содержание
1 - Управление контентом
8 - Конкурс
6 - Стартер разговора
22 - копия
1 - COVID-19
4 - Создайте новую электронную таблицу, используя существующий набор данных
.  1
1 - Управление учетными данными
3 - Любопытный*Маленький
1 - Функция пользовательской формулы
1 - Пользовательские инструменты
1374 - Создание приборной панели
1 - Анализ данных
1 - Анализ данных
2 - Аналитика данных
1 - Вызов данных
103 - Очистка данных
5 - Соединение данных
1 - Исследование данных
2633 - Загрузка данных
1 - Наука о данных
30 - Подключение к базе данных
2332 - Подключения к базе данных
6 - Наборы данных
4018 - Дата
2 - Дата и время
3 - формат даты
1 - Выбор даты
2 - Дата Время
2680 - Формат даты
1 - даты
1 - дата и время разбор
2 - Дефект
10 - Демографический анализ
197 - Дизайнер
1 - Дизайнерское облако
105 - Интеграция дизайнера
107 - Разработчик
3101 - Инструменты разработчика
2632 - Обсуждение
2 - Документация
466 - Человек-собака
3 - Скачать
1072 - Дублирует строки
1 - Дублирование строк
1 - Динамический
1 - Динамический ввод
1 - Динамическое имя
1 - Динамическая обработка
2614 - динамическая замена
1 - динамически создавать таблицы для входных файлов
1 - Электронная почта
708 - Уведомление по электронной почте
1 - Инструмент электронной почты
2 - Встроить
1 - встроенный
1 - Двигатель
86 - Улучшение
4 - Улучшения
2 - Сообщение об ошибке
2234 - Сообщения об ошибках
6 - ЭТС
1 - События
204 - Эксель
1 - Excel динамически объединяет
1 - Макрос Excel
1 - Пользователи Excel
1 - Исследователь
5 - Выражение
1580 - извлечь данные
1 - Запрос функции
4 - Фильтр
1 - фильтр присоединиться
1 - гурман
4 - Формула
2 - формула или фильтр
1 - Инструмент формулы
4 - Формулы
2 - удовольствие
5 - Нечеткое совпадение
701 - Нечеткое соответствие
1 - Галерея
568 - Генерал
175 - Общее предложение
4 - Создание формул строк и многострочных формул
1 - Создать строки
1 - Начало работы
1 - Google Аналитика
181 - группировка
1 - Руководство
16 - Всем привет !
2 - Справка
3583 - Как раскрасить поля в строке на основе значения в другом столбце
1 - Как сделать
1 - Hub20.
 4
4 2 - Я новичок в Альтерикс.
1 - идентификатор
1 - В базе
1117 - В базе данных
1 - Введите
3941 - Входные данные
2 - Вход Выход
3 - Вставка новых строк
1 - Установить
4 - Установка
404 - Интерфейс
3 - Инструменты интерфейса
1644 - Введение
7 - Итеративный макрос
970 - Соединитель Jira
1 - Присоединяйтесь к
1748 - база знаний
1 - Лицензии
1 - Лицензирование
244 - Список бегунов
1 - Погрузчики
18 - Загрузчики SDK
3 - Оптимизатор местоположения
79 - Поиск
1 - Машинное обучение
167 - Макрос
2 - Макросы
2720 - Картирование
1 - Маркето
25 - соответствие
1 - Слияние
1 - МонгоДБ
83 - Создание нескольких переменных
1 - MultiRowFormula
1 - Нужна помощь
1 - нужна помощь: как найти определенную строку во всех столбцах excel и вернуть этот clmn
1 - Нужна помощь по формуле Tool
1 - сеть
1 - Эквивалент функции NetworkDays
1 - Новый инструмент
1 - Новости
1 - Не твое дело
1 - Не по теме
15 - Управление финансов
1 - Нефть и газ
1 - Оптимизация
692 - Любитель активного отдыха
1 - Выход
4572 - Выходные данные
1 - пакет
1 - Разобрать
1995 - Сопоставление с образцом
1 - Люди Человек
5 - процентили
1 - Power BI
191 - практические упражнения
1 - Предиктивный
2 - Прогнозный анализ
1259 - Прогнозная аналитика
1 - Препарат
4966 - Предписывающая аналитика
235 - Опубликовать
275 - Питон
645 - Qlik
57 - квартили
1 - Вопрос
11 - Вопросы
2 - R квадратные значения
1 - Инструмент R
678 - RE GEX конвертировать
1 - проблема с обновлением
1 - Регулярное выражение
1884 - Удалить столбец
1 - Отчетность
2032 - Ресурс
16 - RestAPI
1 - Управление ролями
3 - Выполнить команду
559 - Запуск рабочих процессов
12 - Время выполнения
1 - Продажи
300 - Расписание
1 - Расписание рабочих процессов
3 - Планировщик
436 - Ученый
3 - Поиск
3 - Поиск отзывов
16 - Сервер
454 - Настройки
909 - Установка и конфигурация
93 - SFTP
1 - Sharepoint
434 - Делюсь
2 - Умный лист
1 - Снежинка
1 - Пространственный
1 - Пространственный анализ
782 - студент
9 - Проблема со стилем
1 - Итого
1 - Системное администрирование
2 - Таблица
540 - Столы
1 - Технология
1 - Интеллектуальный анализ текста
288 - Миниатюра
1 - Четверг Мысль
11 - Временной ряд
437 - Прогнозирование временных рядов
1 - Советы и рекомендации
3759 - Улучшение инструмента
9 - Инструменты
1 - Интересующая тема
43 - Трансформация
2915 - Транспонировать
1 - Твиттер
50 - Удасити
137 - Уникальный
2 - Не уверен на подходе
1 - Обновления
3 - Обновления
1 - URL-адрес
1 - Варианты использования
1 - Дизайн взаимодействия с пользователем
2 - Пользовательский интерфейс
45 - Управление пользователями
5 - Видео
2 - ВидеоID
1 - ВПР
1 - Еженедельное испытание
1 - Распределение Вейбулла Weibull.
 Dist
Dist 1 - Количество слов
1 - Рабочий процесс
7399 - Рабочие процессы
1 - Годфракция
1 - Ютуб
1 - YTD и QTD
1
- « Предыдущий
- Следующий »
Как создать формулу в Excel: вычитание, умножение и многое другое!
Перейти к содержимому Как создать формулу в Excel: сложение, вычитание, умножение и деление (+еще)Автор: соучредитель Каспер Лангманн , специалист Microsoft Office.
Научиться создавать формулы в Excel очень просто.
Если вы никогда не знали, как писать формулы в электронных таблицах Excel, вы попали по адресу.
Это руководство расскажет вам о каждом шаге написания формулы в Excel и о том, как ее понять.
Каспер Лангманн , соучредитель Spreadsheeto
К тому времени, как вы прочтете это руководство, вы будете знать, что такое формула и как создать свою собственную.
Оглавление
-
Бонус: бесплатный файл упражнений (скачать)
-
1: Что такое формула?
-
2: Как создать формулу?
-
3: разница между формулой и функцией
-
4: How to add
-
5: How to subtract
-
5: How to multiply
-
6 : Как Divide
-
7: Как использовать Корни
-
8: Как использовать .0054
9: Орден операций
-
Заключение: Обертывание вещей.
 вам нужен набор данных для практики.
вам нужен набор данных для практики.Я включил один для вас (бесплатно).
Нажмите ниже, и мы отправим его прямо сейчас!
облачная загрузкаБОНУС: Загрузите Файл упражнений по формуле (с 12 предварительно загруженными упражнениями) , чтобы присоединиться к этому сообщению.
Что такое «Формула»?Итак, что такое формула?
Это просто оператор, состоящий из «операндов» и «операторов».
Допустим, вы хотите рассчитать скидку 15% от 20 долларов.
В этом выражении есть два «операнда»: цена (20 долларов) и процент скидки (15%).
Оператор умножения (*).
Результат — «Скидка».
Скидка = 20 долларов США (цена) * 15% (процент скидки)
Важно отметить, что формулы всегда должны начинаться со знака равенства (=).
 Если вы не начнете свои формулы со знака равенства, Excel будет рассматривать его как строковый тип данных.
Если вы не начнете свои формулы со знака равенства, Excel будет рассматривать его как строковый тип данных.Каспер Лангманн , соучредитель Spreadsheeto
Теперь давайте посмотрим, как выглядит наша формула скидки в Excel.
Как только вы нажмете ввод, формула рассчитает формулу и покажет результат.
Обратите внимание на формулу, показанную в поле над электронной таблицей. Это «строка формул». Подробнее об этом чуть позже.
Теперь посмотрите на результат, если вы введете формулу без знака равенства.
Кажется, ничто не отличается, кроме отсутствующего знака равенства перед фактической формулой.
А теперь давайте посмотрим, что произойдет, если мы щелкнем мышью за пределами ячейки, содержащей формулу (частично).
Каспер Лангманн , соучредитель Spreadsheeto
Без знака равенства это просто строка текста или чисел в соответствии с Excel.
Как создать формулу
Теперь давайте перейдем к созданию собственных формул.
Первым шагом к созданию формулы является ввод знака равенства в ячейку, в которую вы его поместите.
Теперь вы готовы начать ввод фактической формулы.
Если бы мы хотели разделить 6 на 3, мы бы ввели следующее:
Вы также можете использовать ссылки на ячейки вместо буквенных чисел.
На самом деле в формулах можно смешивать ссылки на ячейки и буквенные числа.
Обратите внимание: ваша формула также отображается в «строке формул» прямо над столбцом «C» рабочего листа.
Вы всегда можете просмотреть полную формулу и даже отредактировать ее из «панели формул».
Если щелкнуть ячейку, содержащую формулу, она появится в «панели формул». Это означает, что вам не нужно дважды щелкать ячейку, чтобы увидеть формулу.
Каспер Лангманн , соучредитель Spreadsheeto
В чем разница между
«Формула» и «Функция»?В отличие от формул, функции представляют собой предварительно созданные формулы , которые предлагает Excel.

Например, функция «СУММ» в Excel упрощает сложение двух и более чисел.
Вместо создания собственной формулы для сложения двух числовых значений используйте функцию «СУММ»!
Хотя функции сами по себе являются заранее построенными формулами, они все равно должны начинаться со знака равенства.
В формуле можно сочетать несколько функций.
Как добавить в ExcelТеперь давайте рассмотрим особенности того, как добавить в Excel.
Как вы уже видели, это довольно простая задача. Но сейчас мы рассмотрим несколько конкретных примеров того, как складывать числовые значения в Excel.
Каспер Лангманн , соучредитель Spreadsheeto
Самый простой способ сделать это — ввести математическое выражение для сложения двух чисел в ячейке.
Например, просто введите «=2 + 2» в ячейку по вашему выбору, и Excel выполнит запрошенный расчет.

Обратите внимание на формулу в «панели формул», в то время как ожидаемый результат находится в ячейке B2.
Вы также можете использовать ссылки на ячейки в качестве условий вашего уравнения вместо буквенных числовых значений.
После ввода знака равенства вы можете ввести ссылку на ячейку вручную или щелкнуть ячейку. Любой метод подойдет.
Теперь давайте рассмотрим смешивание буквенных числовых значений и ссылок на ячейки в нашей формуле.
Что делать, если вам нужно добавить более двух цифр? Ну, вы всегда можете добавить в свою формулу новые числа.
Каспер Лангманн , соучредитель Spreadsheeto
Вы даже можете продолжать добавлять ссылки на ячейки в формулу таким образом…
Но есть более простой способ, который мы уже затрагивали ранее… Функция «СУММ»!
Итак, для добавления множества числовых значений вы можете сделать следующее:
Просто введите =СУММ, а затем числа в круглых скобках, разделенные запятыми.

Вот как создать формулу в Excel для добавления нескольких чисел (см. «строку формул» на рисунке выше) .
Excel значительно упрощает работу при использовании функции «СУММ» с большим количеством ссылок на ячейки. Вместо использования ссылок на отдельные ячейки функция «СУММ» позволяет выбрать весь диапазон.
Каспер Лангманн , соучредитель Spreadsheeto
Вы также можете ввести первую и последнюю ячейки диапазона, разделенные двоеточием (:), и сделать то же самое.
Вы также можете добавить более одного диапазона ссылок на ячейки, используя функцию «СУММ».
Просто разделите диапазоны запятой.
Помните, что вы всегда можете ввести диапазоны вручную. Или вы можете выделить разные диапазоны, разделенные запятыми.
Как вычесть в ExcelТеперь давайте посмотрим, как написать формулу для вычитания в Excel.

Поскольку вы уже знаете, как складывать в Excel, научиться вычитанию легко .
Вы можете вычитать так же, как и складывать, просто заменив знак плюс на знак минус в простой формуле.
То же самое справедливо и при создании формулы для вычитания ссылок на ячейки.
Вы даже можете использовать функцию «СУММ» для создания формулы для вычитания чисел в Excel.
Это просто.
Вам просто нужно убедиться, что вы изменили знаки для чисел или значений в ссылках на ячейки, чтобы сделать это.
Например, если мы хотим использовать функцию «СУММ» для вычитания 2 из 4, нам нужно написать формулу следующим образом.
Каспер Лангманн , соучредитель Spreadsheeto
То же самое относится и к ссылкам на ячейки.
Вы можете изменить знак значения, которое хотите вычесть из другого значения в ячейке.
Затем выберите диапазон, как мы это делали до использования функции «СУММ» при добавлении.

Как только вы измените знак для соответствующего значения, вы можете просто выбрать диапазон для вашей формулы «СУММ».
Хотя это и не так просто, это все же эффективный способ вычитания в Excel.
Как умножать в ExcelТеперь, когда вы узнали, как написать формулу сложения и вычитания в Excel, давайте рассмотрим умножение.
В Excel для умножения чисел необходимо использовать звездочку (*).
Итак, давайте начнем, щелкнув любую ячейку, введя знак равенства, чтобы начать создавать нашу формулу. Затем запишем умножение 3 на 2.
Каспер Лангманн , соучредитель Spreadsheeto
Вы также можете использовать ссылку на ячейку при умножении.
Концепция достаточно проста: функция «ПРОИЗВЕД» позволяет умножать более двух чисел одновременно.
Когда вы начнете вводить «ПРОДУКТ», функция покажет себя и ее объяснение в окне всплывающей подсказки.

Теперь выбираем диапазон ячеек от А2 до А8.
Теперь нажмите «Ввод», и формула рассчитает произведение всех значений в диапазоне «A2:A8».
Как делить в ExcelВ этом разделе мы рассмотрим, как сделать формулу в Excel для деления.
В случае создания формулы для деления в Excel мы будем использовать косую черту (/).
Каспер Лангманн , соучредитель Spreadsheeto
Разделяет делимое и делитель.
Делимое будет слева от косой черты, тогда как делитель будет на справа .
Как и в других формулах, мы начинаем нашу формулу деления со знака и равно.
Затем мы вводим делимое, косую черту и, наконец, делитель.
Когда мы нажимаем Enter, мы получаем результат нашей формулы.
Особое примечание о делении в Excel заключается в том, что вы не можете делить любое число на ноль.

Если вы попытаетесь сделать это в Excel, вы получите следующую ошибку.
Как использовать корни в ExcelВ Excel есть одна встроенная функция, позволяющая находить квадратный корень из числа.
Это «SQRT», и для него требуется только один аргумент: число, из которого вы хотите найти квадратный корень.
Это настолько просто, насколько это возможно.
Но помните, что вы не можете вычислить квадратный корень из отрицательного числа, как и Excel. Если вы попытаетесь это сделать, вы получите #ЧИСЛО! ошибка.
Каспер Лангманн , соучредитель Spreadsheeto
В Excel есть еще одна встроенная функция, которая может помочь в решении этой проблемы. Функция «ABS» возвращает абсолютное значение числа.
Вы можете вложить формулу «ABS» в формулу «SQRT» (как показано ниже) .
Это поможет вам избежать «#ЧИСЛО!», вызванного отрицательным числом.
Как использовать экспоненты в Excel
Вы также можете написать формулы в Excel, чтобы возвести число в некоторую указанную степень.
Это можно сделать двумя способами: 9).
Excel также имеет встроенную функцию, которую вы можете использовать, называемую функцией «POWER».
Первый из двух аргументов — это основание, а второй аргумент — показатель степени.
Функция «СТЕПЕНЬ» вычисляет тот же результат, что и формула с использованием знака вставки.
Порядок действийКакой порядок действий?
Это математический протокол, определяющий математический порядок выполнения операций.
Логика следует за аббревиатурой PEMDAS. Вот что каждая буква означает…
Kasper Langmann , соучредитель Spreadsheeto
- P
7777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777.
 добавление и S удаление
добавление и S удаление
Короче говоря: PEMDAS.
Итак, давайте немного разберем это на нескольких примерах.
Допустим, у вас есть формула вида «=5+3*2».
Умножение 3 на 2 происходит перед операцией сложения.
Окончательный результат равен 11.
Если вы поместите операцию сложения в круглые скобки, порядок операций изменится.
Обратите внимание, что 5 прибавляется к 3, а результат 8 затем умножается на 2, в результате чего получается 16.
Это сильно отличается от результата предыдущего примера.
Посмотрите на следующую формулу и рассмотрите следующий пример. Эта формула вычисляет показатель степени сначала , произведение , второе , и сумму , последнее .
Каспер Лангманн , соучредитель Spreadsheeto
Результат экспоненциальной части равен 25, а результат ‘PRODUCT’ равен 12. Если часть формулы заключить в круглые скобки, порядок действий изменится.
Если часть формулы заключить в круглые скобки, порядок действий изменится.
Это возвращает другой результат…
Сначала вычисляется все, что находится в скобках.
Упрощенно, то есть 12 + 5.
Полученное число 17 затем возводится в степень 2, что дает нам окончательный результат 289. в результатах. Знание этого протокола помогает эффективно устранять неполадки с формулами в Excel.
Каспер Лангманн , соучредитель Spreadsheeto
ЗаключениеЭто завершает наше руководство по созданию формулы в Excel.
Как вы видели, концепции могут быть довольно простыми. Однако существуют разные подходы к формулам, например использование литеральных значений и/или ссылок на ячейки.
Затем у вас есть несколько вариантов, таких как использование некоторых встроенных функций, которые предлагает Excel.
Стоит повторить, что любая формула требует знака равенства, чтобы Excel распознал ее как таковую.


 Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения.
Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения.




 Записываем 3 в ответ под чертой справа
Записываем 3 в ответ под чертой справа Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4 Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6 Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого.
Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого.
 В этом окне выберите Разделить в группе Операция . После этого нажмите OK.
В этом окне выберите Разделить в группе Операция . После этого нажмите OK.