Решаем и пишем правильно — Сайт Беляевой Ирины Анатольевны

Порядок выполнения действий

14 августа, 202214 августа, 2022Leave a comment

1. Найдите значения выражений по двум разным схемам. Почему с одними и теми же числами и действиями получились разные результаты? Потому что отличается порядок выполнения действий: в первом выражения они выполнены слева направо, а во втором справа налево. Вывод: нельзя менять порядок действий 2. Рассмотрим выражение, составленное только с помощью действий сложения и вычитания: 7 – 2 + 3 – 5. С этими действиями знакомятся в школе в 1 классе….

Read More >>

Задачи на деление

12 мая, 202225 августа, 2022

Leave a comment

Какие задачи решают делением? Схемы задач на деление можно получить из схем задач на умножение, ведь деление — это действие, обратное умножению. Из каждой схемы задач на умножение получаются по две схемы задач на деление. В первой из них даны: произведение с и 1-й множитель а, неизвестен 2-й множитель. Во второй даны: произведение с и 2-й множитель b, неизвестен 1-й множитель. Схема 1 а. Есть сколько-то _ _ _ ,…

Read More >>

Задачи на умножение

10 апреля, 202224 августа, 2022Leave a comment

Какие задачи решают умножением? Речь пойдет о часто встречающихся схемах задач, где требуется применить умножение. Схема 1.Есть b _ _ _ , в каждом по а … .Сколько … в них всего? Ответ: а ∙ b … . Как получить из этой схемы конкретные задачи? Как обычно: нужно вместо букв а и b ставить какие-нибудь числа, а вместо пропусков — подходящие существительные (для пунктира из точек — одно и то…

Read More >>

Задачи на вычитание

10 марта, 202222 августа, 2022Leave a comment

Какие задачи решают вычитанием? Раз вычитание — это действие, обратное сложению, то можно догадаться, как получить схемы задач на вычитание.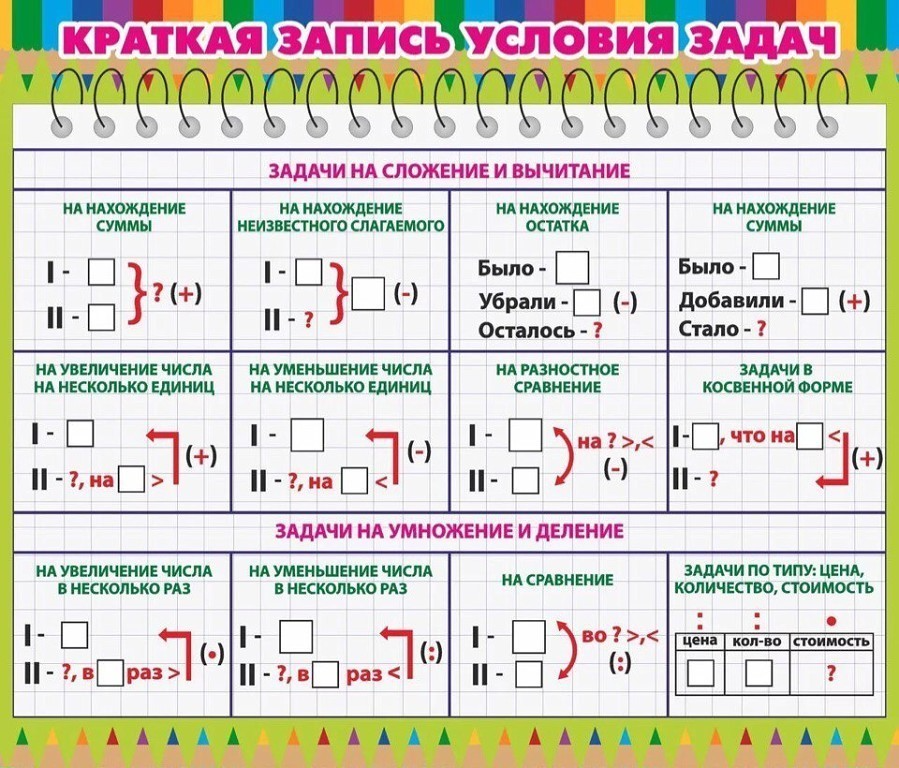 А именно, разбирая схемы задач на сложение, нужно в каждой из них находить одно слагаемое, вычитая из суммы с = a + b другое слагаемое a илиb. Давайте займемся этим и посмотрим, что у нас получится. Схема 1 а.Было с … , убавилось b … .Сколько … осталось? Ответ: с…

Read More >>

Задачи на сложение

12 февраля, 202221 августа, 2022Leave a comment

Простые и составные задачи Простые задачи от составных отличаются не уровнем сложности, а количеством выполняемых арифметических действий. Простая задача подразумевает выполнение только одного действия, а составная – более одного. Поэтому составную задачу можно представить в виде цепочки простых подзадач, позволяющих в конечном итоге ответить на вопрос задачи. И таких цепочек может быть не одна, то есть задача может иметь несколько решений. Такие задачи делят на стандартные и нестандартные (или алгоритмические…

Read More >>

Углы

8 января, 2022Leave a comment

Уважаемые читатели, пришла пора познакомиться с геометрической фигурой – угол. Посмотрите на аппликацию, из каких фигур составлена ракета? Правильно, из треугольников, четырехугольников и шестиугольников. А какое слово спрятано в названиях этих фигур? Совершенно верно, угол. Так что же это за фигура? Сначала разберемся, что из себя представляет прямая линия. Вообразите себе тонкую нить, натянутую между двумя гвоздиками. А теперь представьте, что эти два гвоздика разлетаются в разные стороны до бесконечности….

Read More >>

Единицы длины

27 ноября, 202127 ноября, 2021Leave a comment

Когда возникает необходимость изучить какой-либо объект, то наравне с такой характеристикой, как вес, называют и его размеры. Чтобы определить названные параметры, мы сравниваем их с международным эталоном массы (1 кг) и эталоном длины (1 м). Для удобства введены с помощью приставок ещё дольные и кратные единицы измерения, отличающиеся от основной величины в 10, 100, 1000 и т. д. раз. Кратная единица – единица величины, в целое число раз большая основной единицы. Дольная единица – единица…

Read More >>

Измерение времени

15 июня, 2021

29 июня, 2021Leave a comment

В наши дни используют механические и электронные часы. Электронные часы просто показывают количество пройденных часов и минут от начала суток. Сутки начинаются ночью с нуля часов и нуля минут. 12 часов проходит от этого времени до полудня, а потом ещё 12 часов от полудня до полуночи. Сложнее разобраться с показаниями механических часов, поскольку у таких часов есть две стрелки-указателя: коротенькая – часовая и длинная – минутная. Шкала на таких часах поделена на 12…

Read More >>

Двузначные числа

7 мая, 2021Leave a comment

Десятки  Когда речь идёт о больших числах, то счёт удобно вести десятками или даже сотнями, тысячами и т.д. Если взять один десяток каких-то предметов, то говорят, что взяли десять: 10, если два десятка – двадцать: 20, три десятка – тридцать: 30, четыре десятка – сорок: 40, пять десятков – пятьдесят: 50, шесть десятков – шестьдесят: 60, семь десятков – семьдесят: 70, восемь десятков – восемьдесят: 80, девять десятков – девяносто:…

Read More >>

Перестановка слагаемых

12 апреля, 202114 апреля, 2021Leave a comment

Мальчик держит несколько флажков. На рисунке мы видим слева от него два синих флажка в правой руке и с другой стороны – один красный флажок в левой руке. Найдём, сколько всего флажков держит мальчик. Для этого к двум синим флажкам прибавим один красный флажок. Получаем три флажка: 2 + 1 = 3. Но вот мальчик поменял флажки местами. Теперь слева от него один красный флажок, а с другой стороны –…

Read More >>

Алгебра. Учебник для 6-8 классов

Алгебра. Учебник для 6-8 классов

Барсуков А.Н. Алгебра. Учебник для 6-8 классов. 11-е изд., стер. — М.: Просвещение, 1966. — 296 с. Учебник для средних общеобразовательных школ СССР в 50-60-е годы. Шестое издание „Алгебры» А.Н. Барсукова переработано и приведено в соответствие с новой программой. Переработка учебника и изложение вопросов, вновь включенных в программу восьмилетней школы, выполнены С.И. Новоселовым. Главу „Счётная (логарифмическая) линейка* и о возвышении в квадрат и куб, извлечении квадратного и кубического корней при помощи счётной линейки написал учитель математики школы № 315 Москвы И. Б. Вейцман. Одиннадцатое издание печатается с десятого без изменений. Оглавление ГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ. § 2. Алгебраические выражения. § 3. Допустимые значения букв. § 4. Порядок действий. § 5. Основные законы сложения и умножения. § 6. Краткие исторические сведения. ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА. § 7. Положительные и отрицательные числа. § 8. Числовая ось. § 9. Противоположные числа. § 10. Абсолютная величина числа. § 11. Сравнение рациональных чисел. § 12. Сложение рациональных чисел. § 13. Сложение нескольких чисел. § 14. Законы сложения. § 15. Вычитание рациональных чисел. § 16. Алгебраическая сумма. § 17. Умножение. § 18. Умножение нескольких чисел. § 19. Законы умножения. § 20. Деление. § 21. Свойства деления. § 22. Возведение в степень. § 23. Порядок выполнения действий. § 24. Уравнения. § 25. Решение задач с помощью уравнений. § 26. Графики. § 27. Краткие исторические сведения. (Из истории отрицательных чисел.) ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ. § 28. Одночлен и многочлен. § 29. Тождества и тождественные преобразования. § 30. Коэффициент. § 31. Расположенные многочлены. § 32. Приведение подобных членов. § 33. Сложение одночленов и многочленов. § 34. Противоположные многочлены. § 35. Вычитание одночленов и многочленов § 36. Умножение одночленов. § 37. Умножение многочлена на одночлен. § 38. Умножение многочленов. § 39. Умножение расположенных многочленов. § 40. Возведение одночленов в степень. § 41. Формулы сокращённого умножения. § 42. Общие замечания о делении целых алгебраических выражений. § 43. Деление одночленов. § 44. Деление многочлена на одночлен § 45. Примеры решения уравнений. ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ. § 47. Равносильные уравнения. § 48. Два основных свойства уравнений. § 49. Уравнения, содержащие неизвестное в обеих частях. § 50. Уравнение первой степени с одним неизвестным. § 51. Общие указания к решению уравнений. § 52. Решение задач с помощью уравнений. § 53. Краткие исторические сведения. (Из истории уравнений.) ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ. § 54. Понятие о разложении на множители. § 55. Вынесение за скобки общего множителя. § 56. Способ группировки. § 57. Применение формул сокращённого умножения. § 58. Применение нескольких способов. § 59. Деление многочленов при помощи разложения на множители. ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ. § 60. Понятие об алгебраической дроби. § 61. Основное свойство дроби и сокращение дробей. § 62. Перемена знака у членов дроби. § 63. Целая отрицательная и нулевая степени числа. § 64. Приведение дробей к общему знаменателю. § 65. Сложение дробей. § 66. Вычитание дробей. § 67. Умножение дробей. § 68. Деление дробей. § 69. Возведение дроби в натуральную степень. § 70. Дробные уравнения. § 71. Примеры решения уравнений с буквенными коэффициентами. ГЛАВА СЕДЬМАЯ. КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ. § 72. Координаты точки на плоскости. § 73. Прямо пропорциональная зависимость. § 74. График прямо пропорциональной зависимости. § 75. Линейная зависимость. § 76. Обратно пропорциональная зависимость. ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ. § 77. Уравнение первой степени с двумя неизвестными. § 78. Система двух уравнений первой степени с двумя неизвестными. § 79. Равносильные системы. (1/3) § 130. Примеры графического решения уравнений и систем уравнений.

Умножение и деление предложений — Элементарная математика

Распознавать и формулировать предложения, связанные с умножением и делением

Материалы

Нет

Обзор

Чтобы подготовиться к предстоящей работе с умножением и делением, попросите учащихся попрактиковаться в фактах до 10 × 10. Укажите факт умножения, например 5 × 6, и попросите учащегося назвать факт произведение и его предложение умножения (5 × 6 = 30). Затем попросите другого учащегося дать соответствующее предложение о делении (30 ÷ 6 = 5 или 30 ÷ 5 = 6).

Класс также можно разделить на две команды. Первая команда дает предложение умножения и произведение, а вторая команда дает соответствующее предложение деления и частное. Когда учитель говорит «Переключи!» каждая команда работает с противоположной операцией.

О последовательности

Часть 1 предлагает учащимся попрактиковаться в фактах умножения до 5 × 10 и поделиться соответствующими предложениями об умножении и делении. Часть 2 включает факты до 10 × 10 и факты расширенного теста до 12 × 12, оба с дополнительной практикой предоставления связанных предложений умножения и деления.

Часть 1

Давайте продолжим практиковаться в умножении. Я делюсь фактом, и один доброволец (или команда) дает продукт вместе с предложением умножения, которое идет с ним. Второй доброволец (или команда) разделяет частное и связанное с ним предложение деления. Итак, если я скажу 2 × 6, наш первый доброволец (или команда) скажет, что 2 × 6 = 12, а второй доброволец (команда) скажет, что 12 ÷ 6 = 2 или 12 ÷ 2 = 6. Начнем!

Примеры:

• 2 × 4 = 8 (8 ÷ 4 = 2 или 8 ÷ 2 = 4)
• 3 × 5 = 15 (15 ÷ 5 = 3 или 15 ÷ 3 = 5)
• 4 × 4 = 16 (16 ÷ 4 = 4)
• 5 × 4 = 20 (20 ÷ 4 = 5 или 20 ÷ 5 = 4)
• 4 × 3 = 12 (12 ÷ 3 = 4 или 12 ÷ 4 = 3)
• 3 × 3 = 9 (9 ÷ 3 = 3)
• 2 × 10 = 20 (20 ÷ 10 = 2 или 20 ÷ 2 = 10)
• 1 × 12 = 12 (12 ÷ 12 = 1 или 12 ÷ 1 = 12)
• 2 × 7 = 14 (14 ÷ 7 = 2 или 14 ÷ 2 = 7)
• 3 × 6 = 18 (18 ÷ 6 = 3 или 18 ÷ 3 = 6)

Пока дети наслаждаются своим мастерством, не стесняйтесь повторять. Когда дети хотят большего, попробуйте Часть 2.

Часть 2

Давайте продолжим с еще более важными фактами!

Примеры:

• 10 × 10 = 100 (100 ÷ 10 = 10)
• 9 × 8 = 72 (72 ÷ 8 = 9 или 72 ÷ 9 = 8)
• 7 × 6 = 42 (42 ÷ 6 = 7 или 42 ÷ 7 = 6)
• 8 × 5 = 40 (40 ÷ 5 = 8 или 40 ÷ 8 = 5)
• 6 × 9 = 54 (54 ÷ 9 = 6 или 54 ÷ 6 = 9)
• 7 × 7 = 49 (49 ÷ 7 = 7)
• 9 × 9 = 81 (81 ÷ 9 = 9)
• 6 × 8 = 48 (48 ÷ 8 = 6 или 48 ÷ 6 = 8)
• 9 × 1 = 9 (9 ÷ 1 = 9 или 9 ÷ 9 = 1)

Как всегда, когда дети кажутся взволнованными новой задачей, двигайтесь дальше.

Добавочный номер

Давайте попробуем еще больше фактов.

• 11 × 12 = 132 (132 ÷ 12 = 11 или 132 ÷ 11 = 12)
• 12 × 12 = 144 (144 ÷ 12 = 12)
• 10 × 12 = 120 (120 ÷ 12 = 10 или 120 ÷ 10 = 12)
• 11 × 9 = 99 (99 ÷ 9 = 11 или 99 ÷ 11 = 9)
• 12 × 4 = 48 (48 ÷ 4 = 12 или 48 ÷ 12 = 4)
• 12 × 8 = 96 (96 ÷ 8 = 12 или 96 ÷ 12 = 8)
• 11 × 11 = 121 (121 ÷ 11 = 11)
• 9 × 12 = 108 (108 ÷ 12 = 9 или 108 ÷ 9 = 12)
• 11 × 6 = 66 (66 ÷ 6 = 11 или 66 ÷ 11 = 6)

Умножение и деление | Правила и примеры Умножение и деление

В математике умножение и деление являются двумя важными арифметическими операциями. Операции умножения и деления тесно связаны друг с другом, как сложение и вычитание. Все эти операции выполняются над всеми действительными числами. Правила умножения и деления целых чисел отличаются от правил дробей и десятичных знаков.

Давайте узнаем больше об умножении и делении вместе с правилами и примерами. Также научитесь умножать и делить целые числа, дроби и десятичные дроби.

Содержание: Определение умножения и деления Связь между умножением и делением Правила умножения и деления Умножение и деление целых чисел Умножение и деление дробей Умножение и деление десятичных дробей Умножить и разделить на число, кратное 10 Уравнения Решенные примеры Проблемы со словами Рабочие листы Часто задаваемые вопросы

Что такое умножение и деление в математике?

В математике есть четыре основных операции.

• Дополнение (+)
• Вычитание (-)
• Умножение (×)
• Раздел (÷)

Что такое умножение?

Умножение — это многократное сложение числа. Если мы умножаем m на n, это означает, что m многократно добавляется к самому себе n раз. Символ умножения — «×».

Например, 8 умножить на 4 равно 32. Как? Прибавив к себе 8, 4 раза, получим;

8 + 8 + 8 + 8 = 32

Следовательно, мы можем написать

.

8 х 4 = 32

Что такое дивизия?

Деление – это способ деления или распределения числа на равные части, например, если 16 разделить на 4, то 16 делится на 4 равные части. Таким образом, результирующее значение равно 4,9.0004

16 ÷ 4 = 4

Части деления

Дивиденд ÷ Делитель = Частное

15 ÷ 3 = 5

В приведенном выше примере есть три части для деления.

• 15 дивидендов
• 3 — делитель
• 5 является частным (правая сторона)

Связь умножения и деления

Умножение и деление — операции, обратные друг другу.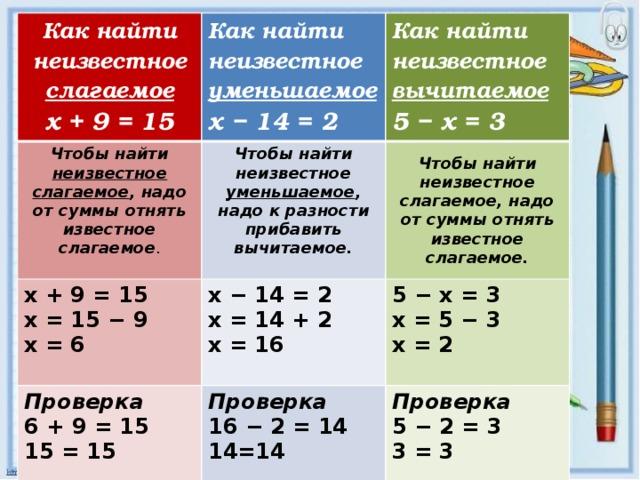 Если мы говорим, что а, умноженное на b, равно с, то с, деленное на b, дает а. Математически это можно представить как:

• а × Ь = с
• с ÷ б = а

Например,

• 4 x 5 = 20   [4 умножить на 5 дает 20]
• 20 ÷ 5 = 4   [20 разделить на 5 возвращает обратно 4]

Правила умножения и деления

Для каждого математического вычисления мы должны следовать правилам. Таким образом, даже для умножения и деления чисел существуют некоторые правила, которым мы должны следовать.

Правило 1: Порядок действий

Порядок операций умножения не имеет значения. Это означает, что если мы расположим числа в другом порядке при их умножении, то результат будет таким же.

Примеры:

3 х 4 = 12

4 х 3 = 12

В приведенном выше примере мы видим, что даже если мы поменяли местами 3 и 4, произведение двух целых чисел равно 12.

Но это правило не применимо для деления. Возьмем другой пример.

12 ÷ 3 = 4

3 ÷ 12 ≠ 4 (равно 0,25)

Таким образом, мы не можем изменить порядок чисел в методе деления.

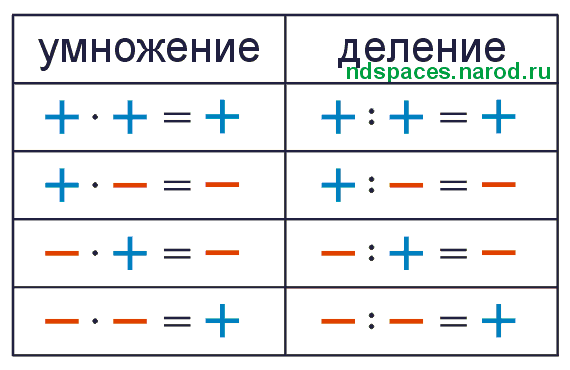
Правило 2. Умножение и деление на положительные числа

Если любое действительное число умножить или разделить на положительное действительное число, то знак полученного числа не изменится.

Примеры:

2 х 3 = 6

-2 х 3 = -6

Так как 2 и 3 являются целыми положительными числами, то произведение 2 и 3 также положительно. Но произведение -2 и 3 — отрицательное число.

4 ÷ 2 = 2

-4 ÷ 2 = -2

Так как 4 и 2 оба положительны, следовательно, 4, деленное на 2, также является положительным числом. Но -4 разделить на 2 — это отрицательное число.

Таким образом, мы можем сделать вывод, что:

(+) х (+)   = (+) (+)  ÷  (+)   = (+) (-)   х  (+)   =  (-) (-)  ÷  (+)   = (-)

Правило 3.

Умножение и деление на отрицательные числа

Умножение и деление любого действительного числа на отрицательное число изменит знак полученного числа. Примеры приведены ниже.

1. Умножить 5 на -2.

5 х -2 = -10

2. Умножить -5 на -2.

-5 х -2 = 10

3. Разделить 10 на 2.

10 ÷ -2 = -5

-10 ÷ -2 = 5

Таким образом, мы можем заключить, что:

(+) х (-) = (-) (+) ÷ (-) = (-) (-) х (-) = (+) (-) ÷ (-) = (+)

Краткое изложение правил умножения и деления

Правила умножения	Правила дивизиона
(+) × (+)  = (+) (-) × (-)  = (+) (+) × (-) = (-) (-) × (+) = (-)	(+) ÷ (+)  = (+) (-) ÷ (-) = (+) (+) ÷ (-) = (-) (-) ÷ (+) = (-)

Умножение и деление целых чисел

Целые числа — это значения, которые не являются дробями и могут быть отрицательными, положительными или нулевыми. Целые числа могут быть легко представлены на числовой прямой. Таким образом, арифметические вычисления над целыми числами могут быть выполнены простым способом.

Умножение и деление любого целого числа на целое число, дробь или само целое число приведены ниже с примерами.

• 3 x 9 = 27 (целое число x целое число)
• 2 x ¼ = ½ (целое число x дробь)
• 2 x -5 = -10 (целое число x целое число)

Умножение и деление дробей

Здесь мы научимся умножать и делить дроби на примерах.

Дробь является частью целого. Например, ½ — это дробь, представляющая половину целого числа или любого значения. Здесь верхняя часть называется числителем, а нижняя — знаменателем. Давайте умножать и делить дроби с примерами.

¼ x ½ = (1 x 1)/(4 x 2) = ⅛

¼ ÷ ½ = (1 x 2)/(1 x 4) = 2/4 = ½

Умножение и деление десятичных дробей

Десятичные числа — это числа с десятичной точкой (например: 2,35). Они представляют часть чего-либо или некоторого значения, например ½ = 0,5. Десятичная запись или точка отличают целую часть от дробной части (например, 2,35 = 2 + 7/20).

Умножение десятичных дробей

При умножении десятичного числа на любое действительное число положение десятичной точки (.) изменяется.

Например: 0,33 х 2 = 0,33 + 0,33 + 0,33. Умножение десятичных чисел аналогично умножению целых чисел. Шаги для умножения десятичных дробей приведены ниже с примером.

Рассмотрим умножение двух чисел, например 2,32 и 3.

Шаг 1: Подсчитайте общее количество знаков (цифр) справа от запятой в обоих числах.

Здесь в 2.32 две цифры справа от десятичной точки, а 3 — это целое число без десятичной точки. Следовательно, общее количество цифр справа от десятичной дроби равно 2,9.0004

Шаг 2: Теперь забудьте о десятичной точке и просто перемножайте числа без десятичной точки.

Шаг 3: После умножения поставьте запятую в ответе на 2 знака (шаг 1) справа, т. е. ответ (2,32 х 3) будет 6,96.

Просто умножьте десятичные числа без запятой, а затем дайте десятичной запятой в ответе столько знаков, сколько общее количество знаков до десятичных запятых в обоих числах.

Деление десятичных дробей

Мы можем использовать тот же прием, что и при умножении десятичных дробей, т. е. удалить десятичные точки и разделить числа как целые числа.

Разделим 40,5 на 0,20. Методы деления этих десятичных чисел следующие:

Способ 1. Преобразуйте десятичные числа в целые, умножив числитель и знаменатель на одно и то же число. Знаменатель всегда должен быть целым числом.

(Умножить и числитель, и знаменатель на 5)

Метод 2. В качестве альтернативы можно преобразовать десятичные числа в целые путем умножения на числа, имеющие степень 10 (10, 100, 1000 и т. д.).

• Возьмем знаменатель, посчитаем количество знаков (цифр) до запятой.

Здесь знаменатель равен 0,20, а количество цифр до запятой равно 2.

40,5 ÷ 0,20 = 40,5 / 0,20

• Возьмем степень 10 такую ​​же, как количество цифр до десятичной точки e. 10 ² = 100

• Умножить числитель и знаменатель на 100.

Умножение и деление десятичных чисел на 10, 100 и 1000

Умножение и деление десятичных дробей на числа, имеющие степень 10, проще, чем на целое число. Правила умножения и деления десятичных чисел на 10, 100 и 1000:

Умножение и деление	Правила	Примеры
Умножить на 10 (10 1 )	число переместится на один разряд влево	5,63 х 10 = 56,3
Умножить на 100 (10 2 )	число переместит значение на две позиции влево	5,63 х 100 = 563
Умножить на 1000 (10 3 )	число переместит значение на три позиции влево	5,63 х 1000 = 5630
Разделить на 10 (10 1 )	число переместится на одну позицию вправо	56,3 ÷  10 =5,63
Разделить на 100 (10 2 )	число переместит значение на две позиции вправо	56,3 ÷  100 =0,563
Разделить на 1000 (10 3 )	число переместится на три позиции вправо	56,3 ÷  1000 =0,0563

Уравнения умножения и деления

Уравнения — это выражения, включающие целые числа, переменные, знаки равенства и арифметические операции. Например,

2а + 9 = 7

Если мы решим приведенное выше уравнение относительно a, то

2а = 7 – 9

а = -2÷2 = -1

Таким образом, мы видим, что в приведенном выше решении использовались как методы умножения, так и деления.

Статьи по теме

• Умножение дробей
• Деление дробей
• Сложение и вычитание десятичных дробей
• Сложение и вычитание целых чисел
• Таблицы умножения
• Трюки с умножением

Решенные примеры — умножение и деление

Q.1: Найдите произведение:

• 22 х 11 = ?
• 3 х 91 = ?
• 444 х 3 = ?
• 1000 х 8 = ?

Решение:

• 22 х 11 = 242
• 3 х 91 = 273
• 444 х 3 = 1332
• 1000 х 8 = 8000

Q. 2: Найти деление:

• 34 ÷ 2 = ?
• 555 ÷ 5 = ?
• 81 ÷ 3 = ?
• 812 ÷ 4 = ?

Решение: Подразделения:

• 34 ÷ 2 = 17
• 555 ÷ 5 = 111
• 81 ÷ 3 = 27
• 812 ÷ 4 = 203

Word задачи на умножение и деление

Q.1: В 1 коробке 90 карандашей. Сколько карандашей в 3 коробках?

Решение: Дано, в 1 коробке 90 карандашей.

Итак, в 3 коробках количество карандашей = 3 х 90 = 270

Таким образом, всего в 3 коробках 270 карандашей.

Q.2: У Раджу в коробке 1615 конфет. Если таких коробок 85, то сколько конфет в каждой?

Решение: Общее количество конфет = 1615

Количество ящиков = 85

Следовательно, в каждой коробке содержится = 1615 ÷ 85 конфет

= 19 конфет.

Практические вопросы — Умножение и деление

1. Заполните пропуски:

• 7    х    9    = ___
• 83 ÷ 2  = __

2. Найдите значение:

• ⅔ х 5/9 = ?
• ⅚ х 12 = ?
• 16 ÷ 4/3 = ?
• 200 ÷ 40 = ?

3. Каждая ириска стоит рупий. 2. Если есть 120 ирисок, то какова их общая стоимость?

4. Школа планирует поездку. В нем 1729 студентов, в каждом автобусе 19 мест. Сколько автобусов необходимо для поездки?

Чтобы решить больше задач на умножение и деление десятичных дробей, загрузите BYJU’S — The Learning App из магазина Google Play и посмотрите интерактивные видеоролики.

Часто задаваемые вопросы об умножении и делении

В каком порядке выполняются операции умножения и деления?

В соответствии с правилом БОДМАС, мы сначала делим, а затем умножаем, если выражение не заключено в скобки.
15 ÷ 3 x 2 = 5 x 2 = 10
15 ÷ (3 x 2) = 15 ÷ 6 = 2,5

Что получится, если умножить целое число на целое число?

Умножение целого числа на целое число приводит к самому целому числу.