Умножение дробей с минусами: Онлайн калькулятор дробей. Вычисления с дробями. Сложение, вычитание, умножение и деление дробей

Содержание

Деление дроби на натуральное число.

Чтобы понять, как делить дроби, изучим правило и на примерах рассмотрим, как его применять.

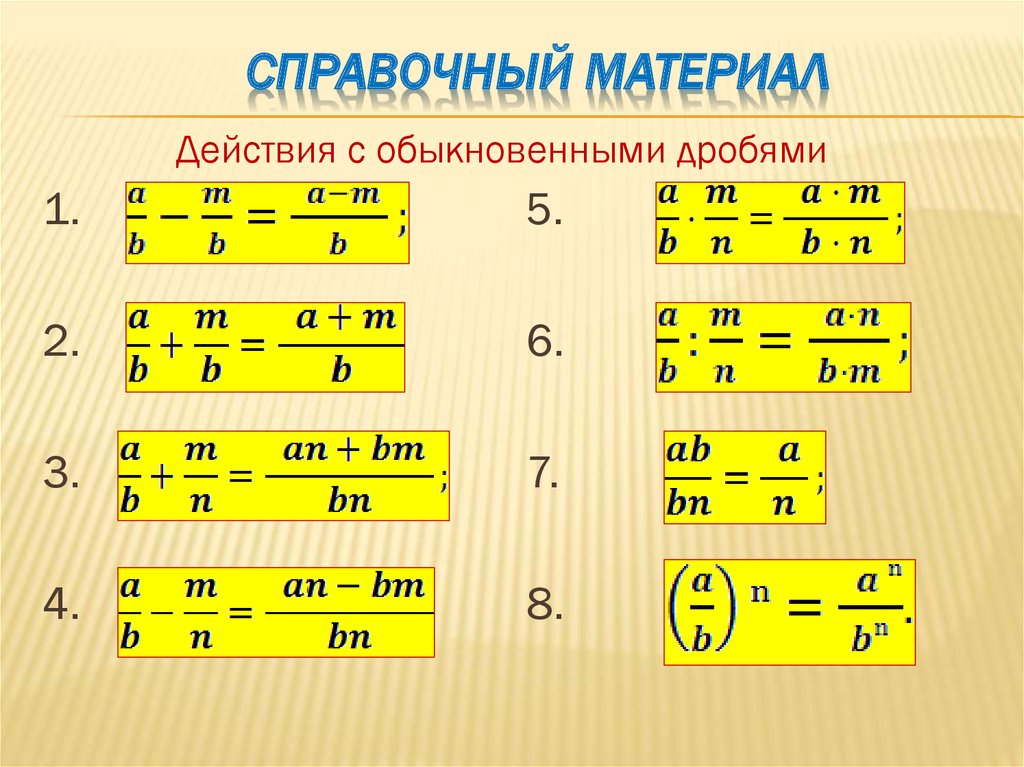
Правило деления обыкновенных дробей

Чтобы разделить две дроби, надо первое число умножить на ко второму (то есть первую дробь умножаем на перевернутую вторую).

Примеры деления обыкновенных дробей :

Чтобы разделить эти дроби, первую дробь переписываем и, обратную ко второй (делимое умножаем на число, обратное делителю). Сократить здесь ничего нельзя.

Чтобы разделить данные дроби, первое число переписываем без изменений и умножаем на число, обратное ко второму.6 и 9 на 3, 20 и 25 — на 5. Полученная в результате дробь 8/15 — правильная и несократимая. Значит, это — окончательный ответ.

Первую дробь оставляем без изменений и умножаем на число, обратное ко второй дроби. Сокращаем 45 и 36 на 9, 65 и 52 — на 13. В результате получили неправильную дробь, из которой .

При деление двух равных чисел получаем единицу, поэтому сразу можем записать ответ.

Чтобы разделить дроби, первую умножаем на число, обратное ко второму. Сокращаем 23 и 23 на 23, 14 и 7 — на 7. Поскольку в знаменателе стоит единица, ответ — целое число.

В следующий раз рассмотрим, как разделить целое число на дробь.

2 августа 2011

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.
Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.

Обозначение:

Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.

В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.

По определению имеем:

Умножение дробей с целой частью и отрицательных дробей

Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.

Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:

Плюс на минус дает минус;
Минус на минус дает плюс.

До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части.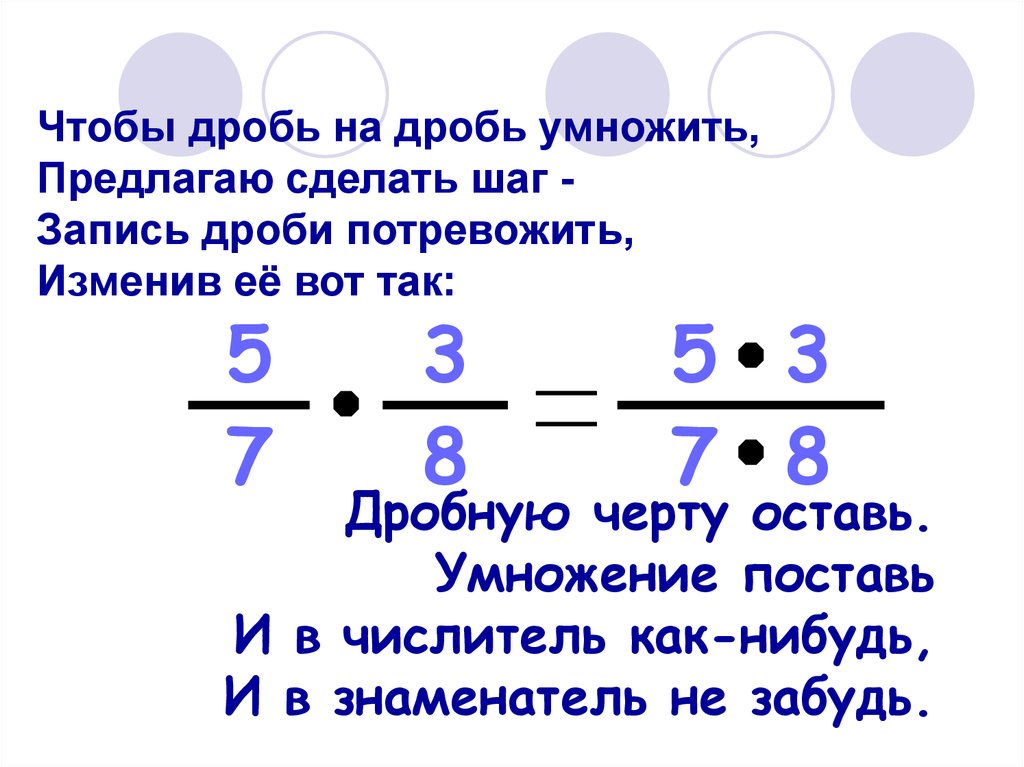 Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:

Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Задача. Найдите значение выражения:

Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:

Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).

Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.

Сокращение дробей «на лету»

Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:

Задача. Найдите значение выражения:

По определению имеем:

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.

Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:

Так делать нельзя!

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:

Правильное решение:

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

Для решения различных заданий из курса математики, физики приходится производить деление дробей. Это сделать очень легко, если знать определенные правила выполнения этого математического действия.

Прежде чем перейти к формулированию правило том, как делить дроби, давайте вспомним некоторые математические термины:

Верхняя часть дроби называется числителем, а нижняя – знаменателем.
При делении числа называются так: делимое: делитель = частное

Как делить дроби: простые дроби

Для выполнения деления двух простых дробей следует умножить делимое на дробь, обратную делителю. Эту дробь по-другому называют еще перевернутой, потому что она получается в результате замены местами числителя и знаменателя. Например:

3/77: 1/11 = 3 /77 * 11 /1 = 3/7

Как делить дроби: смешанные дроби

Если нам предстоит разделить смешанные дроби, то здесь тоже все достаточно просто и понятно. Сначала переводим смешанную дробь в обычную неправильную дробь. Для этого умножаем знаменатель такой дроби на целое число и числитель прибавляем к полученному произведению. В итоге мы получили новый числитель смешанной дроби, а знаменатель ее останется без изменения. Дальше деление дробей будет осуществляться точно так же, как и деление простых дробей. Например:

10 2/3: 4/15 = 32/3: 4/15 = 32/3 * 15 /4 = 40/1 = 40

Как делить дробь на число

Для того чтобы разделить простую дробь на число, последнее следует написать в виде дроби (неправильной). Это сделать очень легко: на месте числителя пишется это число, а знаменатель такой дроби равен единице. Дальше деление выполняется обычным способом. Рассмотрим это на примере:

5/11: 7 = 5/11: 7/1 = 5/11 * 1/7 = 5/77

Как делить десятичные дроби

Нередко взрослый человек испытывает затруднения при необходимости без помощи калькулятора разделить целое число или десятичную дробь на десятичную дробь.

Итак, чтобы выполнить деление десятичных дробей, нужно в делителе просто зачеркнуть запятую и перестать обращать на нее внимание. В делимом запятую нужно передвинуть вправо ровно на столько знаков, сколько было в дробной части делителя, при необходимости дописывая нули. И дальше производят обычное деление на целое число. Чтобы это стало более понятно, приведем следующий пример.

Дробь представляет собой нецелое либо дополненное число, например 1/2 (=0,5) или 7,5/5 (=1,5). Иногда дробь может быть целым числом, например, 20/5 (=4), но тогда её запись не имеет того математического смысла, который вносится в дробь.

Спонсор размещения P&G Статьи по теме «Как делить число на дробь» Как возвести в — 1 степень Как перевести смешанное число в неправильную дробь Как умножать дробь на число

Инструкция

Для начала вспомните, что простая или обыкновенная дробь может быть записана формате X / Y, где X – это числитель, а Y – знаменатель.

Например, 1/4, или 0,25 в цифровой записи. Для удобства дальнейших вычислений рекомендуется записывать дробь вертикально: числитель, горизонтальная полоса деления под ним, и знаменатель под полосой.

Для деления числа на целую дробь, нужно представить число в виде дроби. Так как число – это количество целых частей, то оно отправляется в знаменатель, а в числитель прописывается то, на что это количество частей делится для получения самого же себя – то есть, единица. 8 нужно записать как 8/1, а 263 – как 263/1, и так далее.

После этого вам нужно поделить число на дробь. Предположим, что вы имеете число 127 и дробь 4/15. Тогда операцию 127: 4/15 необходимо записать следующим образом:

Получается трёхэтажная дробь, при которой среднее деление (деление дробей) необходимо заменить умножением, а числитель и знаменатель перевернуть:

Записав это действие обычными дробями с горизонтальным делением, вы получите:

Результат действия 467 1/4.

Пересчитав на калькуляторе каждую дробь, вы получите следующее:

127: 1 = 127
4: 15 = 0,2666…
127: 0,2666… = 476, 2500001 или 476 1/4.

Результаты полностью совпадают.

Как просто

Другие новости по теме:

Дробь в математических науках представляет собой число, которое состоит из единственной или нескольких частей единицы, которые, в свою очередь, называются долями. Количество долей, на которые была разделена единица, представляет собой знаменатель дроби; количество взятых долей представляет собой

Число, которое состоит из одной или многих частей одного целого, в математике и смежных с ней науках принято называть дробью. Части единицы именуют долями. Общее число долей в единице – это знаменатель дроби, а количество взятых долей – ее числитель. Вам понадобится — лист бумаги; — ручка; —

Под словосочетанием «перевернуть дробь» можно понимать различные математические преобразования. Так или иначе, в результате этих преобразований числитель определенным образом должен меняться местами с знаменателем. В зависимости от вида такого преобразования число может как меняться, так и

Рано или поздно, все дети в школе начинают изучать дроби: их сложение, деление, умножение и все возможные действия, которые только возможно выполнять с дробями. Чтобы оказать должную помощь ребенку, родителям самим не стоит забывать, как происходит деление целых чисел на дроби, иначе, вы не сможете ему ничем помочь, а лишь запутаете. Если вам понадобилось вспомнить данное действие, но вы никак не можете свести всю информацию в голове в единое правило, то данная статья вам поможет: вы научитесь делить число на дробь и увидите наглядные примеры.

Как разделить число на дробь

Запишите свой пример на черновик, чтобы у вас была возможность делать заметки и помарки. Помните, что целое число записывается между клеток, прямо на их пересечении, а дробные числа — каждая в своей клетке.

В данном способе вам нужно перевернуть дробь вверх ногами, то есть, знаменатель записать в числитель, а числитель — в знаменатель.
Знак деления нужно поменять на умножение.
Теперь вам осталось выполнить умножение по уже изученным правилам: числитель умножается на целое число, а знаменатель не трогаете.

Конечно, в результате такого действия у вас получится очень большое число в числителе. В таком состоянии оставлять дробь нельзя — учитель попросту не примет этот ответ. Сократите дробь, разделив числитель на знаменатель. Целое число, которое получится в результате, запишите слева от дроби посередине клеток, а остаток и будет новым числителем. Знаменатель остается неизменным.

Этот алгоритм довольно прост, даже для ребенка. Выполнив его пять-шесть раз, малыш запомнит порядок действия и сможет применять его к любым дробям.

Как разделить число на десятичную дробь

Бывают дроби другого вида — десятичные. Деление на них происходит по совсем другому алгоритму. Если вы столкнулись с таким примером, то придерживайтесь инструкции:

Для начала, превратите оба числа в десятичные дроби. Сделать это просто: делитель у вас и так представлен в виде дроби, а делимое натуральное число вы отделяете запятой, получая десятичную дробь. То есть, если делимое было числом 5, вы получаете дробь 5,0. Отделять число нужно на столько цифр, сколько стоит после запятой и делителя.
После этого, обе десятичные дроби вы должны сделать натуральными числами. Сперва, вам покажется это немного запутанным, но это самый быстрый способ деления, который будет занимать у вас секунды, после нескольких тренировок. Дробь 5,0 станет числом 50, дробь 6,23 будет 623.
Выполните деление. Если числа получились большие, либо деление будет происходить с остатком, выполните его в столбик. Так вы наглядно увидите все действия данного примера. Вам не нужно специально ставить запятую, так как она сама появится в процессе деления в столбик.

Данный вид деления изначально кажется слишком запутанным, так как вам нужно превратить делимое и делитель в дробь, а потом снова в натуральные числа. Но после недолгой тренировки, вы сразу станете видеть те числа, которые нужно просто разделить друг на друга.

Помните, что умение правильно делить дроби и целые числа на них могут ни раз пригодиться в жизни, поэтому, знать эти правила и простые принципы ребенку нужно идеально, чтобы в более старших классах они не стали камнем преткновения, из-за которого ребенок не может решать более сложные задачи.

Правила умножения и деления дробей на целое число — Korholding.ru

Содержание:

Правила умножения и деления дробей на целое число

ОБОЙДИ УЖЕ ЭТИ ГРАБЛИ! 🙂

Умножение и деление дробей.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )

Эта операция гораздо приятнее сложения-вычитания! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:

Всё предельно просто. И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…

Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:

Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:

В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:

Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:

Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:

В первом случае (выражение слева):

Во втором (выражение справа):

Чувствуете разницу? 4 и 1/9!

А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:

то делим-умножаем по порядочку, слева направо!

И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:

Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.

Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!

1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.

2. В примерах с разными видами дробей — переходим к обыкновенным дробям.

3. Все дроби сокращаем до упора.

4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).

Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы.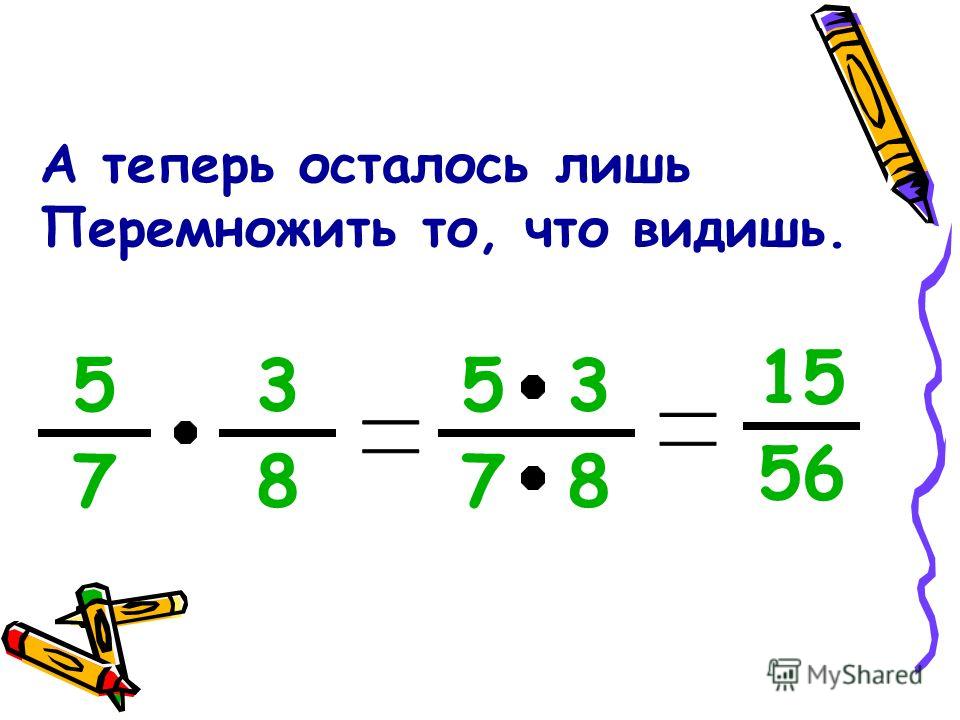

Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.

Итак, решаем в режиме экзамена! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.

Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать. Вот они, ответы, через точку с запятой записаны.

0; 17/22; 3/4; 2/5; 1; 25.

А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет.

Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но. Это решаемые проблемы.

В Особом разделе 555 «Дроби» разобраны все эти (и не только!) примеры. С подробными пояснениями что, зачем и как. Такой разбор здорово помогает при нехватке знаний и навыков!

Да и по второй проблеме там есть кое-что. ) Вполне практический совет, как стать внимательнее. Да-да! Совет, который может применить каждый.

Кроме знаний и внимательности для успеха нужен определенный автоматизм. Где его взять? Слышу тяжелый вздох… Да, только в практике, больше негде.

Можете для тренировки зайти на сайт 321start.ru. Там в опции «Попробовать» есть 10 примеров для всех желающих. С мгновенной проверкой. Для зарегистрированных пользователей — 34 примера от простых до суровых. Это только по дробям.

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Вот здесь можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

А вот здесь можно познакомиться с функциями и производными.

Правило 1.

Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения.

Правило 2.

Чтобы умножить дробь на дробь, надо:

1. найти произведение числителей и произведение знаменателей этих дробей

2. первое произведение записать числителе, а второе — знаменателем.

Правило 3.

Для того, чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

Правило 4.

Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.

Пример 1.

Вычислите

Пример 2.

Вычислите

Пример 3.

Вычислите

Пример 4.

Вычислите

Математика. Другие материалы

Возведение числа в рациональную степень.

(Автор: Покотило Екатерина)

Возведение числа в натуральную степень. (Автор: Покотило Екатерина)

Обобщенный метод интервалов при решении алгебраических неравенств (Автор Колчанов А.В.)

Метод замены множителей при решении алгебраических неравенств (Автор Колчанов А.В.)

Признаки делимости (Лунгу Алена)

Проверь себя по теме ‘Умножение и деление обыкновенных дробей’

Умножение дробей

Умножение обыкновенных дробей рассмотрим в нескольких возможных вариантах.

Умножение обыкновенной дроби на дробь

Это наиболее простой случай, в котором нужно пользоваться следующими правилами умножения дробей.

Чтобы умножить дробь на дробь, надо:

числитель первой дроби умножить на числитель второй дроби и их произведение записать в числитель новой дроби;

знаменатель первой дроби умножить на знаменатель второй дроби и их произведение записать в знаменатель новой дроби;

Прежде чем перемножать числители и знаменатели проверьте нельзя ли сократить дроби. Сокращение дробей при расчётах значительно облегчит ваши вычисления.

Умножение дроби на натуральное число

Чтобы дробь умножить на натуральное число нужно числитель дроби умножить на это число, а знаменатель дроби оставить без изменения.

Если в результате умножения получилась неправильная дробь, не забудьте превратить её в смешанное число, то есть выделить целую часть.

Умножение смешанных чисел

Чтобы перемножить смешанные числа, надо вначале превратить их в неправильные дроби и после этого умножить по правилу умножения обыкновенных дробей.

Другой способ умножения дроби на натуральное число

Иногда при расчётах удобнее воспользоваться другим способом умножения обыкновенной дроби на число.

Чтобы умножить дробь на натуральное число нужно знаменатель дроби разделить на это число, а числитель оставить прежним.

Как видно из примера, этим вариантом правила удобнее пользоваться, если знаменатель дроби делится без остатка на натуральное число.

Деление дроби на число

Как разделить дробь на число быстрее всего? Разберем теорию, сделаем вывод и на примерах посмотрим, как деление дроби на число можно выполнять по новому короткому правилу.

Обычно деление дроби на число выполняют по правилу деления дробей . Первое число (дробь) умножаем на число, обратное второму. Поскольку второе число целое, обратное к нему число — дробь, числитель которой равен единице, а знаменатель — данному числу. Схематически деление дроби на натуральное число выглядит так:

Отсюда делаем вывод:

чтобы разделить дробь на число, надо знаменатель умножить на это число, а числитель оставить прежним. Правило можно сформулировать еще короче:

при делении дроби на число число идет в знаменатель.

Выполнить деление дроби на число:

Чтобы разделить дробь на число, числитель перепишем без изменений, а знаменатель умножим на это число. Сокращаем 6 и 3 на 3.

При делении дроби на число числитель переписываем, а знаменатель умножаем на это число. Сокращаем 16 и 24 на 8.

При делении дроби на число число идет в знаменатель, поэтому числитель оставляем таким же, а знаменатель умножаем на делитель. Сокращаем 21 и 35 на 7.

Умножение и деление дробей

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей»). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Чтобы умножить две дроби , надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.

Чтобы разделить две дроби , надо первую дробь умножить на «перевернутую» вторую.

Задача. Найдите значение выражения:

По определению имеем:

Умножение дробей с целой частью и отрицательных дробей

Плюс на минус дает минус;
Минус на минус дает плюс.

Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Сокращение дробей «на лету»

Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения. Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Так делать нельзя!

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

Деление дробей.

Деление дроби на натуральное число.

Примеры деления дроби на натуральное число

Деление натурального числа на дробь.

Примеры деления натурального числа на дробь

Деление обыкновенных дробей.

Примеры деления обыкновенных дробей

Деление смешанных чисел.

преобразовать смешанные дроби в неправильные;
умножить первую дробь на дробь, обратную второй;
сократить полученную дробь;
если получилась неправильная дробь преобразовать неправильную дробь в смешанную.

Примеры деления смешанных чисел

1 1 2 : 2 2 3 = 1 · 2 + 1 2 : 2 · 3 + 2 3 = 3 2 : 8 3 = 3 2 · 3 8 = 3 · 3 2 · 8 = 9 16

2 1 7 : 3 5 = 2 · 7 + 1 7 : 3 5 = 15 7 : 3 5 = 15 7 · 5 3 = 15 · 5 7 · 3 = 5 · 5 7 = 25 7 = 7 · 3 + 4 7 = 3 4 7

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Дроби. Умножение и деление дробей.

Умножение обыкновенной дроби на дробь.

Чтобы перемножить обыкновенные дроби, необходимо умножить числитель на числитель (получим числитель произведения) и знаменатель на знаменатель (получим знаменатель произведения).

Формула умножения дробей:

Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби. Если получится сократить дробь, то вам легче будет дальше производить расчеты.

Обратите внимание! Здесь не нужно искать общий знаменатель!!

Деление обыкновенной дроби на дробь.

Деление обыкновенной дроби на дробь происходит так: переворачиваете вторую дробь (т.е. меняете числитель и знаменатель местами) и после этого дроби перемножаются.

Формула деления обыкновенных дробей:

Умножение дроби на натуральное число.

Обратите внимание! При умножении дроби на натуральное число, числитель дроби умножается на наше натуральное число, а знаменатель дроби оставляем прежним. Если результатом произведения оказалась неправильная дробь, то обязательно выделите целую часть, превратив неправильную дробь в смешанную.

Деление дробей с участием натурального числа.

Это не так страшно, как кажется. Как и в случае со сложением, переводим целое число в дробь с единицей в знаменателе. Например:

Умножение смешанных дробей.

Правила умножения дробей (смешанных):

преобразовываем смешанные дроби в неправильные;
перемножаем числители и знаменатели дробей;
сокращаем дробь;
если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.

Второй способ умножения дроби на натуральное число.

Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.

Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.

Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.

Многоэтажные дроби.

В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:

Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:

Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.

Обратите внимание, например:

При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:

Практические советы при умножении и делении дробей:

1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.

2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.

3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.

4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Темы по алгебре: обратные и обратные числа

Урок 4: обратные и обратные числа

/en/алгебра-топики/отрицательные-числа/содержание/

Противоположные числа

Каждое число имеет напротив . На самом деле, у каждого числа есть две противоположности : аддитивное , обратное , и , обратное , или , мультипликативное, обратное . Однако не пугайтесь этих технически звучащих названий. На самом деле найти противоположное число довольно просто.

Аддитивная инверсия

Первый тип противоположности вам может быть наиболее знаком: положительных чисел и отрицательных чисел . Например, противоположное 4 равно -4, или минус четыре . На числовой прямой 4 и -4 находятся на одинаковом расстоянии от 0, но на противоположных сторонах.

Этот тип противоположности также называется аддитивной инверсией . Обратное — это просто другое слово для напротив 9.0010 и сложение относится к тому факту, что когда вы складываете эти противоположные числа вместе, они всегда равны 0. делает -20 + 20 и — х + х . На самом деле, любое число, которое вы можете придумать, имеет аддитивную обратную. Независимо от того, насколько большое или маленькое число, сложение его и его инверсия каждый раз будет равняться 0.

Если вы никогда не работали с положительными и отрицательными числами, вы можете просмотреть наш урок об отрицательных числах.

Чтобы найти обратную добавку:

Для положительных чисел или переменных, таких как 5 или x : Добавьте знак минус (-) слева от числа: 5 → -5.
x → -x
3y → -3y
For negative numbers or variables, like -5 or -x : Remove the negative знак: -10 → 10.
-y → Y
-6x → 6x

Использование Additial Inverse

. числа в выражении. (Если вы не знакомы с сокращением, посмотрите наш урок по упрощению выражений.) Когда вы сокращаете число, вы исключаете его из одной части уравнения, выполняя обратное действие на этом числе на обе части уравнения. In this expression, we’re cancelling out -8 by adding its opposite: 8.

x	— 8	=	12
	+ 8		+ 8

Использование аддитивного обратного числа работает для сокращения, потому что число, добавленное к его обратному , всегда равно 0 .

Обратные числа и обратное мультипликативное

Второй тип обратного числа связан с умножением и делением . Это называется мультипликативным обратным , но чаще его называют обратным .

Чтобы понять обратное, вы должны сначала понять, что каждое целое число может быть записано как дробь , равная этому числу, деленному на 1 . Например, 6 также можно записать как 6/1.

Переменные также могут быть записаны таким образом. Например, х = х/1.

, обратное числа, — это перевернутая дробь. Другими словами, у обратной дроби нижнее число исходной дроби — или знаменатель — вверху, а верхнее число — или числитель — внизу. Таким образом, обратное число 6 равно 1/6, потому что 6 = 6/1, а 1/6 — это , обратное 6/1.

Ниже вы можете увидеть больше реципрок. Обратите внимание, что обратная величина числа, которое уже является дробью, — это просто перевернутая дробь.

5y	→	1
		5y

18	→	1
		18

And because reciprocal means opposite , величина, обратная обратной дроби, равна целому числу .

1	→	25
25

Из просмотра этих слоев вы, возможно, уже заметили более простые, чтобы определить рецепт, просто позаботиться о том, чтобы пописать только по номеру: только что написать только по номеру: только что написать целый номер: только что написать целый номер: только что написать целый номер: только что написать целый номер: только что написать целый номер: только что написать целый номер: только что написать целый номер: только что написать целый номер: только что написать целый номер: только что написать целый номер: только что написать целый номер: только что написать целый номер: только что написать целый номер: только что написать. 1 на сверху и исходный номер снизу .

Десятичные числа тоже имеют обратные значения! Чтобы найти обратную величину десятичного числа, замените его на дробь, а затем переверните дробь. Не знаете, как преобразовать десятичное число в дробь? Ознакомьтесь с нашим уроком по преобразованию процентов, десятичных дробей и дробей.

Использование обратных величин

Если вы когда-нибудь умножали и делили дроби , обратная величина может показаться вам знакомой. (Если нет, вы всегда можете просмотреть наш урок по умножению и делению дробей.) Когда вы умножаете две дроби, вы умножаете прямо. Числители умножаются, а знаменатели умножаются.

. числитель внизу, а знаменатель вверху. Другими словами, вы используете обратное . Вы используете число напротив числа , потому что умножение и деление также являются противоположностями.

4	⋅	2	=	8
5	⋅	3	=	15
3	15
3	15
3	15
3

4	÷	2		=		4	⋅	3		=		12
5		3				5		2				10

Практика!

Используйте только что полученные навыки для решения этих задач. После того, как вы решили оба набора задач, вы можете прокрутить вниз, чтобы просмотреть ответы.

Тренировочный набор 1

Найти additive inverse :

5
-8
q

Practice set 2

Find the reciprocal :

5
5/6
0.75

Set 1 answers

-5
8
— Q

Установите 2 Ответы

1/5
6/5
4/3

5553 6/5
4/3
555553
4/3
55553
4/3
5 Продолжать
Предыдущий: Отрицательные числа
Next:Чтение алгебраических выражений
/en/алгебра-темы/чтение-алгебраические-выражения/содержание/
Запросы по математике — сумма и произведение дробей
Процессы математических запросов: Поиск примеров, удовлетворяющих условию; предполагать, обобщать и доказывать. Концептуальная область исследования: Сложение и умножение дробей (расширенное до вычитания и деления).
Это приглашение возникло в задаче, которую Энди Стрикленд (учитель математики из Уортинга, Великобритания) поставил перед собой: можно ли найти пару дробей, удовлетворяющую утверждению? С тех пор как заявление превратилось в подсказку, оно стало отправной точкой для изучения всех типов классов средней школы. Первые комментарии и вопросы включают:
Что означают «сумма» и «произведение»?
Как складывать и умножать дроби?
Всегда ли работает?
Это никогда не сработает (иногда в сопровождении примера).
Можете ли вы показать или доказать, что это правда?
Студенты заинтригованы этим утверждением, потому что, на первый взгляд, это невозможно.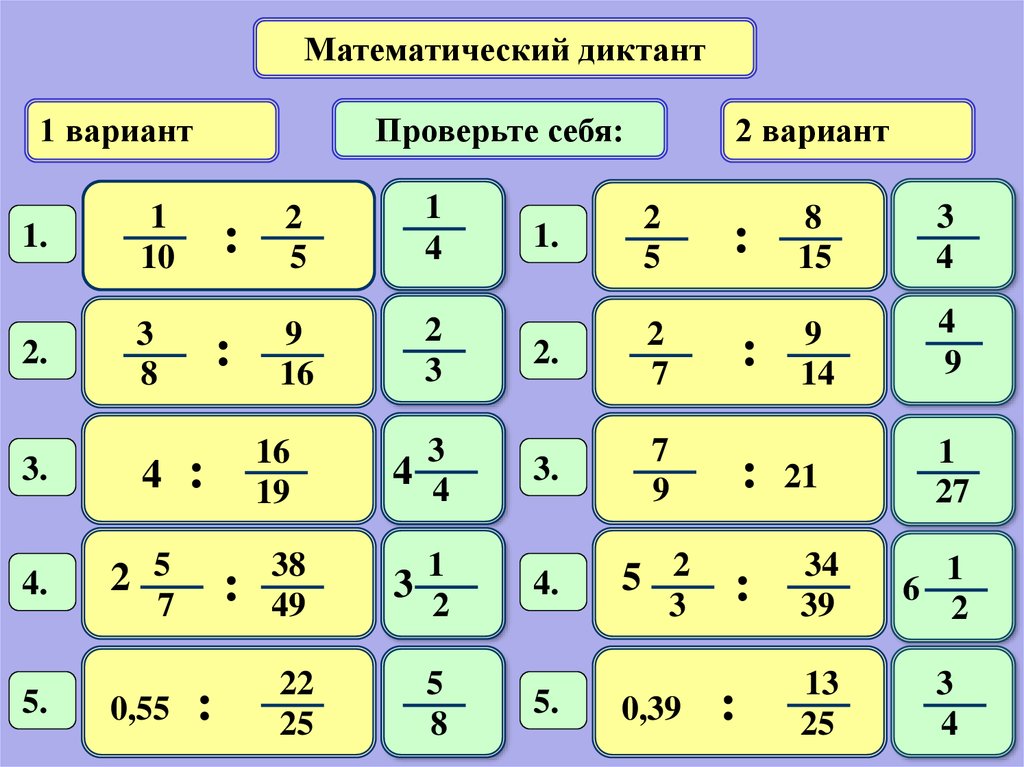 Однако это происходит только потому, что учащиеся склонны определять дроби ограниченным образом, концентрируясь на правильных дробях в своем исследовании. Действительно, правильные дроби не могут удовлетворять условию в подсказке. Учителя могут проиллюстрировать объяснение того, почему нет, используя диаграмму.
Из диаграммы видно, что сумма и произведение двух правильных дробей не равны. Диаграммы можно использовать, чтобы сделать вывод, что сумма и произведение любых двух правильных дробей никогда не будут равны.
При переходе к неправильным дробям (возможно, под руководством учителя) исследование может развиваться по разным путям. (В этот момент учитель может решить исключить тривиальное решение двух дробей, которые обе упрощаются до двух.) В классе исследование проходило через различные фазы, такие как планирование, исследование, обобщение и оценка (см. 9).0009 фазы запроса ). В качестве альтернативы, он зигзагообразно переходил от индуктивных к дедуктивным рассуждениям (см. форм рассуждений ). Учащиеся, начиная с 8-го класса, участвовали в сложении и умножении алгебраических дробей. Старшие школьники показали, что дроби в следующей форме удовлетворяют условию в подсказке:
См. математические заметки для алгебраических направлений исследования.
Вопросы и наблюдения
Это ответы учащегося 10-го класса смешанной успеваемости в Brittons Academy в Рейнхэме (Великобритания) на их первый запрос. Студенты спрашивают о дробях, которые удовлетворяют утверждению, размышляют о знаменателях этих дробей и даже на этом раннем этапе предлагают изменить подсказку. Эмма Роуз , классный руководитель и ведущий практик кафедры математики, сообщает, что «ученики были блестящими».
Обсуждение вопросов
Учащиеся 9-х классов выдвинули приведенные выше идеи в ходе обсуждения подсказки. Фотография была размещена в Твиттере их учителем Айн Кэрролл ‏ . Исследование продвинулось далеко вперед с появлением неправильных дробей в виде ( n + x )/ n и ( n + x )/ x .
Концептуальное понимание
Аманда Джеймс , учитель математики в школе Варндин (Брайтон, Великобритания), использовала подсказку в своем 8-м классе (набор 4 из 5). Приведенные выше вопросы и комментарии отражают первоначальные идеи учащихся. Несмотря на то, что класс кажется уверенным в работе с дробями, Аманда сообщает, что стало ясно, что учащимся не хватает глубокого понимания концепции дроби. По мере того, как расследование продолжалось, Аманда давала ученикам новые подсказки для размышления. первая дополнительная подсказка заявила, что «Нахождение доли чего-то делает ее меньше».
Аманда разработала вторую дополнительную подсказку (ниже) , чтобы способствовать беглости и обобщению:
Аманда сообщила, что процесс исследования привел к более глубокому пониманию дробей: «Класс прокомментировал, насколько они на самом деле понимают что такое дробь сейчас, и это придало им уверенности в выполнении вычислений с дробями Мы потратили больше времени на обсуждение значения дроби, чем они на самом деле вычисляли с ними, но их недавняя оценка показывает, что они понимали глубже, а не поверхностное обучение «сложению дробей» или «нахождению дробей числа».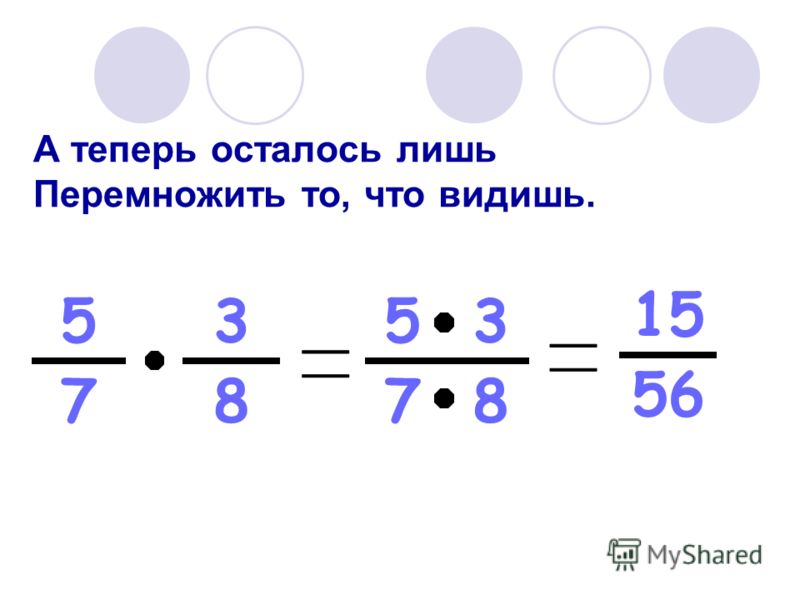 К концу опроса студенты начали использовать неправильные дроби. Затем они попытались выразить свои выводы в общей форме, используя символы.
Номер в алгебре через запрос
Вопросы о подсказке (выше) исходят от 7-го класса дополнительного образования в школе Magdalen College School (Оксфорд, Великобритания). Эта запись запросов охватывает два 35-минутных урока. Учащиеся нашли пару дробей, которые упрощаются до двух, после чего учитель направил их на поиск других дробей, удовлетворяющих условию в подсказке. На втором уроке учащиеся составляли различные алгебраические выражения, а учитель следил за тем, чтобы класс придерживался математических правил (см. ниже).
За два урока учащиеся перешли от частных числовых примеров к общим алгебраическим выражениям. Один студент резюмировал исследование следующим образом: «Это действительно забавно, что мы начали с чего-то, что никто не считал эффективным, но оказалось, что это интересно».
Люк Пирс , классный руководитель, прокомментировал проведение опроса: «Я был очень взволнован, чтобы справиться со своим первым опросом. Сначала он был довольно хаотичным, но есть так много возможностей для настоящей математики. Решаю, когда закончить исследование сложное, и оно легко могло бы привести к большему количеству уроков. Мне нравится процесс исследования, потому что он дает учащимся возможность почувствовать себя настоящими математиками, что слишком редко случается в современных школах. Им это нравилось».
Рэйчел Махони (учитель математики в гимназии Карре в Слифорде (Линкольншир, Великобритания) блоги о структурированном опросе, который она провела со своим классом 8 класса.
Энн Макдональд , учитель математики средней школы, опробовала подсказку в классе 8 для своего первого опыта исследования. Она записала сложные вопросы учеников и комментарии (выше) и отправили Inquiry Maths это описание того, как их математическое мышление связано с факторизацией:
Обычно, когда я впервые знакомлюсь с факторингом, я даю учащимся несколько вопросов с раскрывающимися скобками, а затем прошу их «написать вопрос», когда они получат ответ. Обычно это приводит к тому, что они спрашивают, почему мы иногда хотим, чтобы наши выражения были со скобками, а иногда без них. Мой ответ никогда не звучит убедительно (или убеждает!).
В этот момент я обычно начинаю думать, что преподавание перестановки формул до введения факторизации было бы хорошей идеей, чтобы я мог проиллюстрировать, как факторизация помогает нам изменить тему. Вчера в ходе опроса в 8 классе удалось выяснить следующее:
Две дроби ( a/b и a/c) имеют одинаковый продукт и сумму, когда a = b + c … и тогда это: a/b x a/c = a ² /bc
и, наконец, это: a/b + a/c = (ac + ab)/bc.
Два студента пытались объяснить, почему a ² = ac + ab , и мы говорили, что это трудно объяснить. Тогда я спросил их, знают ли они, как разложить на множители, и оказалось, что они слышали это слово, но не знали, как это сделать. Я объяснил, как разложить приведенное выше на множители, чтобы получить а ² = а ( с + b ) и они могли видеть смысл факторизации!
В этот момент заглянул заместитель директора, и ученики молча слушали меня. Он, вероятно, думал, что я поучаю их до смерти. Хотел бы я, чтобы он был там весь урок, чтобы увидеть, как вся алгебра на доске исходила от них! Я сказал детям, что они создали доску, похожую на доску Шелдона Купера, и им это понравилось (ну, фанатам понравилось!)
Разница двух дробей равна их частному.
Силена , ученица 9 класса, разработала новую линию исследования, когда решила найти две дроби, разность и частное которых равны. Приняв алгебраический подход, который она использовала в конце основного исследования суммы и произведения двух дробей, Силена вывела формулу соотношения между а, b, c и d , когда разность и частное a/b и c/d равны (см. ниже).
Силена использовала формулу, чтобы найти значения a , b , c и d , удовлетворяющие подсказке. В ее первом примере a = 25, b = 6, c = 5 и d = 3. Разница двух дробей (25/6 и 5/3) равна их частному.
Второй и третий примеры, полученные из формулы, также удовлетворяют требованию равенства разности и частного. Однако четвертый пример не сработал. Разность и частное 81/16 и 9/8 ( a = 81, b = 16, c = 9 и d = 8) не равны.
The fourth example led Silena to give more conditions for the relationship between a , b , c and d :
a = c ²
b = 2 d
c и d оба нечетные или четные, c > д.
Последнее условие примера 4 не выполняется, потому что c = 8 и d = 9.
2 = d , что объясняет, почему c и d должны быть как нечетными, так и четными в условии 3. Грамматическая школа (Великобритания) написала в Inquiry Maths о пути, который может развиться из подсказки: «Я рассматривал вопрос «сумма двух дробей равна их произведению» и собираюсь попробовать его на уроке. скоро. Я думал, что, поскольку все решения удовлетворяют x + y = xy , которое преобразуется в y = x/ ( x- 1) полезно нарисовать график возможных ( x,y ) решений. Видно, что если отрицательные дроби не разрешены, то решение будут иметь только неправильные дроби. Кроме того, подстановка x = a/b в преобразованное уравнение дает y = a/ ( a-b ). Можно доказать, что эти два удовлетворяют условию и дают бесконечное число решений».
Расширение запроса
Эти дополнительные подсказки могут расширить запрос:
Общее и частное в математическом запросе
Даниэль Уокер (учитель из северного Лондона, Великобритания) связался с веб-сайтом Inquiry Maths с этим запросом : Подсказка дает конкретный случай общего утверждения, касающегося разности и произведения двух дробей (выше).