как умножить десятичную дробь на натуральное число в 2023 году

Как умножать десятичные дроби: правило?

Алгоритм и правило умножения десятичных дробей звучит так:

Чтобы умножить одну десятичную дробь на другую, надо, не обращая внимания на запятые, перемножить их как целые числа и в произведении поставить запятую с правой стороны на столько десятичных знаков, сколько их было у двух множителей вместе. Если в произведении меньше десятичных знаков, чем следует выделить, то слева нужно дописать соответствующее количество нулей.

Используем данное правило, решая следующие примеры.

Пример. Найти произведение десятичных дробей 3,051 и 0,05.

Сначала умножим целые числа:

3051 ⋅ 5 = 15255

Теперь определим, где в произведении поставить десятичную запятую. В первом множителе – 3 знака после запятой, во втором – 2, следовательно, вместе будет 5 знаков. В произведении 15255 отсчитываем 5 десятичных знаков справа и ставим запятую, получим десятичную дробь 0,15255    

Пример.

Найти произведение десятичных дробей 4,125 и 0,008

Умножаем целые числа:

4125 ⋅ 8 = 33000

Поскольку в множителях 3 + 3 = 6 десятичных знаков после запятой, поэтому к числу 33000, имеющему 5 знаков, дописываем слева один ноль (033000) и отделяем запятой: 0,033000, что равно десятичной дроби 0,033

Чтобы найти произведение десятичных дробей, можно их сначала превратить в обыкновенные дроби и выполнить умножение по правилу умножения обыкновенных дробей.

Пример. Умножить десятичные дроби 1,5 и 0,75

Поскольку 1,5 можно превратить в дробь 15/10, а 0,75 = 75/100, выполнить умножение можно следующим образом:

Умножение десятичных дробей в столбик

Умножение десятичных дробей в столбик происходит по принципу умножения натуральных чисел без учета десятичных ком. После завершения умножения нужно поставить десятичную запятую в произведении на столько десятичных знаков, сколько их было у двух множителей вместе, начиная отсчет справа.

Кроме того, для удобства умножения в столбик первым следует записывать число или дробь с большим количеством цифр. Второе число размещают под первым так, чтобы его последняя цифра стояла под последней цифрой первого множителя

Пример. Выполнить умножение десятичных дробей 38,42 и 0,15 в столбик

Начинаем с умножения множителей без учета запятых.

Поставим десятичную запятую в произведении. Поскольку множители имеют 2 + 2 = 4 десятичных знака, отчислим в произведении 4 знака справа и поставим запятую:

Получили произведение дробей 5,7630, что равнозначно 5,763

Пример. Найти произведение десятичных дробей 4,6125 и 0,023, выполнив умножение в столбик

Выполним умножение, игнорируя запятые

Поставим запятую в произведении, разместив ее через 7 знаков справа (ведь 4 + 3 = 7)

Поскольку в произведении 7 цифр, ставим запятую перед первой цифрой 1, и дописываем ноль слева.

Умножение десятичной дроби на 0,1, 0,01, 0,001 и т.д.

Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001, 0,0001 и т.д., нужно в этой дроби перенести запятую на 1, 2, 3, 4 и т.д. комы влево. Если у дроби не хватает цифр, нужно дописать нули слева.

Пример. Умножить 78,63 на 0,1

Поскольку нужно умножить дробь 78,63 на 0,1, в произведении нужно перенести запятую на 1 знак влево:

78,63 ⋅ 0,1 = 7,863

Проверим, выполнив действие согласно правилу умножения десятичных дробей:

78,63 ⋅ 0,1 = 7863 ⋅1 = 7863. Перенесем запятую на 2 + 1 = 3 знака справа, получим 7,863.

То есть, умножив дроби двумя способами, получили одинаковый результат.

Пример. Умножить 256,32 на 0,001

Поскольку умножение на 0,001 надо перенести запятую влево на 3 знака: 256,32 ⋅ 0,001 = 0,25632

Умножение десятичной дроби на натуральное число

Умножение десятичной дроби на число выполняют по правилу умножения десятичных дробей, то есть перемножают множители, игнорируя запятую. После этого в произведении следует отделить десятичной запятой столько цифр, сколько цифр есть в дроби после запятой.

Пример. Умножить число 8 на десятичную дробь 0,0256

Пример. Умножить число 12 на десятичную дробь 3,45

В результате умножения получили дробь 41,40, ноль слева можно сократить, поэтому 12 ⋅ 3,45 = 41,4

Умножение десятичной дроби на числа 10, 100, 1000, 10000 и т.д.

Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д., нужно в данной дроби перенести запятую справа на столько цифр, сколько нулей записано после 1 в числе, на которое умножаем. Если в десятичной дроби не хватает знаков, то нужно дописать справа необходимое количество нулей.

Пример. Умножить дробь 0,0256 на 10000

Поскольку число 10000 имеет 4 нуля, в дроби 0,0256 при умножении надо перенести запятую вправо на 4 знака:

0,0256 ⋅ 10000 = 256

Пример.  Найти произведение дроби 0,4 и числа 1000

Поскольку число 1000 имеет 3 нуля при умножении в дроби 0,4 надо перенести запятую вправо на 3 знака. В дроби 0,4 после запятой 1 знак, поэтому дописываем 2 нуля:

0,400 ⋅ 1000 = 400

Пример. Умножить дробь 0,0039 на 10

0,0039 ⋅ 10 = 0,039

Пример. Умножить дробь 0,0039 на 10000

0,0039 ⋅ 10000 = 0039,0 = 39

Умножение десятичной дроби на обычную дробь или на смешанное число

Чтобы умножить десятичную дробь на обыкновенную дробь или смешанное число, нужно десятичную дробь превратить в обыкновенную и выполнить умножение.

Пример. Найти произведение 0,4  и 3 5/6

Превратим десятичную дробь в обыкновенную:

0,4 = 4/10 = 2/5

Выполним умножение:

Задача. Максим купил 1 кг мандарин, заплатив 85,5 грн. Сколько стоит 0,5 кг мандарина?

Чтобы найти стоимость 0,5 кг мандарин, нужно 85,5 ⋅0,5 = 42,75 грн.

Ответ: 42,75 грн.

определения, история развития, применение дробей на практике

Содержание:

• Определение
• Историческая справка

Определение

В математике дробь означает число, которое состоящее из одной или нескольких частей (долей) единицы. По способу записи дроби бывают обыкновенные и десятичные.

Первой дробью известной человечеству была половина, далее — треть. Древние египтян и вавилоняне имели специальные обозначения для дробей $\frac{1}{3}$ и $\frac{2}{3}$ , которые отличались от обозначения остальных дробей. Египтяне все дроби старались записать как суммы долей, то есть дробей вида $\frac{1}{n}$ , за исключением единственной дроби — $\frac{2}{3}$ . Но складывать такие дроби было неудобно. Также египтяне умножали и делили дроби.

Вавилоняне работали только с шестидесятеричными дробями. Так как знаменателями таких дробей служат числа 60, 602, 603 и т.п., то такие дроби, как 1/7, нельзя было точно выразить через шестидесятеричные. Выражали через подобные дроби приближенно.

Шестидесятеричные дроби заимствовали у Вавилона греческие и арабские математики и астрономы. Но возникали трудности при работе с натуральными числами, записанными в десятичной системе, и дробями, записанными в шестидесятеричной. Поэтому фламандский математик, механик и инженер Симон Стевин (1548 — 1620) предложил перейти к десятичным дробям.

Своей системой дробей отличался Древний Рим. Эта система основывалась на делении на 12 долей единицы веса, называемой асс. Двенадцатая доля асса называлась унция. В ходу были и следующие названия: «семис» — половина асса, «секстане» — шестая доля асса, «семиунция» — полунции, то есть 1/24 асса. Всего применялось 18 различных названий дробей. Для работы с такими дробями надо было помнить и таблицу сложения, и таблицу умножения. Для облегчения работы составлялись специальные таблицы. Недостатком такой системы было то, что в ней не было дробей со знаменателями 10 или 100, что затрудняло деление на 10, 100 и т. д. Для избежания указанных трудностей римляне стали использовать проценты.

В греческих сочинениях по математике дробей не встречалось, т.к. греческие ученые считали, что математика должна заниматься только целыми числами. Дроби в греческой науке появились благодаря музыке.

Запись дробей с числителем и знаменателем предложили в Индии, только знаменатель писали вверху, а числитель в внизу, а также не ставили черту дроби. Современную запись дробей предложили арабы. Фундамент теории обыкновенных дробей заложили греческие и индийские математики.

Впервые в Европе данный термин употребил в 1202 году первый крупный математик средневековой Европы Леонардо Пизанский (1170 — 1250), более известный как Фибоначчи. Полноценная теория обыкновенных дробей и операций над ними сложилась в XVI веке в работах итальянского математика Никколо Тартальи (1499 — 1557) и немецкого и итальянского математика, астронома Христофора Клавиуса (Клавия) (1537 — 1612). В древней Руси дроби называли долями или ломаными числами. Русский термин «дробь» происходит от латинского слова «fractura», которое в переводе с арабского означает «ломать», «раздроблять». Термин «дробь» используется в «Арифметике» русского математика и педагога Леонтия Филипповича Магницкого (1669 — 1739) как для обыкновенных, так и для десятичных дробей.

Десятичные дроби впервые встречаются в Китае примерно с III века н.э. при вычислениях на счётной доске. В Европе же впервые десятичные дроби применяет еврейский математик и астроном Иммануил Бонфис бен Яаков (1300 — 1377) около 1350 года, но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585).

Читать следующую тему: понятие дроби и виды дробей.

• Понятие дроби. Виды дробей
• Сложение дробей
• Вычитание дробей
• Умножение дробей
• Деление дробей
• Нахождение дроби от числа, нахождение числа по известной величине его дроби
• Понятие десятичной дроби
• Превращение десятичной дроби в обыкновенную, превращение обыкновенной дроби в десятичную
• Действия над десятичными дробями
• Периодические десятичные дроби
• Обыкновенные дроби
• Правильные и неправильные дроби. Смешанные дроби
• Сравнение дробей
• Основное свойство дроби
• Изменение величины дроби с изменением ее членов
• Сокращение дроби
• Раздробление дробей
• Приведение дробей к общему знаменателю

Что такое десятичная дробь? Определение, преобразование, примеры

Определение десятичных дробей

Необходимым условием для понимания десятичных дробей является понимание нормальных дробей. Вы должны знать, что дробь состоит из числителя (верхняя часть) и знаменателя (нижняя часть). Правильный способ записи дроби —

X — числитель в этом примере, а y — знаменатель.
Десятичные дроби — это дроби, в которых знаменатель (y на изображении) должен быть равен 10 или кратен 10, например 100, 1000, 10000 и т. д. Числитель может быть любым целым числом (от -бесконечности до +бесконечности). Эти десятичные дроби обычно выражаются десятичными числами (числа с десятичной точкой).

В алгебре десятичная дробь — это число, имеющее 10 или степени 10, например 10¹, 10², 10³ и т. д. в знаменателе.

Примеры десятичных дробей

• 7/10000 — десятичная дробь, записанная в десятичной форме как 0,0007.
• 19/10 — десятичная дробь, записанная в десятичной форме как 1,9.
• 39/1000 — десятичная дробь, записанная как 0,039.

Непримеры десятичных дробей

Другие дроби, в знаменателе которых не десять чисел, не являются десятичными дробями. Это:

• 37/8
• 2/1083
• 83/145

Чтение десятичных дробей

Рассмотрим сценарий, в котором 1 стоит в числителе. Мы будем рассматривать разные знаменатели, чтобы понять, как эти термины читаются с этим числителем.

• 1/10 читается как одна десятая.
• 1/100 читается как одна сотая.
• 1/1000 читается как тысячная.

Когда значение числителя больше единицы, мы добавляем к имени букву «s». Так, например, 3/10 читается как три десятых.

История десятичных дробей

Китайцы впервые разработали и использовали десятичные дроби в конце 4-го века до нашей эры, которые распространились на Ближний Восток, прежде чем достигли Европы.

Преобразование в десятичные дроби

1. Преобразование из дробей в десятичные дроби : 

• Рассмотрим пример дроби 3/2.
• Первым шагом будет рассмотрение числа, которое дает 10 или кратно 10 при умножении на знаменатель. В этом случае 5, умноженное на 2, дает 10. 
• Теперь умножьте числитель и знаменатель на одно и то же число, чтобы получить десятичную дробь. Здесь 3 x 5/2 x 5 дает 15/10.
• Таким образом, десятичная дробь 3/2 равна 15/10.

2. Преобразование смешанных чисел в десятичные дроби : 

• Преобразование смешанной дроби в нормальную дробь.
• Следуйте инструкциям по преобразованию дробей в десятичные дроби.

3. Преобразование десятичных чисел в десятичные дроби : 

• Запишите исходное десятичное число в форме числителя и знаменателя, поставив 1 в знаменателе: 4,3/1.
• Для каждого пробела, на который вы перемещаете десятичную точку, добавьте ноль рядом с 1 в знаменателе: 43/10 (Как мы видим, на один сдвиг десятичного знака нужно добавить один 0 в знаменателе).

             4.3/1

             43.0/10

• Поскольку число в числителе не является десятичным, вы получили свою десятичную дробь: 4.3 = 43/10.

Применение десятичных дробей в реальной жизни

Десятичные дроби используются для понимания точных величин вместо целых чисел. Вы также будете использовать их для выражения процентов. Например, 97% можно записать как 97/100 для простоты вычисления.

Вот несколько ситуаций, в которых вы можете столкнуться с десятичными дробями:

• Монеты (доли рупий)
• Продукты для взвешивания
• Измерение ингредиентов во время приготовления

Решенные примеры

Пример 1

Преобразуйте 2 ½ в десятичную дробь.

= 2 ½ 

= 5/2

= 5 x 5 / 2 x 5

= 25 / 10

Пример 2

Преобразование 5,4 в десятичную дробь

= 5,4/1

= 54/10

Пример 3

Преобразуйте 8 ⅕ в десятичную дробь.

= 8 ⅕ 

= 41/5

= 41 x 2 / 5 x 2 

= 82/10

Заключение
Десятичные дроби побуждают учащихся изучать точные величины. Это поможет им понять вес, например, 3,2 кг, и расстояние, например, 7,85 км. Первым шагом к лучшему пониманию десятичных чисел является ежедневное выполнение задач с десятичными дробями. Идея взять ручку и бумагу для решения задач скучна и неинтересна для учащихся. Им нужны развлекательные способы, чтобы побудить их к практике сумм.

SplashLearn делает процесс изучения десятичных чисел увлекательным и интерактивным для детей. С десятками игр с десятичными дробями у вашего ребенка никогда не будет недостатка в вариантах для занятий математикой. Вместо этого обучение становится увлекательным благодаря интересным играм, которые привлекают ваших детей к решению задач.

Давайте сделаем это!

Вместо того, чтобы учить детей десятичным дробям и раздавать практические задания, попросите их найти и составить десятичные дроби из десятичных дробей, которые вы называете.

Практические задачи

1

Преобразуйте 6,34 в десятичную дробь.

634/100

634/10

6,34/100

6,34/10

Правильный ответ: 634/100
.

2

Преобразуйте 4 ½ в десятичную дробь.

4/2

4/10

45/100

45/10

Правильный ответ: 45/10
4 ½ можно записать как 4,5, а поскольку после запятой есть только один знак, это десятичная дробь будет 45/10.

3

Преобразуйте 8/5 в десятичную дробь.

16/10

8/100

160/100

16/100

Правильный ответ 16/10
2 и др.) в знаменателе. Эти числа записываются в десятичной форме для удобства решения математических сумм. Например, 4/1000 — это десятичная дробь, записываемая десятичными знаками как 0,004.

Как записать десятичную дробь?

Десятичная дробь записывается как любое число в числителе с 10 и кратным 10 в знаменателе.

Что такое десятичная дробь в простейшем виде?

Простейшей формой десятичной дроби является основная неделимая дробь, полученная путем деления числителя на знаменатель. Например, простейшая форма десятичной дроби 4/10 — это 2/5.

Все ли проценты могут быть выражены десятичными дробями? Приведите пример.

Да. Все проценты могут быть выражены в виде десятичных дробей. Например, 80% записывается как 80/100 в форме десятичной дроби. Это можно разделить, чтобы получить простейшую форму 4/5 десятичной формы.

Где используются десятичные дроби?

Десятичные дроби используются для выражения веса людей и продуктов. Его также можно использовать для определения скидок на цену продуктов и измерения ингредиентов рецепта.

Переосмысление того, как мы обучаем операциям с дробями и десятичными знаками — Смешивание и математика

Позвольте мне начать с того, что я собирался написать этот пост в блоге уже давно. .. очень давно! Это было где-то в ноябре прошлого учебного года, когда я получил откровение (благодаря фантастическому курсу для выпускников и профессору, замечательной научно-исследовательской книге «Расширение детской математики: дроби и десятичные числа» и ученикам, которые были так готовы и способны передать свои математические знания). понимания и борьбы). То, как я преподавал математические стандарты 5-го класса, не позволяло учащимся устанавливать критические связи между дробями и десятичными знаками.

Ну вот…

В математике есть определенные понятия, порядок которых довольно очевиден. Ясно, что учащиеся должны научиться складывать, прежде чем они научатся умножать, или делить целые числа, прежде чем научиться делить десятичные дроби. То, что я обнаружил, не так ясно среди многих учителей и тех руководителей округов, которые пишут наши руководства по темпу, — это то, что важнее всего? Операции с дробями или операции с десятичными? Обе эти концепции играют огромную роль в математике в 5-м классе и обеспечивают критическую основу для изучения математики в старшей школе и за ее пределами.

Не верите мне? Послушайте, что Шерри Пэрриш и Энн Доминик, авторы книги «Беседы о числах: дроби, десятичные числа и проценты», говорят о том, что ученики старших классов не понимают дробей.

«Национальная консультативная группа по математике пришла к выводу, что наиболее важным фундаментальным навыком, не развитым в настоящее время, является владение дробями… Выводы группы были подтверждены опросом 1000 учителей алгебры в США, которые указали, что нехватка дробей знания были второй самой большой проблемой, с которой столкнулись студенты при подготовке к изучению алгебры».

Если это одна из самых больших проблем, с которыми сталкиваются ученики при изучении алгебры в средней школе, важно, чтобы мы делали все возможное, чтобы преподавать дроби (а также десятичные числа и проценты) таким образом, чтобы наши ученики действительно и глубоко понимать дроби. Теперь, когда вы знаете, насколько важно овладеть этими понятиями, чему вы должны учить в первую очередь?

Очень короткий ответ: дроби.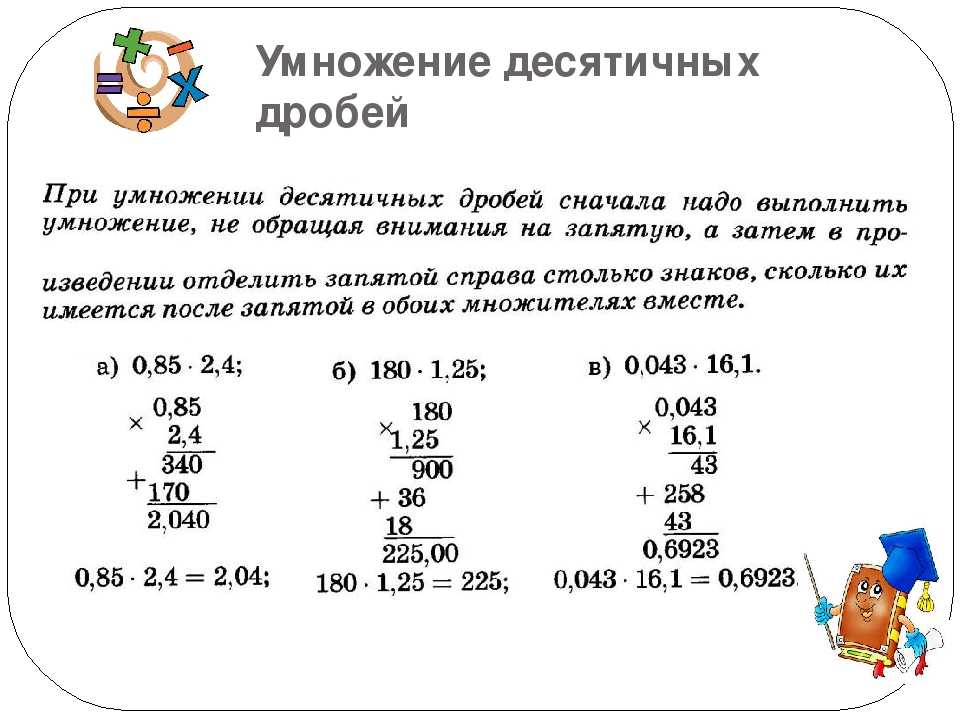

Тогда почему многие руководства по стимуляции делают прямо противоположное? Честно говоря, я считаю, что это потому, что они ожидают, что ученики 5-го класса построили достаточно прочную фракционную основу. Это большое предположение для такого важного математического понятия. Даже имея самую сильную основу в области дробей, учащиеся должны концептуально понять операции с дробями, прежде чем углубляться в операции с десятичными числами. Это очень верно для умножения и деления.

Момент истины…

Долгое время я учил операции с десятичными знаками, а затем операции с дробями, потому что это то, что всегда говорили инструкции по темпу, и я думал, что это, безусловно, лучший способ. Только после того, как я провел собственное обучение и бросил вызов тому, что делал всегда, я понял, что понимание десятичной дроби является самым сильным, когда оно основано на понимании учениками дробей. Посмотрите, звучит ли это знакомо:

Почему 0,01 (одна сотая) меньше, чем 0,1 (одна десятая)? Почему 0,2 составляет одну десятую от 2?   Чтобы объяснить это, вам нужно опираться на представление учащихся о том, что на самом деле представляет собой «одна десятая».

Куда ставить десятичную дробь при умножении двух десятичных чисел?   Независимо от того, сколько моделей мы использовали, этот вопрос, казалось, никогда не исчезал, ПОКА мы не начали работать над умножением с дробями. В этот момент они могли объяснить, почему 0,1 x 0,01 = 0,001 или 1/10 x 1/100 = 1/1000.

Что вообще означает деление 5 на 0,2 и почему я получаю больший ответ? Почему при умножении 5 на 0,2 я получаю меньший ответ? Я думал, что умножение должно увеличивать число, а деление должно уменьшать его! Да, технически вы можете объяснить это, не обязательно вдаваясь в дроби, но разъяснение этого, опираясь на понимание учащимися дробей, гораздо менее абстрактно, чем попытка объяснить это, опираясь на трудное понимание учащимися десятичных дробей. Кроме того, модели, используемые для обучения умножению и делению дробей, прекрасно отвечают на эти два вопроса наглядно.

Ознакомьтесь с ходом обучения десятичным дробям и обратите внимание, как многие стандарты дробей встроены в изучение операций с десятичными дробями в 5-м классе! Не поверишь, десятичные числа гораздо более абстрактны, чем дроби .

Авторы книги «Расширение детской математики: дроби и десятичные дроби» заявляют, что «понимание детьми десятичных дробей одновременно опирается на их понимание дробей и  разрядного значения» (2011 г., стр. xxiv). Я скажу, что иногда учащиеся быстрее добиваются «временного успеха» в операциях с десятичными дробями, чем в операциях с дробями, если обучение сосредоточено на процедурах, а не на концептуальном понимании. Процедуры операций с десятичными дробями обычно более знакомы учащимся, чем процедуры операций с дробями.

Но так ли это на самом деле? Является ли этот тип обучения (процедурным, а не концептуальным) длительным и позволяет ли им устанавливать важные связи в их растущем понимании дробей, десятичных знаков и процентов?

Вместо того, чтобы учить десятичные дроби и постоянно прыгать вперед, чтобы объяснить , почему  или , как , я, наконец, решил просто сделать перерыв в нашей десятичной единице, перейти прямо к нашей дробной единице и позволить учащимся открыть для себя все почему  и как для себя! К тому времени, когда мы вернулись к нашей десятичной единице, я мог направить студентов думать о своем собственном понимании дробей, чтобы ответить на их многочисленные вопросы о десятичных дробях.