Умножение дробей правило: Умножение обыкновенных дробей — урок. Математика, 6 класс.

Содержание

§ Умножение дробей

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

Геометрия: начальная школа
Действия в столбик
Деление с остатком
Законы арифметики
Периметр
Порядок действий
Разряды и классы. Разрядные слагаемые
Счет в пределах 10 и 20

Математика 5 класс

Взаимно обратные числа и дроби
Десятичные дроби
Натуральные числа
Нахождение НОД и НОК
Обыкновенные дроби
Округление чисел
Перевод обыкновенной дроби в десятичную

Площадь
Проценты
Свойства сложения, вычитания, умножения и деления
Среднее арифметическое
Упрощение выражений
Уравнения 5 класс
Числовые и буквенные выражения

Математика 6 класс

Масштаб
Модуль числа
Окружность. Площадь круга
Отношение чисел
Отрицательные и положительные числа
Периодическая дробь
Признаки делимости
Пропорции
Рациональные числа
Система координат
Целые числа

Алгебра 7 класс

Алгебраические дроби
Как применять формулы сокращённого умножения
Многочлены
Одночлены
Системы уравнений
Степени
Уравнения
Формулы сокращённого умножения
Функция в математике

Геометрия 7 класс

Точка, прямая и отрезок
Что такое аксиома и теорема

Алгебра 8 класс

Квадратичная функция. Парабола
Квадратные неравенства
Квадратные уравнения
Квадратный корень
Неравенства
Системы неравенств
Стандартный вид числа
Теорема Виета

Алгебра 9 класс

Возрастание и убывание функции
Нули функции
Область определения функции
Отрицательная степень
Среднее
геометрическое

Алгебра 10 класс

Иррациональные числа

Алгебра 11 класс

Факториал

Правильная постановка вопроса свидетельствует о некотором знакомстве с предметом.

Фрэнсис Бэкон

на главную

Введите тему

Русский язык Поддержать сайт

Дроби. Числитель и знаменатель Сокращение дробей Сравнение дробей Смешанные числа. Выделить целую часть Сложение дробей. Общий знаменатель Вычитание дробей Умножение дробей Деление дробей Нахождение дроби от числа Нахождение целого по известной дроби

Умножение обыкновенных дробей рассмотрим в нескольких возможных вариантах.

Умножение обыкновенной дроби на дробь

Это наиболее простой случай, в котором нужно пользоваться следующими правилами умножения дробей.

Чтобы умножить дробь на дробь, надо:

числитель первой дроби умножить на числитель второй дроби и их произведение записать в числитель новой дроби;

знаменатель первой дроби умножить на знаменатель второй дроби и их произведение записать в знаменатель новой дроби;

Пример.

Прежде чем перемножать числители и знаменатели проверьте нельзя ли сократить дроби. Сокращение дробей при расчётах значительно облегчит ваши вычисления.

Пример.

Умножение дроби на натуральное число

Запомните!

Чтобы дробь умножить на натуральное число нужно числитель дроби умножить на это число, а знаменатель дроби оставить без изменения.

Если в результате умножения получилась неправильная дробь, не забудьте превратить её в смешанное число, то есть выделить целую часть.

Умножение смешанных чисел

Запомните!

Чтобы перемножить смешанные числа, надо вначале превратить их в неправильные дроби и после этого умножить по правилу умножения обыкновенных дробей.

Другой способ умножения дроби на натуральное число

Иногда при расчётах удобнее воспользоваться другим способом умножения обыкновенной дроби на число.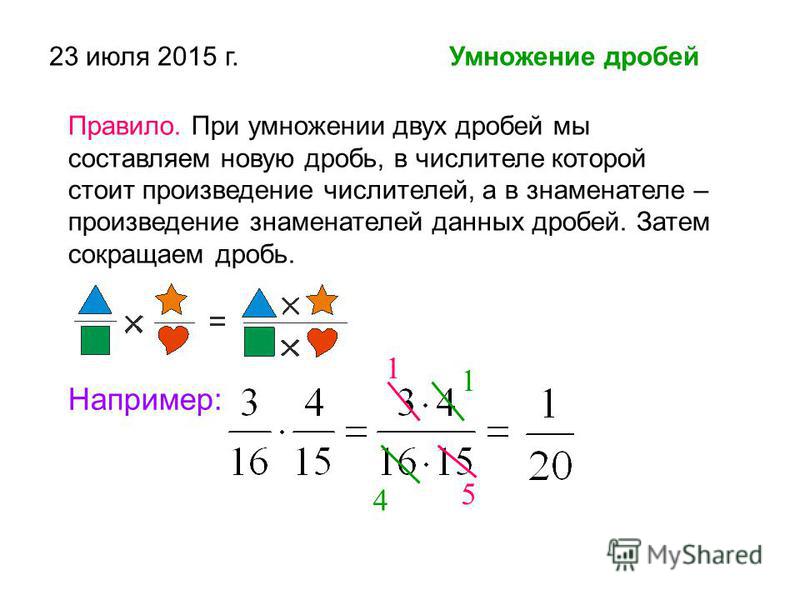

Запомните!

Чтобы умножить дробь на натуральное число нужно знаменатель дроби разделить на это число, а числитель оставить прежним.

Как видно из примера, этим вариантом правила удобнее пользоваться, если знаменатель дроби делится без остатка на натуральное число.

Дробь. Умножение дробей обыкновенных, десятичных, смешанных

В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.

Что такое дробь?

Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного параллелепипеда, площади прямоугольника.

Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.

Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида ⁵/₈, ⁴/₅, ²/₄ называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.

Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель – сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.

Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную ¹/₄ от всего единичного отрезка, а точка В отмечает ²/₈ от данного отрезка.

Разновидности дробей

Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.

Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь – число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.

Правильное дробное выражение всегда меньше единицы, а неправильное – больше либо равно 1.

Что касается десятичных дробей, то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.

Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.

Пример. Представить дробь 7²¹/₁₀₀₀ в десятичной записи.

Алгоритм перевода неправильной дроби в смешанное число и наоборот

Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:

разделить числитель на имеющийся знаменатель;
в конкретном примере неполное частное – целое;
и остаток – числитель дробной части, причем знаменатель остается неизменным.

Пример. Перевести неправильную дробь в смешанное число: ⁴⁷/₅.

Решение. 47 : 5. Неполное частное равняется 9, остаток = 2. Значит, ⁴⁷/₅= 9²/₅.

Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:

целая часть умножается на знаменатель дробного выражения;
полученное произведение прибавляется к числителю;
результат записывается в числителе, знаменатель остается неизменным.

Пример. Представить число в смешанном виде в качестве неправильной дроби: 9⁸/₁₀.

Решение. 9 х 10 + 8 = 90 + 8 = 98 – числитель.

Ответ: ⁹⁸/_10.

Умножение дробей обыкновенных

Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.

Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе – это ошибка, но и назвать верным ответом ее тоже затруднительно.

Пример. Найти произведение двух обыкновенных дробей: ½ и ²⁰/₁₈.

Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ ⁵/₉.

Умножение дробей десятичных

Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:

две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
подсчитать количество цифр после знака запятой в каждом из чисел;
в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.

Пример. Вычислить произведение двух десятичных дробей: 2,25 и 3,6.

Решение.

Умножение смешанных дробей

Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:

перевести числа в смешанном виде в неправильные дроби;
найти произведение числителей;
найти произведение знаменателей;
записать получившийся результат;
максимально упростить выражение.

Пример. Найти произведение 4½ и 6²/_5.

Умножение числа на дробь (дроби на число)

Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить натуральное число на дробь.

Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:

записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
найти произведение, несмотря на запятую;
в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.

Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.

Пример. Вычислить произведение ⁵/₈ и 12.

Решение. ⁵/₈ * 12 = ^{( 12)}/₈= ⁶⁰/₈= ³⁰/₄= ¹⁵/₂= 7¹/_2.

Ответ: 7¹/_2.

Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.

Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.

Пример. Найти произведение 9⁵/₆ и 9.

Решение. 9⁵/₆ х 9 = 9 х 9 + ^{(5 х 9)}/₆= 81 + ⁴⁵/₆= 81 + 7³/₆= 88¹/_2.

Ответ: 88¹/_2.

Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001

Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.

Пример 1. Найти произведение 0,065 и 1000.

Решение. 0,065 х 1000 = 0065 = 65.

Ответ: 65.

Пример 2. Найти произведение 3,9 и 1000.

Решение. 3,9 х 1000 = 3,900 х 1000 = 3900.

Ответ: 3900.

Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.

Пример 1. Найти произведение 56 и 0,01.

Решение. 56 х 0,01 = 0056 = 0,56.

Ответ: 0,56.

Пример 2. Найти произведение 4 и 0,001.

Решение. 4 х 0,001 = 0004 = 0,004.

Ответ: 0,004.

Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.

Умножение дробей

При умножении дробей, чтобы найти произведение двух или более дробей, вам просто нужно выполнить эти три простых шага.

Шаг 1: Перемножьте числители. Числители также называются верхними числами.

Шаг 2: Перемножьте знаменатели. Знаменатели также называются нижними числами.

Шаг 3: Наконец, попробуйте упростить продукт , если это необходимо , чтобы получить окончательный ответ.

Например, обратите внимание, что мы делаем, когда умножаем следующие дроби: 3/4 × 4/6.

Шаг 1: Умножьте 3 и 4, чтобы получить 12, и 12 – числитель произведения

Шаг 2: Умножьте 4 и 6, чтобы получить 24, а 24 – знаменатель произведения

3/4 × 4/6 = (3 × 4)/(4 × 6) = 12/24

Шаг 3: Разделите числитель и знаменатель на 12, чтобы упростить дробь. 12 — это наибольший общий делитель (НОД) чисел 12 и 24.

3/4 × 4/6 = 1/2

Приведенный выше пример прост. Однако при умножении дробей вы можете задаться вопросом о следующих случаях.

Умножение дробей с разными знаменателями
Умножение дробей с одинаковыми знаменателями
Умножение дробей с целыми числами
Умножение дробей со смешанными числами правила, которым нужно следовать, когда вы умножаете дроби на разные типы дробей .
Правила умножения дробей
Правило 1: Самое важное правило – умножать прямо. Другими словами, умножьте числители, чтобы получить новый числитель или числитель произведения. Умножьте знаменатели, чтобы получить новый знаменатель или знаменатель произведения.
Правило 2: Другое важное правило заключается в том, чтобы перед умножением всегда преобразовывать смешанные дроби, также называемые смешанными числами, в неправильные дроби.
Правило 3: Перед умножением преобразовывайте целые числа в дроби.
Правило 4: Умножение дробей — это не то же самое, что сложение дробей. Поэтому не надо искать наименьший общий знаменатель!
Правило 5: Упростите произведение или запишите конечную дробь после выполнения умножения в меньших единицах, если это необходимо.
Умножение дробей с разными знаменателями
При умножении дробей с разными знаменателями помните , правило 4 , указанное выше. Не ищите общего знаменателя! Правила сложения дробей и умножения дробей не совпадают.
Например, обратите внимание, что мы не ищем общий знаменатель при умножении следующих дробей: 1/5 × 2/3.
Шаг 1: Умножьте 1 и 2, чтобы получить 2
Шаг 2: Умножьте 5 и 3, чтобы получить 15 2/15
Шаг 3: 2/15 уже записано в наименьших единицах, поскольку наибольший общий делитель 2 и 15 равен 1.
1/5 × 2/3 = 1/2
Умножение дробей с одинаковым знаменателем
Когда вы умножаете дроби с одинаковым знаменателем, просто делайте то же самое, что вы делаете, когда дроби имеют разные знаменатели.
Пример: Умножение 3/4 и 1/4
3/4 × 1/4 = (3 × 1)/(4 × 4) = 3/16
Умножение дробей с целыми числами

Когда вы умножаете дроби на целые числа, просто имейте в виду правило 3 изложенное выше. Перед умножением преобразуйте целое число в дробь.
Обратите внимание, что любое целое число x можно записать в виде дроби x /1, поскольку любое число, деленное на 1, вернет одно и то же число.
Например, если вы умножаете целое число 5 на другую дробь, перед умножением запишите 5 как 5/1.
Пример: Умножить 5 и 2/3
5 × 2/3 = 5/1 × 2/3
5 × 2/3 = (5 × 2)/(1 × 3) = 10/ 3
Умножение дробей со смешанными числами

При умножении дробей со смешанными числами важно помнить правило 2 . Вы должны сначала преобразовать любое смешанное число в дробь, прежде чем умножать.
Предположим, вы умножаете дробь на 2 1/3. Поскольку 2 1/3 — смешанное число, его необходимо преобразовать в дробь.
2 1/3 = (2 × 3 + 1)/3 = (6 + 1) / 3 = 7/3
Пример: Умножьте 1/6 и 2 1/3
1/6 × 2 1/3 = 1/6 × 7/3
1/6 × 7/3 = (1 × 7)/(6 × 3) = 7/18
Умножение неправильных дробей

Умножение неправильных дробей в исполнении следующих правило 1 . Просто умножьте прямо. Одной вещью, которую вы точно не захотите делать здесь, является преобразование неправильных дробей в смешанные числа.
Это будет очень контрпродуктивно, так как вам придется конвертировать их обратно в неправильные дроби.
Пример: Умножить 9/2 и 3/5
9/2 × 3/5 = (9 × 3)/(2 × 5) = 27/10 умножение дробей
1. Рекомендую ознакомиться с таблицей умножения. Вы сможете выполнять умножение дробей намного быстрее.

2. Иногда полезно упростить дроби перед умножением, чтобы упростить вычисления.
Взгляните на следующий пример:
10 / 20
×
3 / 15
10 / 20
можно упростить как
1 / 2
Разделить числитель и знаменатель на 10
3 / 15
можно упростить как
1 / 5
Разделить числитель и знаменатель на 3
Таким образом, проще выполнить умножение, чтобы получить

1 / 10

2. Иногда полезно упростить дроби перед умножением.
Взгляните на следующий пример:
10 / 20
×
3 / 15

10 / 20
можно упростить как
1 / 2
После деления числителя и знаменателя на 10
3 / 15
можно упростить как
1 / 5

После деления числителя и знаменателя на 3
Таким образом, проще выполнить умножение, чтобы получить
1 / 10

3. Если у вас есть три или более дробей, просто умножьте на все числителей и на все знаменателей
Идем немного глубже! Почему мы умножаем дроби прямо?
Я хотел бы начать тему с интересного примера о пицце.
Предположим, вы купили пиццу среднего размера, и в ней 8 кусков.
Если кто-то съест половину вашей пиццы или 4 куска, у вас останется
4 / 8
На приведенной ниже иллюстрации также видно, что остаток такой же, как и
1 / 2
Если вы решили, что съедите только 1 ломтик из оставшихся 4 ломтиков, вы съедите
1 / 4
из остатков.

Помните, что остатки
1 / 2
Вы также можете возразить, что съели только 1 ломтик из 8 ломтиков или
1 / 8

Таким образом, мы видим, что съесть 1/4 часть 1/2 — это то же самое, что съесть 1/8.
Другой способ получить
1 / 8
заключается в выполнении следующего умножения:

× знак равно
Мы получаем этот ответ, умножая числа сверху (числители): 1 × 1 = 1
и умножая числа внизу (знаменатели): 4 × 2 = 8
Это интересный результат, но все, что вам нужно помните следующее:
Когда вы умножаете дроби, вы должны умножать прямо.

Когда слово « из » помещается между двумя дробями, это означает умножение.
Тест на умножение дробей. Проверьте, можете ли вы теперь умножать дроби.

Умножение дробей — Math28
Contenido
Что такое умножение дробей?
Умножение дробей — одна из основных операций, позволяющая получить третью дробь, которая будет произведением предыдущих, что известно как «Произведение» или «Результат умножения».
Узнать больше о: » Умножение » →
Символ или знак умножения дробей
Умножение дробей представлено символом креста или «х», оно также может быть представлено с помощью средней точки, символ умножения известен как «на».
Узнать больше о: « Операции с дробями » →
Как мы умножаем дроби?
Для получения числового значения в виде дробей существует только одна процедура умножения дробей либо с разными знаменателями, либо с одинаковыми знаменателями.

При умножении дробей числители дробей умножаются, а знаменатели расходятся.
2 / 2
х
1 / 2
=
2 / 4
2/2
1/2
2/4
В следующем примере дроби 1/3 и 2/6 перемножаются, определяются числители обеих дробей, соответствующие 1 и 2, перемножаются и результат помещается в числитель. Теперь определите знаменатели обеих дробей, соответствующие 3 и 6, умножьте и поместите результат в знаменатель.
1 / 3
х
2 / 6
=
1 х 2 / 3 х 6
=
2 / 18
Результат 2/18 можно упростить, потому что и числитель, и знаменатель можно уменьшить вдвое. Таким образом, половина от 2 равна 1, а половина от 18 равна 9.
2 / 18
=
1 / 9
Примечание : Дроби 2/18 и 1/9 эквивалентны, поскольку они представляют одну и ту же сумму.
Пример:
2 / 3
х
4 / 3
=
2 х 4 /
3 х 3
=
8 / 9
5 / 2
х
6 / 2
=
5 х 6 /
2 х 2
=
30 /
4
5 / 6
х
4 / 3
=
5 х 4 /
6 х 3
=
20 /
18
8 / 3
х
2 / 4
=
8 х 2 /
3 х 4
=
16 /
12
Из предыдущих примеров можно упростить 30/4 = 15/2, 20/18 = 10/9 и 16/12 = 4/3.
Упражнение:
А)
5 / 3
х
3 / 3
= ?
Б)
9 / 2
х
5 / 2
= ?
С)
6 / 5
х
4 / 3
= ?
Д)
6 / 8
х
2 / 2
= ?
Умножение трех или более дробей
Процедура похожа на две дроби, умножение выполняется в строке, числитель на числитель и знаменатель на знаменатель.
4 / 2
х
5 / 3
х
3 / 2
=
4 х 5 х 3 / 2 х 3 х 2
=
60 / 12
=
10 /
2
= 5
Пример:
3 / 2
х
4 / 2
х
8 /
2
=
3 х 4 х 8 /
2 х 2 х 2
=
96 /
8
3 / 4
х
5 / 4
х
10 /
4
=
3 х 5 х 10 /
4 х 4 х 4
=
150 /
64
2 / 3
х
4 / 2
х
4 /
6
=
2 х 4 х 4 /
3 х 2 х 6
=
32 /
36
5 / 4
х
4 / 8
х
3 /
2
=
5 х 4 х 3 /
4 х 8 х 2
=
60 /
64
Из предыдущих примеров можно упростить 96/8 = 12, 32/36 = 8/9 и 60/64 = 15/18.
Упражнение:
А)
4 / 3
х
7 / 2
х
3 / 2
= ?
Б)
4 / 2
х
5 / 2
х
3 / 4
= ?
С)
3 / 2
х
7 / 2
х
3 / 2
= ?
Д)
6 / 6
х
7 / 6
х
2 / 6
= ?
Умножение смешанных дробей
При умножении смешанных дробей необходимо, чтобы вся часть выражалась в виде дроби, имеющей тот же знаменатель, что и в сопровождающей ее дробной части.